EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 598 (February 2017) A&A, 598 (2017) A94 Full HTML
Free Access
Issue
A&A
Volume 598, February 2017
Article Number A94
Number of page(s) 7
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201629006
Published online 07 February 2017

© ESO, 2017

1. Introduction

The Quadrantid meteor shower has been a strong and regularly observed shower in the January sky for nearly 200 yr (Fisher 1930) with a zenithal hourly rate of the order of 100. It is thus both one of the strongest and earliest identified meteor showers. However, no records of the Quadrantids appear to exist earlier than the beginning of the nineteenth century, which is fairly remarkable since Chinese and Japanese records date back for two millennia (Hasegawa 1993) and mentions of the Perseids, the Leonids and the Lyrids are plentiful. Murray et al. (1980) demonstrated that perturbations by Jupiter caused small changes in the nodal distance of the mean stream so that the Earth did not intersect the stream prior to the nineteenth century. Numerical integrations by Hughes et al. (1981), Frorschle & Scholl (1982, 1986) and Wu & Williams (1992) all show that large changes in the orbital element of Quadrantid meteoroids can take place within a time-scale of a few thousand years, therefore orbital changes may explain the lack of early observations. However, it is also possible that the strong stream we observe today only formed a few centuries ago as was suggested by Wiegert & Brown (2005). The peak in the activity profile is relatively short, usually less than a day (Shelton 1965; Jenniskens et al. 1997), so there may be two components to the Quadrantids; an old one built up over a long period, and new material ejected into the stream fairly recently. Unlike other showers identified relatively early on, no parent object had been identified and generally accepted for the Quadrantids until fairly recently.

There have been many contenders proposed and these have been summarized in Williams & Collander-Brown (1998), Williams et al. (2004b), but none are really credible. Hasegawa (1979) has suggested that comet C/1490 Y1 (1491 I) was the parent for the Quadrantid stream. The mean orbit of the present Quadrantid stream was numerically integrated back to 1491 by Williams & Wu (1993) and these elements are in remarkably good agreement with those given by Hasegawa for C/1490 Y1, bearing in mind that the observing arc was not long enough to determine eccentricity. They also showed that the comet could experience a close encounter with Jupiter in the middle of the seventeenth century.

McIntosh (1990) suggested that comet 96P/Machholz was a possible candidate since the orbits were similar several millennia ago. The general characteristics of the orbital evolution of the comet and stream are also very similar, both showing changes with a 4000 yr period (Gonczi et al. 1992). The situation changed somewhat when Jenniskens (2004) pointed out the remarkable similarity between the orbits of the Quadrantid meteoroid stream and asteroid 2003 EH1 (now 196256). He also suggested that the asteroid was a fragment from the break-up of C/1490 Y1. This was taken up by Williams et al. (2004a,b) who claimed that the orbit of 2003 EH1 in 1490 could produce the path on the sky described by Hasegawa. A possible scenario here is that fragmentation of 96P/Machholz at various times produced C/1490 Y1 and (196256) 2003 EH1. The broad background in the Quadrantids is generated by normal comet activity while the fragmentation produced large amounts of new material as suggested by Jopek & Williams (2013).

The fact that (196256) 2003 EH1 has been classified as an asteroid does not mitigate the above scenario.There are almost certainly many dormant or extinct cometary nuclei or fragments amongst the near-Earth objects (NEOs) population (Jewitt 2012). They were found not only in the NEO population, but in the main asteroid belt as well. Recently, (Tancredi 2014) has identified 331 asteroids in cometary orbits (ACOs) among over half a million asteroids already discovered using the proposed classification criterion based on the Tisserand’s parameter and some features of the orbital parameters. It was shown that 203 ACOs belong to the Jupiter family type and a suggestion was made that the discovered dormant or extinct comets seem to be a small fraction of the active comets. Note NEA 2003 EH1 was referred to asteroids in cometary orbits by Tancredi (2014). These are normal comets that have shed their volatiles and have gradually become covered by a thick dust mantle after multiple passages around the Sun. The mantle prevents a sublimation of the volatiles through solar heating so that out-gassing ceases and no coma or tail is produced. This makes it very difficult to distinguish between dormant comets and small asteroids using ground-based observations. Further it is very difficult to distinguish between cometary nuclei and dark asteroids by obtaining reflectance spectra; Tubiana et al. (2015) using the 8.2 m VLT at Cerro Paranal found it difficult to reach firm conclusions regarding comet 2P/Encke and associated NEO’s. The dynamical features of the inactive comet do not change significantly and its orbit remains comet-like.

The Quadrantid shower is not the first shower to be apparently associated with an asteroid; (3200) Phaeton and the Geminid shower were found to be associated by Whipple (1983) and Fox et al. (1984). At present, more than 40 NEAs are claimed to be associated with the Taurid complex, alongside comet 2P/Encke (Asher et al. 1993; Porubčan et al. 2004, 2006; Babadzhanov et al. 2008a; Rudawska et al. 2012a,b). Many other associations between asteroids and meteor showers have been identified, examples being Babadzhanov et al. (2009, 2012, 2013, 2015), Trigo-Rodrigues et al. (2009), Madiedo et al. (2013), Micheli et al. (2016).

Many investigations have been carried out into the relationship between the Quadrantids and either or both 96P/Machholz and (196256) 2003 EH1; examples being Jenniskens (2004), Williams et al. (2004a), Babadzhanov et al. (2008b), Neslusan et al. (2013a,b), and there is no doubting that some association exists between them, though the exact chronology of events remains unclear. The main aim of this work is to shed some light on this by investigating the evolution of the nominal orbits of both 96P/Machholz and (196256) 2003 EH1 in order to determine the point in time at which they were most similar to each other using standard methods described in Jopek & Williams (2013) for determining closeness of orbits.

2. The Quadrantid complex

The main bodies that may be relevant for understanding the origin and evolution of the Quadrantid stream are comet 96P/Machholz 1, comet C/1490 Y1, and NEA (196256) 2003 EH1. The orbit of C/1490 Y1 is so poorly determined that little valuable information can be gained by further investigation of its evolution.

Comet 96P/Machholz was discovered by D. Machholz in May 1986, given the initial designation 1986 VIII Machholz, and has been extensively observed since that date. Its perihelion distance q is 0.12 AU and at the present time the comet is approaching perihelion. There are only six known short-period near-Earth comets that make closer approaches to the Sun than comet 96P/Machholz. The orbital period of comet Machholz is 5.28 yr and only 20 known comets have periods shorter than that of comet 96P/Machholz. Only six periodic comets with a straight motion have inclinations of their orbits to the ecliptic plane larger than that of the orbit of 96P/Machholz of 58 deg. This comet is thus a very unusual object. In addition, no pre-discovery images were found in images of the relevant area of the sky taken by telescopes with a large field of view (FoV) and the limiting magnitude of + 19m (Green et al. 1990). However, at least three of the perihelion passages in that time-frame were favorable for observations (Sekanina 1990). It was suggestion that the comet was in an inactive period up until 1986 (Green et al. 1990; Sekanina 1990).

The Amor asteroid (196256) 2003 EH1 was discovered on March 6, 2003, by the LONEOS program. The absolute magnitude H of 2003 EH1 is 15.8m, and the equivalent diameter d is estimated to be in the range 1.7 to 3.9 km1 assuming an albedo in the range 0.04 and 0.20, typical for asteroids of C and S type, respectively. The Tisserand parameter Tj (defined later) is frequently used to distinguish between a comet-like and an asteroid-like orbit, with values less than 3.12 denoting a cometary orbit (Kresak 1982; Kozai 1992). The value of the Tisserand parameter for (196256) 2003 EH1 is Tj = 1.96, suggesting a comet-like orbit.

The elements of the present-day orbits of comet 96P/Machholz, NEA 2003 EH12, and the Quadrantid meteor shower (Babadzhanov et al. 2008b) are summarized in Table 1 where the usual orbital elements: a-semi-major axis, e-eccentricity, q-perihelion distance, i-inclination, ω-argument of perihelia, Ω-longitude of ascending node and the value of Tj are also given. All orbital angular values are given in degrees relative to Equinox J2000.0.

Table 1

Summary of the current orbits of comet 96P/Machholz 1, (196256) 2003 EH1 and the Quadrantid meteor shower (J2000.0).

It is obvious without resorting to quantitative comparison tools that the orbits of (196256) 2003 EH1 and the Quadrantid meteoroid stream are exceedingly similar and they are without question related in some way, either through the simple process of the Quadrantid meteoroid being ejected (196256) 2003 EH1 or through both being formed at roughly the same time through the fragmentation of a larger body. Though the orbits are not as similar at the present time, there are similarities with the orbit of comet 96P/Machholz, and the similarity in orbital evolution mentioned earlier suggests that this body might be comet 96P/Machholz.

Any orbit will effectively intersect the orbit of the Earth when the heliocentric distance of either the ascending node Ra or the descending node Rd are approximately 1 AU. Mathematically, 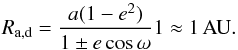Ra,d=a(1−e2)1±ecosω1≈1 AU.\begin{equation} \label{eq:1} R_{\rm a,\rm d}=\frac{a(1-e^{2})}{1\pm e\cos\omega}1\approx 1 \, \rm AU. \end{equation}(1)In one cycle of the argument of perihelion, ω , the values of a and e are changing due to perturbations so that for a given orbit there can be 1, 2, 4, or 8 values of ω satisfying the above equations. For the Quadrantid meteoroid stream, the number is 8, so the stream can produce 8 different meteor showers. Most of these showers have been identified (Babadzhanov et al. 2008b).

For (196256) 2003 EH1 and comet 96P/Machholz ω is also 8 therefore these objects and the Quadrantid stream have the same type of evolution. Note that in order for meteor showers to actually be produced at each of these crossings, the meteoroids must be distributed in significant numbers all around the nominal orbit. This requires meteoroids to be fed into the stream over a significant time period, not just at one point in space and time. In other words, meteoroids are released through continuous release as from a comet rather than from one event such as an asteroid collision. Therefore, (196256) 2003 EH1 is likely to be of cometary origin (Babadzhanov et al. 2008b).

The relationship between the Quadrantid stream and (196256) 2003 EH1, as well as a possible relationship between the Quadrantids and comet 96P/Machholz, have been subject to many investigations already cited in the introduction. Some of these investigations, especially Williams et al. (2004a,b), Neslusan et al. (2013a,b), numerically integrated the motion of (196256) 2003 EH1 and a large family of clones. However, all either look at the association between (196256) 2003 EH1 and the Quadrantids or of comet 96P/Machholz and the Quadrantids. Very little attention has been paid to the association of NEO 2003 EH1 with comet 96P/Machholz and this is the main purpose of this investigation.

3. Investigation of orbital evolution of comet 96P/Machholz and 2003 EH1

First, the close values of Tisserand parameter for the comet and 2003 EH1 should be noted (Table 1). This value indicates that they are both on “comet-like” orbits.

When asteroids and cometary nuclei fragment, the debris separates with velocities of the order of tens of m s-1, that are very small compared with the orbital velocity so that the specific orbital energy and angular momentum of each fragment are very similar. This implies that there are small differences in their initial orbital elements (exact formulae can be found in Williams 2002). Over time, planetary perturbations will cause such differences to increase in a way that can not be predicted analytically. To establish whether or not a pair of currently observed orbits were close in the past, it is necessary to numerically follow the orbital evolution. As these objects move through a chaotic region, it is usually necessary to investigate a family of clones to fully understand the evolution. However, as mentioned already, many investigations, especially (Williams et al. 2004a,b; Neslusan et al. 2013a,b) used a large family of clones. They found that the vast majority of the clones stayed close to the nominal orbit, though a few did not. These few were important in the investigations of Williams et al. (2004a,b) as they were investigating whether or not comet C/1490 Y1 could be an outlying member of the complex. Here we are interested in determining whether or not the major concentrations were once close to each other, and, if these follow the nominal orbit. Because of the vast saving in computing time we thus integrated only the nominal orbit of both bodies. The disadvantage of doing this is that we can conclude nothing if they do not ever get close to one another, since some of the clones, had they been included, still might get close. However, if we find that the nominal orbits get close, then we can conclude that most clones would also have gotten close with a high probability that the two real bodies concerned also did.

The numerical integration of the nominal orbits of comet 96P/Machholz and (196256) 2003 EH1 was performed using the Everhart (1974) integration method with perturbations from all eight major planets included. The integrator RADAU19 with self-adjusting step-length was applied for calculation of evolution of orbits. The step-length for output of the integration’s results to a file was accepted to be one year for detailing of the process and 100 yr for obtaining an overall look of the dynamics.

The integration was carried out, starting at the current epoch backwards to 14 000 BC and forwards to 14 000 AD; a time interval of 28 000 yr in total. Long-period variations of relevant orbital elements of the objects are given in Figs. 1–5.

As can be seen, the duration of one rotation cycle of the argument of perihelion for comet 96P/Machholz is near 7900 yr, and for 196256 is approximately 8500 yr. The orbital evolution of both objects is characterized by the large ranges of variations of the eccentricities, and so of the perihelion distances (from 0.05 to 1.4 AU) and the inclinations (from 10 to 85 deg) of the orbits during one half cycle of the argument of perihelion from 0 to 180 deg (Figs. 2–4). The longitudes of perihelia, that is, π = Ω + ω, librates within a relatively small range from 90 to 115 deg around the value of π = 100 deg (Fig. 5). The period of the libration is approximately 4000 yr, thereby coinciding with the period of the eccentricity or the inclination. As seen from Fig. 1, the semi-major axis of the comet’s orbit is more constant than those of 196256. Variations of the heliocentric distances Ra,Rd versus the time for the asteroid’s and comet’s orbits are plotted in Figs. 6 and 7, respectively. One cycle of secular variations of the radii-vectors to the ascending and descending nodes versus the argument of perihelion ω of the asteroid’s and comet’s orbits is presented in Figs. 8 and 9, respectively. The distance of 1 AU in Figs. 6–9 corresponds to the times when the orbits intersect the Earth’s orbit. Figures 8 and 9 clearly show that intersections with the Earth’s orbit occur at eight different values of the arguments of perihelia. Moreover, the variations of two bodies are practically the same. So, the results of the integrations confirm that these objects have the same evolutionary type, that is, both orbits are octuple Earth crossers.

thumbnail Fig. 1

Long-period variations of the semi-major axis a of the orbits of comet 96P/Machholz 1 and 196256.

thumbnail Fig. 2

Long-period variations of the eccentricity e of the orbits of comet 96P/Machholz 1 and 196256.

thumbnail Fig. 3

Long-period variations of the perihelion distance q of the orbits of comet 96P/Machholz 1 and 196256.

thumbnail Fig. 4

Long-period variations of the inclination i of the orbits of comet 96P/Machholz 1 and 196256.

thumbnail Fig. 5

Long-period variations of the longitude of perihelion π of the orbits of comet 96P/Machholz 1 and 196256.

thumbnail Fig. 6

Long-period variations of the heliocentric distances of ascending Ra and descending Rd nodes of the orbit of 196256.

thumbnail Fig. 7

Long-period variations of the heliocentric distances of ascending Ra and descending Rd nodes of the orbit of comet 96P/Machholz 1.

thumbnail Fig. 8

One cycle of secular variations of the radii-vectors to the ascending and descending nodes of 196256 versus the argument of perihelion ω.

thumbnail Fig. 9

One cycle of secular variations of the radii-vectors to the ascending and descending nodes of comet 96P/Machholz versus argument of perihelion ω.

Finally, one cycle of the secular trajectories of the radii-vectors to the ascending and descending nodes of the comet and 196256 projected on ecliptic plane is given in Fig. 10. It clearly shows that the orbits of 96P/Machholz and 196256 are really octuple Earth crossers and intersect the Earth’s orbit at different longitudes of the Sun. The trajectories of the ascending and descending nodes resemble one another. Therefore, at each point of the trajectory, including the intersection points from 1 to 4, there exist both the ascending and descending nodes.

4. Criteria of orbital similarity

We now need to establish whether the orbits of comet Machholz and 196256 were very close at any point during the considered time interval.

Several distance functions D or criteria have been developed to measure the distance between the orbits. DSH criterion by Southworth & Hawkins (1963) is a more traditional and widely used tool to measure the orbital similarity. It is determined by the expression DS−H2=(e2−e1)2+(q2−q1)2+(2sini2−i12)2 +sini1sini2(2sinΩ2−Ω12)2 +[(e1+e22)2sin(Ω2+ω2)−(Ω1+ω1)2]2,\begin{eqnarray} D_{\rm S-H}^2&=&(e_{2}-e_{1})^2+(q_{2}-q_{1})^2+\left(2\sin\frac{i_{2}-i_{1}}{2}\right)^2\nonumber \\\label{eq:2} &&\quad+\sin i_{1}\sin i_{2}\left(2\sin\frac{\Omega_{2}-\Omega_{1}}{2}\right)^2\nonumber \\ &&\quad+\left[\left(\frac{e_{1}+e_{2}}{2}\right)2\sin\frac{(\Omega_{2}+\omega_{2})-(\Omega_{1}+\omega_{1})} {2}\right]^2, \end{eqnarray}(2)where five orbital elements of the two orbits being compared are used for its calculation; subscripts 1 and 2 refer to these orbits. The orbits are considered to be close if their value of DSH ≤ 0.20 (see e.g., Jenniskens 2006; Jopek & Williams 2013).

In the absence of resonances, the semi-major axes of the orbits have no secular perturbations of the first order and can be considered constant: 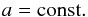a=const.\begin{equation} \label{eq:3} a=\rm const. \end{equation}(3)The perpendicular projection of the vector kinetic moment of the asteroid or comet to the plane of motion of the perturbing planet is also constant: 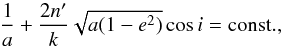1a+2n′ka(1−e2)cosi=const.,\begin{equation} \label{eq:4} \frac{1}{a}+\frac{2n'}{k}\sqrt{a(1-e^{2})}\cos i=\rm const., \end{equation}(4)where e is the eccentricity and i is the inclination of the asteroid orbit, n′ is the mean motion of the planet, and k is the Gauss’ constant.

The Tisserand parameter was obtained by solving the restricted circular problem of three bodies: the Sun, Jupiter, and a comet. This criterion connects the elements of the comet’s orbit, the semi-major axis, inclination, and eccentricity. The value of this criterion relative to the planet p is calculated by the formula: 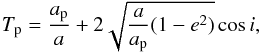Tp=apa+2aap(1−e2)cosi,\begin{equation} \label{eq:5} T_{\rm p}=\frac{a_{\rm p}}{a}+2\sqrt{\frac{a}{a_{\rm p}}(1-e^{2})}\cos i, \end{equation}(5)where ap is the semi-major axis of the orbit of the perturbing planet (Jupiter, or whichever has the greatest effect). The Tisserand parameter is a consequence of the integral (4).

Exploring the secular gravitational perturbations of three body problem, an analytical expression for the second and third integrals of motion was presented (Moiseev 1945; Lidov 1961): 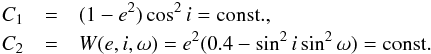C1=(1−e2)cos2i=const.,C2=W(e,i,ω)=e2(0.4−sin2isin2ω)=const.\begin{eqnarray} \label{eq:6} C_{1}&=&(1-e^{2})\cos^{2} i=\rm const., \\ C_{2}&=&W(e,i,\omega)=e^{2}(0.4-\sin^{2}i\sin^{2}\omega)=\rm const.\nonumber \end{eqnarray}(6)These integrals can be used in a doubly-averaged problem of three bodies: the Sun, Jupiter and an asteroid. Consistency follows from the Tisserand parameter, as the semi-major axes of the orbits have no secular perturbations of the first order. Moreover the integrals (6) establish the relations of e(ω) and i(ω).

The condition (2) relates a,e,ω or e,q,ω, as the parameter of the orbit p = a(1−e2) = q(1 + e). Thus, only four independent elements remain. If we consider the relationship of the eccentricity, inclination, and argument of perihelion arising from the integrals (6) then there are only two independent elements, a and ω.

Another formula for the function of a distance was introduced by Drummond (1979, 1981); 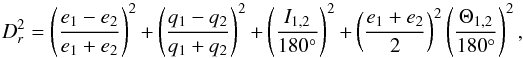Dr2=(e1−e2e1+e2)2+(q1−q2q1+q2)2+(I1,2180◦)2+(e1+e22)2(Θ1,2180◦)2,\begin{equation} \label{eq:7} D_{r}^{2}=\left(\frac{e_{1}-e_{2}}{e_{1}+e_{2}}\right)^{2}+ \left(\frac{q_{1}-q_{2}}{q_{1}+q_{2}}\right)^{2}+\left(\frac{I_{1,2}}{180^{\circ}}\right)^{2}+ \left(\frac{e_{1}+e_{2}}{2}\right)^{2}\left(\frac{\Theta_{1,2}}{180^{\circ}}\right)^{2}, \end{equation}(7)where I1,2 is the angle between the planes of the orbits, determined by the inclinations i and longitudes of the ascending nodes Ω; Θ1,2 is the angle between the directions to perihelia of the orbits. To confirm a closeness of the orbits, the Dr criterion is applied with the same threshold as the DSH criterion.

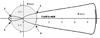thumbnail Fig. 10

One cycle of secular trajectory of the radii-vectors to the ascending and descending nodes of 96P/Machholz and 196256 in the ecliptic plane. The gray zone represents the Earth’s orbit. Intersection points where exist both the ascending and descending nodes are indicated from 1 to 4 by arrows.

Table 2

Orbital elements of comet 96P/Machholz 1 and 196256 and the distance between their orbits at 7415 BC (J2000.0).

In the cases of the large dispersion in the angular elements of orbits, Asher et al. (1993) suggested slightly modifying the D criterion that is used with the same threshold value as the DSH criterion and defined by formula D2=(a1−a23)2+(e1−e2)2+{2sin[(i1−i2)/2]}2.\begin{equation} \label{eq:8} D^{2}=\left(\frac{a_{1}-a_{2}}{3}\right)^{2}+ (e_{1}-e_{2})^{2}+\{2\sin[(i_{1}-i_{2})/2]\}^{2}. \end{equation}(8)The next modification of the DSH criterion was proposed by Jopek (1993) and defined by the following expression; 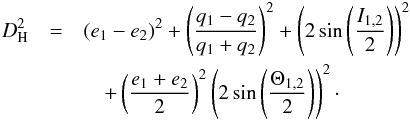DH2=(e1−e2)2+(q1−q2q1+q2)2+(2sin(I1,22))2 +(e1+e22)2(2sin(Θ1,22))2·\begin{eqnarray} \label{eq:9} D_{\rm H}^{2}&=&(e_{1}-e_{2})^{2}+ \left(\frac{q_{1}-q_{2}}{q_{1}+q_{2}}\right)^{2}+ \left(2\sin\left(\frac{I_{1,2}}{2}\right)\right)^{2}\nonumber \\ &&\quad+\left(\frac{e_{1}+e_{2}}{2}\right)^{2} \left(2\sin\left(\frac{\Theta_{1,2}}{2}\right)\right)^{2}\cdot \end{eqnarray}(9)Valsecchi et al. (1999) used the quantities of U and cosθ to identify meteor showers with orbits having different q,e,i,Ω and ω as possibly originating from the same body, due to secular perturbations on the same meteoroid stream. Here, U is the geocentric velocity of the meteoroids when crossing the Earth’s orbit 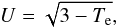U=3−Te,\begin{equation} U=\sqrt{3-T_{\rm e}},\nonumber \end{equation}(10)where Te is the Tisserand parameter calculated relative to the Earth by the equation 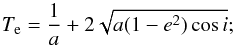Te=1a+2a(1−e2)cosi;\begin{equation} T_{\rm e}=\frac{1}{a}+2\sqrt{a(1-e^{2})\cos i};\nonumber \end{equation}(11)and θ is the elongation of the geocentric radiant from the apex, that is, the angle between U and the direction of motion of the Earth, which depends on U and a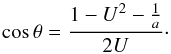cosθ=1−U2−1a2U·\begin{equation} \cos\theta=\frac{1-U^{2}-\frac{1}{a}}{2U}\cdot\nonumber \end{equation}(12)As a result of developing the distance function concept, Valsecchi et al. (1999), Jopek et al. (1999, 2003) have suggested the absolutely new criterion of orbital similarity, based on the known integrals of the restricted circular three body problem. The following DN function for the distance between two orbits was defined as: 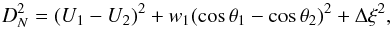DN2=(U1−U2)2+w1(cosθ1−cosθ2)2+Δξ2,\begin{equation} \label{eq:10} D_{N}^{2}=(U_{1}-U_{2})^{2}+w_{1}(\cos\theta_{1}-\cos\theta_{2})^{2}+\Delta\xi^{2}, \end{equation}(13)where w1 is a weighting factor. The value of the third summand –(Δξ)2 characterizes the difference (the angle) between radiant positions of two orbits. The calculation of this parameter is possible only for the orbits that intersect the Earth’s orbit at the ascending or descending nodes. In the case when the orbits do not cross the Earth’s orbit, a simplified form of this criterion, without the last summand – DR, is used: 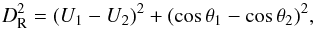DR2=(U1−U2)2+(cosθ1−cosθ2)2,\begin{equation} \label{eq:11} D_{\rm R}^{2}=(U_{1}-U_{2})^{2}+(\cos\theta_{1}-\cos\theta_{2})^{2}, \end{equation}(14)where w1 is set to 1. Since it is assumed that the Tisserand parameter has not changed significantly, the DR value should also be approximately constant. Only three orbital elements are using this criterion and, consequently, it can be applied only at the initial stage of investigation when we need to choose the objects for study of their possible interrelation.

We note that the DSH criterion and its modifications, such as Dr,D, and DH criteria operate with the heliocentric orbital elements. Only the DN criterion is using the geocentric parameters. It is a very useful method for measuring the similarity of meteoroid orbits to identify meteoroid streams and meteor showers. Additionally, it is necessary to note that adopted threshold values of the DSH,Dr,DH,DR criteria, which allow for confirmation of a common origin of the objects, were empirically defined.

5. On orbital similarity of comet 96P/Machholz 1 and 196256

The results of calculations of the DSH,Dr, and the simplified DR criteria for the orbits of comet 96P/Machholz and object 2003 EH1 during a period of 28 000 yr are given in Fig. 11. As seen, all criteria have simultaneously the minimal values from 7415–7465 BC, that is approximately 9500 yr ago. Consequently, the most similarity between the orbits was observed during this period. The elements of the orbits at the moment at which they were closest as well as the corresponding values of the criteria are given in Table 2.

thumbnail Fig. 11

Variations of the criteria of orbital similarity of comet 96P/Machholz 1 and object 2003 EH1 during 28 000 yr.

6. Discussion

As seen, only one point of close similarity has been recorded for the orbits of 96P/Machholz and object 2003 EH1 during the time period studied. Moreover, the intersection of the orbits occurred at the perihelia that were located at a distance near of 1 AU at the period under review. Without perturbations, the orbits should constantly pass through this point of fragmentation, that is, they should cross at this point. But this information is disappearing with time because of the change of the objects’ orbital elements and various gravitational and non-gravitational perturbing actions. Consequently, such intersection of the orbits has not been observed previously and may not be observed in future.

An impact with another object can cause fragmentation of the nucleus of a comet-progenitor. Such an event is highly improbable but cannot be excluded. The tidal forces of the Sun, the Earth, and Venus at the preceding stages of evolution can be considered as another reason for the fragmentation. Investigation of orbital evolution shows that there were many close approaches of objects to the Sun, the Earth, and to Venus at distances of less than 0.05 AU during the considered time interval. Encounters with Jupiter at distances of less than 0.2 AU took place only two or three times. Alternatively, we note that according to the results of orbital evolution, the deviations of the semimajor axes of the objects do not exceed 0.3 AU. So, it is necessary to emphasize that dispersion in semi-major axes can reach the value of 0.3 AU only under the action of close encounters with the planets.

Nonetheless, regardless of a scenario of the splitting of the parent comet’s nucleus, the results of investigations of the orbital evolution have shown that comet 96P/Machholz 1 and the object 2003 EH1 have a common origin. A decay of the parent into these two large fragments occurred approximately 9500 yr ago, and 196256 is, in effect, an extinct remnant of the parent comet.

7. Conclusion

Thus, the moment when the orbits of 96P/Machholz 1 and 196256 are closest to each other may be considered as the moment of a break-up of the nucleus of the comet-progenitor of the Quadrantid meteoroid complex. We have supposed that the comet and asteroid are large fragments of the nucleus of that parent comet. As a result, at present, the Quadrantid complex consists of active comet 96P/Machholz 1, inactive comet (196256) 2003 EH1 and the Quadrantid meteoroid stream with its eight meteor showers observable on the Earth. For reasons given here, it would be reasonable to carry out a search for similar large extinct fragments formed upon decay of a parent comet among both the known and newly discovered near-Earth asteroids.

Acknowledgments

We would like to express our gratitude to an anonymous referee for discussion of results and useful comments which improved the paper. The improvement of the English language of the paper by the Language Editor is also appreciated.

References

  1. Asher, D. J., Clube, S. V. M., & Steel, D. I. 1993, MNRAS, 264, 93 [NASA ADS] [CrossRef] [Google Scholar]
  2. Babadzhanov, P. B., Williams, I. P., & Kokhirova, G. I. 2008a, MNRAS, 386, 1436 [NASA ADS] [CrossRef] [Google Scholar]
  3. Babadzhanov, P. B., Williams, I. P., & Kokhirova, G. I. 2008b, MNRAS, 386, 2271 [NASA ADS] [CrossRef] [Google Scholar]
  4. Babadzhanov, P. B., Williams, I. P., & Kokhirova, G. I. 2009, A&A, 507, 1067 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Babadzhanov, P. B., Williams, I. P., & Kokhirova, G. I. 2012, MNRAS, 420, 2546 [NASA ADS] [CrossRef] [Google Scholar]
  6. Babadzhanov, P. B., Williams, I. P., & Kokhirova, G. I. 2013, A&A, 556, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Babadzhanov, P. B., Kokhirova, G. I., & Obrubov, Yu. V. 2015, Sol. Syst. Res., 49, 165 [NASA ADS] [CrossRef] [Google Scholar]
  8. Drummond, J. D. 1979, in Proc. Southwest Regional Conf. Astron. Astrophys., eds. P. F. Gott, P. S. Riherd, & A. R. Little Rock, 5, 83 [Google Scholar]
  9. Drummond, J. D. 1981, Icarus, 45, 545 [NASA ADS] [CrossRef] [Google Scholar]
  10. Everhart, E. 1974, Celest. Mech., 10, 35 [NASA ADS] [CrossRef] [Google Scholar]
  11. Fox, K., Williams, I. P., & Hughes, D. W. 1984, MNRAS, 208, 11 [NASA ADS] [CrossRef] [Google Scholar]
  12. Fisher, W. J. 1930, Harvard College Observ. Circ., 346, 1 [NASA ADS] [Google Scholar]
  13. Froeschle, C. I., & Scholl, H. 1982, A&A, 111, 348 [Google Scholar]
  14. Froeschle, C. I., & Scholl, H. 1986, A&A, 158, 259 [NASA ADS] [Google Scholar]
  15. Gonczi, R., Rickman, H., & Froeschle, C. 1992, MNRAS, 254, 627 [NASA ADS] [CrossRef] [Google Scholar]
  16. Green, D. W. E., Rickman, H., Porter, A. C., & Meeech, K. J. 1990, Science, 247, 1063 [NASA ADS] [CrossRef] [Google Scholar]
  17. Hasegawa, I. 1979, PASJ, 31, 257 [Google Scholar]
  18. Hasegawa, I. 1993, in Meteoroids and their parent bodies, eds. J. Stohl, & I. P. Williams (Bratislava: Astronomical Institute, Slovak Academy of Sciences), Proc. Intern. Astron. Symp., 209 [Google Scholar]
  19. Hughes, D. W., Williams, I. P., & Fox, K. 1981, MNRAS, 195, 625 [NASA ADS] [CrossRef] [Google Scholar]
  20. Jenniskens, P. 2004, AJ, 127, 3018 [NASA ADS] [CrossRef] [Google Scholar]
  21. Jenniskens, P. 2006, in Meteor Showers and Their Parent Comets (Cambridge, UK: Cambridge Univ. Press), 790 [Google Scholar]
  22. Jenniskens, P., Betlem, H., de Linge, M., Langbroek, M., & van Vliet, M. 1997, A&A, 327, 1242 [NASA ADS] [Google Scholar]
  23. Jewitt, D. C. 2012, AJ, 143, 66 [NASA ADS] [CrossRef] [Google Scholar]
  24. Jopek, T. J. 1993, Icarus, 106, 603 [NASA ADS] [CrossRef] [Google Scholar]
  25. Jopek, T., & Williams, I. P. 2013, MNRAS, 430, 2377 [NASA ADS] [CrossRef] [Google Scholar]
  26. Jopek, T. J., Valsecchi, G. B., & Froeschle, C. l. 1999, MNRAS, 304, 751 [NASA ADS] [CrossRef] [Google Scholar]
  27. Jopek, T. J., Valsecchi, G. B., & Froeschle, C. l. 2003, MNRAS, 344, 665 [NASA ADS] [CrossRef] [Google Scholar]
  28. Kozai, H. 1992, Cel. Mech. Dyn. Astron., 54, 237 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kresak, L. 1982, Astr. Inst. Czech. Bull., 33, 104 [NASA ADS] [Google Scholar]
  30. Lidov, M. L. 1961, Iskusstvennie Sputniki Zemli, 8, 5 [Google Scholar]
  31. Madiedo, J. M., Trigo-Rodriguez, J. M., Williams, I. P., et al. 2013, MNRAS, 431, 2464 [NASA ADS] [CrossRef] [Google Scholar]
  32. McIntosh, B. A. 1990, Icarus, 86, 299 [NASA ADS] [CrossRef] [Google Scholar]
  33. Micheli, M., Tholen, D., & Jenniskens, P. 2016, Icarus, 267, 64 [NASA ADS] [CrossRef] [Google Scholar]
  34. Moiseev, N. D. 1945, Trudy Gos. Astron. Inst. Mosk. Univ., 15, 75 [Google Scholar]
  35. Murray, C. D., Hughes, D. A., & Williams, I. P. 1980, MNRAS, 190, 733 [NASA ADS] [CrossRef] [Google Scholar]
  36. Neslusan, L., Kanuchova, Z., & Tomko, D. 2013a, A&A, 551, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Neslusan, L., Kanuchova, Z., & Tomko, D. 2013b, A&A, 560, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Porubčan, V., Kornos, L., & Williams, I. P. 2004, Earth, Moon & Planets, 95, 697 [Google Scholar]
  39. Porubčan, V., Kornos, L., & Williams, I. P. 2006, Contrib. Astron. Obs. Scalnate Pleso, 36, 103 [Google Scholar]
  40. Rudawska, R., Vaubaillon, J., & Jenniskens, P. 2012a, European Planetary Science Congress 2012, Madrid, Spain, 886 [Google Scholar]
  41. Rudawska, R., Vaubaillon, J., & Jenniskens, P. 2012b, Asteroids, Comets, Meteors 2012, Proc. Conf. May 16−20, 2012, Niigata, Japan, LPI Contribution, 1667, 6222 [Google Scholar]
  42. Sekanina, Z. 1990, AJ, 99, 1268 [NASA ADS] [CrossRef] [Google Scholar]
  43. Shelton, J. W. 1965, AJ, 70, 337 [NASA ADS] [CrossRef] [Google Scholar]
  44. Southworth, R. B., & Hawkins, G. S. 1963, Smith. Contrib. Astrophys., 7, 261 [Google Scholar]
  45. Tancredi, G. 2014, Icarus, 234, 66 [NASA ADS] [CrossRef] [Google Scholar]
  46. Trigo-Rodriguez, J. M., Madiedo, J. M., Williams, I. P., & Castro-Tirado, A. J. 2009, MNRAS, 392, 367 [NASA ADS] [CrossRef] [Google Scholar]
  47. Tubiana, C., Snodgrass, C., Michelsen, R., et al. 2015, A&A, 584, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Valsecchi, G. B., Jopek, T. J., & Froeschle, Cl. 1999, MNRAS, 304, 743 [NASA ADS] [CrossRef] [Google Scholar]
  49. Whipple, F. L. 1983, IAU Circ., 3881, 1 [NASA ADS] [Google Scholar]
  50. Wiegert, P., & Brown, P. 2005, Icarus, 179, 139 [NASA ADS] [CrossRef] [Google Scholar]
  51. Williams, I. P. 2002, in Meteors in the Earth’s atmosphere, eds. E. Murad, & I. P. Williams (Cambridge, UK: Cambridge University Press), 13 [Google Scholar]
  52. Williams, I. P., & Wu, Z. D. 1993, MNRAS, 264, 659 [NASA ADS] [CrossRef] [Google Scholar]
  53. Williams, I. P., & Collander-Brown, S. J. 1998, MNRAS, 294, 127 [NASA ADS] [CrossRef] [Google Scholar]
  54. Williams, I. P., Ryabova, G. O., Baturin, A. P., & Chernitsov, A. M. 2004a, MNRAS, 355, 1171 [NASA ADS] [CrossRef] [Google Scholar]
  55. Williams, I. P., Ryabova, G. O., Baturin, A. P., & Chernitsov, A. M. 2004b, Earth Moon & Planets, 95, 11 [NASA ADS] [CrossRef] [Google Scholar]
  56. Wu, Z., & Williams, I. P. 1992, MNRAS, 259, 617 [NASA ADS] [Google Scholar]

All Tables

Table 1

Summary of the current orbits of comet 96P/Machholz 1, (196256) 2003 EH1 and the Quadrantid meteor shower (J2000.0).

In the text
Table 2

Orbital elements of comet 96P/Machholz 1 and 196256 and the distance between their orbits at 7415 BC (J2000.0).

In the text

All Figures

thumbnail Fig. 1

Long-period variations of the semi-major axis a of the orbits of comet 96P/Machholz 1 and 196256.
In the text
thumbnail Fig. 2

Long-period variations of the eccentricity e of the orbits of comet 96P/Machholz 1 and 196256.
In the text
thumbnail Fig. 3

Long-period variations of the perihelion distance q of the orbits of comet 96P/Machholz 1 and 196256.
In the text
thumbnail Fig. 4

Long-period variations of the inclination i of the orbits of comet 96P/Machholz 1 and 196256.
In the text
thumbnail Fig. 5

Long-period variations of the longitude of perihelion π of the orbits of comet 96P/Machholz 1 and 196256.
In the text
thumbnail Fig. 6

Long-period variations of the heliocentric distances of ascending Ra and descending Rd nodes of the orbit of 196256.
In the text
thumbnail Fig. 7

Long-period variations of the heliocentric distances of ascending Ra and descending Rd nodes of the orbit of comet 96P/Machholz 1.
In the text
thumbnail Fig. 8

One cycle of secular variations of the radii-vectors to the ascending and descending nodes of 196256 versus the argument of perihelion ω.
In the text
thumbnail Fig. 9

One cycle of secular variations of the radii-vectors to the ascending and descending nodes of comet 96P/Machholz versus argument of perihelion ω.
In the text
thumbnail Fig. 10

One cycle of secular trajectory of the radii-vectors to the ascending and descending nodes of 96P/Machholz and 196256 in the ecliptic plane. The gray zone represents the Earth’s orbit. Intersection points where exist both the ascending and descending nodes are indicated from 1 to 4 by arrows.
In the text
thumbnail Fig. 11

Variations of the criteria of orbital similarity of comet 96P/Machholz 1 and object 2003 EH1 during 28 000 yr.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.