| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | L1 | |
| Number of page(s) | 3 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201629947 | |
| Published online | 19 December 2016 | |
Observable properties of strong gravitational lenses
Jodrell Bank Centre for Astrophysics, University of Manchester, Alan Turing Building, Oxford Road, Manchester, M13 9PL, UK
e-mail: nicolas.tessore@manchester.ac.uk
Received: 24 October 2016
Accepted: 15 November 2016
It is shown which properties of a strong gravitational lens can in principle be recovered from observations of multiple extended images when no assumptions are made about the deflector or sources. The mapping between individual multiple images is identified as the carrier of information about the gravitational lens and it is shown how this information can be extracted from a hypothetical observation. The derivatives of the image map contain information about convergence ratios and reduced shears over the regions of the multiple images. For two observed images, it is not possible to reconstruct the convergence ratio and shear at the same time. For three observed images, it is possible to recover the convergence ratios and reduced shears identically. For four or more observed images, the system of constraints is overdetermined, but the same quantities can theoretically be recovered.
Key words: gravitational lensing: strong / methods: analytical
© ESO, 2016
1. Introduction
In a recent article, Wagner & Bartelmann (2016) have shown that derivatives and ratios of derivatives of the lensing potential near critical curves can be constrained directly from observations of strong gravitational lenses without the reconstruction of a lens model. This raises the question of whether or not other lensing quantities can, at least in principle, be constrained from observations alone. In this Letter, an answer is given by explicit construction of the observable properties of strong gravitational lenses. Observables are quantities which can be recovered from observations without the assumption of a specific lens model or reconstruction method, and are necessarily invariant under the mass sheet transform (MST, Falco et al. 1985; Gorenstein et al. 1988; Schneider & Seitz 1995; for a summary see Schneider et al. 2006). The approach presented is a general recipe for the extraction of model-independent information from observations of strong lenses with multiple extended images, which is applied here to recover the convergence and shear.
The structure of the letter is as follows. Section 2 introduces the mapping between multiple images as the essential holder of the observation’s information about a strong gravitational lens. Section 3 shows how observables can be reconstructed from the observed image map. Section 4 generalises the result to more than two observed images and treats the case in which some lens properties can be recovered identically. Section 5 closes with a brief discussion of the idea presented here and a look towards its possible application with future observations.
2. The image map
When no assumptions are made about the mass distribution of the deflector or about the surface brightness distribution of the lensed sources, any inference about a single strong gravitational lens must be based on the observation of multiple images of the background objects. Consider a hypothetical ideal observation of two images Ω and Ω′ of the same source plane region (Fig. 1). The most information that can be extracted, even in principle, from the two images Ω and Ω′ is a map ϕ which connects those points θ ∈ Ω and θ′ ∈ Ω′ that show the same point in the source plane. This image map must therefore contain all the properties of the gravitational lens that can be reconstructed, and observable properties of a strong gravitational lens are precisely those which can be recovered from the image map.
To formally establish the relationship between image map ϕ and the gravitational lens, let Ω,Ω′ ⊂ R2 be two regions in the image plane, each of which shows a multiple image of the same region S ⊂ R2 in the source plane. Considering the lens equation separately for Ω and Ω′, let β and β′ be the individual source position mappings where the regions Ω and Ω′ are suitably restricted to contain only the multiple images (hence β(Ω) = β′(Ω′) = S), and α is the deflection angle of the gravitational lens. The image map ϕ is a mapping between the multiple images Ω and Ω′, 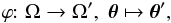 (1)where θ and θ′ = ϕ(θ) map to the same point β(θ) = β′(θ′) in the source plane. It follows that there is a relation between image map ϕ and the source position mappings,
(1)where θ and θ′ = ϕ(θ) map to the same point β(θ) = β′(θ′) in the source plane. It follows that there is a relation between image map ϕ and the source position mappings, 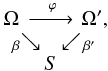 (2)where β and β′ are determined by the gravitational lens. The equivalence between the source position mappings,
(2)where β and β′ are determined by the gravitational lens. The equivalence between the source position mappings, 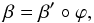 (3)can now be used to infer the properties of the lens from the image map by comparing the left and right-hand sides under various operations.
(3)can now be used to infer the properties of the lens from the image map by comparing the left and right-hand sides under various operations.
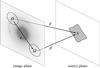 |
Fig. 1 An observation shows multiple images Ω and Ω′ of the source plane region S. The image map ϕ:Ω → Ω′ connects those points θ ∈ Ω and θ′ ∈ Ω′ that show the same point in the source plane, and can be used to relate the source position mappings β′ and β = β′°ϕ. |
3. Convergence and shear
Equation (3) can be expanded to first order on both sides, which yields a relation, 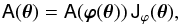 (4)between the magnification matrix A evaluated at θ and θ′ = ϕ(θ), respectively, and the Jacobian matrix Jϕ of the image map. It follows that Jϕ is equal to the relative magnification matrix,
(4)between the magnification matrix A evaluated at θ and θ′ = ϕ(θ), respectively, and the Jacobian matrix Jϕ of the image map. It follows that Jϕ is equal to the relative magnification matrix, 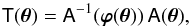 (5)between the multiple images Ω and Ω′. The matrix T is the only model-independent information that can be extracted from the observation at first order.
(5)between the multiple images Ω and Ω′. The matrix T is the only model-independent information that can be extracted from the observation at first order.
Writing the magnification matrix A in terms of convergence κ and the two components g1,g2 of the reduced shear, the matrix equation Jϕ = T can be split into partial differential equations, that generate the image map ϕ, where the unprimed and primed values are taken at θ ∈ Ω and θ′ = ϕ(θ) ∈ Ω′, respectively.
The observable lens properties from two images are then the quantities which can be constructed from combinations of the image map derivatives (8) to (11). For example, the Jacobian determinant of the image map is the local magnification ratio, 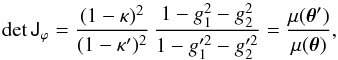 (6)at corresponding points θ ∈ Ω and θ′ = ϕ(θ) ∈ Ω′. This result is well-known and could be obtained more directly by taking the determinant on both sides of Eq. (4).
(6)at corresponding points θ ∈ Ω and θ′ = ϕ(θ) ∈ Ω′. This result is well-known and could be obtained more directly by taking the determinant on both sides of Eq. (4).
Unfortunately, no combination of derivatives (8) to (11) will be able to recover the convergences κ and κ′ directly, since the equations only contain the convergence ratio, 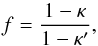 (7)and neither κ nor κ′ in isolation. This also follows from the MST; the convergence κ is not an invariant and therefore cannot be observable. The convergence ratio f, on the other hand, is an invariant, which makes it a prime candidate for an observable. However, Eqs. (8) to (11) still provide only four constraints for the five remaining unknowns
(7)and neither κ nor κ′ in isolation. This also follows from the MST; the convergence κ is not an invariant and therefore cannot be observable. The convergence ratio f, on the other hand, is an invariant, which makes it a prime candidate for an observable. However, Eqs. (8) to (11) still provide only four constraints for the five remaining unknowns 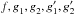 . The image map between two multiple images on its own is hence not enough to recover the convergence ratio and shear at the same time.
. The image map between two multiple images on its own is hence not enough to recover the convergence ratio and shear at the same time.
While it is tempting to augment the system of constraints by considering the magnification ratio μ(θ′) /μ(θ) as observable, this would be incorrect. For the assumed ideal observation, the magnification ratio must be constructed explicitly by mapping areas between the multiple images. This is the same information contained in the image map and it cannot be used twice. The correct way to construct more informative observables is to use more than two multiple images in the reconstruction.
4. Multiple images
Consider now n > 2 multiple images Ω0,Ω1,...,Ωn−1 of the same source plane region S. Keeping Ω0 fixed, it is possible to construct n−1 individual image maps, 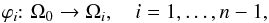 (8)which contain all the information about the multiple images, as any further map ϕij:Ωi → Ωj is the composition
(8)which contain all the information about the multiple images, as any further map ϕij:Ωi → Ωj is the composition 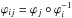 . Every pair of images (Ω0,Ωi) obeys a relation similar to (2),
. Every pair of images (Ω0,Ωi) obeys a relation similar to (2), 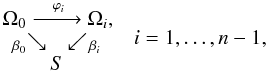 (9)between its image map ϕi and suitably restricted source position mappings β0:Ω0 → S and βi:Ωi → S. In particular, there are now n−1 individual equations that relate β0 and βi in the same manner as Eq. (3)did in the case of two images,
(9)between its image map ϕi and suitably restricted source position mappings β0:Ω0 → S and βi:Ωi → S. In particular, there are now n−1 individual equations that relate β0 and βi in the same manner as Eq. (3)did in the case of two images, 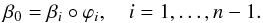 (10)Hence there is a set of Eqs. (8) to (11) for each multiple image i = 1,...,n−1, where the convergence κi and shear gi,1,gi,2 for each image are evaluated at the point ϕi(θ), respectively.
(10)Hence there is a set of Eqs. (8) to (11) for each multiple image i = 1,...,n−1, where the convergence κi and shear gi,1,gi,2 for each image are evaluated at the point ϕi(θ), respectively.
The goal is now to solve the system of Eqs. (17) to (20) for the lens observables. The total number of constraints is Ncon = 4n−4. For the reasons given above, it is necessary to introduce the convergence ratio for each image, 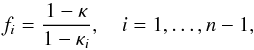 (11)since the n convergences κ0,κ1,... are not directly observable. The observables are then g0,1,g0,2,f1,g1,1,g1,2,..., and the total number of unknowns is Nobs = 3n−1. The system of equations therefore admits three distinct cases.
(11)since the n convergences κ0,κ1,... are not directly observable. The observables are then g0,1,g0,2,f1,g1,1,g1,2,..., and the total number of unknowns is Nobs = 3n−1. The system of equations therefore admits three distinct cases.
For n = 2 multiple images, Ncon < Nobs and the system is underdetermined. This is seen in Sect. 3.
For n = 3 multiple images, Ncon = Nobs and the system is solvable. The lens properties can hence be recovered identically from the image maps by solving Eqs. (17) to (20) for the observables. Taking the combinations of the derivatives of the two image maps (i = 1,2), the reduced shear g0 over multiple image Ω0 is found to be For the additional multiple images Ωi, i = 1,2, the convergence ratio fi and reduced shear gi are most easily expressed in terms of the results for g0,1 and g0,2 as
where 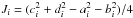 is the Jacobian determinant of image map ϕi.
is the Jacobian determinant of image map ϕi.
For n > 3 multiple images, Ncon > Nobs and the system is overdetermined. In this case, all lens properties can, in principle, still be recovered from observations. The additional constraints are a consistency check of the reconstruction, and could be used to test image maps constructed from observations.
5. Conclusions
It has been known since the discovery of the MST that many properties of a gravitational lens are not observable. The results of Sect. 4 now explicitly show properties that can, at least in principle, be observed from multiple extended images. This is of practical interest: knowing which properties of a lens system are effectively constrained by the observation is necessary to present significant results. Reconstructions should compare maps of the convergence ratios f1,f2,... and reduced shears g0,g1,..., as these are the effectively observable properties of strong lenses.
As it stands, the image map ϕ is a theoretical construct that is introduced here as a tool to find properties of gravitational lenses that can be recovered from multiple observed images. However, it is possible that future telescopes have the necessary resolution to make a point-by-point mapping between multiple images of the largest strong lenses feasible, at least to some degree. In this case, the technique outlined here could lead to a truly model-free reconstruction method for strong lenses that uses no more information than what is provided by observations.
Acknowledgments
The author would like to thank M. Bartelmann, S. Bridle and R. B. Metcalf for their comments and discussions. The anonymous referee helpfully suggested changing the derivation from using complex derivatives to the better-known real-valued expressions, which simplified the discussion. The author further acknowledges support from the European Research Council in the form of a Consolidator Grant with number 681431.
References
- Falco, E. E., Gorenstein, M. V., & Shapiro, I. I. 1985, ApJ, 289, L1 [Google Scholar]
- Gorenstein, M. V., Shapiro, I. I., & Falco, E. E. 1988, ApJ, 327, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., & Seitz, C. 1995, A&A, 294, 411 [NASA ADS] [Google Scholar]
- Schneider, P., Kochanek, C. S., & Wambsganss, J. 2006, Gravitational Lensing: Strong, Weak and Micro (Berlin: Springer-Verlag) [Google Scholar]
- Wagner, J., & Bartelmann, M. 2016, A&A, 590, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 An observation shows multiple images Ω and Ω′ of the source plane region S. The image map ϕ:Ω → Ω′ connects those points θ ∈ Ω and θ′ ∈ Ω′ that show the same point in the source plane, and can be used to relate the source position mappings β′ and β = β′°ϕ. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


