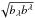EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 596 (December 2016) A&A, 596 (2016) A13 Full HTML
Free Access
Issue
A&A
Volume 596, December 2016
Article Number A13
Number of page(s) 10
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201629157
Published online 21 November 2016

© ESO, 2016

1. Introduction

Low luminosity active galactic nuclei (LLAGN, defined here as Lbol< 10-2LEdd where Lbol and LEdd are the bolometric and Eddington luminosity, respectively) and low-ionization nuclear emission-line region galaxies (LINERs) often display compact radio emissions in their nuclei (Falcke & Markoff 2000; Nagar et al. 2000; Nagar et al. 2005). Their radio cores usually exhibit a flat spectrum (i.e., Fν ~ ν− α where α> −0.5 for ν = 1–100 GHz), and are thought to be associated with the accretion/ejection processes around central supermassive black holes. High resolution very long baseline interferometry (VLBI) observations often reveal that the compact radio cores have morphology of parsec-scale jets streams (see, e.g., Sect. 5.4 in Nagar et al. 2005; Markoff et al. 2008; Doi et al. 2013 for a sample of LLAGN sources with compact jets). Compact radio cores are also associated with quasars jets and blazars, which are much more powerful than LLAGN. These jets are often associated with high-energy processes such as particle acceleration and X-ray or γ-ray emissions (Grandi et al. 2012; Massaro et al. 2015).

One of the big questions is how do black holes form a radio jet in the first place? The general picture is that to form a jet one needs large-scale ordered rotating magnetic fields (B-fields). However, it is unclear whether the observed jets are powered by rotation of an accretion disk in which the B-fields are anchored, or by the spin of the central black hole and rotation of the B-fields owing to frame-dragging effects. It is possible that both mechanisms operate together.

Spinning black holes have a significant amount of rotational energy. This energy can be as large as ~30% of the gravitational energy of a supermassive black hole (Egrav = MBHc2 ≈ 1062 [MBH/ 108M⊙] ergs, Misner et al. 1977). This energy is enough to power the radio lobes of a typical radio galaxy. The energy removal from the black hole by magnetic fields was first discussed by Blandford & Rees (1974), Lovelace (1976) and Blandford & Znajek (1977). Black hole jets associated with the so-called Blandford-Znajek process are referred to as Blandford-Znajek jets (BZ jets). Early analytical models of BZ jets predicted that the jet power would be proportional to the square of a black hole rotation, i.e., 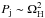where ΩH is the angular velocity of the BH event horizon. Later, a number of numerical general relativistic magnetohydrodynamics (GRMHD) simulations confirmed this dependency (e.g., McKinney & Gammie 2004). Some simulations show even steeper relationship: 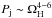(e.g., Tchekhovskoy et al. 2010). The scaling relation found above, which is often called the spin paradigm, was proposed as a way of explaining the diversity of radio jet powers in radio galaxies (FRI-II dichotomy) and the radio loud/quiet dichotomy of quasars (Tchekhovskoy et al. 2010). The latter has recently been discussed in the context of “magnetic flux paradigm” (see e.g., Sikora & Begelman 2013).

The jet power-spin correlation is difficult to test observationally because both the power and the spin of the black hole cannot be measured directly. For example, Narayan & McClintock (2012) estimated the spin of black holes using a thermal continuum-fitting method in five black hole binary systems, and found that jet radio luminosity (which, by assumption, was associated with the jet power) scales as the square of the black hole spin. However Russell et al. (2013) casts doubts on these results by finding no correlation in a larger sample of objects of the same class. The so-called spin paradigm in the context of supermassive black holes in radio loud galaxies was addressed by van Velzen & Falcke (2013), who found a tight correlation between the optical luminosity of the jet core and the radio luminosity of jet lobes. The small scatter in their correlation suggests that a spin of the black hole may not be critical for the production of jets if one assumes that the black hole spin distribution function of black holes is uniform. Falcke & Biermann (1995) suggested that jets and disks are symbiotic features in AGN, and it has been shown that the accretion disk luminosity and jet radio luminosity tightly trace each other over many orders of magnitude in accretion luminosity and black hole mass (Rawlings & Saunders 1991; Falcke et al. 1995; Falcke & Biermann 1996). Later, Merloni et al. (2003) and Falcke et al. (2004) found a fundamental plane of black hole activity, connecting X-ray and radio flux of black holes as a function of mass and accretion rate. Taken at face value, this suggests that a spin is a subdominant factor in the visible radio jet formation and that accretion luminosity and jet radio luminosity scale with spin in a comparable manner.

Hence, the role of black hole spin in the production of visible radio jets is still a highly relevant, but unsolved issue. The usual problem is that the jet radio luminosity is often associated with the jet power. What then is the radio jet that we observe in black hole systems, and how does its luminosity scale with the black hole spin? Here we attempt to address these questions from a theoretical point of view, using advanced numerical simulations of plasma dynamics around spinning black holes. These simulations have recently become sophisticated enough to produce basic observational properties of jets (limb-brightening, flat spectrum, size-wavelength relation, see Mościbrodzka & Falcke 2013; Chan et al. 2015; Mościbrodzka et al. 2016). The models we present here and the results obtained from them, however, only concentrate on low-luminosity supermassive black holes; which have relatively low luminosities (L< 10-6LEdd) and optically-thin radiatively inefficient accretion flows. This significantly simplifies the necessary physics, since we can largely ignore radiative cooling and radiation pressure in the dynamical simulations (e.g., Dibi et al. 2012). However, whether these models can also reproduce the black hole fundamental plane scaling has not been tested yet, nor how they respond to changes in the spin parameter. Fortunately, these GRMHD models can be feasibly combined with a general relativistic radiative transfer model in a post-processing manner. This allows us now to examine the electromagnetic emission from the model from nearly ab initio calculations.

Our jets are produced in time-dependent, fully three dimensional general relativistic magnetohydrodynamic (3D GRMHD) simulations of black hole accretion flows. The black hole is fed by a magnetized torus seeded with a single closed loop magnetic field at the equator of the black hole (Mościbrodzka et al. 2014). In this type of simulations, the BZ-jet naturally emerges, and it can be seen as a bipolar funnel both above and below the black hole. The funnel regions have ordered large-scale magnetic fields that allow for energy extraction from BHs if the black hole is rotating fast. However, the funnel regions are largely evacuated and radiatively dim. In accordance with observations of high-resolution VLBI images of the M 87 jet (Hada et al. 2013), we identify the main radiating part of the jet as the sheath structure of entrained plasma, which forms around the evacuated funnels. In the simulations, the jet sheath is mass loaded in the innermost parts of the accretion disk, and so its matter content is well known since it is self-consistently calculated by GRMHD equations. Hence, in the jet model proposed here there is no need to, for example, inject extra electron/positron pairs to produce radiation from the jet (Mościbrodzka et al. 2011; Levinson & Rieger 2011; Broderick & Tchekhovskoy 2015).

Moreover, our models naturally fit the detailed observations of the closest and best studied flat spectrum radio cores, namely Sgr A* (Mościbrodzka & Falcke 2013; Mościbrodzka et al. 2014; Fraga-Encinas et al. 2016) and M 87 (Mościbrodzka et al. 2016). Our semi-empirical approach allowed us to constrain unknown parameters, such as the electron temperatures in the numerical models, by using observations.

Building upon our previous work which uses a fixed black hole spin, we now present a new suite of numerical models for jets, which are driven from accretion disks around black holes with a range of spins. For the first time, we can investigate how the jet radio emission scales with accretion rate and black hole spin in these models. Also, for the first time, we are able to discuss how the black hole spin affects the scale-invariant jet models that have been introduced to explain the fundamental plane of the black hole activity (e.g., Heinz & Sunyaev 2003).

The paper is organized as follows. In Sect. 2, we describe our simulation setup for the jet formation, and describe how the corresponding radiation from the jets is computed. In Sect. 3, we show general properties of accretion flow models and we present our studies on how radio emission from the jet depends on the black hole spin. We also discuss the energies and masses carried by different components of the simulations (disk, jet sheath, and jet spine). We discuss the result of simulations in the context of a scale-invariant jet model in Sect. 4. The results are summarized in Sect.5.

2. Method

2.1. GRMHD simulations

The dynamics of magnetized plasma near a Kerr black hole is followed by 3D GRMHD simulations. All simulations presented here are carried out using the HARM-3D code (Gammie et al. 2003; Noble et al. 2009). The code solves ideal-MHD equations in a fixed Kerr metric.

At t = 0, the plasma is confined to a geometrically thick donut-shaped torus. The plasma density distribution, internal energy, and velocity is computed using an analytical torus model presented in Fishbone & Moncrief (1976). The inner edge of the torus is rin = 12GM/c2, and the position of the plasma pressure maximum is rmax = 24GM/c2. We follow standard procedures and seed the initial disk with a sub-thermal magnetic field (β = Pgas/Pmag = 10−100), the geometry of which aligns with the iso-density surfaces of the torus (the so-called single loop scenario).

The free parameter of the dynamical simulations is the black hole spin. The spin varies from a∗ = 0.01 to 0.98, where a∗ = cJ/GM2 is the dimensionless angular momentum of the black hole. Table 1 lists all considered models with parameters adopted to set up the computational grid size and resolution. We describe the properties of the GRMHD models in Sect. 3.1.

Table 1

GRMHD models of an accreting black hole with a jet and the parameters that describe the numerical grid.

2.2. Radiative transfer models

To calculate the electromagnetic emission from the GRMHD simulations, we use a ray-tracing radiative transfer method. In this method, the radiative transfer equation is integrated along null geodesics from the vicinity of the black hole to an observer. The radiative transfer includes synchrotron emission and self-absorption from a relativistic, thermal population of electrons described by the Maxwell-Jüttner distribution function. We note that most AGN show evidence for a non-thermal power-law distribution with a low-energy cutoff. A thermal distribution plus a non-thermal tail would be a more appropriate description in this case. However, this would introduce an additional free parameter, and, anyway, it is the low-energy peak that dominates the emission for the self-absorbed flat-spectrum part of jets. In fact, in simple analytic Blandford-Königl type models of flat-spectrum radio cores, thermal and non-thermal distribution functions produce the same scaling behavior (e.g., Falcke & Hehl 2002).

With this distribution function, synchrotron emission maps at a given frequency are calculated. The integration of intensity over the map gives us the model total flux. By producing maps at various frequencies, we construct spectral energy distribution (SED) of synchrotron emission from the model. Radiative transfer calculations are carried out with the general relativistic radiative transfer code mibothros described by Noble et al. (2007). Our numerical code has been tested extensively by the authors. We recently compared our current code with the synchrotron maps produced by an independent code grtrans (Dexter 2016), and confirmed that the emitted radiation is independent of the radiative transfer scheme.

We have to assume an electron temperature as they are not self-consistently computed in our simulations. The usual problem here is that typical GRMHD simulations only provide the proton temperature, Tp. The electron temperature is therefore usually parameterized by a coupling ratio between proton and electron temperatures (Tp/Te). In Mościbrodzka & Falcke (2013), we suggested that the coupling ratio is most likely different in the low-magnetized disk compared to the tenuous, highly-magnetized jet sheath. Indeed, fitting of the SED of Sgr A* and M 87 suggests that the electron-proton coupling is much lower in the disk, compared to the jet. The disk flow is therefore described as a two-temperature plasma, as commonly assumed for advection dominated/radiatively inefficient accretion flow (ADAF/RIAF) solutions (Narayan et al. 1998), while the jet is described as a hot, single temperature electrons. The latter is justified by the almost constant brightness temperatures seen in compact jets and may be due to the continuous re-acceleration/re-heating of electrons along the jet or due to thermal conductivity along the magnetic field lines, balancing some of the adiabatic losses. We note that the electron temperature prescriptions used here and in our previous work are now naturally produced in the axisymmetric extended-GRMHD models that follow the electron and proton temperatures from nearly first-principles (Ressler et al. 2015; Foucart et al. 2016).

In our models, the boundary between the disk and jet regions is defined by using the hydrodynamical Bernoulli parameter, −hut = 1.02, where h is gas enthalpy, and ut is the covariant time component of the gas four-velocity. The fiducial value of the Bernoulli parameter typically corresponds to a jet plasma bulk velocities v> 0.2c, as measured by an observer at infinity. This is, for example, consistent with subluminal speeds detected at the base of, for example, M 87 jet (Hada et al. 2016). This type of a definition consistently associates the magnetically dominant outflow region with the jet component and makes the jet sheath radio bright. We neglect radiation from the highly magnetized and evacuated jet spine because the jet-spine temperatures and matter content are arbitrarily set by the numerical floor quantities (fluid density and internal energy floors) that are necessary for numerical stability of the GRMHD code.

In this study, we are not fitting models to a specific set of observed SEDs; hence, we adopt a constant value, Tp/Te = 20 for the disk, which would fit typical SEDs well. The default jet electron temperature is set as Θe,jet = kTe/mec2 = 20 in electron rest mass energy units. The latter is also motivated by fitting models to Sgr A* spectrum (e.g., Mościbrodzka et al. 2014; Chan et al. 2015; Gold et al. 2016). Tp/Te and Θe,jet are fixed parameters in all the radiative transfer calculations.

Finally, to completely define the radiative transfer problem, we have to scale the GRMHD simulation to a specific source. This requires us to provide the central black hole mass (sets the typical length scale) and mass of the accretion disk (sets the accretion rate onto the black hole). Our fiducial model assumes a mass of the central black hole in a LLAGN to be MBH = 108M⊙. We consider a system in which the black hole is accreting at a rate ṁ = Ṁ/ṀEdd ≈ 10-5, where the Eddington accretion rate is defined as usual, i.e., ṀEdd = LEdd/ 0.1c2 = 4πGMBHmpc/ (σTH0.1c2) ≈ 2.2(MBH/ 108M⊙) [M⊙ yr-1]. In Sect. 4, where we discuss the scale-invariant jet models, the parameters MBH and ṁ are varied.

3. Results

Figure 1 presents a schematic diagram of our 3D GRMHD simulations. During the simulations, three regions with various physical conditions are formed near the black hole. In the disk region, located at the equatorial plane of the grid, the plasma is weakly magnetized and turbulent, and it accretes onto the black hole. The jet-spine is the highly magnetized region above the black hole poles where the plasma content is negligible, and force-free conditions prevail. The evacuated jet-spine is surrounded by the jet sheath. Here we find that this general picture does not change with black hole spin.

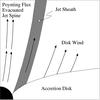thumbnail Fig. 1

Schematic diagram of the geometry and the components of our 3D GRMHD simulations of accretion flow with a jet. Only one hemisphere of the model is shown. The black hole is located in the lower left corner of the plot. The figure is adopted after Hawley & Krolik (2006).

3.1. Structures of jets and their accretion flows

Before presenting the radiative properties of the jets as a function of black hole spin, we first examine some of the properties of the disk, the jet spine, and the jet sheath in models with various black hole spins (models A through F in Table 1).

Figure 2 (top panel) shows the evolution of the mass accretion rate, where the colors distinguish the models with various black hole spins. The accretion rate is calculated using a standard definition, i.e., (1)where ρ0 is the rest mass density, ur is the radial component of the plasma four-velocity, 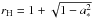is the BH horizon radius, and d 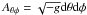is the element of the surface area in the Kerr metric with 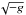being the metric determinant. Evidently, the mass accretion rate (presented in Fig. 2 in arbitrary units) in all models saturates and fluctuates around unity. The accretion rate is variable because of the inhomogeneous structure of the turbulent accretion disk. The accretion rate averaged over later times of the simulation is approximately the same for all black hole spins.

In the BZ model, the power of a black hole jet depends not only on the black hole spin but also on the magnetic field flux accumulated near the black hole horizon, 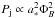. The absolute magnetic field flux that is being accumulated near the black hole horizon as the simulation evolves is computed using 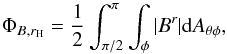(2)where Br is the radial component of the magnetic field vector. Figure 2 (lower panel) shows that, in all models, a similar amount of dimensionless magnetic flux has been accumulated at the black hole horizon, regardless of the black hole spin. Here our purpose is to show that a free parameter of the model ΦB is actually fixed, and so for a constant accretion rate onto the black hole, any eventual differences in the jet power or jet radio luminosity would be due to altering the black hole spin. We note that if we change the accretion rate onto the black hole (by scaling the simulation density), we automatically increase the magnetic field flux at the black hole because the strength of the magnetic field increases. If the mass of the black hole is increased, then the flux near the black hole decreases because we decrease the B-field strength.

thumbnail Fig. 2

Top panel: mass accretion rate onto the black hole as a function of time in models with varying black hole spin. Bottom panel: the poloidal magnetic field flux accumulated near the black hole event horizon as a function of time for various black hole spins. All quantities are shown in dimensionless (code) units.

In our simulations, the jet spine is the evacuated region above the black hole poles and is equivalent to the BZ jet. For a non-rotating black hole, the jet-spine also forms but no energy extraction from the black hole occurs. The electromagnetic power of the jet-spine is defined as 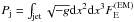, where 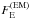is the dimensionless electromagnetic radial energy flux defined as 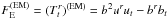. The jet powers, scaled to a system with the fiducial black hole mass MBH = 108M⊙ and accretion rate ṁ = 10-5, are listed in Table 2.

We find that electromagnetic energy is extracted from the black hole for 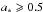, and the jet power increases with the black hole spin according to 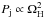(where ΩH(a∗) = a∗/ 2rH and where rH is the radius of the black hole event horizon). These findings are in agreement with the BZ model and with findings from similar simulations by other authors. In our models, the efficiency of the black hole rotational energy extraction, defined as ηj = Pj/Ṁc2 is at most 4%, where Pj and Ṁ are the time-averaged electromagnetic luminosity inside of the evacuated funnel and accretion rate through the black hole horizon, respectively. Typically, the models studied here are called SANE in the current jargon (Standard And Normal Evolution), having low-power jets. For comparison, jets produced in so-called magnetically arrested disks (MADs) are more efficient because, in MADs, ΦB,rH is typically about 10 times larger compared to our values (e.g., Sa¸dowski et al. 2013). Consequently, the energy extraction efficiency in MADs can reach 140% (Tchekhovskoy et al. 2011).

Table 2

Electromagnetic power of the jet-spine Pj as a function of black hole spin a∗.

Next, we present time- and shell-averaged radial profiles of various scalar quantities in the simulations that are important for the radiative transfer calculations since they are used in the synchrotron emissivity and absorptivity functions. The averaging is defined as follows: 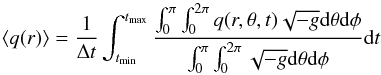(3)where q is a scalar quantity of interest. We time-average the quantities over later times of the simulation when the solutions relax from initial conditions and reach a quasi-stationary state. The integration limits tmin = 6000 GM/c3 and tmax = 7000 GM/c3 are indicated in Fig. 2 as two vertical dashed lines. In Fig. 3, we show the time-averaged radial profiles of plasma density, magnetic field strength and assumed electron temperature (where electron temperature is expressed as Θe = kbTe/mec2). These quantities are shown for the accretion disk region, in the jet sheath and in the jet spine regions.

We first discuss the radial structures of the jet sheath. Examining Fig. 3, it is evident that, in the jet sheath, the plasma density decreases with radius as ρ0 ~ r-2 and the magnetic field strength decreases with distance as B ~ r-1. The same dependence was derived in the simple conical outflows used in analytical modeling of jets in the past. As predicted by Blandford & Königl (1979) and Falcke & Biermann (1995), these jets are expected to produce a nearly flat spectral index in their SEDs when the electron distribution function along the jet is fixed. This is in agreement with our findings here and with Mościbrodzka & Falcke (2013) and Falcke & Markoff (2000). Interestingly, we also find that the density of the jet sheath depends on the black hole spin. This is in agreement with findings by Hawley & Krolik (2006, see their Table 2.) who show that the mass outflow through the jet sheath increases with black hole spin. The spin of the black hole does not affect the radial dependency of the density in the jet-sheath but only the normalization constant. This has interesting implications for the scale-invariant jet models, as discussed in Sect. 4.

Figure 3 also indicates the same radial dependencies of ρ0 and B with radius in the jet spine. However, the mass loading of the jet spine is negligible compared to the jet sheath; hence, most of the visible radiation is generated by the jet sheath. Finally, in the disk the radial dependencies of plasma density and magnetic fields are flatter compared to that in the jet. The electron temperatures in the disk become sub-relativistic beyond 10GM/c2 and so the accretion disk neither emits nor absorbs synchrotron radiation.

thumbnail Fig. 3

Shell- and time-averaged profiles of rest mass density ρ0 (left column), magnetic field strength (middle column), and electron temperature Θe (right column) in the disk (top row), jet sheath (middle row), and jet spine (bottom row) for models with various black hole spins. All quantities are in dimensionless code units. See text (Sect. 3.1) for discussion.

3.2. Radio luminosity of a jet

Throughout this paper, we assume the inclination angle of a jet as i = 60° when calculating its radio emission. Although not shown here, the radio flux computed for a higher inclination angle decreased by a factor of two at most, and vice versa for a lower inclination model. This trend is roughly in agreement with the change in the flux that is due to the relativistic Doppler factor D = Γ-1(1−v/ccos(i))-1 where Γ = 1/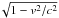, and i is the inclination angle. Hence, for a mildly relativistic jet (v = 0.2−0.5 c), the flux is expected to change by no more than a factor of two.

Figure 4 displays the radio flux emitted by the jet measured at two frequencies by a distant observer as a function of black hole spin. The radio fluxes shown are time-averages of jet radio emission produced within Δt = 1000GM/c3 of the simulation, when the accretion flow and jet are fully relaxed from the initial conditions. For the assumed ṁ ≈ 10-5 and MBH = 108M⊙, the jet synchrotron flux at ν1 = 86 and ν2 = 43 GHz are produced in the optically thick part of the jet base. Two frequencies are shown to demonstrate that the model spectral index α, defined as Fν ~ ν− α, matches the typical observational value of compact, self-absorbed jets. In our models, for all black hole spins, we find α ≈ −0.5, which is often called an inverted spectrum.

Figure 4 (left panel) shows the radio flux densities plotted against the black hole event horizon angular velocity ΩH. Solid and dashed lines in this figure are the parametric fit of the flux density as a function of ΩH. The dependency of the jet radio flux density on ΩH can be described approximately with 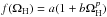. We present the best least square fit values of the free parameters a, b, and p in Table 3. These dependencies are less steep than the BZ jet power dependency on spin: 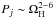. In other words even for a nearly zero spin the jet radio emission persists.

Table 3

Parameters for the best-fit models for the radio flux densities (measured at the frequencies: ν1 = 86 and ν2 = 43 GHz).

In the right panel of Fig. 4, the same jet radio flux densities are plotted against the angular frequency of the inner most stable circular (ISCO) orbit 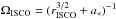(the formula for the angular velocity of a Keplerian disk near a rotating black hole). We found that our disks have similar angular velocities to those of the Keplerian angular velocities. For convenience, the values of ΩISCO are displayed in Table 1. The dependency of the radio flux on ΩISCO can be described by a trivial function of 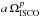. The best fit parameters a and p are summarized in Table 3. The slightly different values of p parameter for different observing frequencies are due to the limited size of our jet which is restricted by the size of out computational grid, and also to the curvature in the spectrum. We argue that the two chosen frequencies bridge the valid range of the model. The observed radio flux is approximately proportional to the Keplerian angular frequency of matter at the ISCO. We argue that the increase in the jet radio flux is a result of a higher mass content of the jet sheath since other relevant variables remain roughly unchanged.

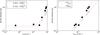thumbnail Fig. 4

Radio flux densities of models plotted as a function of the black hole event horizon angular velocity (left panel), and as a function of the angular velocity of the matter in the disk at the ISCO (right panel). We show the radio flux densities at two frequencies; ν1 = 86 (filled circles) ν2 = 43 (open circles) GHz at which the SEDs are close to flat and optically thick. The flux densities are given in arbitrary units since they depend on the distance to the source that is not specified here. The emission is computed for a fixed mass of the black hole and a fixed accretion rate. The lines show the best fits to the synthetic data points. The best-fit parameters, along with the form of the fitting function, are given in Table 3.

3.3. Mass and energy fluxes carried by the jet

It is interesting to investigate the mass and energy fluxes in the accretion disk and in the two-component jet because the dissipation of energy and radiation in AGN may be also produced by, for example, the jet interacting with the environment of the black hole. It is important to find out whether the mass and energy fluxes depend on the black hole spin and whether the black hole spin could play a role in the black hole feedback.

The radial profiles of mass and total energy flows are defined as 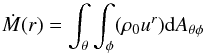(4)and 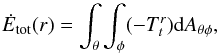(5)where 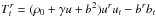is a component of the stress-energy MHD tensor that represents the energy of the plasma and the magnetic field transported in the radial direction, and 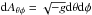is an area element in the θ−φ plane. The symbols in the tensor expression have the following meanings: ρ0 is the plasma rest-mass density, γ is the adiabatic index, u is the specific internal energy of plasma, bμ is the magnetic field four-vector defined in the frame comoving with the plasma, and uμ is the plasma four-velocity. The negative (positive) value of Ṁ and Ėtot indicates inflow (outflow) of the mass/energy from the system. We also calculate the energy flux reduced by the rest mass energy, i.e., 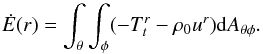(6)Here, Ė is the sum of kinetic, magnetic and thermal energies.

Figure 5 displays Ṁ, Ėtot, and Ė in the disk, jet sheath, and jet spine regions in models A to F. All energy fluxes are given in dimensionless units as used in the numerical code. In the disk region (first row in Fig. 5), the mass is inflowing towards the black hole starting at r ~ 50GM/c2, which corresponds roughly to the pressure maximum of the torus. The massive outflow beyond this radius is caused by the torus wind. Interestingly, the energy in the disk region is positive. This indicates that the energy is removed from the inner parts of the disk. The properties of radial mass and energy fluxes seem independent of the black hole spin, as one would naively expect.

The radial mass and energy fluxes in the jet sheath point outwards and they increase with black hole spin. The mass flux in the jet is dominated by the jet sheath which can expel up to 5% of the mass accreting onto the black hole. In the jet spine, the mass flux is defined by the numerical floor values.

The net mass flux (i.e., integrated over the all angles) is controlled by the accretion disk. However the net energy radial flux points outwards at all radii and the dependency on the black hole spin is evident. Interestingly, both the jet spine and jet sheath contribute to the total energy flux outflow, indicating that both jet components may play some role in the black hole feedback that is then somewhat spin-dependent.

thumbnail Fig. 5

Shell- and time-averaged radial fluxes of mass, total energy, and energy minus rest mass energy (Ṁ, Ėtot, and Ė from left to right, respectively) in the disk, jet sheath, jet spine, and the whole regions for models with various black hole spins.

Finally, we are interested in finding out which component of the energy is dominating the energy in disk, jet sheath, and jet spine regions. Following definitions in McKinney et al. (2012, their Eq. (6)) the radial energy flux Ė(r) can be further split into magnetic (Ėmag), kinetic (Ėkin), and thermal (Ėth) energies. It is straightforward to work out that the radial components of these energy fluxes are

Figure 6 shows that the magnetic, kinetic, and thermal (associated mainly with heavy protons) energies of the three regions in our models. The inner (r< 50GM/c2) accretion disk is dominated by kinetic and thermal energy with weak contribution from magnetic energy. This is expected in weakly magnetized plasma. It is clear that, in the jet sheath, all three energies increase as the black hole spin increases. The energies are roughly in equipartition around r ~ 50GM/c2 and the jet sheath acceleration rate increases with increasing spin. The net magnetic energy of the jet is predominantly within the jet spine. We note that the radiative losses of the jet sheath are comparable to the rotational energy that is being liberated from the black hole in the BZ process that operates in the jet spine. For example, for black hole spin a∗ = 0.94 and fixed ṁ ≈ 10-5 and MBH = 108M⊙, the total luminosity of the system (luminosity integrated over frequencies and averaged over angles) is approximately 6 × 1040 [erg s-1], which is close the BZ power of the jet spine which is 3 × 1040 [erg s-1] (see Table 2).

thumbnail Fig. 6

Shell- and time-averaged radial fluxes of mass, total energy, and energy without rest mass energy included (Ėmag, Ėkin, Ėth from left to right, respectively) in the disk, jet sheath, jet spine, and the whole regions in models with various black hole spins.

4. Scale-invariant jet models

In this section we discuss our results in the context of scale-invariant jet models (Falcke & Biermann 1995; Heinz & Sunyaev 2003). The scale-invariant models were introduced to unify jets physics in black hole systems with various masses and accretion rates, i.e., AGN or X-ray binaries, and to explain the relationship between the black hole mass, radio luminosity, and X-ray luminosity of the object so-called fundamental plane of black holes (Merloni et al. 2003; Falcke et al. 2004). Since our models are fully relativistic, for the first time we can test these analytic models, and inspect the effect of black hole spin for these models. On the other hand, we hoped to constrain more parameters in the GRMHD simulations by comparing them to the fundamental plane of black hole activity and the empirical scaling laws.

The scale-invariant jet model provides a relationship between the observed jet radio flux Fν (where ν is the observing frequency) and the global parameters of the system: the mass of a central black hole MBH, black hole spin (a∗), and the mass accretion rate Ṁ in Eddington units. In the scale-invariant jet model, any dynamically relevant variable f (e.g., plasma density or magnetic field strength) is a product of two decoupled functions: 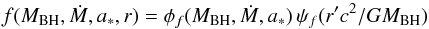(10)where φf describes the dependency of the variable on the central engine mass, accretion rate, and spin and ψf describes the spatial dependency of variable f on the similarity variable r′c2/GMBH, which is simply the distance from the center in units of gravitational radii (that scales with mass of the black hole).

The synchrotron emission from the jet depends on the electron number density ne and the magnetic field strength, B, along the jet. Jets launched by the ADAF models, which are what we effectively have in our numerical simulations, are mechanically cooled jets (by adiabatic decompression), as shown in Fig. 3. Here only φne depends on the black hole spin, while other relevant quantities ψne, φB, and ψB only depend weakly on it. Consequently, our GRMHD simulations produce the following density and magnetic field dependencies: 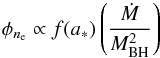(11)and 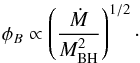(12)Based on our numerical models, we find f(a∗) ~ ΩISCO (Sect. 3.2). The radial dependencies in the jet sheath (Sect. 3.1), as shown in Fig. 3 are:

We find that the above dependencies (except the spin dependency) roughly agree with the conical jet model in Blandford & Königl (1979) or Falcke & Biermann (1995), and with the scale-invariant jet model from ADAFs (Heinz & Sunyaev 2003; Yuan et al. 2002).

We can therefore use the latter model to obtain the general scalings for jet optically thick emission. We plug in our φne, φB, ψne and ψB derived from GRMHD simulations to Eqs. (9), (10), and (12) in Heinz & Sunyaev (2003). This results in similar relationships that are now modified by black hole spin, which enters the radiative transfer integral by scaling the jet particle number density. We find that the jet radio flux (Fν) scales with mass and accretion rate as 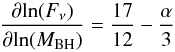(15)and 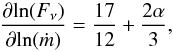(16)where α is the spectral index. Interestingly, because of the logarithmic derivatives, any dependency on the spin cancels out, thus our formulae are identical to those provided by Heinz & Sunyaev (2003). The black hole spin does not affect the scalings of flux with black hole mass and accretion rate but it affects the observed flux (their Eq. (8)) which is also evident in our radiative transfer models (Fig. 4).

Next, we compare the theoretical scalings to the results of fully relativistic radiative transfer calculations. In our radiative transfer simulations, we find that for small changes of ṁ and MBH, Fν ∝ ṁ1.1 and 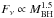(or equivalently Fν ∝ Ṁ1.1 and 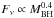) and Fν scalings is independent of the black hole spin. We note that our numerical experiments show that the observed jet radio spectrum in general is not flat (the spectral index α ≠ 0, but rather −0.5). Hence, the numerical dependency on the accretion rate (expressed in dimensionless Eddington units) turn out to be in excellent agreement with Heinz & Sunyaev (2003) prediction 17/12 + 2α/ 3 = 1.08, assuming a spectral slope αν = −0.5, and the dependency on the mass of the black hole 17/12−α/ 3 = 1.58, is also very good. Our value of α ≠ 0 is most probably due to the non-conical shape of the jet near the black hole and the limited extent of the simulation domain.

Finally, the dependency of the flux on the black hole spin parameter is described by the function f(a∗) that enters the radiative transfer integral as a jet density scaling constant. The optically thick part of the radio emission from the jet will simply be proportional to f(a∗).

5. Summary

We have shown that 3D GRMHD simulations of low-luminosity supermassive black holes can reproduce the compact flat-spectrum radio emission for various black hole spins ranging from a∗ ≈ 0.0 to a∗ = 0.98. In our simulations, the visible radio jet is launched from an optically-thin radiatively inefficient accretion flow, and is identified as the plasma outflowing in a thin layer surrounding a pure Poynting flux outflow. In this scenario, the observed radio flux generated by the jet increases with black hole spin. We argue that the increase in the radio flux is caused by more efficient mass loading of the jet sheath. The radio flux detected by the distant observer changes by a factor of less than 10, from a low to a high spin values.

This indeed seems to be a large factor. However, we note that in standard thin disks, the accretion power scales as 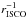, which can vary by a factor of 6 between spinning and non-spinning black holes. This is simply because the matter falls deeper into the potential well and acquires more energy for a smaller ISCO. Hence, the jet radio luminosity normalized to accretion power does not change as a function of spin.

We find that the radio flux scales with the black hole mass and accretion rate are remarkably similar to those found in analytic scale-invariant jet models, in which the spin is a minor factor. This validates some of the basic assumptions of the jet-disk symbiosis and fundamental plane pictures, which require a relatively low scatter between accretion disk luminosities and radio fluxes, or jet powers.

The present model of jet radio emission is not only motivated by observational characteristics of LLAGN, such as flat-to-inverted radio spectra on the self-absorbed side that are typical for astrophysical jets, but also motivated by a couple of other theoretical findings. For example, the jet sheath emission can fit broadband observational data of Sgr A* (e.g., Mościbrodzka et al. 2014; Chan et al. 2015; Gold et al. 2016). We have also recently discussed in detail the application of the bright jet sheath models to model the observations of jet core in M 87 galaxy (see Mościbrodzka et al. 2016), in which the sheath is actually resolved in VLBI observations. In addition, our models of jet emission can be tested in detail using the millimeter and sub-millimeter VLBI observations that will directly image black holes and the surrounding plasma in Sgr A* and M 87 in the near future. The model presented in this work may be applicable to a wide range of black hole jet-disk systems with different masses and accretion rates because we find, essentially, the same scaling laws in our jet-sheath models as in the analytical scale-invariant jet model.

Finally, our model still has a number of uncertainties that may affect the presented results. Neglecting radiative cooling may or may not affect the scaling laws mentioned above as one goes to higher accretion rates. The dependency of radio fluxes may be affected by, for example, relatively low resolution of the numerical grid; our arbitrary definition of the jet and disk zones or initial conditions that are not completely free of spin effects. The most important simplification, however, is the very robust prescription for emitting particles – the Maxwell-Jüttner distribution function that is parametrized with a constant electron temperature. This simplification is also the reason why we have not discussed the high-energy emission from the optically thin parts of the jet. The electrons in jets certainly form a power-law distribution, which has its greatest effect at frequencies higher than radio. The high-energy emission could be entirely dominated by the power-law tail of electrons or inverse-Compton emission produced by the power-law electrons in the jet. If so, the latter could possibly also explain, for example, the observed X-ray/radio correlation in black hole binaries and AGNs (Merloni et al. 2003; Falcke et al. 2004; Plotkin et al. 2012). This should be explored in future studies.

Acknowledgments

We acknowledge support from the ERC Synergy Grant BlackHoleCam – Imaging the Event Horizon of Black Holes (Grant 610058). Authors thank BlackHoleCam collaborators and Ryuichi Kurosawa for comments on the manuscript.

References

  1. Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [NASA ADS] [CrossRef] [Google Scholar]
  2. Blandford, R. D., & Rees, M. J. 1974, MNRAS, 169, 395 [NASA ADS] [CrossRef] [Google Scholar]
  3. Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
  4. Broderick, A. E., & Tchekhovskoy, A. 2015, ApJ, 809, 97 [NASA ADS] [CrossRef] [Google Scholar]
  5. Chan, C.-K., Psaltis, D., Özel, F., Narayan, R., & Saḑowski, A. 2015, ApJ, 799, 1 [NASA ADS] [CrossRef] [Google Scholar]
  6. Dexter, J. 2016, MNRAS, 462, 115 [NASA ADS] [CrossRef] [Google Scholar]
  7. Dibi, S., Drappeau, S., Fragile, P. C., Markoff, S., & Dexter, J. 2012, MNRAS, 426, 1928 [NASA ADS] [CrossRef] [Google Scholar]
  8. Doi, A., Kohno, K., Nakanishi, K., et al. 2013, ApJ, 765, 63 [NASA ADS] [CrossRef] [Google Scholar]
  9. Falcke, H., & Biermann, P. L. 1995, A&A, 293, 665 [NASA ADS] [Google Scholar]
  10. Falcke, H., & Biermann, P. L. 1996, A&A, 308, 321 [NASA ADS] [Google Scholar]
  11. Falcke, H., & Hehl, F. 2002, The Galactic Black Hole (Bristol and Philadelphia: Institute of Physics Publishing, www.iop.org) [Google Scholar]
  12. Falcke, H., & Markoff, S. 2000, A&A, 362, 113 [NASA ADS] [Google Scholar]
  13. Falcke, H., Malkan, M. A., & Biermann, P. L. 1995, A&A, 298, 375 [NASA ADS] [Google Scholar]
  14. Falcke, H., Körding, E., & Markoff, S. 2004, A&A, 414, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Fishbone, L. G., & Moncrief, V. 1976, ApJ, 207, 962 [NASA ADS] [CrossRef] [Google Scholar]
  16. Foucart, F., Chandra, M., Gammie, C. F., & Quataert, E. 2016, MNRAS, 456, 1332 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fraga-Encinas, R., Mościbrodzka, M., Brinkerink, C., & Falcke, H. 2016, A&A, 588, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Gammie, C. F., McKinney, J. C., & Tóth, G. 2003, ApJ, 589, 444 [Google Scholar]
  19. Gold, R., McKinney, J. C., Johnson, M. D., & Doeleman, S. S. 2016, ApJ, submitted [arXiv:1601.05550] [Google Scholar]
  20. Grandi, P., Torresi, E., on behalf of the Fermi-LAT collaboration 2012, 2012 Fermi and Jansky Proceedings − eConf C1111101 [arXiv:1205.1686] [Google Scholar]
  21. Hada, K., Kino, M., Doi, A., et al. 2013, ApJ, 775, 70 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hada, K., Kino, M., Doi, A., et al. 2016, ApJ, 817, 131 [NASA ADS] [CrossRef] [Google Scholar]
  23. Hawley, J. F., & Krolik, J. H. 2006, ApJ, 641, 103 [NASA ADS] [CrossRef] [Google Scholar]
  24. Heinz, S., & Sunyaev, R. A. 2003, MNRAS, 343, L59 [NASA ADS] [CrossRef] [Google Scholar]
  25. Levinson, A., & Rieger, F. 2011, ApJ, 730, 123 [NASA ADS] [CrossRef] [Google Scholar]
  26. Lovelace, R. V. E. 1976, Nature, 262, 649 [NASA ADS] [CrossRef] [Google Scholar]
  27. Markoff, S., Nowak, M., Young, A., et al. 2008, ApJ, 681, 905 [Google Scholar]
  28. Massaro, F., Harris, D. E., Liuzzo, E., et al. 2015, ApJS, 220, 5 [NASA ADS] [CrossRef] [Google Scholar]
  29. McKinney, J. C., & Gammie, C. F. 2004, ApJ, 611, 977 [NASA ADS] [CrossRef] [Google Scholar]
  30. McKinney, J. C., Tchekhovskoy, A., & Blandford, R. D. 2012, MNRAS, 423, 3083 [NASA ADS] [CrossRef] [Google Scholar]
  31. Merloni, A., Heinz, S., & di Matteo, T. 2003, MNRAS, 345, 1057 [NASA ADS] [CrossRef] [Google Scholar]
  32. Misner, C. W., Thorne, K. S., & Wheeler, J. A. 1977, Gravitation (W. H. Freeman and Company) [Google Scholar]
  33. Mościbrodzka, M., & Falcke, H. 2013, A&A, 559, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Mościbrodzka, M., Gammie, C. F., Dolence, J. C., & Shiokawa, H. 2011, ApJ, 735, 9 [NASA ADS] [CrossRef] [Google Scholar]
  35. Mościbrodzka, M., Falcke, H., Shiokawa, H., & Gammie, C. F. 2014, A&A, 570, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Mościbrodzka, M., Falcke, H., & Shiokawa, H. 2016, A&A, 586, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Nagar, N. M., Falcke, H., Wilson, A. S., & Ho, L. C. 2000, ApJ, 542, 186 [NASA ADS] [CrossRef] [Google Scholar]
  38. Nagar, N. M., Falcke, H., & Wilson, A. S. 2005, A&A, 435, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Narayan, R., & McClintock, J. E. 2012, MNRAS, 419, L69 [NASA ADS] [CrossRef] [Google Scholar]
  40. Narayan, R., Mahadevan, R., Grindlay, J. E., Popham, R. G., & Gammie, C. 1998, ApJ, 492, 554 [NASA ADS] [CrossRef] [Google Scholar]
  41. Noble, S. C., Leung, P. K., Gammie, C. F., & Book, L. G. 2007, Class. Quant. Grav., 24, S259 [Google Scholar]
  42. Noble, S. C., Krolik, J. H., & Hawley, J. F. 2009, ApJ, 692, 411 [NASA ADS] [CrossRef] [Google Scholar]
  43. Plotkin, R. M., Markoff, S., Kelly, B. C., Körding, E., & Anderson, S. F. 2012, MNRAS, 419, 267 [NASA ADS] [CrossRef] [Google Scholar]
  44. Rawlings, S., & Saunders, R. 1991, Nature, 349, 138 [NASA ADS] [CrossRef] [Google Scholar]
  45. Ressler, S. M., Tchekhovskoy, A., Quataert, E., Chandra, M., & Gammie, C. F. 2015, MNRAS, 454, 1848 [NASA ADS] [CrossRef] [Google Scholar]
  46. Russell, D. M., Gallo, E., & Fender, R. P. 2013, MNRAS, 431, 405 [NASA ADS] [CrossRef] [Google Scholar]
  47. Sądowski, A., Narayan, R., Penna, R., & Zhu, Y. 2013, MNRAS, 436, 3856 [NASA ADS] [CrossRef] [Google Scholar]
  48. Sikora, M., & Begelman, M. C. 2013, ApJ, 764, L24 [NASA ADS] [CrossRef] [Google Scholar]
  49. Tchekhovskoy, A., Narayan, R., & McKinney, J. C. 2010, ApJ, 711, 50 [NASA ADS] [CrossRef] [Google Scholar]
  50. Tchekhovskoy, A., Narayan, R., & McKinney, J. C. 2011, MNRAS, 418, L79 [NASA ADS] [CrossRef] [Google Scholar]
  51. van Velzen, S., & Falcke, H. 2013, A&A, 557, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Yuan, F., Markoff, S., & Falcke, H. 2002, A&A, 383, 854 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1

GRMHD models of an accreting black hole with a jet and the parameters that describe the numerical grid.

In the text
Table 2

Electromagnetic power of the jet-spine Pj as a function of black hole spin a∗.

In the text
Table 3

Parameters for the best-fit models for the radio flux densities (measured at the frequencies: ν1 = 86 and ν2 = 43 GHz).

In the text

All Figures

thumbnail Fig. 1

Schematic diagram of the geometry and the components of our 3D GRMHD simulations of accretion flow with a jet. Only one hemisphere of the model is shown. The black hole is located in the lower left corner of the plot. The figure is adopted after Hawley & Krolik (2006).
In the text
thumbnail Fig. 2

Top panel: mass accretion rate onto the black hole as a function of time in models with varying black hole spin. Bottom panel: the poloidal magnetic field flux accumulated near the black hole event horizon as a function of time for various black hole spins. All quantities are shown in dimensionless (code) units.
In the text
thumbnail Fig. 3

Shell- and time-averaged profiles of rest mass density ρ0 (left column), magnetic field strength (middle column), and electron temperature Θe (right column) in the disk (top row), jet sheath (middle row), and jet spine (bottom row) for models with various black hole spins. All quantities are in dimensionless code units. See text (Sect. 3.1) for discussion.
In the text
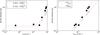thumbnail Fig. 4

Radio flux densities of models plotted as a function of the black hole event horizon angular velocity (left panel), and as a function of the angular velocity of the matter in the disk at the ISCO (right panel). We show the radio flux densities at two frequencies; ν1 = 86 (filled circles) ν2 = 43 (open circles) GHz at which the SEDs are close to flat and optically thick. The flux densities are given in arbitrary units since they depend on the distance to the source that is not specified here. The emission is computed for a fixed mass of the black hole and a fixed accretion rate. The lines show the best fits to the synthetic data points. The best-fit parameters, along with the form of the fitting function, are given in Table 3.
In the text
thumbnail Fig. 5

Shell- and time-averaged radial fluxes of mass, total energy, and energy minus rest mass energy (Ṁ, Ėtot, and Ė from left to right, respectively) in the disk, jet sheath, jet spine, and the whole regions for models with various black hole spins.
In the text
thumbnail Fig. 6

Shell- and time-averaged radial fluxes of mass, total energy, and energy without rest mass energy included (Ėmag, Ėkin, Ėth from left to right, respectively) in the disk, jet sheath, jet spine, and the whole regions in models with various black hole spins.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.