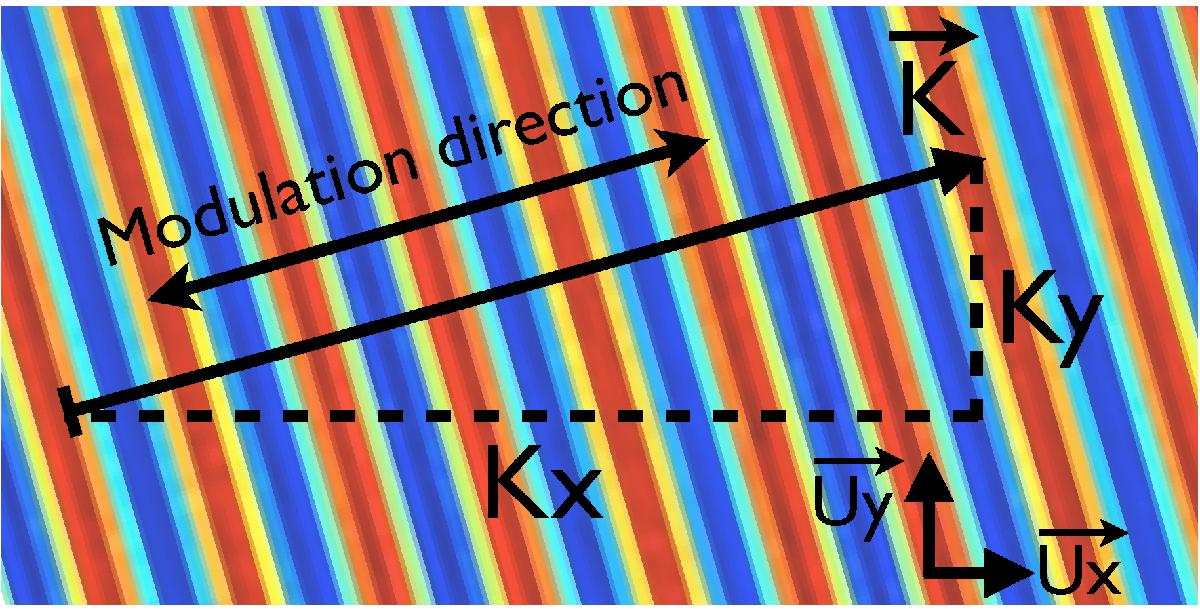
Definition of the wave vector. For a given metrology orientation, the wave vector is defined as K = (K_x(t),K_y(t)), for a plane wave of the form: I(x,y,t) ∝ sin(xK_x(t) + yK_y(t) + φ(t)). The wave vector is by definition perpendicular to the fringes and aligned with the modulation direction, i.e. the apparent motion of the fringes when the phase changes. The default distance unit is the pixel, so the magnitude of the vector is | K | = 2π/λ, with lambda in pixel units.