| Issue |
A&A
Volume 594, October 2016
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527828 | |
| Published online | 13 October 2016 | |
The International Deep Planet Survey
II. The frequency of directly imaged giant exoplanets with stellar mass⋆
1 LESIA, Observatoire de Paris, CNRS,
Université Paris Diderot, Université Pierre et Marie Curie,
5 place Jules Janssen,
92190
Meudon,
France
e-mail: raphael.galicher@obspm.fr
2 Groupement d’Intérêt Scientifique
PHASE (Partenariat Haute résolution Angulaire Sol Espace) between ONERA, Observatoire
de Paris, CNRS and Université Paris Diderot, 75000
Paris,
France
3 National Research Council Canada,
5071 West Saanich Road, Victoria, BC,
V9E 2E7,
Canada
4 Lawrence Livermore National
Laboratory, 7000 East
Ave., Livermore,
CA
94550,
USA
5 Kavli Institute for Particle
Astrophysics and Cosmology, Stanford University, CA
94305,
USA
6 Department of Physics and Astronomy,
University of California, Los
Angeles, CA
90095,
USA
7 Lunar and Planetary Laboratory,
University of Arizona, Tucson
AZ
85721,
USA
8 CASS, University of California San
Diego, La Jolla,
CA
92093-0424,
USA
9 Department of Physics and Astronomy,
University of Georgia, Athens, GA
30602-2451,
USA
10 Arizona State
University, Tempe,
AZ
85281,
USA
11 Département de Physique, Université
de Montréal, C.P.
6128
Succ. Centre-Ville, Montréal,
QC
H3C 3J7,
Canada
12 SETI Institute,
Carl Sagan Center, 189 Bernardo
Avenue, Mountain
View, CA
94043,
USA
Received:
25
November
2016
Accepted:
17
July
2016
Context. Radial velocity and transit methods are effective for the study of short orbital period exoplanets but they hardly probe objects at large separations for which direct imaging can be used.
Aims. We carried out the international deep planet survey of 292 young nearby stars to search for giant exoplanets and determine their frequency.
Methods. We developed a pipeline for a uniform processing of all the data that we have recorded with NIRC2/Keck II, NIRI/Gemini North, NICI/Gemini South, and NACO/VLT for 14 yr. The pipeline first applies cosmetic corrections and then reduces the speckle intensity to enhance the contrast in the images.
Results. The main result of the international deep planet survey is the
discovery of the HR 8799 exoplanets. We also detected 59 visual multiple systems including
16 new binary stars and 2 new triple stellar systems, as well as 2279 point-like sources. We used Monte Carlo
simulations and the Bayesian theorem to determine that 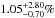 of stars harbor at least one giant planet between
0.5 and 14 MJ and between
20 and 300 AU. This result is obtained assuming
uniform distributions of planet masses and semi-major axes. If we consider power law
distributions as measured for close-in planets instead, the derived frequency is
of stars harbor at least one giant planet between
0.5 and 14 MJ and between
20 and 300 AU. This result is obtained assuming
uniform distributions of planet masses and semi-major axes. If we consider power law
distributions as measured for close-in planets instead, the derived frequency is 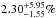 , recalling the strong impact of assumptions on Monte
Carlo output distributions. We also find no evidence that the derived frequency depends on
the mass of the hosting star, whereas it does for close-in planets.
, recalling the strong impact of assumptions on Monte
Carlo output distributions. We also find no evidence that the derived frequency depends on
the mass of the hosting star, whereas it does for close-in planets.
Conclusions. The international deep planet survey provides a database of confirmed background sources that may be useful for other exoplanet direct imaging surveys. It also puts new constraints on the number of stars with at least one giant planet reducing by a factor of two the frequencies derived by almost all previous works.
Key words: planets and satellites: gaseous planets / planets and satellites: fundamental parameters / methods: observational / methods: data analysis / methods: statistical / instrumentation: high angular resolution
Tables 11−15 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/594/A63
© ESO, 2016
1. Introduction
Target list.
After the first discoveries of exoplanets by indirect detections in the late 80s and 90s, several teams performed surveys to obtain direct images of substellar objects in the optical and near-infrared. As the instruments were not optimized for high contrast imaging, the first surveys probed brown dwarfs that are brighter than planets and thus, easier to detect. For example, Becklin & Zuckerman (1988), Schroeder et al. (2000), Gizis et al. (2001), Oppenheimer et al. (2001), and Carson et al. (2009) observed nearby stars, while Neuhäuser & Guenther (2005) and Lowrance et al. (2005) surveyed young systems, and Chauvin et al. (2006) targeted stars harboring planets detected by stellar radial velocity. Taking advantage of new observing modes, such as spectral differential imaging (SDI; Marois et al. 2000) and angular differential imaging (ADI; Marois et al. 2006) and using more powerful adaptive optics systems, later surveys of youthful stars probed fainter and fainter substellar companions down to the young gas-giant extrasolar planet regime (Biller et al. 2007; Kasper et al. 2007; Lafrenière et al. 2007a; Nielsen et al. 2008; Metchev & Hillenbrand 2009; Chauvin et al. 2010; Heinze et al. 2010; Rameau et al. 2013; Yamamoto et al. 2013; Biller et al. 2013; Nielsen et al. 2013; Wahhaj et al. 2013; Brandt et al. 2014).
 |
Fig. 1 IDPS star age, spectral type, and distance distributions. |
For 14 yr, we had been using Keck II, Gemini North and South, and VLT to run two near-infrared imaging surveys: a Keck adaptive optics search for young exoplanets (Kaisler et al. 2003) and the international deep planet survey (IDPS; Marois 2010). In this paper, we merge the two and call IDPS the resulting survey. The targets were 292 young and nearby stars of A to M spectral types with a majority of massive stars. The main objectives of the IDPS were the detection and spectral characterization of new exoplanets, and the determination of the frequency of stars harboring giant planets with long orbital periods.
A first paper (Vigan et al. 2012) presented a fraction of the A stars of the IDPS. In the current paper, we present the complete survey. The target sample is described in Sect. 2. The observations and instruments that we used are presented in Sect. 3. Then, Sect. 4 details the pipeline that we developed for the uniform data processing of the ~30 000 frames. The characteristics of all the detected sources (multistellar systems, exoplanets, and field stars) are listed in Sect. 5. Finally, we run a Monte Carlo analysis in Sect. 6 to constrain the frequency of stars with giant planets.
2. Target sample
As for most of exoplanet direct imaging surveys, the target sample is composed of young and nearby stars (Table 1) with a median age of 120 Myr and a median distance of 45 pc (Fig. 1). The youth ensures that giant planets are bright enough in the near-infrared to be detected assuming evolutionary models like COND and DUSTY (Chabrier et al. 2000; Baraffe et al. 2003). The ages in Table 1 are extracted from previous work (Ref. column) or were derived by our team using the following techniques described in Zuckerman & Song (2004): lithium, X-ray, UV emission, UVW velocity, H-alpha, and color-magnitude diagrams.
All types of main-sequence stars were surveyed with a majority of massive stars: 5, 107, 63, 24, 44, and 49 B, A, F, G, K, M stars. The complete sample is composed of 292 stars.
3. Observations
We obtained near-infrared observations with the adaptive optics systems of Gemini North, Gemini South, Keck II, and VLT. We used public HST data to confirm one of our candidates to be a background object. The observations are described in the following sections and in Table 2. The information about the NACO/VLT observations are gathered in Vigan et al. (2012) and they are not included in this paper although we use the associated detection limits for the statistical study (Sect. 6).
3.1. NIRI at Gemini North
At Gemini North, we observed with the NIRI camera (Hodapp et al. 2003) and the ALTAIR adaptive optics system (Herriot et al. 2000). Data were taken from 2004 to 2014 (programs GN-2007B-Q-59, GN-2008A-Q-77, GN-2008B-Q-64, GN-2009A-Q-80, GN-2009B-Q-17, GN-2011B-Q-11, GN-2012B-Q-14, GN-2012B-Q-70, GN-2013A-Q-34, GN-2013B-Q-16, and GN-2014A-Q-18).
The f/32 camera was used, yielding a 22′′ × 22′′ field of view and 1024 × 1024 pixel images. The spatial sampling is 21.4 mas or 22.0 mas per pixel if the Altair field lens is used (LI in Table 2) or not (LO). The lens improves the off-axis AO correction but induces astrometric distortions (Sect. 4.1). Table 3 gives the specifications of the spectral filters that were used. Images with ~30 s exposure time were recorded in an ADI mode. With NIRI, ADI consists of recording a sequence of many exposures of the target while keeping the instrument rotator off. The camera and the telescope optics thus remain aligned for all exposures, enabling a very accurate point spread function (PSF) correlation between consecutive exposures. Since the field of view rotates when the rotator is off, any off-axis source (companion or background object) moves angularly around the central star with time. For each frame of the sequence, a locally optimized combination of images (LOCI, Lafrenière et al. 2007b; Marois et al. 2010b) produces a reference PSF to subtract. The PSF subtracted frames are then rotated to align north up and they are median combined. Generally, the more the field of view rotates during the sequence, the more efficient the speckle subtraction. Optimal performance is achieved if the observations are acquired as the target is close to the meridian (±1 h from its transit).
During the first observations of each star (apart from 9 that saturated the detector even for the shortest exposure time), unsaturated short exposures were recorded to calibrate the photometry in the ~30 s images. Sometimes, when observing at a second or later epoch, to save time we did not acquire unsaturated images, observe more targets, and follow more exoplanet candidates.
3.2. NIRC2 at Keck II
Most of the IDPS data were obtained with the NIRC2 instrument (McLean & Sprayberry 2003; Wizinowich 2006) at Keck II during ~70 nights or half-nights between 2001 and 2014.
Two observing modes were employed, and both of these modes enabled the use of ADI to subtract the speckle pattern. In the position angle mode (PA in Table 2), north points to the same direction in all frames of a given sequence. The field of view is thus fixed while most of the speckle pattern rotates. One can thus discriminate a fixed off-axis source from the rotating speckle pattern. In the vertical angle mode (V), the pupil rotator is kept off and the field rotates, which is equivalent to the ADI mode used at Gemini. The V mode is usually more effective for speckle calibration, but this mode was not used before 2004 since we were still searching for the best observing strategy at this time.
We sometimes recorded saturated and unsaturated data but usually, we only recorded long exposure sequences using one of the occulting coronagraphic focal plane masks, with diameters of 400, 600, 800, or 1000 mas. The masks are not fully opaque and unsaturated images of the star could be extracted from the long exposures. During the survey, we used several filters that are listed in Table 3.
Most of the data were recorded with the 10′′ × 10′′ narrow field-of-view camera with 9.942 mas/pixels. We also used the 40′′ × 40′′ wide camera with 39.686 mas/pixels (w in Table 2) in peculiar cases to probe planets at more than 10′′ from their star or when the observing conditions where bad.
3.3. NICI at Gemini South
Thirty-four stars were observed with the NICI AO camera (Chun et al. 2008) in 2009, 2012, and 2013 (programs GS-2009B-Q-14, GS-2012B-Q-8, and GS-2013A-Q-24). The camera provided a 18.5′′ × 18.5′′ field of view and a 18 mas plate scale. We recorded 1024 × 1024 pixel images in one or two filters at the same time (Table 3). All data were taken in ADI mode keeping the Cassegrain rotator off (V mode). Sometimes, the SDI mode was also used observing simultaneously at CH4s and CH4l. We always used the F0.32 (320 mas diameter) or F0.65 (650 mas) occulting focal plane masks. As for NIRC2, the occulting masks were not fully opaque and unsaturated images of the star could be extracted from the long exposures.
3.4. NICMOS on HST and other programs
We reduced public data that were not part of the IDPS to obtain a second epoch for some of our candidates. We used NIRI, NICI, NIRC2, NACO, and NICMOS archive data. We list the programs these data come from in Table 2.
4. Image processing
The pipeline we developed for a uniform processing of all the IDPS sequences can be divided into four main steps. First, flat fielding, sky subtraction, bad-pixel and distortion corrections were applied to each frame of a considered sequence (Sect. 4.1). In the second step, all frames were registered within a pixel (Sect. 4.2). The procedures used for these two first steps depended on the instrument and on the sequence (procedures were not the same for registering saturated or unsaturated data for example). The last two steps consisted of obtaining calibrated high contrast images and were common to all the IDPS sequences. In the third step, a LOCI-like algorithm was applied to each sequence to reduce the speckle intensity and provide a final image with high contrast for each target (Sect. 4.3). In cases where the field-of-view rotation was small, north was aligned up in each frame of the sequence and all the frames were stacked, applying no speckle subtracting algorithm. The fourth step calibrated the contrast level in the final images, estimated the astrometry and the photometry of off-axis sources, and gathered the results in a database (Sect. 4.4).
Observation list.
Spectral filter specifications.
4.1. Cosmetic corrections
Considering one IDPS sequence, the first step of our data processing was the selection of the frames. If their quality was degraded because of clouds, high seeing variations, or bad adaptive optics corrections, they were removed from the sequence. When available, a sky frame was subtracted from all frames. In the cases of observations at Lp or Mp-bands, the LOCI background subtraction algorithm presented in Galicher & Marois (2011) was used to subtract the background residuals.
Each frame of the sky-corrected sequence was corrected from flat-fielding using calibration data taken at the telescope. Then, the bad and hot pixels were found from the sky and flat images, and their flux was set to the median value of neighboring pixels of the science image. Sometimes, detectors created a horizontal or vertical stripe pattern in NIRI and NICI images (Fig. 2).
 |
Fig. 2 Stripe pattern induced by detectors in NIRI and NICI images. |
To remove this pattern, we assumed it to be translation invariant. We estimated the stripe intensity and spatial frequency from the 25 first rows for vertical stripes or columns for horizontal stripes and we subtracted the pattern to the rest of the image.
Then, the field distortions were corrected. For the NIRC2 narrow camera images, we used the solution from Yelda et al. (2010) with an accuracy down to ~0.01 pixel (0.5 mas) for static distortion correction. When observing with the wide camera, we applied the Keck routine revised by Cameron1 that corrects for distortions down to a ~4 mas level. For NICI distortions, we used the instrument team solutions that have an accuracy of ~35 mas for 2009 data. To correct for NIRI distortions, we compared NIRI and NIRC2 images of the Trapezium region and we created new distortion maps for images taken with or without the Altair field lens (Fig. 3).
 |
Fig. 3 NIRI distorsion maps for images taken with (top) or without (bottom) the Altair field lens. Arrows indicate the distortions at each position of the detector. For the sake of visibility, we multiplied their length by 10. |
In both cases, the accuracy of the correction is less than a pixel (<21 mas) close to the center of the detector but reaches 2 to 5 pixels (40−100 mas) further than ~4′′ from the center. We did not correct for distortions in NICMOS images and assumed a 1.5 pixel (113 mas) error.
Eventually, we registered all images within ~1 pixels adding zero pixels at the borders of the images to ensure no field-of-view loss when rotating the frames as described in Sect. 4.3.
4.2. Image registration
If images were unsaturated, we used an iterative Gaussian fit procedure to register each frame of the sequence within a fraction of pixel (≲1/50). We used the same procedure to register coronagraphic images since the occulting mask transmissions was partially transmissive and left unsaturated images of the central star on the detector. In NIRC2 and NICI coronagraphic images, the central part of the star image, which was attenuated by the focal plane mask, was slightly shifted with respect to the external part of the star image (i.e., the speckles that were not affected by the focal plane mask). We thus registered all the frames using the deflected central star image and compensated for the bias induced by the mask. Several times during the IDPS, we calibrated the mask deflections at Keck II observing the HD 172649 binary system with the 400, 600, 800, and 1000 mas diameter masks at J, H, and Ks filters.
For NIRI saturated images, we selected the first frame of the sequence and we masked all the pixels but the regions of the spider diffraction pattern. We then found the position that maximized the correlation of the masked image with its 180 deg rotation (spiders are symmetrical). Once the first frame was registered within a pixel, we built a new mask to select the spider diffraction pattern and an annulus where speckles were not saturated and where the detector noise was negligible. We registered all the frames of the sequence maximizing their correlation inside the new mask with the first frame. Sizes of the annulus were sequence dependent.
For NIRC2 saturated images, the procedure was very similar but the centering of the first frame was done by hand (~1 pix error) using the hexagonal diffraction signal as a guide because the spider pattern was not detected.
For NICMOS images, we selected the spider pattern area and found the position that maximized the correlation of the image with its 180 deg rotation.
At this point of the pipeline, all sequences were registered within ≤1 pixel.
4.3. High contrast imaging
For NIRC2 and NIRI data, the speckle pattern was reduced in each frame of the sequence by subtracting an optimized reference image calculated by the SOSIE algorithm (Marois et al. 2010b). To create the reference image, we divided the target image into sections (left in Fig. 4). For each section (blue central region, right in Fig. 4), we selected the frames in the sequence for which the field-of-view rotation would have sufficiently displaced a putative companion (half of the PSF full-width half-maximum, FWHM), and we defined a region (exterior red region) setting a FWHM gap. We found the linear combination of the selected frames that minimized the residual noise in the exterior region.
 |
Fig. 4 SOSIE sections of interest (left and right central blue section) and optimizing region (right exterior red region). |
We then subtracted the linear combination in the section of interest (blue central section). This reduced the speckle intensity because the SOSIE coefficients that are needed to subtract the speckles in the blue region are highly correlated with the SOSIE coefficients that are optimized to subtract the speckles in the red region. The FWHM gap avoids self-subtraction of the planet signal. We tested several geometrical shapes for the sections and found that annuli were a good trade-off between computing time and performance (negligible loss in performance). After subtraction, we derived the north axis from the FITS header keywords for each frame and we rotated all frames to align their field of view with north up. We eventually median combined the frames to enhance the signal-to-noise ratio of putative off-axis sources. In the regions of the image where no reference frames were available to apply the SOSIE algorithm (far from the central star if the telescope was dithered during the sequence or close to the center when the field-of-view rotation was small), we did no speckle subtraction and only median combined the frames.
Intensity attenuation of the PSF behind the NIRC2 and NICI occulting masks.
For sequences taken in PA mode (Sect. 3.2), the pupil rotated between frames rather than the field of view. We rotated each frame to create a sequence with a fixed speckle pattern and a rotating field of view. We then applied our SOSIE algorithm.
When only one spectral filter was used with NICI, we used the same SOSIE algorithm as described before. For images taken at two spectral bands simultaneously, we developed a SOSIE-based algorithm that minimizes the speckle intensity using the spectral images (spectral speckle differential imaging) and the ADI images simultaneously (see also Artigau et al. 2008). This data processing was used only for detection. To avoid the issue of calibration in such ADI/SDI SOSIE images (Maire et al. 2014), we used the ADI SOSIE images (no SDI) to derive the photometry of the candidates and the detection limits.
Usually, NICMOS sequences are composed of only 2−6 frames, which limits the SOSIE performance. To improve the speckle subtraction, we built a NICMOS image database (called IDB) gathering 1012 images that is similar to what Lafrenière et al. (2009) proposed. To reduce the speckle level in one section of one frame, we selected the frames of the same sequence and the 50 most correlated images IDB in this section. Then, we applied the SOSIE algorithm described previously.
As the ADI observing mode was not used before 2004, the SOSIE algorithm could not be applied to a non-negligible number of sequences taken between 2000 and 2004 with NIRC2. For these sequences, we only rotated all the frames to align the north up and we median combined them. We tested a SOSIE algorithm using a library of PSFs taken the same night with the same instrumental configuration (similar to the NICMOS-HST data processing) but no improvement was achieved. The reason is certainly that aberrations vary over the night in a ground-based telescope (pointing, flexures, temperatures, etc.) and thus, the PSF and the speckle pattern evolve over the night.
4.4. Photometry and astrometry calibrations
5σ contrast curves of the IDPS observations.
As for any ADI or SDI technique used for speckle calibration, the astrometry and photometry are biased in the final images. The procedure we used to estimate these biases requires an unsaturated PSF (Galicher et al. 2011). When unsaturated images were available, they were registered following the procedures described in Sect. 4.2 and we median combined them to obtain the needed unsaturated PSF.
In the case of NIRC2 coronagraphic images, we used the attenuated images of the star that were recorded behind the occulting mask. We compensated for the mask transmissions that were calibrated observing binary systems (Sect. 4.2 and Table 4). For the 600 and 800 mas masks at H and Lp, we used images of GJ 803 and HR 8799 taken with and without masks for the calibration.
All the NICI data were recorded with an occulting mask and we also used the attenuated image of the star behind the coronagraph as a reference for photometry. From the NICI documentation, the attenuation of the 0.32 arcsec occulting mask was ~300. We used this value for the CH4 bands as the calibration was performed at CH4l. For the K and H-bands, we used calibrations published in Wahhaj et al. (2011) in which the attenuations were 238 and 191 at H and K, respectively.
For several data sets, saturated and unsaturated sequences were not recorded using the same filters although their central wavelengths and bandwidths were close. We thus considered the median saturated and unsaturated images. We selected an annulus in which the saturated image was not saturated and where the unsaturated image was not dominated by the detector noise. We integrated the flux over the annulus for both images and we determined the factor that gives the photometry in the saturated image from the measured flux in the unsaturated image. We finally obtained an unsaturated PSF that was calibrated in flux with respect to the saturated data. Doing so, we assumed the PSF pattern was similar in the two filters, which was a good approximation as the filter central wavelengths and bandwidths were similar.
When a binary or planet candidate was detected, we used the calibrated unsaturated PSF to estimate its astrometry and photometry (Galicher et al. 2011). First, we roughly estimated the flux and position (within 1 pixel) of the source in the SOSIE image. The pipeline then created a data cube of frames that only contained the unsaturated PSF at the candidate position on the detector accounting for the field-of-view rotation in each frame and for the smearing of off-axis source images as the field of view could rotate during a single exposure. The SOSIE coefficients that were used to obtain the SOSIE image where the candidate was detected were applied on the candidate data cube. The resulting frames were rotated to align north up. The median of these frames provided the estimation of the candidate image in the SOSIE image (Fig. 5).
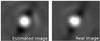 |
Fig. 5 Estimated (left) and real (right) images of an off-axis source. |
We then adjusted the estimated image subpixel position and its flux to minimize the integrated flux of the difference between the real and estimated candidate images. We used a 3 FWHM diameter disk for the minimization. The 1σ error bars were the required excursions in position or in flux to increase the minimum residual flux by a factor of 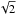 . We empirically determined this factor running tests on sequences in which we injected known fake planets.
. We empirically determined this factor running tests on sequences in which we injected known fake planets.
Using the calibrated unsaturated PSF, we also estimated the SOSIE throughput in all SOSIE sections (central blue section in Fig. 4) following a procedure similar to the one used for the candidate position and flux estimation. The image were thus flux calibrated.
 |
Fig. 6 Typical deep (full line), median (dotted-dashed line), and shallow (dashed line) IDPS 5σ contrast curves against angular separation. Top left: H-band. Top right: CH4-bands. Bottom left: K-band. Bottom right: L-band. |
For every star (IDPS and public data) with unsaturated data, we produced a contrast curve. When off-axis sources were detected in the image, we added a negative object at their position in the raw datacube to remove them from the image and not bias the contrast at their angular separation (Marois et al. 2010a; Galicher et al. 2011). The noise distribution in ADI processed images is well reproduced by a Gaussian function (Marois et al. 2008a) and we estimated the 5σ noise level where σ is the azymuthal standard deviation of the residual flux in annulii of 1 λ/D width rejecting pixels with no flux (out of the field of view). We did not account for the small amount of noise realizations (Mawet et al. 2014) whose impact is negligible at the considered separations. Finally, the 5σ noise levels were divided by the stellar flux estimated from the unsaturated images. Typical contrast curves of the IDPS are plotted in Fig. 6. The shallow curves correspond to the short sequences taken between 2000 and 2004 with NIRC2. The best performance is commonly reached using NIRC2 (after 2004) or NICI. All the IDPS contrast curves are gathered in Table 5.
5. Detections
5.1. Crowded fields
For 5 targets, we detected more than 50 off-axis sources (Table 6). These stars are within 10 deg in latitude from the Galactic plane and the probability that the off-axis sources are background objects is high. Thus, we put a low priority on these stars, and finally, we did not reobserved them.
Targets with crowded field (more than 50 sources).
5.2. Binary and triple systems
During the survey, we detected 59 visual multiple systems with projected separations smaller than 200 AU. Forty of these systems are already known physical binaries and 16 are physical binaries discovered during the IDPS. We also obtained an image of HIP 117452, which is a triple stellar system (De Rosa et al. 2011). Finally, we discovered two triple stars: HIP 104365 (Vigan et al. 2012) and HIP 107948 (Fig. 7). The properties of the binaries (separation, magnitude difference, etc.) are listed in Table 7. We do not derive the stellar type of the companions in this paper.
Binaries detected during the IDPS.
 |
Fig. 7 Multistellar system discovered during the IDPS: HIP 107948. |
5.3. Exoplanet detections
One of the main results of the IDPS is the discovery of the four exoplanets orbiting the HR 8799 star (Marois et al. 2008b, 2010b). We also flagged 2279 point-like objects in the IDPS images, corresponding to ~1100 individual sources detected at 2−3 epochs. We plot in Fig. 8 the contrast and the angular separation with respect to the star for the 1396 IDPS detections whose contrast could be estimated.
 |
Fig. 8 Contrast of 1396 point-like sources detected in the IDPS as a function of their angular separation. |
By observing a given star at multiple epochs and considering proper motions and parallax, we confirmed that most of the detected sources are background objects (Fig. 9).
 |
Fig. 9 Example of the astrometry test for comparing the expected position of a background source (blue and green) to the measured positions (blue and red) for a planet candidate around HIP 12545. Crosses include error bars on the measured astrometry and on the stellar parallax and proper motion. |
Some candidates have not yet been followed up because of very bad weather or technical problems. The characteristics of the 2279 detected sources are reported in Table 8 and are available on a dedicated website2.
6. Occurence of stars with giant planets
The detection limits (Table 5) and the four exoplanet detections of the IDPS can be used to run a Monte Carlo statistical analysis (Sects. 6.2 and 6.3) and calculate an upper limit to the frequency of stars that harbor at least one companion of mass and semimajor axis within given intervals (Sect. 6.4). Moreover, as exoplanets were discovered during the survey, we can put a lower limit on this frequency and we study the impact of the hosting star mass (Sect. 6.5.1). We also study the impact of one of the assumptions that is needed to run the Monte Carlo analysis (Sect. 6.5.2). Finally, we compare our results to previous works (Sect. 6.6).
6.1. Sample
We focus our analysis on single star systems rejecting the binaries (Table 7) from the IDPS sample. We also reject the stars with crowded fields (Sect. 5.1) and the stars for which no contrast curve could be derived from the observations. This leaves 229 stars with a median age of 100 Myr and a median distance of 43 pc (dashed lines in Fig. 10).
To increase the number of stars in the sample and, thus, derive a more accurate frequency of stars with giant planets, we combine the IDPS detection limits and detections to the detection limits of two other surveys: Gemini deep planet survey (Lafrenière et al. 2007a) and a NACO/VLT survey (Chauvin et al. 2010). Thanks to previous collaborations with these teams, we know that our detection limits and theirs are consistent. In future works, it would be interesting to combine all the existing surveys ensuring all the detection limits are consistent but this is out of the scope of our paper.
substellar candidates and background sources observed during the IDPS.
The Lafrenière et al. (2007a) and Chauvin et al. (2010) surveys complete the IDPS because they include more G, K, and M stars (full lines in Fig. 10).
 |
Fig. 10 Distribution of the ages, spectral types, and distances of the IDPS stars with contrast curves (dashed line) and of the sample used for the statistical study (full line). |
The complete sample of 356 stars includes 5, 95, 67, 43, 86, and 60 B, A, F, G, K, M stars. The median age and median distance, which are 100 Myr and 37 pc, are very similar to those of the IDPS. We use this sample in the rest of the paper.
6.2. Formalism and assumptions
The analysis is based on the statistical formalism presented in Lafrenière et al. (2007a). A Monte Carlo simulation is used to create an ensemble of fake planets computing their projected angular separation with respect to their star assuming given distributions of planetary masses and orbital parameters. Then, considering a model of planet atmosphere and the age of the targets, the fake planet fluxes are derived and compared to the detection limits of the survey to determine what fraction of planets should have been detected. Finally, the frequency of stars that harbor at least one exoplanet is derived using the Bayes’ theorem. In this section, we briefly outline the main steps of the analysis specifying the assumptions.
We simulate Npla fake planets for each target star. First, we draw Npla semimajor axis values considering a uniform distribution in the interval [amin,amax]. These values are converted to planet-star separations following the method of Brandeker et al. (2006) and assuming the orbital eccentricity distribution derived by Kipping (2013) from the radial velocity exoplanet sample, which is a Beta distribution with parameters a = 0.867 and b = 3.03. The projected physical separations are converted into angular separations based on the distance of the primary star. Then, we draw Npla masses following a uniform distribution in the interval [mmin,mmax]. Each planet mass is converted into flux in the observing spectral band using the COND03 model (Baraffe et al. 2003) and a random age assuming an asymmetric Gaussian distribution for which the 1σ lower age, 1σ upper age, and average age are given in Table 1. The planet-to-star contrast is then derived from the stellar magnitude. As we compare this contrast to a 1D-contrast curve, we add a random noise to account for the variations of the noise in the 2D-reduced image. The random noise is drawn from a Gaussian distribution of standard deviation that is equal to the noise measured at the separation of the fake planet. Finally, we derive the probability pj of detecting a given planet around the jth star from the fraction of fake planets lying above the 5σ detection limit.
When the star was observed several times, we combine the detection limits (Table 5) taking the deepest contrast at each separation. Doing so, we assume the putative planets do not move in the image from one observation to the others. During the IDPS, the earliest and latest observations of a given star are separated by 3.5 yr in average. Considering the median distance to the stars (~40 pc) and the average minimum angular separation of the observations (0.3′′), the closest detectable planets would have a semimajor axis of 12 AU and, thus, an orbital period of ~30 yr for the massive stars (2 M⊙). The putative planets would then have moved by ~20 pixels in Keck data and 10 pixels in Gemini data between the two observations. Such a motion is small enough so that we can combine the detection limits.
6.3. Exoplanet detection probability
The average of pj over all j values (i.e., over the complete sample) are plotted in Fig. 11 as a function of the projected planet-star separation for planet masses going from 0.5 to 13 Jupiter masses. For each curve, we set the mass of the Npla = 100 000 random planets (mmin = mmax).
 |
Fig. 11 Mean probability of detecting giant planets during the surveys as a function of the projected semimajor axis for several planetary masses. |
The peak sensitivity of the survey occurs for projected separations between 20 and 300 AU. For example, if each star of the sample harbored one 10 MJ at 100 AU, we would have detected 75% of them. The sensitivity declines for separations larger than 200 AU because of the median distance of the targets (37 pc) and the ~10′′ field of view of NIRC2 (the most used instrument during the IDPS).
6.4. Upper limit on the frequency of stars with giant planets
Using the Bayes theorem, the determination of the pj yields a credible interval for the frequency of stars with giant planets under the assumptions made about the planet mass and semimajor axis (uniform distributions), stellar age, and atmosphere model. The boundaries of the interval depend on the level of credibility α that is considered (Eq. (6) in Lafrenière et al. 2007a). For α = 95%, Fig. 12 presents the upper limit on the frequency of stars harboring at least one giant planet as a function of the planet mass and the projected separation.
 |
Fig. 12 Upper limit on the frequency of stars harboring at least one giant planet as a function of the planet mass and projected semimajor axis. |
The large number of targets and the low detection limits of the IDPS, combined with Lafrenière et al. (2007a) and Chauvin et al. (2010) results, enables us to constrain the frequency of stars harboring exoplanets with masses down to 0.5−1 MJ. For example, we find that there are less than 20% of stars harboring one or more 1 MJ exoplanets between 30 and 300 AU; and less than 10% of stars with one or more 2 MJ exoplanets between 30 and 400 AU.
6.5. Frequency of stars with giant planets
Because substellar objects are detected around stars in our sample (Table 9), we can also put a lower limit on the frequency of stars with giant planets following the formalism presented in Lafrenière et al. (2007a, Eq. (6)).
Detected substellar objects in our sample.
When calculating the frequency of stars harboring at least one giant planet within [mmin,mmax] and [amin,amax], only the exoplanets of Table 9, whose mass and separation are included in these intervals are considered detected during the survey. For example, the detected exoplanets for [mmin,mmax] = [0.5,14] MJ and [amin,amax] = [20,300] AU are HR 8799 b, c, d, and HIP 30034 b. Also, even if several of the HR 8799 planets are flagged as detected, the HR 8799 system counts for one detection only, i.e., one star with at least one giant planet.
6.5.1. Mass of the hosting star
Under all the assumptions described in the previous sections, we derive the probability density function of the frequency of stars with at least one giant planet of mass in [mmin,mmax] = [0.5,14] MJ and semimajor axis in [amin,amax] = [20,300] AU (black full line in Fig. 13).
 |
Fig. 13 Probability density function of frequency of stars with at least one giant planet in the given intervals of masses and semimajor axes: [mmin,mmax] = [0.5,14] MJ and [amin,amax] = [20,300] AU. |
The mode of the distribution (i.e., frequency for which the distribution is maximum) is 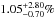 . The error bars give a 95% confidence interval. This means that
. The error bars give a 95% confidence interval. This means that 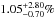 of stars harbors at least one giant planet of 0.5−14 MJ between 20 and 300 AU with a 95% certitude.
of stars harbors at least one giant planet of 0.5−14 MJ between 20 and 300 AU with a 95% certitude.
Surveying exoplanets with orbital periods shorter than four years around stars of 1 to 5 M⊙ (i.e., semimajor axis of <2 AU) and with masses up to 30 MJ, Reffert et al. (2015) found that the frequency of stars with giant planets depends on the stellar mass, reaching a maximum for hosting stars of ~1.9 M⊙. We test this assertion on our sample for stars hosting at least one giant planet between 20 and 300 AU and in the range of 0.5 to 14 MJ. We split our sample into 168 massive stars (B, A, F types, >1.1 M⊙, red dashed line) and 188 low-mass stars (G, K, M-types, <1.1 M⊙, blue mixed line) and we overplot the associated probability density functions in Fig. 13. The mode of the distribution for the massive stars is 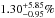 with 95% confidence error bars. For the low-mass stars, we find
with 95% confidence error bars. For the low-mass stars, we find 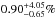 . The two confidence intervals overlap and there is no significant difference at a 95% confidence level between the frequencies of massive and low-mass stars that host an exoplanetary system. We cannot extend the Reffert et al. (2015) result to giant planets orbiting at large separations using our sample.
. The two confidence intervals overlap and there is no significant difference at a 95% confidence level between the frequencies of massive and low-mass stars that host an exoplanetary system. We cannot extend the Reffert et al. (2015) result to giant planets orbiting at large separations using our sample.
6.5.2. Planet mass and semimajor axis distributions
The various assumptions that are made to performed a statistical analysis impact the final results. Although studying each parameter effect is out of the scope of this paper, we tested one effect. Instead of assuming uniform distributions of planet masses and semimajor axes, we now use power laws similar to what was measured for close-in exoplanets by Cumming et al. (2008). Hence, the number dN of simulated exoplanets whose mass is in the interval [m,m + dm] and semimajor axis is in the interval [a,a + da] is proportional to m-1.31a-0.61 dm da. All the other assumptions being the same as before, we obtain that 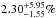 of stars harbor at least one giant planet of 0.5−14 MJ between 20 and 300 AU with a 95% certitude. Thus, changing the assumption on the planet mass and semimajor axis distributions, the derived frequency increases by a factor of ~2: the most probable frequency ranges from 1.05% (uniform distributions, Sect. 6.5.1) to 2.30%, and the 95% interval ranges from [0.35%,3.85%] (uniform distributions) to [0.75%,8.25%]. The two 95% intervals overlap but the impact of the assumed planet mass and semimajor axis distributions is obvious in this case.
of stars harbor at least one giant planet of 0.5−14 MJ between 20 and 300 AU with a 95% certitude. Thus, changing the assumption on the planet mass and semimajor axis distributions, the derived frequency increases by a factor of ~2: the most probable frequency ranges from 1.05% (uniform distributions, Sect. 6.5.1) to 2.30%, and the 95% interval ranges from [0.35%,3.85%] (uniform distributions) to [0.75%,8.25%]. The two 95% intervals overlap but the impact of the assumed planet mass and semimajor axis distributions is obvious in this case.
This result was expected because the power law distributions predict a lot more light and close-in planets than uniform distributions, which are planets the IDPS is less sensitive to. This leads to the open question: which distribution shall we use for the planet mass and semimajor axis? On the one hand, we can argue that the distributions derived by Cumming et al. (2008) come from observations and should be a good a priori. On the other hand, we can wonder whether the formation process is or is not the same for close-in and outer giant planets, and thus, whether the distributions are or are not the same. In any case, future studies are needed to determine the impact of each assumption that is made to derive exoplanet frequencies. In the rest of the current paper, we provide the frequencies for both assumptions on the planet mass and semimajor axis.
6.6. Comparision to other surveys
We compare to previous results the frequencies of stars that harbor at least one giant planet as derived from our sample (Table 10). We use mass and separation intervals as close as possible to those chosen by the other teams and we confirm all results. Having a larger number of stars and deep detection limits, we put stronger constraints reducing the estimated frequencies by a factor of two or more in almost all cases. Also, the difference between the frequencies derived for the two planet mass distributions that we consider (uniform or power laws) is small when we focus on planets more massive than ~1 MJ.
Frequencies of stars harboring at least one giant planet in given intervals of masses and semimajor axes derived from our work and from previous publications.
Whereas each team makes different assumptions, all results are consistent with each other. This is interesting and future works should be done to understand which assumption(s) the derived frequencies mainly depend on.
7. Conclusion
We have completed the IDPS for giant planets around 292 young nearby stars of all spectral types with a majority of massive stars. We developed a pipeline for a uniform processing of the data that have been recorded for 14 yr using several instruments: NIRC2/Keck II, NIRI/Gemini north, NICI/Gemini South, and NACO/VLT. We achieved contrasts of ~12.5 ± 2.5 mag at 1′′ at H, CH4, K and Lp-bands.
We detected a total of 2279 point-like sources. Most of these sources were confirmed to be background objects. Four were confirmed to be exoplanets. They are the now well-characterized HR 8799 planets (Marois et al. 2008b, 2010b). We also discovered 16 stellar binary systems and 2 triple stars.
We used the Bayesian formalism developed in Lafrenière et al. (2007a) to derive the frequency of stars with giant planets from the detection limits of the survey as well as the confirmed exoplanets. To complete the IDPS sample, we combined our results with the Lafrenière et al. (2007a) and Chauvin et al. (2010) surveys that mainly observed low-mass stars (G, K and M stars). The complete sample includes 356 stars of all spectral types with a median age of 100 Myr and a median distance of 37 pc. We determined that 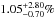 of stars harbor at least one giant planet of 0.5−14 MJ between 20 and 300 AU. We also found no evidence that giant planets at large separations are more likely formed around BAF stars than around GKM stars. We confirm previous results reducing the measured frequencies of stars with at least one giant planet by a factor of two or more in almost all cases. The fact that the results of the different studies are consistent is encouraging, but we should keep in mind that each team uses different assumptions (planet atmosphere models, orbital parameter distributions, star aging, etc.) and one might wonder on which assumption(s) the derived frequencies mainly depend. For example, we showed in this paper that the assumption on the planet mass and semimajor axis distributions can change the conclusions and it will be essential to address this question to prepare the interpretation of the Gemini Planet Imager (Macintosh et al. 2008) and the Spectro-Polarimetric High-contrast Exoplanet REsearch (Beuzit et al. 2008) surveys. Most of their targets are part of the IDPS sample but the extreme adaptive optics systems will probe lighter and closer-to-their-star exoplanets, which will complete our knowledge of giant planets at large separations.
of stars harbor at least one giant planet of 0.5−14 MJ between 20 and 300 AU. We also found no evidence that giant planets at large separations are more likely formed around BAF stars than around GKM stars. We confirm previous results reducing the measured frequencies of stars with at least one giant planet by a factor of two or more in almost all cases. The fact that the results of the different studies are consistent is encouraging, but we should keep in mind that each team uses different assumptions (planet atmosphere models, orbital parameter distributions, star aging, etc.) and one might wonder on which assumption(s) the derived frequencies mainly depend. For example, we showed in this paper that the assumption on the planet mass and semimajor axis distributions can change the conclusions and it will be essential to address this question to prepare the interpretation of the Gemini Planet Imager (Macintosh et al. 2008) and the Spectro-Polarimetric High-contrast Exoplanet REsearch (Beuzit et al. 2008) surveys. Most of their targets are part of the IDPS sample but the extreme adaptive optics systems will probe lighter and closer-to-their-star exoplanets, which will complete our knowledge of giant planets at large separations.
Acknowledgments
The authors acknowledge the referee for constructive comments and suggestions. The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Mauna Kea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this mountain. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France (Wenger et al. 2000). Some of the data presented herein were obtained at the W. M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California, and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W. M. Keck Foundation. This research has made use of the Keck Observatory Archive (KOA), which is operated by the W. M. Keck Observatory and the NASA Exoplanet Science Institute (NExScI), under contract with the National Aeronautics and Space Administration. Based on observations obtained at the Gemini Observatory (acquired through the Gemini Observatory Archive and the Gemini Science Archive), which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (United States), the National Research Council (Canada), CONICYT (Chile), Ministerio de Ciencia, Tecnología e Innovación Productiva (Argentina), and Ministério da Ciência, Tecnologia e Inovação (Brazil).
References
- Argyle, R. W., Alzner, A., & Horch, E. P. 2002, A&A, 384, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Artigau, É., Biller, B. A., Wahhaj, Z., et al. 2008, in SPIE Conf. Ser., 1 [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barrado Y Navascués, D. 2006, A&A, 459, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batalha, C. C., Quast, G. R., Torres, C. A. O., et al. 1998, A&AS, 128, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becklin, E. E., & Zuckerman, B. 1988, Nature, 336, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Bergfors, C., Brandner, W., Janson, M., et al. 2010, A&A, 520, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- Biller, B. A., Close, L. M., Masciadri, E., et al. 2007, ApJSS, 173, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Biller, B. A., Liu, M. C., Wahhaj, Z., et al. 2013, ApJ, 777, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Bowler, B. P., Liu, M. C., Shkolnik, E. L., & Tamura, M. 2015, ApJS, 216, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Brandeker, A., Jayawardhana, R., Khavari, P., Haisch, Jr., K. E., & Mardones, D. 2006, ApJ, 652, 1572 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, T. D., McElwain, M. W., Turner, E. L., et al. 2014, ApJ, 794, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero, J. A. 2010, A&A, 514, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carson, J. C. 2005, Ph.D. Thesis, Cornell University, New York, USA [Google Scholar]
- Carson, J. C., Hiner, K. D., Villar, III, G. G., et al. 2009, AJ, 137, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Udry, S., et al. 2006, A&A, 456, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Bonavita, M., et al. 2010, A&A, 509, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chauvin, G., Vigan, A., Bonnefoy, M., et al. 2015, A&A, 573, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, C. H., Patten, B. M., Werner, M. W., et al. 2005, ApJ, 634, 1372 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C. H., Mittal, T., Kuchner, M., et al. 2014, VizieR Online Data Catalog: J/ApJS/211/25 [Google Scholar]
- Chun, M., Toomey, D., Wahhaj, Z., et al. 2008, in SPIE Conf. Ser., 7015 [Google Scholar]
- Cumming, A., Butler, R. P., Marcy, G. W., et al. 2008, PASP, 120, 531 [CrossRef] [Google Scholar]
- Cvetković, Z., Pavlović, R., Damljanović, G., & Boeva, S. 2011, AJ, 142, 73 [NASA ADS] [CrossRef] [Google Scholar]
- David, T. J., & Hillenbrand, L. A. 2015, ApJ, 804, 146 [NASA ADS] [CrossRef] [Google Scholar]
- De Rosa, R. J., Bulger, J., Patience, J., et al. 2011, MNRAS, 415, 854 [NASA ADS] [CrossRef] [Google Scholar]
- De Rosa, R. J., Patience, J., Vigan, A., et al. 2012, MNRAS, 422, 2765 [NASA ADS] [CrossRef] [Google Scholar]
- De Rosa, R. J., Patience, J., Wilson, P. A., et al. 2014, MNRAS, 437, 1216 [NASA ADS] [CrossRef] [Google Scholar]
- Delfosse, X., Forveille, T., Beuzit, J.-L., et al. 1999, A&A, 344, 897 [NASA ADS] [Google Scholar]
- Desidera, S., Covino, E., Messina, S., et al. 2015, A&A, 573, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Docobo, J. A., Alvarez, C., Lahulla, J. F., Lancharesi, V., & Aguirre, A. 2000, Astron. Nachr., 321, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Dommanget, J., & Nys, O. 2000, A&A, 363, 991 [NASA ADS] [Google Scholar]
- Dommanget, J., & Nys, O. 2002, VizieR Online Data Catalog: I/274 [Google Scholar]
- Eggleton, P. P., & Tokovinin, A. A. 2010, VizieR Online Data Catalog: J/MNRAS/389/869 [Google Scholar]
- Elliott, P., Bayo, A., Melo, C. H. F., et al. 2014, A&A, 568, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elliott, P., Huélamo, N., Bouy, H., et al. 2015, A&A, 580, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabricius, C., & Makarov, V. V. 2000, A&A, 356, 141 [NASA ADS] [Google Scholar]
- Galicher, R., & Marois, C. 2011, in AO4ELT2 Proc., SPIE Conf. Ser., 25 [Google Scholar]
- Galicher, R., Marois, C., Macintosh, B., Barman, T., & Konopacky, Q. 2011, ApJ, 739, L41 [Google Scholar]
- Gizis, J. E., Kirkpatrick, J. D., Burgasser, A., et al. 2001, ApJ, 551, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Hartkopf, W. I., Tokovinin, A., & Mason, B. D. 2012, AJ, 143, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Heinze, A. N., Hinz, P. M., Sivanandam, S., et al. 2010, ApJ, 714, 1551 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández, J., Calvet, N., Hartmann, L., et al. 2005, AJ, 129, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Herriot, G., Morris, S., Anthony, A., et al. 2000, in SPIE Conf. Ser. 4007, ed. P. L. Wizinowich, 115 [Google Scholar]
- Hodapp, K. W., Jensen, J. B., Irwin, E. M., et al. 2003, PASP, 115, 1388 [NASA ADS] [CrossRef] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2009, A&A, 501, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janson, M., Brandner, W., & Henning, T. 2008, A&A, 478, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janson, M., Carson, J. C., Lafrenière, D., et al. 2012, ApJ, 747, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Kaisler, D., Zuckerman, B., & Becklin, B., E. M. 2003, in Scientific Frontiers in Research on Extrasolar Planets, eds. D. Deming, & S. Seager, ASP Conf. Ser., 294, 91 [Google Scholar]
- Kasper, M., Apai, D., Janson, M., & Brandner, W. 2007, A&A, 472, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 434, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, A. L., Shkolnik, E. L., Allers, K. N., & Liu, M. C. 2014, AJ, 147, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Doyon, R., Marois, C., et al. 2007a, ApJ, 670, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Marois, C., Doyon, R., Nadeau, D., & Artigau, É. 2007b, ApJ, 660, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Marois, C., Doyon, R., & Barman, T. 2009, ApJ, 694, L148 [NASA ADS] [CrossRef] [Google Scholar]
- Lowrance, P. J., Becklin, E. E., Schneider, G., et al. 2005, AJ, 130, 1845 [NASA ADS] [CrossRef] [Google Scholar]
- Macintosh, B., Zuckerman, B., Kaisler, D., et al. 2000, BAAS, 32, 1508 [NASA ADS] [Google Scholar]
- Macintosh, B. A., Graham, J. R., Palmer, D. W., et al. 2008, in SPIE Conf. Ser., 7015 [Google Scholar]
- Maire, A.-L., Boccaletti, A., Rameau, J., et al. 2014, A&A, 566, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malo, L., Doyon, R., Lafrenière, D., et al. 2013, ApJ, 762, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Mamajek, E. E. 2012, ApJ, 754, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C. 2010, in In the Spirit of Lyot 2010, Int. Conf., 18 [Google Scholar]
- Marois, C., Doyon, R., Racine, R., & Nadeau, D. 2000, PASP, 112, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Marois, C., Lafrenière, D., Macintosh, B., & Doyon, R. 2008a, ApJ, 673, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Macintosh, B., Barman, T., et al. 2008b, Science, 322, 1348 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marois, C., Macintosh, B., & Véran, J. 2010a, in SPIE Conf. Ser., 7736 [Google Scholar]
- Marois, C., Zuckerman, B., Konopacky, Q. M., Macintosh, B., & Barman, T. 2010b, Nature, 468, 1080 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marshall, J. P., Löhne, T., Montesinos, B., et al. 2011, A&A, 529, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mawet, D., Milli, J., Wahhaj, Z., et al. 2014, ApJ, 792, 97 [NASA ADS] [CrossRef] [Google Scholar]
- McLean, I. S., & Sprayberry, D. 2003, in SPIE Conf. Ser. 4841, eds. M. Iye, & A. F. M. Moorwood, 1 [Google Scholar]
- Melis, C., Zuckerman, B., Rhee, J. H., & Song, I. 2010, ApJ, 717, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Metchev, S. A., & Hillenbrand, L. A. 2009, ApJS, 181, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Moór, A., Ábrahám, P., Derekas, A., et al. 2006, ApJ, 644, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Moór, A., Pascucci, I., Kóspál, Á., et al. 2011, ApJS, 193, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Moór, A., Szabó, G. M., Kiss, L. L., et al. 2013, MNRAS, 435, 1376 [NASA ADS] [CrossRef] [Google Scholar]
- Morales, F. Y., Rieke, G. H., Werner, M. W., et al. 2011, ApJ, 730, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Mugrauer, M., Neuhäuser, R., Guenther, E. W., et al. 2004, A&A, 417, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakajima, T., & Morino, J.-I. 2012, AJ, 143, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Neuhäuser, R., & Guenther, E. W. 2005, in 3th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, eds. F. Favata, G. A. J. Hussain, & B. Battrick, ESA SP, 560, 841 [Google Scholar]
- Nielsen, E. L., & Close, L. M. 2010, ApJ, 717, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Nielsen, E. L., Close, L. M., Biller, B. A., Masciadri, E., & Lenzen, R. 2008, ApJ, 674, 466 [Google Scholar]
- Nielsen, E. L., Liu, M. C., Wahhaj, Z., et al. 2012, ApJ, 750, 53 [Google Scholar]
- Nielsen, E. L., Liu, M. C., Wahhaj, Z., et al. 2013, ApJ, 776, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oppenheimer, B. R., Golimowski, D. A., Kulkarni, S. R., et al. 2001, AJ, 121, 2189 [NASA ADS] [CrossRef] [Google Scholar]
- Paunzen, E. 1997, A&A, 326, L29 [NASA ADS] [Google Scholar]
- Perryman, M. A. C., & ESA, eds. 1997, The Hipparcos and TYCHO catalogues. Astrometric and photometric star catalogues derived from the ESA HIPPARCOS Space Astrometry Mission, eds. M. A. C. Perryman, & ESA, ESA SP, 1200 [Google Scholar]
- Rameau, J., Chauvin, G., Lagrange, A.-M., et al. 2013, A&A, 553, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reffert, S., Bergmann, C., Quirrenbach, A., Trifonov, T., & Künstler, A. 2015, A&A, 574, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rhee, J. H., Song, I., Zuckerman, B., & McElwain, M. 2007, ApJ, 660, 1556 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Rieke, G. H., Su, K. Y. L., Stansberry, J. A., et al. 2005, ApJ, 620, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, D. R., & Zuckerman, B. 2012, ApJ, 745, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, D. R., Zuckerman, B., Kastner, J. H., et al. 2013, ApJ, 774, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Rousseau, J. M., Perie, J. P., & Gachard, M. T. 1996, A&AS, 116, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schroeder, D. J., Golimowski, D. A., Brukardt, R. A., et al. 2000, AJ, 119, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Shkolnik, E. L., Anglada-Escudé, G., Liu, M. C., et al. 2012, ApJ, 758, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Sion, E. M., Holberg, J. B., Oswalt, T. D., McCook, G. P., & Wasatonic, R. 2009, AJ, 138, 1681 [NASA ADS] [CrossRef] [Google Scholar]
- Song, I., Caillault, J.-P., Barrado y Navascués, D., & Stauffer, J. R. 2001, ApJ, 546, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Song, I., Zuckerman, B., & Bessell, M. S. 2003, ApJ, 599, 342 [Google Scholar]
- Song, I., Zuckerman, B., & Bessell, M. S. 2012, AJ, 144, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Tetzlaff, N., Neuhäuser, R., & Hohle, M. M. 2011, MNRAS, 410, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A., Hartung, M., Hayward, T. L., & Makarov, V. V. 2012, AJ, 144, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Turon, C., Creze, M., Egret, D., et al. 1993, Bulletin d’Information du Centre de Données Stellaires, 43, 5 [Google Scholar]
- Vigan, A., Patience, J., Marois, C., et al. 2012, A&A, 544, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wahhaj, Z., Liu, M. C., Biller, B. A., et al. 2011, ApJ, 729, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Wahhaj, Z., Liu, M. C., Nielsen, E. L., et al. 2013, ApJ, 773, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wizinowich, P. L. 2006, in ICO20: Optical Design and Fabrication, eds. J. Breckinridge, & Y. Wang, Proc. SPIE, 6034, 1 [Google Scholar]
- Yamamoto, K., Matsuo, T., Shibai, H., et al. 2013, PASJ, 65, 90 [NASA ADS] [Google Scholar]
- Yelda, S., Lu, J. R., Ghez, A. M., et al. 2010, ApJ, 725, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Monet, D. G., Levine, S. E., et al. 2004, in BAAS, 36, 1418 [Google Scholar]
- Zuckerman, B., & Song, I. 2004, ARA&A, 42, 685 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Zuckerman, B., & Song, I. 2012, ApJ, 758, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Zuckerman, B., Song, I., Bessell, M. S., & Webb, R. A. 2001, ApJ, 562, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Zuckerman, B., Rhee, J. H., Song, I., & Bessell, M. S. 2011, ApJ, 732, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Zuckerman, B., Melis, C., Song, I., et al. 2008, ApJ, 683, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- Zuckerman, B., Vican, L., Song, I., & Schneider, A. 2013, ApJ, 778, 5 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Frequencies of stars harboring at least one giant planet in given intervals of masses and semimajor axes derived from our work and from previous publications.
All Figures
 |
Fig. 1 IDPS star age, spectral type, and distance distributions. |
| In the text | |
 |
Fig. 2 Stripe pattern induced by detectors in NIRI and NICI images. |
| In the text | |
 |
Fig. 3 NIRI distorsion maps for images taken with (top) or without (bottom) the Altair field lens. Arrows indicate the distortions at each position of the detector. For the sake of visibility, we multiplied their length by 10. |
| In the text | |
 |
Fig. 4 SOSIE sections of interest (left and right central blue section) and optimizing region (right exterior red region). |
| In the text | |
 |
Fig. 5 Estimated (left) and real (right) images of an off-axis source. |
| In the text | |
 |
Fig. 6 Typical deep (full line), median (dotted-dashed line), and shallow (dashed line) IDPS 5σ contrast curves against angular separation. Top left: H-band. Top right: CH4-bands. Bottom left: K-band. Bottom right: L-band. |
| In the text | |
 |
Fig. 7 Multistellar system discovered during the IDPS: HIP 107948. |
| In the text | |
 |
Fig. 8 Contrast of 1396 point-like sources detected in the IDPS as a function of their angular separation. |
| In the text | |
 |
Fig. 9 Example of the astrometry test for comparing the expected position of a background source (blue and green) to the measured positions (blue and red) for a planet candidate around HIP 12545. Crosses include error bars on the measured astrometry and on the stellar parallax and proper motion. |
| In the text | |
 |
Fig. 10 Distribution of the ages, spectral types, and distances of the IDPS stars with contrast curves (dashed line) and of the sample used for the statistical study (full line). |
| In the text | |
 |
Fig. 11 Mean probability of detecting giant planets during the surveys as a function of the projected semimajor axis for several planetary masses. |
| In the text | |
 |
Fig. 12 Upper limit on the frequency of stars harboring at least one giant planet as a function of the planet mass and projected semimajor axis. |
| In the text | |
 |
Fig. 13 Probability density function of frequency of stars with at least one giant planet in the given intervals of masses and semimajor axes: [mmin,mmax] = [0.5,14] MJ and [amin,amax] = [20,300] AU. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


