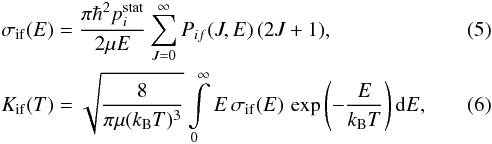© ESO 2016

1. Introduction

Determination of stellar properties, including chemical compositions, from stellar spectra is one of fundamental problems in modern astrophysics (see, e.g., reviews Asplund 2005; Mashonkina 2014; Barklem 2016, and references therein). Non-local thermodynamic equilibrium (non-LTE) modeling of stellar spectra is one of the important tools for such determining of absolute and relative abundances for different chemical elements in stars. For a given atomic species, non-LTE modeling requires detailed and complete information about both the radiative and collision inelastic processes. The most important collisions for non-LTE stellar atmosphere modeling are those with electrons and with hydrogen atoms (Asplund 2005; Mashonkina 2009, 2014; Barklem 2016), as well as their inverse processes involving collisions of positive ions of a treated chemical element with hydrogen negative ions. Information about inelastic processes in collisions with hydrogen gives the main uncertainty for non-LTE studies (Asplund 2005; Mashonkina 2014; Barklem 2016).

Beryllium is a chemical element of interest for stellar atmospheres (Asplund 2005). Galactic evolution of beryllium with non-LTE effects and accuracy of beryllium abundances in metal-poor stars was treated by Garcia Lopez et al. (1995) based on the so-called Drawin formula for inelastic collisions with hydrogen. The most accurate atomic data on inelastic processes in low-energy beryllium-hydrogen collisions would be data calculated by means of full quantum methods, for example, the reprojection method within the framework of the Born-Oppenheimer approach based on ab initio quantum-chemical data. Such full quantum calculations have been recently performed for inelastic processes in collisions of hydrogen with a few chemical elements: helium, lithium, sodium, magnesium (see Belyaev 2015; Barklem 2016; Belyaev et al. 2016, for references). Unfortunately, full quantum calculations are still time-consuming, especially quantum-chemical data. For this reason, approximate approaches are in use. The Drawin formula widely used in the past is not reliable at all (Barklem et al. 2011), so other approximate but reliable approaches should be used. Approximate and physically reliable approaches to treat inelastic collisions of atoms and positive ions of different chemical elements with hydrogen atoms and negative ions have recently been proposed by Belyaev (2013a), Belyaev et al. (2014b) within the framework of the Born-Oppenheimer approach. Since the treated inelastic processes are determined by nonadiabatic transitions, which are quantum by nature, the model approaches are essentially quantum as well. These approaches have been applied to study aluminium (Belyaev 2013b), cesium (Belyaev et al. 2014a), silicon (Belyaev et al. 2014b), and calcium (Belyaev et al. 2016) collisions with hydrogen. The main goal of these approaches is to calculate inelastic rate coefficients with high and moderate values, that is, rates of astrophysical interest, as well as estimate rate coefficients with low values, which are likely to be unimportant. In the present paper, the model quantum approach is applied to low-energy inelastic Be + H and Be⁺ + H⁻ collisions.

It is worth to mention that some adiabatic potentials for several low-lying BeH states have been calculated earlier by ab initio methods by Petsalakis et al. (1992), Pitarch-Ruiz et al. (2008), Roos et al. (2009). Unfortunately, potential energies were not calculated at large internuclear distances, where the main avoided crossings determining inelastic reactions occur. For this reason, Hedberg et al. (2014) calculated the total cross section for the mutual neutralization process Be⁺ + H⁻ → Be^∗ + H based on the model approach, not on ab initio potentials. However, these data are not sufficient for stellar atmosphere modeling: one has to know not only the total cross section for the neutralization process, but also partial cross sections and rate coefficients for all inelastic processes in collisions treated. The present work provides the partial cross sections and rate coefficients for excitation, de-excitation, ion-pair formation and mutual neutralization processes, that is, for all inelastic processes in low-energy beryllium-hydrogen collisions.

2. Model approach

The present study of inelastic processes in beryllium-hydrogen collisions is performed by means of the quantum model approach within the framework of the Born-Oppenheimer formalism (Belyaev 2013a; Belyaev et al. 2014b). The approach is based on the asymptotic method for calculations of adiabatic potentials and on the multichannel Landau-Zener model for computing inelastic transition probabilities. In the first step, adiabatic potentials are obtained using the asymptotic method (Belyaev 2013a). In addition, ab initio potentials for low-lying molecular states can be used, if available. In the second step, state-to-state nonadiabatic transition probabilities should be calculated taking into account the presence of several nonadiabatic regions. At present, this is done by means of the multichannel Landau-Zener model. Since this is the important part of the theoretical treatment, the model is described below in detail.

A nonadiabatic transition probability after a single traverse of a nonadiabatic region is calculated by the adiabatic-potential-based Landau-Zener formula 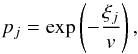${\mathit{p}}_{\mathit{j}}\mathrm{=}\exp \left(\mathrm{-}\frac{{\mathit{\xi }}_{\mathit{j}}}{\mathit{v}}\right)\mathit{,}$(1)where v is the radial velocity in the center of the nonadiabatic region R_C formed by adjacent states j and j + 1 (assuming that state labelling starts from the lowest one), and ξ_j is the Landau-Zener parameter calculated as follows (Belyaev & Lebedev 2011) 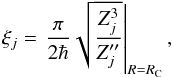${\mathit{\xi }}_{\mathit{j}}\mathrm{=}{\frac{\mathit{\pi }}{\mathrm{2}ħ}\sqrt{\frac{{\mathit{Z}}_{\mathit{j}}^{\mathrm{3}}}{{\mathit{Z}}_{\mathit{j}}^{\mathrm{\prime \prime }}}}|}_{\mathit{R}\mathrm{=}{\mathit{R}}_{\mathrm{C}}}\mathit{,}$(2)Z_j = U_{j + 1} − U_j being the energy splitting between adjacent states (U_j is an adiabatic potential of a molecular state j) and 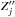${\mathit{Z}}_{\mathit{j}}^{\mathrm{\prime \prime }}$ being the second derivative with respect to the internuclear distance R (see Belyaev & Lebedev 2011, for details).

When one ionic diabatic state interacts with several covalent diabatic states (neglecting covalent-covalent interaction), every pair of adjacent adiabatic states forms only one nonadiabatic region. In this case a series of nonadiabatic regions is passed by a collision system in a particular order and the multichannel formulas (Belyaev & Tserkovnyi 1987; Belyaev 1993; Belyaev & Barklem 2003) to treat mutual neutralization and de-excitation processes are applicable.

However, for de-excitation processes (an initial-state potential asymptote being below the ionic-state one) special care should be taken when collision energy is lower than energy thresholds of higher-lying states. In this case, multiple traverses of nonadiabatic regions can occur due to oscillations in an ionic diabatic potential (see Devdariani & Zagrebin 1984; Belyaev 1985, for a three-channel case). The additional relevant probability can be expressed as a sum of a geometrical progression. The state-to-state inelastic probability P_if for the transition from a given initial state i to a given final state f (f<i) is calculated using the expression $\begin{array}{ccc}{\mathit{P}}_{\mathit{if}}& \mathrm{=}& \mathrm{2}{\mathit{p}}_{\mathit{f}}\mathrm{(}\mathrm{1}\mathrm{-}{\mathit{p}}_{\mathit{f}}\mathrm{)}\mathrm{(}\mathrm{1}\mathrm{-}{\mathit{p}}_{\mathit{i}}\mathrm{)}\left(\underset{\mathit{k}\mathrm{=}\mathit{f}\mathrm{+}\mathrm{1}}{\overset{\mathit{i}\mathrm{-}\mathrm{1}}{\mathrm{􏽙}}}{\mathit{p}}_{\mathit{k}}\right)\\ & & \mathrm{\times }\begin{array}{c}\mathrm{⎧}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎨}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎩}\end{array}\mathrm{1}\mathrm{+}\sum _{\mathit{m}\mathrm{=}\mathrm{1}}^{\mathrm{2}\mathrm{(}\mathit{f}\mathrm{-}\mathrm{1}\mathrm{)}}\underset{\mathit{k}\mathrm{=}\mathrm{1}}{\overset{\mathit{m}}{\mathrm{􏽙}}}\left(\mathrm{-}{\mathit{p}}_{\mathit{f}\mathrm{-}\left[\frac{\mathit{k}\mathrm{+}\mathrm{1}}{\mathrm{2}}\right]}\right)\begin{array}{c}\mathrm{⎫}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎬}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎭}\end{array}\\ & & \mathrm{\times }\begin{array}{c}\mathrm{⎧}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎨}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎩}\end{array}\mathrm{1}\mathrm{-}\frac{\underset{\mathit{k}\mathrm{=}\mathit{i}}{\overset{\mathit{F}}{\mathrm{􏽑}}}{\mathit{p}}_{\mathit{k}}^{\mathrm{2}}\hspace{0.17em}\left\{\mathrm{1}\mathrm{+}\sum _{\mathit{m}\mathrm{=}\mathrm{1}}^{\mathrm{2}\mathrm{(}\mathit{i}\mathrm{-}\mathrm{1}\mathrm{)}}\underset{\mathit{k}\mathrm{=}\mathrm{1}}{\overset{\mathit{m}}{\mathrm{􏽑}}}\left(\mathrm{-}{\mathit{p}}_{\mathit{i}\mathrm{-}\left[\frac{\mathit{k}\mathrm{+}\mathrm{1}}{\mathrm{2}}\right]}\right)\right\}}{\sum _{\mathit{m}\mathrm{=}\mathrm{1}}^{\mathrm{2}\mathit{F}}\underset{\mathit{k}\mathrm{=}\mathrm{1}}{\overset{\mathit{m}}{\mathrm{􏽑}}}\left(\mathrm{-}{\mathit{p}}_{\mathit{F}\mathrm{+}\mathrm{1}\mathrm{-}\left[\frac{\mathit{k}\mathrm{+}\mathrm{1}}{\mathrm{2}}\right]}\right)}\begin{array}{c}\mathrm{⎫}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎬}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎭}\end{array}\mathit{,}\end{array}$(3)where F is the number of energetically open nonadiabatic regions (a region is energetically open when its mean adiabatic potential energy at a center of the region is below the total energy), and square brackets in subscripts denote highest integer values.

The last factor in curly brackets in Eq. (3)leads to the increase of a transition probability when oscillations in the ionic diabatic potential occur. When all channels are energetically open, this factor is equal to unity, and Eq. (3)turns into the multichannel formula for de-excitation processes (Belyaev & Barklem 2003). For the case when the initial channel is ionic, the factor (1 − p_i) is equal to unity since higher-lying covalent states do not create any nonadiabatic regions with the ionic state (since an asymptotic ionic diabatic potential is attractive). In this case, when no oscillation occurs, Eq. (3)turns to the multichannel formula for mutual neutralization processes (Belyaev & Tserkovnyi 1987; Belyaev 1993).

To take tunnelling into account, the probability (1 − p_i) to traverse a nonadiabatic region adiabatically can be multiplied by the tunnelling probability 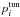${\mathit{p}}_{\mathit{i}}^{\mathrm{tun}}$. In Belyaev (1985) the tunnelling probability was found to have the following form ${\mathit{p}}_{\mathit{i}}^{\mathrm{tun}}\mathrm{=}{\left[\mathrm{1}\mathrm{+}\exp \left(\mathrm{-}\frac{\mathrm{4}\hspace{0.17em}\mathrm{(}\mathit{\mu }{\mathit{v}}_{\mathit{i}}^{\mathrm{2}}\mathrm{+}{\mathit{Z}}_{\mathit{i}}\mathrm{)}\hspace{0.17em}\sqrt{\mathit{\mu }}\hspace{0.17em}{\mathit{\xi }}_{\mathit{i}}}{{\mathit{Z}}_{\mathit{i}}^{\mathrm{3}\mathit{/}\mathrm{2}}}\right)\right]}^{-1}\mathit{,}$(4)μ being the reduced nuclear mass. In the present work, this probability was also taken into account.

Finally, knowing all state-to-state inelastic probabilities P_if for exothermic transitions (f<i), we can determine cross sections and rate coefficients for exothermic inelastic partial processes. Cross sections σ_if(E) and rate coefficients K_if(T) are calculated with the following formulas:

$\begin{array}{ccc}& & {\mathit{\sigma }}_{\mathrm{if}}\mathrm{\left(}\mathit{E}\mathrm{\right)}\mathrm{=}\frac{\mathit{\pi }{ħ}^{\mathrm{2}}{\mathit{p}}_{\mathit{i}}^{\mathrm{stat}}}{\mathrm{2}\mathit{\mu E}}\sum _{\mathit{J}\mathrm{=}\mathrm{0}}^{\mathrm{\infty }}{\mathit{P}}_{\mathit{if}}\mathrm{\left(}\mathit{J,E}\mathrm{\right)}\hspace{0.17em}\mathrm{(}\mathrm{2}\mathit{J}\mathrm{+}\mathrm{1}\mathrm{)}\mathit{,}\\ & & {\mathit{K}}_{\mathrm{if}}\mathrm{\left(}\mathit{T}\mathrm{\right)}\mathrm{=}\sqrt{\frac{\mathrm{8}}{\mathit{\pi \mu }\mathrm{(}{\mathit{k}}_{\mathrm{B}}\mathit{T}{\mathrm{)}}^{\mathrm{3}}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\mathrm{\int }}}\mathit{E}\hspace{0.17em}{\mathit{\sigma }}_{\mathrm{if}}\mathrm{\left(}\mathit{E}\mathrm{\right)}\hspace{0.17em}\exp \left(\mathrm{-}\frac{\mathit{E}}{{\mathit{k}}_{\mathrm{B}}\mathit{T}}\right)\mathrm{d}\mathit{E,}\end{array}$

where E is the collision energy, J the total angular momentum quantum number, T the temperature, 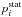${\mathit{p}}_{\mathit{i}}^{\mathrm{stat}}$ the statistical probability for population of the initial channel i, k_B the Boltzmann constant. Cross sections and rate coefficients for endothermic processes are calculated using the detailed balance equations (see, e.g., Belyaev et al. 2014b).

3. Beryllium-hydrogen collision study

In the present model study, one ionic and 13 low-lying covalent states are taken into account. Since the ionic state has the 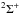${}^{\mathrm{2}}\mathrm{\Sigma }^{\mathrm{+}}$ molecular symmetry, we consider covalent states of the same symmetry only. These states together with the corresponding values of asymptotic energies (in atomic units, a.u.) taken from NIST (Kramida et al. 2012) are listed in Table 1. The adiabatic potentials for these molecular states are calculated by means of the model asymptotic approach described in detail by Belyaev (2013a). The calculated model potentials are plotted in Fig. 1 by solid lines. The same figure shows the ab initio potentials for the ground and first excited states calculated by Pitarch-Ruiz et al. (2008), Roos et al. (2009). As described in the Introduction, the ab initio calculations do not provide enough data to evaluate Landau-Zener parameters for avoided crossings formed by the ionic and higher-lying excited states. For this reason, in the present study of inelastic processes in beryllium-hydrogen collisions, we use the ab initio data only for the nonadiabatic region formed by the ground and first excited states, while the model adiabatic potentials are used for other nonadiabatic regions. As shown by the present nonadiabatic nuclear dynamical calculation and discussed below, the short-range nonadiabatic regions (located at internuclear distances R< 10 atomic units) involving the ground and the first-excited molecular states can affect only cross sections and rate coefficients with negligibly low values, so deviation of the model adiabatic potentials from the ab initio ones (that takes place at short distances, see Fig. 1) is unimportant for the present calculation of the atomic data for non-LTE stellar atmosphere modeling.

Fig. 1 Adiabatic potential energies for the BeH(${}^{\mathrm{2}}\mathrm{\Sigma }^{\mathrm{+}}$) states. Solid lines represent data obtained by the model approach, while symbols stand for the ab initio data taken from Pitarch-Ruiz et al. (2008; crosses) and Roos et al. (2009; circles).

The important issue of the model approach is a calculation of the exchange interaction off-diagonal matrix elements, at present due to the ionic-covalent interaction. In the present study, the great majority of these matrix elements correspond to one-electron transitions between the ionic and covalent states, and hence, they are evaluated by the semi-empirical formula proposed by Olson et al. (1971). However, one molecular state, which is considered in the present study and which asymptotically correlates to the scattering channel Be(2p²¹D) + H, corresponds to a two-electron transition. The Olson-Smith-Bauer formula is not directly applicable for two-electron transition matrix elements. In this case, a more rigorous approach, such as the one described in Belyaev (1993), should be applied. As shown in Belyaev (1993), a two-electron transition matrix element can be expressed through a sum of products of single-electron integrals. This results in the fact that a two-electron transition matrix element can be evaluated by means of the semi-empirical formula of Olson et al. (1971), but some adjustment is needed. In the present study, this adjustment consists of estimating a two-electron transition matrix element as a product of single-electron exchange interaction matrix elements evaluated by the Olson-Smith-Bauer formula and multiplied by the internuclear distance. This two-electron transition off-diagonal matrix element is much smaller than single-electron transition off-diagonal matrix elements and, hence, corresponding cross sections and rate coefficients have lower values.

In the present work, the energy dependence of cross sections and the temperature dependence of rate coefficients for all partial inelastic processes in beryllium-hydrogen collisions between all states listed in Table 1 are calculated. It is found that the highest values for the inelastic cross sections correspond to the mutual neutralization processes. The calculated partial cross sections for the mutual neutralization processes as functions of the collisional energy are shown in Fig. 2.

Fig. 2 Inelastic cross sections for the partial mutual neutralization processes in Be+ + H− collisions.

Other partial mutual neutralization processes, cross sections for which are not plotted in Fig. 2, have smaller cross sections. We can see that the highest values of the mutual neutralization cross sections correspond to the transitions into the Be(2s3s ¹S), Be(2s3p ^1,3P), and Be(2s3d ³D) states as the final states. This finding agrees with the conclusion from Hedberg et al. (2014), though Hedberg et al. (2014) are more in favor of the Be(2s3p ¹P) and Be(2s3d ³D) states than Be(2s3p ^1,3P), see their discussion. We also note the different treatments for the Be(2p²¹D) state, see the discussion above.

The total mutual neutralization cross section calculated in the present work, that is, a sum of all partial mutual neutralization cross sections is in a perfect agreement with that computed by Hedberg et al. (2014). Some deviation in the final state distribution appears due to (i) different formulas for evaluating the exchange interaction matrix elements; (ii) different techniques for computing the Landau-Zener parameters; and (iii) accounting for multiple nonadiabatic regions in a nuclear dynamics (see Eq. (3)for multichannel formulas). Unfortunately, no rate coefficients are published by Hedberg et al. (2014) preventing comparison with the present calculations.

The calculated partial rate coefficients for all processes in beryllium-hydrogen collisions between the states listed in Table 1 are presented in Tables A.1–A.10. The data are also available online at the CDS as supplementary materials to this paper. As an example, the graphical representation of the rate coefficients K_if(T) (in units of cm³/s) for the inelastic processes at T = 6000 K is shown in Fig. 3. The initial and final state labels i and f are defined in Table 1. We see that the highest values of rate coefficients correspond to the mutual neutralization processes Be⁺ + H⁻ → Be(2s3s ¹S) + H(1s ²S), Be(2s3p ^1,3P) + H(1s ²S), Be(2s3d ³D) + H(1s ²S). Figure 4 shows the temperature dependence of the rate coefficients for these processes and for their inverse processes of ion-pair formation from the corresponding covalent states.

Fig. 3 Graphical representation of the rate coefficients Kif(T) (in units of cm3/s) for the inelastic processes in Be + H and Be+ + H− collisions at temperature T = 6000 K. The labels for the initial and the final states are listed in Table 1.

Fig. 4 Temperature dependence of the rate coefficients with the highest values in beryllium-hydrogen collisions.

The inelastic processes in beryllium-hydrogen collisions, as well as the same processes in similar collisions of other chemical elements with hydrogen (see, e.g., Belyaev 2013a; Belyaev et al. 2014b, 2016, and references therein), can be divided into three groups according to their values for inelastic rate coefficients. Analysis of the calculated rate coefficients allows us to define these groups as follows. The first group consists of processes with the highest rate coefficients, typically on an order of magnitude larger than 10^-8 cm³/s. In beryllium-hydrogen collisions, the first group includes the mutual neutralization processes into the atomic states Be(2s3s ¹S), Be(2s3p ^1,3P), Be(2s3d ³D), see Figs. 3 and 4. At T = 6000 K, the highest rate coefficients are equal to 5.1 × 10^-8 cm³/s and 4.5 × 10^-8 cm³/s for the mutual neutralization processes for the final states Be(2s3p ³P) and Be(2s3p ¹P), respectively.

The second group includes processes with moderate values of rate coefficients, typically between 10^-11 and 10^-8 cm³/s. This group consists of the mutual neutralization processes with the final states Be(2s2p ¹P), Be(2s3s ³S), Be(2p²¹D), Be(2s3d ¹D), Be(2s4s ³S), many excitation and de-excitation processes involving atomic states between Be(2s2p ¹P) and Be(2s4s ³S), as well as the ion-pair formation processes involving the states, for which the mutual neutralization processes are included in the first and the second groups. This is the largest group. The mutual neutralization rate coefficients involving the states from the second group as the final states have the values between 10^-10 cm³/ s and 10^-8 cm³/ s. At T = 6000 K, the highest rate coefficient from the second group is equal to 6.5 × 10^-9 cm³/s for the mutual neutralization process for the final state Be(2s3s ³S). Usually, the rate coefficients for the excitation and de-excitation processes are smaller by at least an order of magnitude than the corresponding values for the mutual neutralization processes. At the same temperature of 6000 K, the highest value among all rate coefficients for the excitation and de-excitation processes is equal to 4.0 × 10^-9 cm³/s for the de-excitation process Be(2s3s ¹S) + H → Be(2s3s ³S) + H, which is more than an order of magnitude smaller than the maximum value for the mutual neutralization rate coefficients from the first group.

The processes from the first and the second groups are likely to be important for non-LTE modeling. As shown in the previous model studies (see, e.g., Belyaev 2013a; Belyaev et al. 2014b, 2016, and references therein) and confirmed by the present calculations, the model quantum approach provides reliable data for rate coefficients with high and moderate values, that is, for the processes from the first and the second groups. This is the main goal of the present study.

The third group consists of processes with low rate coefficients, typically lower than 10^-11 cm³/s. In the present case, this group includes the processes involving the two lowest atomic states (that is, the ground state Be(2s²¹S), the channel j = 1, and the first excited state Be(2s2p ³P), the channel j = 2), as well as the high-lying excited states starting from the state Be(2s4s ¹S), the channels j ≥ 12, but ionic. Since the processes from this group have negligibly low values for rate coefficients, the processes from the third group are likely to be unimportant for non-LTE modeling.

4. Conclusion

The atomic data for inelastic processes in low-energy beryllium-hydrogen collisions are calculated by means of the quantum model approach. These data include the energy dependence of the cross sections and the temperature dependence of the rate coefficients for inelastic processes in Be + H and Be⁺ + H⁻ collisions for all transitions between 13 low-lying covalent states plus the ionic state. It is shown that the highest rate coefficients, with values up to 5.1 × 10^-8 cm³/ s at T = 6000 K, correspond to the mutual neutralization processes (in Be⁺ + H⁻ collisions) involving the states Be(2s3s ¹S), Be(2s3p ^1,3P) and Be(2s3d ³D) as the final states. The next group with the second highest rate coefficients, with values up to 6.5 × 10^-9 cm³/ s at T = 6000 K, includes the excitation, de-excitation, ion-pair formation and mutual neutralization processes involving the states between Be(2s2p ¹P) and Be(2s4s ³S), except for the processes included into the first group. The processes from the first and second groups are characterized by rate coefficients with high and moderate values and are likely to be important for non-LTE stellar atmosphere modeling. The processes that involve the ground and first excited states of beryllium, as well the high-lying states starting from the state Be(2s4s ¹S), have negligible rate coefficients and are expected to be unimportant for astrophysical applications. The present data provide a reliable

basis for non-LTE stellar atmosphere modeling of the beryllium spectrum.

Acknowledgments

Authors gratefully acknowledge partial support from the Ministry for Education and Science (Russian Federation). S.A.Y. and A.K.B. gratefully acknowledge partial support from the Max-Planck Institute for Astrophysics (Garching). S.A.Y. also gratefully acknowledges partial support from the Dynasty Foundation (Russian Federation).

References

Appendix A: Additional tables

All Tables

All Figures

	Fig. 1 Adiabatic potential energies for the BeH(${}^{\mathrm{2}}\mathrm{\Sigma }^{\mathrm{+}}$) states. Solid lines represent data obtained by the model approach, while symbols stand for the ab initio data taken from Pitarch-Ruiz et al. (2008; crosses) and Roos et al. (2009; circles).
In the text

	Fig. 2 Inelastic cross sections for the partial mutual neutralization processes in Be+ + H− collisions.
In the text

	Fig. 3 Graphical representation of the rate coefficients Kif(T) (in units of cm3/s) for the inelastic processes in Be + H and Be+ + H− collisions at temperature T = 6000 K. The labels for the initial and the final states are listed in Table 1.
In the text

	Fig. 4 Temperature dependence of the rate coefficients with the highest values in beryllium-hydrogen collisions.
In the text