| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 4 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201628444 | |
| Published online | 03 August 2016 | |
Research Note
Some physical properties predicted for the putative Planet Nine of the solar system
MTA CSFK Konkoly Observatory, Konkoly Thege M. ut 15–17, 1121 Budapest, Hungary
e-mail: tothi@konkoly.hu
Received: 7 March 2016
Accepted: 12 June 2016
Context. Nothing is known as yet about the physical properties of the putative Planet Nine (P9), which is hypothesized to orbit at the fringes of the solar system. Two groups of observers are using the eight-meter Subaru telescope to search for P9. Early estimates and predictions are important to characterize this hypothetic planet. We here predict some properties to compare them with the observed physical properties when Planet Nine has been unambiguously detected comparisons between the predicted and observed physical properties.
Aims. We estimate the size, apparent observable brightness, shortest rotation period, and extension of the stable orbital region of possible satellites of P9.
Methods. Using the predicted mass and adopting a possible mean bulk density range of P9, we computed its radius and assumed a domain for its geometric albedo. We then determined the apparent magnitude along its elliptic orbit. By testing different plausible physical models of a sub-Neptune class planet, we estimated the regions of stability and destruction versus rotational breakup in the radius–rotational period plane. In this plane the shortest rotational period is constrained by the possible size range of P9 and the separation curves. We applied quantitative measures of the stability domain of possible satellites orbiting P9 to quantify the search region in which to find possible satellite companions of the putative trans-Neptunian giant planet of our solar system.
Results. Its predicted apparent magnitude even near aphelion allows discovering P9 with eight-meter class telescopes. P9 is stable against rotational breakup for stronger material if the period is longer than ~6 h, and for weaker material if the period is longer than ~13 h. The Szebehely stability domain for possible satellites of the hypothetical P9 is very large: for a small satellite it extents to ~1.7 au from the planet, and the longest orbital period of the satellite in this orbit is ~396 yr. For a possible twin planet configuration, the radius of the Szebehely stability domain is 1.3 au and the corresponding orbital period is ~280 yr. A twin planet would be brighter by about 0.25 mag than a single planet.
Key words: Kuiper belt: general / planets and satellites: general / planets and satellites: fundamental parameters / planets and satellites: detection / planets and satellites: interiors / planets and satellites: individual: Planet Nine
© ESO, 2016
1. Introduction
Trujillo & Sheppard (2014) noted that a set of trans-Neptunian objects (TNOs) in the distant solar system exhibits unexplained clustering in orbital elements. From analyzing this orbital grouping, Batygin & Brown (2016) very recently announced theoretical evidence of a giant planet orbiting the Sun on a highly elongated orbit in the outer solar system. They called it Planet Nine (P9 for short). This claim is the strongest yet in the long-lasting search for a hypothetic “Planet X” beyond Neptune, and this recent result is a very solid argument (Hand2016; Witze2016). Currently, two observing teams, Batygin and Brown, and Sheppard and Trujillo, are using the large field of view camera of the eight-meter Subaru telescope to search for P9 (Hand 2016). Little is known about the physical properties of this putative planet, which is hypothesized to orbit at the fringes of the solar system. Early estimates and predictions are important to characterize and search for this planet. We present some properties of the hypothetic P9 here: its possible size, geometric albedo, apparent brightness variations along its orbit, constraints on its rotational period, range of its bulk interior parameters such as mean density and tensile strength, and its stability against rotational breakup due to adventitiously too fast rotation. An extension of the orbital stability domain of its possible satellites is also explored.
2. Size, bulk density, geometric albedo, and brightness of P9
First, it is fundamental to know the size, shape, and albedo of the putative planet and to predict its apparent brightness to schedule any survey search program by optical telescopes. To this end, we constructed the variation in the apparent magnitude of P9 along its elliptic orbit.
Calculations performed by Batygin & Brown (2016) suggested that the putative P9 lies on an elongated orbit that is highly inclined to the plane of ecliptic. The authors estimated that it is on an elliptic orbit with semimajor axis of ap ~ 700 au, eccentricity ep ~ 0.6 and would have to be somewhat more massive than mp = 10m⊕ (m⊕ is the mass of Earth), which means that this the lowest possible mass for P9. This mass is at the upper limit of super-Earth-class planets, but lower than that of Neptune-like planets, hence the hypothetic P9 belongs to the sub-Neptune category of planets. Because it orbits in the trans-Neptunian region of our solar system and belongs to the sub-Neptune class, we assume that the physical properties resemble those of the ice giant Neptune. Assuming that the nominal value of the semimajor axis is 700 au, then the perihelion distance is 280 au and aphelion is at 1120 au, which means that this hypothetic sub-Neptune-class object reaches the inner edge of the Oort cloud (Duncan et al. 1987). With this semimajor axis the orbital period of P9 is 18520 yr.
Since the putative P9 is a sub-Neptune-class mass planet, we can assume that its physical properties are analogous or nearly similar to those of Neptune. Recent models of the interior properties of ice giants constrain their internal chemical composition, state, density, and pressure conditions (Knudson et al.2012; Nettelmann et al.2013; Baraffe et al.2014, and references therein).
The mean bulk densities of the ice giants Uranus are 1270 kg m-3 and 1680 kg m-3 for Neptune (Williams 2007). To cover the possible bulk densities, we considered a wide bulk density range from 800 (atmosphere and mantle regions) to 2500 kg m-3 (rocky-ice core) (cf. Fig. 1 of Guillot1999). The geometric albedos of the ice giants Uranus and Neptune are 0.51 and 0.41, respectively (Williams 2007).
Assuming a spherical body and adopting the estimated mass of P9 and mean bulk density range for ice giants of 800–2500 kg m-3 yields radii in the range of 17866 km to 26120 km.
The relation between the optical cross-section and apparent magnitude of a celestial body observed at heliocentric distance rh (au), geocentric distance Δ (au), and at solar phase angle α (deg) (Russell1916; Jewitt1991) is 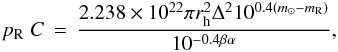 (1)where pR is the red geometric albedo,
(1)where pR is the red geometric albedo, 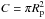 is the optical cross-section of a spherical planet with radius Rp in meters, m⊙ = −27.07 is the R magnitude of the Sun (Hsieh et al.2004 and references therein). mR is the apparent R magnitude of the object, and β is the linear phase coefficient (mag/deg). Here the R magnitude was selected to apply the results for the best sensitivity range of CCD detectors, but of course other optical photometric bands can also be considered. For example, the V band geometric albedo may also be different from that in Rband, but the apparent magnitudes may be taking an assumed (V−R) color into account (e.g., the color of Neptune), hence the object might be slightly brighter in V than in R.
is the optical cross-section of a spherical planet with radius Rp in meters, m⊙ = −27.07 is the R magnitude of the Sun (Hsieh et al.2004 and references therein). mR is the apparent R magnitude of the object, and β is the linear phase coefficient (mag/deg). Here the R magnitude was selected to apply the results for the best sensitivity range of CCD detectors, but of course other optical photometric bands can also be considered. For example, the V band geometric albedo may also be different from that in Rband, but the apparent magnitudes may be taking an assumed (V−R) color into account (e.g., the color of Neptune), hence the object might be slightly brighter in V than in R.
Figure 1 illustrates the heliocentric apparent magnitude variation with the orbital phase of P9 for the extrema of the predicted brightness. Extremal brightnesses come from the following combinations: the brightest case corresponds to the largest size (26120 km in radius) and highest albedo (0.40), and the faintest case corresponds to the smallest size (17 866 km) and lowest albedo. Accordingly, at perihelion, that is, at zero orbital phase, the highest heliocentric brightnesses are 17.17 and 19.49 mag in R band. At aphelion, that is, at orbital phase 0.5, the lowest brightnesses are 23.19 and 25.52 mag in R band. Very recently, Linder & Mordasini (2016) explored the magnitude evolution of candidate P9, and our results agree with their results. Despite its faintness, a search with eight-meter class large ground-based telescopes, for example, with the Subaru telescope, may have a chance to find P9 in the near future. P9 may presumably be found closer than its aphelion according to the allowed zone of location along its orbit (Fienga et al. 2016), and consequently it might be brighter than 23–26 R magnitude.
 |
Fig. 1 Predicted heliocentric apparent R magnitude variation with the orbital phase of the putative P9. The highest brightness is at perihelion (zero orbital phase), and the lowest brightness is at aphelion (0.5 orbital phase). Owing to the very large heliocentric distance of P9, the difference between the opposition geocentric and heliocentric magnitudes is very small: ~0.002 mag. Scaling of the orbital scale: phase = 1 corresponds to one complete orbit around the Sun, which is 18 520 years for a semimajor axis of 700 au. |
3. Stability against rotational breakup
At a critical rotational period (Pcrit), a body is split as a result of the centrifugal force of rapid rotation. It is important to know this allowed shortest rotational period (highest rotational angular velocity), which is constrained by the bulk interior material parameters of P9: size, shape parameter, bulk density, and material strength of the body. To determine the critical rotational period, the key parameters are therfore the tensile strength and bulk density, which can only be estimated by modeling ice giants, which we assume are analogs of P9.
The bulk interior structure and parameters of the outer planets Uranus and Neptune are currently unknown. Their name, ice giants, suggests a composition of predominantly volatiles in ice phase, such as water, methane, and ammonia ice (Cook 1980). Findings by Knudson et al. (2012) showed that a model of highly compressed water can be used as the standard for modeling Neptune and Uranus. The authors applied a scenario of shock compression of water to 700 GPa and 3800 kg m-3 (compressed density), which is relevant to water-rich models of Uranus and Neptune, and the exoplanet GJ436b. We adopted these ranges of internal tensile strength and bulk density for the interior of P9, and this assumption should be used with caution because obviously, we can only assume an analogy between the structures of Neptune and P9.
For the assumption that a solid, homogeneous, rigid, and incompressible body rotates about the axis of its highest moment of inertia (in non-excited rotation mode), models have been developed for the critical rotational periods for spheres (Davidsson 1999) and biaxial ellipsoids: prolate ellipsoids and oblate spheroids (Davidsson 2001). For a simplified model of a major planet, there are obvious limitations to their assumed internal homogenity and constant bulk density and tensile strength. While it is possible to argue that the assumptions for homogeneity, rigidity, shape of failure surfaces, and crack propagation velocities are more or less realistic, no real planet is that simple. We emphasize here that the spherical, solid, homogeneous, rigid, and incompressible body, which is the starting point of most physical models, can too easily be oversimplified (see also Davidsson1999). Even though this analysis is oversimplified, it is suitable to estimate the critical rotational period for P9. The critical period for an oblate spheroid has been derived by Davidsson (2001), and we closely followed this method. For the critical rotation period, the following expression holds in this model: 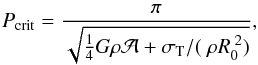 (2)where ρ is the bulk density, σT is the tensile strength, R0 is the effective radius of the body, G is the universal constant of gravity; and with flattening f, the shape parameter
(2)where ρ is the bulk density, σT is the tensile strength, R0 is the effective radius of the body, G is the universal constant of gravity; and with flattening f, the shape parameter 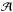 is given by
is given by 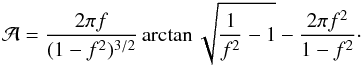 (3)Here we estimated the stability and destruction regions for the oblate spheroid-shaped putative P9 versus rotational breakup in the radius-rotational period plane. By testing different plausible physical models of the Planet-Nine-class sub-Neptune-body equation of state, we show that the plane is divided into two segments: the allowed and forbidden regions. The range of constituent material parameters were adopted from the literature. We then compared the location of Uranus and Neptune with respect to the separation lines. The resulting separation lines and the possible domain of P9 is shown in Fig. 2. For comparison, the loci of Uranus and Neptune are also displayed: these planets are in the stable region of the radius–rotational period plane for all material parameters considered. The shortest critical rotational periods are at the largest tensile strength and bulk density of 100 GPa and 2500 kg m-3: ~6 h. The longest critical rotational periods are at the smallest tensile strength and bulk density of 1 GPa and 800 kg m-3: ~13 h. For the nominal mean bulk density of Neptune, the allowed values of the critical rotational period are between ~7 and ~13 h according to the adopted tensile strength range.
(3)Here we estimated the stability and destruction regions for the oblate spheroid-shaped putative P9 versus rotational breakup in the radius-rotational period plane. By testing different plausible physical models of the Planet-Nine-class sub-Neptune-body equation of state, we show that the plane is divided into two segments: the allowed and forbidden regions. The range of constituent material parameters were adopted from the literature. We then compared the location of Uranus and Neptune with respect to the separation lines. The resulting separation lines and the possible domain of P9 is shown in Fig. 2. For comparison, the loci of Uranus and Neptune are also displayed: these planets are in the stable region of the radius–rotational period plane for all material parameters considered. The shortest critical rotational periods are at the largest tensile strength and bulk density of 100 GPa and 2500 kg m-3: ~6 h. The longest critical rotational periods are at the smallest tensile strength and bulk density of 1 GPa and 800 kg m-3: ~13 h. For the nominal mean bulk density of Neptune, the allowed values of the critical rotational period are between ~7 and ~13 h according to the adopted tensile strength range.
 |
Fig. 2 Stability domains against rotational breakup of P9 shown in the radius-rotational period plane for tensile strengths between 1 and 100 GPa and bulk densities 800 and 2500 kg m-3. Separation lines of 1 GPa (red), 10 GPa (geen), and 100 GPa (green) are indicated. The locations of Uranus (U) and Neptune (N) are also shown for comparison. |
4. Stability domain for possible satellites
Since the hypothetical P9 is a Neptune-class massive planet orbiting the Sun at very large heliocentric distance, hence the solar tidal effect is small, and as a result, the extended orbital stability domain for possible satellites is large. A quantitative measure of stability based on Hill’s definition was evaluated for direct and retrograde satellite orbits (Szebehely1967; Szebehely1978; Hamilton & Burns1991; Hamilton & Krivov1997). The Hill radius RH is the measure of the orbital stability region around the primary body, and it can be computed from the system mass in conjunction with the solar mass and the heliocentric perihelion distance of the planet, according to (e.g., Noll et al.2008) 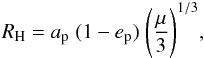 (4)where ap is the semimajor axis, ep is the eccentricity of the elliptical orbit of the primary (P9) orbiting the Sun, and ap(1−ep) is its perihelion distance, μ = mp/m⊙ is the mass-parameter of the system with mass of the primary body mp and the solar mass m⊙ (cf. Szebehely1978, and Eq. (3) of Noll et al.2008).
(4)where ap is the semimajor axis, ep is the eccentricity of the elliptical orbit of the primary (P9) orbiting the Sun, and ap(1−ep) is its perihelion distance, μ = mp/m⊙ is the mass-parameter of the system with mass of the primary body mp and the solar mass m⊙ (cf. Szebehely1978, and Eq. (3) of Noll et al.2008).
However, different criteria of stability limits for satellite motion were compared by Szebehely & McKenzie (1978). The size of the solar-tidal stability region is defined by Szebehely’s stability criterion for satellites on nearly circular orbits (Szebehely1967; Szebehely1978). The lowest result and therefore the most conservative estimate is obtained by the simple formula by Szebehely (1967). It is a critical (highest) value of the satellite’s orbital radius found for stability, and it is a remarkably simple function of the mass parameter μ, 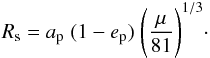 (5)Rs is not the radius of the planetary (primary body) zero velocity Hill oval, but rather Rs = (1 / 3)RH. For objects between Rs and RH instability is possible, objects orbiting outside RH must have unstable orbits. Consequently, the Szebehely stability criterion for a satellite orbit is more conservative, stricter, and safer than Hill’s.
(5)Rs is not the radius of the planetary (primary body) zero velocity Hill oval, but rather Rs = (1 / 3)RH. For objects between Rs and RH instability is possible, objects orbiting outside RH must have unstable orbits. Consequently, the Szebehely stability criterion for a satellite orbit is more conservative, stricter, and safer than Hill’s.
 |
Fig. 3 Orbital period versus semimajor axis (log-log scales) of possible satellites of P9 with two different satellite-to primary- (planet) mass ratios ms/mp: 10-9 for a small satellite and 1 for a possible twin planet system, while the total mass of the system is kept: 10 × Earth masses. The radii of the Hill stability domain (blue dash-dotted vertical lines) and of Szebehely’s domain (red dashed vertical lines) are marked by thin lines for the small satellite case and by thick lines for a possible twin planet case. |
We note that Kavelaars et al. (2004) demonstrated that the size of the search area for satellites (for example based on the Hill criterion) is independent of the distance to the planet (here P9) because the size of a Hill sphere expands with distance from the Sun but the angular search volume does not.
The only information available for the P9 system is the possible lowest mass of the primary (~10 × Earth masses) and the most probable perihelion distance of 280 au (Sect. 2). The mass range of the secondary component of the system can be adopted from the highest and lowest masses of the satellites of Neptune, that is, the satellite-to-planet mass ratios range from 10-9 to ~0.01. In an extreme case, the P9 system might even be in a twin configuration in which the secondary and primary have nearly equal masses, but the total mass of this twin planet system should be ~10 × Earth masses, and consequently, the mass of each component is 5 × Earth masses.
For a global characterization of the possible satellite system of P9, we explored the possible orbital periods within the stability region around the primary. Figure 3 displays the possible orbital periods of the satellites of P9 versus the semimajor axes of their stable orbits. If the mass of the primary is much higher than that of the secondary (case of small satellite), the Hill radius of P9 extends to 5.0 au with an orbital period of 2058 yr and the radius of the Szebehely stability region is 1.7 au with an orbital period of 396 yr. This means that the radius of the more stable region is larger than the semimajor axis of Mars. For a twin planet configuration (case of nearly equal masses) the stability domains are smaller because each has half the mass of the total mass: the Hill radius is 4.0 au with a 1455 yr orbital period, and the radius of the Szebehely stability region is 1.3 au with a 280 yr orbital period. A twin planet configuration would have another consequence: its brightness would be about 26% (0.25 mag) higher than for a single planet. These large extensions are expected because of the Neptune-class mass of P9 and because it is located at the very large heliocentric distance at the inner edge of the Oort cloud. For comparison, the stability domain for the satellites of Neptune is much smaller owing to the smaller perihelion distance of the planet. The Hill radius of Neptune is only 0.26 au and the radius of the Szebehely stability region is 0.10 au. As a consequence of the very long orbital periods of the possible satellites of P9 at the edge of their stability region, their slow apparent motion is as slow as that of the primary itself. This means that the satellites of P9 practically have same apparent motion as the primary.
5. Summary and conclusions
Our recent study of the possible physical characteristics of the hypothetical P9 of the solar system led to the following conclusions:
-
1.
We assumed that the physical properties of the putative P9 are similar to those of Neptune: albedo, mean bulk density, and tensile strength. Based on the bulk density, the radius of P9 ranges between 17866 km and 26120 km, and the heliocentric apparent R magnitude at opposition ranges from ~17 to 25.5 mag.
-
2.
We applied the model of Davidsson (2001) for the rotational stability of oblate spheroids to study the possible location of the putative P9 in the radius–rotational period plane. In doing so, we considered the range of plausible ice giant material strengths and bulk densities as found in the literature for Neptune and similar sub-Neptune class planets. We emphasize here that the solid, homogeneous, rigid, and incompressible body, which is the starting point of most physical models, is oversimplified. We determined a lower limit for the allowed rotational period that keeps the putative P9 in the stable domain against breakup that is due to too fast rotation. The allowed shortest rotational period is 6 h if the tensile strength is 100 GPa, and ~13 h for 1 GPa within the bulk density range adequate for Neptune-class objects.
-
3.
For a small satellite of P9, the Szebehely stability domain is very large: it extends to ~1.7 au from the planet, and the orbital period of the satellite at the edge of this region is 396 yr. For a twin planet configuration the Szebehely stability domain is 1.3 au and the orbital period at the edge of this region is 280 yr. A twin planet would be brighter by 0.25 mag than a single planet.
Acknowledgments
The author thanks the anonymous referee for valuable comments and suggestions.
References
- Baraffe, I., Chabrier, G., Fortney, J., & Sotin, Ch. 2014, Planetary internal structures, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & Th. Henning (Tucson: University of Arizona Press), 763 [Google Scholar]
- Batygin, K., & Brown, M. E. 2016, AJ, 151, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, A. H. 1980, Interiors of the planets – Cambridge Planetary Science Series, eds. W. I. Axford, G. E. Hunt, & T. O. Mutch (Cambridge, UK: Cambridge Univ. Press), 348 [Google Scholar]
- Davidsson, B. J. R. 1999, Icarus, 142, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Davidsson, B. J. R. 2001, Icarus, 149, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, M., Quinn, T., & Tremaine, S. 1987, AJ, 94, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- Fienga, A., Laskar, J., Manche, H., & Gastineau, M. 2016, A&A, 587, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T. 1999, Science, 286, 72 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hamilton, D. P., & Burns, J. A. 1991, Icarus, 92, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Hamilton, D. P., & Krivov, A. V. 1997, Icarus, 128, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Hand, E. 2016, Science, 351, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Hsieh, H. H., Jewitt, D. C., & Fernández, Y. R. 2004, AJ, 127, 2997 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. 1991, in Comets in the Post-Halley Era, eds. R. L. Newburn Jr., M. Neugebauer, & J. Rahe (Dordrecht: Kluwer), 33 [Google Scholar]
- Kavelaars, J. J., Holman, M. J., Grav, T., et al. 2004, Icarus, 169, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Knudson, M. D., Desjarlais, M. P., Lemke, R. W., et al. 2012, Phys. Rev. Lett., 108, 4 [CrossRef] [Google Scholar]
- Linder, E. F., & Mordasini, Ch. 2016, A&A, 589, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nettelmann, N., Helled, R., Fortney, J. J., & Redmer, R. 2013, Planet. Space Sci., 77, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Noll, K. S., Grundy, W. M., Chiang, E. I., Margot, J.-L., & Kern, S. D. 2008, The Solar System Beyond Neptune, eds. M. A. Barucci, H. Boehnhardt, D. P. Cruikshank, & A. Morbidelli (Tucson, AZ: Univ. of Arizona Press), 345 [Google Scholar]
- Russell, N. 1916, ApJ, 43, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Szebehely, V. 1967, Theory of orbits, The restricted problem of three bodies (New York, London: Academic Press) [Google Scholar]
- Szebehely, V. 1978, Cel. Mech., 18, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Szebehely, V., & McKenzie, R. 1978, Cel. Mech., 18, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, Ch. A., & Sheppard, S. S. 2014, Nature, 507, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, D. R. 2007, Planetary Fact Sheets, NASA NSSDC GSFC [Google Scholar]
- Witze, A. 2016, Nature, 529, 266 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Predicted heliocentric apparent R magnitude variation with the orbital phase of the putative P9. The highest brightness is at perihelion (zero orbital phase), and the lowest brightness is at aphelion (0.5 orbital phase). Owing to the very large heliocentric distance of P9, the difference between the opposition geocentric and heliocentric magnitudes is very small: ~0.002 mag. Scaling of the orbital scale: phase = 1 corresponds to one complete orbit around the Sun, which is 18 520 years for a semimajor axis of 700 au. |
| In the text | |
 |
Fig. 2 Stability domains against rotational breakup of P9 shown in the radius-rotational period plane for tensile strengths between 1 and 100 GPa and bulk densities 800 and 2500 kg m-3. Separation lines of 1 GPa (red), 10 GPa (geen), and 100 GPa (green) are indicated. The locations of Uranus (U) and Neptune (N) are also shown for comparison. |
| In the text | |
 |
Fig. 3 Orbital period versus semimajor axis (log-log scales) of possible satellites of P9 with two different satellite-to primary- (planet) mass ratios ms/mp: 10-9 for a small satellite and 1 for a possible twin planet system, while the total mass of the system is kept: 10 × Earth masses. The radii of the Hill stability domain (blue dash-dotted vertical lines) and of Szebehely’s domain (red dashed vertical lines) are marked by thin lines for the small satellite case and by thick lines for a possible twin planet case. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


