| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201628346 | |
| Published online | 19 July 2016 | |
Magnetic fields in ring galaxies
1 School of Mathematics, University of Manchester, Oxford Road, Manchester M13 9PL, UK
2 Department of Physics, Moscow University, 119992 Moscow, Russia
3 Sternberg Astronomical Institute and Department of Physics, Moscow M.V. Lomonosov State University, Universitetskij pr., 13, 119992 Moscow, Russia
4 Chalmers University of Technology, Dept. of Earth and Space Sciences, Onsala Space Observatory, 439 92 Onsala, Sweden
5 MPI für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
6 IZMIRAN, Troitsk, Moscow Region 142190, Russia
Received: 19 February 2016
Accepted: 28 April 2016
Context. Many galaxies contain magnetic fields supported by galactic dynamo action. The investigation of these magnetic fields can be helpful for understanding galactic evolution; however, nothing definitive is known about magnetic fields in ring galaxies.
Aims. Here we investigate large-scale magnetic fields in a previously unexplored context, namely ring galaxies, and concentrate our efforts on the structures that appear most promising for galactic dynamo action, i.e. outer star-forming rings in visually unbarred galaxies.
Methods. We use tested methods for modelling α−Ω galactic dynamos, taking into account the available observational information concerning ionized interstellar matter in ring galaxies.
Results. Our main result is that dynamo drivers in ring galaxies are strong enough to excite large-scale magnetic fields in the ring galaxies studied. The variety of dynamo driven magnetic configurations in ring galaxies obtained in our modelling is much richer than that found in classical spiral galaxies. In particular, various long-lived transients are possible. An especially interesting case is that of NGC 4513, where the ring counter-rotates with respect to the disc. Strong shear in the region between the disc and the ring is associated with unusually strong dynamo drivers in such counter-rotators. The effect of the strong drivers is found to be unexpectedly moderate. With counter-rotation in the disc, a generic model shows that a steady mixed parity magnetic configuration that is unknown for classical spiral galaxies, may be excited, although we do not specifically model NGC 4513.
Conclusions. We deduce that ring galaxies constitute a morphological class of galaxies in which identification of large-scale magnetic fields from observations of polarized radio emission, as well as dynamo modelling, may be possible. Such studies have the potential to throw additional light on the physical nature of rings, their lifetimes, and evolution.
Key words: dynamo / ISM: magnetic fields / Galaxy: disk / galaxies: magnetic fields / galaxies: spiral
© ESO, 2016
1. Introduction
The interstellar medium of spiral galaxies contains large-scale magnetic fields (of scale comparable with the galactic size) that are believed to be excited by a galactic dynamo that is driven by the joint action of differential rotation and mirror-asymmetric turbulent flows. As we know from observations of several nearby spiral galaxies, such as M 51 and also the Milky Way, this large-scale magnetic field is mainly azimuthal in the disc, with field strength of several μG, i.e. the magnetic energy is close to equipartition with the kinetic energy of turbulent motions; see e.g. Beck (2016). In addition to the large-scale magnetic field, a small-scale component of comparable strength is present in the interstellar medium. At least in the large, isolated spiral galaxy NGC 6946, the large-scale magnetic field is organized in magnetic arms located between the stellar arms. These features are more or less related to predictions of galactic dynamo theory (for a review, see e.g. Beck et al. 1996). There are some attempts (e.g. Arshakian et al. 2009) to follow magnetic field evolution in the context of galactic evolution.
 |
Fig. 1 Examples of lenticular (they have no spiral arms but do have discs) galaxies with outer rings: composite-coloured images from the SDSS survey and image from ultraviolet GALEX survey for NGC 4513. (The NGC 4513 image from the SDSS survey shows the ring with a rather low contrast.) |
Observations and modelling of magnetic fields of barred galaxies, considered as a particular morphological class of galaxies, have been combined with interpretation of the results obtained in the framework of galactic dynamos (Moss et al. 1998a, 2001; Beck et al. 1999). Previous experience with barred galaxies has shown the investigation of magnetic fields in galaxies of particular morphological classes to be fruitful (Beck et al. 2002, 2005; Moss et al. 2007), e.g. specific magnetic structures near bars were identified and interpreted as being important in feeding black holes at galactic centres.
Further studies of investigation of magnetic fields in particular morphological classes of galaxies should include examples of classes that appear to be candidates for future observations of polarized radio emission, which is an important indicator of the presence of large-scale magnetic fields. The aim of this paper is to discuss ring galaxies in this context; however radio polarization detections of these galaxies are scarce.
Ring galaxies were defined as a class of disc galaxies by compiling a list and atlas of galaxies in which the rings were separated from the bright central parts of the galaxies (Vorontsov-Velyaminov 1960). Here it was stated that the rings were “structural elements on the same level as bars, spiral arms, and discs”. The typical radii of the outer galactic rings range between 5 and 25 kpc (Theys & Spiegel 1976) and the width might be as large as a few kpc. Though the rings are certainly stellar structures, they often contain gas and demonstrate some level of star formation. For example, a recent catalogue of ring structures derived from the Spitzer Survey of Stellar Structure in Galaxies (Sheth et al. 2010), ARRAKIS (Comerón et al. 2014), includes outer stellar rings detected in 50–60% of all nearby S0 galaxies (Laurikainen et al. 2011; Comerón et al. 2014). Among those, half of all rings in S0s are seen in the ultraviolet, in the NUV-band being mapped by the GALEX space telescope, and so revealing recent star formation (Kostiuk & Sil’chenko 2015). In early-type (S0) disc galaxies the star formation is mainly organized in large-scale rings (Pogge & Eskridge 1993; Salim et al. 2012), and the neutral-hydrogen distributions are also ring-like (Van Driel & van Woerden 1991). The gas in the outer ultraviolet rings is often ionized by young stars (Ilyina et al. 2014). Van Driel & van Woerden (1991), who traced the rotation of the S0 discs far beyond the centre by observing neutral hydrogen in the rings, noted that the rotation curves in the outer discs were flat and so the rotation was obviously differential. In other words, the interstellar matter in ring galaxies has all the features that drive dynamo action in classical nearby galaxies with magnetic fields. The natural question here is: are the dynamo drivers in ring galaxies strong enough to get self-excitation of magnetic fields? Continuum radio emission, indicative of the presence of magnetic fields, has been detected from a number of ring galaxies, e.g. Ghigo (1980), Jeske (1986), Appleton et al. (1999). There is a possible detection of polarized emission from the polar ring galaxy NGC 660 (Wiegert et al. 2015). Estimates presented below are optimistic enough to suggest that further observational studies of these systems may be justified.
In the framework of our paper, we have to recognize that the physical properties of the interstellar medium in ring galaxies and also the dynamo context of the problem, are much less investigated than the corresponding topics for such galaxies as the Milky Way or several nearby galaxies that are considered to be the site of typical examples of galactic dynamos (but see e.g. Horellou et al. 1995). Their properties are quite diverse. Correspondingly, we are interested here in crude preliminary estimates rather than in detailed modelling. Moreover, among the ring galaxies of diverse origins (see the next section) we can select the cases that are particularly promising for development of a dynamo. Fortunately, rings are often found in the same plane as the main stellar disc component1. This means that we can consider ring galaxies as mainly flat systems and use various simplifications of the general dynamo equations previously developed for spiral galaxies. Additionally, the axisymmetry of the discs of ring galaxies simplifies dynamo studies.
2. Interstellar gas in ring galaxies
There are three distinct mechanisms that have been proposed for the origin of the marked outer ring structures in disc galaxies. The most exotic, and so in practice probably the rarest, is the impact mechanism (Freeman & Vaucouleurs 1974; Lynds & Toomre 1976; Theys & Spiegel 1976; Few & Madore 1986; Appleton & Struck-Marcell 1996; Athanassoula et al. 1997) This mechanism involves the infall of a dwarf satellite or of a high-velocity massive cloud impacting very close to the galactic centre; this suggests that the initial configuration is a strongly inclined, almost radial orbit of the satellite or of the cloud around the host galaxy. Such collisions do not destroy the large-scale stellar disc of the host galaxy, but instead can provoke a compression wave running outwards through the large-scale gaseous (and stellar) disc of the host galaxy. The shock compresses the gas of the galaxy, initially quasi-homogeneously distributed over the whole disc, and the compression becomes sufficient to initiate star formation in a ring. Large spiral galaxies with high gas content appear to be the most favourable for this mechanism to operate.
Another scenario, perhaps more frequent, invokes resonance (Schommer & Sullivan 1976; Athanassoula et al. 1982; Buta 1995; Buta & Combes 1996). The resonance scenario requires violation of axisymmetry of the galactic disc and can occur in the presence of a bar or at least of a slightly oval bulge (Jungwiert & Palous 1996). The triaxial gravitational potential causes radial gas motions so that the gas can accumulate at the inner and outer Lindblad resonances of the non-axisymmetric rigidly rotating pattern.
The third possibility for ring formation involves outer gas accretion (Buta & Combes 1996). We believe that this scenario is probably the most common among early-type discs, namely, among lenticular galaxies which possess outer rings in more than half of all cases (Comerón et al. 2014). Interestingly, the frequency of strong bars diminishes among lenticular galaxies compared to spirals (Laurikainen et al. 2011, 2013), while the frequency of outer rings rises (Comerón et al. 2014).
This implies a rather low probability that the outermost rings in lenticular galaxies are due to resonance. The large proportion of observed gas counter-rotation with respect to the stellar components, especially among the S0s in rarified environments, strongly supports an origin through accretion (Katkov et al. 2015). Some examples of the outer star forming rings in visually unbarred galaxies are shown in Fig. 1. This figure presents a particular class of ring galaxies, those with accreted star forming rings in axisymmetric S0s which are especially suitable to host a dynamo process. The class is however far from being homogeneous. Figure 1 illustrates that the ring galaxies of interest can vary considerably in appearance. This is why we have to consider a variety of possible dynamo effects that might contribute to magnetic field formation in such scenarios and experiment with the dynamo numbers that estimate the strengths of the effects. A particular challenge is that NGC 4513, shown in the first panel of Fig. 1, has a counter-rotating ring. IC 5285, UGC 5936, and UGC 9980 do not demonstrate observable radial gas velocities, thus ruling out a collisional origin for their rings (Ilyina & Sil’chenko 2011; Ilyina et al. 2014; Katkov et al. 2015).
In fact, to discriminate between the origin scenarios for an outer ring in a particular galaxy, kinematical data are necessary, and 3D (two spatial coordinates on the plane of sky and one along the wavelength axis Courtes 1995); spectral data are especially useful (Moiseev & Bizyaev 2009). The collisional rings and OLR (Outer Lindblad Resonance) rings generate radial gas outflow while accreted gaseous rings rotate circularly, although sometimes outside the main galactic plane. In addition, the optical spectral data provide the possibility of determining the excitation mechanism for the ionized (warm) gas. The flux ratios of strong emission lines discriminate easily between the mechanisms of shock excitation and of ionization by UV radiation of young stars (Baldwin et al. 1981; Veilleux & Osterbrock 1987). To facilitate the action of a dynamo in magnetic-field generation, we need
-
long-lived (order of Gyrs) rings; hence collisional rings, with their lifetimes of a few hundred Myr, are unlikely to be candidates;
-
a supply of free electrons, hence an ionized state of the gas that can be provided and supported by continuous star formation in the rings;
-
regular circular gas rotation in the main galactic planes, presumably with a flat rotation curve, to provide a differential character for the gas rotation.
In some ways rings, generated by accretion may be be the most favourable for our investigation, with estimated lifetimes possibly approaching the Hubble time (Buta & Combes 1996). Based on the results of Ilyina & Sil’chenko (2011), Ilyina et al. (2014) and Katkov et al. (2015) we select a small sample with the properties mentioned above and present it in Fig. 1. The typical properties of these galaxies will be used in the further theoretical consideration of the dynamo magnetic-field generation in ring galaxies. Some extension of the typical picture can be also considered, by taking into account possible cases of the outer gas counter-rotation, as in NGC 4513 (Ilyina et al. 2014), or strong flaring of the gas layer in the ring area, as in UGC 5936 (Ilyina & Sil’chenko 2011). In this sample, continuum radio emission has been detected from IC 5285 (Condon et al. 1998).
3. Dynamos in ring galaxies
From the viewpoint of galactic dynamos, the main specific problem of ring galaxies is to what extent drivers of the galactic dynamo, i.e. differential rotation and mirror-asymmetric turbulence, can produce a magnetic structure in the ring that is independent of that in the disc, or is propagation of magnetic field generated in the disc into the ring a more realistic process? Of course, the answer depends on properties of the interstellar medium near the boundary between the disc and ring. One possibility here is that rings are overdense regions of warm gas superposed on an exponential disk as in late-type disc galaxies. The other possibility is that there is a gap in density distribution between the disc and ring. The latter option, which is the case in lenticular galaxies where warm ionized gas is often observed only in the rings (Pogge & Eskridge 1993; Salim et al. 2012), is obviously favourable for formation of an independent magnetic structure in the ring and looks a realistic possibility, especially for counter-rotating rings.
In the rings, the dynamo drivers have in addition to overcome the turbulent diffusion of the large-scale magnetic field into the gap between the disc and the ring. We recall that in the standard disc dynamo the drivers only have to compensate for losses of the large-scale magnetic field mainly through the upper and lower boundaries of the disc. We start with an order of magnitude estimate of the role of these losses.
We need somehow to compare the results obtained for ring galaxies with those for spiral galaxies. We proceed as follows. The conventional estimate for the intensity of dynamo action (e.g. Beck et al. 2005) is given in terms of the dynamo number D = 9(Ωh/v)2, where Ω is angular velocity, h is disc thickness, and v the rms turbulent velocity. Usually Ωh ≈ v and D ≈ 10. This estimate is based on the assumption that | rd Ω / dr | = Ω, which is an obvious idealisation for a flat (or outer Brandt) rotation curve. For real rotation curves it seems reasonable to try values D of several dozen, i.e. significantly larger than the normal estimates. This logic is directly applicable for rings that co-rotate with the disc. However a galaxy with a counter-rotating ring has unusually strong shear in the region between the disc and ring. We attempt to parametrize this situation as follows. We present the rotation curve as a combination of two disjoint pieces of a Brandt rotation curve with Ω of opposite signs, but with absolute value matched smoothly through the gap (see Fig. 8), and use the conventional estimate for D. In other words, we describe the anomalous shear in the region between the ring and the disc by the form of rotation curve. A problem here is that we may overestimate the width of the region in which the transition from the region co-rotating with the disc to that co-rotating with the ring occurs. Contemporary observations fail to resolve this transition. In order to take this problem into account we consider values of D up to D = 200, and demonstrate that the results are more or less generically stable.
3.1. Simple estimates
The basic concept of the standard galactic dynamo is that the azimuthal magnetic field Bφ is obtained from the radial field Br by the action of differential rotation Ω, while the radial field is restored from the azimuthal by the α-effect which arises from the mirror asymmetry of interstellar turbulence. Both effects are in competition with the destructive role of turbulent diffusion. This dynamo action can be represented in a very simple model by 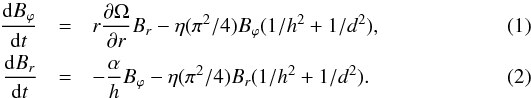 Here η is the turbulent diffusivity, h is the half-thickness of the disc and d is the half-width of the ring. For the crude estimates of interest, we have replaced all derivatives in the dynamo equations by corresponding algebraic terms and introduced numerical factors π2/ 4 to fit numbers known from numerical experiments (e.g. Phillips 2001). We estimate magnetic diffusivity in the framework of conventional mixing length theory as η = lv/ 3, where l is the basic scale of turbulence and v is the rms turbulent velocity, and the numerical factor 3 comes from the dimensionality of space. Another conventional estimate α = Ωl2/h comes from the viewpoint that the mirror asymmetry of interstellar turbulence is caused by Coriolis force action in a stratified medium. This conventional estimate implies that, for the case of a counter-rotating ring, α changes sign in the gap between the disc and the counter-rotating ring. This should be regarded as an order of magnitude estimate; for our purposes the important factor is the dependence on Ω.
Here η is the turbulent diffusivity, h is the half-thickness of the disc and d is the half-width of the ring. For the crude estimates of interest, we have replaced all derivatives in the dynamo equations by corresponding algebraic terms and introduced numerical factors π2/ 4 to fit numbers known from numerical experiments (e.g. Phillips 2001). We estimate magnetic diffusivity in the framework of conventional mixing length theory as η = lv/ 3, where l is the basic scale of turbulence and v is the rms turbulent velocity, and the numerical factor 3 comes from the dimensionality of space. Another conventional estimate α = Ωl2/h comes from the viewpoint that the mirror asymmetry of interstellar turbulence is caused by Coriolis force action in a stratified medium. This conventional estimate implies that, for the case of a counter-rotating ring, α changes sign in the gap between the disc and the counter-rotating ring. This should be regarded as an order of magnitude estimate; for our purposes the important factor is the dependence on Ω.
Dynamo self-excitation means that the linear dynamo equations above have exponential solutions ~expγt,γ> 0. (In particular, it means that all magnetic field components grow with the same rate.) After some algebra, we obtain from Eqs. (1) and (2) a dispersion relation 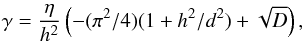 (3)where
(3)where 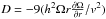 is a dimensionless quantity known as the dynamo number, that measures the intensity of galactic dynamo action. Dynamo self-excitation (positive γ) arises if D exceeds a critical level which for a thin galactic disc is Dcr ≃ π4/ 16 ≃ 6 (to be compared with Dcrit = 7.5 found by Ruzmaikin et al. 1988 in a slightly different approach). For a flat rotation curve
is a dimensionless quantity known as the dynamo number, that measures the intensity of galactic dynamo action. Dynamo self-excitation (positive γ) arises if D exceeds a critical level which for a thin galactic disc is Dcr ≃ π4/ 16 ≃ 6 (to be compared with Dcrit = 7.5 found by Ruzmaikin et al. 1988 in a slightly different approach). For a flat rotation curve 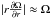 and for h = 500pc, v = 10kms-1 and rotation velocity of 200kms-1, we find that at r = 10 kpc,
and for h = 500pc, v = 10kms-1 and rotation velocity of 200kms-1, we find that at r = 10 kpc, 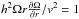 , i.e. D = 9.
, i.e. D = 9.
Diffusive losses in the gap between the ring and disc increase Dcr. It reaches Dcr = 10 for d = 1.5h, giving d = 600pc for h = 400 pc. On the other hand, the above estimates are crude enough that estimates D = 10 ~ 50 can be considered as realistic in a more complete model. Increase of the ring thickness h or differential rotation r∂Ω /∂r promote dynamo self-excitation. Indeed, rotation curves of ring galaxies appear more complicated than given by flat rotation curves (Ilyina et al. 2014) and the rings can be quite thick (Ilyina & Sil’chenko 2011). We conclude that self-excitation of a large-scale dynamo driven magnetic field in the rings looks possible. For h = d dynamo excitation needs D = 30, which seems quite possible for the interstellar medium.
3.2. Towards detailed dynamo models for ring galaxies
A natural development of the above estimates is to use what is known as the no-z approximation (Subramanian & Mestel 1993; Moss 1995). This approximation describes the magnetic field components in the disc plane. The z-component of the field perpendicular to the disc plane is restored by the solenoidality condition assuming that it is much less than the plane components (Br and Bϕ).
In the framework of the no-z model the dynamo equations are![\begin{eqnarray} &&\frac{\partial B_{r}}{\partial t}=-\frac{\alpha B_{\varphi}}{h}\notag\\[1mm] \label{eq1} &&\qquad+\eta \left(-(\pi^2/4)\frac{B_{r}}{h^{2}}+\frac{\partial} {\partial r}\left(\frac{\partial}{r \partial r}(r B_{r})\right) +\frac{1}{r^{2}}\frac{\partial B_{r}}{\partial \varphi}\right),\\[2mm] &&\frac{\partial B_{\varphi}}{\partial t}= r\frac{\partial \Omega}{\partial r} B_{r}-\Omega \frac{\partial B_{\varphi}}{\partial \varphi} \notag\\[1mm] \label{eq2} &&\qquad+\eta \left(-(\pi^2/4)\frac{B_{\varphi}}{h^{2}}+\frac{\partial}{\partial r}\left(\frac{\partial}{r \partial r}(r B_{\varphi})\right) +\frac{1}{r^{2}}\frac{\partial B_{r}}{\partial \varphi}\right) \cdot \end{eqnarray}](/articles/aa/full_html/2016/08/aa28346-16/aa28346-16-eq49.png) The α-coefficient includes saturation of the magnetic field growth when it reaches the equipartition value
The α-coefficient includes saturation of the magnetic field growth when it reaches the equipartition value 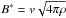 , where ρ is the interstellar medium density. We use an algebraic quenching for dynamo action
, where ρ is the interstellar medium density. We use an algebraic quenching for dynamo action 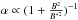 and avoid for the time being more sophisticated parametrisations (e.g. Shukurov 2006; Sur et al. 2007; Mikhailov 2013). For Ω we use a Brandt (1960) rotation curve
and avoid for the time being more sophisticated parametrisations (e.g. Shukurov 2006; Sur et al. 2007; Mikhailov 2013). For Ω we use a Brandt (1960) rotation curve 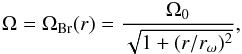 (6)with parameters chosen to give an asymptotic rotational velocity of about 200 km s-1 when rω = 2 kpc. Now α ∝ Ω.
(6)with parameters chosen to give an asymptotic rotational velocity of about 200 km s-1 when rω = 2 kpc. Now α ∝ Ω.
We assume that B∗ = 5μG in the main parts of the and that ρgap is an order of magnitude smaller than the density in the inner parts, and B∗ is there about 0.5 μG (Fig. 2, lower panel). Usually we use zero boundary conditions at the central and outer boundaries of the galactic disc. Additionally, we define L to be the radial extent of the gap between the inner disc and outer ring, and R the radius of the inner disc. As a conservative assumption, we take the rotation curve to be given by Eq. (6) everywhere, including in the gap. The outer boundary of the disc in which we model dynamo action is fixed at a radius of 10 kpc in all cases.
The magnetic field configuration in a ring galaxy depends on the lifetime of the ring and its origin, in particular the nature of the seed magnetic field configuration. The main aim of this paper is to investigate whether a galactic dynamo can generate a magnetic field in the ring. In order to clarify this, we are interested initially in long-lived rings and weak (much smaller than equipartition strength) seed magnetic fields. This is why we choose, as a basic example, to present the field resulting from a weak seed field after t = 1010 yr. We bear in mind that other possibilities should be considered later, after confirming that dynamo generated magnetic fields can be important for ring galaxies. Generally the saturated state is attained in a shorter time, but at the moment we wish mainly to demonstrate the eventual outcome of dynamo action. In the framework of this research, we first perform some preliminary experiments.
 |
Fig. 2 Regular magnetic field generation in the ring for various values of d (2d is the width of ring) and dynamo numbers D. The upper panel shows the magnetic field for t = 1010yr for D = 20; the middle panel the same for D = 50. The solid curves are for a ring with d = 1 kpc, the dashed curve d = 1.5 kpc, and the dot-dashed curve is for d = 2 kpc. The lower panel shows the equipartition field B∗ (which is determined by the kinetic energy of the turbulent gas) vs. radius for a representative case with L = 5 kpc, d = 1 kpc. |
 |
Fig. 3 Dynamo generated magnetic fields for various values of D and L when the seed field is concentrated solely in the inner disc. The ring half-width d = 1 kpc in all cases. The upper panel shows the magnetic field for t = 1010yr when the dynamo number D = 20, the lower shows the same for D = 50. The solid curves are for the gap extent L = 1 kpc, the dashed curves for L = 2 kpc, and the dot-dashed curves are for L = 3 kpc. |
 |
Fig. 4 Upper panel: regular magnetic field generation for various densities in the gap and the seed field in the inner disc. The upper panel shows the magnetic field at t = 1010yr for D = 20; the middle panel gives the same for D = 50. The solid curve shows ρgap = 10-1ρ0, the dashed curve ρgap = 10-2ρ0, and the dot-dashed curve ρgap = 10-3ρ0. R = 5 kpc, L = 2 kpc, d = 1 kpc. Without a ring the outer maximum in B is absent, and B continues to decline with radius. Lower panel: the dependence of pitch angle p = tan-1(Br/Bφ) on radius. |
 |
Fig. 5 Regular magnetic field generation for a counter-rotating ring at a nominal time of 1010 yr . The solid curve shows the magnetic field for | D | = 20, dashed curve for | D | = 50. The upper panel shows α ∝ Ω, middle panel α(r) = α0 > 0, lower panel α(r) = α0< 0. R = 5 kpc, L = 2 kpc. We note that in the lower panel the dynamo action in the disc is suppressed by the choice of sign of α0. |
 |
Fig. 6 Magnetic field evolution for the model with the seed field concentrated in the inner disc only (R = 5 kpc, L = 2 kpc). The solid curve shows t = 2 × 109yr, the dashed curve t = 5 × 109yr, and the dot-dashed curve is for t = 1010yr. |
The modelling is conservative, in that we use the Brandt rotation curve and ignore the fact that differential rotation in ring galaxies is usually more pronounced, and we always consider an inner disc of maximum radius R = 5 kpc, independent of the width of the gap L. Correspondingly, an increase of L moves the ring to a less dynamo-active radius.
4. Results: no-z model
We ran our model for D = 9,20,50 and some other values that seem to be realistic for disc galaxies and their outer rings. For D = 9 the initial magnetic field in the ring decays. Figure 2 shows 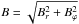 for t = 1010yr for D = 20 (top panel) and D = 50 (middle panel) and the seed field present in the outer ring only (
for t = 1010yr for D = 20 (top panel) and D = 50 (middle panel) and the seed field present in the outer ring only (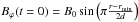 , Br = 0, and rmin and rmax are the inner and the outer radii). We find that the intensity of dynamo action (D) can be (under realistic assumptions) sufficient for magnetic field self-excitation and that the field can reach a field strength that is close to the equipartition value in a few Gyr. Varying the half-widths of the ring from 1 to 2 kpc (the magnetic field decays for smaller d), we find that the magnetic configuration is robust. Wider rings and larger D give however more widely distributed and stronger magnetic field. In order to isolate the effects of dynamo action in the ring we take a seed magnetic field for the dynamo that is present only in the ring. We also can conclude that an initial magnetic field concentrated in the ring can pass into the central parts.
, Br = 0, and rmin and rmax are the inner and the outer radii). We find that the intensity of dynamo action (D) can be (under realistic assumptions) sufficient for magnetic field self-excitation and that the field can reach a field strength that is close to the equipartition value in a few Gyr. Varying the half-widths of the ring from 1 to 2 kpc (the magnetic field decays for smaller d), we find that the magnetic configuration is robust. Wider rings and larger D give however more widely distributed and stronger magnetic field. In order to isolate the effects of dynamo action in the ring we take a seed magnetic field for the dynamo that is present only in the ring. We also can conclude that an initial magnetic field concentrated in the ring can pass into the central parts.
The figure obtained for the large-scale magnetic field strength in the disc is in some cases as large as 30 μG, which appears rather large in the context of magnetic fields in spiral galaxies. This estimate arises because we use Beq = 5 μG and D = 50. Then, using the estimate 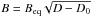 obtained by Shukurov (2007), where D0 = 7 is the generation threshold for the disc, we obtain the above field strength.
obtained by Shukurov (2007), where D0 = 7 is the generation threshold for the disc, we obtain the above field strength.
Then we ran the model with the seed in the inner disc only (Figs. 3 and 4). We see that the outer ring becomes magnetized after sufficient time, but it appears that magnetic field transport from the inner disc is at least as important as in situ dynamo action in the outer ring.
Figure 5 shows that in the framework of our model the dynamo generated magnetic field is not very sensitive to the gas density in the gap between the ring and disc. Without a ring, the outer maxima in Bφ are absent, and Bφ continues to decrease with radius.
The no-z model gives a counter-intuitive result (Fig. 6) for the case of a counter-rotating ring, such as observed in NGC 4513, although we do not attempt to model this galaxy explicitly. Then Ω = f(r)ΩBr(r) where f(r) = 1 in the inner parts, f(r) = −1 in the outer parts and it changes gradually in the gap. Qualitatively, Ω(r) is as shown in Fig. 8, with allowance for differing positions of the gap. Counter-rotation of the ring in respect to the inner disc means very large radial gradients in Ω. A natural expectation is to find effective dynamo action around the gap between the ring and the disc. In practice, we face a problem of how, in the framework of the model, to parametrize the quantity α for the counter rotating ring. A straightforward parametrization α = Ωl2/h assumes that α vanishes in the gap, suppressing dynamo action. Here l is the scale of interstellar turbulence: typically l = 100 pc. α is a quantity which is hard to predict and we also tried the option that α does not change sign in the gap (Fig. 6c). In the absence of counter-rotation, we tested the case of α positive in the disc in the ring and also the case of α negative both in the disc and the ring and found again that the dynamo action in the gap region is moderate.
We see from the above results that the magnetic field can pass through the gap between ring and disc. If the seed is only non-zero in the disc, it penetrates into the ring and vice versa. A theoretical prediction for the field propagation (based on an estimate given in a much more general context in Kolmogorov et al. 1937) is given by (Moss et al. 1998b; Mikhailov 2015),
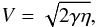 where γ is the growth rate of magnetic field. Taking η = 0.33 kpckms-1,γ = 1.5Gyr-1, we obtain V = 1 kpcGyr-1, which is quite close to the numerical estimate that follows from Fig. 4. We have assumed that the diffusivity, given by properties of the turbulence, is uniform through the inner disc and ring. Of course, this may not be justified.
where γ is the growth rate of magnetic field. Taking η = 0.33 kpckms-1,γ = 1.5Gyr-1, we obtain V = 1 kpcGyr-1, which is quite close to the numerical estimate that follows from Fig. 4. We have assumed that the diffusivity, given by properties of the turbulence, is uniform through the inner disc and ring. Of course, this may not be justified.
We recognize that these times significantly exceed the probable lifetimes of the rings. Among other conservative assumptions in the model, we note that the timescales depend inversely on the value of the diffusivity, which is subject to substantial uncertainty. Also the choice of seed field and the history of the galaxy before the formation of the ring can be important, see the comments in Sect. 5.
The magnetic field in an isolated galactic disc is usually (almost) axisymmetric. A ring however is a relatively thin, azimuthally extended, and relatively isolated, body and it is a priori possible that generation of a bisymmetric magnetic field could occur there. We can note here that dominant bisymmetric magnetic configurations are now considered to be rare in, or completely absent from, normal spiral galaxies (see e.g. Beck 2016). Nevertheless, it seems reasonable to examine briefly this option in thin rings, given that dynamo theory suggests that thin rings are believed to be more favourable for generation of nonaxisymmetric fields. However, we found such a solution only for the case of a free outer boundary of the disc (∂B/∂r = 0 at r = 10 kpc), Ω0 = 67 km s-1 kpc-1, and α = 2.68 kms-1 (corresponding to Rα ≈ 4, Rω ≈ 50) the radius of the inner disc is 5 kpc, the inner radius of the outer ring is 9 kpc, and its outer radius is 10 kpc. The initial field is zero if r< 9 kpc and bisymmetric in the ring. With the standard dynamo parameters of Sect. 4, the bisymmetric field generated only survives for about t = 0.5Gyr and then disappears, to be replaced by an axisymmetric configuration. However, with slightly different dynamo parameters a stable bisymmetric field can be found (Fig. 7). We can conclude that, although possibly of some interest in a dynamo theory context, nonaxisymmetric fields are not likely to be relevant to real ring galaxies.
 |
Fig. 7 Regular magnetic field generated in an outer thin ring in the nonaxisymmetric case (see discussion in the text). |
5. Counter-rotating discs: beyond the no-z model
5.1. Basic model
The rather surprising results obtained above for counter-rotating discs, using the severely truncated no-z model, suggest the need for verification with an alternative model. Of course, such verification would be helpful for the case of a co-rotating disc as well, but in this case previous comparisons show that the no-z model provides a satisfactory approximation to a conventional axisymmetric model with explicit z-dependence. Given that the no-z models of Sect. 4 suggest that fields are axisymmetric, we revisited the problem using an axisymmetric embedded disc model, with cylindrical r,z coordinates. The code used is essentially that of Moss et al. (1998a,b). (This is an α2Ω code, whereas in the previous sections the αΩ approximation is used; however, in the regime of interest, there is little difference between these approaches.) In this Section, we use a slightly different notation: Rgal is now the overall galactic radius, and we define the gap location and size by parameters ri and ro.
The reference rotation curve is again a Brandt curve (Eq. (6)) with rω = 0.2Rgal. In this α2Ω code, the dynamo numbers are given by Rω = Ω0h2/η0,Rα = α0h/η0, where Ω0 is the quantity defining the rotation curve (Eq. (6)), α0 is the corresponding value of α, and η0 is the value of the diffusivity in the disc. The diffusivity is independent of radius, and increases asymptotically to 25ηD in the halo. The value of α varies sinusoidally in the disc (∝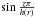 ), and is zero in | z | >h(r). We continue to use a canonical value of ηD = 1026 cm2 s-1 in the later discussion, but always bearing in mind the possibility of some variation as this estimate is rather uncertain. Our probable underestimate of the angular velocity gradients, and hence of the effective dynamo number, might be considered to be compensated by the use of large values of D. The “gap” is between r = ri and r = ro, and the equipartition field strength is uniform outside of the gap, i.e. in r ≤ ri and r ≥ ro. Field strengths are measured in units of this equipartition field (again defined by the kinetic energy of the assumed turbulent gas motions). In the gap the equipartition field drops quadratically to the value Beq1 at r = (ri + ro) / 2. In the initial investigation, the dynamo parameters were slightly different to those used in Sect. 4: Rα = 4, Rω = 50. For the majority of models, in r ≤ ri, the disc thickness h = 0.04Rgal, and in r ≥ ro, h = 0.08Rgal and with a smooth interpolation in the gap. Analogously, in r ≤ ri, Ω = ΩB(r), and in r ≤ ro, Ω = −ΩB(r), with a smooth transition. Correspondingly, with α ∝ Ω, α changes sign smoothly. In the standard case, ri = 0.5Rgal,ro = 0.7Rgal. Figure 8 shows the radial dependence of the key disc quantities.
), and is zero in | z | >h(r). We continue to use a canonical value of ηD = 1026 cm2 s-1 in the later discussion, but always bearing in mind the possibility of some variation as this estimate is rather uncertain. Our probable underestimate of the angular velocity gradients, and hence of the effective dynamo number, might be considered to be compensated by the use of large values of D. The “gap” is between r = ri and r = ro, and the equipartition field strength is uniform outside of the gap, i.e. in r ≤ ri and r ≥ ro. Field strengths are measured in units of this equipartition field (again defined by the kinetic energy of the assumed turbulent gas motions). In the gap the equipartition field drops quadratically to the value Beq1 at r = (ri + ro) / 2. In the initial investigation, the dynamo parameters were slightly different to those used in Sect. 4: Rα = 4, Rω = 50. For the majority of models, in r ≤ ri, the disc thickness h = 0.04Rgal, and in r ≥ ro, h = 0.08Rgal and with a smooth interpolation in the gap. Analogously, in r ≤ ri, Ω = ΩB(r), and in r ≤ ro, Ω = −ΩB(r), with a smooth transition. Correspondingly, with α ∝ Ω, α changes sign smoothly. In the standard case, ri = 0.5Rgal,ro = 0.7Rgal. Figure 8 shows the radial dependence of the key disc quantities.
We first computed a model with Beq1 = 0.1B∗ (Sect. 3.2). Figure 9a shows the dependence of Bφ on radius along the mid-plane z = 0, and Fig. 9b shows the contours of Bφ. The notable feature of these plots is the departure from strict quadrupolar parity; in this case the parity P ≈ −0.5 in the steady state. This feature could not be revealed by the no-z model, which implicitly assumes P = + 1. We have used the standard definition of dynamo field parity, 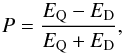 (7)where EQ,ED are the energies respectively of the even and odd parts of the field. Thus a strictly quadrupolar/dipolar field has P = + 1 / −1.
(7)where EQ,ED are the energies respectively of the even and odd parts of the field. Thus a strictly quadrupolar/dipolar field has P = + 1 / −1.
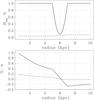 |
Fig. 8 Radial dependence of the key disc properties for the counter-rotating model. Upper panel: Beq (solid, in units of B∗). Lower panel: Ω (solid) and α (broken). |
 |
Fig. 9 a) Dependence of Bφ on radius in the disc plane. b) Bφ contours for the model with Beq1 = 0.1B∗; here ri = 0.5Rgal and ro = 0.7Rgal, with counter-rotation. |
 |
Fig. 10 a) Dependence of Bφ on radius in the disc plane; b) Bφ contours for the model with Beq1 = 0.1B∗ and enforced quadrupolar parity; c) dependence of | Bφ | on radius for the corresponding no-z model. ri = 0.5Rgal,ro = 0.7Rgal, with counter-rotation. Bφ is measured in units of the equipartition field B∗. |
In order to make a better comparison with the no-z model, we recomputed this model in the region z ≥ 0 with quadrupolar parity enforced by the boundary conditions on the plane z = 0. The contours of toroidal field and the radial variation of Bφ on z = 0 are shown in the upper two panels of Fig. 10. The lower panel shows the variation of | B | with radius in the corresponding no-z model. Comparison of the lower two panels of this figure shows a remarkable similarity between the no-z and r,z models, and gives confidence in the modelling, even for these much larger dynamo numbers; see also Phillips (2001).
Varying Beq1 between 1 and 0.01 produces very little variation in the eventual steady configuration, with final parity around P ≈ −0.3. Moving the gap to (ri,ro) = (0.6,0.9) gives a final parity, P ≈ + 0.4, and with (0.35, 0.7) gives P ≈ −0.28. A model with uniform disc thickness, h/Rgal = 0.04, no gap/counter-rotation, α ∝ Ω and Rα = −1.0,Rω = 20 gives a strictly dipolar field, P = −1. This result persists for considerably larger dynamo numbers, for example Rα = −4.0,Rω = 50. This means that the dynamo action in the disc of the model is strong enough to excite a dipolar magnetic field (in which the azimuthal field changes sign at the central plane (antisymmetric), while for a weaker dynamo action magnetic fields in galactic discs have a quadrupolar configuration (with an azimuthal field that is symmetric with respect to the central plane). The counter-rotating ring and associated magnetic field losses resulting from magnetic field transport into the gap makes the parity of the configuration mixed, and the field configuration in the inner parts of the disc is closer to quadrupolar symmetry.
Further models with ri = 0.5Rgal,ro = 0.7Rgal with a) no counter-rotation, α ∝ Ω,Beq1 = 0.1, gave a strictly quadrupolar P = + 1; b) counter-rotation, α ∝ | Ω |, Beq1 = 0.1B∗, resulted in P = + 0.98.
In the counter-rotating case and α ∝ Ω, as the dynamo numbers are reduced, the contribution of the odd parity component also becomes smaller. For example, with Rα = 2,Rω = 25 in the steady state, the final parity is P ≈ 0.12, with Rα = 1,Rω = 25 we find P ≈ 0.47, and Rα = 1,Rω = 20 also gives a mixed parity final state. In the marginally supercritical case Rα = 1,Rω = 15, the steady field is purely quadrupolar, P = + 1; the field in the outer ring decreases in relative strength with a reduction in dynamo numbers.
In summary, we can deduce that mixed parity fields (in which the azimuthal field has no symmetry with respect to the central plane) are a robust feature of the model with counter-rotation and α ∝ Ω. With α ∝ | Ω | the effect is much reduced. The region with α< 0 seems crucial to the effect, counter-rotation with α> 0 everywhere produces only a small effect. The computations described in this Section started from a weak seed field of mixed parity distributed throughout the disc. With our standard ηD = 1026 cm2 s-1, the eventual steady state can take times in excess of 1010 yr to become established for the smaller dynamo numbers, and departure from very near quadrupolar symmetry can then take a substantial fraction of this time. Timescales can be substantially reduced by different choices of the field present at the onset of counter-rotation. We emphasize again that these estimated timescales are sensitive to the value of ηD. Prolonged timescales are plausibly associated with the diffusion of field across the gap between the inner disc and the counter-rotating ring.
5.2. Timescales and evolution
In Sect. 5.1 we have presented the saturated steady magnetic configuration for a particular model. The results presented using the no-z approximation suggest that evolution to the final configuration can be relatively slow; this feature is associated with the diffusion of field across the gap as the final configuration is determined. If we start with an arbitrary seed field then, depending on its strength, evolution to the final saturated configuration can take times longer than the estimated lifetimes of rings, depending on their believed mechanism of formation. For example, for rings formed by accretion Buta & Combes (1996) quote times that may approach the Hubble time, whereas for rings resulting from impacts the models of Athanassoula et al. (1997) suggest lifetimes of less than 1 Gyr. We show in Fig. 11 the evolution of parity and energy for an example where the seed field is weak (with magnitude much smaller than equipartition strength) and of arbitrary parity. After an initial brief fall in parity, a purely quadrupolar configuration persists for about 4 Gyr. The nonlinear regime is then reached and the field moves rapidly to the asymptotic state shown in Fig. 9b. However significant large-scale fields can be present in the ring regions after 3−4 Gyr if the seed field is stronger. Thus we now can consider two evolutionary scenarios. Either the counter-rotating ring is present from time t = 0 with a seed field of unknown strength and geometry, or a merger event occurs creating the ring after a standard even parity field has been established.
 |
Fig. 11 Dependence of global parity and energy on time for a calculation beginning from a weak seed field of mixed parity. |
 |
Fig. 12 The radial distribution of Bφ in the disc plane a) immediately before the counter-rotation is turned on; b)–e) at times 0.9,1.8,2.7,3.6 Gyr afterwards. |
To illustrate this, with a stronger seed field, a significant large-scale field of magnitude comparable with equipartition strength can be established in the ring after 2−3 Gyr, although the dynamo is far from saturation, and a mixed parity field does not appear for another 0.5−1 Gyr with a longer time until the asymptotic state of Fig. 9b is attained.
On the other hand, if the ring forms after an encounter or merger event involving one or two pre-magnetised galaxies with near saturated dynamos, then the effective seed field for subsequent dynamo action may be quite strong and organised. (We do not consider here the possibility that such an event generates turbulence and small-scale magnetic fields of approximately equipartition strength, which would provide a seed for subsequent dynamo action, see e.g. Moss et al. 2013.) To gain some insight into this scenario, we allowed a standard, even parity, steady global field to become established in a model with no counter-rotation and no gap, with reduced strength equipartition field. Counter-rotation was then introduced, with Beq1 = 0.1, i.e. the model of Sect. 5.1. In Fig. 12 we show the dependence of Bφ in the plane z = 0 on radius at times 0,0.9,1.8,2.7, and 3.6 Gyr after the introduction of counter-rotation. A significant field is present in the ring (r> 7 kpc) throughout.
We can conclude that mixed parity fields may be attainable within galactic timescales, depending on the details and history of the model. Other unexplored possibilities include that we underestimated angular velocity gradients near the gap and thus underestimated the strength of the dynamo action in that region, or that the turbulent diffusivity is not constant throughout the disc plane. We have shown that large-scale fields may be present in galactic rings and that there is also the possibility that they may be of mixed parity. With our current state of knowledge we cannot be more specific.
6. Discussions and conclusions
We have demonstrated that dynamo drivers in ring galaxies, i.e. differential rotation and mirror-asymmetry of interstellar turbulence, can be strong enough to excite magnetic fields both in the disc and the rings. Our expectation is that such rings do contain large-scale magnetic fields (probably slightly weaker than in the inner discs) which give rise to polarized radio emission.
We found that the current concepts of galactic dynamo action tell us rather counter-intuitively that the strong angular velocity gradients associated with counter-rotation of galactic rings with respect to that of the disc does not lead to a substantial increase of dynamo action and magnetic field strength near the ring. In other words, observations of magnetic fields in galaxies with counter-rotating rings have the potential to provide a strong test for current galactic dynamo concepts.
Inter alia, this investigation demonstrates the limits of the no-z model. It is known to be satisfactory (and very useful) for studying fields that are believed with a high degree of confidence to have strictly even parity with respect to the galactic equator, but is clearly unreliable where this symmetry cannot be guaranteed, as in the models of Sect. 5 above, where the stable fields are of mixed parity.
A potentially important feature of thin rings is the possibility of generating non-axisymmetric fields. In our model, such fields can more readily be generated if magnetic field propagates freely through the outer boundary of the ring. However dynamo numbers have to be chosen rather selectively to obtain nonaxisymmetric fields, and the result suggests that axisymmetric large-scale fields are the normal case. Potentially more importantly, a magnetic configuration that is asymmetric with respect to the central galactic plane (a mixed parity solution) can arise near the gap between the disc and the counter-rotating ring.
We note that our paper does not cover all dynamo related problems that arise in the context of ring galaxies studies. In particular, it looks natural to investigate possible effects of dynamo action in resonant rings as well as the dynamo driven evolution of a strong (i.e. comparable with the equipartition field strength) and maybe small-scale seed field. A further possibility is the effects of ongoing injections of small-scale fields of approximately equipartition strength generated by turbulent dynamo action, as in Moss et al. (2013). Such extensions of the topic should however be addressed separately.
We further note that to reach steady-state magnetic configurations we sometimes run our code for times that are nominally several times longer than the anticipated lifetimes of the rings. However, the eventual steady-state configurations may not be so significant, see e.g. Fig. 12. Timescales for our models, and their prior evolution, are somewhat uncertain. We have presented a scenario, summarized in Fig. 12 in which fields can be present in galactic rings more or less throughout the lifetime of the rings. Whether the rings live long enough for global mixed parity configurations to become established is more uncertain, although Buta & Combes (1996) suggest that ring lifetimes may be rather extended. Observations of such fields would be challenging anyway. We reiterate that the timescale for magnetic field evolution depends on the value of the turbulent magnetic diffusivity, which is not a directly observable quantity, and that theoretical estimates contain substantial uncertainties. We have adopted a standard figure (1026 cm2 s-1), but need to keep in mind that we may underestimate the speed of magnetic field transport in ring galaxies. On the other hand, our results demonstrate that we can expect various long-lived magnetic transients in ring galaxies, and contemporary magnetic configurations in these objects can be influenced by features of seed magnetic fields (or the field present after the ring forms).
Chyży & Buta (2008) found a coherent magnetic spiral structure crossing the inner pseudo-ring of NGC 4736. It is not exactly comparable with the outer rings discussed here, but it appears to be an interesting system.
We obtained an unexpected result for dynamo models with counter-rotating disc and ring. In spite of a very large shear between the disc and ring, the resulting dynamo action is quite moderate. Even with our definition of dynamo number D the excitation threshold is found numerically to be around D = 13, instead of D = 7.5 for spiral galaxies. Thus the counter-rotating configuration inhibits the efficiency of dynamo action. The eigenfunction near marginal excitation is concentrated in the inner regions, and so this increase in marginal dynamo number is plausibly associated with its reduced radial scale, and an opposition between the inner and outer dynamo drivers.
In general, we can conclude that magnetic field studies in ring galaxies have the potential to provide useful information concerning the nature and evolution of such galaxies.
There are examples of polar rings, i.e. rings inclined to the disc plane (Moiseev et al. 2011). However it is believed that after they are accreted with arbitrary inclined angular momentum, gaseous rings settle to the plane of the galactic disc in a few orbital times: see e.g. Steiman-Cameron & Durisen (1988), Christodoulou & Tohline (1993), Colley & Sparke (1996).
Acknowledgments
E.M. acknowledges support from the Dynasty Foundation and RFBR under grant 16-32-00056. D.S. acknowledges support from RFBR under grant 15-02-01407. R.B. is grateful for support from DFG Research Unit FOR1254. Analysis of the observational data on ring galaxies is supported by the RSF grant N 14-22-0041, and dynamo modelling of the counter-rotating ring by RSF grant 16-17-10097. The authors thank Marita Krause, MPIfR’s internal referee, for helpful comments, and the external referee, Andrew Fletcher for suggesting a number of improvements to the text.
References
- Appleton, P. N., & Struck-Marcell, C. 1996, Fund. Cosmic Phys., 16, 11 [Google Scholar]
- Appleton, P. N., Charmandaris, V., Horellou, C., et al. 1999, ApJ, 527, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Arshakian, T., Beck, R., Krause, M., & Sokoloff, D. 2009, A&A, 494, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Athanassoula, E., Bosma, A., Creze, M., & Schwarz, M. P. 1982, A&A, 107, 101 [NASA ADS] [Google Scholar]
- Athanassoula, E., Puerari, I., & Bosma, A. 1997, MNRAS, 286, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R. 2016, A&ARv, 24, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Brandenburg, A., Moss, D., et al. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Ehle, M., Shoutenkov, V., Shukurov, A., & Sokoloff, D. 1999, Nature, 397, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Shoutenkov, V., Ehle, M., et al. 2002, A&A, 391, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R., Fletcher, A., Shukurov, A., et al. 2005, A&A, 444, 739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandt, J. C. 1960, ApJ, 131, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Buta, R. 1995, PASP, 105, 654 [Google Scholar]
- Buta, R., & Combes, F. 1996, Fundamentals of Cosmic Physics, 17, 95 [Google Scholar]
- Christodoulou, D. M., & Tohline, J. E. 1993, ApJ, 403, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Chyży, K. T., & Buta, R. J. 2008, ApJ, 677, id. L17 [Google Scholar]
- Colley, W. N., & Sparke, L. S. 1996, ApJ, 471, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Comerón, S., Salo, H., Laurikainen, E., et al. 2014, A&A, 562, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Courtes, G. 1995, in Tridimensional Optical Spectroscopic Methods in Astrophysics, eds. G. Comte, & M. Marcelin, IAU Coll., 149, 1 [Google Scholar]
- Few, J. M. A., & Madore, B. F. 1986, MNRAS, 222, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K. C., & de Vaucouleurs, G. 1974, ApJ, 194, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Ghigo, F. D. 1980, AJ, 85, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Horellou, C., Casoli, F., Combes, F., & Dupraz, C. 1995, A&A, 298, 743 [NASA ADS] [Google Scholar]
- Ilyina, M. A., & Sil’chenko, O. K. 2011, Astron. Lett., 37, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Ilyina, M. A., Sil’chenko, O. K., & Afanasiev, V. L. 2014, MNRAS, 439, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Jeske, N. A. 1986, Ph.D. Thesis, Ring galaxies: an investigation of the physical conditions in closely interacting systems (Berkeley: University of California) [Google Scholar]
- Jungwiert, B., & Palous, J. 1996, A&A, 311, 397 [NASA ADS] [Google Scholar]
- Katkov, I. Yu., Kniazev, A. Yu., & Sil’chenko, O. K. 2015, AJ, 150, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Kolmogorov, A. N., Petrovsky, I. G., & Piskunov, N. S. 1937, Mosc. Univ. Bull., 1, 6 [Google Scholar]
- Kostiuk, I. P., & Sil’chenko, O. K. 2015, Astrophys. Bull., 70, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Laurikainen, E., Salo, H., Buta, R., & Knapen, J. H. 2011, MNRAS, 418, 1452 [NASA ADS] [CrossRef] [Google Scholar]
- Laurikainen, E., Salo, H., Athanassoula, E., et al. 2013, MNRAS, 430, 3489 [NASA ADS] [CrossRef] [Google Scholar]
- Lynds, R., & Toomre, A. 1976, ApJ, 209, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Mikhailov, E. A. 2013, Astron. Lett., 39, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Mikhailov, E. 2015, Mosc. Univ. Bull. Phys., 70, 2, 101 [CrossRef] [Google Scholar]
- Moiseev, A. V., & Bizyaev, D. V. 2009, New Astron. Rev., 53, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Moiseev, A. V., Smirnova, K. I., Smirnova, A. A., & Reshetnikov, V. P. 2011, MNRAS, 418, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D. 1995, MNRAS, 275, 191 [NASA ADS] [Google Scholar]
- Moss, D., Shukurov, A., Sokoloff, D. D., Berkhuijsen, E. M., & Beck, R. 1998a, A&A, 335, 500 [NASA ADS] [Google Scholar]
- Moss, D., Shukurov, A., & Sokoloff, D. 1998b, Geophys. Astrophys. Fluid. Dyn., 89, 285 [Google Scholar]
- Moss, D., Shukurov, A., Sokoloff, D., Beck, R., Fletcher, A. 2001, A&A, 380, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Snodin, A. P., Englmaier, P., et al. 2007, A&A, 465, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Beck, R., Sokoloff, D., et al. 2013, A&A, 556, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Phillips, A. 2001, Geophys. Astrophys. Fluid. Dyn., 94, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Pogge, R. W., & Eskridge, P. B. 1993, AJ, 106, 1405 [NASA ADS] [CrossRef] [Google Scholar]
- Ruzmaikin, A., Shukurov, A., & Sokoloff, D. 1988, Magnetic Fields of Galaxies (Dordrecht: Kluwer) [Google Scholar]
- Salim, S., Fang, J. J., Rich, R. M., et al. 2012, ApJ, 755,105 [NASA ADS] [CrossRef] [Google Scholar]
- Schommer, R. A., & Sullivan, W. T. III 1976, Aph. Lett., 17, 191 [Google Scholar]
- Sheth, K., Regan, M., Hinz, J. L., et al. 2010, PASP, 122, 1397 [NASA ADS] [CrossRef] [Google Scholar]
- Shukurov, A., Sokoloff, D., Subramanian, K., & Brandenburg, A. 2006, A&A, 448, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shukurov, A. 2007, In Mathematical aspects of natural dynamos, eds. E. Dormy, & A. M. Soward (Boca Raton: CRC Press), Chap. 7 [Google Scholar]
- Steiman-Cameron, T. Y., & Durisen, R. H. 1988, ApJ, 325, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Subramanian, K., & Mestel, L. 1993, MNRAS, 265, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Sur, S., Shukurov, A., & Subramanian, K. 2007, MNRAS, 377, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Theys, J. C., & Spiegel, E. A. 1976, ApJ, 208, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Van Driel, W., & van Woerden, H. 1991, A&A, 243, 71 [NASA ADS] [Google Scholar]
- Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Vorontsov-Vel’yaminov, B. A. 1960, Sov. Astron., 4, 365 [NASA ADS] [Google Scholar]
- Wiegert, T., Irwin, J., Miskolczi, A., et al. 2013, AJ, 150, 81 [Google Scholar]
All Figures
 |
Fig. 1 Examples of lenticular (they have no spiral arms but do have discs) galaxies with outer rings: composite-coloured images from the SDSS survey and image from ultraviolet GALEX survey for NGC 4513. (The NGC 4513 image from the SDSS survey shows the ring with a rather low contrast.) |
| In the text | |
 |
Fig. 2 Regular magnetic field generation in the ring for various values of d (2d is the width of ring) and dynamo numbers D. The upper panel shows the magnetic field for t = 1010yr for D = 20; the middle panel the same for D = 50. The solid curves are for a ring with d = 1 kpc, the dashed curve d = 1.5 kpc, and the dot-dashed curve is for d = 2 kpc. The lower panel shows the equipartition field B∗ (which is determined by the kinetic energy of the turbulent gas) vs. radius for a representative case with L = 5 kpc, d = 1 kpc. |
| In the text | |
 |
Fig. 3 Dynamo generated magnetic fields for various values of D and L when the seed field is concentrated solely in the inner disc. The ring half-width d = 1 kpc in all cases. The upper panel shows the magnetic field for t = 1010yr when the dynamo number D = 20, the lower shows the same for D = 50. The solid curves are for the gap extent L = 1 kpc, the dashed curves for L = 2 kpc, and the dot-dashed curves are for L = 3 kpc. |
| In the text | |
 |
Fig. 4 Upper panel: regular magnetic field generation for various densities in the gap and the seed field in the inner disc. The upper panel shows the magnetic field at t = 1010yr for D = 20; the middle panel gives the same for D = 50. The solid curve shows ρgap = 10-1ρ0, the dashed curve ρgap = 10-2ρ0, and the dot-dashed curve ρgap = 10-3ρ0. R = 5 kpc, L = 2 kpc, d = 1 kpc. Without a ring the outer maximum in B is absent, and B continues to decline with radius. Lower panel: the dependence of pitch angle p = tan-1(Br/Bφ) on radius. |
| In the text | |
 |
Fig. 5 Regular magnetic field generation for a counter-rotating ring at a nominal time of 1010 yr . The solid curve shows the magnetic field for | D | = 20, dashed curve for | D | = 50. The upper panel shows α ∝ Ω, middle panel α(r) = α0 > 0, lower panel α(r) = α0< 0. R = 5 kpc, L = 2 kpc. We note that in the lower panel the dynamo action in the disc is suppressed by the choice of sign of α0. |
| In the text | |
 |
Fig. 6 Magnetic field evolution for the model with the seed field concentrated in the inner disc only (R = 5 kpc, L = 2 kpc). The solid curve shows t = 2 × 109yr, the dashed curve t = 5 × 109yr, and the dot-dashed curve is for t = 1010yr. |
| In the text | |
 |
Fig. 7 Regular magnetic field generated in an outer thin ring in the nonaxisymmetric case (see discussion in the text). |
| In the text | |
 |
Fig. 8 Radial dependence of the key disc properties for the counter-rotating model. Upper panel: Beq (solid, in units of B∗). Lower panel: Ω (solid) and α (broken). |
| In the text | |
 |
Fig. 9 a) Dependence of Bφ on radius in the disc plane. b) Bφ contours for the model with Beq1 = 0.1B∗; here ri = 0.5Rgal and ro = 0.7Rgal, with counter-rotation. |
| In the text | |
 |
Fig. 10 a) Dependence of Bφ on radius in the disc plane; b) Bφ contours for the model with Beq1 = 0.1B∗ and enforced quadrupolar parity; c) dependence of | Bφ | on radius for the corresponding no-z model. ri = 0.5Rgal,ro = 0.7Rgal, with counter-rotation. Bφ is measured in units of the equipartition field B∗. |
| In the text | |
 |
Fig. 11 Dependence of global parity and energy on time for a calculation beginning from a weak seed field of mixed parity. |
| In the text | |
 |
Fig. 12 The radial distribution of Bφ in the disc plane a) immediately before the counter-rotation is turned on; b)–e) at times 0.9,1.8,2.7,3.6 Gyr afterwards. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


