EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 590 (June 2016) A&A, 590 (2016) A119 Full HTML
Free Access
Issue
A&A
Volume 590, June 2016
Article Number A119
Number of page(s) 7
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201628564
Published online 25 May 2016

© ESO, 2016

1. Introduction

The jets of high-mass microquasars propagate through the wind of the companion star. This wind can strongly affect the jet hydrodynamics within the binary and farther away. This has been studied in a number of papers, that have mostly focussed on dynamics, but sometimes also considered the potential high-energy emission from the interaction, and in some cases accounted for wind inhomogeneities (e.g. Romero et al. 2003; Romero & Orellana 2005; Perucho & Bosch-Ramon 2008, 2012; Owocki et al. 2009; Araudo et al. 2009; Perucho et al. 2010; Barkov & Khangulyan 2012; Yoon & Heinz 2015; Yoon et al. 2016).

In addition to the role of wind thrust intercepting the jet, orbital motion can also have a dynamical influence on the jet on scales larger than those of the binary, inducing a helical pattern in the jet (e.g., see the discussion in Bosch-Ramon 2013). The strength of this influence should be determined by the wind-jet thrust relation: the stronger the jet bending due to wind impact is, the closer to the binary the Coriolis force should affect jet propagation. A similar effect is expected to take place in binary systems hosting a massive star and a non-accreting pulsar, in which the stellar and the pulsar wind collide, and the shocked flows form a strongly non-ballistic spiral structure (Bosch-Ramon & Barkov 2011; Bosch-Ramon et al. 2012, 2015; Bednarek & Sitarek 2013; Barkov & Bosch-Ramon 2016).

In this work, we characterise through analytical estimates the way the stellar wind and orbital motion affect the jet in a high-mass microquasar. The results can be easily scaled to derive conclusions for relevant sources, such as for instance Cyg X-1 or Cyg X-3, two high-mass microquasars suggested to be candidates of wind-jet interaction to explain observations in different energy bands (e.g. Albert et al. 2007; Romero et al. 2010; Dubus et al. 2010; Vilhu & Hannikainen 2013, and see also Sect. 3.3).

thumbnail Fig. 1

Sketch of the scenario studied in this work at small and middle scales; the main ingredients (star, stellar wind, jet), and physical processes and effects (wind-jet bending, Coriolis effect-jet bending) are shown.

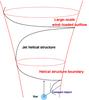thumbnail Fig. 2

Sketch of the scenario studied in this work at large scales; the main physical processes and effects (helical jet, wind-jet outflow) are shown.

2. Wind-jet interaction

Let us first set the scenario in which the wind-jet interaction problem is considered. The scenario consists of a massive star with a strong and fast stellar wind, and a compact object, a black hole or an accreting neutron star, from which a jet is launched. Typical values for the mass-loss rates and wind velocities in OB stars are Ṁw ~ 10-9−10-5M⊙ yr-1 and νw ~ 2 × 108 cm s-1, respectively (e.g. Muijres et al. 2012; Krtička 2014). Figures 1 and 2 show a sketch of the scenario studied here, with the different ingredients, physical processes and effects, and spatial scales discussed in this work. As seen in the figures, the location of the star and the compact object are (0,−d,0) and (0,0,0), respectively. The stellar wind is assumed to be spherically symmetric, centered in the star, and of constant velocity. The initial jet direction is the z-axis (i.e. perpendicular to the orbital plane, which may not necessarily be the case), the y-axis goes first through the star and then through the compact object location, and the x-axis direction corresponds to ex = ey × ez, pointing in the opposite direction to the sense of the orbit.

It has been typically assumed (though not yet proven) that persistent, low-hard state, microquasar jets are mildly relativistic at most (e.g. Fender et al. 2004). Nevertheless, unlike some of the previous studies, which assumed a non-relativistic jet (Yoon & Heinz 2015; Yoon et al. 2016), we consider here that the jet could have a relativistic bulk velocity. This is justified by the fact that even modest Lorentz factors can have a significant impact when computing the jet lateral momentum flux (fjl), and indirectly other physical quantities. It is also worth noting that for a compact object mass of Mco ~ 3 M⊙, a distance of z ~ 1011−1012 cm means ~105−106RSch, RSch = 2GMco/c2 being the Schwarzschild radius if the compact object is a black hole. For a supermassive black hole of 108M⊙ hosted by an active galactic nuclei, this distance would correspond to z ~ 1−10 pc, the typical scale at which the blazar emission, strongly affected by relativistic beaming, is produced (e.g. Nalewajko et al. 2014; Dotson et al. 2015).

The convention Qx = (Q/ 10x) is adopted all through the paper, with Q in cgs units unless otherwise stated.

2.1. Stellar wind impact: recollimation shock

At some distance zi from the compact object, the wind momentum flux can become larger than the lateral momentum flux of the jet, and stop the jet expansion towards the star (e.g. Perucho & Bosch-Ramon 2008).

The distance zi depends on the initial jet half-opening angle, θj, the total stellar wind momentum rate 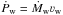Ṗw=Ṁνww\hbox{$\dot{P}_{\rm w}=\dot{M}_{\rm w}\varv_{\rm w}$}, and the jet lateral momentum flux: 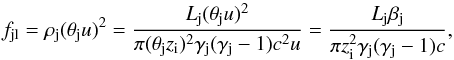fjl=ρj(θju)2=Lj(θju)2π(θjzi)2γj(γj−1)c2u=Ljβjπzi2γj(γj−1)c,\begin{equation} f_{\rm jl}=\rho_{\rm j}(\theta_{\rm j} u)^2=\frac{L_{\rm j}(\theta_{\rm j} u)^2}{\pi (\theta_{\rm j} z_{\rm i})^2 \gamma_{\rm j}(\gamma_{\rm j}-1)c^2u}=\frac{L_{\rm j}\beta_{\rm j}}{\pi z_{\rm i}^2\gamma_{\rm j}(\gamma_{\rm j}-1)c} , \end{equation}(1)with Lj, ρj, u, and γj being the jet power (without accounting for its mass-rest energy), density, velocity, and Lorentz factor, and βj = u/c. 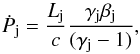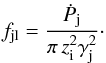The jet lateral momentum flux can also be written as a function of the jet total thrust, Ṗj=Ljcγjβj(γj−1),\begin{equation} \dot{P}_{\rm j}=\frac{L_{\rm j}}{c}\frac{\gamma_{\rm j}\beta_{\rm j}}{(\gamma_{\rm j}-1)} , \end{equation}(2)as fjl=Ṗjπ zi2γj2·\begin{equation} f_{\rm jl}=\frac{\dot{P}_{\rm j}}{\pi\,z_{\rm i}^2\gamma_{\rm j}^2}\cdot \end{equation}(3)Before interacting, the wind propagation and jet expansion are assumed to be supersonic and non-relativistic, whereas as mentioned the jet propagation can be relativistic. Given the wind and jet geometries, the most intense wind-jet lateral interaction takes place within the binary system, on jet scales z ≲ d.

The value of zi can be found from wind and jet-momentum flux balance in the ey-direction: 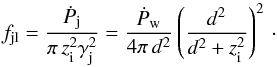fjl=Ṗjπ zi2γj2=Ṗw4π d2(d2d2+zi2)2 ·\begin{equation} f_{\rm jl}=\frac{\dot{P}_{\rm j}}{\pi\,z_{\rm i}^2\gamma_{\rm j}^2}=\frac{\dot{P}_{\rm w}}{4\pi\,d^2}\left(\frac{d^2}{d^2+z_{\rm i}^2}\right)^2\,\cdot \label{balwj} \end{equation}(4)There is a restriction on Eq. (4) to obtain a physical value for zi (see Yoon et al. 2016, for the non-relativistic case): 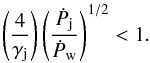(4γj)(ṖjṖw)1/2<1.\begin{equation} \left(\frac{4}{\gamma_{\rm j}}\right)\left(\frac{\dot{P}_{\rm j}}{\dot{P}_{\rm w}}\right)^{1/2}<1. \label{m1} \end{equation}(5)If the condition given in Eq. (5) is fulfilled and the jet supersonic expansion is stopped by the wind, the jet suffers a recollimation shock (e.g. Komissarov & Falle 1997; Perucho & Bosch-Ramon 2008; Bromberg & Levinson 2009; Perucho et al. 2010; Yoon et al. 2016). Otherwise, it implies that the jet is so powerful that fjl is not balanced by the stellar wind at any point, which is the case for jet powers: 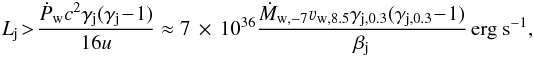Lj>Ṗwc2γj(γj−1)16u≈7 × 1036Ṁw,−7νw,8.5γj,0.3(γj,0.3−1)βj ergs-1,\begin{equation} L_{\rm j}\!>\!\frac{\dot{P}_{\rm w}c^2\gamma_{\rm j}(\gamma_{\rm j}\!-\!1)}{16u} \approx 7\,\times\, 10^{36}\frac{\dot{M}_{\rm w,-7}\varv_{\rm w,8.5}\gamma_{\rm j,0.3}(\gamma_{\rm j,0.3}\!-\!1)}{\beta_{\rm j}}\,{\rm erg~s}^{-1} , \label{recL} \end{equation}(6)with Ṁw units being M⊙ yr-1, and normalizing Ṁw and νw to values typical for high-mass stars.

2.2. Stellar wind impact: jet bending

To calculate the bending angle Φ of the jet due to wind impact, we introduce a non-dimensional parameter, χj, which corresponds to the ratio of jet-intercepting wind and jet thrusts for a conical jet perpendicular to the orbit: 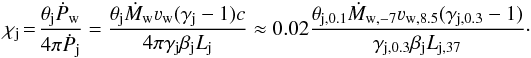χj=θjṖw4πṖj=θjṀwνw(γj−1)c4πγjβjLj≈0.02θj,0.1Ṁw,−7νw,8.5(γj,0.3−1)γj,0.3βjLj,37·\begin{equation} \chi_{\rm j}\!=\!\frac{ \theta_{\rm j}\dot{P}_{\rm w}}{4\pi \dot{P}_{\rm j}}=\frac{\theta_{\rm j}\dot{M}_{\rm w}\varv_{\rm w}(\gamma_{\rm j}-1) c}{4\pi\gamma_{\rm j}\beta_{\rm j} L_{\rm j} }\approx 0.02\frac{\theta_{\rm j,0.1}\dot{M}_{\rm w,-7}\varv_{\rm w,8.5}(\gamma_{\rm j,0.3}-1)}{\gamma_{\rm j,0.3}\beta_{\rm j}L_{\rm j,37}}\cdot \label{eq:Bj} \end{equation}(7)The angle Φ can be then computed numerically in a self-consistent way, i.e. accounting for jet bending. The system of equations solved is presented in Appendix A. An approximate solution to these equations is (see Eq. (A.4)): 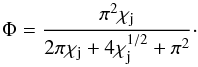Φ=π2χj2πχj+4χj1/2+π2·\begin{equation} \Phi=\frac{\pi^2 \chi_{\rm j}}{2\pi \chi_{\rm j} +4\chi_{\rm j}^{1/2}+\pi^2 }\cdot \label{eq:phi} \end{equation}(8)This approximate solution have the following asymptotical behaviour: 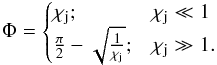Φ={χj≪1χj≫1.\begin{equation} \Phi= \begin{cases} \chi_{\rm j}; & \chi_{\rm j}\ll 1\\ \frac{\pi}{2}-\sqrt{\frac{1}{\chi_{\rm j}}}; & \chi_{\rm j} \gg 1. \end{cases} \label{eq:phiasim} \end{equation}(9)Our approach yields a similar result to the analytical solution obtained by Yoon et al. (2016), but is more general as it is also valid for large jet bending angles.

For bending angles Φ ≲ θj, the wind impact will trigger a weak recollimation shock or a sound wave in the jet, with a negligible impact on the general jet orientation and expansion. For Φ significantly larger than θj, the wind impact can trigger a strong recollimation shock in addition to a substantial deviation of the jet. Bending can be thus considered relevant for the jet evolution if Φ >θj. Since it is expected that θj ≪ 1, one can fix Φ = θj and adopt the solution for χj ≪ 1 to obtain the following constraint for significant jet bending: 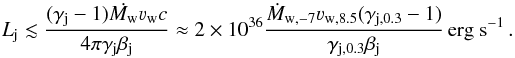Lj≲(γj−1)Mw˙νwc4πγjβj≈2×1036Ṁw,−7νw,8.5(γj,0.3−1)γj,0.3βj ergs-1 .\begin{equation} L_{\rm j}\lesssim \frac{(\gamma_{\rm j}-1)\dot{M_{\rm w}}\varv_{\rm w}c}{4\pi\gamma_{\rm j}\beta_{\rm j}}\approx 2\times10^{36}\frac{\dot{M}_{\rm w,-7}\varv_{\rm w,8.5}(\gamma_{\rm j,0.3}-1)}{\gamma_{\rm j,0.3}\beta_{\rm j}} \,{\rm erg~s}^{-1}\,. \label{eq:ljphi} \end{equation}(10)As the jet becomes bent by the wind impact an angle Φ from the initial jet direction and away from the star, the y-component of the bent jet velocity can be derived as ≈sin [Φ] u.

2.3. Stellar wind impact: orbital effects

Orbital motion affects the propagation of a bent jet through the Coriolis effect. For small jet bending, that is Φ ≲ θj, the jet expansion eventually leads to a jet radius wider than the binary size, and the helical jet pattern gradually smooths out. Otherwise, if Φ is significantly larger than θj, the Coriolis effect should lead to a prominent helical structure of the jet trajectory (see Fig. 2).

If the jet propagates in vacuum, the helical jet trajectory will be ballistic. However, the presence of the wind implies that: (i) the Coriolis force can be enhanced by the wind ram pressure in the ex-direction in the jet flow co-rotating frame; and (ii) the shape of the helical jet on large scales is also affected by the wind presence as the jet, when forced to bend to become helical, pushes against the wind. We discuss (i) in this section, and consider (ii) in Sect. 2.4.

If situation (i) happens, then the distance yturn, covered by the jet in the ey-direction before turning towards the ex-direction because of the Coriolis effect, is significantly smaller than in the ballistic case. Otherwise, the Coriolis force enhancement due to the wind presence can be considered irrelevant.

The ballistic value of yturn is: yturnbal=sin[Φ]uωo≈3×1014sin[Φ]βjωo,−4 cm,\begin{equation} y_{\rm turn}^{\rm bal}=\frac{\sin[\Phi]u}{\omega_{\rm o}}\approx 3\times 10^{14} \frac{\sin[\Phi]\beta_{\rm j}}{\omega_{\rm o,-4}}\,{\rm cm} , \label{balturn} \end{equation}(11)where ωo,−4 = ωo/ 10-4 s is the orbital angular velocity of the compact object, with the normalization corresponding to a period of ~1 day for a circular orbit.

The non-ballistic value of yturn can be roughly estimated assuming balance between the jet momentum flux, and the wind momentum flux in the co-rotating jet flow frame (i.e. in the ex-direction): Ṗj2θbj(yturn2+z2)≈ρwν⊥2=Ṁw4πνw[z2+(yturn+μ d)2](yturn+μ d)2ωo2,\begin{equation} \frac{\dot{P}_{\rm j}}{2\theta_{\rm bj}(y_{\rm turn}^2+z^2)} \!\approx \! \rho_{\rm w}\varv_\perp^2= \frac{\dot{M}_{\rm w}}{4\pi\varv_{\rm w}[z^2+(y_{\rm turn}+\mu\,d)^2]}(y_{\rm turn}+\mu\,d)^2\omega_{\rm o}^2 , \label{nonbal} \end{equation}(12)where θbj ≲ Φ is the half-opening angle of the bent jet, μ = M∗/ (M∗ + Mco), with M∗ being the stellar mass, and the wind momentum flux is computed in the ex-direction adopting the velocity of the co-rotating jet flow frame, ν⊥ = (yturn + μd)ωo. Note that, as the momentum transfer takes place perpendicularly to the jet, the jet thrust has been divided by the lateral surface of the jet.

For yturn ≫ d, Eq. (12) can be simplified to 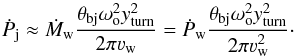Ṗj≈Ṁwθbjωo2yturn22πνw=Ṗwθbjωo2yturn22πνw2·\begin{equation} \dot{P}_{\rm j}\approx \dot{M}_{\rm w} \frac{ \theta_{\rm bj} \omega_{\rm o}^2 y_{\rm turn}^2}{2\pi\varv_{\rm w}}= \dot{P}_{\rm w} \frac{ \theta_{\rm bj} \omega_{\rm o}^2 y_{\rm turn}^2}{2\pi\varv_{\rm w}^2} \cdot \label{yvac1} \end{equation}(13)Making the additional assumption that θbj ~ θj (see Sect. 3.2), and using Eq. (7), one obtains 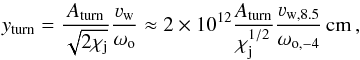yturn=Aturn2χjνwωo≈2×1012Aturnχj1/2νw,8.5ωo,−4 cm ,\begin{equation} y_{\rm turn}= \frac{A_{\rm turn}}{\sqrt{2\chi_{\rm j}}}\frac{\varv_{\rm w}}{\omega_{\rm o}}\approx 2\times 10^{12} \frac{A_{\rm turn}}{\chi_{\rm j}^{1/2}} \frac{\varv_{\rm w,8.5}}{\omega_{\rm o,-4}}\,{\rm cm}\,, \label{yvac2} \end{equation}(14)where Aturn is a constant of the order of one, and accounts (as θbj) for the details of the wind-jet interaction, which are to be characterised through numerical simulations.

For the helical trajectory to be non-ballistic, it is required that 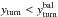yturn<yturnbal\hbox{$y_{\rm turn}<y_{\rm turn}^{\rm bal}$}. Comparing Eqs. (11) and (14), and adopting for simplicity the approximation sin [Φ] ~ Φ ~ χj, the stated condition implies 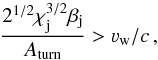21/2χj3/2βjAturn>νw/c ,\begin{equation} \frac{2^{1/2}\chi_{\rm j}^{3/2}\beta_{\rm j}}{A_{\rm turn}}>\varv_{\rm w}/c\,, \end{equation}(15)which can be rewritten as 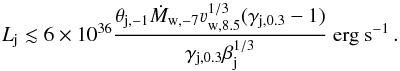Lj≲6×1036θj,−1Ṁw,−7νw,8.51/3(γj,0.3−1)γj,0.3βj1/3ergs-1 .\begin{equation} L_{\rm j}\lesssim 6\times10^{36} \frac{\theta_{\rm j,-1}\dot{M}_{\rm w,-7}\varv_{\rm w,8.5}^{1/3}(\gamma_{\rm j,0.3}-1)}{\gamma_{\rm j,0.3}\beta_{\rm j}^{1/3}} \mbox{ erg s}^{-1}\,. \label{orbL} \end{equation}(16)It is worth noting that, if 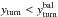yturn<yturnbal\hbox{$y_{\rm turn}<y_{\rm turn}^{\rm bal}$} is fulfilled and the jet were still supersonic when becoming helical, shocks could develop along the non-ballistic trajectory; note that the more relativistic the jet, the stronger the shocks will be (Bosch-Ramon et al. 2012).

2.4. Stellar wind impact: large-scale evolution

The jet flow moves through a channel made of shocked wind and shaped by jet bending plus orbital motion. When the helical trajectory is non-ballistic, the channel forces the jet flow to deviate and the whole helical structure becomes tighter. When the jet starts to become helical, the flow velocity in the ey-direction can be estimated from 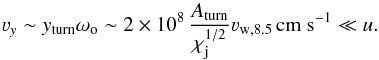νy~yturnωo~2×108 Aturnχj1/2νw,8.5 cms-1≪u.\begin{equation} \varv_y\sim y_{\rm turn}\omega_{\rm o}\sim 2\times 10^8\, \frac{A_{\rm turn}}{\chi_{\rm j}^{1/2}} \varv_{\rm w,8.5} \,{\rm cm~s}^{-1}\ll u . \label{varvy} \end{equation}(17)Such a low value for νy implies that the fast jet flow should be deflected towards the ez- and ex-directions. In addition, while the jet turns, wind is also accumulated in the directions the jet does not temporarily point to. This implies that, as the jet pushes against the accumulated wind material in the ez-direction, the jet flow will slow down in that direction as well. It is therefore expected that, unless the jet flow itself is already strongly braked (or Φ rather small), the flow will move the fastest in the ex-direction; i.e. azimuthally with respect to the binary orbital axis, but in the direction opposite to the orbital motion.

It is difficult to provide a more precise description of the helical jet geometry or the jet flow velocity, as there are several factors that cannot be captured in the present analysis. The hydrodynamics of the wind-jet interaction in the helical structure is complex even assuming that the flows are laminar. In addition, although the jet flow velocity is initially u, its value can be significantly lower if severe jet disruption, and/or wind mass-loading, and/or the formation of a thick shear layer surrounding the jet, occur. All these three processes are related to instability development, which is expected to happen in the present scenario: (i) strong growth of Kelvin-Helmholtz instabilities already on the binary scales (see Perucho & Bosch-Ramon 2008; Perucho et al. 2010; Yoon & Heinz 2015, for numerical computations); (ii) Rayleigh-Taylor instabilities at the wind-jet interface along the helical jet structure (see, e.g., Monceau-Baroux et al. 2014; Ito et al. 2015).

Severe jet disruption can slow down and heat up the jet. On the other hand, pressure decreases away from the binary, and thus the disrupted flow will tend to accelerate. However, strong wind-jet mixing is expected under jet disruption, which will weaken this acceleration. Jet disruption and wind-jet mixing thus affect the jet helical structure, modulating its dynamics and homogenizing it. Unfortunately, it is not known at what distance, or to what degree, the jet and the wind flows mix and the whole structure homogenises, although simulations of high-mass binaries with a non-accreting pulsar (Bosch-Ramon et al. 2012, 2015) suggest that this might happen even after just a few turns of the helical jet.

As explained, both the wind presence and orbital motion tighten the jet helical trajectory, but the jet reacts exerting a force on the surrounding wind, pushing it away from the binary. On the other hand, whereas at binary scales the wind transfers thrust to the jet in the ey-direction, at larger scales orbital motion redistributes this thrust and the final half-opening angle of the jet helical structure should thus be ≲Φ. As noted, the jet pushes wind when turning, hence transferring some momentum back to the wind, although one can consider this shocked/pushed wind surrounding the helical jet as part of the same structure. Far enough from the binary, wind-jet momentum transfer is negligible and the boundary of the helical structure and the unshocked wind motion become parallel (see Fig. 2), pointing radially with respect to the star.

Assuming maximum wind-jet mixing, the final velocity of the helical structure flow away from the binary can be estimated from 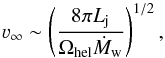ν∞~(8πLjΩhelṀw)1/2,\begin{equation} \varv_{\infty}\sim \left(\frac{8\pi L_{\rm j}}{\Omega_{\rm hel}\dot{M}_{\rm w}}\right)^{1/2}, \end{equation}(18)where Ωhel is the solid angle subtended by the helical jet, as seen from the star at large distances, which can be estimated using Eq. (9) as 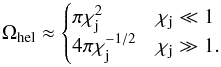Ωhel≈{χj≪1χj≫1.\begin{equation} \Omega_{\rm hel}\approx \begin{cases} \pi \chi_{\rm j}^2 & \chi_{\rm j}\ll 1\\ 4\pi \chi_{\rm j}^{-1/2} & \chi_{\rm j}\gg 1 . \end{cases} \end{equation}(19)We note that the case χj ≫ 1 corresponds to a bent jet pointing in the orbital plane (the relevant angle is then π/ 2−Φ), similar to the case of a high-mass binary hosting a non-accreting pulsar.

For the case of a relatively small Φ-value, one can write 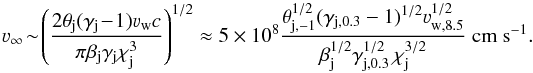ν∞~(2θj(γj−1)νwcπβjγjχj3)1/2≈5 × 108θj,−11/2(γj,0.3−1)1/2νw,8.51/2βj1/2γj,0.31/2 χj3/2cms-1.\begin{equation} \varv_{\infty}\!\sim\! \left(\frac{2\theta_{\rm j}(\gamma_{\rm j}\!-\!1)\varv_{\rm w} c}{\pi\beta_{\rm j} \gamma_{\rm j} \chi_{\rm j}^{3}}\right)^{1/2} \approx 5\,\times\, 10^8 \frac{\theta_{\rm j,-1}^{1/2}(\gamma_{\rm j,0.3}-1)^{1/2}\varv_{\rm w,8.5}^{1/2}}{\beta_{\rm j}^{1/2} \gamma_{\rm j,0.3}^{1/2}\,\chi_{\rm j}^{3/2}} \mbox{ cm s}^{-1}. \label{vinf} \end{equation}(20) This result shows that, on the largest scales, for small bending angles, the jet can eventually recover mildly relativistic velocities, but for moderate Φ-values, say ~0.3, ν∞ is well below u.

2.5. Stellar wind impact: weak-jet case

It is also worth deriving the conditions for the case of a weak jet:

  • (i)

    One way is to set the bending angle to Φ ≳ 1, which yields 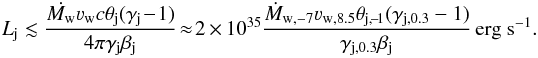Lj≲Mw˙νwcθj(γj−1)4πγjβj≈2 × 1035Ṁw,−7νw,8.5θj,−1(γj,0.3−1)γj,0.3βj ergs-1.\begin{equation} L_{\rm j}\lesssim \frac{\dot{M_{\rm w}}\varv_{\rm w}c\theta_{\rm j}(\gamma_{\rm j}\!-\!1)}{4\pi\gamma_{\rm j}\beta_{\rm j}} \!\approx \! 2\,\times\,10^{35} \frac{\dot{M}_{\rm w,-7}\varv_{\rm w,8.5}\theta_{\rm j,\!-\!1}(\gamma_{\rm j,0.3}-1)}{\gamma_{\rm j,0.3}\beta_{\rm j}} \,{\rm erg~s}^{-1} . \label{eq:ljbj1} \end{equation}(21)

  • (ii)

    A slightly different condition is obtained if one takes ν∞ ~ νw, i.e. 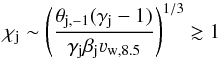χj~(θj,−1(γj−1)γjβjνw,8.5)1/3≳1\begin{equation} \chi_{\rm j}\sim \left(\frac{\theta_{\rm j,-1}(\gamma_{\rm j}-1)}{\gamma_{\rm j}\beta_{\rm j}\varv_{\rm w, 8.5}}\right)^{1/3}\gtrsim 1 \end{equation}(22)yielding 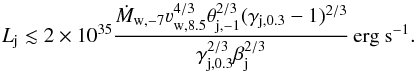Lj≲2×1035Ṁw,−7νw,8.54/3θj,−12/3(γj,0.3−1)2/3γj,0.32/3βj2/3 ergs-1.\begin{equation} L_{\rm j}\lesssim 2\times10^{35} \frac{\dot{M}_{\rm w,-7}\varv_{\rm w,8.5}^{4/3}\theta_{\rm j,-1}^{2/3}(\gamma_{\rm j,0.3}-1)^{2/3}}{\gamma_{\rm j,0.3}^{2/3}\beta_{\rm j}^{2/3}} \,{\rm erg~s}^{-1} . \label{eq:ljbj2} \end{equation}(23)This second condition implies that the large-scale jet evolution is fully dominated by the interaction with the wind and the associated mass-load.

If the jet has less power than these critical values, it will only affect a small volume of the binary surroundings at large distances. The termination regions of such a jet will be strongly affected by the stellar wind dynamics, and not the other way around (e.g. the cases studied for instance in Bosch-Ramon et al. 2011).

3. Summary and discussion

3.1. Results summary

We conclude that if the wind-induced bending angle of the jet is larger than its initial half-opening angle, that is Φ >θj, and the conditions given in Eqs. (10) and (16) are fulfilled, the jets of high-mass microquasars will suffer: (i) asymmetric recollimation shocks within the binary (see Eq. (6)); (ii) bending away from the star (see Eqs. (8) and (10)); (iii) enhanced bending against orbital motion caused by the wind presence under the Coriolis effect (see Eqs. (14) and (16)), and finally (iv) becoming a non-ballistic helical structure. Conclusions (i) and (ii) were already reached by numerical relativistic (Perucho & Bosch-Ramon 2008, 2012; Perucho et al. 2010), and numerical and analytical non-relativistic jet studies (Yoon & Heinz 2015; Yoon et al. 2016), although we generalise here the characterization of the jet bending angle Φ. Conclusions (iii) and (iv) are for the first time discussed in detail here. We also propose that the recollimation shock, jet bending within the binary, and a further non-ballistic helical jet trajectory lead to perturbations that will likely trigger instability growth that will partially or totally disrupt the jet, and can load it with wind material. These perturbations can also be associated to sites for particle acceleration (see Sect. 3.3). Finally, on scales much larger than the binary, we conclude that the jet will likely become a non-relativistic, wind-loaded outflow, with a half-opening angle ≲Φ (see Eq. (20)). On those scales the helical jet pattern and a differentiated wind-jet structure may be more or less washed out depending on the disruptive degree of instabilities within the binary system, and/or in the jet helical structure further up.

3.2. Major sources of uncertainty

The values of the wind and the jet parameters, Ṁw, νw, Lj, γj, and θj, are by themselves uncertain, as it is hard to derive them from observations. Provided that they are known, the wind impact on the jet can be characterised by the angle Φ, which depends on the parameter χj. This angle can be more precisely derived from simulations, although our prescription is consistent with numerical calculations (see Yoon et al. 2016, with the caveat that these simulations were non-relativistic). Additionally, there is the parameter θbj (see Eq. (12)), whose determination particularly requires simulations that have not been carried out yet. The chosen relation θbj ~ θj when deriving Eq. (14) is taken for illustrative purposes, although the θbj-value may easily be larger. Therefore, θbj is possibly the most important source of uncertainty in the estimates derived in this work. This uncertainty ranges from a factor of about one, if the jet is not significantly disrupted on the binary scales, up to an order of magnitude, for full jet disruption at the binary scales. Qualitatively, Φ and θbj are expected to be positively correlated, but only simulations can tell us by how much. Finally, despite being less uncertain than θbj, the parameter that allows for the refinement of yturn in Eq. (14), Aturn, should be also derived from simulations.

3.3. Observational signatures

The periphery of the binary system may be the most suitable region for particle acceleration, and gamma-ray production, and it is also transparent enough to gamma rays above ~10 GeV (e.g. Khangulyan et al. 2008; Bosch-Ramon & Khangulyan 2009). In fact, the wind-jet interaction may be the powering mechanism of the gamma rays in the range ~10-1−104 GeV observed from high-mass microquasars such as Cyg X-1 and Cyg X-3 (Albert et al. 2007; Tavani et al. 2009; Abdo et al. 2009; Sabatini et al. 2010; Malyshev et al. 2013; Bodaghee et al. 2013). The most suitable regions for particle acceleration, and radiation, given the high stellar photon density on these scales, would be the jet recollimation shock. Further up, under the non-ballistic helical jet trajectory, shocks may occur and could accelerate particles, although at those distances energy losses may be dominated already by adiabatic cooling and particle escape, given the different dependences with distance from the binary (r) of radiative versus non-radiative losses, expected to be ∝1 /r2 and 1 /r, respectively. This effect would yield lower radiation efficiencies farther from the binary.

thumbnail Fig. 3

Sketch of the bent jet trajectory (blue dashed line) at binary system scales under the impact of the stellar wind.

Radio emission, produced where the stellar wind is already transparent at low frequencies (e.g. Szostek & Zdziarski 2007; Bosch-Ramon 2009) far enough from the star, could be also detectable. A good candidate could be the region where the jet becomes a helical non-ballistic structure and beyond, where weak shocks and turbulence could occur leading to Fermi I and stochastic particle acceleration (see, e.g. Rieger et al. 2007, in the context of microquasar jets). Regarding radio signatures of wind-jet interaction, there is evidence on milliarcsecond (mas) scales of a sort of helical pattern in the jet of Cyg X-3 (Mioduszewski et al. 2001; Miller-Jones et al. 2004; Tudose et al. 2007), and possible jet bending in Cyg X-1 (Stirling et al. 2001). Unfortunately, we can only provide with approximate quantitative predictions for the jet properties of Cyg X-3 and Cyg X-1 at the onset of the helical pattern, and for the flow velocity very far from the binary. At intermediate distances, numerical simulations accounting for radiation are required to characterise the actual aspect in radio of the helical jet flow, including the opening angle and other features of the radio structures. Nevertheless, one can still consider very approximately two extreme cases regarding the half-opening angle of ≲1° of the jet of Cyg X-1 found by Stirling et al. (2001) (adopting the system inclination of Orosz et al. 2011 for the jet): (i) at the highest end of the possible jet power range (say, up to ~1038 erg s-1, Sell et al. 2015), the jet may be powerful enough for Φ ≲ θj ~ 1°, given the stellar mass-loss rate in the source, ~3 × 10-6M⊙ yr-1 (e.g. Hutchings 1976); (ii) at more moderate but possible values of the jet power, say ~1037 erg s-1, and assuming that the helical jet flow moves vertically with speed ~ucos [Φ], a constraint can be derived for νy<ucos [Φ] /tan [1°] ≈ 5 × 108βjcos [Φ] cm s-1 on scales of ~10 mas (a de-projected linear size of ~6 × 1014 cm). This constraint on νy may be comparable to the value derived from Eq. (17). In fact, the wind and jet properties in Cyg X-1 and Cyg X-3 are such that the jets of these two high-mass microquasars could indeed suffer a recollimation shock within the binary system (see the discussion in Yoon et al. 2016, and references therein). In addition, although the relatively loose restrictions on jet power and wind mass-loss leave the value of Φ rather unconstrained, their winds are powerful and thus a non-ballistic nature for the jets seems likely. On the other hand, evidence of the presence of these jets on arcsecond (e.g. Martí et al. 2000, in the case of Cyg X-3), and even arcminute (e.g. Marti et al. 1996; Gallo et al. 2005, in the case of Cyg X-1), scales implies that they do not fit, as expected, in the category of a weak jet dominated by the wind dynamics (see Eqs. (21) and (23)). In any case, as noted, the high complexity of the process calls for thorough numerical studies for a proper comparison with observations, as the jet dynamics can be strongly non-linear on the multiple scales of interest, and the radio emitting flow may simply be a part of the whole structure.

If one links the wind and the jet properties assuming an accretion scenario (e.g. Bondi spherical accretion), and a magnetically driven jet, one gets a relationship between Lj and Ṁw, as was done in Barkov & Khangulyan (2012). That work conclusions can be used to tentatively predict the value of Φ. For instance, in the case of the powerful gamma-ray binary LS 5039, which hosts a compact object of unknown nature (see the discussion on the nature of the compact object of LS 5039 in Barkov & Khangulyan 2012, and references therein), a putative jet may reach a power ≲1036 erg s-1. For a wind mass-loss ~10-7M⊙ yr-1, this could imply Φ ~ 0.1, meaning that the jet will not be strongly bent. Nevertheless, strong bending cannot be fully discarded in this system, given the parameter uncertainties. It is noteworthy that radio images of this source showed morphology evolution along the orbit. This was attributed to the presence of a non-accreting pulsar in the system (see Moldón et al. 2012), although a bent jet affected by orbital motion cannot be discarded. In fact, a scenario with modest accretion, jet bending plus orbital motion, and some Doppler boosting (to reach the observed gamma-ray fluxes), may explain this source high-energy phenomenology, and is worthy of further study.

3.4. Future prospects

Although simulations of wind interaction with the jets of high-mass microquasars, in the relativistic (e.g. Perucho & Bosch-Ramon 2008, 2012; Perucho et al. 2010) and the non-relativistic (e.g. Yoon & Heinz 2015; Yoon et al. 2016) regimes, have been carried out on binary scales, the impact of orbital motion on the larger scale evolution of these jets has not been studied yet. Here we provide a semi-quantitative description of such a scenario, although numerical computations of relativistic hydrodynamics and eventually magnetohydrodynamics, are required to better characterise the jet evolution, the regions where the jet suffers significant kinetic energy dissipation through shocks, the role of different spatial scales of the non-linear growth of instabilities triggered at the wind-jet interfaces (see, e.g. Bosch-Ramon et al. 2012, 2015; Lamberts et al. 2013, in the context of pulsar-star wind interactions) both on jet disruption and wind-jet mixing, etc. Finally, the magnetic field should be included as, even in the case of low-magnetization plasmas, the field may be amplified in some regions, becoming dynamically important, through flow compression and braking. The magnetic field could also play a role in enhancing or suppressing instability growth, and in radiation.

As a next step, and to check the semi-quantitative predictions done in this work, we plan to carry out three-dimensional, relativistic hydrodynamical simulations including orbital motion, at scales significantly larger than the binary. We note nevertheless that the complexity of the flow evolution, and the different scales of interest (recollimation shock location, jet bending, onset of the helical jet pattern, evolution of the helical structure, etc.), make such numerical calculations very demanding.

Acknowledgments

We thank the anonymous referee for his/her constructive and useful comments. We want to thank Manel Perucho and Dmitry Khangulyan for fruitful discussions and comments. V.B.-R. acknowledges support by the Spanish Ministerio de Economía y Competitividad (MINECO) under grants AYA2013-47447-C3-1-P, and MDM-2014-0369 of ICCUB (Unidad de Excelencia ’María de Maeztu’). This research has been supported by the Marie Curie career integration grant 321520. V.B.-R. also acknowledges financial support from MINECO and European Social Funds through a Ramón y Cajal fellowship. M.V.B. acknowledges partial support by JSPS (Japan Society for the Promotion of Science): No.16H00878, 2503786, 25610056, 26287056, 26800159. M.V.B. also acknowledges MEXT (Ministry of Education, Culture, Sports, Science and Technology): No. 26105521 and RFBR grant 12-02-01336-a.

References

  1. Abdo, A. A., Ackermann, M., et al. (Fermi LAT Collaboration) 2009, Science, 326, 1512 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  2. Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 665, L51 [NASA ADS] [CrossRef] [Google Scholar]
  3. Araudo, A. T., Bosch-Ramon, V., & Romero, G. E. 2009, A&A, 503, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Barkov, M. V., & Bosch-Ramon, V. 2016, MNRAS, 456, L64 [NASA ADS] [CrossRef] [Google Scholar]
  5. Barkov, M. V., & Khangulyan, D. V. 2012, MNRAS, 421, 1351 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bednarek, W., & Sitarek, J. 2013, MNRAS, 430, 2951 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bodaghee, A., Tomsick, J. A., Pottschmidt, K., et al. 2013, ApJ, 775, 98 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bosch-Ramon, V. 2009, A&A, 493, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bosch-Ramon, V. 2013, in Eur. Phys. J. Web Conf., 61, 3001 [Google Scholar]
  10. Bosch-Ramon, V., & Barkov, M. V. 2011, A&A, 535, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bosch-Ramon, V., & Khangulyan, D. 2009, Int. J. Mod. Phys. D, 18, 347 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bosch-Ramon, V., Perucho, M., & Bordas, P. 2011, A&A, 528, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Bosch-Ramon, V., Barkov, M. V., Khangulyan, D., & Perucho, M. 2012, A&A, 544, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bosch-Ramon, V., Barkov, M. V., & Perucho, M. 2015, A&A, 577, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Bromberg, O., & Levinson, A. 2009, ApJ, 699, 1274 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dotson, A., Georganopoulos, M., Meyer, E. T., & McCann, K. 2015, ApJ, 809, 164 [NASA ADS] [CrossRef] [Google Scholar]
  17. Dubus, G., Cerutti, B., & Henri, G. 2010, MNRAS, 404, L55 [NASA ADS] [Google Scholar]
  18. Fender, R. P., Belloni, T. M., & Gallo, E. 2004, MNRAS, 355, 1105 [NASA ADS] [CrossRef] [Google Scholar]
  19. Gallo, E., Fender, R., Kaiser, C., et al. 2005, Nature, 436, 819 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  20. Hutchings, J. B. 1976, ApJ, 203, 438 [NASA ADS] [CrossRef] [Google Scholar]
  21. Ito, H., Matsumoto, J., Nagataki, S., Warren, D. C., & Barkov, M. V. 2015, ApJ, 814, L29 [NASA ADS] [CrossRef] [Google Scholar]
  22. Khangulyan, D., Aharonian, F., & Bosch-Ramon, V. 2008, MNRAS, 383, 467 [NASA ADS] [CrossRef] [Google Scholar]
  23. Komissarov, S. S., & Falle, S. A. E. G. 1997, MNRAS, 288, 833 [NASA ADS] [CrossRef] [Google Scholar]
  24. Krtička, J. 2014, A&A, 564, A70 [Google Scholar]
  25. Lamberts, A., Fromang, S., Dubus, G., & Teyssier, R. 2013, A&A, 560, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Malyshev, D., Zdziarski, A. A., & Chernyakova, M. 2013, MNRAS, 434, 2380 [NASA ADS] [CrossRef] [Google Scholar]
  27. Marti, J., Rodriguez, L. F., Mirabel, I. F., & Paredes, J. M. 1996, A&A, 306, 449 [NASA ADS] [Google Scholar]
  28. Martí, J., Paredes, J. M., & Peracaula, M. 2000, ApJ, 545, 939 [NASA ADS] [CrossRef] [Google Scholar]
  29. Miller-Jones, J. C. A., Blundell, K. M., Rupen, M. P., et al. 2004, ApJ, 600, 368 [NASA ADS] [CrossRef] [Google Scholar]
  30. Mioduszewski, A. J., Rupen, M. P., Hjellming, R. M., Pooley, G. G., & Waltman, E. B. 2001, ApJ, 553, 766 [NASA ADS] [CrossRef] [Google Scholar]
  31. Moldón, J., Ribó, M., & Paredes, J. M. 2012, A&A, 548, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Monceau-Baroux, R., Porth, O., Meliani, Z., & Keppens, R. 2014, A&A, 561, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Muijres, L. E., Vink, J. S., de Koter, A., Müller, P. E., & Langer, N. 2012, A&A, 537, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Nalewajko, K., Begelman, M. C., & Sikora, M. 2014, ApJ, 789, 161 [NASA ADS] [CrossRef] [Google Scholar]
  35. Orosz, J. A., McClintock, J. E., Aufdenberg, J. P., et al. 2011, ApJ, 742, 84 [NASA ADS] [CrossRef] [Google Scholar]
  36. Owocki, S. P., Romero, G. E., Townsend, R. H. D., & Araudo, A. T. 2009, ApJ, 696, 690 [NASA ADS] [CrossRef] [Google Scholar]
  37. Perucho, M., & Bosch-Ramon, V. 2008, A&A, 482, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Perucho, M., & Bosch-Ramon, V. 2012, A&A, 539, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Perucho, M., Bosch-Ramon, V., & Khangulyan, D. 2010, A&A, 512, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Rieger, F. M., Bosch-Ramon, V., & Duffy, P. 2007, Ap&SS, 309, 119 [NASA ADS] [CrossRef] [Google Scholar]
  41. Romero, G. E., & Orellana, M. 2005, A&A, 439, 237 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Romero, G. E., Torres, D. F., Kaufman Bernadó, M. M., & Mirabel, I. F. 2003, A&A, 410, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Romero, G. E., Del Valle, M. V., & Orellana, M. 2010, A&A, 518, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Sabatini, S., Tavani, M., Striani, E., et al. 2010, ApJ, 712, L10 [NASA ADS] [CrossRef] [Google Scholar]
  45. Sell, P. H., Heinz, S., Richards, E., et al. 2015, MNRAS, 446, 3579 [NASA ADS] [CrossRef] [Google Scholar]
  46. Stirling, A. M., Spencer, R. E., de la Force, C. J., et al. 2001, MNRAS, 327, 1273 [NASA ADS] [CrossRef] [Google Scholar]
  47. Szostek, A., & Zdziarski, A. A. 2007, MNRAS, 375, 793 [NASA ADS] [CrossRef] [Google Scholar]
  48. Tavani, M., Bulgarelli, A., Piano, G., et al. 2009, Nature, 462, 620 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  49. Tudose, V., Fender, R. P., Garrett, M. A., et al. 2007, MNRAS, 375, L11 [NASA ADS] [CrossRef] [Google Scholar]
  50. Vilhu, O., & Hannikainen, D. C. 2013, A&A, 550, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Yoon, D., & Heinz, S. 2015, ApJ, 801, 55 [NASA ADS] [CrossRef] [Google Scholar]
  52. Yoon, D., Zdziarski, A. A., & Heinz, S. 2016, MNRAS, 456, 3638 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Set of equations

The evolution of the conical jet bending angle with distance can be described through the following set of ordinary differential equations (ODE), {,\appendix \setcounter{section}{1} \begin{equation} \begin{cases} \displaystyle \frac{{\rm d}\Psi}{{\rm d}t}=-\frac{{\rm d}\theta}{{\rm d}t}-\frac{{\rm d}\phi}{{\rm d}t}= -\frac{\sin[\Psi]}{\sin[\phi+\Psi]}\frac{\beta_{\rm j}}{r} -\frac{2\sin[\Psi]^2}{\cos[\phi]}\frac{\chi_{\rm j}}{r^2} \\ \displaystyle \frac{{\rm d}\phi}{{\rm d}t} = \frac{2\sin[\Psi]^2}{\cos[\phi]}\frac{\chi_{\rm j}}{r^2}\\ \displaystyle \frac{{\rm d}r}{{\rm d}t}=\beta_{\rm j}\cos[\Psi] \end{cases} \label{set} \!\!, \end{equation}(A.1)

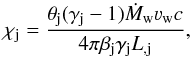where χj=θj(γj−1)Ṁwνwc4πβjγjL,j,\appendix \setcounter{section}{1} \begin{equation} \chi_{\rm j}=\frac{\theta_{\rm j}(\gamma_{\rm j}-1)\dot{M}_{\rm w}\varv_{\rm w} c}{4\pi\beta_{\rm j} \gamma_{\rm j} L_{\rm,j} } , \label{ap:Bj} \end{equation}(A.2)t and r are non-dimensional time and length in units of d/c and d, respectively, Ψ is the angle between the direction from the normal star and the jet velocity, and φ is the angle between the jet velocity and the normal to the orbital plane (see Fig. 3).

We solve the set of ODE (A.1) numerically with the following initial conditions: 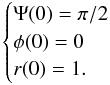{\appendix \setcounter{section}{1} \begin{equation} \begin{cases} \Psi(0)=\pi/2 \\ \phi(0) = 0 \\ r(0)=1. \end{cases} \label{init} \end{equation}(A.3)We then find an approximated formula for the asymptotic solution of the angle φ, where Φ = φ(∞): 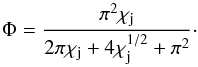Φ=π2χj2πχj+4χj1/2+π2·\appendix \setcounter{section}{1} \begin{equation} \Phi=\frac{\pi^2 \chi_{\rm j}}{2\pi \chi_{\rm j} +4\chi_{\rm j}^{1/2}+\pi^2 }\cdot \label{asimp} \end{equation}(A.4)The approximated formula fits the numerical solution with an accuracy better than 10%.

All Figures

thumbnail Fig. 1

Sketch of the scenario studied in this work at small and middle scales; the main ingredients (star, stellar wind, jet), and physical processes and effects (wind-jet bending, Coriolis effect-jet bending) are shown.
In the text
thumbnail Fig. 2

Sketch of the scenario studied in this work at large scales; the main physical processes and effects (helical jet, wind-jet outflow) are shown.
In the text
thumbnail Fig. 3

Sketch of the bent jet trajectory (blue dashed line) at binary system scales under the impact of the stellar wind.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.