EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 590 (June 2016) A&A, 590 (2016) A85 Full HTML
Free Access
Issue
A&A
Volume 590, June 2016
Article Number A85
Number of page(s) 7
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201628364
Published online 16 May 2016

© ESO, 2016

1. Introduction

Monitoring the eclipsing binaries and their eclipses is a classical technique in stellar astrophysics, which has been used for decades. One can study the eclipsing binary light curve and model its shape, which reveals the physical parameters of both eclipsing components, as well as its orbit (see e.g. Kallrath & Milone 2009). It is still the most precise method to derive the masses, radii, and luminosities of components (see e.g. Southworth 2012).

The role of the eclipsing binaries outside of our Galaxy is undisputable, however their observations have been quite problematic owing to their low brightness and therefore a lack of data for analysis. This issue has changed rapidly during the last two decades thanks to the large surveys like OGLE and MACHO. Owing to the long-lasting photometric monitoring of the Magellanic Clouds, nowadays we know more than 30 000 eclipsing binaries outside of the Galaxy, and many of them are interesting enough for further, more detailed analysis. Hence our contribution to the topic is still valuable.

The study of eclipsing binaries as extragalactic sources was also motivated for another reason. The Magellanic Clouds have slightly different metallicity than our Milky Way Galaxy (see e.g. Westerlund 1997; or Davies et al. 2015), hence one can study whether this effect plays a role in eclipsing binary research, whether it is traceable in the models, or whether our data are sufficiently precise. Another motivation can also be the question of the stellar multiplicity in general. Is the frequency of multiples about the same in Magellanic Clouds as in our own Galaxy? Borkovits et al. (2016) show quite recently that of about 1/12 of all eclipsing binaries observed by the Kepler space telescope probably contain additional components that can be detected only via eclipse timing variations.

Table 1

Identification of the analysed systems.

Table 2

Light curve parameters for the analysed systems, the results from PHOEBE.

2. The system selection

Over the last few years, we performed an analysis of several interesting binaries located in the Magellanic Clouds, which show the apsidal motion (see e.g. Zasche et al. 2015a). All of these binaries are well-detached, slightly eccentric and have orbital periods of the order of couple of days. Thanks to this long-term monitoring of the selected fields, we also collected many useful photometric observations for the stars close to our main targets and checked which of them are adequately interesting for future analysis.

The stars were also checked for their light curves in the Macho (Faccioli et al. 2007), OGLE II (Wyrzykowski et al. 2004), and OGLE III (Graczyk et al. 2011) databases. The data mining from all these data sources, together with our new photometry led to the selection of several quite interesting systems, where the suspicious behaviour of the minima times was found. This was the first selection criterion.

Another selection criterion was the data coverage. Because we focused on periodic variations in the O−C diagrams, we decided to include in our study only systems that have at least one period of the variation already covered (either with the survey data or our own observations). All of the selected stars are of detached or semidetached type.

3. The analysis

For the analysis of the light curves, we used the program PHOEBE (Prša & Zwitter 2005), which is based on the Wilson-Devinney algorithm (Wilson & Devinney 1971). We used the OGLE III data for the light curve modelling, because these are of the best quality, obtained over a long time span and the phase light curves are well covered.

The PHOEBE code enables us to construct the theoretical light curve, which is later used as a template to derive the times of eclipses. Therefore, our light curve fit needs to be as precise as possible. For the light curve fitting, we assumed all the systems were circular, hence the eccentricity was fixed at zero. For the starting ephemerides, we used the same ones as published by Graczyk et al. (2011) in their catalogue. The primary temperatures were derived from the photometric indices as given by Ulaczyk et al. (2012), Massey (2002), and Zaritsky et al. (2004). See Table 1 for more information about the individual systems in our sample.

Table 3

The parameters of the third-body orbits for the individual systems.

Therefore, the set of the fitted quantities was the following: the temperature of the secondary component T2, the inclination angle i, the Kopal’s modified potentials Ωi, and the luminosities of the components Li. Having no information about the radial velocities of the eclipsing pair, the mass ratio value was derived in the following way. For all of the systems, we tried two different configurations – detached as well as semidetached ones. For the detached one we used the method of deriving the mass ratio as introduced in Graczyk (2003), using the assumption that both components are located on the main sequence. For the semidetached ones, the mass ratio was directly computed as a free parameter. For most of the systems the hypothesis of the semidetached configuration led to slightly worse fits with higher values of the χ2 than the detached one. The limb darkening coefficients were interpolated from the van Hammes tables (van Hamme 1993) and the synchronicity parameters (Fi) were also kept fixed at values of Fi = 1. Because we deal with very hot stars here, we also fixed the albedo coefficients Ai at a value 1.0, as well as the gravity darkening coefficients gi = 1.0. And finally, the value of the third light was also computed during the light curve solution. This luminosity L3 cannot necessarily be connected with the eclipsing pair itself (i.e. only an optical double), but here we naturally explain its origin by the third-body hypothesis in the system and directly identify this contribution with the third hidden component. For the results of the fitting process, see the parameters given in Table 2.

To study the period variations in these binaries, we used a well-known light-travel time effect (LTTE) hypothesis (Irwin 1959). This is based on the assumption that there are not only the two stars of the binary, but also a hidden distant third component, orbiting around the eclipsing pair. As the pair moves around a common barycenter of the system, the eclipses of the binary occur earlier or later depending on the current position of the binary with respect to the observer. For a discussion and limitations of the method see e.g. Mayer (1990). A similar method was recently used to discover several dozens of new triple systems in the Kepler data set (see Borkovits et al. 2016 or Gies et al. 2015). Analysis of many eclipsing binaries in the Large Magellanic Cloud (LMC) fields that were observed by our group led to an identification of a few interesting ones, which show some periodic modulation of their orbital period. These systems are now presented in this study in more detail.

During the last few decades, it has been found that most of the early-type stars are multiples (see e.g. Chini et al. 2012 or Duchêne & Kraus 2013). And obviously, all of the stars in our sample are rather massive stars (spectral type B and earlier), hence the LTTE should be detected for many of them. Surprisingly, there is still a lack of studies of the period changes and detection of the third components for the stars in the Magellanic Clouds. Besides a few studies of the apsidal motion in eccentric eclipsing binaries, only one paper was found about the period variations for the systems in the Large Magellanic Cloud (Rittipruk et al. 2015). They state that, after an analysis of 79 EROS systems, nine apsidal motions, eight mass transfers, and 12 LTTE systems were identified. But only one LTTE system is being presented in their paper. However, this one system still has a rather questionable solution with the combination of the mass transfer together with the LTTE hypothesis with the orbital period of about 100 yr (but the data cover only 20 yr).

The times of minima for the analysed systems were derived using the AFP method presented in Zasche et al. (2014). This method uses the light curve template, as derived from PHOEBE, and shifts the template in both x and y axes together with the phased light curve in the particular dataset to achieve the best fit. These datasets were constructed according to the quality and density of the data (for OGLE this usually means one dataset per one year of observations). Using the MACHO, OGLE, and our new data we obtained minima times spread out over 20-yr period for some of the systems. Hence, detecting the orbital periods of the order of several years was possible. All of these data points are given in the table at the CDS, see Table 4 as an example.

The whole fitting process was performed in several steps. At first the ephemerides from Graczyk et al. (2011) were used and the preliminary solution was found in PHOEBE. With this light curve template, the AFP method produced some preliminary minima and we were able to see whether the system was suitable for a further analysis or not. The second step was the period analysis, refining the orbital period, which was then used in PHOEBE for a more detailed modelling of the light curve. With the final light curve template, the final times of minima were derived and the period analysis was performed.

Table 4

Heliocentric minima of the systems used for the analysis.

One can ask what kind of phenomena can be studied in this way and about the suitability of the method of O−C diagram analysis for the eclipsing binaries located in the LMC. A classical explanation of the period changes can be found in various literature published in recent decades, hence we only provide a summary. The periodic modulations of the orbital period are usually explained via the third-body hypothesis and the light-travel time effect (i.e. only the geometrical effect, see above). On the other hand, a dynamical effect of perturbations also exists, which is caused by the third component(s), see, e.g. Borkovits et al. (2015). However, its contribution is only large enough for the tight systems where the third body has a sufficiently short orbital period. The extending, or on the opposite, the shortening of the orbital period of the binary is typically described as the mass transfer between components (or escaping from the system), see, e.g. Hilditch (2001). On the other hand, if we deal with the eccentric orbit and the primary and secondary minima behave in opposite way, we usually apply the hypothesis of the apsidal motion of the binary (Gimenez & Garcia-Pelayo 1983). However, sometimes the changes of period are not strictly periodic, or are even abrupt. The quasiperiodic modulation is often described via some magnetic activity of the components (which is preferably present in the later-type stars), see, e.g. Applegate (1992), and the discontinuous period changes are usually explained as some kind of mass ejections from the components (Wilson & Honeycutt 2014). And, of course, in the real system, all of these mechanisms can be present together, hence their contributions have to be summed up. A review on this topic can be found in, for example, Sterken (2005). The results of our fitting is presented below in Table 3.

thumbnail Fig. 1

Light curves of the analysed systems.

4. Individual systems

In the tables and pictures, we decided to use an abbreviation of the long OGLE names. Therefore, instead of, for example, OGLE-LMC-ECL-06242, we use only the #06242 for increased clarity.

Because the method of analysis is the same for all of the studied systems and the results are sometimes similar, we focus only on the most interesting ones in our sample and discuss them in more detail in the following subsections.

4.1. OGLE-LMC-ECL-08823

The most interesting system in our sample is definitely OGLE-LMC-ECL-08823, which is also the hottest one, of earliest spectral type, and also probably the most massive. This is in fact the only star in our sample that was analysed before. Foellmi et al. (2003) published the study of the Wolf-Rayet stars in Magellanic Clouds and this star was also included. They find that it is of WN4b spectral type, while the secondary is probably an O5 star. The effective temperature of 79 000 K, as listed in Table 2, is taken from this paper. The spectra of the system were studied, but the secondary radial velocities were not derived, hence we only deal with the SB1-type binary.

We used OGLE III data for the light curve modelling. As well as this data set, we used OGLE II and MACHO photometry to determine minima times. With its rather long orbital period of about 18 days, it is also the longest period star in our study. However, owing to its long period, we were not able to obtain any new observation of its eclipses, hence the time span of the minima times is only limited to about 16 yr. For the light curve modelling, we used the assumption that the mass ratio value is q = 2.67 (coming from a rough estimation of masses of WN4 and O5V stars). As one can see in Fig. 1, the light curve fit is not perfect and the whole light curve is probably somehow distorted (upper parts of the primary minimum seems to be wider), and the secondary minima are only shallow. For this reason, we decided to use only the primary minima for the period analysis. From Fig. 2, it is clear that the orbital period is modulated with a period of about 8.9-yr. However, its amplitude is so large, that it produces an unrealistically high value of the mass function for the third component. Thus, its minimal mass (assuming M12 = 55 M⊙) also resulted in more than 100 M⊙, which seems to be a rather improbable solution. Therefore, we have to conclude that, for this system, the LTTE hypothesis probably produces spurious results, or the period changes are abrupt and caused by another mechanism. However, the publications on the period changes in Wolf-Rayet stars are still very rare these days.

thumbnail Fig. 2

O−C diagrams of the analysed systems. The individual primary and secondary minima are denoted by dots and open circles, respectively. Larger symbols correspond to the more precise measurements. The solid lines indicate the final fit.

4.2. OGLE-LMC-ECL-19996

The second very interesting case is OGLE-LMC-ECL-19996, which is also one of the stars with the earliest spectral type in the LMC. This star has not been studied before and only the photometry from the OGLE and MACHO surveys exist.

We carried out the analysis of its light curve (from OGLE-III), as well as the period analysis using all of the available photometry. Our new data from La Silla cover more than 1200 days during seasons 2012−16. Thanks to all of these data, we were able to reliably identify the period variation with the period of about seven years and the surprisingly high amplitude of about 0.040 days, see Table 2. The resulting mass function of the third body is of about 6.48 M⊙ which, as far as we know, is the highest value among LTTE systems ever studied. However, even despite its large value, this kind of solution can still be considered a credible one. It produced the minimal mass of the third body of about 26 M⊙, which is practically the same as the total mass of the eclipsing pair itself (assumed M12 = 26M⊙). However, this is not in contradiction with the light curve solution, because it also resulted in the highest value of the third light in our sample of stars (see Table 2) and its value is in perfect agreement with the predicted third-body mass.

4.3. OGLE-LMC-ECL-20162

Another interesting example is the star OGLE-LMC-ECL-20162, which has also been studied only very briefly in the past. Massey et al. (2012) published its spectral type as O9V. Therefore, we fixed T1 = 33 000 K for our light curve solution (Pecaut & Mamajek 2013).

Performing the light curve fitting, as well as the period analysis of the system, we found that there is also probably the third component with the orbital period of about 5.4 yr. This type of object (located on the main sequence) should have about the same luminosity as the eclipsing components. This result is in rough agreement with our light curve solution as presented in Table 2.

However, what makes this system more interesting is the fact that some kind of flares were observed in the light curve. This is most visible in the OGLE data (see Fig. 3), having the amplitude of about 0.1 mag. However, the MACHO photometry would also indicate some variability of the light curve shape (however, with no flares). The first event is zoomed in Fig. 3, where we also plotted the residuals of the light curve fit. Its nature is still questionable, because a flare, with such a long duration in such an early-type star is rather improbable. On the other hand, its shape would also indicate that the gravitational lensing event is controversial (because it is not perfectly symmetric and its duration is rather long). What seems to be remarkable is the fact that another flare-like event occurs about 2050 days after the first one, while the predicted orbital period of the third body is only about 100 days shorter (forcing the fit to have 2050-day period yielded the χ2 value to be about 7% higher). Therefore, only further analysis would resolve the question about the nature of this phenomenon.

4.4. OGLE-LMC-ECL-09971

The last system, which we would like to feature, is the OGLE-LMC-ECL-09971. No analysis can be found in the literature, hence we deal only with very limited information about the star.

However, the light curve fitting was carried out and the solution is presented in Table 2, where we can see that the third light resulted only in a rather small value. But also the third body, the result of the O−C diagram analysis, has a small mass. On the other hand what makes this system remarkable is the fact that the individual primary and secondary minima in the O−C diagram, plotted in Fig. 2, shows that the orbit could have a non-zero eccentricity. Residuals after subtracting the LTTE fit show that the secondary minima occur slightly later than the primaries, however the difference is only very small and only future dedicated observation or spectroscopy will reveal whether the orbit is slightly eccentric or circular.

thumbnail Fig. 3

Photometry from the OGLE-III survey of the star OGLE-LMC-ECL-20162 (top). The first flare-like/lensing-like event is also plotted and zoomed (bottom) but only with the data that ranges from HJD 2 452 540 to 2 452 740 after subtraction of the light curve fit (i.e. residuals from the solution used for the complete analysis).

5. Results and discussion

The methods for analysing eclipsing binaries are nowadays classical and used almost routinely. However, this kind of analysis can still bring new and surprising results, especially when we apply these methods to new kind of binaries. This is the case of this study, which presents an analysis of the period changes of binaries outside of the Milky Way Galaxy.

We applied classical LTTE hypothesis to eight selected eclipsing systems of early spectral type from the LMC and found that third components probably exist with rather short orbital periods of a couple of years. The significant selection effect has a role because we only deal with limited amounts of data points that cover about 20 years (and, moreover, the selection also has an effect on the sample of binaries, i.e. only massive ones). This is the first study of its kind of extragalactic sources and we have shown that this type of analysis is also suitable for the stars outside of our Galaxy.

People may have quesitons about the quality of the input data and the conclusiveness of the LTTE fit. We are aware that some of the minima times have rather poor quality and their respective uncertainties are comparable with the amplitudes of the LTTE (this applies mostly for the old MACHO data). One the other hand, it is only because of these older data points that we are able to identify the period changes with longer periods.

The analysis has shown that the predicted third bodies found via the period changes have rather high masses in general, but this is also due to the fact that the eclipsing binary components are very massive ones. We deal here with the stars of the highest luminosity, the highest mass, and of the earliest spectral type in the LMC and, consequently, the third bodies should also be massive. This finding was supported by the fact that large fractions of the third light were also detected in the light curve solution and these two numbers coincide well with each other for most of the systems.

Another finding from our study is that the dynamical effects of the third bodies on the eclipsing binary orbits are generally small. This can be seen in the last column in Table 3 where the ratio of periods can tell us something about the influence of the third component on the inner orbit and the ratio 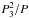P32/P\hbox{$P_3^2/P$} can be considered as a typical timescale of the precession caused by the distant body. As a result, we cannot hope to find any evidence there of precession on a timescale of decades, but rather centuries. This is caused by the inner binary having a relatively short orbital period while, on the contrary, the third body has too long orbital period.

And finally, another remarkable finding is the fact that in our study of eight systems, five orbits were discovered to be circular. If we state that the solution for the system OGLE-LMC-ECL-08823 is odd and cannot be considered as a correct one, hence we deal with of about two-thirds of all circular systems. This result is quite surprising, because our experience of analysing many dozens of LTTE orbits tells us that these systems are mostly eccentric. Also other studies of LTTE in another sets of stars (e.g. Zasche et al. 2015b, or Borkovits et al. 2016) tend to show eccentric solutions. Whether this is also the result of some selection effect or some mechanism of faster circularization for the very massive stars is still not clear.

6. Conclusion

A set of eight luminous eclipsing binaries in LMC were analysed resulting in the finding that all these systems probably contain some additional components. Despite the fact that this is still only a hypothesis, we can consider this finding as a good starting point for future dedicated observations of these systems. Especially those systems like OGLE-LMC-ECL-19996 or OGLE-LMC-ECL-20162 seem to be the most appropriate for follow-up spectroscopic observations because these are relatively bright enough stars, their predicted third components are luminous enough when compared with the eclipsing pairs, and finally the periods of the outer orbits are also relatively short.

Acknowledgments

We acknowledge the anonymous referee for helpful and critical suggestions which significantly improved the manuscript. We thank the MACHO and OGLE teams for making all of the public observations easily available. This work was supported by the Czech Science Foundation grants No. P209/10/0715, and GA15-02112S, and also by the grant MSMT INGO II LG15010. We are also grateful to the ESO team at the La Silla Observatory for their help in maintaining and operating the Danish telescope. The following internet-based resources were used in research for this paper: the SIMBAD database and the VizieR service operated at the CDS, Strasbourg, France, and the NASA’s Astrophysics Data System Bibliographic Services.

References

  1. Applegate, J. H. 1992, ApJ, 385, 621 [NASA ADS] [CrossRef] [Google Scholar]
  2. Borkovits, T., Rappaport, S., Hajdu, T., & Sztakovics, J. 2015, MNRAS, 448, 946 [NASA ADS] [CrossRef] [Google Scholar]
  3. Borkovits, T., Hajdu, T., Sztakovics, J., et al. 2016, MNRAS, 455, 4136 [NASA ADS] [CrossRef] [Google Scholar]
  4. Chini, R., Hoffmeister, V. H., Nasseri, A., Stahl, O., & Zinnecker, H. 2012, MNRAS, 424, 1925 [NASA ADS] [CrossRef] [Google Scholar]
  5. Davies, B., Kudritzki, R.-P., Gazak, Z., et al. 2015, ApJ, 806, 21 [NASA ADS] [CrossRef] [Google Scholar]
  6. Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
  7. Faccioli, L., Alcock, C., Cook, K., et al. 2007, AJ, 134, 1963 [NASA ADS] [CrossRef] [Google Scholar]
  8. Foellmi, C., Moffat, A. F. J., & Guerrero, M. A. 2003, MNRAS, 338, 1025 [NASA ADS] [CrossRef] [Google Scholar]
  9. Gies, D. R., Matson, R. A., Guo, Z., et al. 2015, AJ, 150, 178 [NASA ADS] [CrossRef] [Google Scholar]
  10. Gimenez, A., & Garcia-Pelayo, J. M. 1983, Ap&SS, 92, 203 [NASA ADS] [CrossRef] [Google Scholar]
  11. Graczyk, D. 2003, MNRAS, 342, 1334 [NASA ADS] [CrossRef] [Google Scholar]
  12. Graczyk, D., Soszyński, I., Poleski, R., et al. 2011, Acta Astron., 61, 103 [NASA ADS] [Google Scholar]
  13. Hilditch, R. W. 2001, An Introduction to Close Binary Stars (Cambridge, UK: Cambridge University Press) [Google Scholar]
  14. Irwin, J. B. 1959, AJ, 64, 149 [NASA ADS] [CrossRef] [Google Scholar]
  15. Kallrath, J., & Milone, E. F. 2009, Eclipsing Binary Stars: Modeling and Analysis, Astronomy and Astrophysics Library (New York: Springer-Verlag) [Google Scholar]
  16. Massey, P. 2002, ApJS, 141, 81 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  17. Massey, P., Morrell, N. I., Neugent, K. F., et al. 2012, ApJ, 748, 96 [NASA ADS] [CrossRef] [Google Scholar]
  18. Mayer, P. 1990, Bull. Astron. Inst. Czechosl., 41, 231 [Google Scholar]
  19. Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [NASA ADS] [CrossRef] [Google Scholar]
  20. Prša, A., & Zwitter, T. 2005, ApJ, 628, 426 [NASA ADS] [CrossRef] [Google Scholar]
  21. Rittipruk, P., Hong, K. S., & Kang, Y. W. 2015, PKAS, 30, 211 [NASA ADS] [Google Scholar]
  22. Southworth, J. 2012, in Orbital Couples: Pas de Deux in the Solar System and the Milky Way, Proc. Paris Workshop, 51 [Google Scholar]
  23. Sterken, C. 2005, in The Light-Time Effect in Astrophysics: Causes and cures of the O−C diagram, ASP Conf. Ser., 335, 3 [Google Scholar]
  24. Ulaczyk, K., Szymański, M. K., Udalski, A., et al. 2012, Acta Astron., 62, 247 [NASA ADS] [Google Scholar]
  25. van Hamme, W. 1993, AJ, 106, 2096 [NASA ADS] [CrossRef] [Google Scholar]
  26. Westerlund, B. E. 1997, The Magellanic Clouds (Cambridge, UK: Cambridge University Press) [Google Scholar]
  27. Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [NASA ADS] [CrossRef] [Google Scholar]
  28. Wilson, R. E., & Honeycutt, R. K. 2014, ApJ, 795, 8 [NASA ADS] [CrossRef] [Google Scholar]
  29. Wyrzykowski, L., Udalski, A., Kubiak, M., et al. 2004, AcA, 54, 1 [Google Scholar]
  30. Zaritsky, D., Harris, J., Thompson, I. B., & Grebel, E. K. 2004, AJ, 128, 1606 [NASA ADS] [CrossRef] [Google Scholar]
  31. Zasche, P., Wolf, M., Vraštil, J., et al. 2014, A&A, 572, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Zasche, P., Wolf, M., Vraštil, J., & Pilarčík, L. 2015a, AJ, 150, 183 [NASA ADS] [CrossRef] [Google Scholar]
  33. Zasche, P., Wolf, M., Kučáková, H., et al. 2015b, AJ, 149, 197 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Identification of the analysed systems.

In the text
Table 2

Light curve parameters for the analysed systems, the results from PHOEBE.

In the text
Table 3

The parameters of the third-body orbits for the individual systems.

In the text
Table 4

Heliocentric minima of the systems used for the analysis.

In the text

All Figures

thumbnail Fig. 1

Light curves of the analysed systems.
In the text
thumbnail Fig. 2

O−C diagrams of the analysed systems. The individual primary and secondary minima are denoted by dots and open circles, respectively. Larger symbols correspond to the more precise measurements. The solid lines indicate the final fit.
In the text
thumbnail Fig. 3

Photometry from the OGLE-III survey of the star OGLE-LMC-ECL-20162 (top). The first flare-like/lensing-like event is also plotted and zoomed (bottom) but only with the data that ranges from HJD 2 452 540 to 2 452 740 after subtraction of the light curve fit (i.e. residuals from the solution used for the complete analysis).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.