| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 11 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201628339 | |
| Published online | 10 May 2016 | |
Extended main sequence turn-offs in low mass intermediate-age clusters⋆
1 Observatorio Astronómico, Universidad Nacional de Córdoba,
Laprida 854, 5000 Córdoba, Argentina ;
e-mail:
andres@oac.unc.edu.ar
2
Consejo Nacional de Investigaciones Científicas y Técnicas, Av.
Rivadavia 1917, C1033 AAJ Buenos
Aires, Argentina
3
Astrophysics Research Institute, Liverpool John Moores
University, 146 Brownlow
Hill, Liverpool
L3 5RF,
UK
Received: 18 February 2016
Accepted: 22 March 2016
We present an imaging analysis of four low mass stellar clusters (≲5000 M⊙) in the outer regions of the LMC in order to shed light on the extended main sequence turn-off (eMSTO) phenomenon observed in high mass clusters. The four clusters have ages between 1−2 Gyr and two of them appear to host eMTSOs. The discovery of eMSTOs in such low mass clusters – more than 5 times less massive than the eMSTO clusters previously studied – suggests that mass is not the controlling factor in whether clusters host eMSTOs. Additionally, the narrow extent of the eMSTO in the two older clusters (~2 Gyr) is in agreement with predictions of the stellar rotation scenario, as lower mass stars are expected to be magnetically braked, meaning that their colour magnitude diagrams should be better reproduced by canonical simple stellar populations. We also performed a structural analysis on all the clusters and found that a large core radius is not a requisite for a cluster to exhibit an eMSTO.
Key words: techniques: photometric / Magellanic Clouds / galaxies: individual: LMC
Full Table 2, and Tables 3−5 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/590/A50
© ESO, 2016
1. Introduction
The Large Magellanic Cloud (LMC) hosts a relatively large cluster population with significant numbers of young (less than a few hundred Myr) and intermediate-age (~1−3 Gyr) clusters. Owing to the relative low extinction towards most of them, and the lack of a significant confusion along the line of sight (and known distances), these clusters can often be studied in more detail than their Galactic counterparts. This means that their stellar populations allow for much more stringent tests on isochrones and evolutionary tracks, and the high mass clusters provide an opportunity to study relatively short stellar evolutionary phases.
One surprise that has come from studying the stellar populations of the LMC clusters (and those of its companion, the SMC) is that many of the young and intermediate-age clusters show main sequence turn-offs (MSTOs) that are broader than expected for a single stellar population (SSP; including photometric errors and the effects of binaries). This phenomenon was originally discovered in intermediate-age clusters (e.g. Bertelli et al. 2003; Mackey & Broby Nielsen 2007), but has recently also been found in young massive clusters (e.g. Milone et al. 2015; Correnti et al. 2015; Milone et al. 2016); Bastian et al. 2016. It is now clear that the extended main sequence turn-off (eMSTO) phenomenon is a common feature of massive young (Bastian & Silva-Villa 2013; Niederhofer et al. 2015a; Milone et al. 2016); Bastian et al. 2016 and intermediate-age clusters (e.g. Milone et al. 2009; Goudfrooij et al. 2011; Piatti et al. 2014b). One interpretation of the eMSTOs is that clusters host an age spread of 100−700 Myr within them (e.g. Milone et al. 2009; Goudfrooij et al. 2014). Goudfrooij et al. (2014) suggested a relation between the inferred age spread within the clusters and the escape velocity of the clusters when the clusters were young. In order to correct the current escape velocities of the clusters to the near-initial values, they adopted a model of extreme mass loss, meaning that the clusters would have been significantly more massive in the past. Based on these inferred initial masses (and also that the clusters were significantly more compact in the past), the authors suggest a minimum escape velocity of ~15 km s-1; above this velocity clusters are able to retain stellar ejecta (and accrete material from the surroundings) and form subsequent generations of stars.
Niederhofer et al. (2015a) and Niederhofer et al. (2016), however, found a stronger relation between the inferred age spread and the age of the cluster, with younger clusters hosting smaller age spreads and older clusters hosting larger spreads. This agrees with the observation that younger (< 500 Myr) clusters in the LMC do not show age spreads as large as 300−700 Myr, which are commonly inferred for the intermediate-age clusters (e.g. Bastian & Silva-Villa 2013; Niederhofer et al. 2015b). Niederhofer et al. (2015a) have shown that younger (< 1 Gyr) massive clusters also show evidence of age spreads that continue the age-spread – age relation down to ages of ~50 Myr. Such a correlation between the inferred age spread and the cluster age suggests that the eMSTO phenomenon is not due to true age spreads, but rather to stellar evolutionary effects.
One such stellar evolutionary induced effect that has been suggested is stellar rotation (Bastian & de Mink 2009). Rotation can affect the evolution of the star through increased internal mixing and can also change the colour/magnitude of a star via the geometrical effects of stellar flattening. Brandt & Huang (2015a) used the rotating isochrones from the Geneva models (Ekström et al. 2012; Georgy et al. 2014) and showed that indeed stellar rotation can reproduce the eMSTOs observed in intermediate-age clusters. Niederhofer et al. (2015a) used the same models and found that they predicted a relation between an apparent age spread and cluster age that matches the observations well. D’Antona et al. (2015) modelled the colour magnitude diagram (CMD) of NGC 1856 (~300 Myr, ~105M⊙) and found that rotation could explain the observed eMSTO and also an observed splitting in the CMD just below the MSTO. Whether or not rotation can match the observed “dual main sequences” in young clusters (e.g. NGC 1856; Milone et al. 2015) is still an open question. In principle, rotation is a possible explanation; however, the required rotational velocity distribution may not be able to adequately reproduce the MSTO (e.g. Milone et al. 2016). Further effort in the modelling of stellar rotation is required to address this.
However, the observed splitting of the main sequence is not consistent with an age spread. Future HST-based imaging surveys of more young clusters will be able to explicitly test the prediction of the rotation scenario as the ~100 Myr clusters should show eMSTOs with inferred age spreads of ~30 Myr.
As discussed in Brandt & Huang (2015a, see also Bastian & de Mink 2009, if rotation is the underlying cause of the eMSTO phenomenon, we would expect a peak in the inferred age spread at around 1−1.5 Gyr, followed by a decrease to older ages. For lower mass stars (≲ 1.7 M⊙) magnetic breaking becomes the dominant effect and is expected to slow down rotating stars, minimising the effect of rotation on the host star’s properties. Such a turn-over in the Δ(age)-age plot has been reported by Niederhofer et al. (2016).
While the eMSTO phenomenon has now been routinely observed in the CMDs of massive clusters (with ages between ~100 Myr and ~2 Gyr), there have been suggestions that such a feature is missing in low mass clusters (e.g. Goudfrooij et al. 2014). If age spreads were the cause, this could be due to the lower gravitational potential of these clusters, which would not allow them to retain or accrete the gas required to form a second generation of stars. Hence, a clear prediction of this scenario is that low mass (1000−5000 M⊙) clusters should not show the eMSTO phenomenon (Conroy & Spergel 2011; Goudfrooij et al. 2014). If stellar rotation was the cause, the lack of eMSTOs might be due to the lower number of stars on the MSTO, making any extension difficult to see, or possibly due to a link between the stellar rotation distribution and cluster mass. However, low mass clusters might show the eMSTO in the case of stellar rotation.
If age spreads of the order of ~300−700 Myr were common in massive clusters, we should see evidence of ongoing star-formation (or extended SFHs) in either the observed CMDs of young massive clusters and in the integrated spectra of the clusters. This has been searched for in clusters with ages between a few 10s of Myr and ~600 Myr and masses between 104−107 M⊙. No evidence of such extended star-formation episodes has been found (Bastian et al. 2013; Cabrera-Ziri et al. 2014, 2015; Niederhofer et al. 2015a). This provides evidence against the idea that the eMSTOs are caused by age spreads.
 |
Fig. 1 Spatial distribution of the Bica et al. (2008) catalogue of star clusters in the LMC centred at RA = 05h23m34s, Dec = −69°45′22″ (J2000), projected onto the sky. The objects studied here are shown in colour. |
We present an analysis of four low mass (≲ 5 × 103 M⊙) clusters in the outer regions of the LMC with ages between 1 and 2 Gyr in order to see whether they host the eMSTO phenomenon. Their location in the outer parts of the LMC means that they are not expected to have lost significant fractions of the initial stellar population due to cluster dissolution (e.g. Baumgardt et al. 2013). If eMSTOs are found, this would show that cluster mass (or escape velocity) is not a controlling factor in their appearance, which in turn would suggest that age spreads are not present, i.e. that the eMSTOs are caused by another effect, for example stellar rotation.
This paper is organised as follows. Section 2 provides a description of the data on which this study is based and the data reduction procedures applied. We estimate the extinction, age, and inferred age spread for each of the clusters in Sect. 3 and their structural parameters in Sect. 4. We discuss our results in Sect. 5 and present our main conclusions in Sect. 6.
Observation log of selected clusters.
2. Observations and data reductions
The observations presented here are part of a programme aimed at producing high quality CMDs and radial profiles from g,i photometry of unstudied LMC star clusters located in the outskirts of the LMC and spread over two regions of ~3°× 3° to the south-east following the direction of the Bar and at ~45° clockwise from that direction (see Fig. 1). The selected regions were pointed to provide excellent feedback in exploring comprehensively whether tidal effects have reached the outskirts of the LMC. Other active issues that deserve much more attention are searching for old clusters with masses smaller than 104 M⊙ which should be observable according to the results of recent single stellar population models (Baumgardt et al. 2013) and looking for multiple stellar populations within the cluster sample. Since LMC clusters can be as old as 2−3 Gyr – in addition to the 15 known ancient globular clusters (Piatti 2011; Piatti & Geisler 2013) – we expect that our selected clusters are at most as old as this age regime. The MSTO of a 2−3 Gyr old cluster is at V (≈g) ~21 mag Piatti et al. (2014b), which corresponds to an F0 V dwarf star (Schmidt-Kaler 1982).
We obtained images of four previously selected unstudied LMC clusters with the Gemini South telescope and the GMOS-S instrument through g and i filters. In imaging mode GMOS-S has a field of view of approximately 5.5′× 5.5′ at a scale of 0.16 arcsec per (2 × 2 binned) pixel. The detector array consists of three 2 K × 4 K Hamamatsu chips arranged in a row. Observations were executed in queue mode (under programme GS-2015A-Q-44, PI: Piatti), which enabled the data to be obtained in excellent seeing and under photometric conditions. Short and long exposure images were taken in each filter (g,i) to provide coverage of bright cluster red giant branch stars and of stars at least three magnitudes below the MSTO. The log of observations is presented in Table 1 where the main astrometric, photometric, and observational information is summarised. The data reduction followed the procedures documented in the Gemini Observatory webpage1 and utilised the gemini/gmos (v1.13) package in IRAF2. We performed overscan, trimming, bias subtraction, flattened all data images, etc., once the calibration frames (zeros and flats) were properly combined.
Around 20−50 independent magnitude measurement of stars in the standard fields E5_b F3, 160100-600000 F2, 180000-600000 F1, and 220000-595900 F2 were derived per filter using the apphot task within IRAF in order to secure the transformation from the instrumental to the gi standard system. Standard stars were distributed over an area similar to that of the GMOS array in order to measure magnitudes of standard stars in each of the three chips. The relationships between instrumental and standard magnitudes were obtained by fitting the following equations, 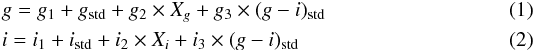 where gj and ij (j = 1, 2, 3) are the fitted coefficients, and X represents the effective airmass. We solved the transformation equations for the three chips with the fitparams task in IRAF simultaneously, and found mean colour terms of −0.025 in g and −0.024 in i, and extinction coefficients of 0.315 in g and 0.216 in i; the rms errors from the transformation to the standard system are 0.029 mag for g and 0.031 for i, respectively, indicating an excellent match to the standard system.
where gj and ij (j = 1, 2, 3) are the fitted coefficients, and X represents the effective airmass. We solved the transformation equations for the three chips with the fitparams task in IRAF simultaneously, and found mean colour terms of −0.025 in g and −0.024 in i, and extinction coefficients of 0.315 in g and 0.216 in i; the rms errors from the transformation to the standard system are 0.029 mag for g and 0.031 for i, respectively, indicating an excellent match to the standard system.
The stellar photometry was performed using the star finding and point spread function (PSF) fitting routines in the daophot/allstar suite of programs (Stetson et al. 1990). For each frame, a quadratically varying PSF was derived by fitting ~100 stars, once the neighbours were eliminated using a preliminary PSF derived from the brightest, least contaminated 30−40 stars. Both groups of PSF stars were interactively selected. We then used the allstar program to apply the resulting PSF to the identified stellar objects and to create a subtracted image, which was used to find and measure magnitudes of additional fainter stars. This procedure was repeated three times for each frame. Finally, we computed aperture corrections from the comparison of PSF and aperture magnitudes by using the neighbour-subtracted PSF star sample. After deriving the photometry for all detected objects in each filter, a cut was made on the basis of the parameters returned by daophot. Only objects with χ< 2, photometric error less than 2σ above the mean error at a given magnitude, and | SHARP | < 1.0 were kept in each filter, and then the remaining objects in the g and i lists were matched with a tolerance of 1 pixel and raw photometry obtained.
We combined all the independent instrumental magnitudes using the stand-alone daomatch and daomaster programs3. As a result, we produced one dataset per cluster containing the x and y coordinates for each star and the respective robust weighted mean magnitudes. The gathered photometric information were standardised using Eqs. (1) and (2). The resulting standardised photometric tables consist of a running number per star, Right Ascension and Declination (J2000.0), the mean g magnitudes and g − i colours, their respective errors σ(g) and σ(g − i), and the number of observations per star. Tables 2 to 5 provide this information for LW 477, LW 483, KMHK 1751, and KMHK 1754, respectively. Only a portion of Table 2 is shown here for guidance regarding their form and content. The complete content of Tables 2−5 is available at the CDS. These tables were used for every subsequent analysis in this work.
In order to evaluate the influence of the photometric errors, crowding effects and the detection limit on the cluster fiducial characteristics in the CMDs, we first examined the quality of our photometry. To do this, we derived the completeness level at different magnitudes by performing artificial star tests on a long exposure image per filter and per cluster. We used the stand-alone addstar program in the daophot package (Stetson et al. 1990) to add synthetic stars, generated bearing in mind the colour and magnitude distributions of the stars in the CMDs (mainly along the main sequence and the red giant branch), and also the radial stellar density profiles of the cluster fields. We evaluated the effect of crowding in five different rings centred on the clusters (0−8, 8−16, 16−32, 32−64 and 64−160 arcsec) and the dependence with the magnitude in bins of 0.5 mag wide along the whole magnitude dynamical range. We added a number of stars equivalent to ~5% of the measured stars in order to avoid significantly higher crowding in the synthetic images than in the original images. On the other hand, to avoid small number statistics, very extensive artificial star tests were performed on each image. We used the option of entering the number of photons per ADU in order to properly add the Poisson noise to the star images.
We then repeated the same steps to obtain the photometry of the synthetic images as described above, i.e. performing three passes with the daophot/allstar routines, making a cut on the basis of the parameters returned by daophot, etc. The errors and star-finding efficiency was estimated by comparing the output and the input data for these stars – within the respective magnitude and colour bins – using the daomatch and daomaster tasks. In our experiments an artificial star is considered recovered if an input–output difference of less than 0.5 mag is found, and if it also satisfies all the photometric selection criteria. In Fig. 2 we show the resultant completeness fractions as a function of magnitude and distance to the centre of LW 483, the most massive cluster in our sample. Figure 2 shows that the 50% completeness level is reached at g ~ 23.5 mag and i ~ 24.0 mag, independently of the distance from the cluster centre (outside the inner 20′′). Thus, we conclude that our photometry is able to reach the 50% completeness level 2−3 mag below the MSTO for the innermost cluster regions. The behaviour of the magnitude and colour errors is represented by error bars in the CMDs shown in Fig. 3.
 |
Fig. 2 Completeness level in g (left) and i (right) bands are shown as a function of the distance from the centre of LW 483. |
3. Fundamental parameters of the clusters
3.1. Cluster ages and extinctions
We first constructed CMDs representing the field along the line of sight towards the individual clusters, which we then used to clean the cluster CMDs. We employed the cleaning procedure developed by Piatti & Bica (2012, see their Fig. 12). The method compares the extracted cluster CMD to a field CMD composed of stars located reasonably far from the object, but not so far as to risk losing the local field-star signature in terms of stellar density, luminosity function, and colour distribution. We decided to clean a circular region around the cluster centre with a radius equal to the cluster radius (rcls, see Sect. 4). The field region was designed to cover an area equal to that of the cluster for an annulus – outer and inner radii equal to 2.236 and 2.0 times rcls – centred on the cluster.
Comparisons of field and cluster CMDs have long been done by comparing the numbers of stars counted in boxes distributed in a similar manner throughout the CMD. However, since some parts of the CMD are more densely populated than others, counting the numbers of stars within boxes of a fixed size is not universally efficient. For instance, to deal with stochastic effects at relatively bright magnitudes (e.g. fluctuations in the numbers of bright stars), larger boxes are required, while populous CMD regions can be characterised using smaller boxes. Thus, the use of boxes of different sizes distributed in the same manner throughout both CMDs leads to a more meaningful comparison of the numbers of stars in different CMD regions. By starting with reasonably large boxes – (Δ(g),Δ(g − i)) = (1.0, 0.5) mag – centred on each star in the annular field CMD and by subsequently reducing their sizes until they separately reach the stars closest in magnitude and colour, we defined boxes which result in the use of larger areas in field CMD regions containing a smaller number of stars, and vice versa. Next, we plotted all these boxes for the field CMD on the cluster CMD and subtracted the star located inside them and closest to each box centre.
 |
Fig. 3 g versus g − i CMDs for the studied clusters. Black filled circles represent stars measured inside the defined field areas, while clear grey filled circles correspond to stars located in the cluster regions (same area size as field regions) which were not eliminated from the field star decontamination procedures. |
We used the cleaned cluster CMDs to estimate some fundamental cluster parameters by matching the observations with the theoretical isochrones of Marigo et al. (2008). In performing this task, it is necessary to deal with the reddening, distance, age, and metallicity. Our strategy consisted of obtaining the reddening values from an independent source, assuming the mean LMC distance modulus for all clusters, and adopting for the mean cluster ages the ages of the isochrones that best reproduced their CMD features. We started with isochrones for a metallicity of [Fe/H] = −0.4 dex (Z = 0.006, Z⊙ = 0.0152), which corresponds to the mean LMC cluster metal content during the last ~2−3 Gyr (Piatti & Geisler 2013), and employed isochrones for other metallicities as required.
Fundamental properties of LMC star clusters.
We made use of the NASA/IPAC Extragalactic Data base4 (NED) to infer Galactic foreground reddening values, E(B − V), for our cluster list (see Table 6). According to Dutra et al. (2001), who studied spectral properties of galaxies behind the LMC, the outermost eastern part of the LMC is optically thin, characterised by an average combined foreground and internal E(B − V) colour excesses of 0.06 ± 0.03 mag. The latter is in excellent agreement with those listed in Table 6. As for the cluster distance moduli, we adopted the same distance modulus for all clusters (m − M)o = 18.49 ± 0.09 mag (de Grijs et al. 2014) and g − Mg = (m − M)o + 3.738 × E(B − V), for RV = 3.1 (Cardelli et al. 1989; Gao et al. 2013); by considering an average depth for the LMC disc of (3.44 ± 1.16) kpc (Δ((m − M)o) ~ 0.15 mag Subramanian & Subramaniam 2009), we derived a smaller age difference than that resulting from the isochrones (characterised by the same metallicity) bracketing the observed cluster features in the CMD.
In the matching procedure, we used subsets of isochrones ranging from Δlog (t yr-1) = −0.3 to +0.3 once they were properly shifted by the corresponding reddening and LMC distance modulus, straddling the initial rough age estimates. We note that by matching different single stellar population (SSP) isochrones we do not take into account the effect of the unresolved binaries or stellar rotation, but focus on the possibility that any unusual broadness at the MSTO might come from the presence of populations of different ages. Mackey et al. (2008a), Magrini et al. (2009), Glatt et al. (2009) and Piatti (2013), among others, showed that a significant fraction of unresolved binaries is not enough to reproduce the eEMSTOs seen in their studied clusters. Moreover, by closely inspecting the matched cluster MSTO regions we have a hint of any uncommon broadness in the studied cluster sample.
Finally, we adopted the cluster age as the age of the isochrone which best reproduced the cluster’s main features in the CMD, namely, the cluster’s main sequence (MS) and red clumps (RCs). Figure 4 shows the results of isochrone matching along with the associated age uncertainties (from Table 6). As far as we are aware, none of the four clusters had been previously studied.
 |
Fig. 4 Cleaned g versus g − i CMDs for stars located within rcls with theortical isochrones superimposed ([Fe/H] = –0.4 dex). The isochrones are separated according to the errors quoted in Table 6. |
3.2. Cluster eMSTOs
3.2.1. Distribution across the MSTO
In order to quantify the MSTO extensions we counted the number of stars (N) located within the parallelograms drawn in Fig. 4 (the clusters CMDs cleaned from field star contamination) using as independent variable the coordinate (X) along the long axis, according to the precepts outlined by Goudfrooij et al. (2011, see their Fig. 14) and used from similar photometry by Piatti (2013). When building the histogram we have taken into account the effects caused by using different binning and by the photometric uncertainties, which cause the points to fall outside their own bin if they do not fall in the bin centre (see e.g. Piatti 2010, 2014; Piatti & Geisler 2013; Piatti et al. 2014a), thus producing a real distribution. For our purposes, we first considered the X range split into bins with sizes 0.10 mag. On the other hand, each X point with its error (σ(X)) covers a segment whose size is given by 2 ×σ(X), and may or may not fall centred on one of the bins, and has dimensions smaller than, similar to, or larger than the bin where it is placed. These scenarios generate a variety of possibilities, in the sense that the X segment could cover from one to five bins depending on its position and size. For this reason, we weighted the contribution of each X point to each of the bins occupied by it, so that the sum of all the weights equals unity. The assigned weight was computed as the fraction of its X segment [2 ×σ(X)] that falls in the bin. In practice, we focused on a single bin and computed the weighted contribution of all the X points to that bin. Then we repeated the calculation for all the bins. The challenge of knowing whether a portion of an X point (an X segment strictly speaking) falls into a bin was solved by taking into account the following possibilities of combination between them. For each interval we looked for X values that fall inside the considered bin, as well as X points where X ± σ(X) could cause them to fall in the considered bin. If X ± σ(X) causes an X point to step over the considered bin, then we consider that the X point may have a value that places it inside the considered interval as well. Therefore, we weighted the contribution of each X point according to their point spread functions. We are confident that our analysis yields accurate morphology and position of the main features in the resulting X distributions.
The resulting histograms are depicted in Fig. 5 with thick black lines, which clearly exhibit extended distributions, particularly for the two younger clusters. We have normalised the histograms for comparison purposes and have avoided the binary sequences, which should be placed to the right of the vertical dotted lines. We then fitted Gaussian functions to Fig. 5 using the IRAF ngaussfit task. These histograms account for the real spread caused by photometric uncertainties. Whenever the latter are not taken into account, we obtain very similars distribuions (see histograms drawn with thick red lines), which suggests that the observed age spread is not driven by photometric errors. The estimated age spreads (including the effects of photometric uncertainties) estimated from the FWHMs are listed in Table 6.
The two younger clusters (LW 477 and especially LW 483) have relatively extended MSTOs with inferred age spreads of ~300 Myr. In contrast, the two older clusters (KMHK 1751 and 1754) have lower inferred age spreads (< 200 Myr). We note that for a given level of photometric error and binarity, and assuming SSPs for all the clusters, we would expect the age spread to increase in the older ones, which is not the case for LW 447 and 483.
 |
Fig. 5 Normalised star counts along the long axis of stars placed within the rectangles drawn in Fig. 4. Thick black and red histograms refer to the star counts obtained by considering or not the photometric uncertainties, respectively. Gaussian distributions fitted to the black histograms are also superimposed. |
3.2.2. Synthetic cluster simulations
In addition to the above tests we also created synthetic clusters under the assumption that they are pure SSPs, and compared them with the observations. The goal of this test is to determine whether the clusters do in fact have MSTOs that are more extended than would be expected for an SSP with photometric errors and binaries in the population.
For each cluster we adopted an age (and extinction/distance modulus) from the previous analyses, and constructed an SSP based on model isochrones. We included errors from the observations and a Salpeter (1955) IMF above 1 M⊙. We sampled the IMF stochastically and included photometric uncertainties taken from the observations. Additionally, we included binaries in our synthetic cluster which we sampled from a flat mass ratio distribution, with a variable binary fraction.
In order to match the synthetic clusters to observations, we took two cuts across the data/models. First, we “verticalised” the main sequence, just below the MSTO and made a histogram of the verticalised colour of observed stars and synthetic populations in a 0.5 mag bin. We adjusted the binary fraction until the observations and models had similar widths (approximated by fitting a Gaussian distribution to the histograms). The number of stars in the synthetic clusters was matched to the observations in this bin. We note that we did not use stars in the observed clusters beyond the mass-ratio = 1 line as these stars are likely old field stars that have not been subtracted with the background. For LW 477 and LW 483 we find binary fractions of 0.6 and 0.35, respectively (within the mass ratio range of 0.5−1.0).
Once the binary fractions were fixed, we then took a cut across the MSTO as discussed above and looked at the histogram of observed/synthetic stars across this cut. Again, the width of the observed distribution and the synthetic populations were approximated by fitting a Gaussian to the distributions. For each cluster we carried out 500 realisations of synthetic clusters with the determined properties (i.e. binary fraction and photometric errors), and compared the widths of the MS (verticalised) and MSTO. The results for LW 477 and 483 are shown in Fig. 6. The x- and y-axes of the panels represents the width difference between the observed and synthetic along the MS and MSTO, respectively.
The fact that the width of the MS for both clusters is similar to the width of the synthetic clusters shows that the stellar populations (binaries and photometric errors) are consistent. On the other hand, the width of the MSTO is larger in both clusters than in average synthetic population. From this we concluded that both LW 477 and LW 483 host extended MSTOs, which are not caused by binarity or photometric errors. However, we note that the observed eMSTO in LW 477 may be consistent with no spread, whereas the spread in LW 483 is much more reliably measured.
On the other hand we found that both KMHK 1751 and 1754 have MSTOs consistent with the expectations of an SSP (plus binaries and photometric errors). Hence, the derived extent of the MSTO in the previous section is an upper limit to their true extent.
 |
Fig. 6 Results of synthetic cluster experiments for LW 477 (top) and LW 483 (bottom). Once the binary populations of each cluster has been estimated (see text for details) we ran 500 stochastic realisations of synthetic clusters with those properties. We then took cuts across the verticalised main sequence (MS) and main sequence turn-off (MSTO), fit the resultant histograms with Gaussian functions, and plotted the difference between the observations and synthetic cluster widths for the MS (x-axis) and MSTO (y-axis). The large filled red circle represents the mean of the 500 realisations. In both clusters the similar MS width between the simulations and observations shows that the clusters are well reproduced by the adopted population properties. However, in both clusters the MSTO is wider in the observations than expected from the simulations, showing that the clusters do indeed host extended MSTOs. |
4. Cluster structural properties
We determined the geometrical centres of the clusters in order to obtain their stellar density radial profiles. The coordinates of the cluster centres and their estimated uncertainties were determined by fitting Gaussian distributions to the star counts in the x and y directions for each cluster. The fits of the Gaussians were performed using the ngaussfit routine in the stsdas/iraf package. We adopted a single Gaussian and fixed the constant to the corresponding background levels (i.e. stellar field densities assumed to be uniform) and the linear terms to zero. The centre of the Gaussian, its amplitude, and its FWHM acted as variables. The number of stars projected along the x and y directions were counted within intervals of 40 pixel wide. In addition, we checked that using spatial bins from 20 to 60 pixels does not result in significant changes in the derived centres. Cluster centres were finally determined with a typical standard deviation of ±10 pixels (~0.4 pc) in all cases. We also took advantage of the deepest g,i images obtained for each cluster to estimate their centres using the stsdas.n2gaussfit routine. During the fitting procedure, we allowed the ellipticity, the position angle, the peak amplitude, and the FWHM to vary from their initial guesses, and kept the background level fixed. From both g,i images we recovered values closer than ±10 pixels from the cluster centres estimated from star counts, which implies that there is no bright star affecting their innermost light profiles.
We then used the resulting centres to check whether the clusters exhibit any elliptical signatures, even though we obtained from n2gaussfit ellipticities equal to zero. To this end, we employed the stsdas.ellipse task, allowing only the ellipticity and the position angle to change (i.e. we held cluster centres fixed). We tried different combinations of first guesses for the ellipticity and the position angle, as well as different steps between successive ellipses, initial semi-major length, etc., in order to be certain that the convergency of the elliptical isophotes fitted at different distances to the clusters’ centres did not depend on those values. The large number of configurations performed led us to conclude that the four clusters do not have any measurable sign of ellipticity.
We also built stellar density profiles based on completeness corrected star counts previously performed within boxes of 40 pixels per side distributed throughout the whole field of each cluster. This box size allowed us to sample the stellar spatial distribution statistically. Thus, the number of stars per unit area at a given radius, r, can be directly calculated through the expression 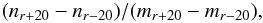 (3)where nj and mj represent the number of stars and boxes, respectively, included in a circle of radius j. We note that this method does not necessarily require a complete circle of radius r within the observed field to estimate the mean stellar density at that distance. This is an important consideration since having a stellar density profile that extends far away from the cluster centre allows us to estimate the background level with high precision. This is necessary in order to derive the cluster radius (rcls). The resulting density profiles expressed as number of stars per arcsec2 are shown in Fig. 7. In the figure, we represented the constructed and background subtracted stellar density profiles with open and filled circles, respectively. Errorbars represent Poisson errors, to which we added the rms error of the background star count to the background subtracted density profiles.
(3)where nj and mj represent the number of stars and boxes, respectively, included in a circle of radius j. We note that this method does not necessarily require a complete circle of radius r within the observed field to estimate the mean stellar density at that distance. This is an important consideration since having a stellar density profile that extends far away from the cluster centre allows us to estimate the background level with high precision. This is necessary in order to derive the cluster radius (rcls). The resulting density profiles expressed as number of stars per arcsec2 are shown in Fig. 7. In the figure, we represented the constructed and background subtracted stellar density profiles with open and filled circles, respectively. Errorbars represent Poisson errors, to which we added the rms error of the background star count to the background subtracted density profiles.
The background corrected surface density profiles were fitted using a King (1962) model through the expression 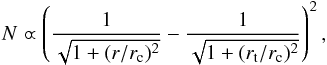 (4)where rc and rt are the core and tidal radii, respectively. The values derived for rc and rt from the fits are listed in Table 7, while the respective King’s curves are plotted with blue solid lines in Fig. 7. As can be seen, the King profiles satisfactorily reproduce the whole cluster extensions. Nevertheless, in order to obtain independent estimates of the cluster half-mass radii, we fitted Plummer’s profiles using the expression
(4)where rc and rt are the core and tidal radii, respectively. The values derived for rc and rt from the fits are listed in Table 7, while the respective King’s curves are plotted with blue solid lines in Fig. 7. As can be seen, the King profiles satisfactorily reproduce the whole cluster extensions. Nevertheless, in order to obtain independent estimates of the cluster half-mass radii, we fitted Plummer’s profiles using the expression 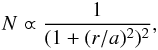 (5)where a is the Plummer radius, which is related to the half-mass radius (rh) by the relation rh~ 1.3a. The resulting rh values are listed in Table 7 and the corresponding Plummer’s curves drawn with orange solid lines in Fig. 7.
(5)where a is the Plummer radius, which is related to the half-mass radius (rh) by the relation rh~ 1.3a. The resulting rh values are listed in Table 7 and the corresponding Plummer’s curves drawn with orange solid lines in Fig. 7.
 |
Fig. 7 Stellar density cluster profiles obtained from star counts for LW 477 (upper left), LW 483 (upper right), KMHK 1751 (bottom left) and KMHK 1754 (bottom right). Open and filled circles refer to measured and background subtracted surface brightness profiles, respectively. Blue and orange solid lines depict the fitted King and Plummer curves, respectively. |
Structural parameters of LMC star clusters.
The masses of the clusters in our sample were derived by comparing the observed integrated magnitude of each cluster (corrected for distance modulus and extinction) to that of the Marigo et al. (2008) SSP models with a Kroupa (2002) stellar initial mass function and a metallicity of Z = 0.008 of the appropriate age. The errors in the mass estimate are driven largely by the choice of models (which were also used in estimating the ages). We estimate the uncertainty in the mass to be σ(log (Mcls/M⊙)) ~ 0.2 dex, i.e. about a factor of ~1.5.
From the derived masses we estimated both the Jacobi tidal radius and the half-mass relaxion time of each cluster. The former was computed from the expression (Chernoff & Weinberg 1990) 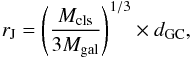 (6)where Mcls is the total cluster mass (see Table 6), Mgal is the LMC mass inside 8.7 kpc ((1.7 ± 0.7) × 1010 M⊙; van der Marel & Kallivayalil 2014), and dGC is the cluster deprojected galactocentric distance. We computed dGC by assuming that the clusters are part of a disc having an inclination i = 35.8° and a position angle of the line of nodes of Θ = 145° (Olsen & Salyk 2002). We refer the reader to Table 1 of Subramanian & Subramaniam (2010), which includes a summary of orientation measurements of the LMC disc plane and other LMC disc quantities, supporting the present adopted values. Table 7 lists the resulting dGC and rJ values. By comparing the rJ values with the cluster tidal radii (see Table 7) we conclude that the four clusters are not tidally truncated, i.e. they are not limited. This means that the clusters are not expected to have lost significant amounts of stellar mass, so that the current masses should reflect their initial masses.
(6)where Mcls is the total cluster mass (see Table 6), Mgal is the LMC mass inside 8.7 kpc ((1.7 ± 0.7) × 1010 M⊙; van der Marel & Kallivayalil 2014), and dGC is the cluster deprojected galactocentric distance. We computed dGC by assuming that the clusters are part of a disc having an inclination i = 35.8° and a position angle of the line of nodes of Θ = 145° (Olsen & Salyk 2002). We refer the reader to Table 1 of Subramanian & Subramaniam (2010), which includes a summary of orientation measurements of the LMC disc plane and other LMC disc quantities, supporting the present adopted values. Table 7 lists the resulting dGC and rJ values. By comparing the rJ values with the cluster tidal radii (see Table 7) we conclude that the four clusters are not tidally truncated, i.e. they are not limited. This means that the clusters are not expected to have lost significant amounts of stellar mass, so that the current masses should reflect their initial masses.
On the other hand, for the half-mass relaxation times we used the equation (Spitzer & Hart 1971) 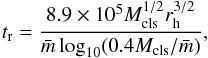 (7)where Mcls is the cluster mass (see Table 6), rh is the half-mass radius (see Table 7), and
(7)where Mcls is the cluster mass (see Table 6), rh is the half-mass radius (see Table 7), and 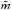 is the average mass of the cluster stars. For simplicity we assume a constant average stellar mass of 1 M⊙. The derived relaxation times are listed in Table 6. These values are in excellent agreement with those obtained from Fig. 20 in Pijloo et al. (2015). Indeed, we found no difference between them (Δ(tr) = 1.3 ± 9.5 Myr), even when the Pijloo et al. (2015) values were interpolated by considering scenarios with and without mass segregation. Additionally, we found a half-mass density range of 6−16 M⊙ pc3 for the studied clusters. These value are much larger than the minimum density a cluster needs to have in order to be stable against the tidal disruption of a galaxy (~0.1 M⊙ pc3, Bok 1934). Accordingly, Wilkinson et al. (2003) also showed that the tidal field of the LMC does not cause any perturbation on the clusters.
is the average mass of the cluster stars. For simplicity we assume a constant average stellar mass of 1 M⊙. The derived relaxation times are listed in Table 6. These values are in excellent agreement with those obtained from Fig. 20 in Pijloo et al. (2015). Indeed, we found no difference between them (Δ(tr) = 1.3 ± 9.5 Myr), even when the Pijloo et al. (2015) values were interpolated by considering scenarios with and without mass segregation. Additionally, we found a half-mass density range of 6−16 M⊙ pc3 for the studied clusters. These value are much larger than the minimum density a cluster needs to have in order to be stable against the tidal disruption of a galaxy (~0.1 M⊙ pc3, Bok 1934). Accordingly, Wilkinson et al. (2003) also showed that the tidal field of the LMC does not cause any perturbation on the clusters.
5. Discussion
Two low mass clusters studied in the present work show evidence of eMSTOs. This feature has now been commonly observed in intermediate-age (1−2 Gyr) clusters as well as younger clusters (NGC 1856, ~300 Myr), although most of the clusters studied to date have much higher stellar masses than those in the current study. The four clusters have masses ≲ 5 × 103 M⊙, and because they are tidally under-filling, they are not expected to have lost significant a number of stars via tidal interactions or two-body relaxation.
Our results suggest that cluster mass (and correspondingly, cluster escape velocity) is not directly linked to the eMSTO phenomena. This is in contradiction to the scenario of Goudfrooij et al. (2014), who suggested that only clusters with escape velocities > 15 km s-1 when they were young (~10 Myr) would be able to retain stellar ejecta and accrete material from the cluster surroundings to undergo extended star-formation episodes (lasting hundreds of Myr). In this scenario, the inferred age spreads from the eMSTO would correspond to actual age spreads within the clusters.
On the other hand, our results confirm recent suggestions that the inferred age spreads found in clusters is related to the age of the cluster, with younger clusters having small inferred age spreads, and older clusters showing larger age spreads, with a peak at ~1.5 Gyr and the inferred age spread decreasing afterwards until it disappears around ~2 Gyr (Brandt & Huang 2015a; Niederhofer et al. 2015a, 2016). This strong correlation with cluster age suggests that a stellar evolutionary effect is the underlying cause, and one potential mechanism is stellar rotation (Bastian & de Mink 2009; Brandt & Huang 2015a; Niederhofer et al. 2015a).
6. Conclusions
We have analysed deep g,i images of four low mass clusters in the outer regions of the LMC. We have used the images to derive the structural parameters of the clusters. We built their number density radial profiles from star counts carried out throughout the observed fields using the final photometric catalogues. Then, we fitted King and Plummer models to derive cluster core, half-mass and tidal radii.
The four clusters were found to be of relatively small size (<22 pc) and are tidally under-filling as well; their Jacobi radii are larger than the cluster radii. The four clusters have core radii of 2.7 pc, which are smaller than the values expected for intermediate-age massive clusters with eMSTOs (e.g. Mackey et al. 2008b; Keller et al. 2011). Indeed, Keller et al. (2012) proposed that the eMSTOs are a common pathway for massive stellar clusters. The studied cluster sample seems to be dynamically evolved since their estimated relaxation times are many times smaller than the cluster ages (age/tr ~ 4−13).
One of the goals of the present work was to search for the eMSTOs, which are now a commonly observed feature of young (100−300 Myr) and intermediate-age (1−2 Gyr) massive clusters in the LMC/SMC. We have constructed g − i versus g CMDs and fit isochrones to the data after accounting for the distance modulus and extinction. We find that LW 477 and LW 483 have similar ages, 1.25 Gyr, while clusters KMHK 1751 and 1754 are older, both with an age of ~2 Gyr.
We find that the two young clusters (LW 477 and 483) show eMSTOs with inferred age spreads (corrected for photometric errors) of ~300 Myr. The eMSTO in LW 483 appears to be more robust than LW 477. These inferred age spreads are in agreement with those of much more massive clusters of similar age (e.g. Rubele et al. 2010, 2011; Goudfrooij et al. 2011; Niederhofer et al. 2016, ~400−500 Myr). This is the first time that eMSTOs have been observed in such low mass clusters, the discovery of which suggests that mass is not an important factor in controlling whether clusters host eMSTOs. This is in contradiction to the scenario of Goudfrooij et al. (2014) who suggest mass (in fact, escape velocity) is the controlling factor in the eMSTO phenomenon.
For the two older clusters in our sample (KMHK 1751 and 1754), we find that both are consistent with a small age spread (< 200 Myr), much smaller than that found for the two young clusters. This is consistent with the stellar rotation scenario, which predicts that after 1−1.5 Gyr the inferred age spreads should decrease as lower mass stars (which are affected by magnetic breaking) enter the MSTO (Brandt & Huang 2015a; Niederhofer et al. 2015a).
Our observations have explicitly tested the role of cluster mass in the eMSTO phenomenon, and we find that it does not play a significant part. Taken together with other recent results in the literature (Li et al. 2014; Brandt & Huang 2015b,a; Niederhofer et al. 2015b,a, 2016), our results do not favour actual age spreads as the origin of the eMSTO phenomenon, and favour a stellar evolutionary effect, such as stellar rotation. While stellar rotation may explain the MSTO phenomenon, high-precision CMDs of younger clusters have revealed features (e.g. dual main sequences) that may be difficult to explain within the rotational scenario. The present results point to the need of high precision HST imaging of these and other low mass intermediate-age clusters to further constrain the populations within the clusters.
http://ned.ipac.caltech.edu/. NED is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with NASA.
Acknowledgments
N.B. gratefully acknowledges financial support from the Royal Society (University Research Fellowship) and the European Research Council (ERC-CoG-646928, Multi-Pop). Based on observations obtained at the Gemini Observatory (Programme: GS-2015A-Q-44), which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (US), the Science and Technology Facilities Council (United Kingdom), the National Research Council (Canada), CONICYT (Chile), the Australian Research Council (Australia), Ministério da Ciència, Tecnologia e Inovação (Brazil) and Ministerio de Ciencia, Tecnología e Innovación Productiva (Argentina). We thank the anonymous referee whose thorough comments and suggestions allowed us to improve the manuscript.
References
- Bastian, N., & de Mink, S. E. 2009, MNRAS, 398, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., & Silva-Villa, E. 2013, MNRAS, 431, L122 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., Cabrera-Ziri, I., Davies, B., & Larsen, S. S. 2013, MNRAS, 436, 2852 [Google Scholar]
- Baumgardt, H., Parmentier, G., Anders, P., & Grebel, E. K. 2013, MNRAS, 430, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Bertelli, G., Nasi, E., Girardi, L., et al. 2003, AJ, 125, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Bica, E., Bonatto, C., Dutra, C. M., & Santos, J. F. C. 2008, MNRAS, 389, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Bok, B. J. 1934, Harvard College Observatory Circular, 384, 1 [Google Scholar]
- Brandt, T. D., & Huang, C. X. 2015a, ApJ, 807, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, T. D., & Huang, C. X. 2015b, ApJ, 807, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera-Ziri, I., Bastian, N., Davies, B., et al. 2014, MNRAS, 441, 2754 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera-Ziri, I., Bastian, N., Longmore, S. N., et al. 2015, MNRAS, 448, 2224 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chernoff, D. F., & Weinberg, M. D. 1990, ApJ, 351, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., & Spergel, D. N. 2011, ApJ, 726, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Correnti, M., Goudfrooij, P., Puzia, T. H., & de Mink, S. E. 2015, MNRAS, 450, 3054 [NASA ADS] [CrossRef] [Google Scholar]
- D’Antona, F., Di Criscienzo, M., Decressin, T., et al. 2015, MNRAS, 453, 2637 [NASA ADS] [Google Scholar]
- de Grijs, R., Wicker, J. E., & Bono, G. 2014, AJ, 147, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Dutra, C. M., Bica, E., Clariá, J. J., Piatti, A. E., & Ahumada, A. V. 2001, A&A, 371, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gao, J., Jiang, B. W., Li, A., & Xue, M. Y. 2013, ApJ, 776, 7 [Google Scholar]
- Georgy, C., Granada, A., Ekström, S., et al. 2014, A&A, 566, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glatt, K., Grebel, E. K., Gallagher, III, J. S., et al. 2009, AJ, 138, 1403 [NASA ADS] [CrossRef] [Google Scholar]
- Goudfrooij, P., Puzia, T. H., Kozhurina-Platais, V., & Chandar, R. 2011, ApJ, 737, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Goudfrooij, P., Girardi, L., Kozhurina-Platais, V., et al. 2014, ApJ, 797, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, S. C., Mackey, A. D., & Da Costa, G. S. 2011, ApJ, 731, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, S. C., Mackey, A. D., & Da Costa, G. S. 2012, ApJ, 761, L5 [NASA ADS] [CrossRef] [Google Scholar]
- King, I. 1962, AJ, 67, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Li, C., de Grijs, R., & Deng, L. 2014, Nature, 516, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Mackey, A. D., & Broby Nielsen, P. 2007, MNRAS, 379, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Mackey, A. D., Broby Nielsen, P., Ferguson, A. M. N., & Richardson, J. C. 2008a, ApJ, 681, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Mackey, A. D., Wilkinson, M. I., Davies, M. B., & Gilmore, G. F. 2008b, MNRAS, 386, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Magrini, L., Sestito, P., Randich, S., & Galli, D. 2009, A&A, 494, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milone, A. P., Bedin, L. R., Piotto, G., & Anderson, J. 2009, A&A, 497, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milone, A. P., Bedin, L. R., Piotto, G., et al. 2015, MNRAS, 450, 3750 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Marino, A. F., D’Antona, F., et al. 2016, MNRAS, 458, 4368 [NASA ADS] [CrossRef] [Google Scholar]
- Niederhofer, F., Georgy, C., Bastian, N., & Ekström, S. 2015a, MNRAS, 453, 2070 [NASA ADS] [CrossRef] [Google Scholar]
- Niederhofer, F., Hilker, M., Bastian, N., & Silva-Villa, E. 2015b, A&A, 575, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Niederhofer, F., Bastian, N., Kozhurina-Platais, V., et al. 2016, A&A, 586, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olsen, K. A. G., & Salyk, C. 2002, AJ, 124, 2045 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E. 2010, A&A, 513, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piatti, A. E. 2011, MNRAS, 418, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E. 2013, MNRAS, 430, 2358 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E. 2014, MNRAS, 437, 1646 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E., & Bica, E. 2012, MNRAS, 425, 3085 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E., & Geisler, D. 2013, AJ, 145, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E., del Pino, A., Aparicio, A., & Hidalgo, S. L. 2014a, MNRAS, 443, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Piatti, A. E., Keller, S. C., Mackey, A. D., & Da Costa, G. S. 2014b, MNRAS, 444, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Pijloo, J. T., Portegies Zwart, S. F., Alexander, P. E. R., et al. 2015, MNRAS, 453, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Rubele, S., Kerber, L., & Girardi, L. 2010, MNRAS, 403, 1156 [NASA ADS] [CrossRef] [Google Scholar]
- Rubele, S., Girardi, L., Kozhurina-Platais, V., Goudfrooij, P., & Kerber, L. 2011, MNRAS, 414, 2204 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt-Kaler, T. 1982, Landolt-Börnstein: Numerical Data and Functional Relationships in Science and Technology, New Series, group VI, Vol. 2b [Google Scholar]
- Spitzer, Jr., L., & Hart, M. H. 1971, ApJ, 164, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B., Davis, L. E., & Crabtree, D. R. 1990, in CCDs in astronomy, ed. G. H. Jacoby, ASP Conf. Ser., 8, 289 [NASA ADS] [Google Scholar]
- Subramanian, S., & Subramaniam, A. 2009, A&A, 496, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Subramanian, S., & Subramaniam, A. 2010, A&A, 520, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Marel, R. P., & Kallivayalil, N. 2014, ApJ, 781, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkinson, M. I., Hurley, J. R., Mackey, A. D., Gilmore, G. F., & Tout, C. A. 2003, MNRAS, 343, 1025 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Spatial distribution of the Bica et al. (2008) catalogue of star clusters in the LMC centred at RA = 05h23m34s, Dec = −69°45′22″ (J2000), projected onto the sky. The objects studied here are shown in colour. |
| In the text | |
 |
Fig. 2 Completeness level in g (left) and i (right) bands are shown as a function of the distance from the centre of LW 483. |
| In the text | |
 |
Fig. 3 g versus g − i CMDs for the studied clusters. Black filled circles represent stars measured inside the defined field areas, while clear grey filled circles correspond to stars located in the cluster regions (same area size as field regions) which were not eliminated from the field star decontamination procedures. |
| In the text | |
 |
Fig. 4 Cleaned g versus g − i CMDs for stars located within rcls with theortical isochrones superimposed ([Fe/H] = –0.4 dex). The isochrones are separated according to the errors quoted in Table 6. |
| In the text | |
 |
Fig. 5 Normalised star counts along the long axis of stars placed within the rectangles drawn in Fig. 4. Thick black and red histograms refer to the star counts obtained by considering or not the photometric uncertainties, respectively. Gaussian distributions fitted to the black histograms are also superimposed. |
| In the text | |
 |
Fig. 6 Results of synthetic cluster experiments for LW 477 (top) and LW 483 (bottom). Once the binary populations of each cluster has been estimated (see text for details) we ran 500 stochastic realisations of synthetic clusters with those properties. We then took cuts across the verticalised main sequence (MS) and main sequence turn-off (MSTO), fit the resultant histograms with Gaussian functions, and plotted the difference between the observations and synthetic cluster widths for the MS (x-axis) and MSTO (y-axis). The large filled red circle represents the mean of the 500 realisations. In both clusters the similar MS width between the simulations and observations shows that the clusters are well reproduced by the adopted population properties. However, in both clusters the MSTO is wider in the observations than expected from the simulations, showing that the clusters do indeed host extended MSTOs. |
| In the text | |
 |
Fig. 7 Stellar density cluster profiles obtained from star counts for LW 477 (upper left), LW 483 (upper right), KMHK 1751 (bottom left) and KMHK 1754 (bottom right). Open and filled circles refer to measured and background subtracted surface brightness profiles, respectively. Blue and orange solid lines depict the fitted King and Plummer curves, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


