| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201628256 | |
| Published online | 20 May 2016 | |
Brackett γ radiation from the inner gaseous accretion disk, magnetosphere, and disk wind region of Herbig AeBe stars
1 Pulkovo Astronomical Observatory of the Russian Academy of Sciences, Pulkovskoe shosse 65, 196140 St. Petersburg, Russia
e-mail: lvtamb@mail.ru
2 The V.V. Sobolev Astronomical Institute of the St. Petersburg University, Petrodvorets, 198904 St. Petersburg, Russia
e-mail: grinin@gao.spb.ru
3 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: weigelt@mpifr-bonn.mpg.de
Received: 5 February 2016
Accepted: 23 March 2016
Various disk and outflow components such as the magnetosphere, the disk wind, the gaseous accretion disk, and other regions may contribute to the hydrogen line emission of young Herbig AeBe stars. Non-LTE modeling was performed to show the influence of the model parameters of each emitting region on the intensity and shape of the Brγ line profile, to present the spatial brightness distribution of each component, and to compare the contribution of each component to the total line emission. The modeling shows that the disk wind is the dominant contributor to the Brγ line rather than the magnetosphere and inner gaseous accretion disk. The contribution of the disk wind region to the Hα line is also considered.
Key words: radiative transfer / techniques: spectroscopic / stars: pre-main sequence / stars: variables: T Tauri, Herbig Ae/Be / stars: winds, outflows / accretion, accretion disks
© ESO, 2016
1. Introduction
Studies over the past several decades have revealed many details of the environments of solar mass young stellar objects, but the environments of intermediate mass Herbig Ae/Be (HAEBEs) stars are relatively poorly understood. The star formation theory developed for T Tauri stars (TTSs) successfully explains various phenomena such as magnetospheric accretion (e.g., Hartmann et al. 1994; Muzerolle et al. 1998, 2001; Kurosawa et al. 2006; Kurosawa & Romanova 2012), and magneto-centrifugal disk wind and jet formation (Königl 1991; Königl & Pudritz 2000; Königl & Salmeron 2011; Ferreira 2007, 2013; Ferreira et al. 2006; Frank et al. 2014, and references therein). To improve our understanding of the physical processes in Herbig Ae/Be stars, it is useful to investigate them with theoretical models developed for TTSs taking into account the special features of HAEBEs (e.g., the high luminosity, rapid rotation, weak magnetic fields).
One promising method of probing the inner environment of young stars is to develop physical models that are able to simultaneously reproduce both the hydrogen emission spectra and the observables of infrared long-baseline interferometry, that is, visibilities, wavelength-differential phases, and closure phases (e.g., Weigelt et al. 2011; Garcia Lopez et al. 2015; Caratti o Garatti et al. 2015; Mendigutía et al. 2015). In the modeling process, all regions emitting hydrogen lines must be taken into account and the individual contribution of each region studied. An important near-infrared emission line for such studies is the Brγ line because it probes the innermost part of the accretion and outflow regions. Infrared interferometry is able to significantly constrain several model parameters used for line profile fitting. The gas that emits hydrogen lines consists of several components. Important components are the magnetosphere of the star where the gas can move within magnetic funnels to the star surface, and the disk wind that can be emitted by different mechanisms: magneto-centrifugal, conical, and X-wind (Königl & Pudritz 2000; Shu et al. 1994a,b; Najita & Shu 1994; Shang et al. 2002; Romanova et al. 2009). At high accretion rates, the midplane of the disk can be heated up to 104 K owing to the dissipation of mechanical energy of turbulent motions (Muzzerolle et al. 2004). At this temperature, the accretion disk itself can be a source of the emission in lines and continuum. In our recent paper (Tambovtseva et al. 2014, TGW14), we considered some of these components – the magnetospheric accretion region, magneto-centrifugal disk winds, and X-winds – and investigated the main properties of these regions.
The centrifugally driven disk wind model was developed by Blandford & Payne (1982) for black holes and later realized by Pudritz & Norman (1986) for young stellar objects, specifically TTSs. It was shown that in the presence of a large-scale magnetic field of the disk whose poloidal component makes an angle of less than 60° with the disk surface, the gas can be lifted along the field lines and accelerated. At great distances from the disk, the toroidal component of the magnetic field can collimate outflows into jets moving perpendicular to the disk. Many aspects of magneto-centrifugal disk winds in TTSs have been studied successfully (e.g., Königl 1991; Wardle & Königl 1993; Königl & Pudritz 2000; Ferreira & Pelletier 1993, 1995; Ferreira & Casse 2004; Ferreira 2007; Lima et al. 2010). Safier (1993) and Garcia et al. (2001) have argued that the rising gas is rapidly heated by ambipolar diffusion. Some observations of jets from TTSs favor models of extended centrifugally driven winds (Ferreira et al. 2006).
In addition to wind regions, in the present paper we consider two regions that can contribute to the Brγ line emission: (1) the inner gaseous accretion disk and hot (evaporating) disk atmosphere and (2) the magnetospheric accretion region. The paper is organized as follows. In Sect. 2 we present the method of solving the radiative transfer problem. Section 3 presents a description of the disk wind model and the results of modeling. In Sect. 4 we describe models of accretion disks emitting in the Brγ line and the results of modeling. We consider both emission from the hot atmosphere of the accretion disk and from the inner region of the accretion disk heated by an internal source (due to the viscous accretion). In these sections, we compare the Brγ line profiles coming from the disk wind and the accretion disk. Section 5 is devoted to modeling the magnetospheric accretion region. The line profiles obtained in these models are also compared with those from the disk-wind models. In Sect. 6 we present Hα line profiles calculated for models with a hot atmosphere of the accretion disk. Section 7 presents a discussion of results and conclusion.
2. Radiative transfer problem
For all emitting components, we performed non-LTE modeling solving the radiative transfer problem. Differences were in the geometry of the regions (flat disk, sphere, and disk wind) and, consequently, in the form of the mass continuity equation and velocity gradient. In principle, the solution to the radiative transfer problem was obtained as follows. We calculated the excitation and ionization state with the help of numerical codes developed by Grinin & Katysheva (1980), Grinin & Mitskevich (1990), and Tambovtseva et al. (2001) for media with large velocity gradients. The radiative terms in the equations of the statistical equilibrium, which takes into account transitions between the discrete levels, are calculated in Sobolev approximation (Sobolev 1960). The intensity of the disk wind radiation emergent at frequencies within the spectral line has been calculated by exact integration over spatial coordinates in the approximation of the full redistribution on the frequency in the co-moving coordinate system (i.e., moving together with gas parcel). We considered 15 atomic levels and continuum. The influence of the higher levels was taken into account under the assumption that they are in thermodynamical equilibrium with the free electrons. For the sake of convenience in the calculations, the population of the atomic levels were expressed through the corresponding Menzel parameters.
The algorithm of the calculations is as follows:
- 1)
We compute the velocity and density distribution throughout the region by choosing the appropriate parameters that determine the wind and accretion geometry, its kinematics, and mass loss/accretion rate;
- 2)
We solve the equation system of statistical equilibrium for the hydrogen atoms in each cell and find the populations of the atomic levels and ionization state in the media by dividing the region of the integration into a grid with cells over coordinates [l,θ,ϕ], and assuming a wind/accretion temperature distribution;
- 3)
We compute intensities of the hydrogen line at the given frequencies in the integration region.
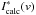 . Then, the required calculated intensity scaled to the star plus disk continuum Icalc(v) is equal to
. Then, the required calculated intensity scaled to the star plus disk continuum Icalc(v) is equal to 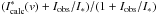 , where 1 refers to the star continuum.
, where 1 refers to the star continuum.
3. Magneto-centrifugal disk wind
We used our disk wind model developed to explain the observed Br line profiles, line visibilities, differential phases, and closure phases in several Herbig Ae/Be stars (Weigelt et al. 2011; Garcia Lopez et al. 2015; Caratti o Garatti et al. 2015). A detailed description of this model and the algorithm for the model computation are given in Grinin & Tambovtseva (2011). Spectral features of the other hydrogen line profiles (including Br γ) depending on the model parameters can be found in Grinin & Tambovtseva (2011) and TGW14. The disk wind model is based on the magneto-centrifugal disk wind model of Blandford & Payne (1982), adapted for the particular case of Herbig AeBe stars. For simplicity, the disk wind consists of hydrogen atoms with constant temperature (~10 000 K) along the wind streamlines. This approximation is in agreement with the so-called warm disk wind models (Safier 1993; Garcia et al. 2001), in which the wind is rapidly heated by ambipolar diffusion to a temperature of ~10 000 K. In these models, the wind electron temperature in the acceleration zone near the disk surface is not high enough to excite the Br line emission. Therefore, in our model, the low-temperature region below a certain height does not contribute to the line emission.
A full description of the disk wind model, can be found in Grinin & Tambovtseva (2011) and Weigelt et al. (2011). We briefly summarize the main model parameters. The list of model parameters is as follows: ω1 and ωN are footpoints of the disk wind launch region for the first and last trajectories of motion or streamlines, respectively, and θ1 is the half opening angle between the first streamline and the vertical axis.
The tangential velocity component u(ω) and poloidal velocity component v(l) change along the streamlines, as given by 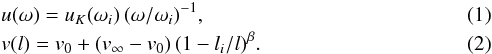 Here, uK (ωi) = (GM∗/ωi)1/2 at the starting point ωi; v0 and v∞ are the initial and terminal velocities, respectively; G is the gravitation constant; M∗ is the stellar mass; and β is a parameter. We assume v0 to be the sound velocity in the disk wind; v∞ =fuK(ωi), where uK(ωi) is the Keplerian velocity at distance ωi from the star; and f is a scale factor. The two last parameters are the mass loss rate Ṁw and γ. The latter regulates the mass loading among the streamlines.
Here, uK (ωi) = (GM∗/ωi)1/2 at the starting point ωi; v0 and v∞ are the initial and terminal velocities, respectively; G is the gravitation constant; M∗ is the stellar mass; and β is a parameter. We assume v0 to be the sound velocity in the disk wind; v∞ =fuK(ωi), where uK(ωi) is the Keplerian velocity at distance ωi from the star; and f is a scale factor. The two last parameters are the mass loss rate Ṁw and γ. The latter regulates the mass loading among the streamlines.
We assume that the accretion disk is transparent to radiation up to the distance of the sublimation radius. Beyond the sublimation radius, the disk is opaque obscuring the disk wind moving away from the observer.
Figure 1 presents the Brγ line profiles for inclinations from pole-on to edge-on calculated for the disk wind models with the following parameters: Ṁw = 1 × 10-7M⊙ yr-1 (model DW1, left), 3 × 10-8M⊙ yr-1 (model DW2, middle), and 1 × 10-8M⊙ yr-1 (model DW3, right). All other parameters are identical in all calculations and are as follows: θ1 = 30°, ω1−ωN = 2R∗−20R∗, γ = 3, β = 5, and f = 5.
 |
Fig. 1 Profiles of the Brackett γ line (normalized to the star continuum) for disk wind models with Ṁw = 1 × 10-7M⊙ yr-1 (model DW1; left), 3 × 10-8M⊙ yr-1 (model DW2; middle), and 1 × 10-8M⊙ yr-1 (model DW3; right). Inclination angles are shown in each panel. |
4. Brackett γ radiation emitted from the inner region of the accretion disk
In order to radiate in Brγ lines (or other hydrogen lines), the accretion disk has to be heated to a temperature exceeding a certain value. Weak Brγ emission appears at the electron temperature of ~6000 K; typical values of electron temperatures which are required for Brγ emission are 8000−10 000 K (as discussed below). Another condition for hydrogen line emission is an acceptable density of the gas. The inner gaseous disk (inward of ~0.1 AU) in the Herbig Ae/Be stars as an emitter in the hydrogen lines has not been the subject of many studies (see, e.g., the review by Dullemond & Monnier 2010). There are two sources of inner gaseous accretion disk heating, external and internal. We will consider both of them.
4.1. External heating of the upper layers of the accretion disk
External mechanisms of disk heating in young stellar objects have been described in many papers (see, e.g., Glassgold et al. 2004, 2007; Gorti & Hollenbach 2004, 2008, 2009; Hollenbach & Gorti 2009, Ercolano et al. 2008, 2009; Gorti et al. 2011). A comprehensive review of the disk photoevaporation and heating mechanisms of the disk surface layer in the young stellar objects is reported in Protostars and Planets VI (PPVI) in the chapter by Alexander et al. (2014). Heating of the disk by high-energy radiation (UV or X-rays) to temperatures of ~103−104 K leads to outflows of matter from the disk surface as a centrifugally launched, pressure-driven wind, which is called a photoevaporative wind. Photoevaporative disk modeling was applied to low-mass T Tauri stars (e.g., TW Hya, Pascucci et al. 2011, 2012). Our calculations of the gas density in the disk surface layers in Herbig Ae stars (see below) show that at great distances from the star, the concentration of the gas is too low to lead to Brγ line emission. Therefore, we consider the hot surface layers of the disk in the range from 2R∗ (~0.02 AU) to 1000R∗ (~10 AU) where the hot gas does not yet evaporate but is able to contribute to the Brγ emission. Since we do not solve the thermal balance problem, we consider an isothermal gas being in the Keplerian motion. Values of the gas temperature were chosen in the range of 6000−10 000 K.
The height of the hot layers were obtained as follows. At each fixed cylindric radius r, we calculated the surface density distribution 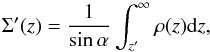 (3)where α is the angle between the incident radiation of the star and the disk surface. We treated it in the same manner as in Kenyon & Hartmann (1987). The mass density at fixed r is
(3)where α is the angle between the incident radiation of the star and the disk surface. We treated it in the same manner as in Kenyon & Hartmann (1987). The mass density at fixed r is 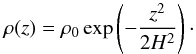 (4)Here ρ0 is the initial mass density at r, H the height of the disk determined as H(r) = H0(r/Rin)p, H0 the initial disk height at the distance Rin (Kenyon & Hartmann 1987), and Rin the inner boundary of the disk. Integration is performed in the vertical direction along z. We choose H0 equal to 0.1Rin and the power index p = 9/8 and 5/4. The latter corresponds to a more flared disk geometry, in which case the disk surface is better illuminated. Since the disks of Herbig Ae stars can be both self-shadowed or flared1 (e.g., Meeus et al. 2001, 2012; Dullemond et al. 2001; Dullemond & Dominik 2004;) we considered both disk geometries. The initial density ρ0 at each cylindric radius was obtained using the expression for the surface density Σ(r) in the minimum mass solar nebula (MMSN) model (e.g., Weidenschilling 1977; Hayashi 1981):
(4)Here ρ0 is the initial mass density at r, H the height of the disk determined as H(r) = H0(r/Rin)p, H0 the initial disk height at the distance Rin (Kenyon & Hartmann 1987), and Rin the inner boundary of the disk. Integration is performed in the vertical direction along z. We choose H0 equal to 0.1Rin and the power index p = 9/8 and 5/4. The latter corresponds to a more flared disk geometry, in which case the disk surface is better illuminated. Since the disks of Herbig Ae stars can be both self-shadowed or flared1 (e.g., Meeus et al. 2001, 2012; Dullemond et al. 2001; Dullemond & Dominik 2004;) we considered both disk geometries. The initial density ρ0 at each cylindric radius was obtained using the expression for the surface density Σ(r) in the minimum mass solar nebula (MMSN) model (e.g., Weidenschilling 1977; Hayashi 1981): 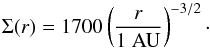 (5)Then
(5)Then 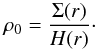 (6)Integration in Eq. (3) is performed until the value of Σ′(z) is equal to the column density Ncol = 1019 atoms cm-2, the value which approximately corresponds to the free pass length of the extreme-ultraviolet (EUV) radiation (see, e.g., Gorti & Hollenbach 2008; Hollenbach & Gorti 2009; Gorti et al. 2011). When integrating, we fix two values of the disk height: the vertical height above the disk midplane z′ at which this condition is fulfilled and the height above the disk midplane z′′ at which Σ′(z) = 1/2Ncol. The difference z′−z′′ gives us the decision height of the heated layer h at the radius r from the star. The double value of this height (2h) can be used as an effective height of the heated surface layer heff. This permits us to use a uniform density distribution for the calculation of the population of atomic levels.
(6)Integration in Eq. (3) is performed until the value of Σ′(z) is equal to the column density Ncol = 1019 atoms cm-2, the value which approximately corresponds to the free pass length of the extreme-ultraviolet (EUV) radiation (see, e.g., Gorti & Hollenbach 2008; Hollenbach & Gorti 2009; Gorti et al. 2011). When integrating, we fix two values of the disk height: the vertical height above the disk midplane z′ at which this condition is fulfilled and the height above the disk midplane z′′ at which Σ′(z) = 1/2Ncol. The difference z′−z′′ gives us the decision height of the heated layer h at the radius r from the star. The double value of this height (2h) can be used as an effective height of the heated surface layer heff. This permits us to use a uniform density distribution for the calculation of the population of atomic levels.
 |
Fig. 2 Height of the heated disk surface layer h vs. distance from the star for two flared geometries: p = 9/8 (solid line) and 5/4 (dashed line). |
Figure 4 in the paper by Gorti et al. (2011) presents the vertical temperature and density distribution in the inner disk of the T Tauri star TW Hya at 0.1 AU. These results were obtained from the solution of the thermal balance problem. Based on these results and on results of the temperature distribution at more remote distances (Gorti & Hollenbach 2008; Gorti et al. 2011), we restricted our model to the outer boundary Rout = 1000R∗ (≈10 AU). Parameters of the disk surface layer models are presented in Table 1.
Figure 2 shows changes in the effective height of the heated disk surface layer with the distance from the star. The results of modeling with the disk height of 0.2R∗ are presented in Fig. 3. The Brγ emission is scarcely seen on the background of the photospheric profiles broadened by the rotation of the star. Therefore, we present only the emission of the Brγ line (without photospheric profiles) normalized to the star continuum. The more flared disk intercepts more radiation from the star, which means that its luminosity is higher (mainly in the far-infrared wavelength region). Nevertheless, in such disks the density of the matter decreases more quickly with distance and height (the temperature is assumed to be the same in both models). Hydrogen lines calculated in these models are formed in the optically thin gaseous atmosphere of the disk owing to recombinations. Under these conditions, the emissivity per unit volume is proportional to the electron number density squared, which results in the smaller line emission for model S2 (p = 5/4) than for model S1 (p = 9/8). In order to obtain more accurate results, it is necessary to solve the thermal balance problem in each model.
 |
Fig. 3 Model profiles of the Brackett γ line (normalized to the star continuum) emitted from the hot layers of an accretion disk. Te = 104 K. Inclination angles are shown. The disk is flared with p = 9/8 (model S1, left) and p = 5/4 (model S2, right). See details in the text. |
Accretion disk model parameters. External heating.
 |
Fig. 4 Left: sketch of the absorption of the hard stellar radiation (red line) by the disk wind. The green line is a shadow zone. Right: points on the disk surface (not to scale). See details in the text. |
Because the heating of the disk atmosphere is caused by the ultraviolet and X-ray radiation generated as a result of the gas accretion onto the star, the efficiency of the photoevaporation process has to be highest when the accretion is in a high phase. However, this is not the case because the intense disk wind and gas in the magnetosphere are able to absorb a significant part of this radiation (Fig. 4). A decrease in the accretion rate during the evolution is followed by a decrease in the mass outflow rate. However, the UV and X-ray luminosity also rapidly decrease (see Fig. 3 in Drake et al. 2014). This question is discussed in the literature on photoevaporative winds. It is expected that at an accretion rate lower than 10-8M⊙ yr-1, the ionizing radiation freely passes the disk wind and accretion column and heats (ionizes) the upper layers of the disk atmospheres (see review by Alexander et al. 2014 and the references therein).
Using our models of the magneto-centrifugal disk wind for two Herbig AeBe stars (Garcia Lopez et al. 2015; Caratti o Garatti et al. 2015), we calculated the column density between the source of external radiation (the polar region of the stellar disk) and the point on the disk surface. The principle scheme of the task is shown in Fig. 4. The disk wind is able to absorb the hard radiation of the central source resulting in a shadow zone (the green line on the disk surface). In this case, the layers heated to temperatures needed for the excitation of the hydrogen lines (~104 K) will be beyond this shadow zones. We took into account that the disk surface is flared and also the changes in the surface disk height with the distance from the star. The results are presented in Fig. 5.
The main parameters of the disk wind models used are as follows. The compact disk wind of the Herbig Ae star HD 163296 (MWC 275; black line in Fig. 5) has a launch region of 0.02−0.04 AU, a half opening angle of 45°, and a mass loss rate of Ṁw = 5 × 10-8M⊙ yr-1. The extended disk wind of the Herbig Be star HD 98922 (red line in Fig. 5) is launched from the region 0.1−1 AU, half opening angle of 30°, and mass loss rate Ṁw = 2 × 10-7M⊙ yr-1. Both models have acceleration parameter β = 5, γ = 3, and gas temperature 10 000 K. The disk wind is transparent for X-rays (0.3−1 kev, NX ~ 1021−1022 cm-2) and far-ultraviolet (FUV; 13.6−6 ev, NFUV> 1022 cm-2, if the radiation is absorbed by the dust) radiation, and it is opaque for EUV radiation (>13.6 ev, NEUV ~ 1017−1018 cm-2). The X-ray and FUV radiation has a large free path length and can heat the gas to temperatures of 2000−3000 K, which is enough for the photoevaporation of the periphery regions of the disk. However, the ionization and heating of the gas to the higher temperatures needed for the formation of the hydrogen emission lines (~104 K) is provided by the EUV radiation (Hollenbash & Gorti 2009; Ercolano & Owen 2010). It has much smaller free path length and is absorbed rather easily near the base of the disk wind. As a result, the circumstellar disk in the region of the disk wind formation and in the region of the shadow created by the disk itself is heated by the FUV and X-ray radiation to a relatively low temperature on the order of few thousand K.
Hollenbach & Gorti (2009), Ercolano & Owen (2010), and Owen et al. (2010) have calculated the intensities of hydrogen lines originating in photoevaporating disk atmospheres. It has been shown that the recombination mechanism of the atomic level excitation leads to very low luminosity of the emission lines in comparison with [NeII] (12.8 μm). In our calculations, we took into account all mechanisms of the populations of the atomic levels including electron collisions. Nevertheless, as is seen from Fig. 3, the Brγ line, which is formed in the disk atmosphere ionized by the EUV radiation, is essentially not seen on the background of the photospheric spectrum of the star.
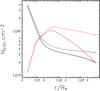 |
Fig. 5 Column gas density in the disk wind between the star and an arbitrary point on the disk surface. Here we used our disk wind models for the Herbig Ae star HD 163296 (MWC 275; black lines) and Herbig Be star HD 98922 (red lines; see text). The disk is flared with p = 9/8 (dashed lines) and p = 5/4 (solid lines). |
4.2. Internal heating of the accretion disk due to accretion viscosity
Another possibility for heating the inner gas disk is to use the accretion viscosity. This is an internal heating mechanism. The vertical temperature structure of such an accretion disk has been described by Calvet et al. (1991, 1992) and D’Alessio et al. (1998). Muzerolle et al. (2004) modified it by replacing the dust opacities with the gas mean opacities to obtain a model of this part of the disk. They used it to study the inner disk structure in Herbig Ae stars, namely UX Ori type stars, in terms of a magnetospheric accretion models. They showed that for accretion rates lower than 10-8M⊙ yr-1, the inner gaseous disk is optically thin, and for mass accretion rates Ṁa ≳ 10-8M⊙ yr-1, the inner disk may be optically thick. According to their calculations, only for Ṁa ~ (10-6−10-7) M⊙ yr-1 the midplane disk temperature can reach the value of 10 000 K. Muzerolle et al. (2004) treated the inner disk as a region between the magnetospheric radius ≲0.04 AU and ~0.5 AU.
Based on these considerations, we adopt the following model of the inner gaseous disk. Our disk starts at the inner radius of 2R∗ (~0.02 AU) and extends till Rout, which is assumed to be 10R∗ (~0.1 AU). The gas temperature obeys the law 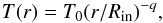 (7)where T0 is the gas temperature at r = Rin and q is a parameter. We considered several disk models with fixed height above the midplane h0 and the fixed boundaries mentioned above. The mass accretion rate and T0 were in the range from 10-8 to 10-6 and from 6000 K to 10 000 K, respectively.
(7)where T0 is the gas temperature at r = Rin and q is a parameter. We considered several disk models with fixed height above the midplane h0 and the fixed boundaries mentioned above. The mass accretion rate and T0 were in the range from 10-8 to 10-6 and from 6000 K to 10 000 K, respectively.
We calculated populations of the hydrogen atomic levels for the cases when h0 is constant and equal to 0.1R∗ and h0 ~ r(h0 = 0.1R∗ at Rin). The mass conservation law is 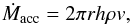 (8)where Ṁacc is the accretion rate, r the distance from the star, h = 2h0 the full height of the disk, ρ the mass density, and v the radial component of the gas velocity.
(8)where Ṁacc is the accretion rate, r the distance from the star, h = 2h0 the full height of the disk, ρ the mass density, and v the radial component of the gas velocity.
We estimated the optical depths as τ = hNiαν0, where Ni is the population of the ith series (the second level for the Balmer series, the third for the Paschen, and the fourth for the Brackett), and αν0 is an atomic absorption coefficient (Allen 1963). Figure 6 presents the opacity of the disk in the Balmer continuum at its inner boundary in the diagram of electron temperature vs. mass accretion rate in both cases. In the case of ρ ∝ r-1 (Fig. 6, left), the inner disk is practically opaque in the Balmer continuum, and becomes transparent only for the relatively low electron temperatures (6000 K) at 10-6M⊙ yr-1 and for the higher electron temperatures (8000 K) at 10-8M⊙ yr-1. This agrees with results of the Muzerolle et al. (2004) who obtained the latter as a boundary value between optically thick and optically thin disks. The situation for another case with ρ ∝ r-2 (Fig. 6, right) is different. The disk is opaque at high temperatures (≥8000 K) for Ṁacc = 10-6M⊙ yr-1, and becomes completely transparent at 10-8M⊙ yr-1.
 |
Fig. 6 Zones of optically thin disks in the case of different density structures. left: ρ ∝ r-1, right: ρ ∝ r-2. |
Based on these estimates, we calculated the accretion disk models shown in Table 2. For each model, we chose the electron temperature at which the disk becomes transparent for the radiation of the star in the Balmer continuum at the given mass accretion rate (Fig. 6). In the mass continuity equation, we use a formal parameter v, which we assume equal to 30 km s-1 in order to obtain the behavior of the density; the tangential velocity is equal to the Keplerian velocity. Our model is simplified because we did not consider changes in the temperature and the density with the height as we did for the surface layers. We chose this simplification because the inner regions of the disk considered interacts with the magnetosphere of the star; as a result, the thermal and density regimes can be different from those in the standard disk (farther from the star). The external heating is also able to influence the vertical T and ρ structure.
Accretion disk model parameters.
Figure 7 presents the Brγ line profiles for the accretion disk of the Herbig Ae star in models M1, M2, M4, and M5. Inclinations vary from 0° to 80° from top to bottom. The results of the calculations of model M3 with a steeper slope of the electron temperature with distance from the star compared to model M2 showed that the line profiles in both models have the same shape for all inclination angles but the M3 model profiles have systematically smaller intensities (about 5% lower than those in model M2). The profiles are typical for disks in the Keplerian rotation: single and narrow profiles for pole-on view and double-peaked and wide for large inclinations. An analysis of the line profiles in model M1 shows that in spite of the relatively low electron temperatures, the intensity of the lines above the star continuum is not small. This can be explained by the fact that the populations of the levels are influenced mainly by radiative processes, not by electron collisions. The line profiles at such a high mass loss rate do not have a deep central absorption for large inclinations. The lines obtained for models M4 and M5 are much weaker than in the case of the flat geometry (M1−M3) in spite of the higher values of the electron temperatures. As seen from Fig. 6, the medium becomes thinner at higher temperatures and mass accretion rates, but the density becomes lower. Because of the small intensities of the lines, we present only their emission since they can hardly be seen on the background of the photospheric profiles.
 |
Fig. 7 Profiles of the Brγ line (normalized to the star continuum) for the accretion disk models M1, M2, M4, and M5. Inclination angles from 0 to 80 are shown. |
Figure 8 compares the Brγ line profiles emitted from the accretion disks models (red profiles) with those from the disk wind model (black profiles). Examples of the inclination angles of 20° and 60° are shown. Figure 8 compares model M1 with the disk wind model DW1 (left), model M2 with the disk wind model DW2 (middle), and model M2 with the disk wind model DW3 (right). The other models from table 2 have weaker lines than models M1 and M2. The region of the magneto–centrifugal disk wind dominates in the line emission.
 |
Fig. 8 Comparison of the Brackett γ line profiles (normalized to the star continuum) for the disk wind model (black) and accretion disk model (red) for a Herbig Ae star: left: M1 and DW1, middle: M2 and DW2, right: M2 and DW3. The profiles for 20 and 60 degree inclination angles are presented. |
5. Magnetospheric accretion
In our previous papers (Tambovtseva et al. 2001, 2014), we adapted the classical magnetospheric accretion model for TTSs to intermediate-mass Herbig Ae/Be stars. Taking into account that HAEBEs are luminous and rapidly rotating stars, the main difference is their size and geometry: we used a very compact disk-like magnetosphere with rotating gas in free-fall motion. Strictly speaking, this configuration can be used if the stellar magnetic field is weak enough to allow the accreting gas to approach the star surface at low latitudes. We presented examples of the Hα and Brγ line profiles in our recent paper (TGW14). Another configuration of the accreting zone (Fig. 9) is expected if the magnetic field of the star is strong enough to transport the gas onto the pole regions (Shu et al. 1994a,b). In this case we can model the magnetospheric accretion zone by bi-polar thin cones. These regions contribute much more to the hydrogen line emission than the other outer parts of magnetospheric accretion regions (these outer parts are not shown in Fig. 9) owing to the lower gas temperatures in the outer regions. This configuration is close to that suggested by Eisner et al. (2010, 2014) with the following main differences: 1) We restricted ourselves to the outer radius equal to the corotation radius Rc, which is rather small (2−3R∗)2; and 2) we performed non-LTE calculations to obtain the atomic level populations for the cone geometry and emergent intensity in the Br γ line.
 |
Fig. 9 Geometry of the magnetosphere model assumed in this paper. The matter accretes onto the star within thin cones (gray) with the inner and outer half opening angles θin and θout. The outer parts of the magnetospheric accreting regions are assumed to be negligible as contributors to the line emission because of their lower gas temperature. |
Parameters of the models are as follows: accreting gas flows from the outer radius Rout to the star surface within two cones having half-opening angles θin and θout. The radial v and tangential u velocity components are 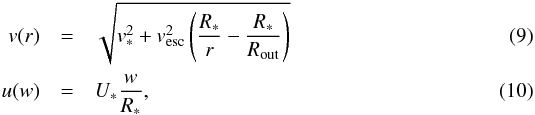 where r is a distance from the star center, w a distance from the vertical axis, v∗ the velocity at the star surface, vesc the escape velocity, U∗ the rotational velocity at the equator of the star, and R∗ the stellar radius. The electron temperature Te is chosen constant or obeys the law
where r is a distance from the star center, w a distance from the vertical axis, v∗ the velocity at the star surface, vesc the escape velocity, U∗ the rotational velocity at the equator of the star, and R∗ the stellar radius. The electron temperature Te is chosen constant or obeys the law 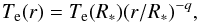 (11)where Te(R∗) is the electron temperature of the gas at the star surface and q is parameter.
(11)where Te(R∗) is the electron temperature of the gas at the star surface and q is parameter.
In our calculations, we took into account only the inner region of the magnetosphere shown in Fig. 9. This assumption is appropriate because it is the hottest part of the magnetosphere and it dominates in the line emission in comparison with the outer regions. Following the geometry shown in Fig. 9, we calculated several models with the parameters from Table 3 and investigated the dependence of the line profiles on these parameters. In models with missing q values (see Eq. (11)), the gas temperature is constant and equal to Te(R∗).
Magnetosphere model parameters.
The corotation radius Rc plays an important role. Figure 10 presents the dependence of the shape and width of the line profiles on Rc. It presents models with three values of Rc: 3, 2.5, and 2R∗ (MS4, MS6, and MS11 respectively). The line profiles are calculated for different inclinations (the inclination angle is counted from the vertical symmetry axis) from pole-on view to nearly edge-on view. As expected, the intensity of the line decreases with decreasing corotation radius because the emitting volume decreases. In addition, the line profiles become narrower with decreasing corotation radius because the gas rotates, and near the star (at the pole regions) the rotation is slower than at Rc. It should be noted that for moderate inclinations the line profiles have an inverse P Cygni form, but for large inclinations they are single.
 |
Fig. 10 Dependence of the Brγ line profiles (normalized to the star continuum) on the corotation radius rc in magnetospheric models (HAE star): rc = 3R∗ (MS4), 2.5R∗ (MS6), and 2R∗ (MS11). Inclination angles are shown in the right panels. |
 |
Fig. 11 Left: dependence of the Brγ line profiles (normalized to the star continuum) on the outer boundary of the cone θout in the magnetospheric models: θout = 40° (left column) and 45° (right column). Right: dependence of the Brγ line profiles on the inner boundary of the cone θin in the magnetospheric models: θin = 20° (left column) and 30° (right column). Inclination angles are shown in the right panel. |
We do not know the exact geometry of the magnetosphere in Herbig AeBe stars because of the poor knowledge of the magnetic field (Wade et al. 2011; Alecian et al. 2013; Hubrig et al. 2015). Therefore, we can only indirectly determine the geometry via the reproduction of the model line profiles. This is the reason why we change model parameters in a wide range. We also do not know the precise opening angles of the cone, but suggest that they are narrow. Therefore, we investigated the dependence of the line profile on inner and outer half opening angles θin and θout with few changes in the latter. Figure 11 presents the results of this study.
The left panels of Fig. 11 show how the Brγ line profiles depend on the outer half opening angle θout (40° and 45°). Models MS9 and MS10 are compared. One of the results is trivial: the line profiles of the models with larger θout (model MS10) are wider. However, there is also a non-obvious result: for moderate inclinations (40°) the double-peaked shape changes to an inverse P Cygni shape. The right panels in this figure present the dependence of the line profile shape on the inner half opening angle Rin (20° and 30°). Models MS10 and MS12 are compared. With θin = 20°, the line profiles are narrower for large inclinations and wider for small ones in comparison with the case of θin = 30°. The line profile for 20° changed substantially from an inverse P Cygni profile to a double-peaked.
 |
Fig. 12 Comparison of the Brγ line profiles (normalized to the star continuum) for the disk wind model DW3 (blue) and magnetospheric accretion model MS6 (red) for a Herbig Ae star. The total line profile (the combination of the disk wind and magnetospheric accretion model profiles) is shown as a black line. The profiles for 20° and 60° inclination angles are presented. |
 |
Fig. 13 Hα line profiles (normalized to the continuum) emitted from the disk wind region (model DW3, left) and hot layers of the accretion disk regions: model S1 (middle) and S2 (right). Inclination angles are shown. |
Figure 12 compares the Brγ line profiles from the disk wind model (DW3, blue line) and magnetospheric accretion model (MS9, red line); the ratio Ṁw/Ṁacc = 0.1. Since the shape of the line profile at inclination 20° has an inverse P Cygni profile, we present the total line profile (black line) obtained by summing the emissions from the different regions taking into account the different absorption in each of them. The same is done for the profiles at 60° inclination. Figure 12 shows that emission from the magnetospheric accretion region does not significantly change the total line profiles at large inclinations, but can influence the shape of the profile at nearly pole-on view. If the mass loss rate of the disk wind is greater, this effect will be less noticeable.
6. Hα line profiles
Because of the importance of the Hα line, the strongest one in the emission spectra of young Herbig Ae/Be stars, we also present here Hα profiles calculated with disk wind model DW3 and models of hot layers of the accretion disk S1 and S2 (see Table 1) with different flared parameter p. For models S1 and S2 we present only emission components (without photospheric profile). All profiles presented in Fig. 13 are normalized to the continuum3. We did not aim to investigate the Hα line in detail; this will be done in a forthcoming paper. Our results show that the hot layers of the accretion disk of a Herbig Ae star contribute substantially less to Hα than the magneto-centrifugal disk wind. Nevertheless, this emission is not negligible (e.g., in model S1): it is able to change the central part of the line profile, namely to decrease the central gap.
7. Discussion and conclusion
The problem of the Brγ origin in Herbig AeBe stars is currently a matter of intense debate. The study of this line is very important for improving our understanding of the physics of the young stars because it traces the close environment of these stars. It has been suggested that Brγ is emitted from the inner gaseous accretion disk (e.g., Kraus et al. 2008); from a stellar wind (Malbet et al. 2007; Lumsden et al. 2012), the accretion disk, and magnetospheric accretion columns in the pole regions or bi-polar infalling matter (Eisner et al. 2010, 2014); from the boundary accretion layers (Mendigutía et al. 2011, 2012, 2015; Fairlamb et al. 2015); and from the magneto-centrifugal disk winds and that there is less contribution from magnetospheric accretion (Weigelt et al. 2011; Garcia Lopez et al. 2015; Caratti o Garatti et al. 2015).
This problem can be studied with the help of the non-LTE modeling of all regions that are able to emit this line. In our recent papers (Weigelt et al. 2011; Garcia Lopez et al. 2015; Caratti o Garatti et al. 2015) we argued that the disk wind contributes more in Brγ than the magnetosphere. We arrived at this conclusion on the basis of detailed physical modeling of infrared interferometric observations. The comparison of the Brγ line profiles caused by (1) the disk wind and (2) the magnetosphere in the case of the boundary accretion layers (TGW14) and bi-polar accretion (this paper) favors the disk wind region. However, the emission of the magnetosphere region cannot be neglected because it can change the shape of the line profiles, especially in the case of low mass accretion rates (see Grinin & Tambovtseva 2011).
As discussed in Sect. 4, the hot layers of the inner gaseous accretion disk are not able to contribute strongly to the Brγ line emission, but together with the emission from the outer photoevaporating wind they are able to modify the shape of the line profile, for example, to fill in a small gap between two peaks with additional emission and transform the shape of the profile from double-peaked to single-peaked. The accretion disk hot surface layers together with photoevaporating wind are good candidates for such a transformation because, owing to low rotational velocities, they provide single and very narrow line profiles for any inclination angles (Owen et al. 2010; Ercolano & Owen 2010, and this paper). A similar conclusion is obtained for the Hα line.
As argued by Ferreira (2013), the bulk of the observational data cannot be explained by a single component; it is necessary to use a combination of components. This is also valid in the problem of the hydrogen line emission. Our modeling shows that the contributions strongly depend on the object type (T Tauri stars or Herbig AeBe stars; Herbig Ae or Be stars). Owing to the specific properties of the Herbig AeBe stars (rapid rotation), the magnetosphere (if it exists) does not play the dominant role in the hydrogen emission because of its compactness. However, it can provide a small emission source to the main contributor, the disk wind.
All calculations of the line profiles in this paper were performed for intermediate-mass Herbig Ae stars. There are still many unsolved questions, for example, the presence and configuration of the magnetosphere as well as properties of the surface layers of the accretion disks in hot and luminous Herbig Be stars. Our conclusions refer to Herbig Ae stars only, and are as follows.
The emission from the magnetospheric accretion region is able to change the shape of the line profile, for example, to increase the wings of the profile and/or make it asymmetric. The emission coming from the hot midplane of the inner gaseous accretion disk can also slightly change the line profile and increase the intensity of the line profile. It can also emit in the continuum. This has to be taken into account when modeling line profiles. Finally, the emission from hot layers of the disk together with the remote photoevoparation wind is able to fill in the central absorption in the line profiles and transform double-peaked line profiles to single or single-like line profiles.
All components of the environment of young Herbig Ae star such as hot layers of the inner gaseous accretion disk (inward of 10 AU) or the innermost hot midplane of the accretion disk heated by viscous dissipation (inward of 0.1 AU), and the magnetospheric accretion region contribute less Brγ line emission than the magneto-centrifugal disk wind.
Acke et al. (2010) detected polycyclic aromatic hydrocarbon (PAH) features in 70% of their sample (53 HAEBEs), which argued in favor of the disks with a flared structure.
Cauley & Johns-Krull (2014) also argued that in Herbig Ae stars (HAEs) magnetospheres are smaller than in TTSs, whereas in HBEs one should expect a boundary layer accretion, and that smaller magnetospheres are less efficient at driving outflows than classical TTS magnetospheres.
Acknowledgments
We thank the referee for the comments and suggestions that helped to improve the manuscript. This research has been supported in part by the Russian Foundation for Basic Research (Projects 15-02-05399 and 15-02-09191).
References
- Acke, B., Bouwman, J., Juhasz, A., et al. 2010, ApJ, 718, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Alecian, E., Wade, G. A., Catala, C., et al. 2013, MNRAS, 429, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, R., Pascucci, I., Andrews, S., Armitage, P., & Cieza, L. 2014, Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 914, 475 [Google Scholar]
- Allen, C. W. 1963, Astrophysical quantities (London: University of London, Athlone Press) [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., Patino, A., Magris G. C., & D’Alessio, P. 1991, ApJ, 380, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., Magris, G. C., Patino, A., & D’Alessio, P. 1992, Rev. Mex. Astron. Astrophys., 24, 27 [Google Scholar]
- Caratti o Garatti, A., Tambovtseva, L. V., Garcia Lopez, R., et al. 2015, A&A, 582, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cauley, P. W., & Johns-Krull, C. M. 2014, ApJ, 797, 112 [NASA ADS] [CrossRef] [Google Scholar]
- D’Alessio, P., Canto, J., Calvet, N., & Lizano, S. 1998, ApJ, 500, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, J. J., Braithwaite, J., Kashyap, V., et al. 2014, ApJ, 786, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004, A&A, 421, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., & Monnier, J. D. 2010, ARA&A, 48, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, J. A., Monnier, J. D., Woillez, R. L., et al. 2010, ApJ, 718, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, J. A., Hillenbrand, L. A., & Stone, J. M. 2014, MNRAS, 443, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Ercolano, B., Young, P. R., Drake, J. J., & Raymond, J. C. 2008, ApJS, 175, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Ercolano, B., Clarke, C. J., & Drake, J. J. 2009, ApJ, 699, 1639 [NASA ADS] [CrossRef] [Google Scholar]
- Ercolano, B., & Owen, E. 2010, MNRAS, 406, 1553 [NASA ADS] [Google Scholar]
- Fairlamb, J. R., Oudmaijer, R. D., Mendigutía, I., et al. 2015, MNRAS, 453, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J. 2007, in Jets from Young Stars, Lect. Notes Phys. (Berlin: Heidelberg: Springer-Verlag), 723, 181 [Google Scholar]
- Ferreira, J. 2013, in Angular Momentum Transport During Star Formation and Evolution, eds. P. Hennebelle, & C. Charbonnel, EAS Pub. Ser., 62, 169 [Google Scholar]
- Ferreira, J., & Pelletier, G. 1993, A&A, 276, 625 [NASA ADS] [Google Scholar]
- Ferreira, J., & Pelletier, G. 1995, A&A, 295, 807 [NASA ADS] [Google Scholar]
- Ferreira, J., & Casse, F. 2004, ApJ, 601, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J., Dougados, C., & Cabrit, S. 2006, A&A, 453, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frank, A., Ray, T. P., Cabrit, S., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 451 [Google Scholar]
- Garcia Lopez, R., Tambovtseva, L. V., Schertl, D., et al. 2015, A&A, 576, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcia, P. J. V., Ferreira, J., Cabrit, S., & Binette, L. 2001, A&A, 377, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glassgold, A. E., Najita, J., & Igea, J. 2004, ApJ, 615, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Glassgold, A. E., Najita, J., & Igea, J. 2007, ApJ, 656, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Gorti, U., & Hollenbach, D. 2004, ApJ, 613, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Gorti, U., & Hollenbach, D. 2008, ApJ, 683, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Gorti, U., & Hollenbach, D. 2009, ApJ, 690, 1539 [Google Scholar]
- Gorti, U., Hollenbach, D., Najita, J., & Pascucci, I. 2011, ApJ, 735, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Grinin, V. P., & Katysheva, N. A. 1980, Izv. Krymsk. Astrofiz. Obs. (Bulletin of the Crimean Astrophys. Observatory), 62, 59 [NASA ADS] [Google Scholar]
- Grinin, V. P., & Mitskevich, A. S. 1990, Astrophysics, 32, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Grinin, V. P., & Tambovtseva, L. V. 2011, Astron. Rep., 55, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Hewett, R., & Calvet, N. 1994, ApJ, 426, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, in Fundamental problems in the theory of stellar evolution; Proceedings of the Symposium, Kyoto, Japan, July 22−25, 1980 (Dordrecht: D. Reidel Publishing Co.), 1981, 113 [Google Scholar]
- Hollenbach, D., & Gorti, U. 2009, ApJ, 703, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- Hubrig, S., Caroll, T. A., Schöller, M., & Ilyin, I. 2015, MNRAS, 449, L118 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1987, ApJ, 323, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, S., Hofmann, K.-H., Benisty, M., et al. 2008, A&A, 489, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Königl, A. 1991, ApJ, 370, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Königl, A., & Pudritz, R. E. 2000, in Protostars and Planets IV, eds. V. Mannings, A. P. Boss, & S. S. Russell (Tucson: University of Arizona Press), 759 [Google Scholar]
- Königl, A., & Salmeron, R. 2011, in Physical Processes in Circumstellar Disks around Young Stars, ed. P. J.V. Garcia (Chicago, IL: University of Chicago Press), 283 [Google Scholar]
- Kurosawa, R., & Romanova, M. 2012, MNRAS, 426, 2901 [NASA ADS] [CrossRef] [Google Scholar]
- Kurosawa, R., Harries, T. J., & Symington, N. H. 2006, MNRAS, 370, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 1979, ApJSS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lima, G. H. R. A., Alencar, S. H. P., Calvet, N., et al. 2010, A&A, 522, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lumsden, S. L., Wheelwright, H. E., Hoare, M. G., et al. 2012, MNRAS, 424, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Malbet, F., Benisty, M., de Wit, W.-J., et al. 2007, A&A, 464, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meeus, G., Waters, L. B. F. M., Bouwman, J., et al. 2001, A&A, 365, 476 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meeus, G., Montesinos, B., Mendigutia, I., et al. 2012, A&A, 544, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendigutía, I., Eiroa, C., Montesinos, B., et al. 2011, A&A, 529, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendigutía, I., Mora, A., Montesinos, B., et al. 2012, A&A, 543, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendigutía, I., de Wit, W. J., Oudmaijer, R., et al. 2015, MNRAS, 453, 2126 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., Calvet, N., & Hartmann, L. 1998, ApJ, 492, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., Calvet, N., & Hartmann, L. 2001, ApJ, 550, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., D’Alessio, P., Calvet, N., & Hartmann, L. 2004, ApJ, 617, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Najita, J. R., & Shu, F. H. 1994, ApJ, 429, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, J. E., Ercolano, B., Clarke, C. J., & Alexander, R. D. 2010, MNRAS, 401, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Pascucci, I., Sterzik, M., Alexander, R., Alencar, S., & Gorti, U. 2011, ApJ, 736, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Pascucci, I., Gorti, U., & Hollenbach, D. 2012, ApJ, 751, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Pudritz, R. E., & Norman, C. A. 1986, ApJ, 301, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2009, MNRAS, 399, 1802 [NASA ADS] [CrossRef] [Google Scholar]
- Safier, P. 1993, ApJ, 408, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Shang, H., Glassgold, A. E., Shu, F. H., & Lizano, S. 2002, ApJ, 564, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Najita, J., Ostriker, E., & Wilkin, F. 1994a, ApJ, 429, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Najita, J., Ruden, S. P., & Lizano, S. 1994b, ApJ, 429, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolev, V. V. 1960, Moving Envelopes of Stars (Harvard Univ., Cambridge; Leningr. Gos. Univ., Leningrad) [Google Scholar]
- Tambovtseva, L. V., Grinin, V. P., Rodgers, B., & Kozlova, O. V. 2001, Astron. Rep., 45, 442 [NASA ADS] [CrossRef] [Google Scholar]
- Tambovtseva, L. V., Grinin, V. P., Weigelt, G. 2014, A&A, 562, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, G. A., Alecian, E, Grunhut, J., et al. 2011, in Proc. Conference on Astronomical Polarimetry 2008: Science from Small to Large Telescopes, Quebec, Canada, 6–11 July 2008, eds. P. Bastien, & N. Manset, ASP Conf. Ser., 449, 262 [Google Scholar]
- Wardle, M., & Kónigl, A. 1993, ApJ, 410, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977, Astrophys. Space Sci., 51, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Weigelt, G., Grinin, V. P., Groh, J. H., et al. 2011, A&A, 527, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Profiles of the Brackett γ line (normalized to the star continuum) for disk wind models with Ṁw = 1 × 10-7M⊙ yr-1 (model DW1; left), 3 × 10-8M⊙ yr-1 (model DW2; middle), and 1 × 10-8M⊙ yr-1 (model DW3; right). Inclination angles are shown in each panel. |
| In the text | |
 |
Fig. 2 Height of the heated disk surface layer h vs. distance from the star for two flared geometries: p = 9/8 (solid line) and 5/4 (dashed line). |
| In the text | |
 |
Fig. 3 Model profiles of the Brackett γ line (normalized to the star continuum) emitted from the hot layers of an accretion disk. Te = 104 K. Inclination angles are shown. The disk is flared with p = 9/8 (model S1, left) and p = 5/4 (model S2, right). See details in the text. |
| In the text | |
 |
Fig. 4 Left: sketch of the absorption of the hard stellar radiation (red line) by the disk wind. The green line is a shadow zone. Right: points on the disk surface (not to scale). See details in the text. |
| In the text | |
 |
Fig. 5 Column gas density in the disk wind between the star and an arbitrary point on the disk surface. Here we used our disk wind models for the Herbig Ae star HD 163296 (MWC 275; black lines) and Herbig Be star HD 98922 (red lines; see text). The disk is flared with p = 9/8 (dashed lines) and p = 5/4 (solid lines). |
| In the text | |
 |
Fig. 6 Zones of optically thin disks in the case of different density structures. left: ρ ∝ r-1, right: ρ ∝ r-2. |
| In the text | |
 |
Fig. 7 Profiles of the Brγ line (normalized to the star continuum) for the accretion disk models M1, M2, M4, and M5. Inclination angles from 0 to 80 are shown. |
| In the text | |
 |
Fig. 8 Comparison of the Brackett γ line profiles (normalized to the star continuum) for the disk wind model (black) and accretion disk model (red) for a Herbig Ae star: left: M1 and DW1, middle: M2 and DW2, right: M2 and DW3. The profiles for 20 and 60 degree inclination angles are presented. |
| In the text | |
 |
Fig. 9 Geometry of the magnetosphere model assumed in this paper. The matter accretes onto the star within thin cones (gray) with the inner and outer half opening angles θin and θout. The outer parts of the magnetospheric accreting regions are assumed to be negligible as contributors to the line emission because of their lower gas temperature. |
| In the text | |
 |
Fig. 10 Dependence of the Brγ line profiles (normalized to the star continuum) on the corotation radius rc in magnetospheric models (HAE star): rc = 3R∗ (MS4), 2.5R∗ (MS6), and 2R∗ (MS11). Inclination angles are shown in the right panels. |
| In the text | |
 |
Fig. 11 Left: dependence of the Brγ line profiles (normalized to the star continuum) on the outer boundary of the cone θout in the magnetospheric models: θout = 40° (left column) and 45° (right column). Right: dependence of the Brγ line profiles on the inner boundary of the cone θin in the magnetospheric models: θin = 20° (left column) and 30° (right column). Inclination angles are shown in the right panel. |
| In the text | |
 |
Fig. 12 Comparison of the Brγ line profiles (normalized to the star continuum) for the disk wind model DW3 (blue) and magnetospheric accretion model MS6 (red) for a Herbig Ae star. The total line profile (the combination of the disk wind and magnetospheric accretion model profiles) is shown as a black line. The profiles for 20° and 60° inclination angles are presented. |
| In the text | |
 |
Fig. 13 Hα line profiles (normalized to the continuum) emitted from the disk wind region (model DW3, left) and hot layers of the accretion disk regions: model S1 (middle) and S2 (right). Inclination angles are shown. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


