| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 5 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201628135 | |
| Published online | 13 May 2016 | |
Research Note
Normalizing a relativistic model of X-ray reflection
Definition of the reflection fraction and its implementation in relxill
1
Remeis Observatory & ECAP, Universität
Erlangen-Nürnberg,
Sternwartstr. 7,
96049
Bamberg,
Germany
e-mail:
thomas.dauser@sternwarte.uni-erlangen.de
2
Harvard-Smithsonian Center for Astrophysics, 60 Garden
Street, Cambridge,
MA
02138,
USA
3
Jet Propulsion Laboratory, California Institute of
Technology, Pasadena,
CA
91109,
USA
4
Cahill Center for Astronomy and Astrophysics, California Institute
of Technology, Pasadena, CA
91125,
USA
5
X-ray Astrophysics Laboratory, NASA Goddard Space Flight Center, Greenbelt, MD
20771,
USA
Received: 14 January 2016
Accepted: 13 April 2016
Aims. The only relativistic reflection model that implements a parameter relating the intensity incident on an accretion disk to the observed intensity is relxill. The parameter used in earlier versions of this model, referred to as the reflection strength, is unsatisfactory; it has been superseded by a parameter that provides insight into the accretion geometry, namely the reflection fraction. The reflection fraction is defined as the ratio of the coronal intensity illuminating the disk to the coronal intensity that reaches the observer.
Methods. The relxill model combines a general relativistic ray-tracing code and a photoionization code to compute the component of radiation reflected from an accretion that is illuminated by an external source. The reflection fraction is a particularly important parameter for relativistic models with well-defined geometry, such as the lamp post model, which is a focus of this paper.
Results. Relativistic spectra are compared for three inclinations and for four values of the key parameter of the lamp post model, namely the height above the black hole of the illuminating, on-axis point source. In all cases, the strongest reflection is produced for low source heights and high spin. A low-spin black hole is shown to be incapable of producing enhanced relativistic reflection. Results for the relxill model are compared to those obtained with other models and a Monte Carlo simulation.
Conclusions. Fitting data by using the relxill model and the recently implemented reflection fraction, the geometry of a system can be constrained. The reflection fraction is independent of system parameters such as inclination and black hole spin. The reflection-fraction parameter was implemented with the name refl_frac in all flavours of the relxill model, and the non-relativistic reflection model xillver, in v0.4a (18 January 2016).
Key words: accretion, accretion disks / line: profiles / galaxies: active / X-rays: galaxies
© ESO, 2016
1. Introduction
An important issue in the study of active galactic nuclei (AGNs) and Galactic black hole binaries is that of the nature of the accretion flow in the vicinity of the central accretion disk. This flow is usually modelled as a hot corona sandwiching the disk (see, e.g., Haardt & Maraschi 1991; Stern et al. 1995), but it may be a more complicated structure, such as an outflow. The goal is to constrain the geometry of this flow and its physical properties. The chief means of addressing this problem is by studying the spectrum of X-rays “reflected” from the optically thick accretion disk due to its illumination by hard X-rays produced in a surrounding corona (see, e.g., the early work by George & Fabian 1991; Matt et al. 1991). The result is a rich spectrum of radiative recombination continua, absorption edges, and fluorescent lines, most notably the Fe K complex in the 6–8 keV energy range (Matt et al. 1992). Determining the intensity of the reflected spectrum relative to the spectrum that illuminates the disk can provide important constraints on the geometry of the corona. In the simplest case of Euclidean geometry, it is straightforward to parameterize the relative intensity of the reflected component of emission. It is proportional to the fraction of the disk that is covered by the corona, which is the assumption underlying the widely used reflection model pexrav (Magdziarz & Zdziarski 1995).
 |
Fig. 1 Reflection spectra in the non-relativistic case and a neutral accretion disk for three models; the inclination angle increases from left to right. The incident power-law spectrum is the black curve; the xillver, pexrav, and a Monte Carlo simulation are shown as red, blue, and yellow curves, respectively. We use wilm abundances (Wilms et al. 2000), except for xillver for which we use grsa abundances (Grevesse & Sauval 1998). The highlighted area shows the energy band of the Compton hump, which is used to calculate the reflection strength. |
For astrophysical black holes, however, the problem of parameterizing the relative intensity of the reflected component is far more complicated. The relative intensity and the features in the reflected spectrum are strongly affected by relativistic effects such as light bending, special relativistic Doppler boosting, and gravitational redshift. Relativistic reflection is commonly observed in both AGNs (see, e.g., Wilms et al. 2001; Fabian et al. 2004; Dauser et al. 2012; Risaliti et al. 2013; Walton et al. 2013), and in Galactic black holes such as Cyg X-1 (see, e.g., Fabian et al. 1989; Duro et al. 2011; Tomsick et al. 2014; Parker et al. 2015) and GX 339−4 (see, e.g., Miller et al. 2008; García et al. 2015). In the presence of relativistic effects, the relationship between the relative intensity of the reflected spectrum and the geometry of the accretion flow becomes complex and non-linear. For example, in the extreme limit where the reflected component is dominant, the relative strength of this component can be used to constrain the spin of a black hole (Dauser et al. 2014; Parker et al. 2014).
The purpose of this Research Note is to provide a clear definition of a reflection-fraction parameter that captures the complex relationship between the strength of the reflection signal and the geometry (which has often been loosely referred to as the reflection fraction; see, e.g., Walton et al. 2013; Keck et al. 2015). We use the relxill model, which is currently the only relativistic reflection model that implements a reflection-fraction parameter. For a specific geometry, namely an on-axis and isotropic point source, and by thorough consideration of light-bending effects, we precisely define a normalization parameter, the reflection fraction, which relates the incident and observed spectra to the geometry of the system.
2. Definitions
We define two principal quantities that serve to normalize the observed spectrum relative to the coronal spectrum incident on the disk: the reflection strength Rs and the reflection fraction Rf. Although they differ fundamentally, we show that they are nevertheless related. Our focus is on Rf in the relativistic case, and on its implementation in the relxill model.
2.1. Reflection strength Rs
The simple approach to parameterizing the strength of the reflection is to use the ratio of the observed fluxes of the reflected component and the incident component in some specified energy band. To this end, we define the reflection strength to be this ratio in the 20–40 keV band, a definition that has been used by e.g., Keck et al. (2015) and Tao et al. (2015). This energy range, which encompasses the peak of the Compton hump, is a good choice because the reflection spectrum is dominated there by Compton scattering and therefore depends weakly on the Fe abundance or ionization state of the reflector. We note that some authors use a similar definition, but employ a wider energy band (see, e.g., Wilkins et al. 2015; Fürst et al. 2015).
2.2. Reflection fraction Rf: the non-relativistic case
One disadvantage of the reflection strength, Rs, is its strong dependence on the inclination of the system, which makes it difficult to relate this observable to the geometry of the illuminating source. We therefore define a different quantity that is independent of inclination and the condition of the reflector, namely the reflection fraction, which is the ratio of the coronal intensity that illuminates the disk to the coronal intensity that reaches the observer. For a semi-infinite slab (i.e., a 2 π accretion disk) and Rf = 1, the intensity of the coronal component that illuminates the disk is the same as that seen by the observer. In the non-relativistic case, this is the standard assumption built into such widely used reflection models such as pexrav (Magdziarz & Zdziarski 1995), reflionx (Ross & Fabian 2005), and xillver (García et al. 2013). We note that xillver and pexrav include a parameter that characterizes the strength of the reflection spectrum, but that reflionx does not.
Figure 1 shows reflection spectra computed using the models pexrav (Magdziarz & Zdziarski 1995), xillver (García et al. 2013), and a Monte Carlo code for three inclination angles θ (defined with respect to the normal of the accretion disk). All the simulations are for the standard lamp post geometry: i.e., an on-axis, isotropic point source, which is emitting the power-law spectrum plotted in the figure. The spectrum illuminating the disk is the same as that seen by the observer, i.e., Rf = 1.
In the limited bandpass considered in Figure 1 (i.e., the X-ray band), the reflected flux decreases with increasing inclination because flux is redistributed to energies below 100 eV (e.g., see García et al. 2013). For the xillver model, the reflection strength Rs for θ = 18°, 49°, and 76° is 0.93, 0.71, and 0.32, respectively, with very similar values for the other models. The modest differences between the models are due to the use of different abundances and to the approximation used in xillver’s treatment of Compton scattering, which limits its applicability to energies below approximately 100 keV.
 |
Fig. 2 Relativistic reflection spectra for accretion disks that are all illuminated by an isotropic on-axis point source with precisely the same luminosity in all cases. Inclination increases to the right; each panel shows four models corresponding to four values of lamp post height h ranging from 2rg to 100rg. The dashed lines show the incident power-law spectra, while the solid lines depict the observed reflection spectra. For all models, the spin is a = 0.998, the power-law index Γ = 2, the high energy cutoff Ecut = 300 keV, and the gas is neutral (log ξ = 0). The highlighted area shows the energy band of the Compton hump used in computing the reflection strength. |
2.3. Relativistic reflection
We now focus on the relevant and interesting case of relativistic reflection with the spectrum blurred by gravitational redshift and by Doppler and light-bending effects, a subject that has been widely studied (see, e.g., Fabian et al. 1989; Laor 1991; Dauser et al. 2010; and the review by Middleton 2015). However, the only relativistic model that parameterizes the relative strength of the reflected spectrum is relxill (Dauser et al. 2014). The model relxill combines our reflection code xillver (García & Kallman 2010; García et al. 2013) and the relativistic ray tracing code relline (Dauser et al. 2010, 2013).
The definition of the reflection-fraction parameter Rf in the relxill model is identical to that given in Sect. 2.2 for the xillver and pexrav models1. There is a crucial complication that results from the effects of light bending: in order to precisely define Rf one must specify the geometry of the illuminating source because the observer no longer sees the same spectrum that illuminates the disk. For example, many photons initially directed toward infinity will strike the disk, thereby boosting the value of Rf. Meanwhile, photons captured by the black hole or crossing the midplane beyond the outer radius of the disk are disregarded when computing Rf. Because the black hole’s gravity preferentially bends light rays back toward the disk and away from the observer, values of Rf> 1 are the norm, as illustrated by Dauser et al. (2014, their Fig. 2)2.
Figure 2 shows, for each of three values of inclination, a set of reflected spectra and the corresponding spectra of the power-law that illuminates the disk. The emissivity profiles are those appropriate for a lamp post geometry (see, e.g., Martocchia & Matt 1996; Martocchia et al. 2002; Dauser et al. 2013), where an on-axis source is located above the black hole at heights of h = 2, 3rg, 6rg, and 100rg (rg = GM/c2), which correspond to reflection fractions of Rf = 5.9 of 3.3, 1.8, and 0.8, respectively (see Dauser et al. 2014, for more details and other parameter combinations). The luminosity of the point source is the same in all cases. Therefore, the flux in the incident power-law spectra (dashed lines) decreases with h as the gravitational redshift increases.
As the figure shows, the reflection spectrum depends strongly on inclination. Interestingly, for small values of h the reflection strength Rs increases with inclination, while for large h it decreases. One reason for this effect is that redshift and Doppler-boost effects depend strongly on the radial velocity of the disk material, and hence on the inclination of the disk. A second reason is that the emission angle, the angle at which the observer views the disk, is altered by relativistic effects that diminish with radius (see García et al. 2014). The emission angle strongly affects the reflected spectrum because the spectrum is dominated by those portions of the disk that are viewed face-on, i.e., the regions that are near the black hole that exhibit the strongest Doppler boosting. Also important is the height h of the point source above the black hole: The relativistic effects are strong for a point source that is near, but for a source located far from the hole the relativistic effects are muted and the dependence of the reflected spectrum on inclination becomes similar to that for the non-relativistic case (Sect. 2.2).
In summary, for relativistic reflection in the lamp post geometry (or any other fully specified geometry), we can compute the reflection fraction. As the lamp post geometry is the only geometry fulfilling these conditions, and this geometry is implemented in relativistic reflection models, it is the focus of the following discussion. By comparing the observed value of the reflection fraction to the model values, we are able to place constraints on the geometry of the system, specifically the height h of the illuminating source and the disk inclination angle. We close this section with two conclusions. First, for lamp post geometry and an isotropic point source of constant luminosity, the strongest reflection is produced for small values of h and high inclination where relativistic effects are strong, and for large values of h and low inclination where they are weak. Second, for a constant value of the reflection fraction Rf, the ratio of the incident to the reflected flux (i.e., the reflection strength Rs) is strongly dependent on h and inclination.
 |
Fig. 3 Comparison of the reflection fraction Rf (solid lines) and the reflection strength Rs (dashed lines) for increasing lamp post geometry (from left to right) and two values of spin, a = 0 (blue curves) and a = 0.99 (red curves). The ratio of Rf to Rs is shown in the lower panels. |
3. Relationship of Rf to Rs
We now consider the relationship of the reflection fraction Rf to the reflection strength Rs. This latter parameter is a straightforward observable and its value is meaningful, and sometimes quoted, when fitting data using non-relativistic models such as pexrav and pexrav (Sect. 2.1). However, its value is very limited in modelling strongly relativistic systems, e.g., when using relxill.
Figure 3 illustrates the relationship between Rf and Rs for three values of inclination as a function of the height h of the lamp post. The quantities themselves are plotted in the top panels, and their ratio is plotted in the lower panels. These results are based on the same ray-tracing calculations used to generate the spectra plotted in Fig. 2. For most cases, Rf>Rs. For low and moderate inclinations, this ratio is roughly a factor of two, and decreases rather abruptly for small values of h. The high inclination case is quite different: for large h, Rf is about an order of magnitude greater than Rs, while for small h and high spin the ratio plummets and Rs greatly exceeds Rf.
It is interesting to compare the different results for low-spin and high-spin black holes. In the low-spin case, both Rf and Rs are ≲1. For rapidly spinning black holes and h ≲ 5, on the other hand, both reflection parameters are much larger, making their corresponding reflection spectra relatively more prominent. This is a plausible observational selection effect that helps to explain the observed prevalence of high-spin black holes (see, e.g., Reynolds 2014; Middleton 2015), but we also note that this effect can be partly explained by a larger radiative efficiency of the rapidly rotating black holes (see Vasudevan et al. 2016).
Because relxill is currently the only relativistic model that implements a reflection-fraction parameter, we have no point of comparison. We note, however, that values of reflection fraction have been quoted for the relativistic model reflionx (see, e.g., Keck et al. 2015), even though this parameter is not explicitly included in the model. In these cases, the values quoted are for the reflection strength Rs (and not Rf).
4. Reflection fraction in the relxill model
In the following we present the implementation of Rf (in place of Rs) in the example relxill model and also state our reasons for this choice. First, it is applied to the lamp post geometry, the only geometry implemented in a relativistic reflection model, which is fully specified. Second, we emphasize the uncertain interpretation of Rf for the standard power-law emissivity version of relxill, presenting a case which does not provide a strict geometrical definition. For completness, the specific normalizations of the xillver and relxill models are spelled out in Appendix A.
4.1. Adoption of the reflection fraction
We have consistently used the parameter Rf to quantify the normalization of the reflected component in all flavours of the relxill model since we released version 0.4a on 2016 January 18. Previously, we used the reflection strength, which is not simply related to Rf (Sect. 3). Figure 3 provides a rough idea of the relationship between the two parameters.
The principal reason for adopting Rf is that for the lamp post version of relxill this observable allows constraints to be placed on the geometry of the system, specifically the lamp post height h and inclination angle (Sect. 2.3; Dauser et al. 2014). The reflection strength, by comparison, does not provide insight into the geometry of the system. Furthermore, the reflection strength depends on such parameters as the inclination and the black hole’s spin, while Rf is independent of these parameters.
Moreover, as demonstrated by Dauser et al. (2014), when fitting observational data with the lamp post version of relxill, additional constraints can be obtained on the spin parameter by excluding values of Rf that are unrealistic. This is possible because Rf is closely tied to the accretion geometry, while at the same time it is computed for the observed disk spectrum (i.e., ignoring relativistic effects on light rays traveling from the disk to the observer). As an example of a constraint enabled by Rf, Dauser et al. (2014) show that for the larger inner-disk radius of a low-spin black hole, large values of Rf are excluded because a substantial fraction of the photons are captured by the black hole.
The parameter Rf was implemented for the xillver model at the same time as for the relxill model. Conveniently, the widely used pexrav model employs the same normalization, which allows a direct comparison between the two non-relativistic reflection models pexrav and xillver.
4.2. Standard relxill model with emissivity index
A principal virtue of the lamp post version of relxill is that its geometry is completely defined. This is not true of the standard version of relxill, which follows the venerable tradition of describing the illumination profile of the disk by a broken power law (Fabian et al. 1989). In this case, the geometry of the illuminating source is undefined because many conceivable geometries could produce the same power-law illumination profile. In defining Rf for the standard model, we assume that the geometry of the illuminating source is a razor-thin layer that hugs the entire disk. Hence, unlike the lamp post geometry, the photons illuminating the disk are not shifted in energy, and light-bending is irrelevant.
This simplistic geometry is very unlikely to represent physical systems, and it is particularly inappropriate for models with steep emissivity profiles in the inner-disk region. Given that a unique geometry cannot be specified for the emissivity-index model, and given the simplistic geometry we have adopted, fitted values of Rf for this version of the relxill model are of quite limited value when assessing the geometry of a system.
5. Summary and conclusions
We have discussed two normalization parameters for use in models of X-ray reflection. The first of these, the reflection strength Rs, is the ratio of the flux incident on the disk to the reflected component of flux in the 20–40 keV band. One disadvantage of the reflection strength is its dependence on system parameters such as inclination and black hole spin. Furthermore, it does not provide insight into the geometry of the system.
Because of these flaws, we adopted a new normalization parameter, the reflection fraction Rf, which was first implemented in both the relxill and xillver models in v0.4a (18 January 2016) use the same date format throughout the paper ; the parameter name in the models is refl_frac. The reflection fraction is defined as the ratio of the coronal intensity that illuminates the disk to the coronal intensity that reaches the observer. In computing Rf, all relativistic effects are included for light rays traveling from the illuminating source to the disk, but these effects do not act on photons traveling from the disk to the observer. A principal virtue of Rf is that if the geometry is specified, then the geometrical parameters can be constrained by observation, as in the case of the lamp post scenario. Another virtue is that Rf does not depend on the system parameters of inclination and black hole spin.
Basak & Zdziarski (2016) propose an alternative definition, namely that the reflection fraction is the ratio of the coronal flux emitted towards the accretion disk to the coronal flux emitted towards the observer. The substantial difference to our definition is that only the direction of emission is used, not including the directional change due to light-bending; therefore, if the photon actually arrives at infinity or hits the accretion disk, it implies that Rf = 1 for any isotropically emitting lamp post source.
While results obtained using the non-relativistic model pexrav cannot be directly compared to those obtained using relxill, the definition of Rf is the same for both models (Sect. 2.2).
Acknowledgments
We thank John E. Davis for the development of the SLxfig module used to prepare the figures in this Research Note and Andrzej Zdziarski for helpful comments. This research has made use of ISIS functions (ISISscripts) provided by ECAP/Remeis observatory and MIT (http://www.sternwarte.uni-erlangen.de/isis/). We also thank the anonymous referee for comments that improved the manuscript.
References
- Basak, R., & Zdziarski, A. A. 2016, MNRAS, 458, 2199 [NASA ADS] [CrossRef] [Google Scholar]
- Dauser, T., Wilms, J., Reynolds, C. S., & Brenneman, L. W. 2010, MNRAS, 409, 1534 [NASA ADS] [CrossRef] [Google Scholar]
- Dauser, T., Svoboda, J., Schartel, N., et al. 2012, MNRAS, 422, 1914 [NASA ADS] [CrossRef] [Google Scholar]
- Dauser, T., García, J., Wilms, J., et al. 2013, MNRAS, 687 [Google Scholar]
- Dauser, T., García, J., Parker, M., et al. 2014, MNRAS, 444, L100 [NASA ADS] [CrossRef] [Google Scholar]
- Duro, R., Dauser, T., Wilms, J., et al. 2011, A&A, 533, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Miniutti, G., Gallo, L., et al. 2004, MNRAS, 353, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Fürst, F., Nowak, M. A., Tomsick, J. A., et al. 2015, ApJ, 808, 122 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., & Kallman, T. R. 2010, ApJ, 718, 695 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., Dauser, T., Reynolds, C. S., et al. 2013, ApJ, 768, 146 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., Dauser, T., Lohfink, A., et al. 2014, ApJ, 782, 76 [NASA ADS] [CrossRef] [Google Scholar]
- García, J. A., Steiner, J. F., McClintock, J. E., et al. 2015, ApJ, 813, 84 [NASA ADS] [CrossRef] [Google Scholar]
- George, I. M., & Fabian, A. C. 1991, MNRAS, 249, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Keck, M. L., Brenneman, L. W., Ballantyne, D. R., et al. 2015, ApJ, 806, 149 [Google Scholar]
- Laor, A. 1991, ApJ, 376, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Martocchia, A., & Matt, G. 1996, MNRAS, 282, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Martocchia, A., Matt, G., Karas, V., et al. 2002, A&A, 387, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matt, G., Perola, G. C., & Piro, L. 1991, A&A, 247, 25 [NASA ADS] [Google Scholar]
- Matt, G., Perola, G. C., Piro, L., & Stella, L. 1992, A&A, 257, 63 [NASA ADS] [Google Scholar]
- Middleton, M. 2015, in Astrophysics of Black Holes – From fundamental aspects to latest developments, ed. C. Bambi, Astrophysics and Space Science Library (Springer), in press [arXiv:1507.06153] [Google Scholar]
- Miller, J. M., Reynolds, C. S., Fabian, A. C., et al. 2008, ApJ, 679, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, M. L., Wilkins, D. R., Fabian, A. C., et al. 2014, MNRAS, 443, 1723 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, M. L., Tomsick, J. A., Miller, J. M., et al. 2015, ApJ, 808, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S. 2014, Space Sci. Rev., 183, 277 [Google Scholar]
- Risaliti, G., Harrison, F. A., Madsen, K. K., et al. 2013, Nature, 494, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, R. R., Fabian, A. C. 2005, MNRAS, 358, 211 [Google Scholar]
- Stern, B. E., Poutanen, J., Svensson, R., et al. 1995, ApJ, 449, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Tao, L., Tomsick, J. A., Walton, D. J., et al. 2015, ApJ, 811, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Tomsick, J. A., Nowak, M. A., Parker, M., et al. 2014, ApJ, 780, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., Fabian, A. C., Reynolds, C. S., et al. 2016, MNRAS [Google Scholar]
- Walton, D. J., Nardini, E., Fabian, A. C., et al. 2013, MNRAS, 428, 2901 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, D. R., Gallo, L. C., Grupe, D., et al. 2015, MNRAS, 454, 4440 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Reynolds, C. S., Begelman, M. C., et al. 2001, MNRAS, 328, L27 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Normalization of the xillver and relxill models
The xillver model is normalized for an incident spectrum (currently, a cutoff power-law) with flux FX(E) such that 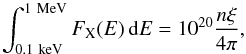 (A.1)where the density and ionization parameter are fixed to the values n = 1015 cm3 and ξ = 1 erg cm s-1, respectively (see also García et al. 2013). While the normalization of relxill (which is based on xillver) is identical, the flux reaching the observer differs because of the relativistic effects described above.
(A.1)where the density and ionization parameter are fixed to the values n = 1015 cm3 and ξ = 1 erg cm s-1, respectively (see also García et al. 2013). While the normalization of relxill (which is based on xillver) is identical, the flux reaching the observer differs because of the relativistic effects described above.
All Figures
 |
Fig. 1 Reflection spectra in the non-relativistic case and a neutral accretion disk for three models; the inclination angle increases from left to right. The incident power-law spectrum is the black curve; the xillver, pexrav, and a Monte Carlo simulation are shown as red, blue, and yellow curves, respectively. We use wilm abundances (Wilms et al. 2000), except for xillver for which we use grsa abundances (Grevesse & Sauval 1998). The highlighted area shows the energy band of the Compton hump, which is used to calculate the reflection strength. |
| In the text | |
 |
Fig. 2 Relativistic reflection spectra for accretion disks that are all illuminated by an isotropic on-axis point source with precisely the same luminosity in all cases. Inclination increases to the right; each panel shows four models corresponding to four values of lamp post height h ranging from 2rg to 100rg. The dashed lines show the incident power-law spectra, while the solid lines depict the observed reflection spectra. For all models, the spin is a = 0.998, the power-law index Γ = 2, the high energy cutoff Ecut = 300 keV, and the gas is neutral (log ξ = 0). The highlighted area shows the energy band of the Compton hump used in computing the reflection strength. |
| In the text | |
 |
Fig. 3 Comparison of the reflection fraction Rf (solid lines) and the reflection strength Rs (dashed lines) for increasing lamp post geometry (from left to right) and two values of spin, a = 0 (blue curves) and a = 0.99 (red curves). The ratio of Rf to Rs is shown in the lower panels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


