| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 5 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201628170 | |
| Published online | 14 April 2016 | |
Research Note
Detection of H3+ auroral emission in Jupiter’s 5-micron window
1 Atmospheric, Oceanic & Planetary Physics, Department of Physics, University of Oxford, Clarendon Laboratory, Parks Road, Oxford OX1 3PU, UK
e-mail: rohini.giles@physics.ox.ac.uk
2 Department of Physics and Astronomy, University of Leicester, University Road, Leicester LE1 7RH, UK
Received: 21 January 2016
Accepted: 11 March 2016
We use high-resolution ground-based observations from the VLT CRIRES instrument in November 2012 to identify sixteen previously undetected H3+ emission lines from Jupiter’s ionosphere. These emission lines are located in Jupiter’s 5-micron window (4.5−5.2 μm), an optically-thin region of the planet’s spectrum where the radiation mostly originates from the deep troposphere. The H3+ emission lines are so strong that they are visible even against this bright background. We measure the Doppler broadening of the H3+ emission lines in order to evaluate the kinetic temperature of the molecules, and we obtain a value of 1390 ± 160 K. We also measure the relative intensities of lines in the ν2 fundamental in order to calculate the rotational temperature, obtaining a value of 960 ± 40 K. Finally, we use the detection of an emission line from the 2ν2(2)-ν2 overtone to measure a vibrational temperature of 925 ± 25 K. We use these three independent temperature estimates to discuss the thermodynamic equilibrium of Jupiter’s ionosphere.
Key words: planets and satellites: gaseous planets / planets and satellites: aurorae / planets and satellites: atmospheres
© ESO, 2016
1. Introduction
Observations of H lines are a valuable tool in studying Jupiter’s upper atmosphere. It can be used to measure ionospheric temperatures and to trace energy inputs from high-energy particles and solar radiation. The species itself also directly affects the ionospheric conditions, both acting as a stabilising “thermostat” and providing the main contribution to ionospheric conductivity. Further details on the role of H
lines are a valuable tool in studying Jupiter’s upper atmosphere. It can be used to measure ionospheric temperatures and to trace energy inputs from high-energy particles and solar radiation. The species itself also directly affects the ionospheric conditions, both acting as a stabilising “thermostat” and providing the main contribution to ionospheric conductivity. Further details on the role of H in planetary atmospheres can be found in Miller et al. (2006).
in planetary atmospheres can be found in Miller et al. (2006).
The first spectroscopic detection of H emission from Jupiter’s ionosphere was made by Drossart et al. (1989) in the 2ν2(l = 2) overtone band at 2 μm in the K-band. This was almost immediately followed by detections of the ν2 fundamental at 4 μm in the L-band (e.g. Oka & Geballe 1990), and more recently by detection of the 2ν2(0)-ν2 (4 μm) and 3ν2(3)-ν2 (2 μm) overtones (Stallard et al. 2002; Raynaud et al. 2004). The strongest H
emission from Jupiter’s ionosphere was made by Drossart et al. (1989) in the 2ν2(l = 2) overtone band at 2 μm in the K-band. This was almost immediately followed by detections of the ν2 fundamental at 4 μm in the L-band (e.g. Oka & Geballe 1990), and more recently by detection of the 2ν2(0)-ν2 (4 μm) and 3ν2(3)-ν2 (2 μm) overtones (Stallard et al. 2002; Raynaud et al. 2004). The strongest H signature is localised around the northern and southern auroral ovals (Drossart et al. 1992); in these regions of the planet, high-energy electrons are accelerated along the magnetic field lines into the upper atmosphere, where they ionise Jupiter’s neutral gases to produce H
signature is localised around the northern and southern auroral ovals (Drossart et al. 1992); in these regions of the planet, high-energy electrons are accelerated along the magnetic field lines into the upper atmosphere, where they ionise Jupiter’s neutral gases to produce H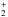 . H
. H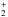 and H2 can then combine to produce H
and H2 can then combine to produce H and H, a reaction that is so efficient that very little H
and H, a reaction that is so efficient that very little H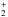 remains in the upper atmosphere. In addition to this auroral effect, there is a planet-wide signal due to extreme ultra-violet radiation from the Sun which also causes ionisation (Miller et al. 1997).
remains in the upper atmosphere. In addition to this auroral effect, there is a planet-wide signal due to extreme ultra-violet radiation from the Sun which also causes ionisation (Miller et al. 1997).
Studying the H emission lines can provide us with several different types of temperature measurements for Jupiter’s ionosphere. The kinetic temperature, Tkin, can be derived from the Doppler broadening of individual lines. The rotational temperature, Trot, can be derived by comparing the relative intensities of different rotational lines within the same vibrational manifold. The vibrational temperature, Tvib, can be derived by simultaneously measuring lines from multiple vibrational levels. If the gas is in local thermodynamic equilibrium (LTE), then these three temperatures should be the same. The kinetic temperature of H
emission lines can provide us with several different types of temperature measurements for Jupiter’s ionosphere. The kinetic temperature, Tkin, can be derived from the Doppler broadening of individual lines. The rotational temperature, Trot, can be derived by comparing the relative intensities of different rotational lines within the same vibrational manifold. The vibrational temperature, Tvib, can be derived by simultaneously measuring lines from multiple vibrational levels. If the gas is in local thermodynamic equilibrium (LTE), then these three temperatures should be the same. The kinetic temperature of H in Jupiter’s ionosphere has been measure once before (Drossart et al. 1993), the vibrational temperature has been measured twice (Stallard et al. 2002; Raynaud et al. 2004), and several studies have measured the rotational temperature (Drossart et al. 1989; Oka & Geballe 1990; Maillard et al. 1990).
in Jupiter’s ionosphere has been measure once before (Drossart et al. 1993), the vibrational temperature has been measured twice (Stallard et al. 2002; Raynaud et al. 2004), and several studies have measured the rotational temperature (Drossart et al. 1989; Oka & Geballe 1990; Maillard et al. 1990).
In this work, we use high-resolution ground-based observations to identify previously undetected H emission lines in the 4.5−5.2 μm range, which belong to the ν2 fundamental and to the 2ν2(2)-ν2 overtone. These emission lines are located in Jupiter’s 5-micron atmospheric window; at these wavelengths, Jupiter’s atmosphere is optically thin, allowing us to view bright radiation from deep in the planet’s troposphere. We then measure the broadening of these lines to evaluate Tkin, and we measure the relative intensities of the ν2 lines to evaluate Trot. Finally, we compare the fundamental and overtone lines to evaluate Tvib. This is first time that all three temperatures have been measured simultaneously.
emission lines in the 4.5−5.2 μm range, which belong to the ν2 fundamental and to the 2ν2(2)-ν2 overtone. These emission lines are located in Jupiter’s 5-micron atmospheric window; at these wavelengths, Jupiter’s atmosphere is optically thin, allowing us to view bright radiation from deep in the planet’s troposphere. We then measure the broadening of these lines to evaluate Tkin, and we measure the relative intensities of the ν2 lines to evaluate Trot. Finally, we compare the fundamental and overtone lines to evaluate Tvib. This is first time that all three temperatures have been measured simultaneously.
2. Observations and data reduction
Observations of Jupiter were made using the CRIRES instrument at the European Southern Observatory’s Very Large Telescope (VLT). These observations took place on 12 November 2012 at 05:00−05:40 UT. CRIRES is a cryogenic high-resolution infrared echelle spectrograph that provides long-slit spectroscopy with a resolving power of 96 000 (Käufl et al. 2004). The observations were made in 14 different wavelength settings that together cover the entirety of Jupiter’s 5-micron atmospheric window. Each wavelength setting was observed at a slightly different time, so corresponds to a slightly different longitude, ranging from 87°W to 108°W. The 0.2 × 40′′ slit was aligned north-south along Jupiter’s central meridian. On this date, Jupiter’s angular diameter was 48” so the observations cover the north pole, but not the south pole. Observations were also made of a standard star, HIP 22509 (A1 Vn type, RA: 04:50:36.72, Dec: 08:54:00.56).
The initial data reduction was performed using the EsoRex pipeline (Ballester et al. 2006). This included bias-subtraction, flat-fielding, wavelength-calibration using known telluric lines and noise calculation using sky observations. Corrections were subsequently performed to account for tilting in both the spectral and spatial directions. In the spectral direction, this was achieved using telluric lines, and in the spatial direction, this was achieved by cross-correlating the latitudinal profile at different wavelengths. The Jovian spectra were divided through by the standard star observations to account for telluric absorption and to provide radiometric calibration. The estimated flux loss due to the narrow slit (0.2′′ compared to a seeing of 0.4′′) was accounted for in this calibration. We find that the 5-micron brightness temperatures vary between 200 K in the coolest parts of the planet and 260 K in the brightest regions. This is roughly consistent with the Cassini VIMS 5-μm observations, which showed a 190−240 K range (Giles et al. 2015). Any differences are likely to be due to how centrally the standard star was located within the narrow slit. It should be noted that the absolute calibration does not impact the quantitative results in this paper, since we only measure the widths and relative intensities of the emission lines.
Geometric data were calculated using the angular size of the planet, the angular size of each pixel, and the location of the planet’s limb. We assumed that the slit was aligned with Jupiter’s central meridian.
3. Analysis
3.1. Line identification
We detected sixteen H emission lines in this spectral region. These lines were identified using the spectroscopic line list of Kao et al. (1991) and are listed in Table 1. Fifteen of the lines belong to the ν2 fundamental band, and the remaining line (located at 4.6118 μm) belongs to the 2ν2(2)-ν2 overtone. This is the first time that an emission line from this overtone has been observed in Jupiter’s atmosphere. All of the lines are in the P-branch of the vibrational manifold, and the line identification describes the (J, K, l) quantum numbers of the lower state.
emission lines in this spectral region. These lines were identified using the spectroscopic line list of Kao et al. (1991) and are listed in Table 1. Fifteen of the lines belong to the ν2 fundamental band, and the remaining line (located at 4.6118 μm) belongs to the 2ν2(2)-ν2 overtone. This is the first time that an emission line from this overtone has been observed in Jupiter’s atmosphere. All of the lines are in the P-branch of the vibrational manifold, and the line identification describes the (J, K, l) quantum numbers of the lower state.
Identified H emission features in Jupiter’s 5-micron window.
emission features in Jupiter’s 5-micron window.
The first emission line to be identified was the P(5, 5) line at 4.48401 μm. Using this emission line, we explored how the strength of the H emission varied with latitude. To improve the signal-to-noise, the data was smoothed with a spatial bin width of three pixels. At each pixel, we used the IDL MPFIT routine (Markwardt 2009) to fit the P(5, 5) emission line. As CRIRES is an echelle spectrometer, the instrumental line shape is triangular, and the resolving power of 96 000 translates into a resolution of ~ 5 × 10-5μm. Because the slit is very narrow, the broadening that occurs from Jupiter’s rotation and the horizontal flow of gas is expected to be negligible. The function used to fit the data was therefore a convolution of a known triangular lineshape (from the instrument) and an unknown Gaussian curve (from the Doppler broadening). There were six variables used: three for the Gaussian component (line centre, line width, line strength) and three for the background (a quadratic fit).
emission varied with latitude. To improve the signal-to-noise, the data was smoothed with a spatial bin width of three pixels. At each pixel, we used the IDL MPFIT routine (Markwardt 2009) to fit the P(5, 5) emission line. As CRIRES is an echelle spectrometer, the instrumental line shape is triangular, and the resolving power of 96 000 translates into a resolution of ~ 5 × 10-5μm. Because the slit is very narrow, the broadening that occurs from Jupiter’s rotation and the horizontal flow of gas is expected to be negligible. The function used to fit the data was therefore a convolution of a known triangular lineshape (from the instrument) and an unknown Gaussian curve (from the Doppler broadening). There were six variables used: three for the Gaussian component (line centre, line width, line strength) and three for the background (a quadratic fit).
Figure 1a shows how the integrated radiance of the emission line varies with latitude. For comparison, Fig. 1b shows the continuum radiance. The strength of the H emission is a factor of ~100 higher in the polar regions than in the equatorial regions, which is consistent with the fact that H
emission is a factor of ~100 higher in the polar regions than in the equatorial regions, which is consistent with the fact that H is predominantly an auroral species. Since the northern polar region has the strongest H
is predominantly an auroral species. Since the northern polar region has the strongest H signature, data from this region (84−86°N) was used to search for additional emission lines. The results of that search are the sixteen lines described in Table 1, and they are each shown in Fig. 2.
signature, data from this region (84−86°N) was used to search for additional emission lines. The results of that search are the sixteen lines described in Table 1, and they are each shown in Fig. 2.
 |
Fig. 1 a) Integrated radiance of the H |
 |
Fig. 2 Identification of H |
3.2. Kinetic temperature
The kinetic temperature of the H ions can be determined by measuring the width of the emission lines. We restricted our analysis to the same northern polar region (84−86°N) as shown in Fig. 2, where the emission lines are strongest; at other latitudes, the low signal-to-noise prevents reliable results. As in the previous section, we used the MPFIT routine to fit a convolution of a triangle and a Gaussian to the sixteen observed lines. These fits are shown by the red lines in Fig. 2 and the Gaussian FWHM of each line is given in Table 1. These Doppler line widths can then then converted into a kinetic temperature, Tkin, via Eq. (1) (e.g. Emerson 1996):
ions can be determined by measuring the width of the emission lines. We restricted our analysis to the same northern polar region (84−86°N) as shown in Fig. 2, where the emission lines are strongest; at other latitudes, the low signal-to-noise prevents reliable results. As in the previous section, we used the MPFIT routine to fit a convolution of a triangle and a Gaussian to the sixteen observed lines. These fits are shown by the red lines in Fig. 2 and the Gaussian FWHM of each line is given in Table 1. These Doppler line widths can then then converted into a kinetic temperature, Tkin, via Eq. (1) (e.g. Emerson 1996): 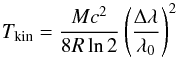 (1)where M is the molar mass of the molecule, c the speed of light, R the molar gas constant, Δλ the Doppler line width, and λ0 the wavelength at the centre of the line.
(1)where M is the molar mass of the molecule, c the speed of light, R the molar gas constant, Δλ the Doppler line width, and λ0 the wavelength at the centre of the line.
If a 10% error is assumed for the resolving power of the CRIRES instrument, then the average kinetic temperature is 1390 ± 160 K. This is reasonably consistent with the value of 1150 ± 60 K that was obtained by Drossart et al. (1993) using an emission line at 3.5 μm.
3.3. Rotational temperature
The rotational temperature of the H ions can be determined by measuring the relative intensities of different rotational lines within the same vibrational manifold. In this dataset, we have observations of fifteen lines from the same ν2 fundamental band. Since multiple wavelength settings were used to make these observations, we do not have the full set of H
ions can be determined by measuring the relative intensities of different rotational lines within the same vibrational manifold. In this dataset, we have observations of fifteen lines from the same ν2 fundamental band. Since multiple wavelength settings were used to make these observations, we do not have the full set of H lines at any given spatial location and so different lines correspond to different longitudes. However, there is some overlap between the segments, such that several emission lines were observed twice. If we assume that the H
lines at any given spatial location and so different lines correspond to different longitudes. However, there is some overlap between the segments, such that several emission lines were observed twice. If we assume that the H temperature is constant across this region and that the only variations are in in the H
temperature is constant across this region and that the only variations are in in the H abundance, then we can scale the different lines so they can be compared. Once scaled, we have three sets of lines that can be directly compared: (i) P(5, 0), P(5, 1), P(5, 2) and P(5, 3) at 94°W, (ii) P(5, 4), P(5, 5), P(6, 1) and P(6, 2) at 101°W, (iii) P(6, 4), P(7, 4) and P(7, 5) at 86°W. Within each set, the H
abundance, then we can scale the different lines so they can be compared. Once scaled, we have three sets of lines that can be directly compared: (i) P(5, 0), P(5, 1), P(5, 2) and P(5, 3) at 94°W, (ii) P(5, 4), P(5, 5), P(6, 1) and P(6, 2) at 101°W, (iii) P(6, 4), P(7, 4) and P(7, 5) at 86°W. Within each set, the H abundance should be consistent, but the abundance may vary between the sets. The normalised intensities of these lines are shown by the grey bars in Fig. 3.
abundance should be consistent, but the abundance may vary between the sets. The normalised intensities of these lines are shown by the grey bars in Fig. 3.
 |
Fig. 3 Relative intensity of observed H |
In the optically thin limit, the integrated radiance of the emission line (relative to the continuum) is proportional to the optical depth, and therefore to the line intensity. As described in Stallard et al. (2002), if LTE is assumed, then the line intensity, I, of a particular transition is given by 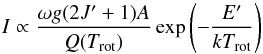 (2)where ω is the wavenumber of the transition, g the nuclear spin degeneracy factor, J′ the rotational quantum number of the upper state, A the Einstein A coefficient, Q(T) the partition function (Miller et al. 2013), E′ the energy of the upper state, and Trot the rotational temperature.
(2)where ω is the wavenumber of the transition, g the nuclear spin degeneracy factor, J′ the rotational quantum number of the upper state, A the Einstein A coefficient, Q(T) the partition function (Miller et al. 2013), E′ the energy of the upper state, and Trot the rotational temperature.
For each emission line, the parameters ω, g, J′, A, and E′ are known (Neale et al. 1996). We can therefore search for a temperature Trot that reproduces the relative intensities shown in Fig. 3. We used MPFIT to apply a least-squares fit, with four variables: Trot and three scaling factors for each of the three sets of emission lines, which are proportional to the H3+ abundance in each case.
This fitting process produced a best-fit Trot of 960 ± 40 K. This fit is shown by the red line in Fig. 3. The retrieved relative abundances are 1.47 (94°W), 1.00 (101°W) and 1.26 (86°W), and the grey bars in Fig. 3 have been scaled according to these values. To confirm that this fitting process was reliable, the three sets of lines were also fit independently, using just two parameters in each case (Trot and a scaling factor). This produced results of 880 ± 110, 980 ± 40, 830 ± 170 K, which is consistent with the overall value of 960 ± 40 K. This result is also consistent with previously published results for the rotational temperature of H in Jupiter’s atmosphere, which range from 670 K (Oka & Geballe 1990) to 1250 K (Drossart et al. 1993).
in Jupiter’s atmosphere, which range from 670 K (Oka & Geballe 1990) to 1250 K (Drossart et al. 1993).
3.4. Vibrational temperature
The vibrational temperature of the H ions can be determined by measuring the relative intensities of emission lines from different vibrational manifolds. In this dataset, we have simultaneous observations of one emission line from an overtone band, P(5,6+), alongside several emission lines from the fundamental band: P(5, 0), P(5, 1) and P(5, 3). Equation (2) can be expressed as
ions can be determined by measuring the relative intensities of emission lines from different vibrational manifolds. In this dataset, we have simultaneous observations of one emission line from an overtone band, P(5,6+), alongside several emission lines from the fundamental band: P(5, 0), P(5, 1) and P(5, 3). Equation (2) can be expressed as ![\begin{equation} T _{\rm vib} = \frac{E'_2 - E'_1}{k}\left[\ln{\left(\frac{I_1}{I_2}\frac{(2J'_2+1)\omega_2A_2}{(2J'_1+1)\omega_1A_1}\right)}\right]^{-1} \end{equation}](/articles/aa/full_html/2016/05/aa28170-16/aa28170-16-eq37.png) (3)where the subscripts 1 and 2 refer to two different emission lines. If we compare the intensity of the overtone line with each of the three fundamental band lines, we obtain vibrational temperatures of 940 ± 50 K, 910 ± 80, and 920 ± 30 K. The mean value of Tvib is therefore 925 ± 25 K. Previous studies found Tvib values of 900−1250 K (Stallard et al. 2002) and 960 ± 50 (Raynaud et al. 2004).
(3)where the subscripts 1 and 2 refer to two different emission lines. If we compare the intensity of the overtone line with each of the three fundamental band lines, we obtain vibrational temperatures of 940 ± 50 K, 910 ± 80, and 920 ± 30 K. The mean value of Tvib is therefore 925 ± 25 K. Previous studies found Tvib values of 900−1250 K (Stallard et al. 2002) and 960 ± 50 (Raynaud et al. 2004).
4. Discussion and conclusions
In this work, we used high-resolution ground-based observations from the CRIRES instrument at the VLT to identify previously undetected H emission lines in Jupiter’s 5-micron spectrum: fifteen lines from the ν2 fundamental, and one line from the 2ν2(2)-ν2 overtone. By considering the broadening and relative intensities of these lines, we measured an average Tkin of 1390 ± 160 K, an average Trot of 960 ± 40 K and an average Tvib of 925 ± 25 K. All of these values are consistent with previous measurements of H
emission lines in Jupiter’s 5-micron spectrum: fifteen lines from the ν2 fundamental, and one line from the 2ν2(2)-ν2 overtone. By considering the broadening and relative intensities of these lines, we measured an average Tkin of 1390 ± 160 K, an average Trot of 960 ± 40 K and an average Tvib of 925 ± 25 K. All of these values are consistent with previous measurements of H in Jupiter’s ionosphere.
in Jupiter’s ionosphere.
By comparing these temperatures, we can gain insight into whether the assumption of LTE is valid. The Einstein A coefficients of the rotational transitions are very small, so at the temperatures and densities present in Jupiter’s ionosphere, the rotational states are expected to be in LTE (Melin et al. 2005). This in turn means that the derived rotational temperature should match the kinetic temperature. We find that Trot is slightly lower than Tkin, which could suggest that this assumption is not valid. The only previous study to compare Tkin and Trot found consistent values (1150 K and 1250 K, Drossart et al. 1993). However, the Trot in this case was higher than the temperature derived by most other studies. It is less surprising that Tvib is lower than Tkin, since the theoretical work Melin et al. (2005) has shown that vibrational levels depart from LTE in Jupiter’s upper atmosphere, and the observational work of Raynaud et al. (2004) also found this to be the case.
Departures from LTE will primarily affect the high altitudes (>2000 km above 1 bar), where the atmosphere is both hot and tenuous (Melin et al. 2005). This significantly reduces the ability of H to act as a thermostat in Jupiter’s upper atmosphere, since the energy inputs from charged particles and solar radiation are not offset by the cooling provided by H
to act as a thermostat in Jupiter’s upper atmosphere, since the energy inputs from charged particles and solar radiation are not offset by the cooling provided by H . In addition, non-LTE effects alter the apparent H
. In addition, non-LTE effects alter the apparent H column density, which in turn affects the inferred conductivity of the ionosphere. The degree to which LTE holds is therefore important in understanding the energy budget of the upper atmosphere.
column density, which in turn affects the inferred conductivity of the ionosphere. The degree to which LTE holds is therefore important in understanding the energy budget of the upper atmosphere.
It should be noted that this suggested violation of rotational LTE must await direct confirmation by future measurements. The key challenge of this study was the use of H lines in multiple different wavelength settings, observed at different times, meaning that we are potentially convolving different temperatures and ionospheric wind speeds, in addition to different H
lines in multiple different wavelength settings, observed at different times, meaning that we are potentially convolving different temperatures and ionospheric wind speeds, in addition to different H abundances. Only an instrument capable of simultaneous observations of multiple H
abundances. Only an instrument capable of simultaneous observations of multiple H lines over a broad wavelength range could allow confirmation that Trot and Tkin are genuinely out of equilibrium. This study may be possible with future observations, including IRTF/ISHELL and the refurbished CRIRES.
lines over a broad wavelength range could allow confirmation that Trot and Tkin are genuinely out of equilibrium. This study may be possible with future observations, including IRTF/ISHELL and the refurbished CRIRES.
Previous studies of H have focussed on the L- and K-bands. This work opens up a new atmospheric window for future studies: the M-band. This increases the range of instruments that can be used to observe H
have focussed on the L- and K-bands. This work opens up a new atmospheric window for future studies: the M-band. This increases the range of instruments that can be used to observe H auroral emission, and will also allow for simultaneous studies of both the upper and deep atmospheres.
auroral emission, and will also allow for simultaneous studies of both the upper and deep atmospheres.
References
- Ballester, P., Banse, K., Castro, S., et al. 2006, in Proc. SPIE, 6270 [Google Scholar]
- Drossart, P., Maillard, J., Caldwell, J., et al. 1989, Nature, 340, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Drossart, P., Prangé, R., & Maillard, J.-P. 1992, Icarus, 97, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Drossart, P., Maillard, J.-P., Caldwell, J., & Rosenqvist, J. 1993, ApJ, 402, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Emerson, D. 1996, Interpreting Astronomical Spectra (John Wiley & Sons) [Google Scholar]
- Giles, R. S., Fletcher, L. N., & Irwin, P. G. 2015, Icarus, 257, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Kao, L., Oka, T., Miller, S., & Tennyson, J. 1991, ApJSS, 77, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Käufl, H. U., Ballester, P., Biereichel, P., et al. 2004, in Proc. SPIE, 5492 [Google Scholar]
- Maillard, J.-P., Drossart, P., Watson, J., Kim, S., & Caldwell, J. 1990, ApJ, 363, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, ASP Conf. Ser., 411, 251 [NASA ADS] [Google Scholar]
- Melin, H., Miller, S., Stallard, T., & Grodent, D. 2005, Icarus, 178, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, S., Achilleos, N., Ballester, G. E., et al. 1997, Icarus, 130, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, S., Stallard, T., Smith, C., et al. 2006, Phil. Trans. Roy. Soc. Lond. A: Mathematical, Physical and Engineering Sciences, 364, 3121 [CrossRef] [Google Scholar]
- Miller, S., Stallard, T., Tennyson, J., & Melin, H. 2013, J. Phys. Chem. A, 117, 9770 [CrossRef] [Google Scholar]
- Neale, L., Miller, S., & Tennyson, J. 1996, ApJ, 464, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, T., & Geballe, T. 1990, ApJ, 351, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Raynaud, E., Lellouch, E., Maillard, J.-P., et al. 2004, Icarus, 171, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Stallard, T., Miller, S., Millward, G., & Joseph, R. D. 2002, Icarus, 156, 498 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 a) Integrated radiance of the H |
| In the text | |
 |
Fig. 2 Identification of H |
| In the text | |
 |
Fig. 3 Relative intensity of observed H |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


