| Issue |
A&A
Volume 589, May 2016
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201527617 | |
| Published online | 20 April 2016 | |
Electron trapping and acceleration by kinetic Alfvén waves in solar flares
1 Space Research Institute, RAS, 117342 Moscow, Russia
e-mail: ante0226@gmail.com
2 Department of Earth, Planetary, and Space Sciences and Institute of Geophysics and Planetary Physics, University of California, Los Angeles, CA 90095, USA
3 Department of Physics, University of Alberta, Edmonton, Alberta AB T6G 2R3, Canada
Received: 22 October 2015
Accepted: 16 March 2016
Context. Theoretical models and spacecraft observations of solar flares highlight the role of wave-particle interaction for non-local electron acceleration. In one scenario, the acceleration of a large electron population up to high energies is due to the transport of electromagnetic energy from the loop-top region down to the footpoints, which is then followed by the energy being released in dense plasma in the lower atmosphere.
Aims. We consider one particular mechanism of non-linear electron acceleration by kinetic Alfvén waves. Here, waves are generated by plasma flows in the energy release region near the loop top. We estimate the efficiency of this mechanism and the energies of accelerated electrons.
Methods. We use analytical estimates and test-particle modelling to investigate the effects of electron trapping and acceleration by kinetic Alfvén waves in the inhomogeneous plasma of the solar corona.
Results. We demonstrate that, for realistic wave amplitudes, electrons can be accelerated up to 10−1000 keV during their propagation along magnetic field lines. Here the electric field that is parallel to the direction of the background magnetic field is about 10 to 103 times the amplitude of the Dreicer electric field. The acceleration mechanism strongly depends on electron scattering which is due to collisions that only take place near the loop footpoints.
Conclusions. The non-linear wave-particle interaction can play an important role in the generation of relativistic electrons within flare loops. Electron trapping and coherent acceleration by kinetic Alfvén waves represent the energy cascade from large-scale plasma flows that originate at the loop-top region down to the electron scale. The non-diffusive character of the non-linear electron acceleration may be responsible for the fast generation of high-energy particles.
Key words: acceleration of particles / Sun: flares / magnetic reconnection
© ESO, 2016
1. Introduction
The classical scenario of electron acceleration in solar flares corresponds to the direct magnetic energy release in the loop-top (or above-loop-top) reconnection region (Masuda et al. 1994; Aschwanden 2002; Zharkova et al. 2011). This scenario gives rise to a problem of compensation of electric currents induced by precipitating electrons (Knight & Sturrock 1977). The generation of parallel electric field E∥ (electrostatic Brown & Bingham 1984; induction Spicer & Sudan 1984; or both van den Oord 1990), caused by precipitating electron beams can induce the reverse current to compensate for the extremely strong current density of the primary electron beam. There is some observational evidence of these parallel electric fields existing (Battaglia & Benz 2008). Presence of counter-streaming electron currents and ion flows that originate from the X-line (a loop-top reconnection region) results in the generation of wave turbulence, which significantly scatters and accelerates the precipitating electrons (see, for example Karlicky 1997; Karlický et al. 2008), e.g. ion-sound turbulence (Vlahos & Papadopoulos 1979), whistler turbulence (Larosa et al. 1994), fast magnetosonic turbulence (Miller et al. 1996; Miller 1997), and double-layers (Volwerk & Kuijpers 1994; Karlický 2012).
The ion (i.e. Alfvén and drift) or hybrid (i.e. fast magnetosonic) wave modes can be effectively generated in solar loops by ion flows accelerated in the X-line. For example, ion flows excite kinetic Alfvén waves (KAWs) in the solar corona efficiently (Voitenko 1998; Zhao et al. 2011; Malovichko et al. 2014) with power-law spectrum and amplitudes of up to 0.1 V/m (Bian et al. 2010). (Moreover, Chen et al. 2014, show that electron beams can also generate KAWs in the flare loop plasma.) This is a typical situation for magnetic reconnection in the Earth magnetotail where in situ spacecraft observations often detect the generation of KAWs by ion flows (e.g. Chaston et al. 2012) and following electron heating by these waves in the near-planet region where the magnetic field is strong (e.g. Watt & Rankin 2012). Moreover, various magnetohydrodynamic (MHD) waves that originated in the reconnection region can transform into KAWs by phase mixing (Heyvaerts & Priest 1983), or generate KAWs non-linearly (Voitenko & Goossens 2004; Zhao et al. 2015). In both systems (flare loops and the Earth magnetotail) the magnetic reconnection is the impulsive process (Melrose 2012) where a significant portion of magnetic field energy is released in a form of fast plasma (ion) flows (Birn & Hesse 2009) and large-amplitude MHD waves (Heyn & Semenov 1996; Longcope & Priest 2007). Thus, the scenario of electron acceleration in solar corona can include the generation of KAWs by ion flows (or MHD wave transformation) and follows the interaction of KAWs with electrons via a finite parallel electric field that is induced by these waves (Haerendel 2009, 2012; Melrose 2012).
Fast magnetosonic waves, drift waves, and KAWs that propagate in inhomogeneous plasma generate electric fields (Génot et al. 2004; Tsiklauri 2006; Vranjes & Poedts 2009). These fields effectively accelerate particles via the Landau resonance (Tsap 2000; Tsiklauri 2012), the mechanism of particle reflection from the corresponding electrostatic potential (Fletcher & Hudson 2008; McClements & Fletcher 2009), or turbulent heating (Petrosian & Bykov 2008; Bykov & Fleishman 2009; Vranjes 2011). This kind of local acceleration of electrons travelling from the primary reconnection region towards the footpoints can play a principal role (Brown et al. 2009; Varady et al. 2014). Waves that are generated in the course of magnetic reconnection can store a significant portion of released energy and transport this energy into the footpoint region (Russell & Stackhouse 2013; Russell & Fletcher 2013) where plasma is more dense and, therefore, stronger fluxes of accelerated particles can be produced (Zaitsev 2005). Thus, the scenario of electron acceleration by waves seems promising for the description of electron acceleration in the region with higher electron density. Landau wave damping and particle reflection from waves can be responsible for moderate electron acceleration (electrons can gain velocity of about two local Alfvén speeds (Fletcher & Hudson 2008; Vasko et al. 2015). However, the inhomgeneous magnetic field of solar loops and the parallel electric field, which is induced by waves, can run the non-linear mechanism of electron acceleration, including particle trapping (e.g. Artemyev et al. 2012, 2014a). This mechanism is shown to be effective for electron acceleration by KAWs in the Earth’s magnetosphere (Watt & Rankin 2009; Artemyev et al. 2015b). In this paper, we study a possible application of this mechanism for electron acceleration by KAWs in solar loops. In Sect. 2, we describe the physical system that was studied and the main equations. Sections 3 and 4 each show numerical and analytical solutions to these equations. Discussion and conclusions of the work are presented in Sect. 5.
2. System geometry and main equations
We consider the magnetic field configuration that corresponds to solar corona loop (Aschwanden et al. 1999), while a plasma density is described by a Newkirk (1961) model. We also take into account the significant jump in the density of plasma around ~2 Mm above the photosphere (e.g. Vernazza et al. 1981). The simplified system geometry and scenario of electron acceleration are schematically shown in Fig. 1. At some distance from the footpoints the energy release process runs the generation of Alfvén waves. Plasma beta in the solar corona loops is generally larger than the square root of the electron to portion mass ratio (Gary 2001). Thus, because of the plasma density and magnetic field gradients, Alfvén waves are transformed to KAWs with a finite spatial scale across the magnetic field (Voitenko 1998; Zhao et al. 2011; Malovichko et al. 2014). The parallel electric field generated by KAWs (Hasegawa & Maclennan 1990) effectively traps electrons and transport them to the footpoints. During this transportation, electrons are accelerated by the electric wave field.
 |
Fig. 1 Schematic view of electron acceleration scenario. |
We consider equations of the relativistic electron (rest mass is m, charge is −e, speed of light is c) motion along inhomogeneous magnetic field B(h) (for implicity we neglect the effect of the magnetic field line curvature) and parallel electric field E∥F(φ) of KAW with a phase 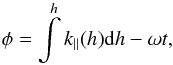 (1)where the parallel wavenumber k∥ is given by KAW dispersion relation (Hasegawa 1976)
(1)where the parallel wavenumber k∥ is given by KAW dispersion relation (Hasegawa 1976) 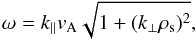 (2)and k⊥ is about (0.5−1)ρs for the maximum growth rate (Voitenko 1998; Chen et al. 2014), and ρs is plasma sound scale. Function F(φ) determines the profiles of the KAW packet. We use a simple function F(φ) = cosφexp(−φ2/ 100), which corresponds to five wave periods within one packet.
(2)and k⊥ is about (0.5−1)ρs for the maximum growth rate (Voitenko 1998; Chen et al. 2014), and ρs is plasma sound scale. Function F(φ) determines the profiles of the KAW packet. We use a simple function F(φ) = cosφexp(−φ2/ 100), which corresponds to five wave periods within one packet.
 |
Fig. 2 Six trajectories of electrons accelerated by KAW: three values of wave amplitude and two values of the electron initial pitch angle are considered. |
We concentrate on the Landau resonance of KAWs and electrons when the magnetic moment 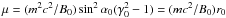 is conserved, where α0 is an initial pitch-angle, γ0 is an initial gamma-factor, B0 is B(h) value in the initial particle position. In this case, the equation of motion can be written in the gyroaveraged form (e.g. Artemyev et al. 2012):
is conserved, where α0 is an initial pitch-angle, γ0 is an initial gamma-factor, B0 is B(h) value in the initial particle position. In this case, the equation of motion can be written in the gyroaveraged form (e.g. Artemyev et al. 2012):
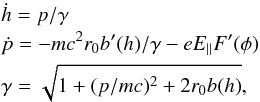 (3)where p is a particle parallel momentum, b = B/B0, b′ = db/ dh, F′ = dF/ dφ. We introduce dimensionless variables: s = h/Rs, p → p/mc, t → tc/Rs (Rs is the Sun radius). The parallel dimensionless wavenumber can be written as
(3)where p is a particle parallel momentum, b = B/B0, b′ = db/ dh, F′ = dF/ dφ. We introduce dimensionless variables: s = h/Rs, p → p/mc, t → tc/Rs (Rs is the Sun radius). The parallel dimensionless wavenumber can be written as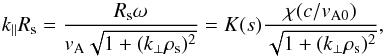 (4)where χ = Rsω/c, vA0 is the Alfvén velocity at the initial particle position, and
(4)where χ = Rsω/c, vA0 is the Alfvén velocity at the initial particle position, and 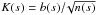 with n(s) is the plasma density normalized on the plasma density n0, which is evaluated at the initial particle position. In this case, system 4 takes the form
with n(s) is the plasma density normalized on the plasma density n0, which is evaluated at the initial particle position. In this case, system 4 takes the form
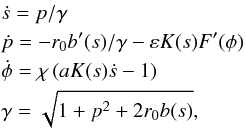 (5)where ε = eE∥Rs/mc2,
(5)where ε = eE∥Rs/mc2, 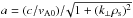 . Equation (6) shows that the effective wave amplitude ε is determined as a ratio of the electric field force ~eE∥ and mirror force ~1 /Rs. The non-linear regime of wave-particle resonant interaction (including effects of particle trapping) corresponds to ε> 1.
. Equation (6) shows that the effective wave amplitude ε is determined as a ratio of the electric field force ~eE∥ and mirror force ~1 /Rs. The non-linear regime of wave-particle resonant interaction (including effects of particle trapping) corresponds to ε> 1.
Following Zhao et al. (2013), we measure wave amplitude E∥ in the Dreicer field ED = nee3lnΛ/4πTe ≈ 7 × 10-3 V/m (where Te ~ 100 eV, ne ~ 109 cm-3, and Coulomb logarithm lnΛ ≈ 17). The dispersion relation for KAWs shows that magnetic field perturbations of KAWs relate to E∥ as δB ~ E∥(ck⊥/vAk∥) (Stasiewicz et al. 2000). Thus, for the background magnetic field B0 measured in Gauss, we can estimate the relative amplitude of the KAW magnetic field δB/B0 ~ (k⊥/k∥)(E∥/ED)(0.01G /B0)2. For weakly oblique waves (k⊥/k∥ ~ 10) and the magnetic field B0 ~ 10 G we have δB/B0 ~ 10-5(E∥/ED), i.e. electric field amplitudes E∥/ED ≤ 103 correspond to the reasonable perturbation of the magnetic field δB/B0 ~ 10-2.
Finally, we add the collision term −νp/γ to equations of motion 6 where a dimensionless collision frequency is ![\begin{equation} \nu \approx 10^{3} \cdot \left( {n_{\rm e} /10^7 \,{\rm cm}^{{\rm - 3}} } \right)\left( {T_{\rm e} [{\rm eV}]} \right)^{-3/2}(\ln \Lambda/17) \label{eq06} . \end{equation}](/articles/aa/full_html/2016/05/aa27617-15/aa27617-15-eq61.png) (6)
(6)
3. Electron acceleration
To demonstrate the effect of particle acceleration by KAWs we solve Eq. (6) numerically for several trajectories. Figure 2 shows the particle energies E = (γ−1)mc2 along the trajectory (as a function of particle coordinates h) for three values of wave amplitude E∥/ED and two values of the initial pitch angle α0. We assume that waves are generated around h ≈ 200 Mm and propagate towards the footpoints. The height of initial particle position is taken to be artificially large owing to the simple magnetic field model: we use B(h) from the quiet loop model where the magnetic field decreases with h slowly. This means that to have the initial Alfvén velocity 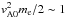 keV, we should use large enough initial h (see Discussion). The process of wave generation is modelled by effective amplitude growth from zero value up to the maximum value for h from 200 Mm down to 180 Mm. Electrons are trapped by waves near the region of the wave generation and propagate with waves until they escape from the resonance. Figure 2 demonstrates that trapped electrons are efficiently accelerated up to 10−100 keV (with the initial energy about 1 keV) depending on the wave amplitude. The time-scale of acceleration of trapped electrons is determined by the profile of Alfvén velocity vA(h). For the chosen magnetic field model, we obtain the time-scale of trapped motion of about 3−4 s (for the trajectories shown in Fig. 2). This time-scale does not depend on electron energy and pitch angle, because trapped electrons move towards the footpoints with the KAW phase velocity ~vA. After escaping from the resonance (when electron energy stops increasing), electrons continue moving towards the footpoints and lose energy because of collisions. The position of the electron escape from the resonance is determined by a competition between the electric wave field and the inhomogeneous magnetic field. With high enough wave amplitude, electrons can penetrate down to a few Mm, where the strong increase of the plasma density (and frequency of collisions) results in electrons escaping from the resonance as a result of the collisions.
keV, we should use large enough initial h (see Discussion). The process of wave generation is modelled by effective amplitude growth from zero value up to the maximum value for h from 200 Mm down to 180 Mm. Electrons are trapped by waves near the region of the wave generation and propagate with waves until they escape from the resonance. Figure 2 demonstrates that trapped electrons are efficiently accelerated up to 10−100 keV (with the initial energy about 1 keV) depending on the wave amplitude. The time-scale of acceleration of trapped electrons is determined by the profile of Alfvén velocity vA(h). For the chosen magnetic field model, we obtain the time-scale of trapped motion of about 3−4 s (for the trajectories shown in Fig. 2). This time-scale does not depend on electron energy and pitch angle, because trapped electrons move towards the footpoints with the KAW phase velocity ~vA. After escaping from the resonance (when electron energy stops increasing), electrons continue moving towards the footpoints and lose energy because of collisions. The position of the electron escape from the resonance is determined by a competition between the electric wave field and the inhomogeneous magnetic field. With high enough wave amplitude, electrons can penetrate down to a few Mm, where the strong increase of the plasma density (and frequency of collisions) results in electrons escaping from the resonance as a result of the collisions.
For calculations of the trajectories shown in Fig. 2 we use the plasma model provided by Newkirk (1961). However, this model assumes that one can use an additional multiplication factor fn, increasing the plasma density to test the effect of collisions on particles. To consider the influence of plasma density on the acceleration process, we integrate three trajectories with an additional force −fnνp/γ and ν, given by Eq. (6). Figure 3 demonstrates that collisions control the decrease in particle energy, but the position of particle escape from the resonance mainly depends on the electric wave field amplitude. For moderate (but reasonable) wave amplitudes E∥/ED ~ 100 (Zhao et al. 2013) particles escape from the resonance around h = 10−30 Mm (see Fig. 3), i.e. much higher than the position of the plasma density jump between the corona and chromosphere at h ~ 2 Mm. Moreover, the increase in the plasma density results in a decrease of the initial Alfvén velocity vA0 and, thus, results in a decrease in the initial energies of trapped particles.
 |
Fig. 3 Three profiles of the energy of trapped electrons for three values of fn factor. |
To obtain statistically representative results of electron acceleration by KAWs we integrate 106 trajectories with two different initial energy distributions (Maxwellian distributions with 300 eV temperature and 1 keV temperature). For each trajectory, we choose an initial pitch angle in such a way that the resonant condition p/γ = 1 /aK is satisfied within the region of wave generation. Thus, only trapped particles are considered. Figure 4 shows the comparison of initial and final spectra of electrons for the two cases. Trapping the acceleration shifts the whole spectrum towards the higher energy with a formation of a prolonged plateau. Thus, trapped acceleration can make a slope of the final particle spectrum (resonant particles plus background) that is significantly lower than the initial Maxwellian one. The energy range of accelerated particles is up to several hundreds of keVs.
 |
Fig. 4 Two examples of evolution of electron spectra owing to electron acceleration by KAWs (the solid curve corresponds to the initial temperature, which is equal to 1 keV, and dashed curve is for 300 eV). Grey colour shows the initial spectra. |
4. Analytical estimates
Wave phase φ in system 6 varies fast due to χ ≫ 1. Thus, we can change variables from (s,p) to 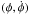 and use s as a slow changing system parameter (see details of this approach in Artemyev et al. 2013). For
and use s as a slow changing system parameter (see details of this approach in Artemyev et al. 2013). For 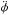 we can write
we can write 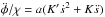 , while
, while 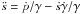 . If we consider the system in the vicinity of the resonance
. If we consider the system in the vicinity of the resonance 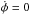 , when ṡ ≈ vR = 1 /aK(s), the we can write the expressions for γ and
, when ṡ ≈ vR = 1 /aK(s), the we can write the expressions for γ and 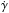 :
: 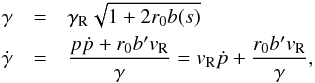 (7)where γR = 1/
(7)where γR = 1/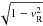 . We use Eq. (7) and equation
. We use Eq. (7) and equation 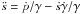 to obtain:
to obtain: 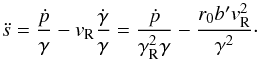 (8)Thus, for
(8)Thus, for 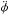 we have the following equation:
we have the following equation: 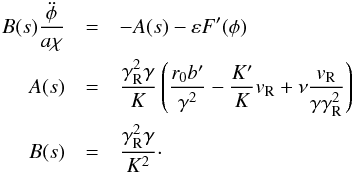 (9)Equation (9) shows that φ variation is described by Hamiltonian (Artemyev et al. 2013, 2014b):
(9)Equation (9) shows that φ variation is described by Hamiltonian (Artemyev et al. 2013, 2014b): 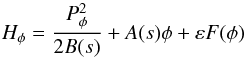 (10)where
(10)where 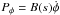 is the conjugated variable to φ. Phase portrait of the Hamiltonian 10 is shown in Fig. 5a, and profiles of B(s) and A(s) coefficients are shown in Fig. 5b. Closed trajectories can be found in the phase plane (Pφ,φ) for A<ε. Particles moving along these trajectories oscillate around
is the conjugated variable to φ. Phase portrait of the Hamiltonian 10 is shown in Fig. 5a, and profiles of B(s) and A(s) coefficients are shown in Fig. 5b. Closed trajectories can be found in the phase plane (Pφ,φ) for A<ε. Particles moving along these trajectories oscillate around 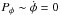 , i.e. these particle are trapped around the resonance. Trapped particles move with the wave (ṡ = vR) and gain energy owing to the conservation of the magnetic moment:
, i.e. these particle are trapped around the resonance. Trapped particles move with the wave (ṡ = vR) and gain energy owing to the conservation of the magnetic moment: 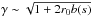 and b(s) increases along the trajectory (see Figs. 2 and 3).
and b(s) increases along the trajectory (see Figs. 2 and 3).
In the system without collisions, being trapped with some energy γ0, particles should escape from the resonance with energy 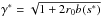 /
/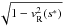 , where an escape position s∗ is defined by equation A(s∗) ≈ ε (see the equations in Artemyev et al. (2013) for more accurate estimate of the escape positions). Collisions can decrease the final energy of trapped particles. To be trapped by waves, particles should have the resonant velocity in the region of the wave generation s = s0. A range of these velocities correspond to a finite width of the resonance (Karney 1978; Neishtadt 2014). However, the main population of trapped particles corresponds to the condition
, where an escape position s∗ is defined by equation A(s∗) ≈ ε (see the equations in Artemyev et al. (2013) for more accurate estimate of the escape positions). Collisions can decrease the final energy of trapped particles. To be trapped by waves, particles should have the resonant velocity in the region of the wave generation s = s0. A range of these velocities correspond to a finite width of the resonance (Karney 1978; Neishtadt 2014). However, the main population of trapped particles corresponds to the condition 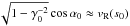 . The combination of this equation and the condition of escape from the resonance A(s∗) = ε gives the final particle energy as a function of γ0. This is an estimate of the maximum possible energy for the main particle population, but some resonant particles can have smaller α0 and, as a result, propagate to smaller s∗. These particles gain more energy than γ∗. For two wave amplitudes, we solve these two equations and plot γ∗ as a function of γ0 in Fig. 6 (left panel). As can be seen, waves with amplitudes of ~100ED can accelerate 1 keV particles up to 100−300 keV. The larger initial energy corresponds to larger α0 and, as a result, to a more rapid escape from the resonance with a weaker relative acceleration (smaller γ∗/γ0). To test this estimate of the maximum gained energy we plot profiles of the average energy gained by resonant particles (where each point corresponds to the numerical integration of 103 trajectories). Figure 6 shows that averaged energies are smaller than the estimated maximum energies, but a general dependence of the final energy on the initial energy is the same for both maximum and average values.
. The combination of this equation and the condition of escape from the resonance A(s∗) = ε gives the final particle energy as a function of γ0. This is an estimate of the maximum possible energy for the main particle population, but some resonant particles can have smaller α0 and, as a result, propagate to smaller s∗. These particles gain more energy than γ∗. For two wave amplitudes, we solve these two equations and plot γ∗ as a function of γ0 in Fig. 6 (left panel). As can be seen, waves with amplitudes of ~100ED can accelerate 1 keV particles up to 100−300 keV. The larger initial energy corresponds to larger α0 and, as a result, to a more rapid escape from the resonance with a weaker relative acceleration (smaller γ∗/γ0). To test this estimate of the maximum gained energy we plot profiles of the average energy gained by resonant particles (where each point corresponds to the numerical integration of 103 trajectories). Figure 6 shows that averaged energies are smaller than the estimated maximum energies, but a general dependence of the final energy on the initial energy is the same for both maximum and average values.
 |
Fig. 6 Left panel: maximum energy gained by the majority of trapped particles is shown as a function of the initial energy. Right panel: average energy gained by the majority of trapped particles is shown as a function of the initial energy. Data are shown for two wave amplitudes. |
5. Discussion and conclusions
We have demonstrated that KAWs effectively accelerate trapped electrons in conditions that are typical for solar corona. However, electron acceleration should result in wave damping. Moreover, in the solar corona KAWs undergo various linear and non-linear dissipation mechanisms, such as collisional dissipation, Landau damping, or non-linear spectral spreading (Voitenko & Goossens 2000). Therefore, there is a question about the energy source that is necessary for the existence of KAWs during wave propagation toward the footpoints of flare loops. In our study, we assume that ion flows (generated in the reconnection region) create this energy source for KAWs, i.e. KAWs propagate in the unstable plasma media with a positive wave growth rate. In this case, trapped electron acceleration (as well as Landau damping of KAWs on thermal electrons) can be considered as an energy transfer between initially accelerated ions (the magnetic reconnection transfers the major part of the magnetic field energy into the ion flows) and electrons, i.e. KAWs serve as a mediator between two particle populations and the wave energy can be much smaller than energies of ions and accelerated electrons. A similar scenario is often considered for electron acceleration in the inner magnetosphere of planets, where lower energy electrons (or ions) excite and support electromagnetic waves, which accelerate a high-energy electron population (e.g. Shklyar 2011).
In our model, we use a simplified assumption that the KAW amplitude does not vary during the wave propagation. However, mechanisms responsible for the conservation of wave amplitude are unknown even for magnetosphere plasma where in situ spacecraft measurements provide simultaneous observations of electromagnetic wave fields and local plasma parameters. The quasi-linear relaxation of the ion outflow beam looks to be a reasonable explanation. Also, the ion beam breaking (due to the increase in the strength of the magnetic field) can limit a time-scale of the KAW supported by ions. Non-linear processes (e.g. the generation of electrostatic double layers within KAWs) can also modify the KAW dispersion properties and reduce the time-scale of the resonant interaction between KAWs and ions. This whole process can limit the energy transfer from ion flows to KAWs and, thus, can result in the conservation of KAW amplitudes. However, to solve the question about actual values and the evolution of KAW amplitudes in the system with an inhomogeneous magnetic field and ion flows, both numerical simulations (full kinetic) and statistical observations are necessary.
The evolution of particle energy distribution owing to the trapping of electron acceleration (see Fig. 6) demonstrates that the trapped population is shifted to high energy values at reasonable wave amplitudes. Of course, only a relatively small population of particles become trapped by waves, e.g. only particles that are located in the region of wave generation have a chance of being trapped (Neishtadt 2014). Thus, the accelerated population represents some beams in energy space. The relaxation of this kind of beam in inhomogeneous plasma results in the generation of low-frequency electrostatic waves (Mottez & Génot 2011). As a result, electron acceleration by KAWs may increase a level of electrostatic turbulence, which effectively scatters electrons. In this case, we deal with the energy cascade from large MHD scales (ion flows from the primary reconnection region), to ion scale (KAWs with ion transverse scale), to scale of hot electrons trapped by KAWs, and finally to cold background electrons that are accelerated by electrostatic turbulence generated by hot electron beams (Génot et al. 2004). The latter process can be enhanced by electron collisions in the near footpoint region (e.g. Lenters & Miller 1998).
We use a simple model of magnetic fields in solar loop without additional deformation related to a local reconnection process. This simplification resulted in the overestimated amplitude of the magnetic field in the region of wave generation and, thus, we obtained an overestimated value of the Alfvén velocity, vA0. This effect does not influence the mechanism of particle acceleration, but requires the consideration of high initial electron energies (~1 keV) to put particles into resonance with KAWs. If we assume that magnetic reconnection (responsible for ion flow generation and following the excitation of KAWs) appears within the localized region where magnetic field amplitude drops significantly, for example, if Alfvén velocity in the region of energy release was estimated to be about 1000 km s-1 (e.g. Takasao et al. 2012; Su et al. 2013), then the corresponding initial energy of trapped electrons would decrease to ~10−100 eV. However, this modification does not change the final energy of accelerated electrons substantially since this energy is defined by the ratio of the magnetic field amplitudes in the wave-generation region and near the escape position. Thus, the effect of the decrease of the initial electron energy should be compensated for by the increase in the ratio of magnetic field amplitudes.
To accelerate electrons significantly (~102−103 times), we have to assume that the reconnection site is high in the corona at h ≈ 200 Mm. This value is quite large for impulsive flares, for which observations indicate that the heights of the reconnection and electron acceleration sites are less than 50−100 Mm (e.g. Aschwanden 2002; Sui et al. 2004; Liu et al. 2008; Reid et al. 2011; Su et al. 2013). It seems that the proposed acceleration mechanism is more suitable for long duration events, which are associated with the formation of huge magnetic arc-shaped structures (e.g. Svestka 1984; West & Seaton 2015) and delayed bursts of hard X-ray emission (e.g. Warmuth et al. 2009; Zimovets & Struminsky 2012). On the other hand, as is mentioned above, we use the simple profile of a magnetic field, which does not take the stretching of field lines into account properly. Taking this into account can, in principle, allow the reconnection site height in the model to be decreae and applied to the impulsive flare too.
To estimate the effect of collisions on trapped electron acceleration, we include the term ~ν into equations of electron motion, see Eq. (6). However, collisions not only decrease the electron parallel energy, but also result in the scattering of the electron pitch angle. In this case, trapped particles can escape from the resonance as a result of the destruction of the resonant conditions. There is a general approach for the estimation of the role of particle scattering on trapped motion (Artemyev et al. 2015a). This approach enables us to derive the diffusion equation in the space of adiabatic invariants of trapped particles and estimate the time-scale of invariant destruction (i.e. particle escape from the resonance). A rough estimate of the pitch angle scattering effect can be obtained using the parameter K = 2πΩccσ/vAν2ε, where σ ~ (Te/γmec2)2ν is a power of magnetic moment scattering and Ωc = eB/mc (see Sect. V in Artemyev et al. 2015a). If K is much less than one, the pitch angle scattering does not influence the trapping acceleration. For 10−100 keV trapped electrons, our estimates gives K ~ 10-3−10-1, thus, according to Artemyev et al. (2015a) the pitch angle scattering can result in the detrapping of less than 30% of trapped particles. Therefore, the proposed mechanism of trapped electron acceleration is quite stable relative to the charged particle scattering. However, a further investigation of this question is necessary.
In this paper, we have considered the mechanism of electron non-linear acceleration by KAWs that are produced in the flare loop-top region. We have demonstrated that reasonable wave amplitudes provide a strong enough parallel electric field to generate the effective potential well for ~1 keV electrons. Being trapped in this potential well results in electron acceleration of up to 100−1000 keV. Trapped electrons gain energy that moves along magnetic field lines toward the footpoints. Reasonable amplitudes of collision frequency cannot significantly decrease the acceleration rate. We have suggested that the proposed mechanism can explain a formation of relativistic electron population within flare loops. The main advantage of the proposed mechanism, in comparison to the classical scenario of electron acceleration in the loop-top reconnection region, consists of the transport of released magnetic energy into the region with more dense plasma, where more electrons can be accelerated.
Acknowledgments
The work of A., V.A., and I.V.Z. was supported by the Russian Foundation for Basic Research (projects No. 15-32-21078).
References
- Artemyev, A., Krasnoselskikh, V., Agapitov, O., Mourenas, D., & Rolland, G. 2012, Phys. Plasmas, 19, 122901 [NASA ADS] [CrossRef] [Google Scholar]
- Artemyev, A. V., Vasiliev, A. A., Mourenas, D., Agapitov, O., & Krasnoselskikh, V. 2013, Phys. Plasmas, 20, 122901 [NASA ADS] [CrossRef] [Google Scholar]
- Artemyev, A. V., Agapitov, O., Mozer, F., & Krasnoselskikh, V. 2014a, Geophys. Res. Lett., 41, 5734 [NASA ADS] [CrossRef] [Google Scholar]
- Artemyev, A. V., Vasiliev, A. A., Mourenas, D., Agapitov, O. V., & Krasnoselskikh, V. V. 2014b, Phys. Plasmas, 21, 102903 [NASA ADS] [CrossRef] [Google Scholar]
- Artemyev, A. V., Mourenas, D., Agapitov, O. V., et al. 2015a, Phys. Plasmas, 22, 082901 [NASA ADS] [CrossRef] [Google Scholar]
- Artemyev, A. V., Rankin, R., Blanco, M. 2015b, J. Geophys. Res., 120, 10305 [CrossRef] [Google Scholar]
- Aschwanden, M. J. 2002, Space Sci. Rev., 101, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Newmark, J. S., Delaboudinière, J.-P., et al. 1999, ApJ, 515, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, M., & Benz, A. O. 2008, A&A, 487, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bian, N. H., Kontar, E. P., & Brown, J. C. 2010, A&A, 519, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birn, J., & Hesse, M. 2009, Ann. Geophys., 27, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., & Bingham, R. 1984, A&A, 131, L11 [NASA ADS] [Google Scholar]
- Brown, J. C., Turkmani, R., Kontar, E. P., MacKinnon, A. L., & Vlahos, L. 2009, A&A, 508, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bykov, A. M., & Fleishman, G. D. 2009, ApJ, 692, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Chaston, C. C., Bonnell, J. W., Clausen, L., & Angelopoulos, V. 2012, Geophys. Res. Lett., 117, 9202 [Google Scholar]
- Chen, L., Wu, D. J., Zhao, G. Q., Tang, J. F., & Huang, J. 2014, ApJ, 793, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L., & Hudson, H. S. 2008, ApJ, 675, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, G. A. 2001, Sol. Phys., 203, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Génot, V., Louarn, P., & Mottez, F. 2004, Ann. Geophys., 22, 2081 [NASA ADS] [CrossRef] [Google Scholar]
- Haerendel, G. 2009, ApJ, 707, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Haerendel, G. 2012, ApJ, 749, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, A. 1976, Geophys. Res. Lett., 81, 5083 [Google Scholar]
- Hasegawa, A., & Maclennan, C. G. 1990, Geophys. Res. Lett., 17, 1605 [NASA ADS] [CrossRef] [Google Scholar]
- Heyn, M. F., & Semenov, V. S. 1996, Phys. Plasmas, 3, 2725 [NASA ADS] [CrossRef] [Google Scholar]
- Heyvaerts, J., & Priest, E. R. 1983, A&A, 117, 220 [NASA ADS] [Google Scholar]
- Karlicky, M. 1997, Space Sci. Rev., 81, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Karlický, M. 2012, ApJ, 750, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Karlický, M., Nickeler, D. H., & Bárta, M. 2008, A&A, 486, 325 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karney, C. F. F. 1978, Phys. Fluids, 21, 1584 [NASA ADS] [CrossRef] [Google Scholar]
- Knight, J. W., & Sturrock, P. A. 1977, ApJ, 218, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Larosa, T. N., Moore, R. L., & Shore, S. N. 1994, ApJ, 425, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Lenters, G. T., & Miller, J. A. 1998, ApJ, 493, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Petrosian, V., Dennis, B. R., & Jiang, Y. W. 2008, ApJ, 676, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Longcope, D. W., & Priest, E. R. 2007, Phys. Plasmas, 14, 122905 [NASA ADS] [CrossRef] [Google Scholar]
- Malovichko, P., Voitenko, Y., & De Keyser, J. 2014, ApJ, 780, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Masuda, S., Kosugi, T., Hara, H., Tsuneta, S., & Ogawara, Y. 1994, Nature, 371, 495 [NASA ADS] [CrossRef] [Google Scholar]
- McClements, K. G., & Fletcher, L. 2009, ApJ, 693, 1494 [NASA ADS] [CrossRef] [Google Scholar]
- Melrose, D. B. 2012, ApJ, 749, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. A. 1997, ApJ, 491, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. A., Larosa, T. N., & Moore, R. L. 1996, ApJ, 461, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Mottez, F., & Génot, V. 2011, Geophys. Res. Lett., 116, [Google Scholar]
- Neishtadt, A. I. 2014, Russian Mathematical Surveys, 69, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Newkirk, Jr., G. 1961, ApJ, 133, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Petrosian, V., & Bykov, A. M. 2008, Space Sci. Rev., 134, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, H. A. S., Vilmer, N., & Kontar, E. P. 2011, A&A, 529, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russell, A. J. B., & Fletcher, L. 2013, ApJ, 765, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, A. J. B., & Stackhouse, D. J. 2013, A&A, 558, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shklyar, D. R. 2011, Ann. Geophys., 29, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Spicer, D. S., & Sudan, R. N. 1984, ApJ, 280, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Stasiewicz, K., Bellan, P., Chaston, C., et al. 2000, Space Sci. Rev., 92, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Su, Y., Veronig, A. M., Holman, G. D., et al. 2013, Nat. Phys., 9, 489 [Google Scholar]
- Sui, L., Holman, G. D., & Dennis, B. R. 2004, ApJ, 612, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Svestka, Z. 1984, Sol. Phys., 94, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Takasao, S., Asai, A., Isobe, H., & Shibata, K. 2012, ApJ, 745, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Tsap, Y. T. 2000, Sol. Phys., 194, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Tsiklauri, D. 2006, A&A, 455, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsiklauri, D. 2012, Phys. Plasmas, 19, 082903 [NASA ADS] [CrossRef] [Google Scholar]
- van den Oord, G. H. J. 1990, A&A, 234, 496 [NASA ADS] [Google Scholar]
- Varady, M., Karlický, M., Moravec, Z., & Kašparová, J. 2014, A&A, 563, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasko, I. Y., Agapitov, O. V., Mozer, F., & Artemyev, A. V. 2015, Geophys. Res. Lett., submitted [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Vlahos, L., & Papadopoulos, K. 1979, ApJ, 233, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Voitenko, Y. M. 1998, Sol. Phys., 182, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Voitenko, Y., & Goossens, M. 2000, A&A, 357, 1086 [NASA ADS] [Google Scholar]
- Voitenko, Y., & Goossens, M. 2004, Nonl. Processes Geophys., 11, 535 [Google Scholar]
- Volwerk, M., & Kuijpers, J. 1994, ApJS, 90, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Vranjes, J. 2011, MNRAS, 415, 1543 [NASA ADS] [CrossRef] [Google Scholar]
- Vranjes, J., & Poedts, S. 2009, MNRAS, 400, 2147 [NASA ADS] [CrossRef] [Google Scholar]
- Warmuth, A., Holman, G. D., Dennis, B. R., et al. 2009, ApJ, 699, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Watt, C. E. J., & Rankin, R. 2009, Phys. Rev. Lett., 102, 045002 [NASA ADS] [CrossRef] [Google Scholar]
- Watt, C. E. J., & Rankin, R. 2012, Washington DC American Geophysical Union Geophysical Monograph Series, 197, 251 [NASA ADS] [Google Scholar]
- West, M. J., & Seaton, D. B. 2015, ApJ, 801, L6 [Google Scholar]
- Zaitsev, V. V. 2005, Astron. Lett., 31, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, J. S., Wu, D. J., & Lu, J. Y. 2011, ApJ, 735, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, J. S., Wu, D. J., & Lu, J. Y. 2013, ApJ, 767, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, J. S., Voitenko, Y., De Keyser, J., & Wu, D. J. 2015, ApJ, 799, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., Arzner, K., Benz, A. O., et al. 2011, Space Sci. Rev., 159, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Zimovets, I. V., & Struminsky, A. B. 2012, Sol. Phys., 281, 749 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Schematic view of electron acceleration scenario. |
| In the text | |
 |
Fig. 2 Six trajectories of electrons accelerated by KAW: three values of wave amplitude and two values of the electron initial pitch angle are considered. |
| In the text | |
 |
Fig. 3 Three profiles of the energy of trapped electrons for three values of fn factor. |
| In the text | |
 |
Fig. 4 Two examples of evolution of electron spectra owing to electron acceleration by KAWs (the solid curve corresponds to the initial temperature, which is equal to 1 keV, and dashed curve is for 300 eV). Grey colour shows the initial spectra. |
| In the text | |
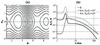 |
Fig. 5 Panel a): phase portrait of system 10 for A/ε< 1. Panel b): profiles of A/ε and B. |
| In the text | |
 |
Fig. 6 Left panel: maximum energy gained by the majority of trapped particles is shown as a function of the initial energy. Right panel: average energy gained by the majority of trapped particles is shown as a function of the initial energy. Data are shown for two wave amplitudes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


