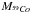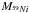| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 5 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201527762 | |
| Published online | 22 March 2016 | |
Abundances of 59Co and 59Ni in the cosmic ray flux
Astronomy DepartmentUniversity of Geneva,
Ch. d’Ecogia 16,
1290
Versoix,
Switzerland
e-mail:
andrii.neronov@unige.ch
Received: 16 November 2015
Accepted: 11 February 2016
Context. Two main hypotheses for the origin of Galactic cosmic rays are the supernova and superbubble origin hypotheses.
Aims. We analyse the evidence for the superbubble hypothesis provided by the measurements of the relativive abundances of isotopes of cobalt and nickel in the cosmic ray flux.
Methods. We compare the measured upper limit on the abundance of 59Ni in the cosmic ray flux with the 59Ni abundance predictions of the most recent stellar evolution models. Non-detection of 59Ni in the cosmic ray flux has previously been attributed to a long time delay of the order of 105 yr between the moment of supernova explosion and the onset of particle acceleration process. This long time delay was considered as an argument in favour of the superbubble scenario.
Results. We show that the recent calculation of the 59Ni yield of massive stars, which takes the initial mass range up to 120 solar masses into account and includes stellar rotation, results in prediction of low 59Ni abundance relative to its decay product 59Co. The predicted abundance is consistent with the upper bound on 59Ni abundance in the cosmic ray flux for the supernova parameters assumed. This result removes the necessity of decay of 59Ni in the time interval between the supernova explosion and the onset of acceleration process and restores the consistency of measurements of 59Ni /59Co abundances with the “supernova” hypothesis of the CR origin.
Key words: nuclear reactions, nucleosynthesis, abundances / stars: massive / supernovae: general / acceleration of particles / cosmic rays
© ESO, 2016
1. Introduction
Observations of γ-ray emission from star forming galaxies demonstrate that acceleration of cosmic rays (CRs) is a by-product of star formation activity (Ackermann et al. 2012). Two alternative possibilities for the star-formation-induced CR acceleration could be considered. CR injection could occur in supernovae and in objects related to the supernovae (Baade & Zwicky 1934) via shock acceleration (Krymskii 1977; Bell 1978; Blandford & Ostriker 1978; Drury 1983; Bell & Lucek 2001) occurring in supernova remnants, pulsar wind nebulae, and/or gamma-ray bursts (see Blasi 2013; Grenier et al. 2015 for recent reviews). Evidence for such a scenario is found in γ-ray observations that reveal the presence of high-energy protons in supernova remnants (Ackermann et al. 2013). Alternatively, CR acceleration might occur in the superbubbles formed by the collective effects of multiple supernovae and winds from massive stars (Bykov & Fleishman 1992; Higdon et al. 1998; Parizot et al. 2004; Binns et al. 2005; Bykov 2014). Evidence for this scenario could also be found in the γ-ray data, which reveal injection of cosmic rays in the nearby superbubble in Cygnus X region (Ackermann et al. 2011).
The chemical composition of the CR flux carries valuable information on the CR sources (Wiedenbeck& Grenier 1981; Maeder & Meynet 1993; Binns et al. 2005; Prantzos 2012). The abundances of different nuclei in the CR flux deviate from the abundances in the solar system. This is expected in both the individual supernova and the superbubble scenarios. In the case of supernovae, the ejecta and the circumstellar medium around the supernova are enriched with the heavy elements produced at different stages in the evolution of the massive star. If the acceleration of CRs occurs early enough after the supernova explosion, at the free expansion stage and/or at the beginning of the Sedov-Taylor phase, the abundance pattern of the accelerated CRs is also expected to be enriched with heavy elements. In contrast, if the acceleration occurs late in the Sedov-Taylor phase, the medium that provides the source of the accelerated particles already has the composition close to that of the ISM, and CRs produced at this stage would have an abundance pattern similar to that of the ISM. The details of the enrichment are sensitive to the dynamics of the propagation of the forward shock of the expanding supernova shell into the cavity carved by the wind produced by the progenitor massive star (Prantzos 2012).
In a similar way, the composition of the medium inside the superbubble changes from the standard ISM composition at the onset of the star formation to the composition enriched with heavy elements injected by the massive star winds and supernovae (Casse & Paul 1982; Binns et al. 2005). Composition of the CRs accelerated at the multiple shocks produced by the supernovae and stellar wind bubbles would also change in the course of the evolution of the superbubble.
Particularly interesting indications about the details of the CR acceleration process might be provided by the ratios of abundances of isotopes such as the “anomalous” 22Ne/20Ne (Mewaldt et al. 1980; Casse & Paul 1982; Binns et al. 2005) and 59Ni/59Co ratios (Wiedenbeck et al. 1999; Israel et al. 2005). Information provided by the isotope ratios is potentially free of uncertainties related to the uncertainty of the mechanism of injection of charged particles into the acceleration site. The injection efficiency most probably depends on the characteristics of particular elements, such as mass, charge, the first ionisation potential, volatility, etc. (Ellison et al. 1997). Dependence of the injection efficiency on these parameters might lead to distorting the abundance pattern of elements in the CR flux, as convincingly demonstrated, for example, for the first ionisation potential correlation with the elemental abundance (Wiedenbeck et al. 2007).
Nickel isotope 59Ni is unstable and decays into 59Co on the decay time scale td = 7.6 × 104 yr through the electron capture. However, it could not decay in this way if accelerated and converted into a cosmic ray soon after the supernova explosion. Non-detection of 59Ni in the cosmic ray flux apparently indicates that the 59Ni had the possibility of decaying before the cosmic ray acceleration process started. This fact supports the hypothesis that the CR acceleration process does not occur in young supernova remnants and is instead efficient only in the superbubble environment.
The conclusion on the decay of 59Ni before the onset of the cosmic ray acceleration process is based on the comparison of the upper bound on the 59Ni/59Co ratio in the CR flux to the 59Ni and 59Co yields of massive stars ending their life in supernova explosions. The predictions for the abundances of these isotopes are taken from the calculations of Woosley & Weaver (1995). These calculations describe the elemental yields produced throughout the life cycle of stars, including the moment of supernova explosion. The predicted ratio fNi = 59Ni/(59Co+59Ni) varies in the 0.2−0.9 range with the median value ≃0.5. Comparing this value with the CR measurements that constrain fNi< 0.18 in the CR flux has led Wiedenbeck et al. (1999) to the conclusion that 59Ni decays before the onset of the acceleration process.
In what follows we notice that the models of Woosley & Weaver (1995) did not extend to the entire relevant range of the initial masses of massive stars. Wiedenbeck et al. (1999) have used the results of calculations of Woosley & Weaver (1995) up to the initial mass 25 M⊙ to estimate fNi. We notice that stars of higher masses, being less abundant, could still provide a sizeable amount of 59Co and 59Ni. We use more recent calculations of the elemental yields by Chieffi & Limongi (2013) to show that account of these heavier stars can result in the model prediction of fNi which is consistent with the upper bound found on fNi in the CR flux.
2. 59Co and 59Ni yield from massive stars and supernovae
Different isotopes of the iron group nuclei, including cobalt and nickel could be produced at different stages of stellar evolution, starting from the helium hydrostatic burning stage up to the explosive nucleosynthesis at the moment of the supernova explosion. It happens that a significant amount if not most of 59Co is synthesised during the hydrostatic burning phases through neutron captures by iron-peak elements, the so-called s-process, while 59Ni is mainly made during the very last stages of the evolution of massive stars, during Si-burning. This can be seen for instance by looking at Table 9 in Woosley & Weaver (1995), where the quantities of 59Co and of 59Ni in the star are given at different stage of the evolution of a solar metallicity 25 M⊙ model. Typically, the amount of 59Co at the end of the core He-burning stage is already not far from the final amount ejected, while that of 59Ni is still very low at that stage and takes its final value mainly as a result of the explosive nucleosynthesis. Thus, the quantities ejected of these two isotopes depend on very different physical ingredients of the models. The ejected mass of 59Co is quite sensitive to the mass of the helium core (larger amounts for higher He-core masses), but depends weakly on the physics of the explosion. In contrast, the amount of 59Ni does not depend much on the size of the He core but is very sensitive to the physics of the explosion. Of course many other parameters enter into this game: the initial mass of the star, its rotation velocity, metallicity, magnetic field strength, nuclear reaction rates, etc. The uncertainty of these parameters unavoidably introduces uncertainties into the calculation of the pre-supernova relative abundance of 59Co and 59Ni. The amounts of 59Co and 59Ni produced also depend on the parameters for which no direct observational data is available and which could be assessed only through numerical simulations, such as the time-dependent neutron excess. Finally, calculations of elemental yields of massive stars include phenomenological parameters that parametrise our uncertainty of the knowledge of the physical mechanisms behind certain phenomena. An example of such a parameter is the “mass cut”, which sets a boundary between the material in the interior of the star that is ejected by the supernova explosion and the material that ultimately forms the compact remnant of the explosion. Increase in the computing power opens possibilities for gradual improvement in the precision of the stellar evolution models and accounts for larger numbers of relevant parameters regulating the evolutionary path stars (see Woosely et al. 2002, for a review).
The most recent calculation of the elemental yields of massive stars, which includes the predictions of the 59Co and 59Ni isotopes is the set of models of Chieffi & Limongi (2013). These yields are compared to those of Woosley & Weaver (1995) in Fig. 1. A few interesting points can be noted.
-
The yields in 59Co of Chieffi & Limongi (2013) are significantly greater than those of Woosley & Weaver (1995), although they present a qualitative similar dependence with the initial mass (increasing with it). These differences are at least in part due to the fact that the models of Chieffi & Limongi (2013) have, for a given initial mass, a larger He core than the models of Woosley & Weaver (1995).
-
In both series of models, 59Co is essentially made during the hydrostatic burning stages. In the case of the models by Chieffi & Limongi (2013), this conclusion is based on a comparison we performed between their 59Co yields and those obtained recently by Frischknecht et al. (2016), who just computed the contribution of the s-process occurring during the hydrostatic burning stages. If we superpose 59Co yields for the masses between 15 and 40 M⊙ with and without rotation for these two papers, we obtain a nearly perfect match. This confirms that indeed 59Co is mainly made by the s-process.
-
For 59Ni, the yields of Chieffi & Limongi (2013) are generally smaller than those of Woosley & Weaver (1995) in the mass domain between 13 and 25 M⊙ and larger for masses above 25 M⊙. This is quite consistent with the fact that below 25 M⊙, the mass cuts (the kinetic energy of the explosion) in the models of Chieffi & Limongi (2013) are larger (smaller) than in the models by Woosley & Weaver (1995) and the reverse for the masses above 25 M⊙. As mentioned above, the 59Ni yields are very dependent on the physics of the explosion.
-
In the mass domain between 11 and 25 M⊙, the models by Woosley & Weaver (1995) indicate strong variations in the 59Ni yields with the initial mass. Typically, the yields for the 20, 22, and 25 M⊙ are (in units of 10-4M⊙) 0.95, 3.67, and 1.74, respectively. It is difficult to give a very clear physical reason for that behaviour. We can just note that the mass of 56Ni also shows strong variations (0.088, 0.205, and 0.129 M⊙). On the other hand, the models by Chieffi & Limongi (2013) give yields of 59Ni for the 20 and 25 M⊙ rotating models (they have no predictions for a 22 M⊙ model) equal to 1.19 and 0.77 × 10-4M⊙ and yields in 56Ni equal to 0.1 M⊙. (Actually in these models the mass cut has been chosen to obtain this amount of 56Ni.)
We used the models by Chieffi & Limongi (2013) for our calculation of fNi. The top panel of Fig. 2 shows the cumulative masses of 59Co and 59Ni produced by a population of massive stars with Salpeter initial mass function (Salpeter 1955) in the mass range between 13 M⊙ (the lowest mass of the models of Chieffi & Limongi 2013) up to the maximum mass shown as the x axis value. The values correspond to the time moment 2.5 × 104 s after the explosion, i.e. much before the decay of 59Ni into . One can see that the 59Co mass accumulates linearly at a steady rate up to the stellar mass range ≃40 M⊙ and at a somewhat lower rate in the mass range M> 40 M⊙. Still, consideration of the full dynamic range of initial stellar masses is important for a fair judgement of the amount of 59Co produced.
 |
Fig. 1 Ejected masses of 59Co and 59Ni by star of different initial masses and computed by different authors: WW95 stands for Woosley & Weaver (1995) and CL13 for Chieffi & Limongi (2013). Both models are for solar metallicity. The models from Woosley & Weaver (1995) correspond to their A series, and the models of Chieffi & Limongi (2013) correspond to their rotating models. In both cases, the yields for the radionuclides are given 2.5 × 104 s after the explosion. That means that 59Ni had no time to decay (half-life is about 105 years). The masses in 59Ni of Woosley & Weaver (1995) present a kind of sawtooth behaviour below 25 M⊙ (see the red continuous lines), a hatched area covers that zone to guide the eye a bit. This was also done for the mass of 59Co from Woosley & Weaver (1995), although here the variations are much smaller. |
 |
Fig. 2 Cumulative mass yields |
Figure 2 shows that a large part of 59Ni is produced by the stars in the mass range up to (20−30) M⊙. This explains the decrease in the nickel-59 relative abundance fNi with the increase in the maximum initial stellar mass. Integration of the 59Co and 59Ni yields over the entire mass range results in the 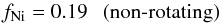 (1)59Ni fraction.
(1)59Ni fraction.
An essential difference of the models of Chieffi & Limongi (2013) from the models of Woosley & Weaver (1995) is the account of the rotation in the calculation of the stellar evolution. The bottom panel of Fig. 2 shows the 59Co and 59Ni yields of stars rotating with an initial equatorial velocity 300 km s-1. In spite of the similar qualitative behaviour of the cumulative yields of 59Co and 59Ni , the rotating models predict systematically lower 59Ni to 59Co fractions, which gives 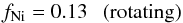 (2)after integration over the entire initial stellar mass range. Similar integrations performed with the yields of Woosley & Weaver (1995) provide values of fNi between 0.6 and 0.7 depending on whether the integration is made between 11 and 40 M⊙ or between 11 and 25 M⊙.
(2)after integration over the entire initial stellar mass range. Similar integrations performed with the yields of Woosley & Weaver (1995) provide values of fNi between 0.6 and 0.7 depending on whether the integration is made between 11 and 40 M⊙ or between 11 and 25 M⊙.
Lower values of fNi from the models of Chieffi & Limongi (2013) result mainly because the high mass range show very low 59Ni to 59Co fraction, while this mass domain still contributes significantly to 59Co. As we shall see, this has important consequences for interpreting the observed upper limit of fNi in cosmic rays (see next section).
An additional uncertainty of fNi estimate is introduced by the uncertainty of the position of the “mass cut” separating the ejecta from the collapsar. The predicted amounts of both 56Ni and 59Ni increases if the mass cut is moved deeper in the iron elements rich core. As a result, fNi increases with the increase in the assumed 56Ni yield. This is illustrated by Fig. 3, which compares the dependence of fNi on the maximum initial mass calculated for different 56Ni yields. One sees that a variation in 56Ni yields from 0.05 M⊙ to 0.2 M⊙ (around the reference value 0.1 M⊙ assumed by Chieffi & Limongi 2013) results in changes oinfNi in the 0.1−0.3 range. Observationally, the yield of 56Ni is observed to be about 0.1 M⊙ for stars with progenitor masses ≲25 M⊙ and is perhaps spread over more than an order of magnitude for higher mass progenitors (Nomoto et al. 2013).
 |
Fig. 3 59Ni fractions as a function of the assumed 56Ni yield for non-rotating star models. |
What are the effects that could modify fNi, in addition to those produced by considering different sets of stellar models? A main effect comes from the uncertainties about the fate of stars producing a black hole at the end of their evolution. Do these stars swallow all their mass into the newly formed black hole or do they still expel some material in a supernova event? In case the transition between neutron star and black hole production were around 25 M⊙ (Heger et al. 2003), and if, when a black hole is formed, no matter ejection occurs, then the integration for obtaining fNi should be made only in the mass range below 25 M⊙ as was done in Wiedenbeck et al. (1999). We see that, in that case, even using the models by Chieffi & Limongi (2013) would produce high fNi values. This would then support the view that some time delays took place between the ejection of 59Ni ejection and its acceleration into the cosmic rays. Although such a possibility cannot be totally discarded at the moment, there are a few arguments indicating that reality might be more complex:
-
First, the domain of initial masses giving neutron stars and black holes is not defined very well. Hydrodynamical simulations in 1 D by Ugliano et al. (2012) and Ertl et al. (2016) obtain successful SN explosions with neutron star formation for some models with initial masses between 20 and 40 M⊙, and even up to 120 M⊙, while failed explosion with BH formation also seem possible for progenitors below 20 M⊙!
-
Second, there are observations of the surface abundances of stars near a black hole, showing clear evidence for the star having been enriched by the ejecta of the SN that occurred at the time of the black hole formation. This indicates that, at least in some cases, a BH can form with a SN explosion (Israelian et al. 1999; González Hernández et al. 2004, 2008, 2011).
-
At solar metallicity, the most massive stars lose mass by stellar winds. Only 59Co has a chance of being ejected by the stellar winds (when the star is a Wolf-Rayet star of the type WC, i.e. where the He-burning products appear at the surface). Thus, if these stars ejected no material at the time of the supernova event, they would only contribute to the enrichment in 59Co. It remains, however, to be checked whether the amounts of 59Co ejected in that way are sufficient to lower fNi.
The above arguments cannot be taken as proof that we must make the integration over the whole mass range in the way we did above, but at least it shows that restricting its computation to only the mass domain below 25 M⊙ is probably not realistic.
3. Implications for the CR origin problem
Recent calculations of the yields of 59Co and 59Ni based on the detailed modelling of the pre-supernova evolution of massive stars over a wide energy range from 13 M⊙ to 120 M⊙ with account of rotation (Chieffi & Limongi 2013) differ from previous calculations of Woosley & Weaver (1995). In particular they result in a systematically lower 59Ni to 59Co fraction after the moment of supernova explosion (for the reference models normalised on 0.1 M⊙56Ni yield).
This fact has important consequences for the physics of Galactic CRs. The absence of 59Ni in the CR flux has been considered as evidence for a long time delay between the moment of supernova explosion and the onset of particle acceleration. This long time delay of ~105 yr was necessary to allow 59Ni to decay to 59Co via electron capture reaction. After such a time delay, supernovae exploding in the massive star formation regions could not be considered as isolated objects. On this time scale, interactions of supernova shell with the superbubble environment have to be taken into account. Therefore, a long time delay between the explosion and the moment of particle acceleration has been considered as an argument for the superbubble hypothesis of the CR production.
The revised calculation of the 59Ni and 59Co yield removes the requirement of 59Ni decay prior to the acceleration. The non-detection of 59Ni in the CR flux might be explained by the relatively small amount of 59Ni ejected by the ensemble of supernovae produced by stars with different initial masses and rotation velocities. This removes the contradiction between the supernova hypothesis of CR production and the measurements of 59Ni to 59Co ratio.
Estimating fNi as done above by integrating over the massive star range, implicitly assumes that the material of the cosmic rays is made from a well-mixed reservoir of many different core collapse supernova events. This is very much in line with the fact that the composition of the cosmic rays is indeed quite similar, with a few exceptions (see Sect. 1), to the interstellar medium abundances whose abundance also results, at least in part, from the contributions of many core collapse supernovae.
The above discussion tells us that (i) present-day observations are compatible with the acceleration of fresh ejecta of core collapse supernova material into the cosmic rays, provided the recent yields from the rotating stellar models of Chieffi & Limongi (2013) are used, (ii) that the whole mass domain from 13 up to at least 45−50 M⊙ contribute; and (iii) that for computing the SN contribution, mass cuts giving 0.1 M⊙ of 56Ni or lower are used.
Now what happens when the yields of type Ia supernovae are accounted for? These supernovae may contribute up to about two thirds of the iron peak element content in the current Universe (Matteucci & Greggio 1986). According to the work by Travaglio et al. (2004), type Ia supernovae typically produce as much 59Co as 59Ni in amounts equal to 5−8 × 10-4M⊙. In this case, the iron peak elements accelerated into the cosmic rays would also be made of two thirds of type Ia material, which would give fNi that is a bit smaller than 0.5 using the yields by Chieffi & Limongi (2013) and a bit larger than 0.5 using the yields by Woosley & Weaver (1995). This would again support the view that some time delay has occurred between the ejection of 59Ni and its acceleration into the cosmic rays.
However, we must keep in mind several differences between the core collapse supernovae and the type Ia supernovae. First, type Ia and core collapse supernovae are distributed differently in the Galaxy. The core collapse supernovae follow the star formation rate. Their density is enhanced in the regions of active star formation, such as the Galactic arms. Passage of a Galactic arm induces an enhancement of the core collapse supernovae contribution to the cosmic ray population on the time scale of cosmic ray residence in the Galactic disk, ~107 yr (Shaviv 2003; Overholt et al. 2009; Benyamin et al. 2013). On the contrary, the Type Ia supernovae rate does not follow temporal and spatial variations in the star formation rate. Instead, it is sensitive to the time integral of the star formation rate averaged over the Galactic volume. Even if the injection efficiency of cosmic rays by the core collapse and Type Ia supernovae is the same, the relative importance of the Type Ia and core collapse supernovae contributions to the cosmic ray flux could vary from place to place depending on the details of the recent massive star formation rate around the point of measurement (Neronov et al. 2012; Kachelriess et al. 2015).
Next, type Ia supernovae are believed to leave no remnant, while core-collapse supernovae do. If supernova remnants play an important role in the acceleration mechanism (Neronov & Semikoz 2012), the core collapse supernovae might be more efficient accelerators owing to the presence of the remnants.
Finally, the core collapse supernova initially expands in the bubble created by the wind of the progenitor star, while the type Ia supernova shell could expand in the interstellar medium already in the early stages of its evolution. In this case the forward shock of the type Ia supernova sweeps the material with the composition of the interstellar medium. If acceleration at the forward shock provides a dominant contribution to the cosmic ray yield of the type Ia supernovae (Warren et al. 2005) composition of the cosmic rays coming from this shock is not directly related to the elemental yield of the supernova. The interstellar medium feeding the shock contains no 59Ni so that even cosmic rays from the type Ia supernovae could be characterised by low fNi.
Actually, the last argument could also be valid for the core-collapse supernovae. Any assumption that cosmic ray production in these supernovae is also dominated by acceleration at the forward shock would just invalidate the “naive” assumption that cosmic-ray elemental yields of a supernova only repeat the elemental yields of the star after the explosion implicitly adopted by Wiedenbeck et al. (1999) and also in the previous sections of this paper. Instead, the composition of material accelerated at the forward shock at a particular moment of time (say, at the onset of Sedov-Taylor phase) would be influenced by the composition of portion of the stellar wind swept up by the supernova shell by that time (Prantzos 2012).
It is interesting to note that the 59Ni fraction predicted by the stellar evolution models of Chieffi & Limongi (2013) is close to the measured upper bound on fNi in the CR flux. This indicates that a moderate increase in sensitivity of CR detectors capable to distinguish iron group isotopes, like CRIS (Wiedenbeck et al. 1999), should lead to the detection of the 59Ni component of the
CR flux, if the accelerated particles originate in the core collapse supernova ejecta. Detection of 59Ni would provide a strong constraint on the mechanism of cosmic ray acceleration, because it would indicate that the supernova ejecta participate in the cosmic ray acceleration process and limit the time delay between the supernova explosion and the acceleration period to less than ~104−105 yr, which is a typical time scale on which the supernova remnants reach the Sedov-Taylor phase (Woltjer 1972; Vink 2012).
References
- Ackermann, M., Ajello, M., Allafort, A., et al. 2011, Science, 334, 1103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2012, ApJ, 755, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2013, Science, 339, 807 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Baade, W., & Zwicky, F. 1934, PNAS, 20, 259 [Google Scholar]
- Bell, A. R. 1978, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. & Lucek, S. G. 2001, MNRAS, 321, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Benyamin, D., Nakar, E., Piran, T., & Schaviv, N. J. 2014, ApJ, 782, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Binns, W. R., Wiedenbeck, M. E., Arnould, M., et al. 2005, ApJ, 634, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Ostriker, J. P. 1978, ApJ, 221, L29 [Google Scholar]
- Blasi, P. 2013, A&ARv., 21, 70 [Google Scholar]
- Bykov, A. M. 2014, A&ARv, 22, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Bykov, A. M., & Fleischman, G. D. 1992, MNRAS, 255, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Casse, M., & Paul, J. A. 1982, ApJ, 258, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Chieffi, A., & Limongi, M. 2013, ApJ, 764, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L. O. 1983, Rep. Progr. Phys. 46, 973 [Google Scholar]
- Ellison, D. C., Drury, L. O’C., & Meyer, J.-P. 1997, ApJ, 487, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Ertl, T., Janka, H.-T., Woosley, S. E., Sukhbold, T., & Ugliano, M. 2016, ApJ, 818, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Frischknecht, U., Hirschi, R., Pignatari, M., et al. 2016, MNRAS, 456, 1803 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J. I., Rebolo, R., Israelian, G., et al. 2004, ApJ, 609, 988 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J. I., Rebolo, R., Israelian, G., et al. 2008, ApJ, 679, 732 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J. I., Casares, J., Rebolo, R., et al. 2011, ApJ, 738, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Grenier, I. A., Black, J. H., & Strong, A. W. 2015, ARA&A, 53, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Higdon, J. C., Lingenfelter, R. E., & Ramaty, R. 1998, ApJ, 509, L33 [CrossRef] [Google Scholar]
- Israel, M. H., Binns, W. R., Cummings, A. C., et al. 2005, Nucl. Phys. A., 758, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Israelian, G., Rebolo, R., Basri, G., Casares, J., & Martín, E. L. 1999, Nature, 401, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Kachelriess, M., Neronov, A., & Semikoz, D. V., 2015, Phys. Rev. Lett. 115, 181103 [NASA ADS] [CrossRef] [Google Scholar]
- Krymskii, G. F. 1977, Akademiia Nauk SSSR Doklady, 234, 1306 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 1993, A&A, 278, 406 [NASA ADS] [Google Scholar]
- Matteucci, F., & Greggio, L. 1986, A&A, 154, 279 [NASA ADS] [Google Scholar]
- Mewaldt, R. A., Spalding, J. D., Stone, E. C., & Vogt, R. E. 1980, ApJ, 235, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Neronov, A., & Semikoz, D. V. 2012, Phys. Rev. D85, 083008 [NASA ADS] [Google Scholar]
- Neronov, A., Semikoz, D. V., & Taylor, A. M. 2012, Phys. Rev. Lett., 108, 051105 [Google Scholar]
- Nomoto, K., Kobayashi, C., & Tominaga, N. 2013, ARA&A, 51, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Overholt, A. C., Melott, A. L., & Pohl, M. 2009, ApJ, 705, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Parizot, E., Marcowith, A., van der Swaluw, E., Bykov, A. M., & Tatischeff, V. 2004, A&A, 424, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N. 2012, A&A, 538, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Shaviv, N. J. 2003, New Astron., 8, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Travaglio, C., Hillebrandt, W., Reinecke, M., & Thielemann, F.-K. 2004, A&A, 425, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ugliano, M., Janka, H.-T., Marek, A., & Arcones, A. 2012, ApJ, 757, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. 2012, A&ARv, 20, 49 [Google Scholar]
- Warren, J. S., Hughes, J. P., Badenes, C., et al. 2005, ApJ, 634, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Wiedenbeck, M. E., & Grenier, D. E. 1981, Phys. Rev. Lett., 46, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Wiedenbeck, M. E., Binns, W. R., Christian, E. R., et al. 1999, ApJ, 523, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Wiedenbeck, M. E., Binns, W. R., Cummings, A. C., et al. 2007, Space Sci. Rev., 130, 415 [Google Scholar]
- Woltjer, L. 1972, ARA&A, 10, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Ejected masses of 59Co and 59Ni by star of different initial masses and computed by different authors: WW95 stands for Woosley & Weaver (1995) and CL13 for Chieffi & Limongi (2013). Both models are for solar metallicity. The models from Woosley & Weaver (1995) correspond to their A series, and the models of Chieffi & Limongi (2013) correspond to their rotating models. In both cases, the yields for the radionuclides are given 2.5 × 104 s after the explosion. That means that 59Ni had no time to decay (half-life is about 105 years). The masses in 59Ni of Woosley & Weaver (1995) present a kind of sawtooth behaviour below 25 M⊙ (see the red continuous lines), a hatched area covers that zone to guide the eye a bit. This was also done for the mass of 59Co from Woosley & Weaver (1995), although here the variations are much smaller. |
| In the text | |
 |
Fig. 2 Cumulative mass yields |
| In the text | |
 |
Fig. 3 59Ni fractions as a function of the assumed 56Ni yield for non-rotating star models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.