| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | L2 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201628068 | |
| Published online | 12 February 2016 | |
Rapid rotational crust-core relaxation in magnetars
Institute for Theoretical Physics, J. W. Goethe University, 60438 Frankfurt am Main, Germany
e-mail: sedrakian@th.physik.uni-frankfurt.de
Received: 1 January 2016
Accepted: 24 January 2016
If a magnetar interior B-field exceeds 1015 G, it will unpair the proton superconductor in the stellar core by inducing diamagnetic currents that destroy the Cooper pair coherence. Then, the P-wave neutron superfluid in these non-superconducting regions will couple to the stellar plasma by scattering of protons off the quasiparticles that are confined in the cores of neutron vortices by the strong (nuclear) force. The dynamical timescales associated with this interaction span from several minutes at the crust-core interface to a few seconds in the deep core. We show that (a) the rapid crust-core coupling is incompatible with oscillation models of magnetars that completely decouple the core superfluid from the crust and (b) magnetar precession is damped by the coupling of normal fluids to the superfluid core and, if observed, needs to be forced or continuously excited by seismic activity.
Key words: dense matter / magnetic fields / stars: neutron
© ESO, 2016
1. Introduction
Magnetars are a class of compact stars that exhibit powerful X-ray and soft γ-ray outburst activity, which is attributed to the energy release stored in their internal magnetic fields (Thompson & Duncan 1995). Their surface B-fields are measured to be a factor of thousand stronger than the fields inferred for rotationally powered pulsars. The interior fields of magnetars are unknown, but could be several orders of magnitude stronger than the surface field (for recent reviews see Turolla et al. 2015; Mereghetti et al. 2015). For interior fields B16 ~ 1, where B16 is the field value in units of 1016 G, the electromagnetic interactions become of the order of characteristic nuclear scales (~MeV). As a consequence, the S-wave condensate of protons in the stellar core, which contains charged Cooper pairs with opposite spins, becomes affected by the B-field. It is eventually destroyed at the second critical field Hc2 that is known from the theory of ordinary superconductivity (Tinkham 1996). This unpairing effect arises because the charge of Cooper pairs is coupled to the electromagnetic field, which winds up the trajectories of protons in strong magnetic fields over distances smaller than the coherence length of a Cooper pair.
In the context of magnetars, it was shown previously that the strong density dependence of the proton pairing gaps causes the quenching of the superconductivity to be non-uniform. As a consequence, intermediate field magnetars with 0.1 ≤ B16 ≤ 5 are partially superconducting, while high-field magnetars are B16 ≥ 5 are fully non-superconducting (Sinha & Sedrakian 2015a,b). If the fields are by an order of magnitude larger, B16 ≥ 10, the neutron S-wave condensate is unpaired by the magnetic field because of the paramagnetic interaction of spins of neutrons with the B-field (Stein et al. 2016). On the other hand, the neutron P-wave superfluid, which features spin-1 Cooper pairs, is unaffected by the magnetic fields at the fundamental level. Because it is uncharged, it cannot show Landau diamagnetism; its paramagnetic response to a B-field is non-destructive because the pairing involves neutrons with parallel spins.
The purpose of this work is to discuss the rotational coupling of neutron superfluid in magnetar cores in the case where the fields are large enough to unpair proton condensate. We show that unpairing opens a new channel of coupling of electron-proton plasma to the neutron vorticity in the core. This new channel (which is suppressed if protons are superconducting) is the scattering of protons off neutron quasiparticles in the vortex cores by nuclear force. This process needs to be contrasted with the scattering of electrons off magnetized neutron vortices by purely electromagnetic forces, which provides an upper bound on the electron mean-free-path in a type-I superconducting case, that is, in the absence of proton vorticity (Alpar & Sauls 1988).
The coupling strength of the superfluid to the unpaired plasma has important implications for the macroscopic observable manifestations of magnetars. We give two specific examples below. Gabler et al. (2013) conducted numerical simulations of axisymmetric, torsional, magneto-elastic oscillations of magnetars with a superfluid core to explain the observed quasiperiodic oscillations of these objects. In doing so, it was assumed that the superfluid is completely decoupled in the core of the star (i.e., the neutron and proton fluids are coupled only by gravity). The assumptions above require a computation of the coupling time between the neutron superfluid and charged plasma in magnetars, in particular, in a situation where protons form normal fluids, as assumed by Gabler et al. (2013). A second example is the precessional motion of magnetars, more specifically, the influence of an interior fluid on such motions. Link (2007) discussed the implications of the observation of precession in ordinary neutron stars on the state of proton superconductivity in their cores by focusing on the incompatibility of the type II superconductivity with free precession. An alternative is the type I superconductivity in the cores of neutron stars with a low magnetic field (Link 2003; Sedrakian 2005; Charbonneau & Zhitnitsky 2007). A natural extension of this discussion to magnetars requires the knowledge of dynamical coupling of the neutron P-wave superfluid, when the proton superfluidity is quenched by magnetic fields and protons form a normal fluid.
Current observations of magnetars do not place any significant constraints on the structure and strength of internal magnetic fields, although it is known that purely poloidal or toroidal configurations are unstable to certain types of instabilities. The internal fields are likely to contain both components, but their location is unknown: they can penetrate deep inside the core of the star or can be confined to its crust. We assume a constant field in the core for concreteness when discussing the unpairing effect below, while the coupling timescales we find are local quantities that are independent of the large-scale structure of the field. This assumption is motivated by the fact that the composition of plasma does change over the core (setting aside the possibility of phase transitions in ultra-dense matter). The density dependence of the B-field has been phenomenologically parametrized such that the field increases as some function of the density toward the stellar center (see, for example, Sinha 2014). While this dependence can be easily incorporated in our discussion, it adds little insight without a self-consistent solution of the Einstein-Maxwell equations (Chatterjee et al. 2015).
This paper is structured as follows. In Sect. 2 we review the unpairing effect in the cores of magnetars and the implied structure of superfluid and superconducting shells. The relaxation times-scales for the coupling of the magnetar core to the crust are computed in Sect. 3. We discuss the implications of our findings in Sect. 4 and provide a summary in Sect. 5.
2. Unpairing effect
As is well known (see, for example, Tinkham 1996), in type II superconductors the Ginzburg-Landau (GL) parameter, defined as κ = λ/ξp, where λ is the London penetration depth of B-field in a superconductor, ξp is the coherence length, is in the range 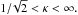 The magnetic field is carried by electromagnetic vortices with quantum flux Φ0 = π/e (here and below ħ= c = 1) if the B-field is in the range between the lower and upper critical fields, that is, Hc1 ≤ B ≤ Hc2. If the B-field is larger than Hc2, it unpairs the Cooper pairs and destroys the superconductivity.
The magnetic field is carried by electromagnetic vortices with quantum flux Φ0 = π/e (here and below ħ= c = 1) if the B-field is in the range between the lower and upper critical fields, that is, Hc1 ≤ B ≤ Hc2. If the B-field is larger than Hc2, it unpairs the Cooper pairs and destroys the superconductivity.
The unpairing effect in a superfluid neutron and superconducting proton mixture was explored within the GL theory on the basis of the following functional (Sinha & Sedrakian 2015a) ![\begin{eqnarray} \label{GL_Functional} \mathscr{F} [\phi,\psi] = \mathscr{F}_n[\phi,\psi] + \mathscr{F}_{\rm p}[\phi,\psi] +\frac1{4m_{\rm p}}\vert \vecD\psi\vert^2 + \frac{B^2}{8\pi}, \end{eqnarray}](/articles/aa/full_html/2016/03/aa28068-16/aa28068-16-eq21.png) (1)where ψ and φ are the proton and neutron condensate wave-functions, mp is the proton mass, D = −i∇−2eA is the gauge-invariant derivative, and Fn [φ,ψ] and Fp [φ,ψ] are the energy-density functionals of neutron and proton condensates. The proximity to Hc2 guarantees that the proton condensate wave-function is small and its functional can be written as a power series
(1)where ψ and φ are the proton and neutron condensate wave-functions, mp is the proton mass, D = −i∇−2eA is the gauge-invariant derivative, and Fn [φ,ψ] and Fp [φ,ψ] are the energy-density functionals of neutron and proton condensates. The proximity to Hc2 guarantees that the proton condensate wave-function is small and its functional can be written as a power series ![\begin{eqnarray} \mathscr{F}_{\rm p}[\phi,\psi] = \alpha\tau \vert \psi\vert^2 +\frac{b}{2}\vert \psi\vert^4 +b'\vert \psi\vert^2 \vert \phi\vert^2, \end{eqnarray}](/articles/aa/full_html/2016/03/aa28068-16/aa28068-16-eq28.png) (2)where τ = (T−Tcp) /Tcp with T being the temperature and Tcp the critical temperature of superconducting phase transition of protons, α and b are the familiar coefficients of GL expansion, while b′ describes the coupling between the neutron and proton condensates. The equations of motions of the proton condensate associated with the GL functional (1)are given by the variations δF [φ,ψ] /δψ = 0 and δF [φ,ψ] /δA = 0. Close to the critical field, the GL equations can be linearized assuming further that A is locally linear in coordinates, so that the B-field is locally constant. The solution of the pair of linearized GL equations that correspond to non-vanishing ψ provide the highest possible value of the field that is still compatible with superconductivity, which is then identified with the upper critical field (Sinha & Sedrakian 2015a)
(2)where τ = (T−Tcp) /Tcp with T being the temperature and Tcp the critical temperature of superconducting phase transition of protons, α and b are the familiar coefficients of GL expansion, while b′ describes the coupling between the neutron and proton condensates. The equations of motions of the proton condensate associated with the GL functional (1)are given by the variations δF [φ,ψ] /δψ = 0 and δF [φ,ψ] /δA = 0. Close to the critical field, the GL equations can be linearized assuming further that A is locally linear in coordinates, so that the B-field is locally constant. The solution of the pair of linearized GL equations that correspond to non-vanishing ψ provide the highest possible value of the field that is still compatible with superconductivity, which is then identified with the upper critical field (Sinha & Sedrakian 2015a) ![\begin{eqnarray} \label{eq:Hc2_1} H_{c2} &=&\frac{\Phi_0}{2\pi\xi_{\rm p}^2} \left[1 + \beta(b')\right], \end{eqnarray}](/articles/aa/full_html/2016/03/aa28068-16/aa28068-16-eq38.png) (3)where mp | ατ | = (2ξp)-2. The critical value of the field is enhanced by β ≃ 0.2 through the density-density coupling between neutron and proton condensates. The dependence of the Hc2 field on density is illustrated in Fig. 1, where we adopted the same input physics as described in Sinha & Sedrakian (2015a). Independent of the details of microphysical input, the maximum of Hc2 is attained close to the crust-core interface (corresponding to nb = 0.5n0, where n0 is the nuclear saturation density). As a consequence, magnetars with approximately constant interior fields below Hc2 will contain two physically distinct regions: (a) the inner core, which is void of superconductivity; and (b) the outer core, where protons are superconducting and, consequently, proton flux-tubes (vortices) are present along with the neutron vortex lattice induced by the rotation. The magnetic B-field in type II superconductor forms quantized electromagnetic vortices with density Np = B/ Φ0. These phases are enveloped by the crust, which is threaded by non-quantized magnetic field.
(3)where mp | ατ | = (2ξp)-2. The critical value of the field is enhanced by β ≃ 0.2 through the density-density coupling between neutron and proton condensates. The dependence of the Hc2 field on density is illustrated in Fig. 1, where we adopted the same input physics as described in Sinha & Sedrakian (2015a). Independent of the details of microphysical input, the maximum of Hc2 is attained close to the crust-core interface (corresponding to nb = 0.5n0, where n0 is the nuclear saturation density). As a consequence, magnetars with approximately constant interior fields below Hc2 will contain two physically distinct regions: (a) the inner core, which is void of superconductivity; and (b) the outer core, where protons are superconducting and, consequently, proton flux-tubes (vortices) are present along with the neutron vortex lattice induced by the rotation. The magnetic B-field in type II superconductor forms quantized electromagnetic vortices with density Np = B/ Φ0. These phases are enveloped by the crust, which is threaded by non-quantized magnetic field.
 |
Fig. 1 Dependence of the critical unpairing field Hc2 on baryonic density (solid line). The density is normalized to the nuclear saturation density n0 = 0.16 fm-3 and the equation of state and composition of matter is the same as in Sinha & Sedrakian (2015a). This arrangment of flux-free and flux-featuring phases arises in the case of intermediate field magnetars with average constant field B<Hc2, which is indicated by the dashed line. |
3. Rotational crust-core coupling timescales
Neutron superfluid rotates by forming an array of quantized vortices. The areal number density of neutron vortices is given by 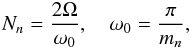 (4)where mn is the bare neutron mass, Ω is the rotation frequency of the star, and ω0 is the quantum of neutron circulation.
(4)where mn is the bare neutron mass, Ω is the rotation frequency of the star, and ω0 is the quantum of neutron circulation.
Any variation in the angular velocity of the magnetar causes the free vortices to move and leads to their new quasi-equilibrium distribution. Hence the vortex distribution depends on their velocity field vL. This velocity field is determined by the equation of motion of a vortex, which because of the negligible vortex mass reduces to the requirement that the sum of forces acting on its unit segment vanishes, ![\begin{equation} \label{eq:force_balance} \rho_n\omega_0 [(\vecv_S-\vecv_L)\times \vecnu] - \eta (\vecv_L-\vecv_N) =0. \end{equation}](/articles/aa/full_html/2016/03/aa28068-16/aa28068-16-eq53.png) (5)Here the first term is the Magnus force, the second is the friction force between the vortices and the normal liquid, ρn is the mass density of the superfluid component, vN is the velocity of the normal component, and η is the coordinate-dependent longitudinal (with respect to vL−vN) friction coefficient. We first consider the flux-tube free (unpaired) region and demonstrate that it is coupled to the plasma of the star on short dynamical coupling timescales. First we note that the non-superconducting proton fluid will couple to the electron fluid on plasma timescales, which are much shorter than the hydrodynamical timescales. Therefore, the unpaired core of a magnetar can be considered as a two-fluid system with neutron condensate forming the superfluid component and the proton plus electron fluids forming the normal component. Neutron vortices (and the neutron superfluid) couples to this normal component electromagnetically (Sauls et al. 1982). However, because protons are unpaired (i.e., excitations out of Fermi surface can be created without the energy cost of breaking a Cooper pair), they will scatter efficiently off neutron vortex core quasiparticles by the nuclear force. The solution of the Boltzmann equation for protons in the relaxation time approximation leads to the microscopic relaxation timescale (Sedrakian 1998)
(5)Here the first term is the Magnus force, the second is the friction force between the vortices and the normal liquid, ρn is the mass density of the superfluid component, vN is the velocity of the normal component, and η is the coordinate-dependent longitudinal (with respect to vL−vN) friction coefficient. We first consider the flux-tube free (unpaired) region and demonstrate that it is coupled to the plasma of the star on short dynamical coupling timescales. First we note that the non-superconducting proton fluid will couple to the electron fluid on plasma timescales, which are much shorter than the hydrodynamical timescales. Therefore, the unpaired core of a magnetar can be considered as a two-fluid system with neutron condensate forming the superfluid component and the proton plus electron fluids forming the normal component. Neutron vortices (and the neutron superfluid) couples to this normal component electromagnetically (Sauls et al. 1982). However, because protons are unpaired (i.e., excitations out of Fermi surface can be created without the energy cost of breaking a Cooper pair), they will scatter efficiently off neutron vortex core quasiparticles by the nuclear force. The solution of the Boltzmann equation for protons in the relaxation time approximation leads to the microscopic relaxation timescale (Sedrakian 1998) 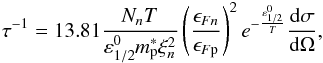 (6)where ϵFn and ϵFp are the Fermi energies of neutrons and protons,
(6)where ϵFn and ϵFp are the Fermi energies of neutrons and protons, 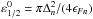 is the lowest energy state of a neutron quasiparticle confined in the vortex, Δn is the pairing gap, dσ/dΩ is the differential neutron-proton scattering cross-section, and ξn is the neutron condensate coherence length. Here and below, for simplicity, we do not distinguish between the neutron and proton effective masses, meaning that we set
is the lowest energy state of a neutron quasiparticle confined in the vortex, Δn is the pairing gap, dσ/dΩ is the differential neutron-proton scattering cross-section, and ξn is the neutron condensate coherence length. Here and below, for simplicity, we do not distinguish between the neutron and proton effective masses, meaning that we set 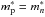 .
.
 |
Fig. 2 Relaxation timescales for protons scattering off the quasiparticles that are confined in the neutron vortex core (upper panel) the drag-to-lift ratio (middle panel), and dynamical relaxation time (lower panel) for T = 0.01 MeV (solid line) and T = 0.05 MeV (dashed line) and the rotation frequency Ω = 1 Hz. The results are valid in the entire density domain if the constant field in the core satisfies B> max Hc2; for fields lower than Hc2 , the results are valid to the right of the superconducting-normal boundary (assuming the arrangement of phases as in Fig. 1). |
The force exerted by proton quasiparticles per single vortex is given by (Bildsten & Epstein 1989) 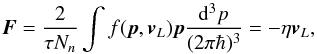 (7)where f(p,vL) is the non-equilibrium distribution function, which we expand assuming small perturbation about the equilibrium distribution function f0, that is, f(p,vL) = f0(p) + (∂f0/∂ϵ)(p·vL). In the low-temperature limit ∂f0/∂ϵ ≃ −δ(ϵ−ϵFp). The friction coefficient, after phase space integrations in (7), is given by
(7)where f(p,vL) is the non-equilibrium distribution function, which we expand assuming small perturbation about the equilibrium distribution function f0, that is, f(p,vL) = f0(p) + (∂f0/∂ϵ)(p·vL). In the low-temperature limit ∂f0/∂ϵ ≃ −δ(ϵ−ϵFp). The friction coefficient, after phase space integrations in (7), is given by 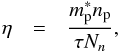 (8)where np is the proton number density and Nn is defined in Eq. (4). The quantity characterizing the macroscopic relaxation of superfluid is the ratio of the strengths of viscous friction force and the Magnus force or the drag-to-lift ratio,
(8)where np is the proton number density and Nn is defined in Eq. (4). The quantity characterizing the macroscopic relaxation of superfluid is the ratio of the strengths of viscous friction force and the Magnus force or the drag-to-lift ratio, 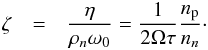 (9)Finally, the macroscopic dynamical coupling time of the superfluid to the plasma is given by
(9)Finally, the macroscopic dynamical coupling time of the superfluid to the plasma is given by 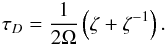 (10)We adopt the same equation of state and nucleonic composition as in Sinha & Sedrakian (2015a) to compute the numerical values of the quantities of interest and do not repeat the details of the input here. We do not consider hyperonic or deconfined quark degrees of freedom. The hyperonic scattering contribution will be subdominant or of the same order of magnitude as the proton scattering because the abundances of these species are similar in hyperon-rich matter. The relevant relaxation timescales in two-flavor quark matter have been computed for color-magnetic flux tubes interacting through the Aharonov-Bohm effect with leptons and unpaired quarks, in which case again the strong force is involved (Alford & Sedrakian 2010).
(10)We adopt the same equation of state and nucleonic composition as in Sinha & Sedrakian (2015a) to compute the numerical values of the quantities of interest and do not repeat the details of the input here. We do not consider hyperonic or deconfined quark degrees of freedom. The hyperonic scattering contribution will be subdominant or of the same order of magnitude as the proton scattering because the abundances of these species are similar in hyperon-rich matter. The relevant relaxation timescales in two-flavor quark matter have been computed for color-magnetic flux tubes interacting through the Aharonov-Bohm effect with leptons and unpaired quarks, in which case again the strong force is involved (Alford & Sedrakian 2010).
Figure 2 shows the key results of this study: the relaxation time (6), the drag-to-lift ratio (9), and the dynamical coupling timescale (10)as a function of baryon density in the stellar core for T = 0.01 and 0.05 MeV, or equivalently for T = 1.2 × 108 K and T = 5.8 × 108 K. An average energy and angle-independent neutron-proton cross section σ ≃ 60 fm2 and rotation frequency Ω = 1 Hz were assumed. The relaxation time increases with decreasing temperature mainly due to the exponential Boltzmann factor in (6). The results shown in Fig. 2 are relevant in the entire density range if the field in the star satisfies the condition B> max Hc2, or in other words, if the unpairing effect acts in the entire core. If B< max Hc2, then the results are valid above a certain density threshold (see Fig. 1). Below this threshold density, the dynamics of the core is determined by the vortex-flux interactions and the coupling of the electron liquid to this conglomerate, which is not well understood. For typical magnetar periods of about 10 s, that is, for spin rotations of about 1 Hz, Fig. 2 implies that the unpaired core couples to the plasma on short dynamical timescales, which lie in the range of several minutes at the crust-core boundary to a few seconds deep in the magnetar core.
4. Implications for superfluid oscillations and precession
We now briefly comment on some applications of the results above. Superfluid oscillations were studied by Gabler et al. (2013) under the assumption that protons form a normal fluid (in line with the unpairing effect, which is alluded to by these authors), but assuming that the superfluid core is completely decoupled from the crust. This leads to a higher Alfvén speed in the core because only protons take part in magneto-elastic oscillations and stronger penetration of these modes inside the crust. In addition, a less massive core takes part in the magneto-elastic oscillations, which means that the coupling to the crust is stronger. The rapid relaxation times obtained in Sect. 3 imply that the two assumptions above are incompatible because once protons are normal, they will couple the proton-electron normal fluid to the neutron superfluid by scattering off the neutron vortex core quasiparticles. We note that for rotation periods characteristic of magnetars, the core is threaded by a mesh of neutron vortices with an areal density given by Nn ~ 3.3 × 102(Ω/1 Hz) cm-2 according to Eq. (4).
In the region where P-wave superfluidity vanishes, the coupling between neutron and proton fluids will be faster than our result above by many orders of magnitude. The agreement of numerical finds of Gabler et al. (2013) with the data on oscillations of magnetars may indicate a type II proton superconductivity and not a normal proton fluid, in which case the coupling of neutron and proton fluids depends on the complex ways the vortex lattices pin in the core of the star (see, for example, Link 2014 and references therein). For models of magnetar oscillations in the case of type II superconducting matter, see, for example, Andersson et al. (2009), van Hoven & Levin (2008).
 |
Fig. 3 Eigenfrequencies of precessional modes (solid lines) and their damping (dashed lines) of a compact star with a superfluid component (Sedrakian et al. 1999). The slow mode (upper panel) is normalized to the classical precession frequency ϵΩ, where ϵ is the eccentricity. The fast mode (lower panel) is a fraction of the rotational frequency. |
Free precession of magnetars will be possible in a range of couplings between the superfluid neutron fluid and the normal proton-electron component in the core and the crust material. The eigenmodes of precessional motion for a star with a superfluid interior were derived for arbitrary drag-to-lift ratios in Sedrakian et al. (1999) and are illustrated in Fig. 3. Observationally interesting are the slow precessional modes with eigenfrequency ~ϵΩ, where ϵ is the eccentricity and Ω is the rotation frequency. This mode is precisely the counterpart of ordinary precession in astronomical bodies. The fast mode with eigenfrequency ~Ω is observationally irrelevant in the electromagnetic spectrum, but it might be an important source of gravitational waves (Jones 2010). It is seen that for ζ > 1 the damping of the slow mode exceeds the eigenmode frequency, which implies that the precession is damped within a cycle. For ζ ≪ 1 precession is undamped by the superfluid component. A comparison with the values of ζ in Fig. 2 shows that the low-density outer core (ζ ≃ 0.2) does not affect free precession, while the high-density inner core (ζ ≃ 0.4) can cause significant damping of precession over a cycle or so. Thus, precession of magnetars is sensitive to the crust-coupling in the case when protons are non-superconducting because the drag-to-lift ratios we find are within the range of the crossover from undamped to damped precession. Because the inner core unpairs at lower fields (see Fig. 1), we may conclude that unpairing will lead to damping of free precession in magnetars. Our arguments apply to free precession; it can still be observed if there is a continuous source of excitation, such as magnetic energy, which can induce seismic activity (Lander et al. 2015).
5. Summary
The key result of this work is the demonstration that if the B-field in the interior of a magnetar is large enough to unpair the proton condensate (unpairing effect), the magnetar core will couple to the crust on short dynamical timescales. We also computed the relevant values of the drag-to-lift ratio that measure the influence of the superfluid on the dynamics of normal fluid plasma. The obtained range of this parameter lies in the region of the crossover from undamped precession to its complete damping, therefore an observation of precession in magnetars can shed light on the dynamical coupling mechanism of their core to the crust. Our results indicate that long-term precession is unlikely in magnetars and, if observed, needs to be induced by seismic activity. We anticipate that our results may be useful in other contexts, such as the quasi-radial oscillations of magnetars, their glitch and anti-glitch relaxations, and vortex shear modes.
Acknowledgments
The support of this research by the Deutsche Forschungsgemeinschaft (Grant No. SE 1836/3-1) and by the European NewCompStar COST Action MP1304 is gratefully acknowledged.
References
- Alford, M. G., & Sedrakian, A. 2010, J. Phys. G Nucl. Phys., 37, 075202 [Google Scholar]
- Alpar, M. A., & Sauls, J. A. 1988, ApJ, 327, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, N., Glampedakis, K., & Samuelsson, L. 2009, MNRAS, 396, 894 [NASA ADS] [CrossRef] [Google Scholar]
- Bildsten, L., & Epstein, R. I. 1989, ApJ, 342, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, J., & Zhitnitsky, A. 2007, Phys. Rev. C, 76, 015801 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, D., Elghozi, T., Novak, J., & Oertel, M. 2015, MNRAS, 447, 3785 [NASA ADS] [CrossRef] [Google Scholar]
- Gabler, M., Cerdá-Durán, P., Stergioulas, N., Font, J. A., & Müller, E. 2013, Phys. Rev. Lett., 111, 211102 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, D. I. 2010, MNRAS, 402, 2503 [NASA ADS] [CrossRef] [Google Scholar]
- Lander, S. K., Andersson, N., Antonopoulou, D., & Watts, A. L. 2015, MNRAS, 449, 2047 [NASA ADS] [CrossRef] [Google Scholar]
- Link, B. 2003, Phys. Rev. Lett., 91, 101101 [NASA ADS] [CrossRef] [Google Scholar]
- Link, B. 2007, Ap&SS, 308, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Link, B. 2014, ApJ, 789, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Mereghetti, S., Pons, J. A., & Melatos, A. 2015, Space Sci. Rev., 191, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Sauls, J. A., Stein, D. L., & Serene, J. W. 1982, Phys. Rev. D, 25, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Sedrakian, A. 1998, Phys. Rev. D, 58, 021301 [NASA ADS] [CrossRef] [Google Scholar]
- Sedrakian, A. 2005, Phys. Rev. D, 71, 083003 [NASA ADS] [CrossRef] [Google Scholar]
- Sedrakian, A., Wasserman, I., & Cordes, J. M. 1999, ApJ, 524, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, M., Sedrakian, A., Huang, X.-G., & Clark, J. W. 2016, Phys. Rev. C, 93, 015802 [NASA ADS] [CrossRef] [Google Scholar]
- Sinha, M. 2014, J. Phys. Conf. Ser., 496, 012011 [NASA ADS] [CrossRef] [Google Scholar]
- Sinha, M., & Sedrakian, A. 2015a, Phys. Rev. C, 91, 035805 [NASA ADS] [CrossRef] [Google Scholar]
- Sinha, M., & Sedrakian, A. 2015b, Phys. Part. Nucl., 46, 1510 [CrossRef] [Google Scholar]
- Thompson, C., & Duncan, R. C. 1995, MNRAS, 275, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Tinkham, M. 1996, in Introduction to superconductivity (New York: McGraw-Hill) [Google Scholar]
- Turolla, R., Zane, S., & Watts, A. L. 2015, Rep. Prog. Phys., 78, 116901 [Google Scholar]
- van Hoven, M., & Levin, Y. 2008, MNRAS, 391, 283 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Dependence of the critical unpairing field Hc2 on baryonic density (solid line). The density is normalized to the nuclear saturation density n0 = 0.16 fm-3 and the equation of state and composition of matter is the same as in Sinha & Sedrakian (2015a). This arrangment of flux-free and flux-featuring phases arises in the case of intermediate field magnetars with average constant field B<Hc2, which is indicated by the dashed line. |
| In the text | |
 |
Fig. 2 Relaxation timescales for protons scattering off the quasiparticles that are confined in the neutron vortex core (upper panel) the drag-to-lift ratio (middle panel), and dynamical relaxation time (lower panel) for T = 0.01 MeV (solid line) and T = 0.05 MeV (dashed line) and the rotation frequency Ω = 1 Hz. The results are valid in the entire density domain if the constant field in the core satisfies B> max Hc2; for fields lower than Hc2 , the results are valid to the right of the superconducting-normal boundary (assuming the arrangement of phases as in Fig. 1). |
| In the text | |
 |
Fig. 3 Eigenfrequencies of precessional modes (solid lines) and their damping (dashed lines) of a compact star with a superfluid component (Sedrakian et al. 1999). The slow mode (upper panel) is normalized to the classical precession frequency ϵΩ, where ϵ is the eccentricity. The fast mode (lower panel) is a fraction of the rotational frequency. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


