| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 13 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201527598 | |
| Published online | 28 January 2016 | |
Center-to-limb variation of intensity and polarization in continuum spectra of FGK stars for spherical atmospheres⋆
1
Kiepenheuer-Institut für Sonnenphysik (KIS),
Schöneckstrasse 6,
79104
Freiburg,
Germany
e-mail: kostogryz@kis.uni-freiburg.de; sveta@kis.uni-freiburg.de
2
Max-Planck Institute for solar system research
(MPS), Justus-von-Liebig-Weg
3, 37077
Göttingen,
Germany
3
Astronomical Observatory Belgrade, Volgina 7, 11060
Belgrade,
Serbia
4
Hamburger Sternwarte, Gojenbergsweg 112,
21029
Hamburg,
Germany
Received: 19 October 2015
Accepted: 2 December 2015
Aims. One of the necessary parameters needed for the interpretation of the light curves of transiting exoplanets or eclipsing binary stars (as well as interferometric measurements of a star or microlensing events) is how the intensity and polarization of light changes from the center to the limb of a star. Scattering and absorption processes in the stellar atmosphere affect both the center-to-limb variation of intensity (CLVI) and polarization (CLVP). In this paper, we present a study of the CLVI and CLVP in continuum spectra, taking into consideration the different contributions of scattering and absorption opacity for a variety of spectral type stars with spherical atmospheres.
Methods. We solve the radiative transfer equation for polarized light in the presence of a continuum scattering, taking into consideration the spherical model of a stellar atmosphere. To cross-check our results, we developed two independent codes that are based on Feautrier and short characteristics methods, respectively,
Results. We calculate the center-to-limb variation of intensity (CLVI) and polarization (CLVP) in continuum for the Phoenix grid of spherical stellar model atmospheres for a range of effective temperatures (4000−7000 K), gravities (log g = 1.0−5.5), and wavelengths (4000−7000 Å), which are tabulated and available at the CDS. In addition, we present several tests of our codes and compare our calculations for the solar atmosphere with published photometric and polarimetric measurements. We also show that our two codes provide similar results in all considered cases.
Conclusions. For sub-giant and dwarf stars (log g = 3.0−4.5), the lower gravity and lower effective temperature of a star lead to higher limb polarization of the star. For giant and supergiant stars (log g = 1.0−2.5), the highest effective temperature yields the largest polarization. By decreasing the effective temperature of a star down to 4500−5500 K (depending on log g), the limb polarization decreases and reaches a local minimum. It increases again with a corresponding decrease in temperature down to 4000 K. For the most compact dwarf stars (log g = 5.0−5.5), the limb polarization degree shows a maximum for models with effective temperatures in the range 4200−4600 K (depending on log g) and decreases toward higher and lower temperatures.
Key words: polarization / radiative transfer / scattering / stars: atmospheres / methods: numerical
The intensity and polarization profiles are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/586/A87
© ESO, 2016
1. Introduction
Center-to-limb variation (i.e., the angular variation) of intensity (CLVI) and polarization (CLVP) are necessary to interpret the light curves of a star during exoplanetary transits (e.g., Müller et al. 2013; Kostogryz et al. 2015) of eclipsing binary systems (e.g., Bass et al. 2012; Kemp et al. 1983) as well as for interpreting interferometric observations (e.g., Wittkowski et al. 2004; Chiavassa et al. 2010), microlensing observations (e.g., An et al. 2002), and helioseismology (Kuhn et al. 1997; Toutain et al. 1999; Kuhn et al. 2012).
A robust interpretation of exoplanet light curves that results from high-precision photometry (e.g., obtained by the Kepler mission) requires precise computations of center-to-limb variations of the intensity (i.e., limb darkening/brightening) for stars of different spectral classes. Limb darkening calculations for the extensive grids of plane-parallel 1D hydrostatic stellar model atmospheres were made by different authors (see, e.g., Claret 2000; Sing 2010). In our previous works, we studied the CLV of intensity and polarization for plane-parallel stellar atmosphere models of different spectral classes (FGK) and surface gravities log g = 3.0−5.0 (Kostogryz & Berdyugina 2015). Recently, Harrington (2015) calculated linear polarization in continuum for MARC stellar atmosphere models (Gustafsson et al. 2008) and found it systematically higher than ours for the same effective temperatures and log g. It was suggested that this difference results from the contribution of spectral lines. Spectral lines are important for blue wavelengths where there may be little real continuum observed but, for 4000 Å and longer, the difference in our results may be due to considering different stellar model atmospheres (see, for example, the comparison of continuum polarization for several solar models by Kostogryz & Berdyugina 2015). We investigate line contribution in a separate paper.
However, for lines of sight near the limb of the star, the approximation of a plane-parallel model atmosphere is not valid. The reason for this is that these “rays” take significantly different paths from what is predicted by a plane-parallel assumption. The more extended the stellar atmosphere (lower surface gravity) is, the more pronounced this effect. Therefore, to obtain precise values of intensity near the limb of the star one needs to calculate CLVI using spherical model atmospheres. There are several theoretical studies where limb-darkening coefficients in different photometric bands are computed for stars with spherical model atmospheres (see, for example Claret et al. 2012, 2013; Neilson & Lester 2013a,b).
If we consider, for example, an exoplanetary transit. As the ingress and egress moments are critical for describing the light curves, accurate calculations, especially close to the limb, are necessary to interpret the light curves. In some cases it is not sufficient to use polynomial fit in μ to describe stellar limb darkening.
On the other hand, the center-to-limb variation of linear polarization in the continuum is not so well studied, despite the fact that it yields a lot of information about stellar atmospheres. Recently, Kostogryz et al. (2015) have shown that variation of linear polarization during a transit provides information on the physical parameters of stellar spots (such as size and position), as well as on the orbital parameters of exoplanets (for example, the longitude of the ascending node that cannot be derived from the photometric light curve). The crucial input in these calculations is the center-to-limb variation of the linear polarization.
In this paper we calculate the CLVI and CLVP in continuum spectra of different spectral classes under the assumption of spherical geometry. In addition, we expand the range of effective temperatures and surface gravities compared to our previous study (Kostogryz et al. 2015). As there are no earlier results for CLVP for the spherical atmosphere of different stars to compare our calculations to, we developed two independent codes to solve the radiative transfer equation for polarized light in the presence of continuum scattering to cross-check our results. In the next section we describe the two methods of solving the radiative transfer equations in detail. Section 3 contains the comparative tests and results of our calculations of solar and stellar CLVI and CLVP. The conclusions of our paper are presented in the fourth section.
2. Methods of calculation
Polarized radiation is fully described by four Stokes parameters I, Q, U, and V. It is customary to assume a coordinate system where Stokes parameter Q is either parallel or perpendicular to the local limb (here we choose the former, as in Kostogryz & Berdyugina 2015). In this paper we consider the continuum polarization that is due to scattering by atoms and free electrons (Rayleigh and Thomson scattering, respectively). This means that, as in one-dimensional models there is no way of breaking the axial symmetry, Stokes U is equal to zero. The same applies for the V component, as neither scattering nor magnetic fields can produce circular polarization in the continuum. In the case of spectral lines, both Stokes U and V can be non-zero, via mechanisms known as the Hanle and Zeeman effects, respectively, see, for example, the monograph by Landi Degl’Innocenti & Landolfi (2004).
Therefore, in the problem we face, the Stokes vector can be described as follows:  (1)where μ = cosθ and θ defines a line of sight direction with respect to the atmospheric normal. For the direction corresponding to the center of stellar disk μ = 1, while for the stellar limb μ = 0. Here, r is the radial coordinate (our models are spherically symmetric and hence one-dimensional) and λ is the wavelength of the radiation.
(1)where μ = cosθ and θ defines a line of sight direction with respect to the atmospheric normal. For the direction corresponding to the center of stellar disk μ = 1, while for the stellar limb μ = 0. Here, r is the radial coordinate (our models are spherically symmetric and hence one-dimensional) and λ is the wavelength of the radiation.
To obtain the emergent Stokes vector, one has to solve the polarized radiative transfer equation in the stationary spherically symmetric media (e.g. Hubeny & Mihalas 2014),  (2)where η is emission the term that comes from both the thermal emission (free-free and free-bound processes) and from scattering processes. The values kc and σc stand for coefficients of absorption and scattering, respectively. Their sum gives the total absorption coefficient. It is common to refer to the ratio of emission and absorption coefficients as the “source function”. The source function (S) in the continuum can be written as
(2)where η is emission the term that comes from both the thermal emission (free-free and free-bound processes) and from scattering processes. The values kc and σc stand for coefficients of absorption and scattering, respectively. Their sum gives the total absorption coefficient. It is common to refer to the ratio of emission and absorption coefficients as the “source function”. The source function (S) in the continuum can be written as  (3)where B(λ) describes the photon creation from the thermal pool of the gas and is described by the Planck function
(3)where B(λ) describes the photon creation from the thermal pool of the gas and is described by the Planck function  (4)Ss(r,μ,λ) defines the contribution from scattering sources, and is given by
(4)Ss(r,μ,λ) defines the contribution from scattering sources, and is given by  (5)where μ′ is the direction of the incident radiation, and PR is the Rayleigh phase matrix that takes the angular dependence of Rayleigh and Thomson scattering (e.g., Stenflo 1994)
(5)where μ′ is the direction of the incident radiation, and PR is the Rayleigh phase matrix that takes the angular dependence of Rayleigh and Thomson scattering (e.g., Stenflo 1994) 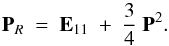 (6)Matrix E11 only has one non-zero element, E11 = 1, that describes unpolarized, isotropic scattering. The matrix P2 describes the linear polarization scattering and has the following form:
(6)Matrix E11 only has one non-zero element, E11 = 1, that describes unpolarized, isotropic scattering. The matrix P2 describes the linear polarization scattering and has the following form:  (7)To solve the radiative transfer equation in a spherical coordinate system (Eq. (2)), it is advantageous to describe the angular and spatial dependence of the radiation field by a set of parallel rays that are tangential to the discrete radial shells. This is known as the “along-the-ray” approach (Avrett & Loeser 1984). The new coordinate system is described by the impact parameter p that illustrates rays and the distance along z (Fig. 1). The radius in the new coordinate system can be written through the p and z as follows:
(7)To solve the radiative transfer equation in a spherical coordinate system (Eq. (2)), it is advantageous to describe the angular and spatial dependence of the radiation field by a set of parallel rays that are tangential to the discrete radial shells. This is known as the “along-the-ray” approach (Avrett & Loeser 1984). The new coordinate system is described by the impact parameter p that illustrates rays and the distance along z (Fig. 1). The radius in the new coordinate system can be written through the p and z as follows:  (8)Each ray p intersects the radial shells r at an angle θ whose cosine μ is written as
(8)Each ray p intersects the radial shells r at an angle θ whose cosine μ is written as  (9)Then the differential operator in z is given by
(9)Then the differential operator in z is given by  (10)It is common to introduce a new variable, the optical depth, defined as
(10)It is common to introduce a new variable, the optical depth, defined as  (11)After all the transformations, we have the spherical radiative transfer equation of the rays travelling along ± z for each ray with its impact parameter p as follows:
(11)After all the transformations, we have the spherical radiative transfer equation of the rays travelling along ± z for each ray with its impact parameter p as follows:  (12)We emphasize that Eqs. (3), (5), and (12) are coupled. Substituting Eq. (5) into Eq. (3) and then in Eq. (12) would lead to an integro-differential equation for the specific intensity and polarization. With given boundary conditions, this integro-differential equation can be solved directly but it turns out that the iterative solution of the coupled systems of Eqs. (3), (5) and (12) is faster and more robust. Starting with an initial guess for the source function (usually SI = B and SQ = 0) one computes the angular and spatial distribution of the intensity and polarization and uses these to compute the new value of the source functions. The process is then repeated and iterated until there is convergence. This approach is known as Λ iteration. For a much wider and more detailed insight into the problem, see, for example, the new edition of the classical reference, Stellar Atmospheres, by Hubeny & Mihalas (2014).
(12)We emphasize that Eqs. (3), (5), and (12) are coupled. Substituting Eq. (5) into Eq. (3) and then in Eq. (12) would lead to an integro-differential equation for the specific intensity and polarization. With given boundary conditions, this integro-differential equation can be solved directly but it turns out that the iterative solution of the coupled systems of Eqs. (3), (5) and (12) is faster and more robust. Starting with an initial guess for the source function (usually SI = B and SQ = 0) one computes the angular and spatial distribution of the intensity and polarization and uses these to compute the new value of the source functions. The process is then repeated and iterated until there is convergence. This approach is known as Λ iteration. For a much wider and more detailed insight into the problem, see, for example, the new edition of the classical reference, Stellar Atmospheres, by Hubeny & Mihalas (2014).
In this work we use an iterative approach for the problem. The main issue then is to numerically solve Eq. (12), given the current values of the source function. This equation is known as the formal solution. We perform the formal solution using two different techniques that are described in the next two subsections.
 |
Fig. 1 Description of p − z coordinate system that is employed for the solution of radiative transfer equation of polarized light. |
2.1. Feautrier solution of the radiative transfer equation
The first approach to the numerical solution of the radiative transfer equation that we consider in our paper is the Feautrier method, which is modified for a spherically symmetric coordinate system (Hummer & Rybicki 1971; Mihalas 1978; Sen & Wilson 1998; Hoffmann et al. 2014, etc.). In this method the two radiative transfer equations (one for I and one for Q) (Eq. (12)) can be rewritten as a two-point boundary problem in the form of second order differential equations. We define the mean-intensity-like and flux-like variables as follows ![\begin{eqnarray} \left\{ \begin{array}{@{}l l@{}} \displaystyle \vec{u}(z, p, \lambda)~&=~\displaystyle \frac{\vec{I}^+(z, p, \lambda)+\vec{I}^-(z, p, \lambda)}{2} \\[4mm] \displaystyle \vec{v}(z, p, \lambda)~&=~\displaystyle \frac{\vec{I}^+(z, p, \lambda)-\vec{I}^-(z, p, \lambda)}{2}\cdot \label{uvdef}\end{array} \right. \end{eqnarray}](/articles/aa/full_html/2016/02/aa27598-15/aa27598-15-eq55.png) (13)Note that u and v are vector quantities given by
(13)Note that u and v are vector quantities given by  , and
, and  , respectively. Substituting Eq. (13) in Eq. (12), the latter can be rewritten as two differential equations:
, respectively. Substituting Eq. (13) in Eq. (12), the latter can be rewritten as two differential equations: ![\begin{eqnarray} \left\{ \begin{array}{@{}l l@{}} \displaystyle \frac{\partial\vec{u}(z, p, \lambda)}{\partial\tau(z, p, \lambda)}~&=~\displaystyle \vec{v}(z, p, \lambda) \\[4mm] \displaystyle \frac{\partial\vec{v}(z, p, \lambda)}{\partial\tau(z, p, \lambda)}~&=~\displaystyle \vec{u}(z, p, \lambda) -\vec{S}(z, p, \lambda).\end{array} \right. \end{eqnarray}](/articles/aa/full_html/2016/02/aa27598-15/aa27598-15-eq60.png) (14)The combination of these two equations yields the second order differential radiative transfer equation:
(14)The combination of these two equations yields the second order differential radiative transfer equation:  (15)To solve the differential equation one needs boundary conditions. The upper boundary condition at r = r1 (see Fig. 1) where we assume no incident radiation (I− ≡ 0) is
(15)To solve the differential equation one needs boundary conditions. The upper boundary condition at r = r1 (see Fig. 1) where we assume no incident radiation (I− ≡ 0) is  (16)which, further, results in the following expression at the boundary condition z = zmax:
(16)which, further, results in the following expression at the boundary condition z = zmax:  (17)where
(17)where  .
.
At the lower boundary, two cases should be distinguished: the rays that intersect the core (p ≤ rND, “core rays”) from those that do not (p>rND, “surface rays”; see Fig. 1). For the core rays, we assume that radiation coming up from the bottom of the star is not polarized (Q+ = 0), and we use the diffusion approximation for the intensity  . For the surface rays we use a “reflecting” boundary I+ = I− both for intensity and polarization:
. For the surface rays we use a “reflecting” boundary I+ = I− both for intensity and polarization: ![\begin{eqnarray} \left\{ \begin{array}{@{}l l@{}} \displaystyle \frac{\partial{u^I}(z, p, \lambda)}{\partial\tau(z, p, \lambda)}\Biggr\rvert_{\tau_{\max}}~&=~\displaystyle I_{\rm core}-u^I(z, p, \lambda) \\[4mm] \displaystyle \frac{\partial{u^Q}(z, p, \lambda)}{\partial\tau(z, p, \lambda)}\Biggr\rvert_{\tau_{\max}}~&=~\displaystyle u^Q(z, p, \lambda) \label{corebc}\end{array} \right. \end{eqnarray}](/articles/aa/full_html/2016/02/aa27598-15/aa27598-15-eq73.png) (18)for the core rays, and
(18)for the core rays, and ![\begin{eqnarray} \left\{ \begin{array}{@{}l l@{}} \displaystyle \frac{\partial{u^I}(z, p, \lambda)}{\partial\tau(z, p, \lambda)}\Biggr\rvert_{\tau_{\max}}~&=~\displaystyle 0 \\[4mm] \displaystyle \frac{\partial{u^Q}(z, p, \lambda)}{\partial\tau(z, p, \lambda)}\Biggr\rvert_{\tau_{\max}}~&=~\displaystyle 0 \label{non_corebc}\end{array} \right. \end{eqnarray}](/articles/aa/full_html/2016/02/aa27598-15/aa27598-15-eq74.png) (19)for the surface rays.
(19)for the surface rays.
Therefore, we numerically solve the radiative transfer equation Eq. (15) with boundary conditions Eqs. (17)–(19), which, after making the variables discrete, leads to a block tri-diagonal system. More details on the solution of radiative transfer equation in spherical coordinates can be found in Peraiah (2001).
2.2. Short characteristics solution
The short characteristics method for the numerical formal solution (Kunasz & Auer 1988; Mihalas et al. 1978) is based on the integral form of the radiative transfer equation, i.e. on the “formal” solution on the line segment connecting appropriately chosen upwind point U and local point L:  (20)where IL and IU are specific monochromatic intensities in the local and upwind point, respectively, Δ is monochromatic optical path between the points, and S is the source function. Now, to numerically solve the integral in Eq. (20), one usually assumes either low-order polynomial or spline behavior of the source function on the interval UL, which leads to the following scheme for the formal solution:
(20)where IL and IU are specific monochromatic intensities in the local and upwind point, respectively, Δ is monochromatic optical path between the points, and S is the source function. Now, to numerically solve the integral in Eq. (20), one usually assumes either low-order polynomial or spline behavior of the source function on the interval UL, which leads to the following scheme for the formal solution:  (21)where w are weights that depend on Δ, and
(21)where w are weights that depend on Δ, and  is the derivative of the source function in the local point along the direction of the propagation of radiation (i.e. “along-the-ray”). This derivative is evaluated either explicitly or expressed through SL, SU and, in some schemes by means of an additional point, D, in the downwind direction of the ray propagation. In one-dimensional schemes, upwind and downwind points are chosen to be the previous and following grid points, with respect to the direction of propagation of the radiation. Originally, first or second order polynomials have been used to obtain weights in Eq. (21), but strictly monotonic Bezier splines lead to a better behaved numerical solution (Auer 2003; de la Cruz Rodríguez & Piskunov 2013). In the computations presented in this paper, we have used Bezier splines of the second order. In the case of the linearly polarized radiation, we consider that the formal solution for the Stokes vector is obtained by performing the formal solution for I and Q components separately. To recap this brief description, it is important to remember that, to obtain the specific intensity in the local point, one needs appropriate intensity in the upwind point and values of emissivity and opacity in upwind, local, and, depending on the numerical scheme, possibly downwind point.
is the derivative of the source function in the local point along the direction of the propagation of radiation (i.e. “along-the-ray”). This derivative is evaluated either explicitly or expressed through SL, SU and, in some schemes by means of an additional point, D, in the downwind direction of the ray propagation. In one-dimensional schemes, upwind and downwind points are chosen to be the previous and following grid points, with respect to the direction of propagation of the radiation. Originally, first or second order polynomials have been used to obtain weights in Eq. (21), but strictly monotonic Bezier splines lead to a better behaved numerical solution (Auer 2003; de la Cruz Rodríguez & Piskunov 2013). In the computations presented in this paper, we have used Bezier splines of the second order. In the case of the linearly polarized radiation, we consider that the formal solution for the Stokes vector is obtained by performing the formal solution for I and Q components separately. To recap this brief description, it is important to remember that, to obtain the specific intensity in the local point, one needs appropriate intensity in the upwind point and values of emissivity and opacity in upwind, local, and, depending on the numerical scheme, possibly downwind point.
As noted in the previous subsection, radiative transfer in spherical media is simplified by the use of the so-called along-the-ray approach (Avrett & Loeser 1984). In this approach, the short characteristics method is straightforward to apply. To obtain the full radiation field, the radiative transfer equation is solved ray-by-ray, where rays are described by the impact parameter p. Consider the ray described by the line segment AB in Fig. 1: to formally solve the radiative transfer equations on segment AB is, because of the symmetry arguments, identical to solving the equation on segment AM in the direction A→M, with the boundary condition IA = 0, followed by the solution in the opposite direction, with the boundary condition  . This is identical to treating the segment AM as a single, one-dimensional, plane-parallel atmosphere with two rays propagating in directions μ = −1 and μ = 1. The procedure for the ray A′B′ is similar, except the boundary condition in B′ is different and follows from the diffusion approximation (Stokes I component), or is equal to zero (Stokes Q component).
. This is identical to treating the segment AM as a single, one-dimensional, plane-parallel atmosphere with two rays propagating in directions μ = −1 and μ = 1. The procedure for the ray A′B′ is similar, except the boundary condition in B′ is different and follows from the diffusion approximation (Stokes I component), or is equal to zero (Stokes Q component).
After the intensity has been computed at all points and for each ray, we can compute the source function using Eq. (5). The process is repeated until convergence. A standard way of accelerating this convergence is to use a Jacobi iteration, also known as “operator splitting”, “operator perturbation” or Accelerated Lambda Iteration (ALI). In the cases considered here, this is not necessary since the optical thickness of the medium is quite moderate but, usually, this leads to an increase in convergence by an order of magnitude. For a review of ALI see, for example, Hubeny (2003).
In principle, the only difference between the two approaches we used is in the formal solution (Feautrier versus the short characteristics), which is, again, the most important part of the computation since the angular integration of the specific intensity to obtain the source function is quite straightforward. We now describe the stellar models we used and discuss the main contributors to the continuum opacity.
2.3. Stellar models and opacities
Emergent polarized intensity is uniquely determined by the atmospheric model, i.e. the change of temperature and pressure with geometrical height in the atmosphere. We use the spherically symmetric PHOENIX local thermodynamic equilibrium model atmospheres (Husser et al. 2013). We consider effective temperatures in the range 4000 ≤ Teff ≤ 7000 K in steps of 100 K and surface gravities 1.0 ≤ log g ≤ 5.5 in steps of 0.5. The metallicity is chosen to be equal to the solar for all models.
Similarly to Kostogryz & Berdyugina (2015), we calculate the scattering and absorption opacities for different wavelengths using SLOC code (Berdyugina 1991). The main contributions to continuum opacities for several representative stellar model atmospheres are presented in Fig. 2. We consider contributions from: Thomson scattering on free electrons e− and Rayleigh scattering on HI,HeI,H2,CO,H2O, and other molecules (the thin dashed lines in Fig. 2). For calculating absorption opacities we take into account free-free (ff) and bound-free (bf) transitions in H−, HI, HeI, He−, H , H
, H , and metal photoionization (the thin solid lines in Fig. 2). The optical depth scale is computed using the total opacity at a given wavelength.
, and metal photoionization (the thin solid lines in Fig. 2). The optical depth scale is computed using the total opacity at a given wavelength.
 |
Fig. 2 Normalized opacities as a function of optical depth. Titles on each of the panels describe the model parameters for the calculation of the opacities. Solid lines show all important absorption opacities and dashed lines represent all scattering opacities. Thick solid and thick dashed lines are the normalized total absorption and total scattering opacities, respectively. |
As it is seen from Figs. 2a–d in the upper layer of the atmosphere, absorption by the negative ion hydrogen H− gives the greatest contribution to the opacity at visible wavelengths. In the deeper layers (for τ ≥ 1), absorption by H− is perhaps not the most dominant but is still an important contributor for solar type and cooler stars. For the hotter giant stars (Figs. 2e, f) absorption by H− is essential in the upper layers of the stellar atmosphere, while deeper in the atmosphere (τ ≥ 1) it decreases and becomes almost negligible. Another absorption opacity source that plays an important role in the deeper layers of atmosphere for solar type and cooler stars is 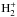 . For hotter giant stars, absorption by
. For hotter giant stars, absorption by 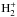 is negligible and the most important opacity source is neutral hydrogen HI. We note that these absorption opacities do not produce any polarization.
is negligible and the most important opacity source is neutral hydrogen HI. We note that these absorption opacities do not produce any polarization.
The main contributions to the polarization of the stellar continuum spectrum are scattering sources: Rayleigh scattering on neutral hydrogen HI (Chandrasekhar 1960) and on molecular hydrogen H2. The latter is more important in cooler atmosphere of dwarf stars (Figs. 2b). For cool giant stars, the scattering by H2 turns out to be less influential (Figs. 2c, d). Instead, Thomson scattering by free electrons e− becomes more significant and even dominates in the hot and low-gravity stellar atmospheres (Figs. 2e, f).
The behavior of the total scattering (thick dashed line) and absorption (thick solid line) opacity is convenient for a qualitative understanding ofthe amount of scattering polarization in the atmosphere. The deeper is the “critical” optical depth in the atmosphere, where the scattering becomes dominant over the absorption, the higher linear polarization is to be expected. Therefore, according to Fig. 2, for the stellar atmosphere with Teff = 4000 K, log g = 1.5 and for the wavelength 4000 Å, where the scattering dominates at τ ≤ 7 × 10-1 (Fig. 2c), the polarization is expected to be very high, as well as for Teff = 7000 K, log g = 1.5, and for all wavelengths. On the contrary, for solar-type models with Teff = 5800 K, log g = 4.5 at the same wavelength, the critical height between scattering and absorption is about τ ≈ 10-5, which should lead to smaller amounts of polarized light. We find that this is, indeed, the case (see Sect. 3.3).
3. Results
Independently, we have developed a spherical radiative transfer code to compute center-to-limb variation of intensity and scattering polarization in the continuum. Both codes are based on the iterative solution of the scattering problem but use two different methods for the numerical formal solution: Feautrier and short characteristics, described in the previous section. The codes usually agree down to the relative difference of few hundredth. In the following subsections, we comment further on the differences. We also note that all the results in the paper have been double-checked using both codes.
3.1. Test of our codes
3.1.1. Model atmosphere with equal absorption and scattering opacity
In this subsection, we describe the test of both our approaches to the formal solution presented above. We consider an isothermal spherical atmosphere with inner and outer boundaries at 1 and 30 stellar radii, respectively, as described in Avrett & Loeser (1984). The total opacity (kc + σc) is given by C/r2, where the constant C is determined by the requirement that the total radial optical depth of the atmosphere is equal to 4. This results in C = 120 / 29, where the radial optical depth is given by:  (22)We assume a constant monochromatic scattering coefficient σc = 0.5. Then, it follows that kc ≡ 1 − σc = 0.5. For the given model atmosphere, i.e., variation of temperature, opacity, and scattering coefficient with radius (we note that, contrary to the plane-parallel case where τ is chosen as an independent coordinate, we actually require the geometrical scale expressed in physical units), we can self-consistently solve the scattering problem and obtain values of the polarized source function at all points in the atmosphere, as well as the angular variation of emergent polarized intensity (I and Q). No solutions of this specific test case are availablefor the polarized radiation so we start by comparing the mean intensity defined as
(22)We assume a constant monochromatic scattering coefficient σc = 0.5. Then, it follows that kc ≡ 1 − σc = 0.5. For the given model atmosphere, i.e., variation of temperature, opacity, and scattering coefficient with radius (we note that, contrary to the plane-parallel case where τ is chosen as an independent coordinate, we actually require the geometrical scale expressed in physical units), we can self-consistently solve the scattering problem and obtain values of the polarized source function at all points in the atmosphere, as well as the angular variation of emergent polarized intensity (I and Q). No solutions of this specific test case are availablefor the polarized radiation so we start by comparing the mean intensity defined as  (23)between the two codes and also with other results found in the literature.
(23)between the two codes and also with other results found in the literature.
 |
Fig. 3 Averaged intensity variation a) and residuals (relative percentage difference) compared to those calculated by the Feautrier method b) in different layers in the test model atmosphere. Solid and dashed lines in a) correspond to our calculations with the Feautrier and the short characteristics solution of radiative transfer equation. The solid line in b) describes the difference between the Feautrier and short characteristics solutions. Different symbols correspond to values of J(r) obtained by different authors: (crosses) are from Mihalas et al. (1975), (stars) – from Rogers (1982), (squares) – from Avrett & Loeser (1984), (diamonds) – from Gros et al. (1997), (triangles) – from Atanackovic-Vukmanovic (2003). |
The dependence J(r) is well-known for this test case of the spherical atmosphere (Mihalas et al. 1975; Rogers 1982; Avrett & Loeser 1984; Gros et al. 1997; Atanackovic-Vukmanovic 2003). Figure 3a presents the results of calculations using the Feautrier method (solid lines) and short characteristics (dashed lines) as compared to other studies: Mihalas et al. (1975), Rogers (1982), Avrett & Loeser (1984), Gros et al. (1997), Atanackovic-Vukmanovic (2003).
As it is difficult to see the difference between calculations, in Fig. 3b we present the relative percentage difference (residuals) between those calculated with the Feautrier approach (JF) and others (J) in % obtained as  (24)The discrepancies for all results are about 1−2% for different cases (different symbols), which can be explained by different discretization in r and different approximations for source function behavior between any two depth points. The solid line in Fig. 3b describes the residuals between our two codes, which are calculated according to Eq. (24), where J ≡ JSC is the solution with the short characteristics method, which is about 0.5% at most. Thus, we can conclude that for the test model atmosphere, our calculations agree within 0.5%.
(24)The discrepancies for all results are about 1−2% for different cases (different symbols), which can be explained by different discretization in r and different approximations for source function behavior between any two depth points. The solid line in Fig. 3b describes the residuals between our two codes, which are calculated according to Eq. (24), where J ≡ JSC is the solution with the short characteristics method, which is about 0.5% at most. Thus, we can conclude that for the test model atmosphere, our calculations agree within 0.5%.
In addition to the mean intensity, we are interested in the relative difference between our two approaches when computing CLVI and CLVP for this test model atmosphere. The comparison is presented in Figs. 4a, c. The results obtained with the Feautrier technique are shown with solid lines, and the one obtained with short characteristics method are presented by dashed lines. The residuals for both CLVI and CLVP are given in Figs. 4b, d. The differences between our codes for the intensity are very small (order of percent). The relative difference for the polarization is also very small for the major part of the Q/I(μ) curve. It is only for μ very close to 1 that our codes show a more significant difference, up to 20%. This is due to the different nature of the formal solution: the short characteristics method using Bezier splines imposes monotonicity of the interpolant (in this case the source function). This approach suppresses numerical overshooting but can potentially decrease the accuracy. In the Feautrier formal solution, on the other hand, it is implicitly assumed that the source function behaves as the second order polynomial. The difference between the two approaches is especially prominent in the cases where the source function varies a lot between the adjacent depth points which is the case here. Namely, for the ray with emergent μ close to (but not equal to) one, “local” μ changes significantly along the ray path. This leads to the significant variation of the polarized source function SQ as it strongly depends on the scattering angle. This, in turn, leads to different results for the emergent intensity after the formal integration. However, these differences become important only for the rays with μ → 1, which are of no interest for our investigation since the polarization there is very small. In the remainder of the paper, we compare the results of the two codes for the realistic model atmospheres. We found that the relative differences are much lower, down to a few percent.
 |
Fig. 4 Center-to-limb variation of intensity a) and polarization c) for the test model atmosphere. The solid line corresponds to the formal solution of differential radiative transfer equations for polarized light using a modified Feautrier method for spherical geometry and the dashed line shows the formal solution of integral radiative transfer equation, using the short characteristics method. The residuals between two approaches are depicted in b) and d) for the center-to-limb variation for intensity and polarization, respectively. |
3.1.2. Purely scattering atmosphere
Similar to our previous study (Kostogryz & Berdyugina 2015), by way of a test of our codes, we investigate a center-to-limb variation of linear polarization in the case of a purely scattering atmosphere. We set the scattering coefficient equal to the total opacity, while the absorption coefficient is zero. Based on these assumptions, the intensity and polarization of the outgoing continuum radiation become independent of the frequency and of all thermodynamic properties and, therefore, any initial plane-parallel atmosphere can be used.
 |
Fig. 5 Center-to-limb variation of polarization for the pure scattering atmosphere. The solid line is obtained for stellar model with Teff = 5800 K and log g = 1.5 at 4000 Å. Two other curves (dashed and dotted-dash) are for the models with the same log g = 4.5 but different effective temperatures, 4000 K and 5800 K at 4000 Å and 7000 Å, respectively. The star symbols indicate the solution for plane-parallel atmosphere obtained by Chandrasekhar (1960). |
According to Chandrasekhar (1960), who solved the radiative transfer equation for an ideal purely scattering atmosphere in the plane-parallel approximation, polarization increases from the center to the limb and can reach up to 11.7%. Later, Peraiah (1975) solved the radiative transfer equation in a spherically symmetric purely scattering homogeneous medium for different ratios of extended atmosphere radius to the radius of stellar “surface” and showed that, for the spherical atmosphere, the CLVP can be higher than for the plane-parallel atmosphere. We solve the radiative transfer equation for several Phoenix stellar model atmospheres with effective temperatures of 4000 K and 5800 K, log g of 4.5, and 1.5, and for two different wavelengths of 4000 and 7000 Å, in which the scattering and absorption coefficients are redefined to get a purely scattering atmosphere. In the left panel of Fig. 5, the CLVP for different models are shown. The star symbols describe the exact solution for a purely scattering plane-parallel atmosphere (Chandrasekhar 1960). For stars which do not have extended atmospheres (e.g., solar-type stars), we can detect a small deviation of CLVP from the plane-parallel atmosphere only at the limb, while extended atmospheres show much higher polarization. Here, we notice that the scattering polarization emerging from a purely scattering spherical atmopshere depends on the extension of the atmosphere. For a more extended atmosphere, i.e. smaller log g, we obtain larger differences with respect to plane-parallel geometry. In particular the polarization is higher, which agrees with Peraiah (1975).
Following the solar terminology, the limb position of the star is defined as a line of sight where the largest gradient of CLVI occurs. The limb position can only be defined using the solution of radiative transfer equation in a spherical atmosphere. Therefore, to explain limb-darkening measurements, we need to find the limb position and recalculate all μ taking into account that μ at the limb should be equal to zero (i.e. we make a difference between geometrical and observational μ). In the right panel of Fig. 5, we present the same curves but for the recalculated values of μ. In this panel we still see a small difference for a theoretical extended atmosphere from Chandrasekhar’s solution, while dwarf star atmospheres with different effective temperatures and for a different wavelengths show very good agreement with the exact solution for plane-parallel atmosphere (Chandrasekhar 1960). This shows that scattering has been correctly calculated in the codes.
 |
Fig. 6 Same as in Fig. 4 but for Phoenix model atmosphere with Teff = 5800 K, log g = 4.5, and wavelength λ = 4500 Å. |
 |
Fig. 7 Center-to-limb variation of intensity for the Sun. Solid lines (shifted on μ according to the limb position) and dotted line (not-shifted) correspond to the formal solution of differential radiative transfer equations for polarized light using the modified Feautrier method for spherical geometry with the HSRA solar model atmosphere. Dashed line shows the interpolation of observations by Neckel & Labs (1994) |
3.2. Solar limb darkening and limb polarization
Direct measurements of CLVI and CLVP have been obtained only for the Sun. Therefore, in this subsection we are going to investigate how our calculations fit the solar photometric and polarimetric observations.
Before exploring how our calculations fit the observations, the difference between our two codes is studied for the solar atmosphere to estimate the difference in numerical calculations. As is seen from Fig. 6, the correlation of our calculations are more than sufficient. The relative difference in intensity (Fig. 6c) is less then 0.1−0.2%, except for the place with residuals equal to 1%, where the intensity gradually decreases and defines the limb position. The part of the calculated CLVI for values of μ outside the limb, are not needed for fitting the measurements. For CLVP (Figs. 6b, d) we also have very close agreement (residuals are about 3%) for the very small values of polarization. From polarimetric solar disk measurements, the error at μ = 0.1 is about 15% and it becomes larger toward the center of the disk and smaller toward the limb of the Sun (Wiehr & Bianda 2003). Therefore, we can conclude that the difference between our two approaches for solving the radiative transfer equation is negligible for solar-type stars.
 |
Fig. 8 Center-to-limb variation of polarization at 4506 Å for different solar model atmospheres, which are depicted by different line types and labeled on the plot. The stars with error bars depict the measurements obtained by Wiehr & Bianda (2003). The Phoenix model has parameters that are the closest to the solar one, such as Teff = 5800 K and log g = 4.5. |
A comparison between observations and calculations for CLVI and CLVP has already been made by Kostogryz & Berdyugina (2015), where the plane-parallel approximation for model atmosphere was assumed. Kostogryz & Berdyugina (2015) employed the semi-empirical model atmosphere HSRA (averaged quiet Sun) derived by Gingerich et al. (1971) and show that, within some natural brightness variations, the simulation for CLVI fitted the observations very well. In this study, we use the same observations, which were obtained by Neckel & Labs (1994) and presented in Fig. 7 as analytical polynomial function P5(μ). This function was obtained by fitting it to the continuum measurements and correcting it for scattered light. We solve the radiative transfer equation by considering spherical symmetry for HSRA to investigate the match between our calculation to observations. In Fig. 7 we present two calculated curves of CLVI for the different wavelengths 4000, 5000, and 6000 Å that describe the CLVI with initial and recalculated μ, according to the determined limb position on the solar disk. We show that our calculation represents the observation very well for 5000 Å, while there are small discrepancies for 4000 Å and 6000 Å that can either be associated with natural variations of the solar brightness or with an imperfect solar model atmosphere or with polynomial interpolation of the observations. We conclude that the CLVI for both plane-parallel and spherical atmospheres can be used to interpret solar observations. The advantage of taking into account a spherical geometry appears at the very limb, where it better describes the edge of the solar disk and thus provides information about the solar radius.
 |
Fig. 9 Center-to-limb variation of intensity calculated in the B filter by Claret et al. (2013; dashed lines), Neilson & Lester (2013a; dash-dotted line), Magic et al. (2015; dash-triple dotted line) as well as our continuum computation for 4500 Å (solid lines). Different panels correspond to different effective temperatures and surface gravities that are labeled in the title of each plot. |
In addition to CLVI, we calculate center-to-limb variation of continuum polarization for different solar model atmospheres of the quiet Sun, such as FALC (averaged quiet Sun), FALA (the supergranular cell center), FALP (the plage model) obtained by Fontenla et al. (1993), HSRA (averaged quiet Sun) and the spherical PHOENIX model for Teff = 5800 K, log g = 4.5 for various wavelengths (4000, 5000, and 6000 Å). The CLVP calculated for plane-parallel approximation showed very close correspondence with different observations in the continuum (Kostogryz & Berdyugina 2015). Here we compare the calculated CLVP for spherical geometry with polarimetric measurements in the continuum obtained by Wiehr & Bianda (2003) (Fig. 8) to investigate the possibility of interpretation of CLVP with spherical atmosphere. As is seen from Fig. 8, the theoretical CLVPs for various model atmospheres can describe the behavior of measured polarization and the best fit is found for HSRA at a particular wavelength. We note that the variation of polarization for different model atmosphere in a spherical geometry is more significant than in a plane-parallel one. It means that the calculated CLVP with spherical geometry is more sensitive to the solar model atmosphere and can be used for model verification.
3.3. Stellar limb darkening and polarization
Stellar center-to-limb variation of intensity is studied by different authors in spherical one-dimensional model atmosphere for different spectral bands and considering different stellar models (Claret et al. 2012, 2013; Neilson & Lester 2013b,a) and also in three-dimensional plane-parallel model atmosphere (Magic et al. 2015). We compare our single wavelength (4500 Å) continuum computation for Phoenix spherical stellar models with other studies for the B filter (Fig. 9). The filter includes contributions from many spectral lines, especially for cooler atmospheres, so we don’t expect a perfect match.
As is seen from the first panel in Fig. 9, where four various limb darkening curves are presented, the different stellar atmospheric models and different authors present diverse results that can be used to test stellar model atmospheres. As expected for hot stars, we can reproduce broadband simulations well since there are not many spectral lines and the continuum dominates. At the very limb, the curve from Claret et al. (2013; solid line) has artificial negative limb darkening that may come from the fitting with 4-parameters and not from calculations.
Because the various stellar models provide different results, to avoid these uncertainties in the second and the third panels in Fig. 9, we compare our calculations with those from non-linear limb-darkening law (Claret et al. 2013) for the same spherical Phoenix stellar models. In our previous study of CLVI with plane parallel approximation (Kostogryz & Berdyugina 2015) we discussed the model atmosphere with the same surface gravity and with a lower temperature than 5800 K, which showed a larger deviation from Claret et al. (2013). However, analyzing the CLVI that was calculated for different surface gravities, we can also add to the previous conclusion that a low gravity star shows a larger discrepancy between CLVI in the continuum at 4500 Å and the one calculated in the broadband B filter. Naturally, to explain broadband observations of the CLVI, we need to take all the spectral lines contributing to the passband of the filter into account, while our calculations are useful for explaining the monochromatic measurements at the continuum level.
To estimate the maximum difference between our two numerical approaches, we solve the radiative transfer equation for the most extended model atmosphere with log g = 1.0, effective temperature 4000 K at wavelength 4000 Å. The relative difference between our two approaches is about 1.0−1.5% in intensity and about 2.0−3.0% in polarization, which is smaller than the observational error bars that can be 10% or more even for solar measurements (Wiehr & Bianda 2003).
For plane-parallel atmospheres, the center to limb variation of intensity, assuming isotropic scattering, is almost identical to CLVI from a solution with dipole scattering (i.e., one including polarization). To check if this holds for extended spherical atmospheres, we calculate CLVI for isotropic and anisotropic scattering, i.e., excluding and including polarization, respectively. In Fig. 10, we present the results of our calculations for Phoenix model atmosphere with Teff = 4000 K, log g = 1.0 and wavelength λ = 4000 Å. For this model the relative difference between these two calculations for CLVI is about 8% at the limb, while for more compact stellar model atmospheres this effect is smaller.
 |
Fig. 10 a) Center-to-limb variation of intensity for Phoenix model atmosphere with Teff = 4000 K, log g = 1.0 and wavelength λ = 4000 Å with neglecting polarization (dashed line) and with taking it into account (solid line). b) Relative difference between two curves from panel a). |
We solve the radiative transfer equation for polarized light taking spherical symmetry of a star into account for the grid of spherical Phoenix model atmospheres within the range of effective temperatures from 4000 to 7000 K at steps of 100 K and for log g from 1.0 to 5.5 at steps of 0.5. For different wavelengths, effective temperatures, log g, and various position on the stellar disk μ, we present the values of CLVI in Table 1 and of CLVP in Table 2. In addition, we present μlimb that is equal to the calculated μ where the largest gradient in the limb-darkening curve occurs and corresponds to the real radius of a star, which is calculated and presented in Table 1 as well. This is important when interpreting exoplanet transit data which provide only a planet-to-star radii ratio.
In Fig. 11 the dependence of stellar continuum polarization on the spherical model atmosphere with different effective temperatures, surface gravities, and wavelengths are presented. For the fixed surface gravity (log g = 4.5) and the wavelength (λ = 4000 Å), given as titles in Fig. 11a, the cooler atmosphere shows larger CLVP. Fixing the surface gravity and temperature, one can investigate the behavior of continuum polarization in different wavelengths. Figure 11b shows that, at shorter wavelengths, higher polarization can be obtained. However, there are some cases in our grid of model atmospheres where we have larger polarization for longer wavelengths and hotter temperatures. This is true for giant and supergiant stars with log g ≤ 1.5, where the main source of scattering opacity is Thomson scattering on free electrons (see Figs. 2e, f), which is independent of wavelength but increases with increasing temperature. The last panel (Fig. 11c) shows that the higher gravity of a star leads to lower linear polarization.
In Fig. 12 we present the distribution of the integrated value of polarization within the range of μ = 0.0−0.3, depending on the effective temperature and gravity of a star at λ = 4000 Å. We see that the polarization degree depends on the atmosphere extension (i.e., scale height), which varies with the effective temperatures and surface gravities. As is seen from Fig. 12, the coolest stars with log g = 3.0−4.5 show larger polarization, while for very compact dwarf stars with log g = 5.0−5.5 the highest polarization is seen for Teff ≈ 4200−4600 K (depending on log g) and decreases for lower temperatures. For giant and supergiant stars (log g< 3.0), the situation is different. The limb polarization is the largest for the hottest stars where the Thomson scattering plays an important role in opacity, then it decreases for the stars with effective temperatures of about 4500−5500 K (depending on log g), and cooler stars again show an increase of polarization because of Rayleigh scattering that dominates in scattering opacity (see Fig. 2). For the coolest and most compact dwarfs, limb polarization decreases. This complex behavior can be explained by the interplay of opacity and geometry that depends on the variation of physical parameters in the atmosphere, such as effective temperature and density.
Calculated center-to-limb variation of intensity for different stellar parameters. All values of I(μ) /I(1.0) = 1.0 at μ = 1.0.
Calculated center-to-limb variation of linear polarization in continuum spectra of different stars. All values of Q/I(μ) = 0.0 at μ = 1.0.
 |
Fig. 11 Center-to-limb variation of continuum polarization for different spherical stellar model atmospheres. The title above each of the panels indicates the fixed parameters, while labels on each plot describe different curves. Continuum polarizations are given in a logarithmic scale. |
We therefore conclude that for the range of effective temperatures of 4000−7000 K and surface gravities of 3.0–5.0 (also considered in our previous study (Kostogryz & Berdyugina 2015), using the plane-parallel approximation), the continuum polarization is the largest for low-gravity cool stars. The extension of the grid of stellar model atmospheres, especially at smaller log g, shows an increase in CLVP for hot stars, where the Thomson scattering becomes dominat in scattering opacities and also an increase of CLVP for cool stars, where Rayleigh scattering on HI is still the most important scattering opacity. For the range of temperatures of 4500−5500 K (depending on log g) the decrease of limb polarization in continuum occurs.
4. Conclusions
In this paper we developed two independent codes to solve the radiative transfer equation of polarized light in continuum, taking into consideration spherical stellar atmospheres, and we presented the center-to-limb variations of intensity and polarization for the range of effective temperatures of 4000−7000 K, surface gravities of log g = 1.0−5.5, and for several wavelengths (4000,4500,5000,6000,7000 Å). We showed that two different formal solutions, such as the Feautrier method and short characteristics, provide very similar results within small deviations that are discussed in the paper.
For the test isothermal model atmosphere with inner and outer boundaries at 1 and 30 stellar radii and constant opacity (σ = 0.5), we calculated the mean intensity and compared our results with the already published values. It was shown that the discrepancies for all results are about 1−2%, which can be explained by different discretizations in r and different approximations of source function. As we have the same discretization in r but different approximations for description of the source function, the differences between our results are within 0.5%. For this test model, the CLVI and CLVP calculations with two different formal solutions were compared and showed that the intensity varies within 0.4%, while the deviation in polarization is larger. In any case, for the most extended real atmosphere the deviations between the two codes are approximately 2−3%.
With observations, we obtained very good agreement for CLVI and CLVP for the solar atmosphere. Moreover, we compare our previous calculations for a plane-parallel atmosphere with calculations in a spherical atmosphere and showed that CLVI in a spherical atmosphere is more informative at the limb and provides information about the radius of the Sun. The CLVP in a spherical atmosphere for different models has larger deviations than in plane-parallel atmosphere and can be used for testing solar model atmospheres.
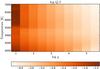 |
Fig. 12 Center-to-limb variation of continuum polarization for different stellar models. The color scale shows the logarithm of integrated continuum polarization within μ from 0 to 0.3 at wavelength 4000 Å. |
For extended stellar atmospheres (giant and super-giant stars) with log g = 1.0−2.5, all models provide significant polarization with two maxima for cooler and for hotter atmospheres. These two maxima in polarization consist of two different scattering processes for hot and cool atmospheres. In other words, Thomson scattering on free electrons are important and even dominate scattering process for hot giant stars, while for cool giant stars Rayleigh scattering on HI is the main contributor to total scattering opacity source. Naturally, the polarization for cool giant stars is greater for shorter wavelengths, while for hot giant stars it does not depend on wavelengths so much.
In sub-giant and dwarf stellar atmospheres with log g = 3.0−4.5, Rayleigh scattering on HI is the most important opacity. Therefore, the greatest polarization can be detected in low-gravity cool star at shorter wavelengths.
For very compact cool dwarf stars (log g = 5.0−5.5) the maximum polarization can be obtained for model atmospheres within the range of Teff ≈ 4200−4600 K and it decreases for the cooler and for the hotter atmospheres.
The radius of the star for each model atmospheres is tabulated and can be used for interpreting exoplanet transit curves since it yields information only about planet-to-star radii ratio.
Acknowledgments
This work was supported by the European Research Council Advanced Grant HotMol(ERC-2011-AdG291659). I.M. acknowledges partial support of Serbian Ministry of Education and Science, through the project 176004, “Stellar Physics”. We thank to our referee, Patrick Harrington, for helpful comments and suggestions, Marianne Faurobert and Taras Yakobchuk for useful discussions.
References
- An, J. H., Albrow, M. D., Beaulieu, J.-P., et al. 2002, ApJ, 572, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Atanackovic-Vukmanovic, O. 2003, Serb. Astron. J., 167, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Auer, L. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 3 [Google Scholar]
- Avrett, E. H., & Loeser, R. 1984, Line transfer in static and expanding spherical atmospheres, ed. W. Kalkofen (Cambridge University Press), 341 [Google Scholar]
- Bass, G., Orosz, J. A., Welsh, W. F., et al. 2012, ApJ, 761, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V. 1991, Bull. Crimean Astrophys. Obs., 83, 89 [NASA ADS] [Google Scholar]
- Chandrasekhar, S. 1960, Radiative transfer (New York: Dover) [Google Scholar]
- Chiavassa, A., Collet, R., Casagrande, L., & Asplund, M. 2010, A&A, 524, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Claret, A., Hauschildt, P. H., & Witte, S. 2012, A&A, 546, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., Hauschildt, P. H., & Witte, S. 2013, A&A, 552, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de la Cruz Rodríguez, J., & Piskunov, N. 2013, ApJ, 764, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Fontenla, J. M., Avrett, E. H., & Loeser, R. 1993, ApJ, 406, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Gingerich, O., Noyes, R. W., Kalkofen, W., & Cuny, Y. 1971, Sol. Phys., 18, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Gros, M., Crivellari, L., & Simonneau, E. 1997, ApJ, 489, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harrington, J. P. 2015, in IAU Symp., 305, 395 [Google Scholar]
- Hoffmann, T. L., Sauer, D. N., Pauldrach, A. W. A., & Hultzsch, P. J. N. 2014, A&A, 569, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubeny, I. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 17 [Google Scholar]
- Hubeny, I., & Mihalas, D. 2014, Theory of Stellar Atmospheres (Princeton, NJ: Princeton University Press) [Google Scholar]
- Hummer, D. G., & Rybicki, G. B. 1971, MNRAS, 152, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kemp, J. C., Henson, G. D., Barbour, M. S., Kraus, D. J., & Collins, II, G. W. 1983, ApJ, 273, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Kostogryz, N. M., & Berdyugina, S. V. 2015, A&A, 575, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kostogryz, N. M., Yakobchuk, T. M., & Berdyugina, S. V. 2015, ApJ, 806, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhn, J. R., Bogart, R., Bush, R., et al. 1997, in Sounding Solar and Stellar Interiors, eds. J. Provost, & F.-X. Schmider, IAU Symp., 181, 103 [Google Scholar]
- Kuhn, J. R., Bush, R., Emilio, M., & Scholl, I. F. 2012, Science, 337, 1638 [NASA ADS] [CrossRef] [Google Scholar]
- Kunasz, P., & Auer, L. H. 1988, J. Quant. Spec. Radiat. Transf., 39, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines, Astrophys. Space Sci. Library, 307 [Google Scholar]
- Magic, Z., Chiavassa, A., Collet, R., & Asplund, M. 2015, A&A, 573, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mihalas, D. 1978, Stellar atmospheres, 2nd edn. (San Francisco: WH. Freeman and Co), 650 [Google Scholar]
- Mihalas, D., Kunasz, P. B., & Hummer, D. G. 1975, ApJ, 202, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D., Auer, L. H., & Mihalas, B. R. 1978, ApJ, 220, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. M., Huber, K. F., Czesla, S., Wolter, U., & Schmitt, J. H. M. M. 2013, A&A, 560, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neckel, H., & Labs, D. 1994, Sol. Phys., 153, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Neilson, H. R., & Lester, J. B. 2013a, A&A, 554, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neilson, H. R., & Lester, J. B. 2013b, A&A, 556, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peraiah, A. 1975, A&A, 40, 75 [NASA ADS] [Google Scholar]
- Peraiah, A. 2001, An Introduction to Radiative Transfer: Methods and Applications in Astrophysics (Cambridge University Press) [Google Scholar]
- Rogers, C. P. 1982, Ph.D. Thesis, University of Toronto (Canada), 43, 0759 [NASA ADS] [Google Scholar]
- Sen, K. K., & Wilson, S. J. 1998, Radiative transfer in moving media: basic mathematical methods for radiative transfer in spherically symmetrical moving media (Berlin Heidelberg: Springer Verlag), 254 [Google Scholar]
- Sing, D. K. 2010, A&A, 510, A21 [Google Scholar]
- Stenflo, J. O. 1994, Solar Magnetic Fields: Polarized Radiation Diagnostics (Dordrecht: Kluwer Academic Publishers) [Google Scholar]
- Toutain, T., Berthomieu, G., & Provost, J. 1999, A&A, 344, 188 [NASA ADS] [Google Scholar]
- Wiehr, E., & Bianda, M. 2003, A&A, 398, 739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittkowski, M., Aufdenberg, J. P., & Kervella, P. 2004, A&A, 413, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Calculated center-to-limb variation of intensity for different stellar parameters. All values of I(μ) /I(1.0) = 1.0 at μ = 1.0.
Calculated center-to-limb variation of linear polarization in continuum spectra of different stars. All values of Q/I(μ) = 0.0 at μ = 1.0.
All Figures
 |
Fig. 1 Description of p − z coordinate system that is employed for the solution of radiative transfer equation of polarized light. |
| In the text | |
 |
Fig. 2 Normalized opacities as a function of optical depth. Titles on each of the panels describe the model parameters for the calculation of the opacities. Solid lines show all important absorption opacities and dashed lines represent all scattering opacities. Thick solid and thick dashed lines are the normalized total absorption and total scattering opacities, respectively. |
| In the text | |
 |
Fig. 3 Averaged intensity variation a) and residuals (relative percentage difference) compared to those calculated by the Feautrier method b) in different layers in the test model atmosphere. Solid and dashed lines in a) correspond to our calculations with the Feautrier and the short characteristics solution of radiative transfer equation. The solid line in b) describes the difference between the Feautrier and short characteristics solutions. Different symbols correspond to values of J(r) obtained by different authors: (crosses) are from Mihalas et al. (1975), (stars) – from Rogers (1982), (squares) – from Avrett & Loeser (1984), (diamonds) – from Gros et al. (1997), (triangles) – from Atanackovic-Vukmanovic (2003). |
| In the text | |
 |
Fig. 4 Center-to-limb variation of intensity a) and polarization c) for the test model atmosphere. The solid line corresponds to the formal solution of differential radiative transfer equations for polarized light using a modified Feautrier method for spherical geometry and the dashed line shows the formal solution of integral radiative transfer equation, using the short characteristics method. The residuals between two approaches are depicted in b) and d) for the center-to-limb variation for intensity and polarization, respectively. |
| In the text | |
 |
Fig. 5 Center-to-limb variation of polarization for the pure scattering atmosphere. The solid line is obtained for stellar model with Teff = 5800 K and log g = 1.5 at 4000 Å. Two other curves (dashed and dotted-dash) are for the models with the same log g = 4.5 but different effective temperatures, 4000 K and 5800 K at 4000 Å and 7000 Å, respectively. The star symbols indicate the solution for plane-parallel atmosphere obtained by Chandrasekhar (1960). |
| In the text | |
 |
Fig. 6 Same as in Fig. 4 but for Phoenix model atmosphere with Teff = 5800 K, log g = 4.5, and wavelength λ = 4500 Å. |
| In the text | |
 |
Fig. 7 Center-to-limb variation of intensity for the Sun. Solid lines (shifted on μ according to the limb position) and dotted line (not-shifted) correspond to the formal solution of differential radiative transfer equations for polarized light using the modified Feautrier method for spherical geometry with the HSRA solar model atmosphere. Dashed line shows the interpolation of observations by Neckel & Labs (1994) |
| In the text | |
 |
Fig. 8 Center-to-limb variation of polarization at 4506 Å for different solar model atmospheres, which are depicted by different line types and labeled on the plot. The stars with error bars depict the measurements obtained by Wiehr & Bianda (2003). The Phoenix model has parameters that are the closest to the solar one, such as Teff = 5800 K and log g = 4.5. |
| In the text | |
 |
Fig. 9 Center-to-limb variation of intensity calculated in the B filter by Claret et al. (2013; dashed lines), Neilson & Lester (2013a; dash-dotted line), Magic et al. (2015; dash-triple dotted line) as well as our continuum computation for 4500 Å (solid lines). Different panels correspond to different effective temperatures and surface gravities that are labeled in the title of each plot. |
| In the text | |
 |
Fig. 10 a) Center-to-limb variation of intensity for Phoenix model atmosphere with Teff = 4000 K, log g = 1.0 and wavelength λ = 4000 Å with neglecting polarization (dashed line) and with taking it into account (solid line). b) Relative difference between two curves from panel a). |
| In the text | |
 |
Fig. 11 Center-to-limb variation of continuum polarization for different spherical stellar model atmospheres. The title above each of the panels indicates the fixed parameters, while labels on each plot describe different curves. Continuum polarizations are given in a logarithmic scale. |
| In the text | |
 |
Fig. 12 Center-to-limb variation of continuum polarization for different stellar models. The color scale shows the logarithm of integrated continuum polarization within μ from 0 to 0.3 at wavelength 4000 Å. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


