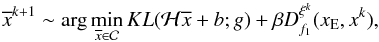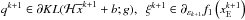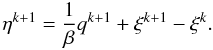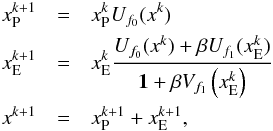| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 9 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201526960 | |
| Published online | 20 January 2016 | |
Deconvolution of post-adaptive optics images of faint circumstellar environments by means of the inexact Bregman procedure
1
Dipartimento di Matematica e Informatica, Università di
Ferrara, via Saragat
1, 44122
Ferrara,
Italy
e-mail:
alessandro.benfenati@unife.it
2
Dipartimento di Informatica, Bioingegneria, Robotica e Ingegneria
dei Sistemi (DIBRIS), Università di Genova, via Dodecaneso 35, 16145
Genova,
Italy
3
Laboratoire Lagrange, Université Côte d’Azur, Université Nice
Sophia-Antipolis/Observatoire de la Côte d’Azur/CNRS, Parc Valrose, 06100
Nice,
France
Received: 14 July 2015
Accepted: 5 October 2015
Aims. High-dynamic range images of astrophysical objects present some difficulties in their restoration because of the presence of very bright point-wise sources surrounded by faint and smooth structures. We propose a method that enables the restoration of this kind of images by taking these kinds of sources into account and, at the same time, improving the contrast enhancement in the final image. Moreover, the proposed approach can help to detect the position of the bright sources.
Methods. The classical variational scheme in the presence of Poisson noise aims to find the minimum of a functional compound of the generalized Kullback-Leibler function and a regularization functional: the latter function is employed to preserve some characteristic in the restored image. The inexact Bregman procedure substitutes the regularization function with its inexact Bregman distance. This proposed scheme allows us to take under control the level of inexactness arising in the computed solution and permits us to employ an overestimation of the regularization parameter (which balances the trade-off between the Kullback-Leibler and the Bregman distance). This aspect is fundamental, since the estimation of this kind of parameter is very difficult in the presence of Poisson noise.
Results. The inexact Bregman procedure is tested on a bright unresolved binary star with a faint circumstellar environment. When the sources’ position is exactly known, this scheme provides us with very satisfactory results. In case of inexact knowledge of the sources’ position, it can in addition give some useful information on the true positions. Finally, the inexact Bregman scheme can be also used when information about the binary star’s position concerns a connected region instead of isolated pixels.
Key words: methods: numerical / methods: data analysis / techniques: image processing / techniques: high angular resolution
© ESO, 2016
1. Introduction
High-dynamic range (HDR) astrophysical objects, often consisting of both very bright central stars and faint diffuse surrounding structures, are first of all difficult to detect because of the various detector noises, and atmospheric turbulence which, if not sufficiently corrected, does not permit the necessary long exposure.
Recent very efficient adaptive optics (AO) systems, often called extreme AO (XAO) systems such as, for example, the SAXO system (Petit et al. 2012) of the instrument SPHERE aboard VLT (Beuzit et al. 2006), make it possible to reach the high sensitivity needed. Additional high-performance coronagraphs can in addition allow even better detections of these faint circumstellar structures. This, however, is at the price of a very high space variance of the point-spread function (PSF) off axis, which prevents deconvolving the final images.
In the present work, we focus on a new deconvolution method that permits us to benefit from the high sensitivity allowed by the XAO system to treat the two different components of the image in a suitable manner (i.e. the very bright central stars, on the one hand, and the faint circumstellar environment, on the other hand). In order to tackle this method realistically, we also consider the central bright component as composed by a slightly unresolved binary star. Moreover, we compare the results of our method with the previously proposed HDR method in La Camera et al. (2012, 2014).
The paper is organized as follows: in Sect. 2 we detail our methods while Sect. 3 describes the end-to-end simulations performed in order to produce realistic data. The obtained results are hence presented in Sect. 4, and conclusions are summarized in Sect. 5.
2. Methods
In this section we describe the mathematical models of the image acquisition system and the variational formulation considered for image reconstruction. Firstly, we present our proposed method, the inexact Bregman procedure, with a brief description of the scaled gradient projection (SGP) method, employed to solve the inner subproblems and tailored for the HDR images case. Then, we briefly present the multi-component Richardson-Lucy (MCRL) method, described in La Camera et al. (2012, 2014). The core of the method is based on the well-known Richardson-Lucy (RL) algorithm (see Richardson 1972 and Lucy 1974), and it is similar to the new method we present. Therefore, we use the MCRL method as a term of comparison for the reconstructed images.
2.1. Generalities
We assume that the acquired image g ∈ Rm is the realization of a multi-valued random variable with expected value ![\begin{eqnarray*} {E}[g] = Hx^* +b , \end{eqnarray*}](/articles/aa/full_html/2016/02/aa26960-15/aa26960-15-eq2.png) where x∗ ∈ Rn is a vector representing the unknown object, H ∈ ℳm × n(R) denotes the imaging matrix coming from the discretization of the (supposedly known, actually estimated) PSF K and satisfying
where x∗ ∈ Rn is a vector representing the unknown object, H ∈ ℳm × n(R) denotes the imaging matrix coming from the discretization of the (supposedly known, actually estimated) PSF K and satisfying 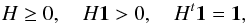 (1)where 1 ∈ Rn is a constant vector with 1 on all entries, and b is the (almost everywhere) constant background emission due to the sky emission and to the detector. The noise perturbing the acquired image is a mixture of Gaussian and Poisson noise, the former due to the read-out noise (RON) and the latter to the counting process. One can consider the RON as a Poisson process (Snyder et al. 1995) and hence the sole noise affecting the image is Poisson noise.
(1)where 1 ∈ Rn is a constant vector with 1 on all entries, and b is the (almost everywhere) constant background emission due to the sky emission and to the detector. The noise perturbing the acquired image is a mixture of Gaussian and Poisson noise, the former due to the read-out noise (RON) and the latter to the counting process. One can consider the RON as a Poisson process (Snyder et al. 1995) and hence the sole noise affecting the image is Poisson noise.
In image reconstruction problems, the aim is to obtain an estimation 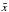 of the unknown object x∗: adopting a Bayesian approach,
of the unknown object x∗: adopting a Bayesian approach, 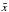 can be computed by solving the following variational problem:
can be computed by solving the following variational problem: 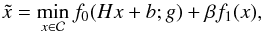 (2)where
(2)where 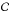 represents the constraints on the solution, such as non–negativity or flux conservation; f0 is called fit-to-data functional: in our case, in presence of Poisson noise, a suitable choice is the generalized Kullback-Leibler functional, known as Csizár I-divergence (Csiszar 1991)
represents the constraints on the solution, such as non–negativity or flux conservation; f0 is called fit-to-data functional: in our case, in presence of Poisson noise, a suitable choice is the generalized Kullback-Leibler functional, known as Csizár I-divergence (Csiszar 1991) 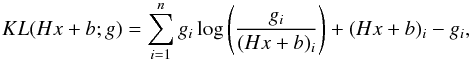 (3)with the agreement 0log (0) = 0, and where the ratio is defined component-wise. Since in real applications b> 0, the logarithm is well defined.
(3)with the agreement 0log (0) = 0, and where the ratio is defined component-wise. Since in real applications b> 0, the logarithm is well defined.
The functional f1 is called regularization functional: it has been introduced to preserve some characteristics on 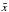 , such as sharp edges or smooth regions. The parameter β is named regularization parameter and it measures the trade-off between f0 and f1. In practical application, one needs the value that gives the best reconstruction, but actually this value is very difficult to estimate (see Bertero et al. 2010; Bardsley & Goldes 2009, for the Poisson case).
, such as sharp edges or smooth regions. The parameter β is named regularization parameter and it measures the trade-off between f0 and f1. In practical application, one needs the value that gives the best reconstruction, but actually this value is very difficult to estimate (see Bertero et al. 2010; Bardsley & Goldes 2009, for the Poisson case).
The problem we are facing consists in the reconstruction of two maps of a given region of an astrophysical object: the former consists in point sources, such as stars, of very high intensity, the latter of smooth structures surrounding these sources. The standard approach, i.e. simply solving Eq. (2), fails since the presence of the point sources destroys all the information about the smooth structures. Hence, the main idea is to consider the object x as the sum of two components, namely x = xP + xE, where xP represents the point sources and xE the extended source. This approach was proposed for the first time in De Mol & Defrise (2004), assuming that the positions of the point sources are known. Denoting by pj the position of the jth source, we can write 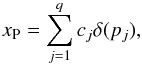 (4)where q is the total number of sources, cj is the jth unknown intensity, and δ(pj) is the delta function centred in pj. Thus, xP is a vector with zero entries except in the q positions corresponding to the known locations of the sources. Then, instead of computing f1 on the whole object x in Eq. (2), we only regularize the extended source, since the structure induced on xP already works as a regularization. This requires a slightly modification in the computation of f0. We introduce the vector c = (c1,c2,...,cq)t containing the intensities of the sources, and we define
(4)where q is the total number of sources, cj is the jth unknown intensity, and δ(pj) is the delta function centred in pj. Thus, xP is a vector with zero entries except in the q positions corresponding to the known locations of the sources. Then, instead of computing f1 on the whole object x in Eq. (2), we only regularize the extended source, since the structure induced on xP already works as a regularization. This requires a slightly modification in the computation of f0. We introduce the vector c = (c1,c2,...,cq)t containing the intensities of the sources, and we define 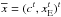 and the matrix
and the matrix ![\hbox{$\mathcal{H}=[\overline{H}, H]$}](/articles/aa/full_html/2016/02/aa26960-15/aa26960-15-eq31.png) , where
, where ![\hbox{$\overline{H}=[h_{p_1},h_{p_2},\dots,h_{p_q}]$}](/articles/aa/full_html/2016/02/aa26960-15/aa26960-15-eq32.png) , with hj denoting the jth column of H. We are hence led to solve
, with hj denoting the jth column of H. We are hence led to solve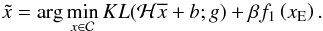 (5)It may happen that
(5)It may happen that 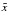 has a loss in contrast, even using the optimal value for β. To overcome this difficulty, we then propose the use of the inexact Bregman procedure, which permits the use of an overestimation of the regularization parameter, and at the same time allows us to obtain a contrast enhancement.
has a loss in contrast, even using the optimal value for β. To overcome this difficulty, we then propose the use of the inexact Bregman procedure, which permits the use of an overestimation of the regularization parameter, and at the same time allows us to obtain a contrast enhancement.
2.2. Inexact Bregman procedure for HDR images
The main idea of the inexact Bregman procedure (Bregman 1967), and it consists in solving Eq. (2) by an iterative procedure in which f1 is substituted with its Bregman distance at the current iterate. In computing this distance, we use the ε-subgradients, obtaining 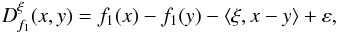 (6)where ξ ∈ ∂εf1(y); ∂εf1(y) denotes the ε-subdifferential of f1 at y (see Rockafellar 1970 for all the technical details). The whole procedure is described below as follows:
(6)where ξ ∈ ∂εf1(y); ∂εf1(y) denotes the ε-subdifferential of f1 at y (see Rockafellar 1970 for all the technical details). The whole procedure is described below as follows:
-
set x0 s.t 0 ≡ ξ0 ∈ ∂f1(x0), ε0 = 0, β> 0. Choose sequences { μk }, { νk } s.t.
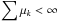 and
and 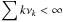 .
.
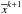 is then an approximated solution. The introduction of the ε-subgradients allows us to take into account the inexactness arising from the use of an iterative solver for the subproblems of Eq. (7). In Benfenati & Ruggiero (2013) the convergence of this method is proven in a general framework.
is then an approximated solution. The introduction of the ε-subgradients allows us to take into account the inexactness arising from the use of an iterative solver for the subproblems of Eq. (7). In Benfenati & Ruggiero (2013) the convergence of this method is proven in a general framework.
As already stated, the main feature of this procedure consists in its regularization behaviour, and, moreover, it allows to use an overestimation of the parameter β (see Sect. 4 for more details). Furthermore, this overestimation induces a contrast enhancement in the restored image.
2.3. Scaled gradient projection
The choice of the iterative solver for the subproblems of Eq. (7) ranges between a huge number of methods. We make use of the SGP method, presented in Bonettini et al. (2009). The aim of the SGP method is to solve the problem 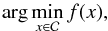 (8)where f is a convex, proper, and differentiable function, and
(8)where f is a convex, proper, and differentiable function, and 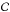 is a convex constraint set. Provided x0,y0, its iteration can be generally described as follows:
is a convex constraint set. Provided x0,y0, its iteration can be generally described as follows: ![\begin{eqnarray} \label{2_SGPalg} &&y^i = {P}_\mathcal{C}\left(x^i-\alpha_iS_i\nabla f(x^i)\right)\\ &&x^{i+1} = x^i+\theta_i(y^i-x^i), \quad \theta_i\in(0,1] , \end{eqnarray}](/articles/aa/full_html/2016/02/aa26960-15/aa26960-15-eq60.png) where
where 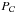 denotes the projection operator on the set
denotes the projection operator on the set 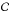 , θi is the line-search parameter, αi is the steplength, and Si denotes a diagonal, positive definite scaling matrix. The parameter θi is determined by a standard monotone line-search strategy, while αi and Si updating rules are devised in order to induce an acceleration on the convergence rate. In the SGP version used within the numerical experiments, at each ith step the steplength αi is determined by using the Barzilai-Borwein rules (see Barzilai & Borwein 1988; Frassoldati et al. 2008). The Si matrix plays a crucial role in achieving acceleration; in order to obtain this kind of an acceleration and, at the same time, to avoid an increasing computational cost, we define the diagonal entries sl of Si, employing a splitting of the gradient of the objective function f (Lanteri et al. 2002),
, θi is the line-search parameter, αi is the steplength, and Si denotes a diagonal, positive definite scaling matrix. The parameter θi is determined by a standard monotone line-search strategy, while αi and Si updating rules are devised in order to induce an acceleration on the convergence rate. In the SGP version used within the numerical experiments, at each ith step the steplength αi is determined by using the Barzilai-Borwein rules (see Barzilai & Borwein 1988; Frassoldati et al. 2008). The Si matrix plays a crucial role in achieving acceleration; in order to obtain this kind of an acceleration and, at the same time, to avoid an increasing computational cost, we define the diagonal entries sl of Si, employing a splitting of the gradient of the objective function f (Lanteri et al. 2002), 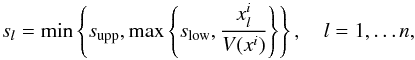 (11)where 0 <slow<supp are positive constants,
(11)where 0 <slow<supp are positive constants, 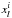 denotes the lth component of the ith iterate and the vector V(xi) is such that
denotes the lth component of the ith iterate and the vector V(xi) is such that 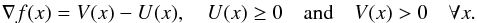 (12)It is obvious that this kind of splitting always exists and is not unique.
(12)It is obvious that this kind of splitting always exists and is not unique.
2.4. Regularization functionals
We provide more details about the implementation of the inexact Bregman procedure, with SGP as inner solver, for the regularization functionals we consider. We define fβ(·) = KL(H· + b;g) + βf1(·). The choices made are the classical Tikhonov (T0) regularization 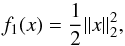 (13)and the hyper surface (HS) potential
(13)and the hyper surface (HS) potential 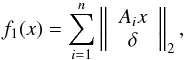 (14)where Ai ∈ ℳ2 × n,
(14)where Ai ∈ ℳ2 × n, ![\hbox{$A=[A_1^t, A_2^t,\dots;A_n^t]^t$}](/articles/aa/full_html/2016/02/aa26960-15/aa26960-15-eq77.png) is the discrete version of the gradient and δ ≥ 0 is a thresholding parameter. We point out that for δ> 0 the HS potential is differentiable, while for δ = 0 we obtain the well-known total variation functional. We use the HS potential.
is the discrete version of the gradient and δ ≥ 0 is a thresholding parameter. We point out that for δ> 0 the HS potential is differentiable, while for δ = 0 we obtain the well-known total variation functional. We use the HS potential.
The construction of the scaling matrix Sl in the SGP method requires the splitting of the gradient of the objective functional as ∇fβ = Vβ − Uβ, and, since 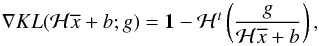 (15)we have
(15)we have 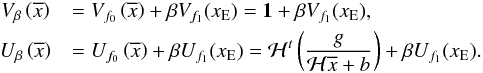 (16)For the Tikhonov case, we simply have Uf1 = 0 and Vf1(x) = x , while for the HS case we follow the formulae presented in Zanella et al. (2009).
(16)For the Tikhonov case, we simply have Uf1 = 0 and Vf1(x) = x , while for the HS case we follow the formulae presented in Zanella et al. (2009).
In both the Tikhonov case and the HS case, the regularization functional is differentiable, thus we can write 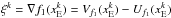 , and, moreover, εk = 0 for any k.
, and, moreover, εk = 0 for any k.
Remark 1.From a numerical point of view, the set-up of the sequence νk can be easily obtained from 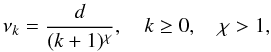 where χ and d are two positive constants. With this approach, at the first iteration, the tolerance is equal to d, while in the successive iterations it becomes more and more severe. A practical rule to set the value for d is to solve the very first subproblem with a mild tolerance and to use a standard stopping criterion, then set d = ∥ η1 ∥. Hence, the only setting required is the value of χ.
where χ and d are two positive constants. With this approach, at the first iteration, the tolerance is equal to d, while in the successive iterations it becomes more and more severe. A practical rule to set the value for d is to solve the very first subproblem with a mild tolerance and to use a standard stopping criterion, then set d = ∥ η1 ∥. Hence, the only setting required is the value of χ.
The convergence property of this tailored version of the Bregman procedure, for a general class of regularization functionals, including the Tikhonov case and the HS case, can be found in Benfenati & Ruggiero (2015).
2.5. Multi-component Richardson Lucy
As mentioned at the beginning of this section, we briefly describe here the so-called MCRL method. The approach is similar to the method presented in this paper. Again, as the name of the method itself suggests, we consider the unknown object x as the sum of the two components x = xP + xE and we want to solve Eq. (5). For the minimization of the functional f = f0(Hx + b;g) + βf1(xE), we use the split-gradient method (SGM) introduced by Lanteri et al. (2002), as in the previous case for the inner solver SGP.
With respect to the version presented in La Camera et al. (2014), we developed an updated version of the method, which has several regularizations, in particular, Tikhonov and HS, described in the next section.
Each step of MCRL consists of an RL iteration on xP and of an SGM iteration on xE. The algorithm is
-
given nonnegative
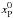 and
and 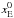 ,
, -
stop the iteration according to a given stopping rule.
In the previous equation the terms Uf0,Uf1 and Vf1 are defined according to Eq. (17). In our simulations we pushed the algorithm to convergence, i.e. we stopped the iterations when the relative variation of the objective function 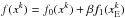 was smaller than a given threshold.
was smaller than a given threshold.
Finally, we remark on the initialization of the two components. We choose 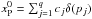 , where the position pj of each star is supposed to be known. At each iteration, because of the properties of RL, only the pixels in the positions pj remain positive, while the other pixels are kept fixed to the initial zero value. In other words, the method introduces a sparsity regularization in the point-like component of the reconstructed object. We initialize
, where the position pj of each star is supposed to be known. At each iteration, because of the properties of RL, only the pixels in the positions pj remain positive, while the other pixels are kept fixed to the initial zero value. In other words, the method introduces a sparsity regularization in the point-like component of the reconstructed object. We initialize 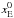 with a constant array. We do not have information about the flux of the diffuse component (only on the sum of the two), thus we simply take
with a constant array. We do not have information about the flux of the diffuse component (only on the sum of the two), thus we simply take 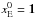 . We verified in our simulations that the algorithm is able to reproduce the correct flux values for both components.
. We verified in our simulations that the algorithm is able to reproduce the correct flux values for both components.
Remark 2.
Since the Bregman procedure consists in two nested cycles when one does not have the explicit solution of the inner problems of Eq. (7), we need a fast solver for the inner subproblems. The SGP algorithm provides reliable results with a lower number of iterations with respect to the MCRL method (see Sect. 4 for details); thus, we preferred SGP as inner solver for the problems of Eq. (7).
Obviously, the Bregman scheme allows us to choose the inner solver in a wide class of methods. Another valuable option is a particularly tailored version of the alternating direction method of multipliers (ADMM; see Figueiredo & Bioucas-Dias 2010), which also permits the use of non-differentiable regularization functionals. We focused on the SGP algorithm as inner solver since the main aim of this work lies in the study of the behaviour of the Bregman procedure, regardless of the method used in the inner cycle.
 |
Fig. 1 From left to right: object, PSF, image, noisy image. Pixel size is ~8.74 mas, i.e. (λ/D) / 6.4, and only the central 256×256-px part is shown here (i.e. a field-of-view of ~2.24×2.24 arcsec). Each image is normalized to its maximum and represented at the power of 0.1 for sake of clarity. |
3. Simulations: case study
The HDR case study considered here consists in AO-aided (hence high angular resolution) observations of a bright unresolved binary star with a faint circumstellar environment made of dust, with the particular aim of imaging the circumstellar structure. The dust forms at a given close-by distance from the star, there is a gap around the star before the start of the faint environment. We chose the very timely case of near-infrared images obtained with the help of a ground-based, 8-m class telescope equipped with a high-Strehl AO system.
We do not focus on characterizing the binarity of the central component (with a binary separation of less than half a resolution element at the central observing band, 2.17 μm). This must be addressed separately, for example by means of the super-resolution algorithm described in Anconelli et al. (2005) and applied to real data in Carbillet et al. (2013). Considering this binarity of the central component implies an additional difficulty in properly imaging the morphology of the circumstellar dust, and, in particular, in reconstructing the exact shape of the very close-by and sharp transition between the hole and the dust.
The circumstellar environment is modelled as Gaussian, with a full-width at half maximum (FWHM) of ~306 mas (35 px). Its central obscuration, characterizing the hole evoked before, has a diameter of ~79 mas (9 px). The pixel size is equivalent to a resolution element of the telescope at 2.17 μm (hence λ/D ≃ 56 mas), divided by 6.4. The total flux of the object is distributed into one-third for each binary component and one-third for the Gaussian circumstellar environment. The total considered magnitude in the observing band (with a bandwidth of 0.3 μm) is 6.
Then, images in that near-infrared band, through the instrument SPHERE/IRDIS aboard VLT (Beuzit et al. 2006), were numerically simulated from a deeply detailed numerical modelling involving atmospheric and instrumental wavefront perturbations, AO corrections through the SPHERE XAO system SAXO (Petit et al. 2012), and broad-band imaging (with no coronagraph). We performed the entire modelling by means of the ad-hoc Software Package SPHERE (Carbillet et al. 2008), which is already used in a number of instrumental (Boccaletti et al. 2008; Carbillet et al. 2011) and image processing (Smith et al. 2009; Vigan et al. 2010) works involving SPHERE/IRDIS, and developed within the CAOS problem-solving environment (Carbillet et al. 2004, 2010). We also considered fundamental noises at the level of the detector (photon noise and RON) and sky background. The time exposure is also limited to a saturation limit given by the detector characteristics, and resulting here in a 23s-only frame. Detailed parameters of the performed end-to-end simulation are given in Table 1.
Detailed parameters of the end-to-end simulation.
The resulting object, PSF, and image are represented in Fig. 1. The blurring effect of the PSF, on the one hand, and the effect of the detector noises, on the other hand, can be clearly noticed.
4. Results
We now introduce the metrics used to evaluate our results. The first is the relative reconstruction error on the true object x∗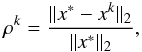 where xk is the restored image at the kth iteration and ∥ ·∥ 2 is the Euclidean norm. We define the optimal value βopt for the regularization parameter in terms of ρk: selecting in an interval [ βd,βu ] some values for β, we chose the one that provides the restored image with the minimum reconstruction error. Actually, instead of considering the whole 1024 × 1024 image in computing ρk, we only take into account a smaller, centred portion of the xE component, within the window w ranging from the 470th pixel to the 555th one in both dimensions. We denote this error ρw (for sake of completeness, we point out that we enumerate the pixels from 1 to 1024 in both directions). As previously mentioned, in practical applications, only an estimate of βopt can be obtained (see Bertero et al. 2010; Bardsley & Goldes 2009). Moreover, the numerical experience (see Benfenati & Ruggiero 2015) has shown that these methods cannot provide satisfactory results for some classes of images (such as the image treated in this work) because of the hypothesis underlying these techniques.
where xk is the restored image at the kth iteration and ∥ ·∥ 2 is the Euclidean norm. We define the optimal value βopt for the regularization parameter in terms of ρk: selecting in an interval [ βd,βu ] some values for β, we chose the one that provides the restored image with the minimum reconstruction error. Actually, instead of considering the whole 1024 × 1024 image in computing ρk, we only take into account a smaller, centred portion of the xE component, within the window w ranging from the 470th pixel to the 555th one in both dimensions. We denote this error ρw (for sake of completeness, we point out that we enumerate the pixels from 1 to 1024 in both directions). As previously mentioned, in practical applications, only an estimate of βopt can be obtained (see Bertero et al. 2010; Bardsley & Goldes 2009). Moreover, the numerical experience (see Benfenati & Ruggiero 2015) has shown that these methods cannot provide satisfactory results for some classes of images (such as the image treated in this work) because of the hypothesis underlying these techniques.
Another quality measurement is obtained by considering the radius of the reconstructed hole in the centre of the image (see Fig. 1). This radius is computed following the steps below, supposing that the centre of this hole is in the middle of the image:
-
at each kth step, we detect the pixel P corresponding to the maximum within the window of interest w. We compute its distance d from the centre. If the maximum is attained in more than one pixel, we compute all the distances of these pixels from the centre and then only consider the maximal distance among these values, namely d;
-
we identify the pixels lying in the circle whose radius is d and we take the square containing this circle; and
-
via a Canny edge detector algorithm, we identify the profile of the hole and then compute the mean radius rk of the reconstructed hole.
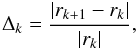 one can choose as a stopping criterion for the inexact Bregman procedure the request that Δk<ϵ, where ϵ is a given tolerance.
one can choose as a stopping criterion for the inexact Bregman procedure the request that Δk<ϵ, where ϵ is a given tolerance.
We have then used two different metrics for error measurements: the first (relative reconstruction error) can provide a numerical measurement of the reconstruction. This error measurement is classical, but it is not applicable to real cases, since x∗ is not available. The other measurement is suggested by the particular structure of the image treated, where the main interest lies in reconstructing the centred hole. Then we developed a procedure to measure the radius of the hole. We assumed this radius to be a quality index of the restored images. This second technique can also be applied in real case studies for a class of images presenting similar structures.
Regarding MCRL, in the case of HS regularization, the proposed method for finding the optimal value βopt based on the minimization of the reconstruction error failed. Therefore, we analysed the reconstructed objects (at different values of β) and we chose the βopt value that provides the smallest value of the mean radius rβ of the reconstructed hole.
 |
Fig. 2 Experiments results. Line plots: the lines depicted represent the 513th row of the image, from pixel 470 to 555. The images shown are the restored images by SGP, MCRL, and inexact Bregman procedure, in column-wise order. The results shown are related to the minimum ρw obtained. |
4.1. Exact knowledge of the positions of the sources
A first set of experiments is done by supposing to know the exact positions of the sources.
The first choice for the regularization function is the Tikhonov functional, using SGP algorithm with βopt = 5 × 10-6. The stopping criterion used is based on the relative difference of two successive objective function values. Setting the tolerance for this criterion to 10-7, in 178 iterations the obtained image has a relative reconstruction error ρw = 13.4%, and the radius of the hole is 4.90 ± 0.91 pixels (while the exact value is 4.5 pixels). Moreover, we can compute the minimum value attained in the reconstructed hole, which in this case is equal to 2% of the maximum value to be compared with the exact percentage (0%). In the plot on the left of Fig. 2 (first row), we show the profile line of the 513rd row (the one in which the binary star lies) of the true object x∗ and the reconstructions of the same row obtained with the different methods. The black dashed line is related to the true object, and the red line and green line represent the SGP and MCRL reconstructions, respectively. Finally, blue line corresponds to the restored image by the Bregman procedure. The SGP method combined with Tikhonov regularization with βopt cannot provide satisfactory results regarding the edges of the hole. In fact, Tikhonov regularization cannot recognize sharp edges.
The MCRL method has a very similar behaviour to SGP, since it cannot recognize the steepness of the hole. The MCRL method provides a restored image with ρw = 11.1% and a radius of 4.77 ± 0.98 using β = 3 × 10-6. Moreover, it reaches a higher minimum value of the hole (6%). On the other hand, MCRL seems to produce fewer artifacts than SGP, as one can observe in the restored image shown again in Fig. 2.
The inexact Bregman procedure is set with β = 10βopt, an initial tolerance of 10-7 and χ = 1.5. We force the procedure to run for 100 iterations. At the 5th external iteration (with a total number of iterations for SGP of 499), we obtain the restored image with ρw = 13.2%. As evidenced by the blue profile line in the upper left plot of Fig. 2, the bottom of the hole (i.e. the value 0) is reached, while the hole’s radius is very similar to the previous case: 4.89 ± 0.91. Requiring Δk< 10-3, the procedure has to be terminated at the 9th iteration, obtaining a reconstruction with ρw = 13.4%, which is slightly higher than the minimum error achieved.
The Tikhonov regularization cannot achieve a satisfactory reconstruction of the image because of the presence of sharp edges: then we use the HS function, with δ = 10-4. The results are shown in the second row of Fig. 2. When SGP method is employed with the optimal value for β (βopt = 5.97 × 10-3), we obtain a restored image with ρw = 9.4%, and a reconstructed radius of 4.24 ± 0.80. The minimum intensity achieved in the hole is 11.1%. This intensity is higher than that achieved by Tikhonov regularization, but one can observe that the flatness of the hole’s bottom is well restored by checking the red profile line in Fig. 2.
The MCRL method is used setting β = 10-3. The relative reconstruction error ρw achieved after 783 iterations is 10.1%, while the restored radius is 5.02 ± 0.89. The minimum value reached in the hole is 6%, which is a better result compared to the value provided by the SGP algorithm. Moreover, the MCRL method provides a more accurate reconstruction of the top boundary of the hole as evidenced by the line plot in Fig. 2 (second row). Although the MCRL method gives a general satisfactory estimation of the hole in terms of depth and radius, among the rest of the diffuse component some anomalies arise that are similar to those in the Tikhonov case.
The inexact Bregman procedure is set as in the Tikhonov case, i.e. with β = 10βopt, an initial tolerance of 10-5 and χ = 1.001. The contrast-enhancement behaviour (see Benfenati & Ruggiero 2013) of this procedure is evident here: at the 32nd iteration (362 total iterations for SGP), we obtain a restored image with ρw = 8.2% and a minimum value achieved in the hole of 2%. On the other hand, this kind of behaviour reveals some artifacts: for example, the peak appearing in the blue profile line, which becomes evident in the restored image. These artifacts are most probably due to the diffraction of the spider arms of the telescope, which are somehow emphasized during the reconstruction process. By adopting the inexact Bregman procedure, the restored hole has a radius equal to 4.33 ± 0.89 at the 32nd iteration, and requiring Δk< 10-3 leads us to stop at the 10th iteration, where r10 = 4.40 ± 0.91 and ρw = 8.6%.
Considering the restored images related to the minimum reconstruction error, the HS regularization, as a result of its edge-preserving behaviour, appears more suitable in this type of restoration problem since it allows us to obtain a more satisfactory reconstruction of the hole in terms of shape and depth. Moreover, the Tikhonov regularization seems to produce more artifacts in the diffuse component. Similar artifacts also tend to appear in the HS case, when one lets the methods (SGP, MCRL, and Bregman) proceed with a high number of iterations.
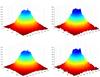 |
Fig. 3 Surface plots of the restored images. First row: surface plots related to the minimum error; second row: surfaces corresponding to the images for which Δk< 10-3. The regularization functions considered are HS and Tikhonov in column-wise order, respectively. |
Comparing the results obtained by SGP and MCRL with those provided by the inexact Bregman procedure, one can observe that the enhancing contrast, characteristic of this kind of procedure, allows us to recognize the centred hole, improving its depth and radius. In Fig. 3 we present the surface plots of the restored images in four cases: in the first row, we show the reconstructions obtained by the Bregman procedure related to the minimum ρw (with HS and Tikhonov regularizations on the left and right, respectively); and, in the second row, we show the restored images, which satisfy Δk< 10-3 (with HS and Tikhonov regularizations on the left and right, respectively).
Tikhonov images are affected by numerous artifacts: in fact, looking at the top of the hole, we can see that the surface on its edge present a number of anomalies. We must also point out that the edge-preserving regularization provides results with some artifacts (the peaks are quite evident).
4.2. Inexact positions of the sources
In this experiment, we set the coordinates of one point source on the wrong pixel on purpose. Since in the previous experiments, the edge-preserving functional turned out to be more suitable, we use this type of function in this experiment. The inexact Bregman procedure is set again by taking β = 10βopt with an initial tolerance of 10-5 and χ = 1.001; in Fig. 4 the image with minimum reconstruction error is shown, together with the line-plot of the 513rd rows of the true object x∗ and of the restored image.
 |
Fig. 4 Results obtained by setting the coordinates of one point source to the wrong pixel. Upper panel: line plot of the 513rd row of the original image, from pixel 470 to 555; black dashed line is the original object, while the red one is the line related to the reconstruction. Lower panel: image of the window of interest (normalized to its maximum and represented at the power of 0.1). |
Setting inexact coordinates for the position of one point source means that a very bright source is present in the diffuse component xd. Hence the method emphasizes a very bright source, as is clearly evident in the large blue spot of high intensity in Fig. 4. Although we set the position of one point source to the wrong coordinates, we can obtain some useful information. In fact, the image in Fig. 4 suggests that we have located the hole (red large spot), but actually one (or more) bright source(s) are present, identified by the high blue peak. Hence, considering the pixels corresponding to the high intensity spot inside the hole, one can search for other bright sources among this region.
4.3. Connected xP region
In order to avoid the case described in previous subsection, we consider that the positions of the sources pj,j = 1,...,q are known, but are in a region composed by each pj and the relative 8-connected pixels.
We tested this approach in our case study. Since the binary star has a separation of two pixels, considering the eight connected pixels around the stars means that we are considering a region of 3 × 6 pixels in the xP component. We expect to restore a larger hole than in the previous cases. The inexact Bregman procedure is set with β = 15βopt and with an initial tolerance of 10-5 and χ = 1.001. In Fig. 5 the results with minimum reconstruction errors are shown.
 |
Fig. 5 Considering a larger region for the point source component. Upper panel: line plot of true object (black dashed line) and reconstruction (red line). Lower panel: image of the window of interest (normalized to its maximum and represented at the power of 0.1). |
As expected, the restored image has a larger hole (its radius is 7.77 ± 0.86), but the position of the hole is clearly identified. The reconstruction error ρw is higher (32.2%) than in the previous cases because of the large connected region set in the xP component. The positive aspect of this approach regards the satisfactory identification of the hole: hence, we have properly divided the image in its two components xP and xE, i.e. we did not include any bright source in the diffuse part. As a successive step, we suggest reducing the region in which the stars are spread to achieve a better estimation of the positions of the sources.
5. Conclusions
Table 2 gives a summary of the final results obtained. The benefit obtained thanks to the approach presented in the present paper is the opportunity to use an overestimation of the regularization parameter β instead of searching for the optimal one, since in presence of Poisson noise this is a very tricky task. A practical strategy consists in estimating β with one of the methods mentioned previously in the paper (e.g. Bertero et al. 2010; Bardsley & Goldes 2009), and then multiply the obtained value (namely 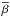 ) by a factor γ> 1. Four scenarios may arise by adopting this strategy:
) by a factor γ> 1. Four scenarios may arise by adopting this strategy:
-
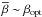 : using
: using 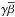 (we suggest γ between 10 and 20) the Bregman procedure acts as previously shown, inducing a contrast enhancement in the restored images;
(we suggest γ between 10 and 20) the Bregman procedure acts as previously shown, inducing a contrast enhancement in the restored images; -
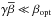 : in this case, the regularization behaviour of the whole procedure is not evident. The value
: in this case, the regularization behaviour of the whole procedure is not evident. The value 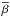 is so small that even
is so small that even 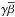 is not sufficient to trigger the regularization behaviour, then γ must be increased;
is not sufficient to trigger the regularization behaviour, then γ must be increased; -
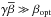 : the restored images, at each outer iteration, present losses in details and contrast. The regularization functional has too much influence with respect to the data fidelity functional, and γ is too large;
: the restored images, at each outer iteration, present losses in details and contrast. The regularization functional has too much influence with respect to the data fidelity functional, and γ is too large; -
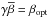 : in this case, the very first step of the Bregman procedure consists in a classical regularization procedure. The successive steps cannot provide better reconstructions (the best one, in terms of relative reconstruction error, is already reached), but it may happen that some benefits in terms of contrast enhancement could emerge.
: in this case, the very first step of the Bregman procedure consists in a classical regularization procedure. The successive steps cannot provide better reconstructions (the best one, in terms of relative reconstruction error, is already reached), but it may happen that some benefits in terms of contrast enhancement could emerge.
This kind of strategy, taking previous considerations into account, allows us thus to simplify the selection procedure of β in real applications.
Although with this overestimation, the restored images (both with Tikhonov and HS regularizations) present satisfactory characteristics in terms of quality and numerical results, such as the radius of the hole and the estimation of the depth of the hole.
Final results obtained.
The whole procedure proposed here relies on a previous step of determination of the exact position of the source, or sources, in the case of a central (possibly unresolved) binary star. This is supposed to be performed with the help of a classical RL deconvolution, and even super-resolution (as described before). This also assumes a signal-to-noise ratio that is high enough for the central object zone of the data to be able to push the iterations of RL far enough (towards a single pixel reconstruction mode). If this step failed to resolve the possible binarity of the central component, it will at least reconstruct a typical elongation, which can be used as described in Sect. 4.3. If the position of one (or more) of the components badly resolved is not exact, the method we propose will feature the typical artifact described in Sect. 4.2, emphasizing the misplaced source, and one can then search again for its correct position. Hence, the inexact Bregman procedure proposed here is not only able to reconstruct the circumstellar environment, but can also help in reconstructing more correctly the central stellar component (if binary/multiple) by successive iterations of the procedure.
A first perspective of this work will be to verify the performance of the method proposed when the PSF is not perfectly calibrated, which was an implied assumption of the present paper (the so-called inverse crime case, a usual and reasonable first step when testing the intrinsic limit of a new method). Nevertheless, we do not expect drastic changes since, e.g. for the SPHERE/VLT instrument taken as a case study here, the PSF calibration procedure is performed very accurately. Hence, the procedure is numerically modelled within the ad hoc Software Package SPHERE (Carbillet et al. 2008), considering 97% of common wavefronts between the calibrated PSF and the PSF used for imaging the object observed.
A successive perspective will be to study the deconvolution of post-coronagraphic data, which present the tricky characteristics of a strong space variance of the PSF around the centre of the field, but can possibly lead to reach higher dynamic ranges.
Acknowledgments
The referee and the editor are thanked for their remarks and questions that permitted us to enhance the readiness of the paper. Nicolas Basalgète is also thanked for proof-reading of the revised version of the manuscript, and Mario Bertero is acknowledged for his theoretical help regarding the issue of Poisson noise vs. Gaussian noise. The idea of searching for ad hoc methods permitting to properly reconstruct evolved objects, such as the close binary star surrounded by dust modelled in the present paper, was born during a Master training stage co-supervised by MC and Olivier Chesneau in year 2011 (Belokogne 2011). The present work is dedicated to the memory of the bright scientist Olivier was.
References
- Anconelli, B., Bertero, M., Boccacci, P., & Carbillet, M. 2005, A&A, 431, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bardsley, J. M., & Goldes, J. 2009, Inverse Problems, 25, 095005 [NASA ADS] [CrossRef] [Google Scholar]
- Barzilai, J., & Borwein, J. M. 1988, IMA J. Num. Anal., 8, 141 [Google Scholar]
- Belokogne, I. 2011, How to push the limits of evolved stars observations with SPHERE/VLT (Université de Nice Sophia-Antipolis) [Google Scholar]
- Benfenati, A., & Ruggiero, V. 2013, Inverse Problems, 29, 5016 [CrossRef] [Google Scholar]
- Benfenati, A., & Ruggiero, V. 2015, Communications in Nonlinear Science and Numerical Simulation, 21, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Bertero, M., Boccacci, P., Talenti, G., Zanella, R., & Zanni, L. 2010, Inverse Problems, 26, 10500 [Google Scholar]
- Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2006, ESO Messenger, 125, 29 [Google Scholar]
- Boccaletti, A., Carbillet, M., Fusco, T., et al. 2008, in Adaptive Optics Systems, SPIE Proc., 7015, 70156 [Google Scholar]
- Bonettini, S., Zanella, R., & Zanni, L. 2009, Inverse Problems, 25, 015002 [NASA ADS] [CrossRef] [Google Scholar]
- Bregman, L. M. 1967, USSR Computational Mathematics and Mathematical Physics, 7, 200 [Google Scholar]
- Carbillet, M., Vérinaud, C., Guarracino, M., et al. 2004, in Advancements in Adaptive Optics, SPIE Proc., 5490, 550 [Google Scholar]
- Carbillet, M., Boccaletti, A., Thalmann, C., et al. 2008, in Adaptive Optics Systems, SPIE Proc., 7015, 70156 [Google Scholar]
- Carbillet, M., Desiderà, G., Augier, E., et al. 2010, in Adaptive Optics Systems II, SPIE Proc., 7736, 773644 [CrossRef] [Google Scholar]
- Carbillet, M., Bendjoya, P., Abe, L., et al. 2011, Exp. Astron., 30, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Carbillet, M., La Camera, A., Chesneau, O., et al. 2013, in Adaptive Optics for Extremely Large Telescopes, Proc. 3rd AO4ELT Conf., Firenz, Italy [Google Scholar]
- Csiszar, I. 1991, Ann. Statist., 19, 2032 [CrossRef] [Google Scholar]
- De Mol, C., & Defrise, M. 2004, Proc. Int. Symp. on Electromagnetic Theory, 798, 800 [Google Scholar]
- Figueiredo, M. A. T., & Bioucas-Dias, J. M. 2010, IEEE Transactions on Image Processing, 19, 3133 [Google Scholar]
- Frassoldati, G., Zanni, L., & Zanghirati, G. 2008, J. Industrial and Management Optimization, 4, 299 [Google Scholar]
- La Camera, A., Antoniucci, S., Bertero, M., et al. 2012, in Optical and Infrared Interferometry III, Proc. SPIE, 8445, 84453D [CrossRef] [Google Scholar]
- La Camera, A., Antoniucci, S., Bertero, M., et al. 2014, PASP, 126, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Lanteri, H., Roche, M., & Aime, C. 2002, Inverse Problems, 18, 1397 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1974, AJ, 79, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, C., Sauvage, J.-F., Sevin, A., et al. 2012, in Adaptive Optics Systems III, SPIE Proc., 8447, 84471 [Google Scholar]
- Richardson, W. H. 1972, J. Opt. Soc. Am., 62, 55 [Google Scholar]
- Rockafellar, R. T. 1970, Convex Analysis (Princeton, NJ: Princeton University Press) [Google Scholar]
- Smith, I., Bertero, M., Boccacci, P., Carbillet, M., & Lantéri, H. 2009, IEEE Trans. on Signal Proc., 57, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Snyder, D. L., Helstrom, C. W., Lanterman, A. D., White, R. L., & Faisal, M. 1995, J. Opt. Soc. Am. A, 12, 272 [Google Scholar]
- Vigan, A., Moutou, C., Langlois, M., et al. 2010, MNRAS, 407, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Zanella, R., Boccacci, P., Zanni, L., & Bertero, M. 2009, Inverse Problems, 25, 045010 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 From left to right: object, PSF, image, noisy image. Pixel size is ~8.74 mas, i.e. (λ/D) / 6.4, and only the central 256×256-px part is shown here (i.e. a field-of-view of ~2.24×2.24 arcsec). Each image is normalized to its maximum and represented at the power of 0.1 for sake of clarity. |
| In the text | |
 |
Fig. 2 Experiments results. Line plots: the lines depicted represent the 513th row of the image, from pixel 470 to 555. The images shown are the restored images by SGP, MCRL, and inexact Bregman procedure, in column-wise order. The results shown are related to the minimum ρw obtained. |
| In the text | |
 |
Fig. 3 Surface plots of the restored images. First row: surface plots related to the minimum error; second row: surfaces corresponding to the images for which Δk< 10-3. The regularization functions considered are HS and Tikhonov in column-wise order, respectively. |
| In the text | |
 |
Fig. 4 Results obtained by setting the coordinates of one point source to the wrong pixel. Upper panel: line plot of the 513rd row of the original image, from pixel 470 to 555; black dashed line is the original object, while the red one is the line related to the reconstruction. Lower panel: image of the window of interest (normalized to its maximum and represented at the power of 0.1). |
| In the text | |
 |
Fig. 5 Considering a larger region for the point source component. Upper panel: line plot of true object (black dashed line) and reconstruction (red line). Lower panel: image of the window of interest (normalized to its maximum and represented at the power of 0.1). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.