EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 585 (January 2016) A&A, 585 (2016) A108 Full HTML
Free Access
Issue
A&A
Volume 585, January 2016
Article Number A108
Number of page(s) 5
Section The Sun
DOI https://doi.org/10.1051/0004-6361/201527343
Published online 05 January 2016

© ESO, 2016

1. Introduction

Magnetic flux ropes are common in the interplanetary space (Shimazu & Marubashi 2000; Janvier et al. 2014) and in the solar corona (e.g., Nindos et al. 2015). Owing to their finite size and the solenoidality of magnetic fields, they are curved and often form loop-like structures. They can therefore be, at least locally, approximated by toroidal magnetic field configurations. The first candidates are linear force-free fields. In the cylindrical geometry, they were successfully applied to the very local description of magnetic fields in the most prominent interplanetary magnetic flux ropes, magnetic clouds (Burlaga 1988; Lepping et al. 1990).

For the toroidal geometry, there are several known solutions of linear force-free fields. Miller & Turner (1981) found an approximate solution for a toroidal flux rope with a high aspect ratio (ratio of the major to minor radii), that is, for thin toroids. Tsuji (1991) derived a general solution for a toroidal flux rope with an arbitrary aspect ratio and cross section, but it is very complex, even for the case of a toroid with a circular cross section (see Vandas & Romashets 2015). Romashets & Vandas (2009) suggested a different way of constructing toroidal linear force-free fields with an azimuthal symmetry (the symmetry around the rotational axis of the toroid). However, this solution yields flux ropes with complex cross sections. We here continue in this approach with the aim to construct toroidal flux ropes with an imposed cross-section shape (e.g., elliptic).

Toroidal magnetic fields are used to interpret some magnetic field observations in magnetic clouds. Ivanov et al. (1989) and Marubashi (1997) applied solutions for linear force-free fields in an ideal toroid (toroid with a circular axis and a constant circular cross section) with a high aspect ratio to fit magnetic field measurements in several magnetic clouds, the Miller & Turner (1981) solution in the former case, and the cylindrically adjusted Lundquist solution (see Vandas & Romashets 2015) in the latter case. For the same purpose, Romashets & Vandas (2003) and Marubashi & Lepping (2007) used the toroidal non-linear force-free field in an ideal toroid, also valid only for a high aspect ratio, derived by Romashets & Vandas (2003). Hidalgo (2014) fit magnetic cloud measurements by his solution in a non-ideal toroid, which has a loop-like axis and varying cross section, but the magnetic field is not force-free.

Vandas & Romashets (2015) derived a simple formula for the magnetic helicity of the linear force-free field in an ideal toroid, based on the Miller & Turner (1981) solution. In this work we test if this formula is applicable to flux ropes with elliptic cross sections, that is, not only to circular ones. The toroidal solution is described in Sect. 2, and it is used to construct toroidal flux ropes with simple cross sections (i.e., circular and elliptic) in Sect. 3. In Sect. 3.1 we use it to calculate their helicity. We conclude in Sect. 4.

2. Construction of a new linear force-free solution

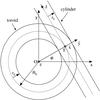thumbnail Fig. 1

Construction of a toroidal solution. The global system connected with the toroid has the origin O and axes x, y, and z. The local system of a cylinder has the origin T and axes ˜x\hbox{$\tilde{x}$}, ˜y\hbox{$\tilde{y}$}, and ˜z\hbox{$\tilde{z}$}.

A force-free magnetic field B is defined by the condition curlB = αB, where α is a scalar function of coordinates. If α = const., α ≠ 0, we speak about a linear or constant-alpha force-free field.

Romashets & Vandas (2009) started with the linear force-free field in a cylinder, found by Lundquist (1950), ˜Bρ=0,˜Bθ=B0J1(αρ),˜BZ=B0J0(αρ),\begin{eqnarray} \label{BrL}\tilde{B}_\rho & = & 0 , \\ \label{BtL}\tilde{B}_\theta & = & B_0 \mathrm{J}_1(\alpha \rho) , \\ \label{BZL}\tilde{B}_Z & = & B_0 \mathrm{J}_0(\alpha \rho) , \end{eqnarray}where ρ, θ, and Z are cylindrical coordinates, α is a constant, B0 scales the field, and Jn are the Bessel functions of the first kind. We consider a toroid with the major radius R0 and minor radius r0 (see Fig. 1). We call this a generating toroid. Its rotational axis coincides with the z axis, and its circular axis (shown by the dashed circle in Fig. 1) lies in the xy plane. We select a point T at this circular axis. Its position is determined by the azimuthal angle ϕ. We have a cylinder with the radius r0 that is tangent to the toroid at the point T, that is, its axis (shown by the dashed straight line in Fig. 1) is tangent to the toroid’s circular axis and lies in the xy plane. The tangent cylinder and its position defines a force-free field in all space, which is given in the intrinsic cylindrical system ρ, θ, and Z of the cylinder by expressions (1)–(3). The field in the global system x, y, and z with the origin O (see Fig. 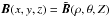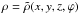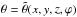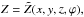1) may be expressed as B(x,y,z)=˜B(ρ,θ,Z)\hbox{${\vec B}(x,y,z) = \tilde{{\vec B}}(\rho,\theta,Z)$} with ρ=˜ρ(x,y,z,ϕ)\hbox{$\rho=\tilde{\rho}(x,y,z,\varphi)$}, θ=˜θ(x,y,z,ϕ)\hbox{$\theta=\tilde{\theta}(x,y,z,\varphi)$}, and Z=˜Z(x,y,z,ϕ),\hbox{$Z=\tilde{Z}(x,y,z,\varphi),$} where we stress that coordinates in the intrinsic cylindrical system of a point determined in the global system by [ x,y,z ] also depend on the cylinder’s position (ϕ). The intrinsic system of the cylinder has its origin at T, its Cartesian 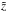˜z\hbox{$\tilde{z}$} axis is along the cylinder axis (the dashed straight line in Fig. 1), its 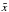˜x\hbox{$\tilde{x}$} axis is parallel to the z axis, and the 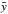˜y\hbox{$\tilde{y}$} axis crosses origins O and T, so it holds 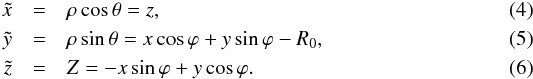˜x=ρcosθ=z,˜y=ρsinθ=xcosϕ+ysinϕ−R0,˜z=Z=−xsinϕ+ycosϕ.\begin{eqnarray} \label{tx} \tilde{x} &=& \rho \cos \theta = z , \\ \label{ty} \tilde{y} &=& \rho \sin \theta = x \cos \varphi + y \sin \varphi - R_0 , \\ \label{tz} \tilde{z} &=& Z = -x \sin \varphi + y \cos \varphi . 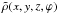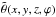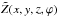\end{eqnarray}These relations (transformation) define the functions ˜ρ(x,y,z,ϕ)\hbox{$\tilde{\rho}(x,y,z,\varphi)$}, ˜θ(x,y,z,ϕ)\hbox{$\tilde{\theta}(x,y,z,\varphi)$}, and ˜Z(x,y,z,ϕ)\hbox{$\tilde{Z}(x,y,z,\varphi)$}, for example, 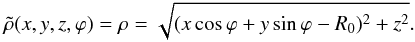˜ρ(x,y,z,ϕ)=ρ=(xcosϕ+ysinϕ−R0)2+z2.\begin{eqnarray} \label{rho} \tilde{\rho}(x,y,z,\varphi) = \rho = \sqrt{(x \cos \varphi+y \sin \varphi-R_0)^2+z^2} . \end{eqnarray}(7)We consider a second cylinder that is tangent at another point T′ of the circular generating-toroid’s axis; its azimuthal angle is ϕ′ ≠ ϕ. This cylinder determines another force-free field in the same way as the first one. 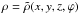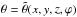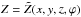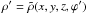We define a superposition of these fields as B(x,y,z)=12[˜B(ρ,θ,Z)+˜B(ρ′,θ′,Z′)],\hbox{${\vec B}(x,y,z) = \frac{1}{2} [\tilde{{\vec B}}(\rho,\theta,Z)+ \tilde{{\vec B}}(\rho^\prime,\theta^\prime,Z^\prime)],$} where ρ=˜ρ(x,y,z,ϕ)\hbox{$\rho=\tilde{\rho}(x,y,z,\varphi)$}, θ=˜θ(x,y,z,ϕ)\hbox{$\theta=\tilde{\theta}(x,y,z,\varphi)$}, Z=˜Z(x,y,z,ϕ)\hbox{$Z=\tilde{Z}(x,y,z,\varphi)$}, ρ′=˜ρ(x,y,z,ϕ′)\hbox{$\rho^\prime=\tilde{\rho}(x,y,z,\varphi^\prime)$}, θ′=˜θ(x,y,z,ϕ′)\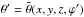hbox{$\theta^\prime=\tilde{\theta}(x,y,z,\varphi^\prime)$}, and Z′=˜Z(x,y,z,ϕ′)\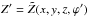hbox{$Z^\prime=\tilde{Z}(x,y,z,\varphi^\prime)$}. The field B is also force-free with the same constant α. This procedure can continue with other tangent cylinders. In a limit, a new force-free field results from contributions of tangent cylinders at every point of the circular generating-toroid’s axis; the summation is replaced by an integration, and we have (Romashets & Vandas 2009) B(x,y,z)=12π∫02π˜B[˜ρ(x,y,z,ϕ),˜θ(x,y,z,ϕ),˜Z(x,y,z,ϕ)] dϕ.\begin{eqnarray} \label{B} {\vec B}(x,y,z) = \frac{1}{2 \pi} \int\limits_0^{2 \pi} \tilde{{\vec B}}[\tilde{\rho}(x,y,z,\varphi),\tilde{\theta}(x,y,z,\varphi), \tilde{Z}(x,y,z,\varphi)] \, \mathrm{d}\varphi . \end{eqnarray}(8)Owing to its construction, the field is a linear force-free field with constant α and it is axially symmetric.

Romashets & Vandas (2009) expressed the components of the field of Eq. (8) in cylindrical coordinates, evaluated integrals, and obtained formulae with multiple sums. However, the sums slowly converge, and it was found that integrals are much more convenient for numerical calculations. Therefore we stopped our field derivation at Eq. (8), and all following calculations are numerical.

thumbnail Fig. 2

Magnetic field magnitude distribution on a cross section of a toroidal flux rope. The generating toroid has the aspect ratio 2.5, and the Lundquist field (1)–(3) was used to construct the field. The field is equivalent to the generalized Lundquist field (9)–(11) with the following free parameters: M = 0, d0 = 1. The closed lines are cross sections of magnetic surfaces that have (non-ideal) toroidal shapes and on which helical magnetic field lines lie. Bmax is the field maximum inside the flux rope.

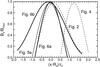thumbnail Fig. 3

Axial components of the flux ropes. The profiles are labeled by the corresponding figures, and they are drawn by the dashed lines for the cases from Figs. 2 and 4, by the thin solid line for the case from Fig. 5a, and by the thick lines for cases from Figs. 6a and b.

An example of a field configuration is shown in Fig. 2, and other examples are shown in Figs. 2 by Romashets & Vandas (2009, 2013). The constant α in the Lundquist solution (1)–(3) was set to α = a0/r0, where a0 is the first root of the Bessel function J0 (a0 ≈ 2.4048). This is a common assignment and ensures that the axial component of the field (BZ) reaches zero at the cylinder’s boundary (ρ = r0). The boundaries of the toroidal flux ropes shown in the cited figures have a small axial field component, but it is not zero because we require the flux-rope cross sections to be convex. This is often not the case for magnetic surfaces on which the axial field is zero. Figure 3 displays the profile of the axial field, which is the By component, for the cross section plotted in Fig. 2. The axial field at the boundary is lower than 15% of the maximum field magnitude. In any case, the mentioned flux ropes have only one axial polarity. Their cross-section shapes depend on the aspect ratio of the generating toroid (R0/r0). Its value may be arbitrary, even lower than 1 (see Romashets & Vandas 2013). However, the shapes of the flux ropes are often irregular or even peculiar.

In order to have them simpler (e.g., circular or elliptical), we replaced the Lundquist solution (1)–(3) by a more general form of cylindrical constant-alpha force-free field (Romashets 1992; Romashets & Vandas 2005) ˜Bρ=B0∑m=0MmJm(αρ)αρ(−dmsinmθ+emcosmθ),˜Bθ=B02∑m=0M[Jm+1(αρ)−Jm−1(αρ)](dmcosmθ+emsinmθ),˜BZ=B0∑m=0MJm(αρ)(dmcosmθ+emsinmθ).\begin{eqnarray} \label{BrR}\tilde{B}_\rho & = & B_0 \sum\limits_{m=0}^M m \frac{\mathrm{J}_m(\alpha \rho)}{\alpha \rho} (-d_m \sin m \theta + e_m \cos m \theta) , \\ \label{BtR}\tilde{B}_\theta & = & \frac{B_0}{2} \sum\limits_{m=0}^M \left[ \mathrm{J}_{m+1}(\alpha \rho)-\mathrm{J}_{m-1}(\alpha \rho)\right] (d_m \cos m \theta + e_m \sin m \theta) , \nonumber \\ && \\ \label{BZR}\tilde{B}_Z & = & B_0 \sum\limits_{m=0}^M \mathrm{J}_m(\alpha \rho) (d_m \cos m \theta + e_m \sin m \theta) . \end{eqnarray}Coefficients dm and em and the value of M are free parameters. The coefficient e0 is not defined since the corresponding terms always vanish. Each harmonic (determined by m) is force-free independently. Similarly to the Lundquist field (1)–(3), the field (9)–(11) does not depend on Z, it reduces to the Lundquist field when M = 0, but for M> 0 the field is not axially symmetric (depends on θ).

thumbnail Fig. 4

Magnetic field magnitude distribution on a cross section of a toroidal flux rope. The generating toroid has the aspect ratio 2.5, and the generalization of the Lundquist field (9)–(11) was used for the field construction. Its free parameters were M = 1, d0 = 0, d1 = 0, e1 = 1. The closed lines are cross sections of magnetic surfaces that have (non-ideal) toroidal shapes and on which helical magnetic field lines lie.

The above described procedure makes the field toroidal and axially symmetric through Eq. (8), but for an arbitrarily chosen set of free parameters we again mostly obtain an irregular/peculiar profile of a flux rope. Figure 4 shows an example of a toroidal flux rope when only the coefficient e1 is non-zero, and Fig. 3 contains the profile of its axial component.

3. Toroidal flux ropes of simple shapes

We consider a simple toroidal shape, for instance, with a circular cross section. The normal component of the field to the flux rope boundary must vanish. Using this condition, we can write equations B·n = 0 for many points on the boundary (for a given M). The B field is given by Eq. (8), and n is the normal vector for a point at the boundary. The equations represent an overdetermined system of equations for a set of unknown coefficients dm and em. The system can be solved, for instance, by the singular value decomposition (SVD) method (Press et al. 2002) to obtain an approximate linear force-free solution for a desired shape.

Figure 5a shows an example, a linear force-free field in an ideal toroid. It was achieved by the above described method. The resulting field has a nearly circular cross section. Comparison with the exact constant-alpha force-free field solution in an ideal toroid (Tsuji 1991; Vandas & Romashets 2015) shows that the fields are practically identical. For instance, the difference between the magnetic field magnitude plotted in Fig. 5a and the exact solution does not exceed 2%. The axial field is very small at the boundary in this case, in accord with the exact solution, which has zero value there. The profile of the axial field is shown in Fig. 3, it is symmetric and running from −1 to 1 along the horizontal axis. It is interesting to note that only five coefficients are needed to describe the solution (we set M = 5 and the SVD method yielded odd dm and even em coefficients close to zero, probably due to symmetry). The magnetic field magnitude distribution and magnetic surfaces in the generating cylinder and outside it are shown in Fig. 5b. The magnetic-field maximum in the toroidal flux rope (Fig. 5a) is shifted toward the toroid hole from the center. It is reflected by the field-maximum shift along the 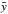˜y\hbox{$\tilde{y}$} axis in the negative direction in Fig. 5b. For aspect ratios lower than 2.5, the procedure yields flux ropes, the cross sections of which deviate more and more from a circle.

thumbnail Fig. 5

a) Magnetic field magnitude distribution inside a toroidal flux rope with practically circular cross section. The closed lines are cross sections of magnetic surfaces. The values of free parameters are M = 5, d0 = 1, d1 = 0., e1 = 1.698, d2 = 2.099, e2 = 0., d3 = 0., e3 = 0.554, d4 = 1.699, e4 = 0., d5 = 0., and e5 = −0.841. b) Magnetic field magnitude distribution and magnetic surfaces of the field defined by the generating cylinder, which was used for the construction of the flux rope shown in panel a), i.e., the field (9)–(11). In contrast to panel a), they are shown in the whole field of view because the magnetic field from all space contributes to the solution displayed in panel a). The cross section of the generating cylinder is plotted by the dashed circle, and the tilde coordinates are the local coordinates defined in Fig. 1. The magnetic-field magnitude scale is the same, but the values of Bmax are different and correspond to the maxima in the displayed fields in panels a) and b). The thick lines indicate magnetic surfaces on which the axial magnetic field is zero.

This method is able to generate toroidal flux ropes with another cross sections. Figure 6 displays shapes very close to ellipses, a prolate shape in Fig. 6a and an oblate one in Fig. 6b. Only ten coefficients were used to define these fields (it was M = 10, and half of the coefficients were close to zero, as in the previous case). The axial field does not vanish at the boundary shown, but it is small, as is shown in Fig. 3.

There are limitations of our procedure. One has been mentioned: it was not commonly possible to obtain the desired shape of the flux rope for low aspect ratios. But even if the desired shape is obtained, the flux rope may be multipolar, that is, with the axial field reversed inside. For instance, the generating toroid of the flux rope shown in Fig. 6a has an oblateness 2:3, but the flux rope has a dual polarity. Therefore we limited it to the inner unipolar part, displayed in Fig. 6a, which has a smaller oblateness and a different aspect ratio (if defined as R0/a) from 5. If the generating toroid has an oblateness or prolateness larger than about two, unipolar flux-rope cross sections deviate from desired elliptic shapes (they more resemble a rectangular shape).

thumbnail Fig. 6

Magnetic field magnitude distribution inside toroidal flux ropes with practically elliptic cross sections. The closed lines are cross sections of magnetic surfaces. The values of free parameters are a) M = 10, d0 = 1, e1 = 1.096, d2 = 1.754, e3 = 0.918, d4 = 1.125, e5 = 0.999, d6 = 0.730, e7 = 1.248, d8 = 1.111, e9 = 0.656, and d10 = 1.601; b)M = 10, d0 = 1, e1 = −0.0641, d2 = 0.0972, e3 = 1.057, d4 = 0.355, e5 = 0.0442, d6 = 0.1477, e7 = 0.541, d8 = −0.01687, e9 = −0.769, and d10 = 1.202. The other coefficients are (numerical) zero.

3.1. Calculating the helicity

It is relatively easy to (numerically) calculate the helicities of these flux ropes. Introducing toroidally curved cylindrical coordinates r, φ, and ψ in our global system, 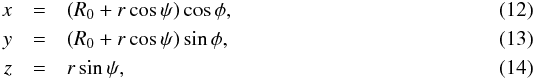x=(R0+rcosψ)cosφ,y=(R0+rcosψ)sinφ,z=rsinψ,\begin{eqnarray} x & = & (R_0 + r \cos \psi) \cos \phi , \\ y & = & (R_0 + r \cos \psi) \sin \phi , \\ z & = & r \sin \psi , \end{eqnarray}the helicity for toroidal flux ropes with an axially symmetric linear force-free field (Vandas & Romashets 2015) is 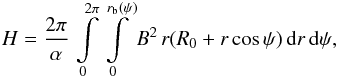H=2πα ∫02π∫0rb(ψ)B2 r(R0+rcosψ) dr dψ,\begin{eqnarray} \label{H} H = \frac{2 \pi}{\alpha} \, \int\limits_0^{2 \pi} \int\limits_0^{r_{\rm b}(\psi)} B^2 \, r (R_0 + r \cos \psi) \, \mathrm{d}r \, \mathrm{d}\psi , \end{eqnarray}(15)where rb(ψ) determines the boundary; r and ψ are polar coordinates in a cross-section plane (like in Figs. 5 and 6, where we should have rb = r0 for the case of Fig. 5a and 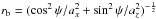rb=(cos2ψ/ax2+sin2ψ/az2)−12\hbox{$r_{\rm b}=(\cos^2 \psi/a_x^2+\sin^2 \psi/a_z^2)^{-\frac{1}{2}}$} for Fig. 6, where ax and az are semi-axes of the boundary ellipses; for a more general boundary, rb would be defined numerically from the results).

To compare different flux ropes, Vandas & Romashets (2015) used the unitless quantity h derived from the helicity H by 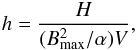h=H(Bmax2/α)V,\begin{eqnarray} \label{h} h = \frac{H}{(B_\mathrm{max}^2/\alpha) V} , \end{eqnarray}(16)where V is the volume of the toroidal flux rope and Bmax is the maximum field magnitude inside it. We calculated this quantity for the three flux ropes shown in Figs. 5a and 6. The h for the Miller & Turner solution can be calculated analytically (Vandas & Romashets 2015), and we checked how this formula is applicable for our flux ropes. The flux rope from Fig. 5a has a circular cross section, so the formula can be applied directly. The value differs by 2.5% from the helicity calculated numerically for this flux rope. The aspect ratio of this rope is quite low, and the Miller & Turner solution is applicable to high aspect ratios (see Fig. 8 in Vandas & Romashets 2015). When the accurate solution (Tsuji 1991; Vandas & Romashets 2015) is used to calculate the helicity, the difference is below 1%. The elliptic flux ropes displayed in Fig. 6 have higher aspect ratios, therefore the Miller & Turner solution is more relevant, but it assumes a circular cross section, so it is not obvious which value is to be used for the minor radius. We tested the geometric mean of the semi-axes, 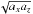axaz\hbox{$\sqrt{a_x a_z}$}, to substitute the radius because the areas of the cross sections (circle and the original ellipse) are the same. The difference in h was below 2%.

4. Conclusions

We presented a procedure for constructing toroidal linear force-free magnetic fields with axial symmetry. The fields are the superposition of cylindrical linear force-free magnetic fields, the generating cylinders of which are tangent to the generating toroid; in other words, if the generating toroid has R0 and r0 as the major and minor radii, respectively, then the generating

cylinders’ radii are r0, and their axes are tangent to the circular axis of the generating toroid with the radius R0. The toroidal field depends on a set of free coefficients. The selection of the coefficients determines the shape (cross section) of the toroidal flux rope and the magnetic field magnitude distribution inside it. This enables controlling the flux rope shape to some extent, for example, to construct toroidal flux ropes with circular or elliptic cross sections. We tested whether the simple analytic formula for the helicity calculation in toroidal flux ropes, which assumes an ideal toroid, is applicable to flux ropes with elliptic cross sections. Numerical comparison suggests that it is usable when the minor radius is set to the geometric mean of the semi-axes of the elliptic cross section. This suggestion is a hypothesis that needs to be verified on more elliptic flux ropes, which we plan to compute in future papers. This model can be applied to interpret magnetic field measurements in interplanetary magnetic clouds, which have a complicated structure, and their different curved parts are treated as parts of toroids with different small and large radii. A grid of models of toroidal flux ropes can be created (identified by aspect ratios and precomputed coefficients) to be used in standard least-squares fitting procedures (e.g., Lepping et al. 2006; Marubashi & Lepping 2007; Vandas et al. 2015) to match magnetic cloud observations with a model.

Acknowledgments

This work was supported by project 14-19376S from GA ČR and by the AV ČR grant RVO:67985815.

References

  1. Burlaga, L. F. 1988, J. Geophys. Res., 93, 7217 [NASA ADS] [CrossRef] [Google Scholar]
  2. Hidalgo, M. A. 2014, ApJ, 784, 67 [NASA ADS] [CrossRef] [Google Scholar]
  3. Ivanov, K. G., Harshiladze, A. F., Eroshenko, E. G., & Styazhkin, V. A. 1989, Sol. Phys., 120, 407 [NASA ADS] [CrossRef] [Google Scholar]
  4. Janvier, M., Demoulin, P., & Dasso, S. 2014, Sol. Phys., 289, 2633 [NASA ADS] [CrossRef] [Google Scholar]
  5. Lepping, R. P., Jones, J. A., & Burlaga, L. F. 1990, J. Geophys. Res., 95, 11957 [NASA ADS] [CrossRef] [Google Scholar]
  6. Lepping, R. P., Berdichevsky, D. B., Wu, C.-C., et al. 2006, Ann. Geophys., 24, 215 [NASA ADS] [CrossRef] [Google Scholar]
  7. Lundquist, S. 1950, Ark. Fys., 2, 361 [Google Scholar]
  8. Marubashi, K. 1997, in Coronal Mass Ejections, Geophys. Monogr. Ser., eds. N. Crooker, J. Joselyn, & J. Feyman (Washington, D. C.: AGU), 99, 147 [Google Scholar]
  9. Marubashi, K., & Lepping, R. P. 2007, Ann. Geophys., 25, 2453 [NASA ADS] [CrossRef] [Google Scholar]
  10. Miller, G., & Turner, L. 1981, Phys. Fluids, 24, 363 [NASA ADS] [CrossRef] [Google Scholar]
  11. Nindos, A., Patsourakos, S., Vourlidas, A., & Tagikas, C. 2015, ApJ, 808, 117 [NASA ADS] [CrossRef] [Google Scholar]
  12. Press, V. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2002, Numerical Recipes in C, The Art of Scientific Computing, 2nd edn. (New York: Cambridge University Press) [Google Scholar]
  13. Romashets, E. P. 1992, Geomag. Aeronom., 32, 29 [NASA ADS] [Google Scholar]
  14. Romashets, E. P., & Vandas, M. 2003, Geophys. Res. Lett., 30, 2065 [Google Scholar]
  15. Romashets, E. P., & Vandas, M. 2005, Adv. Space Res., 35, 2167 [Google Scholar]
  16. Romashets, E. P., & Vandas, M. 2009, A&A, 499, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Romashets, E., & Vandas, M. 2013, Sol. Phys., 284, 235 [NASA ADS] [CrossRef] [Google Scholar]
  18. Shimazu, H., & Marubashi, K. 2000, J. Geophys. Res., 105, 2365 [NASA ADS] [CrossRef] [Google Scholar]
  19. Tsuji, Y. 1991, Phys. Fluids B, 3, 3379 [NASA ADS] [CrossRef] [Google Scholar]
  20. Vandas, M., & Romashets, E. 2015, A&A, 580, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Vandas, M., Romashets, E., & Geranios, A. 2015, A&A, 583, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Figures

thumbnail Fig. 1

Construction of a toroidal solution. The global system connected with the toroid has the origin O and axes x, y, and z. The local system of a cylinder has the origin T and axes ˜x\hbox{$\tilde{x}$}, ˜y\hbox{$\tilde{y}$}, and ˜z\hbox{$\tilde{z}$}.
In the text
thumbnail Fig. 2

Magnetic field magnitude distribution on a cross section of a toroidal flux rope. The generating toroid has the aspect ratio 2.5, and the Lundquist field (1)–(3) was used to construct the field. The field is equivalent to the generalized Lundquist field (9)–(11) with the following free parameters: M = 0, d0 = 1. The closed lines are cross sections of magnetic surfaces that have (non-ideal) toroidal shapes and on which helical magnetic field lines lie. Bmax is the field maximum inside the flux rope.

In the text
thumbnail Fig. 3

Axial components of the flux ropes. The profiles are labeled by the corresponding figures, and they are drawn by the dashed lines for the cases from Figs. 2 and 4, by the thin solid line for the case from Fig. 5a, and by the thick lines for cases from Figs. 6a and b.

In the text
thumbnail Fig. 4

Magnetic field magnitude distribution on a cross section of a toroidal flux rope. The generating toroid has the aspect ratio 2.5, and the generalization of the Lundquist field (9)–(11) was used for the field construction. Its free parameters were M = 1, d0 = 0, d1 = 0, e1 = 1. The closed lines are cross sections of magnetic surfaces that have (non-ideal) toroidal shapes and on which helical magnetic field lines lie.

In the text
thumbnail Fig. 5

a) Magnetic field magnitude distribution inside a toroidal flux rope with practically circular cross section. The closed lines are cross sections of magnetic surfaces. The values of free parameters are M = 5, d0 = 1, d1 = 0., e1 = 1.698, d2 = 2.099, e2 = 0., d3 = 0., e3 = 0.554, d4 = 1.699, e4 = 0., d5 = 0., and e5 = −0.841. b) Magnetic field magnitude distribution and magnetic surfaces of the field defined by the generating cylinder, which was used for the construction of the flux rope shown in panel a), i.e., the field (9)–(11). In contrast to panel a), they are shown in the whole field of view because the magnetic field from all space contributes to the solution displayed in panel a). The cross section of the generating cylinder is plotted by the dashed circle, and the tilde coordinates are the local coordinates defined in Fig. 1. The magnetic-field magnitude scale is the same, but the values of Bmax are different and correspond to the maxima in the displayed fields in panels a) and b). The thick lines indicate magnetic surfaces on which the axial magnetic field is zero.
In the text
thumbnail Fig. 6

Magnetic field magnitude distribution inside toroidal flux ropes with practically elliptic cross sections. The closed lines are cross sections of magnetic surfaces. The values of free parameters are a) M = 10, d0 = 1, e1 = 1.096, d2 = 1.754, e3 = 0.918, d4 = 1.125, e5 = 0.999, d6 = 0.730, e7 = 1.248, d8 = 1.111, e9 = 0.656, and d10 = 1.601; b)M = 10, d0 = 1, e1 = −0.0641, d2 = 0.0972, e3 = 1.057, d4 = 0.355, e5 = 0.0442, d6 = 0.1477, e7 = 0.541, d8 = −0.01687, e9 = −0.769, and d10 = 1.202. The other coefficients are (numerical) zero.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.