| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 7 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201527106 | |
| Published online | 09 December 2015 | |
Accurate multiconfiguration calculations of energy levels, lifetimes, and transition rates for the silicon isoelectronic sequence
Ti IX – Ge XIX, Sr XXV, Zr XXVII, Mo XXIX⋆
1 Group for Materials Science and Applied Mathematics, Malmö
University, Sweden
e-mail:
per.jonsson@mah.se
2
Institute of Theoretical Physics and Astronomy, Vilnius
University, A. Goštauto
12, 01108
Vilnius,
Lithuania
3
Chimie Quantique et Photophysique, Université Libre de
Bruxelles, 1050
Brussels,
Belgium
4
BioISI – Biosystems & Integrative Sciences Institute,
Faculdade de Ciências da Universidade de Lisboa, 1749-016
Lisbon,
Portugal
5
Division of Mathematical Physics, Department of Physics, Lund
University, 22100
Lund,
Sweden
6
National Institute of Standards and Technology,
Gaithersburg, MD
20899,
USA
7
Oxford University, Mathematical Institute,
Oxford
OX2 6GG,
UK
8
Cambridge University, Department of Applied Mathematics and
Theoretical Physics, Centre for
Mathematical Sciences, Cambridge
CB3 0WA,
UK
Received: 3 August 2015
Accepted: 11 September 2015
Multiconfiguration Dirac-Hartree-Fock (MCDHF) calculations and relativistic configuration interaction (RCI) calculations are performed for states of the 3s23p2, 3s3p3 and 3s23p3d configurations in the Si-like ions Ti IX – Ge XIX, Sr XXV, Zr XXVII and Mo XXIX. Valence and core-valence electron correlation effects are accounted for through large configuration state function expansions. Calculated energy levels are compared with data from other calculations and with experimental data from the reference databases. Lifetime and transition rates along with uncertainty estimations are given for all ions. Energies from the calculations are in excellent agreement with observations and computed wavelength are almost of spectroscopic accuracy, aiding line identification in spectra.
Key words: atomic data / atomic processes
Full Tables 2, 3, and 5 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/585/A26
© ESO, 2015
1. Introduction
The emission spectrum of Si-like Fe (Fe XIII) in the extreme ultraviolet (EUV) range provides important lines for electron density diagnostics of the solar and stellar coronal plasma (Keenan et al. 2007). These lines have been observed using for example the EUV Imaging Spectrometer (EIS) on board the Hinode satellite, the Coronal Diagnostic Spectrometer (CDS) on board the SOHO satellite and by the Solar EUV Rocket Telescope and Spectrograph (SERTS), see for example Watanabe et al. (2009). Much work has been devoted to benchmark and validate atomic data for Fe XIII against high-resolution spectroscopic observations of the solar corona (Del Zanna 2011) and against well-defined laboratory plasma (Yamamoto et al. 2008; Nakamura et al. 2011). Also, lines from Ni XV can be used for electron density diagnostics in high-temperature (3 MK) plasmas, such as those of solar active region cores, as discussed in Del Zanna (2013). Del Zanna et al. (2014) provided a complete set of rates and a list of the strongest lines that are observable in astrophysical plasmas, and revised previous identifications.
Excitation energies in cm-1 for Fe XIII as a function of the increasing size of the CSF expansion.
The diagnostic value of the EUV lines in Si-like ions relies on accurate atomic data. A large number of theoretical studies have been conducted for the sequence as well as for individual ions and here we can only discuss a few of the more recent studies. Froese Fischer et al. (2006) reported on energies, lifetimes, and transition rates for low-lying states in ions up to Fe XIII from multiconfiguration Hartree-Fock calculations with Breit-Pauli relativistic corrections (MCHF-BP) as part of the large compilation of atomic data for ions in the sodium-to argon-like sequences. For the Si-like ions, only valence electron correlation was considered. Kohstall et al. (1998) performed fully relativistic multiconfiguration Dirac-Hartree-Fock (MCDHF) calculations for seven ions in the sequence giving energies, lifetimes, and transition rates. Again, only valence correlation was accounted for. Brage and coworkers (Huang et al. 2005; Andersson & Brage 2007) used both the MCHF-BP and MCDHF methods to study energies and transition rates along the sequence. The effects of valence- and core-valence electron correlation were analyzed with the conclusion that core-valence correlation is important at the low-Z end, but that the effects decrease with Z. For higher Z it is important to use a fully relativistic approach. As part of the comparison of theoretical emission-line-intensity ratios with high-resolution spectra from the SERTS, Keenan et al. (2007) provided MCDHF energy and transition data involving 301 levels in Fe XIII, originally from a work by Aggarwal & Keenan (2004). Storey & Zeippen (2010) did R-matrix calculations of rate coefficients for electron collisional excitation and oscillator strengths for Fe XIII. Turning to Ni XV, Landi & Bhatia (2012) did FAC calculations of electron impact collision strengths, energy levels, oscillator strengths, and transition rates, while Gupta & Msezane (2012) used the CIV3 code to compute excitation energies from the ground state as well as oscillator strengths and radiative transition rates. Much theoretical data has been provided by Ishikawa and Vilkas using the relativistic multireference many-body perturbation (MR-MP) method. In a number of publications energies and transition probabilities were presented for various ions in the sequence (Ishikawa & Vilkas 2001, 2002; Vilkas & Ishikawa 2003a,b, 2004a,b). The excitation energies were computed with spectroscopic accuracy and a number of experimental misidentifications were detected. Also, the calculations allowed new lines to be identified; see, for example, Träbert et al. (2011). On the experimental side, Träbert and coworkers have reported lifetimes as well as spectra for line identification from accelerator based work (Träbert et al. 1985, 1988, 1989, 2003; Träbert 1986, 1998, 2005).
Calculated excitation energies can be directly validated against observations and conversely, once a computational method and strategy was shown to be accurate, computed excitation energies aid further line identifications. For transition parameters, such as oscillator strengths and transition rates, the situation is very different. There are no experimental data for individual transitions; only lifetimes for a few states are available. In addition, lifetime measurements are in many cases associated with large uncertainties resulting in sizable error bars; see, for example, Träbert et al. (1989). Also transition parameters from calculations are problematic in that they often scatter substantially. One example is provided in Watanabe et al. (2009). In Table 1 of this paper, rates for diagnostically important transitions in Fe XIII from different calculations and tabulations are compared. For some transitions the rates from the quoted studies differ by a factor of 3.
Calculated transition rates can be internally validated by looking at convergence of the rates as the calculations are systematically enlarged (Froese Fischer & Brage 1993). The agreement between transition parameters calculated in length and velocity form can also be used as an indication of the uncertainties (Ekman et al. 2014). However, very few studies report convergence trends to facilitate this kind of an internal validation and, thus, it is difficult to say anything about the accuracy or to discriminate between different calculations. Given this background, it is important to provide accurate and consistent atomic data for the Si-like sequence, which can be used for line identifications and astrophysical diagnostics as well as for benchmarking. In this work, relativistic multiconfiguration methods are used to obtain excitation energies accurate to within 0.01% to 0.03% for levels in the silicon isoelectronic sequence (Z = 22–32, 38, 40, 42). Lifetimes for all levels are computed in length and velocity form and compared with available values from beam-foil and storage ring experiments. Transition rates and oscillator strengths, along with theoretical uncertainty estimates, are given for all transitions with rates A greater than 104 s-1. Transition data are also given for transitions with rates A greater than a fraction 10-4 of the total A value of the upper level. The latter condition ensures that astrophysically important transitions in the ground 3P triplet are not left out.
2. Relativistic multiconfiguration calculations
The calculations were performed using the fully relativistic multiconfiguration Dirac-Hartree-Fock (MCDHF) method in jj-coupling (Grant 2007).
2.1. Multiconfiguration Dirac-Hartree-Fock
According to quantum mechanics an electronic state of an N-electron system is determined by a wave function Ψ, which is a solution to the wave equation 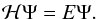 (1)Here ℋ is the Hamiltonian operator and E the total energy of the system. The common starting point for fully relativistic calculations is the Dirac-Coulomb Hamiltonian
(1)Here ℋ is the Hamiltonian operator and E the total energy of the system. The common starting point for fully relativistic calculations is the Dirac-Coulomb Hamiltonian 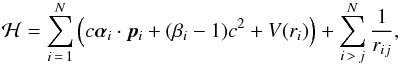 (2)where V is the potential from a two-parameter Fermi nuclear charge distribution, α and β are the 4 × 4 Dirac matrices, and c is the speed of light in atomic units. In the multiconfiguration Dirac-Hartree-Fock method, the wave function Ψ(γPJM) for a state labeled γPJM, where J and M are the angular quantum numbers and P is the parity, is expanded in antisymmetrized and symmetry-adapted configuration state functions (CSFs), yielding
(2)where V is the potential from a two-parameter Fermi nuclear charge distribution, α and β are the 4 × 4 Dirac matrices, and c is the speed of light in atomic units. In the multiconfiguration Dirac-Hartree-Fock method, the wave function Ψ(γPJM) for a state labeled γPJM, where J and M are the angular quantum numbers and P is the parity, is expanded in antisymmetrized and symmetry-adapted configuration state functions (CSFs), yielding 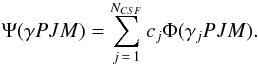 (3)The CSFs are built from products of one-electron Dirac orbitals, where the radial parts are numerically represented on a grid. The label γj denotes appropriate information about the configuration state function j, such as orbital occupancy and angular coupling scheme.
(3)The CSFs are built from products of one-electron Dirac orbitals, where the radial parts are numerically represented on a grid. The label γj denotes appropriate information about the configuration state function j, such as orbital occupancy and angular coupling scheme.
The wave functions were determined in the extended optimal level (EOL) scheme and the radial parts of the Dirac orbitals and the expansion coefficients of a number of targeted states were obtained iteratively from a set of equations, which results from applying the variational principle on a weighted energy functional of the states (Dyall et al. 1989). The transverse interaction in the low-frequency limit, or the Breit interaction (McKenzie et al. 1980), ![\begin{eqnarray} \label{eq:Breit} H_{\mbox{{\footnotesize Breit}}} = - \sum_{i\,<\,j}^N \frac{1}{2 r_{ij}} \Biggl[ \bm{\alpha}_{i} \cdot \bm{\alpha}_{j} + \frac{ (\bm{\alpha}_{i} \cdot {\bm{ r_{ij} }}) (\bm{\alpha}_{j} \cdot {\bm{ r_{ij} }}) } {r_{ij}^2} \Biggr], \end{eqnarray}](/articles/aa/full_html/2016/01/aa27106-15/aa27106-15-eq62.png) (4)and leading quantum electrodynamic (QED) effects (vacuum polarization and self-energy) were included in subsequent configuration interaction (RCI) calculations, where only the expansion coefficients cj of Eq. (3) were determined by diagonalizing the Hamiltonian matrix. All calculations were performed with an updated parallel version of the GRASP2K code (Jönsson et al. 2007, 2013). To calculate the spin-angular part of the matrix elements, the second quantization method in coupled tensorial form and quasispin technique (Gaigalas et al. 1997) was adopted.
(4)and leading quantum electrodynamic (QED) effects (vacuum polarization and self-energy) were included in subsequent configuration interaction (RCI) calculations, where only the expansion coefficients cj of Eq. (3) were determined by diagonalizing the Hamiltonian matrix. All calculations were performed with an updated parallel version of the GRASP2K code (Jönsson et al. 2007, 2013). To calculate the spin-angular part of the matrix elements, the second quantization method in coupled tensorial form and quasispin technique (Gaigalas et al. 1997) was adopted.
2.2. Transition parameters
Transition parameters, such as transition rates or weighted oscillator strengths, between two states γ′P′J′ and γPJ, were expressed in terms of the transition moment 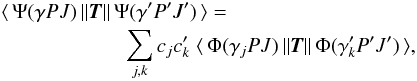 (5)where T is the transition operator (Grant 1974). In cases where the wave functions of the two states γ′P′J′ and γPJ were separately determined, the radial orbitals are not orthogonal. To deal with this complication, a transformation to a biorthonormal orbital basis was applied together with a counter transformation of the expansion coefficients cj and
(5)where T is the transition operator (Grant 1974). In cases where the wave functions of the two states γ′P′J′ and γPJ were separately determined, the radial orbitals are not orthogonal. To deal with this complication, a transformation to a biorthonormal orbital basis was applied together with a counter transformation of the expansion coefficients cj and 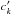 (Olsen et al. 1995) before the reduced matrix elements were evaluated using standard Racah algebra techniques.
(Olsen et al. 1995) before the reduced matrix elements were evaluated using standard Racah algebra techniques.
For electric multipole transitions, there are two forms of the transition operator, the length form and the velocity form (Grant 1974). The length form is usually preferred. The agreement between transition rates Al and Av computed in length and velocity forms can be used as an indicator of accuracy of the underlying wave functions (Froese Fischer 2009; Ekman et al. 2014). The quantity 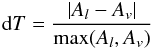 (6)was therefore used as an accuracy indicator. The values of dT do not represent an uncertainty estimate for each individual transition. Instead, they should be considered statistical indicators of uncertainties within given sets of transitions.
(6)was therefore used as an accuracy indicator. The values of dT do not represent an uncertainty estimate for each individual transition. Instead, they should be considered statistical indicators of uncertainties within given sets of transitions.
Comparison of calculated and observed excitation energies in cm-1.
2.3. Calculations
Calculations were performed for the five states belonging to the 3s23p2 even configuration and the 22 states belonging to the 3s3p3 and 3s23p3d odd configurations. The calculations were made by parity, meaning that the even and odd states were determined in separate calculations in the EOL scheme. As a starting point, two MCDHF calculations were performed in the EOL scheme for, respectively, the weighted average of the even and odd parity states. The calculation for the even states was based on the CSF expansion formed from the 3s23p2, 3s23d2, 3s3p23d, 3p23d2, 3p4 configurations that define the multireference (MR) for the even states and the calculation for the odd states was based on the CSF expansion obtained from the 3s3p3, 3s23p3d, 3s3p3d2, 3p33d, 3p3d3 configurations, which define the MR for the odd states. The two initial calculations account for the static electron correlation that results from the close degeneracy of the orbitals. To include dynamic electron correlation and improve on the computed energies and wave functions, the initial calculations were followed by separate MCDHF calculations for the odd and even parity states, where the CSF expansions were obtained from configurations generated by allowing single and double (SD) substitutions from the configurations in the MR to active orbital sets with principal quantum numbers up to n = 7 and with orbital angular momenta up to l = 6. Only CSFs that have non-zero matrix elements with the CSFs belonging to the configurations in the MR were retained. No substitutions were allowed from the 1s shell, which defines an inactive closed core. Furthermore, the substitutions were restricted in such a way that only one substitution was allowed from the 2s and 2p subshells of the configurations in the MR, and thus the generated expansions account for valence and core-valence correlation. The neglected core-core correlation is comparatively unimportant for both the energy separations and the transition probabilities. The MCDHF calculations were followed by RCI calculations, including the Breit-interaction and leading QED effects. The number of CSFs in the final even and odd state expansions were approximately 1 500 000 and 4 600 000, respectively, distributed over the different J symmetries.
Comparison of lifetimes in s.
2.4. Labeling of states
The wave functions were obtained as expansions over jj-coupled CSFs. To adhere to the LS label system in, for example, the tables of the National Institute of Standards and Technology (NIST; NIST Atomic Spectra Database 2013), a transformation from jj- to LS-coupling (Gaigalas et al. 2003; Jönsson et al. 2013) was made and in all tables of this paper the quantum states are labeled with the leading term of the LS-percentage composition. The labels obtained with this approach are, however, not unique; this is further discussed in the next section.
3. Results and discussion
3.1. Energies
In Table 1 we present the computed energies in Fe XIII for increasing active sets of orbitals labeled with the highest principal quantum number n of the orbitals in the set. For comparison, observed energies from Del Zanna (2011) are given as well. The relative difference between theory and observation is 1.51%, 0.48%, 0.20%, 0.09%, and 0.03% for calculations based on the expansion from the MR and the expansions from SD excitations to orbital sets with the highest principal quantum numbers n = 4–7. Thus, the calculations are comparatively well converged with respect to the increasing orbital set. It is obvious that the uncertainties would be further decreased by extending the orbital set. This, however, results in very large expansions. A general observation is that the excitation energy of the 3s3p S
S high-spin state from the 3s23p23P0 ground state is too low. This because that electron correlation effects missing from the calculation are smaller in states with high spin than in states with lower spin (Galvez et al. 2005; Froese Fischer et al. 1997), such as the ground state, and there is a slight imbalance in the amount of electron correlation that not has been accounted for in the two states. The excitation energies for the 3s23p3d 1F
high-spin state from the 3s23p23P0 ground state is too low. This because that electron correlation effects missing from the calculation are smaller in states with high spin than in states with lower spin (Galvez et al. 2005; Froese Fischer et al. 1997), such as the ground state, and there is a slight imbalance in the amount of electron correlation that not has been accounted for in the two states. The excitation energies for the 3s23p3d 1F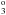 and 3s23p3d 1P
and 3s23p3d 1P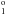 states, on the contrary, are too high, but they are lowered as the orbital set is extended.
states, on the contrary, are too high, but they are lowered as the orbital set is extended.
In Table 2, full table is available on-line, we present the computed energies based on the largest orbital set n = 7 together with energies from MR-MP calculations by Vilkas & Ishikawa (2004a), and with observed energies from the NIST database and, for some ions, from other sources as noted in the table. To make the comparison easier, the difference between the computed and observed energies are also given. The agreement between the computed transition energies and the observed energies is generally excellent. The present calculations and the MR-MP calculations by Vilkas & Ishikawa (2004a) give energies of spectroscopic accuracy, i.e., the computed transition wavelengths are so accurate they can be used to identify unknown lines in spectra without having to revert to semiempirical fitting procedures. In some ions, for which there are fewer measurements and observations, there are levels for which the agreement between theory and observation is less satisfactory with differences up to a few thousand cm-1. In these cases we have reason to believe that the observed levels are incorrect and wrongly assigned. For some ions the energies given in the NIST tables are based on experimental extrapolations. In many cases, it seems these extrapolations give good values in agreement with calculations. In some cases, the extrapolations give energies that differ substantially from calculated energies. A slight imbalance in energies for high- and low-spin states persists in the present calculations throughout the sequence. A method that better balances the MR, and thus the electron correlation, is thus desirable and would lead to even better energy predictions (Froese Fischer et al. 2013).
For Ti IX, V X and Cr XI state 19 and 21 have the same leading LS term label. A closer look at the LS-percentage composition indicates that it is sensible to label the two states as 3p3d 3P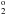 and 3p3d 1D
and 3p3d 1D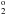 , respectively. These labels are the same as those used in the NIST tables. For Ni XV states 20 and 23 have the same leading LS term label. In this case, both states are an almost 50–50% mix of 3p3d 3P
, respectively. These labels are the same as those used in the NIST tables. For Ni XV states 20 and 23 have the same leading LS term label. In this case, both states are an almost 50–50% mix of 3p3d 3P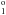 and 3p3d 3D
and 3p3d 3D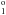 . Following the NIST tables, we give state 20 the label 3p3d 3P
. Following the NIST tables, we give state 20 the label 3p3d 3P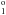 and state 23 the label 3p3d 3D
and state 23 the label 3p3d 3D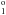 . It is interesting to see how the term mixing gives rise to a very irregular finestructure. Finally, there are several states in Sr XXV, Zr XXVII and Mo XXIX that have the same leading LS term labels. Since LS coupling is not a good approximation, it is difficult to resolve these ambiguities. For the states in Sr XXV, Zr XXVII and Mo XXIX we keep the leading LS term label, but add an extra index A,B to obtain unique labels.
. It is interesting to see how the term mixing gives rise to a very irregular finestructure. Finally, there are several states in Sr XXV, Zr XXVII and Mo XXIX that have the same leading LS term labels. Since LS coupling is not a good approximation, it is difficult to resolve these ambiguities. For the states in Sr XXV, Zr XXVII and Mo XXIX we keep the leading LS term label, but add an extra index A,B to obtain unique labels.
3.2. Lifetimes and transition rates
Comparison of lifetimes in ns for 3s23p3d 3F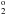 and 3s23p3d 3F
and 3s23p3d 3F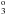 in length (l) and velocity (v) form from calculations and from experiment.
in length (l) and velocity (v) form from calculations and from experiment.
Transition data from the present calculation.
Transition rates for Fe XIII lines appearing in EIS at shorter wavelengths, adapted from Watanabe et al. (2009).
The lifetimes of the excited states were calculated from E1 transition rates in both the length and velocity forms as well as from M1 transition rates. The contributions to the lifetimes from E2 and higher multipoles are negligible. The average relative difference between the lifetimes in the length and velocity forms is less than 0.9%, which is highly satisfactory. In Table 3, full table is available on-line, we compare calculated lifetimes in length and velocity forms with lifetimes obtained with the MCHF Breit-Pauli method (Froese Fischer et al. 2006). The latter only accounts for valence electron correlation and this affects the accuracy of the lifetimes and transition rates mainly for low Z ions (Huang et al. 2005; Andersson & Brage 2007). In some sense, the difference between the present lifetimes and lifetimes by Froese Fischer et al. illustrates the effects of core-valence correlation. In Table 4 we compare lifetimes for the 3s23p3d 3F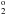 and 3s23p3d 3F
and 3s23p3d 3F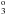 states with values obtained from MCDHF calculations by Kohstall et al. (1998) and MR-MP calculations by Vilkas & Ishikawa (2004a) and with experimental lifetime values from beam-foil measurements by Träbert (1998). The current lifetimes are shorter than those of the other calculations in better agreement with the experiment. In Table 5, full table is available on-line, transition energies, wavelengths, transition rates A, and weighted oscillator strengths gf are given along with the uncertainty indicator dT. For most of the stronger E1 transitions dT is below 1%. For the weaker transitions, as shown in the scatter plot of dT versus the line strength S for Fe XIII, the uncertainty dT is somewhat larger, from a few percent up to 10%. The weaker E1 transitions are often intercombination transitions, where the smallness of the rates comes from cancellations in the contributions to the transition matrix elements ⟨ Ψ(γPJ) ∥ T ∥ Ψ(γ′P′J′) ⟩. Intercombination transitions are known to be difficult to compute accurately. There are two transitions, 3s23p3d 1P
states with values obtained from MCDHF calculations by Kohstall et al. (1998) and MR-MP calculations by Vilkas & Ishikawa (2004a) and with experimental lifetime values from beam-foil measurements by Träbert (1998). The current lifetimes are shorter than those of the other calculations in better agreement with the experiment. In Table 5, full table is available on-line, transition energies, wavelengths, transition rates A, and weighted oscillator strengths gf are given along with the uncertainty indicator dT. For most of the stronger E1 transitions dT is below 1%. For the weaker transitions, as shown in the scatter plot of dT versus the line strength S for Fe XIII, the uncertainty dT is somewhat larger, from a few percent up to 10%. The weaker E1 transitions are often intercombination transitions, where the smallness of the rates comes from cancellations in the contributions to the transition matrix elements ⟨ Ψ(γPJ) ∥ T ∥ Ψ(γ′P′J′) ⟩. Intercombination transitions are known to be difficult to compute accurately. There are two transitions, 3s23p3d 1P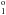 –3s23p
–3s23p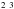 P2 and 3s23p3d 1P
P2 and 3s23p3d 1P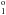 –3s23p21D2, for which dT is much larger. These two transitions are affected by strong cancellations. The two E2 transitions, 3s23p21S0–3s23p23P2 and 3s23p21S0–3s23p21D2, are associated with relatively large values of dT. For the other E2 transitions dT is at most a few percent. In Table 6, we present transition rates for important lines in Fe XIII appearing in EIS at shorter wavelengths. The rates from the different calculations scatter, but there is a reasonable agreement between the rates from the present calculations and the rates given by CHIANTI v7.1.4 (Landi et al. 2013). Table 6 is an adaptation of Table 1 in Watanabe et al. (2009).
–3s23p21D2, for which dT is much larger. These two transitions are affected by strong cancellations. The two E2 transitions, 3s23p21S0–3s23p23P2 and 3s23p21S0–3s23p21D2, are associated with relatively large values of dT. For the other E2 transitions dT is at most a few percent. In Table 6, we present transition rates for important lines in Fe XIII appearing in EIS at shorter wavelengths. The rates from the different calculations scatter, but there is a reasonable agreement between the rates from the present calculations and the rates given by CHIANTI v7.1.4 (Landi et al. 2013). Table 6 is an adaptation of Table 1 in Watanabe et al. (2009).
 |
Fig. 1 Scatterplot of dT against the line strength S for Fe XIII. For the strong transitions, dT is smaller than a few percent. For the weakest transitions, dT is between 5% and 10%. There are two transitions with large values of dT. |
3.3. Summary and conclusions
We performed MCDHF and subsequent RCI calculations for states of the 3s23p2, 3s3p3, and 3s23p3d configurations in the Si-like ions Ti IX – Ge XIX, Sr XXV, Zr XXVII, Mo XXIX. Excitation energies, lifetimes, and transition rates are presented. Energies from the RCI calculations are in excellent agreement with observations. The computed wavelengths are almost of spectroscopic accuracy, aiding line identification in spectra. Uncertainties of the transition rates are estimated by dT, as suggested by Ekman et al. (2014). For most of the stronger transitions, dT is below 1%. For the weaker transitions, the uncertainty dT is somewhat larger, from a few percent up to 10%. We thus argue that the transition rates are highly accurate and may serve as a benchmark for other calculations.
Acknowledgments
The authors are thankful for the high performance computing resources provided by the Information Technology Open Access Center of Vilnius University. This work has been partly supported (MG) by the BriX IAP Research Program P7/12 (Belgium). The authors thank Dr. Jörgen Ekman and Prof. Elmar Träbert for valuable comments.
References
- Aggarwal, K. M., & Keenan, F. P. 2004, A&A, 418, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andersson, M., & Brage, T. 2007, J. Phys. B: At. Mol. Opt. Phys., 40, 709 [CrossRef] [Google Scholar]
- Brown, C. M., Feldman, U., Seely, J. F., & Korendyke, C. M. 2008, ApJS, 176, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Dyall, K. G., Grant, I. P., Johnson, C. T., Parpia, F. A., & Plummer, E. P. 1989, Comput. Phys. Commun., 55, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Del Zanna, G. 2011, A&A, 533, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G. 2013, A&A, 558, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., Storey, P., & Manson, H. E. 2014, A&A, 567, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekman, J., Godefroid, M. R., & Hartman, H. 2014, Atoms, 2, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Froese Fischer, C. 2009, Phys. Scr. T, 134, 014019 [Google Scholar]
- Froese Fischer, C., & Brage, T. 1993, Phys. Scr. T, 47, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Froese Fischer, C., Brage, T., & Jönsson, P. 1997, Computational Atomic Structure – an MCHF approach (CRC Press) [Google Scholar]
- Froese Fischer, C., Tachiev, G., & Irimia, A. 2006, At. Data and Nucl. Data Tables, 92, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Froese Fischer, C., Verdebout, S., Godefroid, M., et al. 2013, Phys. Rev. A, 88, 062506 [NASA ADS] [CrossRef] [Google Scholar]
- Gaigalas, G., Rudzikas, Z., & Froese Fischer, C. 1997, J. Phys. B: At. Mol. Opt. Phys., 30, 3747 [Google Scholar]
- Gaigalas, G., Žalandauskas, T., & Rudzikas, Z. 2003, At. Data and Nucl. Data Tables, 84, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Galvez, F. J., Buendia, E., & Sarsa, A. 2005, J. Chem. Phys., 123, 034302 [NASA ADS] [CrossRef] [Google Scholar]
- Grant, I. P. 1974, J. Phys. B, 7, 1458 [Google Scholar]
- Grant, I. P. 2007, Relativistic Quantum Theory of Atoms and Molecules (New York: Springer) [Google Scholar]
- Gupta, G. P., & Msezane, A. Z. 2012, Phys. Scr., 86, 015303 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, M., Andersson, M., Brage, T., et al. 2005, J. Phys. B: At. Mol. Opt. Phys., 38, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Ishikawa, Y., & Vilkas, M. J. 2001, Phys. Rev. A, 63, 042509 [NASA ADS] [CrossRef] [Google Scholar]
- Ishikawa, Y., & Vilkas, M. J. 2002, Phys. Scr., 65, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Jönsson, P., He, X., Froese Fischer, C., & Grant, I. P. 2007, Comput. Phys. Commun., 177, 597 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jönsson, P., Gaigalas, G., Bieroń, J., Froese Fischer, C., & Grant, I. P. 2013, Comput. Phys. Commun., 184, 2197 [NASA ADS] [CrossRef] [Google Scholar]
- Keenan, F. P., Jess, D. B., Aggarwal, K. M., et al. 2007, MNRAS, 376, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Kohstall, C., Fritzsche, S., Fricke, B., & Sepp, W.-D. 1998, At. Data and Nucl. Data Tables, 70, 63 [Google Scholar]
- Landi, E., & Bhatia, A. K. 2012, At. Data and Nucl. Data Tables, 98, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., Young, P. R., Dere, K. P., Del Zanna, G., & Mason, H. E. 2013, ApJ, 763, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, N., Watanabe, E., Sakaue, H., et al. 2011, ApJ, 739, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Kramida, A., Ralchenko, Yu., Reader, J., & and NIST ASD Team 2012 NIST Atomic Spectra Database (ver. 5.0) [Online], available: http://physics.nist.gov/asd+ (2013, March 10), National Institute of Standards and Technology, Gaithersburg, MD [Google Scholar]
- McKenzie, B. J., Grant, I. P., & Norrington, P. H. 1980, Comput. Phys. Commun., 21, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Olsen, J., Godefroid, M., Jönsson, P., et al. 1995, Phys. Rev. E, 52, 4499 [NASA ADS] [CrossRef] [Google Scholar]
- Storey, P., & Zeippen, C. 2010, A&A, 511, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Träbert, E. 1986, Z. Phys. Atoms, Molecules and Clusters, 2, 213 [Google Scholar]
- Träbert, E. 1998, MNRAS, 297, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Träbert, E. 2005, Phys. Scr. T, 120, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Träbert, E., Blanke, J. H., Heckmann, P. H., Hellmann, H. M., & Hucke, R. 1985, Z. Phys. Atoms and Nuclei 321, 359 [Google Scholar]
- Träbert, E., Heckmann, P. H., Hutton, R., & Martinson, I. 1988, J. Opt. Soc. Am. B, 5, 2173 [Google Scholar]
- Träbert, E., Reistad, N., Martinson, I., & Hutton, R. 1989, Z. Phys. Atoms, Molecules and Clusters, 11, 207 [Google Scholar]
- Träbert, E., Calamai, A. G., Gwinner, G., et al. 2003, J. Phys. B, 36, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Träbert, E., Ishikawa, Y., Santana, J. A., & Del Zanna, G. 2011, Can. J. Phys., 89, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Vilkas, M. J., & Ishikawa, Y. 2003a, J. Phys. B: At. Mol. Opt. Phys., 36, 4641 [NASA ADS] [CrossRef] [Google Scholar]
- Vilkas, M. J., & Ishikawa, Y. 2003b, Phys. Rev. A, 68, 012503 [NASA ADS] [CrossRef] [Google Scholar]
- Vilkas, M. J., & Ishikawa, Y. 2004a, J. Phys. B: At. Mol. Opt. Phys., 37, 1803 [NASA ADS] [CrossRef] [Google Scholar]
- Vilkas, M. J., & Ishikawa, Y. 2004b, Phys. Rev. A, 69, 062503 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, T., Hara, H., Yamamoto, N., et al. 2009, ApJ, 692, 1294 [NASA ADS] [CrossRef] [Google Scholar]
- Yamamoto, N., Kato, T., Funaba, H., et al. 2008, ApJ, 689, 646 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Excitation energies in cm-1 for Fe XIII as a function of the increasing size of the CSF expansion.
Comparison of lifetimes in ns for 3s23p3d 3F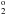 and 3s23p3d 3F
and 3s23p3d 3F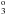 in length (l) and velocity (v) form from calculations and from experiment.
in length (l) and velocity (v) form from calculations and from experiment.
Transition rates for Fe XIII lines appearing in EIS at shorter wavelengths, adapted from Watanabe et al. (2009).
All Figures
 |
Fig. 1 Scatterplot of dT against the line strength S for Fe XIII. For the strong transitions, dT is smaller than a few percent. For the weakest transitions, dT is between 5% and 10%. There are two transitions with large values of dT. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


