| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A123 | |
| Number of page(s) | 6 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201526938 | |
| Published online | 07 January 2016 | |
Origin of the long-term modulation of radio emission of LS I +61°303
1 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: mmassi@mpifr-bonn.mpg.de
2 INAF – Osservatorio Astrofisico di Arcetri, L.go E. Fermi 5, Firenze, Italy
e-mail: torricel@arcetri.astro.it
Received: 10 July 2015
Accepted: 26 October 2015
Context. One of the most unusual aspects of the X-ray binary LS I +61°303 is that at each orbit (P1 = 26.4960 ± 0.0028 d) one radio outburst occurs whose amplitude is modulated with Plong, a long-term period of more than 4 yr. It is still not clear whether the compact object of the system or the companion Be star is responsible for the long-term modulation.
Aims. We study here the stability of Plong. Such a stability is expected if Plong is due to periodic (P2) Doppler boosting of periodic (P1) ejections from the accreting compact object of the system. On the contrary it is not expected if Plong is related to variations in the mass loss of the companion Be star.
Methods. We built a database of 36.8 yr of radio observations of LS I +61°303 covering more than 8 long-term cycles. We performed timing and correlation analysis. We also compared the results of the analyses with the theoretical predictions for a synchrotron emitting precessing (P2) jet periodically (P1) refilled with relativistic electrons.
Results. In addition to the two dominant features at P1 and P2, the timing analysis gives a feature at Plong = 1628 ± 48 days. The determined value of Plong agrees with the beat of the two dominant features, i.e. Pbeat = 1 / (ν1−ν2) = 1626 ± 68 d. Lomb-Scargle results of radio data and model data compare very well. The correlation coefficient of the radio data oscillates at multiples of Pbeat, as does the correlation coefficient of the model data.
Conclusions. Cycles in varying Be stars change in length and disappear after 2-3 cycles following the well-studied case of the binary system ζ Tau. On the contrary, in LS I +61°303 the long-term period is quite stable and repeats itself over the available 8 cycles. The long-term modulation in LS I +61°303 accurately reflects the beat of periodical Doppler boosting (induced by precession) with the periodicity of the ejecta. The peak of the long-term modulation occurs at the coincidence of the maximum number of ejected particles with the maximum Doppler boosting of their emission; this coincidence occurs every 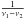 and creates the long-term modulation observed in LS I +61°303.
and creates the long-term modulation observed in LS I +61°303.
Key words: stars: emission-line, Be / gamma rays: stars / X-rays: individuals: LS I +61303 / radio continuum: stars / stars: jets / X-rays: binaries
© ESO, 2016
1. Introduction
The system LS I +61°303, which has an orbital period P1 = 26.4960 ± 0.0028 days (Gregory 2002), is composed of a compact object and a massive star; the star has an optical spectrum typical of a rapidly rotating B0 V star with a decretion disc (Casares et al. 2005). At each orbit one radio outburst occurs whose amplitude is modulated with a long-term period Plong of 1605−1667 d (Marti & Paredes 1995; Gregory 2002). In this paper we study the origin of the long-term modulation. If it is attributable to periodic Doppler boosting effects, due to the precession of a jet associated with the compact object (Massi & Torricelli-Ciamponi 2014), then the long-term modulation has a stable periodicity. If it is attributable to an identical variation in the mass loss of the Be star (Gregory & Neish 2002), then the long-term modulation is rather unstable as it is in variable Be stars (Rivinius et al. 2013).
After examining the relationship between the long-term modulation and the period of the radio outburst (Sect. 2), we describe the precessing model (Sect. 3) and cyclic variability in Be stars (Sect. 4). In Sect. 5 we perform a timing and a correlation analysis on a radio data base of 36.8 yr, that covers more than 8 cycles of the long-term modulation. Finally, in Sect. 6 we discuss the implications of our results.
2. Relationship between the long-term modulation and the period of the radio outburst
In this section we analyse the relationship between the long-term period Plong and the radio outburst period Paverage. Their relationship, as shown below, is their mutual connection to the intrinsic periodicities of the system LS I +61°303, i.e. to the orbital period P1 and to the precession P2 of the jet.
2.1. Period of radio outbursts Paverage
The long-term periodicity Plong in LS I +61°303 is a phenomenon affecting not only the amplitude of the radio outburst, but also its position along the orbit (Paredes et al. 1990; Gregory 1999, 2002). The variation in the position of the outburst along the orbit, i.e. the orbital phase shift, depends on the timing residual between the orbital period P1 and the actual occurrence of the radio outburst. The radio outburst occurs nearly but not exactly at P1. Gregory (1999) showed that when radio outbursts are predicted to occur with P1 then there are timing residuals of up to several days that follow a sawtooth trend with period Plong. The same phenomenon has been analysed in terms of orbital phase shift by Paredes et al. (1990). An example is given in Fig. 1. The top panel shows one outburst before the maximum of the long-term modulation at 49 418 MJD (red), one outburst during the maximum at 49 980 MJD (black), and one outburst towards the minimum at 50 594 MJD (blue). In Fig. 1-centre we plot the three outbursts as function of the orbital phase Φ, ![\begin{equation} \Phi(P_1)={(t-t_0)\over P_1} -{\rm int} \left[{(t-t_0)\over P_1} \right] , \end{equation}](/articles/aa/full_html/2016/01/aa26938-15/aa26938-15-eq16.png) (1)where t0 = 43 366.275 MJD (Gregory 2002). The figure shows that the first outburst peaks at phase Φ(P1) ~ 0.5, whereas the second outburst is shifted at Φ ~ 0.6, and the third at Φ ~ 0.8. As can be seen in both Figs. 1-top and centre, there is a variation in the amplitude of the outburst at the same time as the orbital phase shift. The period of the amplitude modulation and the period of the sawtooth function are the same (Gregory 1999, 2002), so clearly the origin of the two phenomena are also the same. Why is there an orbital phase shift? or better, Why is there a timing residual with respect to the orbital period P1? A saw-tooth function in the residuals is indicative of a systematic error, otherwise residuals should be randomly distributed. An intuitive answer is that P1 is not the periodicity of the radio outburst. The first group to notice that the radio outburst periodicity is not equal to the orbital periodicity is Ray et al. (1997). In 1997 they reported a period for the radio outburst of 26.69 ± 0.02 d and discuss how their best estimate of the period is significantly different (9σ) from the best previously published value of 26.496 ± 0.008 d (Taylor & Gregory 1984). Based on the analysis of 6.5 yr of Green Bank Interferometer (GBI) radio data, the period of Paverage = 26.704 ± 0.004 d for the radio outbursts in LS I +61°303 has been confirmed, and noise-limited timing residuals between radio outbursts and predicted outbursts at Paverage have been determined (Jaron & Massi 2013). The bottom panel of Fig. 1 shows that the three outbursts at the three different epochs all occur at the same Φ(Paverage). The reason why the outburst period is called Paverage is explained in the following section.
(1)where t0 = 43 366.275 MJD (Gregory 2002). The figure shows that the first outburst peaks at phase Φ(P1) ~ 0.5, whereas the second outburst is shifted at Φ ~ 0.6, and the third at Φ ~ 0.8. As can be seen in both Figs. 1-top and centre, there is a variation in the amplitude of the outburst at the same time as the orbital phase shift. The period of the amplitude modulation and the period of the sawtooth function are the same (Gregory 1999, 2002), so clearly the origin of the two phenomena are also the same. Why is there an orbital phase shift? or better, Why is there a timing residual with respect to the orbital period P1? A saw-tooth function in the residuals is indicative of a systematic error, otherwise residuals should be randomly distributed. An intuitive answer is that P1 is not the periodicity of the radio outburst. The first group to notice that the radio outburst periodicity is not equal to the orbital periodicity is Ray et al. (1997). In 1997 they reported a period for the radio outburst of 26.69 ± 0.02 d and discuss how their best estimate of the period is significantly different (9σ) from the best previously published value of 26.496 ± 0.008 d (Taylor & Gregory 1984). Based on the analysis of 6.5 yr of Green Bank Interferometer (GBI) radio data, the period of Paverage = 26.704 ± 0.004 d for the radio outbursts in LS I +61°303 has been confirmed, and noise-limited timing residuals between radio outbursts and predicted outbursts at Paverage have been determined (Jaron & Massi 2013). The bottom panel of Fig. 1 shows that the three outbursts at the three different epochs all occur at the same Φ(Paverage). The reason why the outburst period is called Paverage is explained in the following section.
 |
Fig. 1 Orbital phase shift in LS I +61°303. Top: consecutive radio outbursts in LS I +61°303. Three outbursts are indicated: one before the maximum of the long-term modulation, one at the maximum, one towards the minimum. Centre: the radio light curves are folded with the orbital phase Φ(P1). The outburst does not follow the orbital periodicity and shifts at different epochs to different orbital phases. Bottom: the same light curves are here folded with Paverage, the periodicity of the radio outburst (Jaron & Massi 2013). |
 |
Fig. 2 Radio data of LS I +61°303 at 5, 8, 10, and 15 GHz from the literature. At the top x-axis are cycles of the long-term modulation, i.e. t−t0/ 1626 (see Sect. 4). The archive covers more than 8 cycles. |
2.2. Beat between P1 and P2
Another peculiarity of the radio emission from this system is the variability of its morphology. Radio images at high angular resolution show an elongated feature that changes from a double-sided to a one-sided morphology and that continuosly changes position angle as well. A precession period of 27–28 d was estimated by VLBA astrometry (Massi et al. 2012). The observed flux density (So) of a synchrotron source is the intrinsic flux density (Si) times the Doppler boosting factor (DB), which depends on the ejection angle. A periodic change in ejection angle of a radio emitting source, because of precession, changes the Doppler factor periodically; as a consequence, a periodicity should be observed in the flux density. Timing analysis of GBI radio data has revealed two periods (Massi & Jaron 2013), the already known orbital period P1 = 26.49 ± 0.07 d (ν1 = 0.03775 d-1) and a new period P2 = 26.92 ± 0.07 d (ν2 = 0.03715 d-1) consistent with the precessional period of 27–28 d indicated by the VLBA astrometry (Massi et al. 2012). The orbital period can result in a timing analysis if there is a periodical variation in the intrinsic flux density (Si). The hypothesis that the compact object in LS I +61°303, which accretes material from the Be wind, undergoes a periodical (P1) increase in the accretion rate Ṁ at a particular orbital phase along an eccentric orbit has been suggested and developed by several authors (Taylor et al. 1992; Marti & Paredes 1995; Bosch-Ramon et al. 2006; Romero et al. 2007). Recently, the presence of P1 and P2 have been confirmed as stable features in more recent Fermi-LAT and OVRO monitorings of the GeV gamma-ray emission (Jaron & Massi 2014) and of the radio emission (Massi et al. 2015), respectively.
The aim of the timing analysis was to obtain a better determination of the precessional period, but there was an additional and totally unexpected result: when combining ν1 and ν2 one obtains 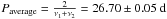 and
and 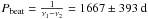 (Massi & Jaron 2013). In other words, the beat of P1 and P2 creates Pbeat (i.e. Plong) that modulates their average Paverage. LS I +61°303 seems to be one more case in astronomy of a “beat”. The first astronomical case was a class of Cepheids, afterwards called Beat-Cepheids (Oosterhoff 1957). This phenomenon occurs when two physical processes create stable variations of nearly equal frequencies (ν1,ν2). The very small difference in frequency creates a long term variation (ν1−ν2) modulating their average (ν1 + ν2)/2.
(Massi & Jaron 2013). In other words, the beat of P1 and P2 creates Pbeat (i.e. Plong) that modulates their average Paverage. LS I +61°303 seems to be one more case in astronomy of a “beat”. The first astronomical case was a class of Cepheids, afterwards called Beat-Cepheids (Oosterhoff 1957). This phenomenon occurs when two physical processes create stable variations of nearly equal frequencies (ν1,ν2). The very small difference in frequency creates a long term variation (ν1−ν2) modulating their average (ν1 + ν2)/2.
3. Precessing jet model
In our previous paper (Massi & Torricelli-Ciamponi 2014), we linked the two periodicities P1 and P2 to two physical processes: the periodic (P1) increase of relativistic electrons in a conical jet due to Ṁ variations and the periodic (P2) Doppler boosting of the emitted radiation by relativistic electrons due to jet precession. We have shown that the synchrotron emission of such a jet, calculated and fitted to the GBI observations, reproduces both the long-term modulation and the orbital phase shift of the radio outburst (Massi & Torricelli-Ciamponi 2014). The peak of the long-term modulation occurs when the jet electron density is around its maximum and the approaching jet forms the smallest possible angle with the line of sight. This coincidence of the maximum number of emitting particles and the maximum Doppler boosting of their emission occurs every 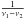 and creates the long-term modulation observed in LS I +61°303. In this context, if no significant variations in P1 and P2 occur in the time interval under examination, then in that interval the long-term modulation remains stable.
and creates the long-term modulation observed in LS I +61°303. In this context, if no significant variations in P1 and P2 occur in the time interval under examination, then in that interval the long-term modulation remains stable.
4. Cyclic variability in the disc of some Be stars
The known long-term variability in Be stars is that of the violet-to-red cycles (V/R variations) in which the two peaks of the emission lines vary in height against each other. The variations correspond to an evolution of the disc itself where the disc undergoes a global one-armed oscillation instability that manifests itself in the V/R variability. This instability (progressing density wave) may eventually lead to the disruption of the disc, which after years or decades fills again (Grudzinska et al. 2015, and reference therein), and to cycle lengths that are not constant but vary from cycle to cycle (Rivinius et al. 2013, and references therein). We examine in detail the well-studied case of ζ Tau, which is also a Be star in a binary system. Over the last 100 yr ζ Tau has gone through active stages characterized by pronounced long-term variations and quiet stages. From 1920 to about 1950 there were no variations. A very clear variability started afterwards and lasted until 1980 with 2 cycles of 2290 days and 1290 days. From 1980 to 1990 the star was again stable. Around 1990 the disc again entered into an active stage and 3 consecutive cycles of 1419 d, 1527 d, and 1230 d were determined (Štefl et al. 2009, and references therein). In this context, radio variations induced by variations in the Be disc are predicted to be rather unstable, i.e. to have cycles of different lengths and, at some epochs, to disappear.
5. Radio data base of LS I +61°303
 |
Fig. 3 Model data (red) and radio observations (black) of LS I +61°303 averaged over one day (Sect. 5). |
We collected data of LS I +61°303 from the literature at 5, 8, 10, and 15 GHz (see Appendix) covering the interval 43 367−56 795 MJD, i.e. 36.8 yr. To date, this is the largest archive on LS I +61°303. The data are shown in Fig. 2. The top x-axis shows the number of cycles for a long-term period of 1626 d (see below): the data set covers 8 long-term cycles. In Fig. 3 we show the data overlapped with our physical model of the precessing jet assuming the same sampling and ν = 8 GHz. Our model was fitted previously (Massi & Torricelli-Ciamponi 2014) on 6.7 yr of radio data (49 380 MJD − 51 823 MJD). As we show in Fig. 3, the model also reproduces well 36.8 yr of data.
 |
Fig. 5 Correlation coefficient vs. time for observations (left) and model data (right), both averaged over three days. |
In order to search for possible periodicities we used the Lomb-Scargle method, which is very efficient on irregularly sampled data (Lomb 1976; Scargle 1982). We use the algorithms of the UK Starlink software package, PERIOD1. The statistical significance of a period is calculated in PERIOD following the method of Fisher randomization as outlined in Linnel Nemec & Nemec (1985). One thousand randomized time series are formed and the periodograms are calculated. The proportion of permutations in a given frequency window that give a peak power higher than that of the original time series provides an estimate of p, the probability that there is no such periodic component. A derived period is considered significant for p< 0.01 and marginally significant for 0.01 <p< 0.10 (Linnel Nemec & Nemec 1985).
The spectrum is shown in Fig.4. We have two dominant features at P1 = 26.496 ± 0.013 d and P2 = 26.935 ± 0.013 d, evident in the zoom in the upper right panel. Period P1 coincides with the orbital period (Gregory 2002) and period P2 with the precession period (Massi & Jaron 2013; Massi et al. 2015). In the spectrum there is a third feature at Plong = 1628 ± 49 d. For all periods the randomization test gives 0.00 <p< 0.01. It is interesting to compare this spectrum with that of the model shown in Fig. 4-right. Periods P1, P2, and Plong are all there. Period Plong shows two side lobes at 1265 d and at 2335 d; the small feature to the right of Plong in Fig. 4-left corresponds to 2335 d.
By comparing the light curves in Fig. 3 and the spectra, i.e. Fig. 4-left with Fig. 4-right, it is clear that the precessing jet model able to reproduce the light curve of 36.8 yr of radio data of LS I +61°303 also reproduces well its Lomb-Scargle spectrum. The most important result from the analysis of the largest archive of data available until now on LS I +61°303 is that it is evident for the first time that Plong is not a main characteristic of the Lomb-Scargle spectrum; the main characteristics are P1 and P2. We can compute the beating of the found P1 and P2 and check how Pbeat compares with Plong. The result is Pbeat = (P1P2)/(P2−P1) = 1626 ± 68 d, clearly in agreement with Plong = 1628 ± 49 d.
How stable is the found Plong over the 8 cycles? This is the fundamental question of this work. A powerful method for studying the stability of a periodic signal over time is its autocorrelation. If a period is stable the correlation coefficient should appear as an oscillatory sequence with peaks at multiples of that period. We first examine the correlation coefficient for model data. The result is shown in Fig. 5-right. In the Lomb-Scargle spectrum, Plong – given by the beating of P1 and P2 – is a minor feature; however, it becomes apparent in the plot of the correlation coefficient. We draw lines at multiples of Pbeat = 1626. Since P1 and P2 are constant in our model, it is clear that the model predicts a stable repetition of their beating frequency. We now compare the correlation of model data with the correlation of the observations. The correlation coefficient is shown in Fig. 5-left. Except for a slight drop in the correlation in the first cycles, the correlation coefficient of LS I +61°303 observations compares well with the correlation coefficient of the model data. The small drop in correlation is likely attributable to the data at 5 GHz present in the first 3.7 cycles (see Appendix). The scattering of the correlation coefficient around cycle 6 is due to the lack of data around that cycle (see Fig. 2); scattering is also present in the correlation of model data (Fig. 5-right).
6. Discussion and conclusions
We built a radio archive of 36.8 yr for the source LS I +61°303 and performed timing and correlation analysis. Our conclusions are the following:
-
1.
In the system LS I +61°303 aperiodic radio outburst is observed ofPaverage = 26.704 ± 0.004 d modulated by a long-term period of 1628 ± 49 d. However, the Lomb-Scargle spectrum is dominated by two other periodicities, P1 = 26.496 ± 0.013 d and P2 = 26.935 ± 0.013 d, and the observed periodicities Paverage and Plong are equal to the beat of P1 and P2.
-
2.
Synchrotron emission from a precessing jet model, with precession period P2, regularly (with period P1) refilled with relativistic electrons, reproduces the observed 36.8 yr light curve of LS I +61°303 and also its Lomb-Scargle spectrum.
-
3.
The correlation coefficient of the observations shows a regular oscillation, as does the correlation coefficient of the model data with peaks at multiple of Plong.
The period Plong = 1628 ± 49 d is stable over 8 cycles. This is not what is expected from Be wind variations, which are rather unstable and change from cycle to cycle or even disappear. A stable Plong is what is expected for a beat of periods P1 (orbital period) and P2 (precession) with no significant variations during the 8 examined cycles. The peak of the long-term modulation occurs when the jet electron density is around its maximum and the approaching jet forms the smallest possible angle with the line of sight. This coincidence of the maximum number of emitting particles and the maximum Doppler boosting of their emission occurs every 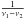 and creates the long-term modulation observed in the radio emission of LS I +61°303.
and creates the long-term modulation observed in the radio emission of LS I +61°303.
Finally, periods P1 and P2 have also been determined in the Lomb-Scargle spectrum of gamma-ray emission at apastron of Fermi-LAT data (Jaron & Massi 2014). Moreover, Paredes-Fortuny et al. (2015) discovered that the orbital phase shift also affects the variations in the equivalent width (EW) of the Hα emission line from LS I +61°303. The orbital phase shift (Sect. 2.1) suggests that Paverage is the true period for the EW variations. The EW variations show a long-term modulation as well (Zamanov et al. 2013). The presence of both long-term period and Paverage, as well as the direct detection of P1 and P2, indicates therefore that the precessing jet also induces variations in EW(Hα) and gamma-ray emission.
Acknowledgments
We are grateful to Hovatta Talvikky for providing the OVRO data and to Guy Pooley for providing the Ryle data. We acknowledge several helpful discussions with Frederic Jaron and Jürgen Neidhöferr. We acknowledge Atsuo Okazaki for suggesting the case of the Be star ζ Tau. We would like to thank the anonymous referee for the helpful comments. The OVRO 40 m Telescope Monitoring Program is supported by NASA under awards NNX08AW31G and NNX11A043G, and by the NSF under awards AST-0808050 and AST-1109911. This research is based on observations with the 100 m telescope of the MPIfR (Max-Planck-Institut fär Radioastronomie) at Effelsberg. The Green Bank Interferometer is a facility of the National Science Foundation operated by the NRAO in support of NASA High Energy Astrophysics programs.
References
- Bosch-Ramon, V., Paredes, J. M., Romero, G. E., & Ribó, M. 2006, A&A, 459, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casares, J., Ribas, I., Paredes, J. M., Martí, J., & Allen de Prieto, C. 2005, MNRAS, 360, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Coe, M. J., Bowring, S. R., Court, A. J., Hall, C. J., & Stephen, J. B. 1983, MNRAS, 203, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C. 1999, ApJ, 520, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C. 2002, ApJ, 575, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C., & Neish, C. 2002, ApJ, 580, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C., Xu, H.-J., Backhouse, C. J., & Reid, A. 1989, ApJ, 339, 1054 [Google Scholar]
- Grudzinska, M., Belczynski, K., Casares, J., et al. 2015, MNRAS, 452, 2773 [NASA ADS] [CrossRef] [Google Scholar]
- Jaron, F., & Massi, M. 2013, A&A, 559, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jaron, F., & Massi, M. 2014, A&A, 572, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linnell Nemec, A. F., & Nemec, J. M. 1985, AJ, 90, 2317 [NASA ADS] [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Martí, J. 1993, Ph.D. Thesis, University of Barcelona, Radio emitting X-ray binaries [Google Scholar]
- Marti, J., & Paredes, J. M. 1995, A&A, 298, 151, A&A, 480, 289 [NASA ADS] [Google Scholar]
- Massi, M. 2014, Proc. 12th European VLBI Network Symposium and Users Meeting (EVN 2014), 7−10 October, Cagliari, Italy, PoS(EVN 2014)062. [Google Scholar]
- Massi, M., & Jaron, F. 2013, A&A, 554, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massi, M., & Kaufman Bernadó, M. 2009, ApJ, 702, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Massi, M., & Torricelli-Ciamponi, G. 2014, A&A, 564, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massi, M., Ribó, M, Paredes, J. M., et al. 2004, A&A, 414, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massi, M., Ros, E., & Zimmermann, L. 2012, A&A, 540, A14 [Google Scholar]
- Massi, M., Jaron, F., & Hovatta, T. 2015, A&A, 575, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oosterhoff, P. T. 1957, Bull. Astr. Inst. Netherlands, 13, 320 [Google Scholar]
- Paredes, J. M., Estalella, R., & Rius, A. 1987, A&A, 186, 177 [NASA ADS] [Google Scholar]
- Paredes, J. M., Estalella, R., & Rius, A. 1990, A&A, 232, 377 [NASA ADS] [Google Scholar]
- Paredes-Fortuny, X., Ribó, M., Bosch-Ramon, V., et al. 2015, A&A, 575, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peracaula, M., Marti, J., & Paredes, J. M. 1997, A&A, 328, 283 [NASA ADS] [Google Scholar]
- Pooley, G. G. 2006, VI Microquasar Workshop: Microquasars and Beyond, PoS(MQW6)019 [Google Scholar]
- Ray, P. S., Foster, R. S., Waltman, E. B., Tavani, M., & Ghigo, F. D. 1997, ApJ, 491, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Rivinius, T., Carciofi, A. C., & Martayan, C. 2013, A&ARv, 21, 69 [Google Scholar]
- Romero, G. E., Okazaki, A. T., Orellana, M., & Owocki, S. P. 2007, A&A, 474, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263 [Google Scholar]
- Štefl, S., Rivinius, T., Carciofi, A. C., et al. 2009, A&A, 504, 929 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, A. R., & Gregory, P. C. 1982, ApJ, 255, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. R., & Gregory, P. C. 1984, ApJ, 283, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. R., Kenny, H. T., Spencer, R. E., & Tzioumis, A. 1992, ApJ, 395, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. R., Young, G., Peracaula, M., Kenny, H. T., & Gregory, P. C. 1996, A&A, 305, 817 [NASA ADS] [Google Scholar]
- Zamanov, R., Stoyanov, K., Martí, J., et al. 2013, A&A, 559, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zimmermann, L., Fuhrmann, L., & Massi, M. 2015, A&A, 580, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Selection of frequencies for the radio data base
We selected from the literature data at 5, 8, 10, and 15 GHz. To reduce inhomogeneities in the archive, we excluded frequencies lower than 5 GHz because of the high flux that the “second peak” can have at low frequency. The periodic radio outburst in LS I +61°303 is in fact not a simple, one-peak outburst. It may have a rather complex structure, mainly dominated by two consecutive peaks. These two peaks are 5−8 d apart and have different spectral characteristics; the first peak has a flat/inverted spectrum and the second outburst is optically thin, i.e. it dominates at low frequencies. At 8 GHz the second peak is often a minor peak, hardly traceable; instead, simultaneous observations at 2 GHz show a strong second peak, even larger at some epochs than the first peak (Massi & Kaufman Bernadó 2009; Massi 2014; Zimmermann et al. 2015).
We included data at 5 GHz to be able to cover the first cycles. However, at this frequency the second peak still seems to be significant and biases the correlation analysis slightly. The small drop in correlation coefficient from 1 to 0.7−0.8 (Fig. 5-left) is likely attributable to the second peak at 5 GHz; for example in Table 1 in Taylor & Gregory (1982), a second peak of 91 ± 9 mJy can be seen at 2444106.95 JD following the first peak (six days earlier) of 100 ± 10 mJy.
All Figures
 |
Fig. 1 Orbital phase shift in LS I +61°303. Top: consecutive radio outbursts in LS I +61°303. Three outbursts are indicated: one before the maximum of the long-term modulation, one at the maximum, one towards the minimum. Centre: the radio light curves are folded with the orbital phase Φ(P1). The outburst does not follow the orbital periodicity and shifts at different epochs to different orbital phases. Bottom: the same light curves are here folded with Paverage, the periodicity of the radio outburst (Jaron & Massi 2013). |
| In the text | |
 |
Fig. 2 Radio data of LS I +61°303 at 5, 8, 10, and 15 GHz from the literature. At the top x-axis are cycles of the long-term modulation, i.e. t−t0/ 1626 (see Sect. 4). The archive covers more than 8 cycles. |
| In the text | |
 |
Fig. 3 Model data (red) and radio observations (black) of LS I +61°303 averaged over one day (Sect. 5). |
| In the text | |
 |
Fig. 4 Lomb-Scargle timing analysis of the observations (left) and the model data (right) of Fig. 3. |
| In the text | |
 |
Fig. 5 Correlation coefficient vs. time for observations (left) and model data (right), both averaged over three days. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


