| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 4 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526888 | |
| Published online | 09 December 2015 | |
GTC/CanariCam observations of (99942) Apophis
1
Instituto de Astrofísica de Canarias (IAC),
C/Vía Láctea s/n, 38205
La Laguna, Tenerife,
Spain
e-mail:
jlicandr@iac.es
2
Departamento de Astrofísica, Universidad de La
Laguna., 38206, La
Laguna, Tenerife,
Spain
3
Max-Planck-Institut für extraterrestrische Physik,
Postfach 1312,
Giessenbachstrasse, 85741
Garching,
Germany
4
UNS-CNRS-Observatoire de la Côte d’Azur,
BP 4229, 06304
Nice Cedex 4,
France
Received: 3 July 2015
Accepted: 2 October 2015
Context. The potentially hazardous asteroid (PHA) (99942) Apophis is one of the most remarkable near-Earth asteroids (NEA) in terms of impact hazard. A good determination of its surface thermal inertia is very important in order to evaluate the Yarkovsky effect on its orbital evolution.
Aims. We present thermal infrared observations obtained on January 29, 2013, with CanariCam mid-infrared camera/spectrograph attached to the Gran Telescopio CANARIAS (GTC, Roque de los Muchachos Observatory, La Palma, Spain) using the Si2-8.7, Si6-12.5, and Q1-17.65 filters with the aim of deriving Apophis’ diameter (D), geometric albedo (pV), and thermal inertia (Γ).
Methods. We performed a detailed thermophysical model analysis of the GTC data combined with previously published thermal data obtained using Herschel Space Observatory PACS instrument at 70, 100, and 160 μm.
Results. The thermophysical model fit of the data favors low surface roughness solutions (within a range of roughness slope angles rms between 0.1 and 0.5), and constrains the effective diameter, visible geometric albedo, and thermal inertia of Apophis to be Deff = 380–393 m, pV = 0.24–0.33 (assuming absolute magnitude H = 19.09 ± 0.19) and Γ = 50–500 Jm-2-0.5 K-1, respectively.
Key words: minor planets, asteroids: individual: (99942) Apophis / methods: observational / infrared: planetary systems
© ESO, 2015
1. Introduction
The potentially hazardous asteroid (PHA) (99942) Apophis (hereafter Apophis) is a near-Earth asteroid (NEA) that has a small but non-zero chance of impacting the Earth and it is one of the most remarkable NEAs in terms of impact hazard. With the available data, it is known that Apophis will have an extremely close approach on April 13, 2029, at 5.7 Earth radii from the Earth’s center, just below the altitude of geosynchronous Earth satellites; by means of a statistical analysis, Farnocchia et al. (2013) find an impact probability greater than 10-6 for an impact in 2068.
The computation of the orbital evolution of this object is limited by the insufficient knowledge of the role played by the non-gravitational Yarkovsky effect, which produces a steady orbital drift as a consequence of the momentum carried away by the thermal emission of the object (see, e.g., Bottke et al. 2002; Giorgini et al. 2002). The Yarkovsky effect depends upon several poorly known parameters, such as the albedo, size, thermal inertia, and pole orientation of the object. Recently Vokrouhlický et al. (2015) evaluated the Yarkovsky effect on the orbital evolution of Apophis.
In addition, improved knowledge of the physical properties of Apophis is desirable for other reasons: (1) the European Commission H2020-PROTEC-2014 funded project NEOShield-2 will base its study of NEO mitigation strategy on the case of Apophis and (2) the possible implications would need to be addressed if an impact were to occur.
A first determination from polarimetric observations of the geometric albedo pV = 0.33 ± 0.08 is presented in Delbo et al. (2007). They also obtained an absolute magnitude of H = 19.7 ± 0.4 mag, which led to an effective diameter Deff = 270 ± 60 m, slightly smaller than earlier estimates in the range of 320 to 970 m depending on the assumed albedo. Müller et al. (2014) published the first far-infrared observations of Apophis using the Herschel Space Observatory PACS instrument. They obtained data at 70, 100, and 160 μm at two epochs and performed a detailed thermophysical model (TPM) analysis. They used the spin and shape model and absolute magnitude H = 19.09 ± 0.19 by Pravec et al. (2014) and obtained an effective diameter 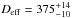 m, a geometric albedo in the V-band
m, a geometric albedo in the V-band 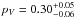 , and a thermal inertia of
, and a thermal inertia of 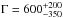 Jm-2 s-0.5 K-1. The albedo determinations agree very well; the difference between the Deff determined by Müller et al. and the value derived by Delbo et al. (2007) from their pV determination is the result of a different value of H (H = 19.09 and H = 19.7, respectively). The Vokrouhlický et al. (2015) results use the Pravec et al. (2014) and Müller et al. (2014) results to evaluate the Yarkovsky effect on the orbital evolution of Apophis; in particular, they use the range of Γ values provided by Müller et al. (2014).
Jm-2 s-0.5 K-1. The albedo determinations agree very well; the difference between the Deff determined by Müller et al. and the value derived by Delbo et al. (2007) from their pV determination is the result of a different value of H (H = 19.09 and H = 19.7, respectively). The Vokrouhlický et al. (2015) results use the Pravec et al. (2014) and Müller et al. (2014) results to evaluate the Yarkovsky effect on the orbital evolution of Apophis; in particular, they use the range of Γ values provided by Müller et al. (2014).
In this paper we present thermal infrared observations obtained on January 29, 2013, with the CanariCam mid-infrared instrument attached to the Gran Telescopio CANARIAS (GTC, Roque de los Muchachos Observatory, La Palma, Spain). Images of Apophis were obtained using three different filters (Si2-8.7, Si6-12.5, and Q1-17.65). These fluxes, obtained at wavelengths which are closer to the wavelengths in which the Apophis thermal emission peaks than the Herschel measurements, are used together with Herschel data to better constrain the thermophysical model presented in Müller et al. (2014).
The paper is organized as follows. In Sect. 2 we present the observations and describe the reduction process and photometry. The TPM is described and the results are presented in Sect. 3. Finally the discussion and conclusions are presented in Sect. 4.
2. Observations and data reduction
The observations were performed on January 29, 2013, with CanariCam (see Telesco et al. 2003) in imaging mode at the 10.4 m Gran Telescopio CANARIAS. Non-sidereal guiding was not available at the time of the observations (it was fully implemented in 2013, but later on) and therefore Apophis had to be tracked by applying offsets to the telescope every time the target was about to move off the CanariCam field of view (FOV) (25′′ × 19′′). The standard star HD 59381 was also observed on the same night as a flux calibrator. The data were taken in the Si2-8.7, Si6-12.5, and Q1-17.65 filters whose central wavelengths are 8.7, 12.5, and 17.65 μm, respectively (see Table 1). The telescope’s secondary mirror was chopping at 2 Hz with a chop throw of 7′′ along the east-west direction. Nodding of the telescope axes was performed every 47 seconds with a nod throw of 7′′, also in the east-west direction, to minimize the radiative offset.
Log of observations.
Data were processed using a set of dedicated PyRAF 1 scripts developed within our group. CanariCam raw images consist of a series of individual frames (savesets). The savesets are stored in multi-extension FITS files (MEF), which have the structure of [320, 240, 2, M ] [ N ]. The first two numbers represent the detector’s X and Y dimensions in pixels (320 × 240). The third dimension represents the number of chop positions, namely on-source and off-source positions. M represents the number of savesets in each nod position and N the number of nods (nod beams A and B), which follow the sequence A-BB-A. Off-source savesets were subtracted from the corresponding on-source savesets for each nod beam. For each individual saveset, we determined the source centroid using SExtractor (Bertin & Arnouts 1996). Savesets were then geometrically aligned using the shifts calculated from the centroid positions with respect to centroid from the first saveset and stacked to produce the final net signal image. This shift-and-add technique improves the image quality, and therefore the sensitivity. Shift-and-add is particularly important for the Apophis data since the object was drifting accross the CanariCam detector by several pixels from one saveset to the next. Additionally, owing to the relatively short on-source time in each saveset (5.9 s) and the rapid movement of Apophis accross the FOV, it was not possible to calculate image centroid in all savesets. Hence, those savesets where the centroid was not obtained were discarded from the total signal, yielding an effective on-source time smaller than the observed on-source time (see Table 2). The resulting images of Apophis and the standard star used are shown in Fig. 1.
 |
Fig. 1 Composed images of Apophis (upper panels) and HD 59381 flux standard star (lower panel) in the three filters used. |
Photometric data.
Aperture photometry was performed in the reduced images using PyRAF. An aperture of radius 0.6′′ was used in all filters in the Apophis as well as in the standard star HD 59381 images. A sky annulus with a radius of 2.4′′ and width of 0.8′′ was used to determine the sky as the median of all pixel values within the annulus area. The in-band flux in Jy for each CanariCam filter was obtained by integrating the standard star template spectrum (Cohen et al. 1999) multiplied by the filter transmission curve. Finally, the in-band flux for HD 59381 was divided by the measured ADU/s within the 0.6′′ radius aperture and then multiplied by the measured ADU/s within the same aperture in Apophis. No color correction is applied as it is much smaller (<1%) than the uncertainties. The final flux densities and the FWHM of the PSF in each image can be found in Table 2.
3. Thermophysical modeling
Thermophysical models are powerful tools used to derive asteroid sizes from their thermal infrared data. If the shape, the spin axis orientation, and the rotational period of the object are well characterized and if enough data are available, TPMs also allow the thermal inertia and the macroscopic roughness of the surface to be constrained. In brief, TPMs model the temperature on each surface element of the shape model – typically triangular facets – at every observation epoch by accounting for the corresponding energy budget, i.e., how much incident solar radiation is absorbed at and conducted onto the surface. This depends on the distance from the asteroid to the Sun and on the physical properties of the surface (albedo, emissivity, macroscopic roughness, conductivity, etc.), but it also depends critically on the shape of the object and its rotational phase at the moment of the observations since they determine the illumination geometry of each facet. Thus, the TPM requires any available convex shape model in combination with the spin axis orientation and rotational properties as input.
The heat conduction onto the surface is controlled by the thermal inertia Γ, while the infrared beaming effects are calculated via a surface roughness model implemented as concave, spherical crater segments on the surface and parametrized by the root mean square (rms) slope angle. Once the temperatures are modeled, the model fluxes that the observer would measure can be computed given the particular observational geometry and they can be fit to the data. The observational geometry refers to the heliocentric and geocentric distances and the phase angle – the angle subtended by the observer and the Sun from the point of view of the asteroid.
Müller et al. (2014) applied a TPM based on the work by Lagerros (1996, 1997, 1998) and Müller & Lagerros (1998, 2002) to model the thermal data of Apophis obtained with the Herschel Space Observatory PACS instrument. Taking the tumbling rotational state and shape model given by Pravec et al. (2014), Müller et al. obtained a thermal inertia of 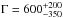 Jm-2 s-0.5 K-1, an effective diameter of
Jm-2 s-0.5 K-1, an effective diameter of 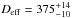 m, and a corresponding visible (V-band) geometric albedo of
m, and a corresponding visible (V-band) geometric albedo of 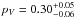 for Apophis. In this paper we use the same TPM and rotational state model to study a combination of GTC and Herschel data to better constrain the Müller et al. (2014) results. We combined all GTC and Herschel data using the results obtained in Müller et al. (2014), with Herschel data alone as a starting guess. We assumed a constant emissivity of 0.9 at all wavelengths. We also used the mean absolute magnitude HV = 19.09 ± 0.19 mag derived by Pravec et al. (2014) under the assumption of a slope parameter of G = 0.24 ± 0.11. The observational circumstances of Herschel Space Observatory data are summarized in Table 1 of Müller et al. (2014); GTC observations were obtained with the asteroid at heliocentric and geocentric distances rhelio = 1.080 AU and Δobs = 0.113, respectively, and a phase angle α = −31.7 degrees. The illumination is similar to that shown in Müller et al. (2014), Fig. 3, right panel, except that it is at a smaller phase angle (CanariCam: −31.7 deg, PACS: −61.4 deg) and a different orientation of the body (as seen from GTC). In Fig. 2 we plot the reduced χ2-values calculated for the radiometric analysis of the combined GTC and Herschel data for different roughness slope angles versus thermal inertia. The roughness slope angles (rms) range from 0.0 to 0.9.
for Apophis. In this paper we use the same TPM and rotational state model to study a combination of GTC and Herschel data to better constrain the Müller et al. (2014) results. We combined all GTC and Herschel data using the results obtained in Müller et al. (2014), with Herschel data alone as a starting guess. We assumed a constant emissivity of 0.9 at all wavelengths. We also used the mean absolute magnitude HV = 19.09 ± 0.19 mag derived by Pravec et al. (2014) under the assumption of a slope parameter of G = 0.24 ± 0.11. The observational circumstances of Herschel Space Observatory data are summarized in Table 1 of Müller et al. (2014); GTC observations were obtained with the asteroid at heliocentric and geocentric distances rhelio = 1.080 AU and Δobs = 0.113, respectively, and a phase angle α = −31.7 degrees. The illumination is similar to that shown in Müller et al. (2014), Fig. 3, right panel, except that it is at a smaller phase angle (CanariCam: −31.7 deg, PACS: −61.4 deg) and a different orientation of the body (as seen from GTC). In Fig. 2 we plot the reduced χ2-values calculated for the radiometric analysis of the combined GTC and Herschel data for different roughness slope angles versus thermal inertia. The roughness slope angles (rms) range from 0.0 to 0.9.
 |
Fig. 2 Reduced χ2 values for models considering different roughness slope angles rms = 0.0, 0.1, 0.2, 0.3, 0.5 and 0.9. Notice that the minima of the reduced χ2-values are lower for low-roughness solutions, but we find acceptable fits (with χ2-values lower than 1.55 shown as an horizontal line) for all levels of roughness. |
 |
Fig. 3 Observed GTC/CanariCam (this paper) and Herschel/PACS (from Müller et al. 2014) divided by model fluxes for the two extreme cases with roughness slope angles rms = 0.0 (upper) and 0.9 (lower). Notice that observed-to-modeled fluxes of the GTC/CanariCam data are particularly sensitive to roughness and worsen for larger roughness, which led us to favor the solutions with low surface roughness in our analysis. |
The minimum reduced χ2 would be ~0.8 and the statistical error would be σ ~ 0.6 so we find acceptable fits (with χ2-values lower than 1.55) for all levels of roughness (see, e.g., Press et al. 1986), which means that we cannot unambiguously constrain roughness and thermal inertia: low-roughness combined with low Γ fit similarly well to high-roughness and high-Γ solutions. On the other hand, the minima of the reduced χ2-values are lower for low-roughness solutions. This is also illustrated in the ratios of observed-to-modeled fluxes presented in Fig. 3, where we compare the ratios of the observed fluxes to our modeled fluxes for the extreme roughness cases. We note in particular that observed-to-modeled fluxes of the GTC/CanariCam data are particularly sensitive to roughness and are a slightly less sensitive for larger roughness. These considerations led us to favor the solutions with low surface roughness in our analysis. Thus, within a range of rms between 0.1 and 0.5, we constrain the size, visible geometric albedo, and thermal inertia of Apophis to be Deff = 380–393 m, pV = 0.27–0.29, and Γ = 50–500 Jm-2 s-0.5 K-1. We note that the given range of pV is obtained assuming the absolute magnitude H = 19.09 from Pravec et al. (2014), considering the uncertainty in H (H = 19.09 ± 0.19) and so the range of possible albedo is wider (pV = 0.24–0.33).
4. Discussion and conclusions
Images of Apophis were obtained using three different filters (Si2-8.7, Si6-12.5, and Q1-17.65) with the CanariCam instrument in imaging mode at the 10.4 m Gran Telescopio CANARIAS (GTC) at El Roque de los Muchachos Observatory (La Palma, Canary Islands, Spain). The derived fluxes, which are closer to the wavelengths in which Apophis’ thermal emission peaks than those reported by Müller et al. (2014) using Herschel space telescope data, are used together with Müller et al. reported fluxes to better constrain the thermophysical model of Apophis also presented in Müller et al.
Our fitting of the TPM to the combined GTC/CanariCam and Herschel/PACS favors the solutions with low surface roughness (within a range of rms roughness slope angles between 0.1 and 0.5) and it constrains the size, visible geometric albedo, and thermal inertia of Apophis to be Deff = 380–393 m, pV = 0.27–0.29, and Γ = 50–500 Jm-2 s-0.5 K-1.
Deff, pV, and Γ values corresponding to the minimum χ2 value of the TPM fits using fixed values of rms in the 0.0 to 0.9 range.
These results agree very well within the uncertainties with those reported by Müller et al. (2014) using only the Herschel data (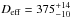 m,
m, 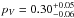 , a thermal inertia Γ in the range 250–800 Jm-2 s-0.5 K-1, with a best solution at Γ = 600 Jm-2 s-0.5 K-1 for rms = 0.5), but point to a somewhat lower
, a thermal inertia Γ in the range 250–800 Jm-2 s-0.5 K-1, with a best solution at Γ = 600 Jm-2 s-0.5 K-1 for rms = 0.5), but point to a somewhat lower
value of thermal inertia, closer to the lower range given in Müller et al. and a slightly larger effective size (closer to the wider range given in Müller et al.). The albedo value also agrees with the value reported by Delbo et al. (2007; pV = 0.33 ± 0.08) derived from polarimetric observations. The thermal inertia of Apophis also closely fits the trend of Γ vs. Deff reported by Delbo & Tanga (2009).
Finally, the presented improvement in the determination of the thermal inertia is very important in order to evaluate the Yarkovsky effect on the orbital evolution of Apophis (Vokrouhlický et al. 2015). Using the Müller et al. (2014) range of possible Γ-values, they estimate the drift of the Apophis orbital semimajor axis ⟨ da/dt ⟩ to be in a range between −11 × 10-4 and −15 × 10-4 au/Myr. Using the range of thermal inertia obtained in this paper, the range of ⟨ da/dt ⟩ that can be derived from Fig. 1 in Vokrouhlický et al. (2015) is slightly smaller, between −6 × 10-4 and −14 × 10-4 au/Myr.
Acknowledgments
We acknowledge Ben Rositis for his useful comments that helped to improve the manuscript. Based on observations made with the Gran Telescopio Canarias (GTC), installed in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias, in the island of La Palma. We acknowledge Petr Scheirich and Petr Pravec for the provision of shape orientation, spin-axis orientation, rotational properties, etc for the GTC observing epochs, and Ben Rositis for his useful comments that helped to improve the manuscript. J.L. acknowledges support from the project ESP2013-47816-C4-2-P (MINECO, Spanish Ministry of Economy and Competitiveness). M.D. and V. Ali-Lagoa acknowledge support from the NEOShield-2 project that has received funding from the European Unions Horizon 2020 research and innovation program under grant agreement No. 640351. The work of V. Ali-Lagoa and MDB was supported by the French Agence National de la Recherche (ANR) SHOCKS.
References
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bottke, W. F., Morbidelli, A., Jedicke, R., et al. 2002, Icarus, 156, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M., Walker, R. G., Carter, B., et al. 1999, AJ, 117, 1864 [NASA ADS] [CrossRef] [Google Scholar]
- Delbo, M., & Tanga, P. 2009, Planet. Space Sci., 57, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Delbo, M., Cellino, A., & Tedesco, E. 2007, Icarus, 188, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Farnocchia, D., Chesley, S. R., Chodas, P. W., et al. 2013, Icarus, 224, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Giorgini, J., Ostro, J., Benner, L., et al. 2002, Science, 296, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Lagerros, J. S. V. 1996, A&A, 310, 1011 [NASA ADS] [Google Scholar]
- Lagerros, J. S. V. 1997, A&A, 325, 1226 [NASA ADS] [Google Scholar]
- Lagerros, J. S. V. 1998, A&A, 332, 1123 [NASA ADS] [Google Scholar]
- Müller, T., & Lagerros, J. S. V. 1998, A&A, 338, 340 [NASA ADS] [Google Scholar]
- Müller, T., & Lagerros, J. S. V. 2002, A&A, 381, 324 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T., Kiss, C., Scheirich, P., et al. 2014, A&A, 566, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pravec, P., Scheirich, P., Durech, J., et al. 2014, Icarus, 233, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Flannery, B. P., & Teukolsky, S. A. 1986, Numerical recipes (Cambridge: University Press) [Google Scholar]
- Telesco, C. M., Ciardi, D., French, J., et al. 2003, in SPIE Conf. Ser., 4841, 913 [Google Scholar]
- Vokrouhlický, D., Farnocchia, D., Capek, D., et al. 2015, Icarus, 252, 277 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Deff, pV, and Γ values corresponding to the minimum χ2 value of the TPM fits using fixed values of rms in the 0.0 to 0.9 range.
All Figures
 |
Fig. 1 Composed images of Apophis (upper panels) and HD 59381 flux standard star (lower panel) in the three filters used. |
| In the text | |
 |
Fig. 2 Reduced χ2 values for models considering different roughness slope angles rms = 0.0, 0.1, 0.2, 0.3, 0.5 and 0.9. Notice that the minima of the reduced χ2-values are lower for low-roughness solutions, but we find acceptable fits (with χ2-values lower than 1.55 shown as an horizontal line) for all levels of roughness. |
| In the text | |
 |
Fig. 3 Observed GTC/CanariCam (this paper) and Herschel/PACS (from Müller et al. 2014) divided by model fluxes for the two extreme cases with roughness slope angles rms = 0.0 (upper) and 0.9 (lower). Notice that observed-to-modeled fluxes of the GTC/CanariCam data are particularly sensitive to roughness and worsen for larger roughness, which led us to favor the solutions with low surface roughness in our analysis. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


