| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201526656 | |
| Published online | 09 December 2015 | |
Probing the Local Bubble with diffuse interstellar bands
I. Project overview and southern hemisphere survey⋆
1 Lennard-Jones Laboratories, Keele University, ST5 5BG, UK
e-mail:
mandybailey22@gmail.com
2
Astrophysics Research Institute, Liverpool John Moores
University, IC2, Liverpool Science
Park, Liverpool
L3 5RF,
UK
3
School of Astronomy, Institute for Research in Fundamental
Sciences (IPM), PO Box
19395-5746, Tehran,
Iran
4
School of Chemistry, The University of Nottingham, University
Park, Nottingham,
NG7 2RD,
UK
5
Royal Astronomical Society, Burlington House,
Piccadilly, London
W1J 0BQ,
UK
Received: 2 June 2015
Accepted: 26 September 2015
Context. The Sun traverses a low-density, hot entity called the Local Bubble. Despite its relevance to life on Earth, the conditions in the Local Bubble and its exact configuration are not very well known. Besides that, there is some unknown interstellar substance that causes a host of absorption bands across the optical spectrum, called diffuse interstellar bands (DIBs).
Aims. We have started a project to chart the Local Bubble in a novel way and learn more about the carriers of the DIBs, by using DIBs as tracers of diffuse gas and environmental conditions.
Methods. We conducted a high signal-to-noise spectroscopic survey of 670 nearby early-type stars to map DIB absorption in and around the Local Bubble. The project started with a southern hemisphere survey conducted at the European Southern Observatory’s New Technology Telescope and has since been extended to an all-sky survey using the Isaac Newton Telescope.
Results. In this first paper in the series, we introduce the overall project and present the results from the southern hemisphere survey. We make available a catalogue of equivalent-width measurements of the DIBs at 5780, 5797, 5850, 6196, 6203, 6270, 6283, and 6614 Å, of the interstellar Na i D lines at 5890 and 5896 Å, and of the stellar He i line at 5876 Å. We find that the 5780 Å DIB is relatively strong throughout, as compared to the 5797 Å DIB, but especially within the Local Bubble and at the interface with a more neutral medium. The 6203 Å DIB shows similar behaviour with respect to the 6196 Å DIB. Some nearby stars show surprisingly strong DIBs, whereas some distant stars show very weak DIBs, indicating small-scale structure within, as well as outside, the Local Bubble. The sight lines with non-detections trace the extent of the Local Bubble especially clearly and show it opening out into the halo.
Conclusions. The Local Bubble has a wall that is in contact with hot gas and/or a harsh interstellar radiation field. That wall is perforated, though, causing leakage of radiation and possibly hot gas. On the other hand, compact self-shielded cloudlets are present much closer to the Sun, probably within the Local Bubble itself. As for the carriers of the DIBs, our observations confirm the notion that these are large molecules whose differences in behaviour are mainly governed by their differing resilience and/or electrical charge, with more subtle differences possibly related to varying excitation.
Key words: ISM: atoms / ISM: bubbles / ISM: lines and bands / ISM: molecules / ISM: structure / local insterstellar matter
Full Tables 1 and 3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/585/A12
© ESO, 2015
1. Introduction
The solar system moves through a region of unusually low gas density – the Local Bubble – initially discovered from the very low values of interstellar attenuation of starlight within 100 pc of the Sun (Fitzgerald 1968; Lucke 1978; cf. Lallement et al. 2014a). Lallement et al. (2003) and Welsh et al. (2010) mapped the Local Bubble in Na i and Ca ii interstellar absorption, revealing a central region of very low neutral/singly-ionized atomic gas absorption out to a distance of about 80 pc in most Galactic directions and vertically for hundreds of parsecs – presumably as far as the Galactic halo. However, the Ca ii maps did not show any sharp increase in absorption at a distance of 80 pc, leaving considerable uncertainty about the interface (“wall”) between the tenuous local and denser surrounding interstellar medium (ISM).
It has also been surprisingly difficult to assess the contents of the Local Bubble. Its possible origin in multiple supernova explosions (Frisch 1981; Cox & Anderson 1982; Maíz-Apellániz 2001; Breitschwerdt et al. 2009) has seemed to be corroborated at first by the detection of a diffuse soft-X-ray background (Snowden et al. 1998). While the putative million-degree gas was not seen in the expected extreme-UV emission by the CHIPS satellite (Hurwitz et al. 2005) nor in O vi 1032 Å absorption (Cox 2005; Barstow et al. 2010), recent works making use of soft X-ray shadows, Planck mm-wavelength data, and Local Bubble maps have now considerably reinforced the idea that there is such hot gas within the cavity (Snowden et al. 2015). The picture is complicated by the interaction between the heliosphere and surrounding ISM, such as charge exchange between the solar wind ions and interstellar atoms (e.g., Lallement et al. 2014b; Zirnstein et al. 2015; but see Galeazzi et al. 2014), indicating local “fluff” of a more neutral kind (Frisch 1998). Any novel way or tracer that can be used to map the Local Bubble is therefore highly desirable.
Bring on the diffuse interstellar bands (DIBs). These are a set of over 400 broad optical absorption features that are ubiquitous in the ISM (Herbig 1995; Sarre 2006). The nature of their carriers has been much debated since Mary Lea Heger first observed them almost a century ago (Heger 1922); the current consensus is that they are large carbonaceous molecules with some resistance to UV radiation (Tielens 2014). Observations of DIBs have shown that they are sensitive to their environment; for instance, the ratio of the 5780 and 5797 Å DIBs is a diagnostic of the level of irradiation and/or kinetic temperature (Cami et al. 1997). Differences in absorption between close binary stars have been detected, indicating that DIBs also trace tiny-scale structure in the ISM (Cordiner et al. 2013).
In this project we use DIBs to map the Local Bubble, by observing hundreds of early-type stars within a few hundred pc of the Sun. These stars have well-determined distances and proper motions, and future observations could reveal tiny-scale structure. Also, by probing very local interstellar matter the sight lines suffer less from overlapping cloud structures, so the behaviour of the various tracers may be simpler to interpret and more telling. DIBs have been used successfully to map extra-planar gas (van Loon et al. 2009; Baron et al. 2015) and the Magellanic Clouds (van Loon et al. 2013; Bailey et al. 2015), as well as parts of the Milky Way (Kos et al. 2014; Zasowski et al. 2015). The elusiveness of the gas within the Local Bubble, however, requires very low noise levels on the measurements and thus calls for dedicated observations. We have initiated such a dedicated observing campaign, first covering the southern hemisphere presented here and subsequently extending it to also cover the northern hemisphere (Farhang et al. 2015a, b, hereafter Papers II and III). The combined, all-sky survey is used to apply inversion techniques to reconstruct a complete three-dimensional map of the density of the DIB carriers (Farhang et al., in prep., hereafter Paper IV). In a fifth paper in the series we examine time variations of interstellar absorption due to the proper motions of the stars, incorporating measurements for stars in common with previous works (e.g., Raimond et al. 2012; Puspitarini et al. 2013).
2. Measurements – southern hemisphere survey
2.1. Targets
Catalogue of observed stars.
The targets were chosen from the Na i D Local Bubble survey of Lallement et al. (2003). The criteria used to select the targets were that they should be bright stars with B-band magnitudes <8.7, be of spectral type earlier than A5 (to provide a clean continuum), have well-known distances from Hipparcos and accurately known, high proper motions (for any future time-variability studies of the tiny scale structure of the ISM). In all, 238 stars were observed, with V-band magnitudes ranging from 2.9 to 8.4. Of these, 109 are of early-A spectral type, 128 of spectral type B, and one of spectral type O9.5. Information on the observed stars is listed in Table 1, the full version of which is available electronically at the Centre de Données astronomiques de Strasbourg (CDS).
The locations on the sky are shown in Fig. 1. There are some regions which have not been sampled as uniformly as others; this is partly due to the distribution of potential targets – with most of them being concentrated towards the Galactic plane – and partly due to adverse observing conditions. To gain a better appreciation of the sampling, we show the distributions of nearest-neighbour distance in 3D (in pc) in Fig. 2; typical sampling of 3D space is on 10–40 pc scales.
 |
Fig. 1 Distribution on the sky of the 238 observed stars as part of the southern hemisphere DIBs survey. The size of the symbol indicates the distance from the Sun. |
 |
Fig. 2 Distribution of nearest-neighbour distance, in pc, in the southern hemisphere DIBs survey. |
2.2. Observations
We obtained long-slit spectroscopic data using the 3.5 m New Technology Telescope (NTT) at the European Southern Observatory, La Silla, Chile. The observations were performed in visitor mode on the nights of 21st−23rd March 2011 and 15th−17th August 2011 (ESO programme 087.C-0405(A+B); PI: M.Bailey) and 19th−22nd August 2012 (ESO programme 0.89.C-0797; PI: M.Bailey).
The Faint Object Spectrograph and Camera (EFOSC2) were used with grism #20 and the 0.′′3 blue offset slit; this gave a resolving power of R = λ/Δλ = 5500, resulting in a two-pixel sampled spectral resolution of ≈1.1 Å (no binning of pixels on the CCD). This combination of grism and offset slit covers the wavelength range 5672–6772 Å, which includes the major λ5780, 5797, 5850, 6196, 6203, 6269, 6283 and 6614 DIBs. Grism #20 introduces a lateral shift of the beam. Therefore, the target was placed at column 1680 during acquisition to ensure the photons arrived approximately at Col. 1107 once the grism was put in place, which is an area on CCD#40 that is free from bad pixels (the dispersion direction runs along the columns of the CCD).
Exposure times were determined with the goal of reaching maximum count levels of ~40 000−50 000 counts per pixel, which is close to but below the CCD saturation level (65 535 counts); these ranged from 3.4 s to 847 s. The CCD was read out in its fast mode, as the read-out-noise was negligible compared to the photon noise. A minimum of three exposures were taken for each target to achieve a total signal-to-noise level (S/N) of ~2000 after the spectra had been combined. If the maximum counts per pixel was <20 000 a further three exposures were made. Exposure times were altered to accommodate changing conditions – the seeing varied between 0.′′4 and 2.′′4; some exposures resulted in saturation of the detector during moments of excellent seeing as the centering on the narrow slit became problematic.
Before the start of each night a set of calibration frames were taken. These comprised a large number of bias frames (>30), to remove the electronic offset level; dome flat fields (~60, using 4 × 1000 W quartz–halogen lamps) to correct for pixel-to-pixel sensitivity and throughput variations across the CCD; and He+Ar arc lamp exposures for wavelength calibration. The large number of bias and flat field frames was necessary in order for these not to limit the S/N on the calibrated spectra.
2.3. Data processing
Standard data reduction steps were applied: creation of master frames representing the bias level and flat field, respectively; subtraction of the master bias frame from the master flat and science frames; division of the science frames by the master flat; wavelength calibration on the basis of the He+Ar arc lamp spectrum. The spectra were then extracted from the calibrated 2D frames using the optimal (weighted) extraction method of Horne (1986). This also removed some particularly bright cosmic ray impacts upon the detector – though these were few in number due to the generally short integration times.
Two issues were encountered during data processing: bias instability and wavelength calibration offsets (for more details see Bailey 2014). The fast read-out mode makes use of two amplifiers, resulting in different bias levels for both halves of the detector. The bias level was found to vary over the course of the measurements in an unpredictable manner. It was thus decided in the second and third of the three observing runs to also obtain a bias frame after every science observation. The offset slit results in part of the CCD remaining unilluminated and we therefore decided to use the recorded count level at the edge furthest away from the illuminated part of the CCD, to determine an offset value with which to correct the master bias frame1.
EFOSC2 was originally designed to be mounted at the Cassegrain focus (of the ESO 3.6 m telescope) where the aperture wheel moved in a horizontal plane only inclining with the telescope. Now that EFOSC2 is located at the Nasmyth focus (of the NTT), flexure problems are experienced. This is due to the fact that the instrument is now turned on its side and gravity can influence the position of the slits depending on the rotator position of the instrument. The effect of the flexure is a variation of the position of the slit on the detector in the dispersion direction, which results in shifts of the wavelength scale that can be as big as several Å (EFOSC2 User’s Manual). We corrected for these offsets by recalibrating each spectrum using the telluric O2 absorption line at λ = 6278.1 Å.
2.4. Methodology
We here first describe the analysis of the 5780 Å DIB. A shallow broad absorption as well as a stellar absorption line at 5785 Å were fitted with a second-order polynomial and a Gaussian function, respectively, at the same time as fitting a Gaussian function to the 5780 Å DIB. While we considered fitting a Lorentzian instead, the above strategy worked well and is more in line with the choice of Gaussian found in the literature (Herbig 1975; Hobbs et al. 2008; Jenniskens & Désert 1994; Krełowski & Westerlund 1988; Westerlund & Krełowski 1988). The wavelength and typical width of the DIB was taken from the DIB catalogue of Jenniskens & Désert (1994), but these were allowed to vary by ±2 Å and 0.5 and 2 ×, respectively (±2 Å and ±0.2 Å for the stellar line). The instrumental resolution of 1.1 Å was sufficiently less than the expected width of the 5780 DIB (~2 Å) to determine the intrinsic profile shape, but this was not the case for the other DIBs under consideration here (~0.6−1.2 Å) except for the 6270 Å DIB (~3−4 Å). The actual fitting was coded in IDL using the mpfit routines, in the range 5773−5788 Å.
The equivalent width EW was determined by integrating the Gaussian function: 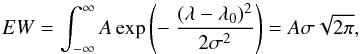 (1)where A is the peak intensity, λ0 the central wavelength and σ the width (with the Full Width at Half Maximum, FWHM = 2.355σ). The errors e0 resulting from mpfitexpr were scaled according to the χ2 deviations from the fit and the degrees of freedom f (the number of spectral elements minus the number of fitting parameters) as in:
(1)where A is the peak intensity, λ0 the central wavelength and σ the width (with the Full Width at Half Maximum, FWHM = 2.355σ). The errors e0 resulting from mpfitexpr were scaled according to the χ2 deviations from the fit and the degrees of freedom f (the number of spectral elements minus the number of fitting parameters) as in: 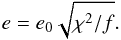 (2)Hence the error in the equivalent width is obtained from:
(2)Hence the error in the equivalent width is obtained from: ![\begin{equation} e[EW] = \sqrt{2\pi \left((e[A] \sigma)^2+(A e[\sigma])^2\right)}. \end{equation}](/articles/aa/full_html/2016/01/aa26656-15/aa26656-15-eq58.png) (3)The constraints on the fitting to the other absorption lines and DIBs are summarised in Table 2. In particular, the wavelengths of the other DIBs were guided by that of the strongest, 5780 Å DIB and allowed to vary much less (typically ±0.5 Å) to avoid spurious results. Likewise, the wavelength of the D1 (red) component of the Na i doublet was tied to that of the stronger D2 (blue) component; both components were fitted simultaneously. The spectral baseline was fitted with a first-order polynomial rather than the second-order polynomial above, except in some cases such as the Na i doublet where a shallow, broad absorption component was accounted for with a second-order polynomial – a second fit was obtained using a first-order polynomial, which was divided by the initial fit (including the second-order polynomial and two Gaussian functions) to reveal the broad absorption component. The 6196 and 6203 Å DIBs were also fitted simultaneously and here too a second-order polynomial was required for the continuum fitting. A second-order polynomial was also required for the 6270 Å DIB continuum as well as to take account of the telluric O2 line near the 6283 Å DIB (before fitting the DIB with a Gaussian and first-order polynomial). Finally, a second-order polynomial was required to account for modest fringing near the reddest of the DIBs under consideration, at 6614 Å.
(3)The constraints on the fitting to the other absorption lines and DIBs are summarised in Table 2. In particular, the wavelengths of the other DIBs were guided by that of the strongest, 5780 Å DIB and allowed to vary much less (typically ±0.5 Å) to avoid spurious results. Likewise, the wavelength of the D1 (red) component of the Na i doublet was tied to that of the stronger D2 (blue) component; both components were fitted simultaneously. The spectral baseline was fitted with a first-order polynomial rather than the second-order polynomial above, except in some cases such as the Na i doublet where a shallow, broad absorption component was accounted for with a second-order polynomial – a second fit was obtained using a first-order polynomial, which was divided by the initial fit (including the second-order polynomial and two Gaussian functions) to reveal the broad absorption component. The 6196 and 6203 Å DIBs were also fitted simultaneously and here too a second-order polynomial was required for the continuum fitting. A second-order polynomial was also required for the 6270 Å DIB continuum as well as to take account of the telluric O2 line near the 6283 Å DIB (before fitting the DIB with a Gaussian and first-order polynomial). Finally, a second-order polynomial was required to account for modest fringing near the reddest of the DIBs under consideration, at 6614 Å.
Overview of the Gaussian fitting constraints, in Å.
Spectral line measurements. EW stands for equivalent width, with e [ EW ] its uncertainty.
All spectra and fits were vetted by eye, guided by the value for EW/e [ EW ], and only fits deemed reliable were retained. The full table of measurements is available at CDS, with the first three entries shown in Table 3.
 |
Fig. 3 Correlations between the 5780, 5797, 6196 and 6614 Å DIBs. Distinction is made on the basis of the Na i absorption. Linear regression fits are overplotted, including some from the literature. |
3. Results
3.1. Detected spectral lines and bands
The He i (D3) line is stellar in origin but the Na i D1 & D2 doublet is mostly interstellar. The latter sits on a broader shallow absorption component, which is a combination of several telluric water lines typically one per cent of the continuum level (see Bailey 2014 for more details). The weak Na i absorption, ~5% of the continuum on average, illustrates how challenging it is to map the ISM within ~100 pc around the Sun.
The DIBs are more challenging still, less than one per cent of the continuum. The 5780 Å DIB is ~0.7% deep on average, but clearly detected in many of our targets. The nearby and diagnostic comparison 5797 Å DIB is <0.2% below the continuum. The 5850 Å DIB is very feeble and being next to a much stronger stellar feature to the red it is omitted from further analysis. The 6196 & 6203 Å DIBs are only ~0.1% deep on average, but sharp and more isolated and thus more useful. The 6270 Å DIB has a depth of typically a few 0.1% and is safe from the telluric O2 absorption to red, but it is broader and difficult to detect in individual targets and hence it is omitted from further analysis. Likewise, the 6283 Å DIB is omitted; it is but a mere fraction of a per cent of continuum and sits on the wing of the strong telluric O2 absorption to the blue. The 6614 Å DIB, on the other hand, is only 0.2% on average but it is well detected often enough to be useful for analysis.
3.2. Correlations
Linear regression analysis of DIB–DIB correlations of the form Y = a + bX with correlation coefficient r.
Figure 3a shows an excellent correlation between the equivalent widths of the 5780 and 5797 Å DIBs, up to some point beyond which increasing strength of the 5797 Å DIB is not accompanied by a noticeable increase in the strength of the 5780 Å DIB. This occurs for EW(5797) ≥ 0.04 Å, around EW(5780) ~ 0.15 Å. Compared to the Friedman et al. (2011) regression fit our sightlines seem to probe relatively strong 5780 Å DIBs except for the sight lines with the strongest 5797 Å DIB. The 5797 Å DIB favours a neutral environment, whereas the 5780 Å DIB favours an ionized environment so a strong detection of one should not necessarily be accompanied by a strong detection of the other. In Table 4 the results are summarised from a linear regression analysis and a Student t test: the correlation is significant if t>tcritical, where 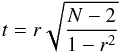 (4)with correlation coefficient r and N data points (N−2 degrees of freedom in this case). These analyses have not taken into account the uncertainties of the individual measurements. However, inspection of Fig. 3 shows that either the errors are fairly uniform in the cases where the scatter does not vary much along the correlation, or they increase with increasing equivalent widths in concert with the scatter. The exact treatment of the uncertainties should therefore not have a huge impact as they are already reflected in the scatter among the values. Hence we conclude that a good correlation is seen when the absorptions are fairly weak but the correlation breaks down above EW(5797) ≥ 0.04 Å.
(4)with correlation coefficient r and N data points (N−2 degrees of freedom in this case). These analyses have not taken into account the uncertainties of the individual measurements. However, inspection of Fig. 3 shows that either the errors are fairly uniform in the cases where the scatter does not vary much along the correlation, or they increase with increasing equivalent widths in concert with the scatter. The exact treatment of the uncertainties should therefore not have a huge impact as they are already reflected in the scatter among the values. Hence we conclude that a good correlation is seen when the absorptions are fairly weak but the correlation breaks down above EW(5797) ≥ 0.04 Å.
As examples of variations in the EW(5780) /EW(5797) ratio, Fig. 4 shows the spectra of HD 146284 and HD 169009. They have a similar EW(5780) but the EW(5797) = 0.058 Å of HD 169009 is twice the EW(5797) = 0.028 Å of HD 146284. While HD 146284 is further away from the Sun (d = 315 pc) than HD 169009 is (d = 102 pc), HD 146284 also is further away from the Galactic plane (z = 102 pc) than HD 169009 (z = 2.9 pc): while the longer column towards HD 146284 through the more tenuous extra-planar medium results in relatively strong diffuse band absorption, the harsher environment results in a relatively weaker 5797 Å DIB (cf. van Loon et al. 2009).
 |
Fig. 4 The 5780 and 5797 Å DIBs in the spectra of two stars at different distance to the Sun (d) and Galactic plane (z): top: HD 169009 at d,z = 102,2.9 pc; bottom: HD 146284 at d,z = 315,102 pc. The blue spectrum is the original spectrum before removing the stellar absorption line around 5785 Å; the red and green curves are the Gaussian fits to the 5780 and 5797 Å DIBs, respectively. |
A good correlation is found between the 6196 and 6614 Å DIBs (Fig. 3d). This particular pair of DIBs is said to have a “near perfect correlation” (McCall et al. 2010). However, at the generally low EW values in our study there appears to be a change from a tight steep slope up to EW(6196) < 0.01 Å and EW(6614) < 0.02 Å, to a shallower relation at greater EW values (cf. Table 4). Considering a continuous, monotonic relation throughout, and the regression fit from McCall et al., there is a suggestion in our data that some sight lines have an anomalously weak 6196 Å DIB – e.g., the datum at EW(6614) = 0.051, EW(6196) = 0.006 Å (HD 145102). Oddly enough, the McCall et al. data also showed some deviations at the weak end but in the opposite sense, with the 6614 Å DIB being weaker. This exemplifies the bias that can be introduced when sampling different sight lines, as well as distances (longer columns may sample multiple clouds hence yielding smoother relationships).
The 5780 and 5797 Å DIBs correlate well with the 6196 and 6614 Å DIB overall (Figs. 3b,c), but the correlations involving the 5797 Å DIB are much tighter than those involving the generally strong(er) 5780 Å DIB (cf. Table 4). This exemplifies the different diagnostic power of the 5780 Å DIB as compared to the other three DIBs – even though we noted that differences between the 6196 and 6614 Å DIB exist too (indeed, there is more scatter in the relations between the 5780 and 5797 Å DIBs with the 6614 Å DIB than with the 6196 Å DIB). Compared to the regression fits from Friedman et al. (2011), the 5780 and 6196 Å DIBs show an identical relation but the 6614 Å DIB seems to be much stronger in certain (but not all) sight lines; we confirm the Friedman et al. suggestion that the 5780 Å DIB is already seen when the 6614 Å DIB is not (a positive value for a at more than 4σ significance). As an example, Fig. 5 shows two sight lines where the spectra have been superimposed for the regions around the 5780, 5797 and 6614 Å DIBs; HD 18650 has a larger Galactic latitude (b = −25°) than HD 179406 (b = −8°). Clearly, their EW(5780) /EW(5797) ratio differs by about a factor two, but the EW(5797) /EW(6614) ratio is very similar.
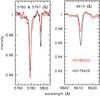 |
Fig. 5 The 5780, 5797 and 6614 Å DIBs in the spectra of HD 186500 and HD 179406; the latter is located closer to the Galactic plane. |
The DIBs weakly correlate with the Na i absorption, but with a lot of scatter; this indicates that in the typical warm neutral/weakly-ionized medium both are seen and they thus each correlate with overall gas column density. In Fig. 6 the behaviour of the 5780 and 5797 Å DIBs is compared to that of the Na i D2 line. There seems to be a threshold for the 5797 Å DIB only to be seen above EW(Na i D2) > 0.1 Å; instead, the 5780 Å DIB can sometimes be seen already at EW(Na i D2) ~ 0.05 Å. While this is in keeping with the 5780 Å DIB being stronger than the 5797 Å DIB, the data in Fig. 6 clearly show the emergence of the 5797 Å DIB above the threshold whereas the 5780 Å DIB appears to reach zero strength at zero Na i D2 absorption. This observation may be understood if the 5797 Å DIB needs a minimum gas column density for the environment to be sufficiently cool and/or shielded from UV radiation, whilst the 5780 Å DIB (and Na i) are also seen in more exposed diffuse ISM.
 |
Fig. 6 Correlations between the 5780 and 5797 Å DIBs, and Na i D2. Distinction is made according to Galactic latitude. |
Curiously, at moderate EW(Na i D2) ~ 0.2−0.3 Å the DIBs – especially the 5780 Å one – are particularly strong. Certainly the 5780 Å DIB is not anymore as strong once EW(Na i D2) ~ 0.4 Å. This could correspond to a greater ubiquity of material within which the carriers of the DIBs thrive, at moderate gas densities, with the 5780 Å DIB disappearing at high(er) densities. The strong DIB absorption is, however, only seen close to the Galactic plane, within about | b | < 40° (cf. Figs. 6a,b).
The EW(5780) /EW(5797) ratio shows an intriguing behaviour with respect to the Na i absorption (Fig. 6c): values EW(5780) /EW(5797) < 5 are seen across the entire range of Na i strength, but values EW(5780) /EW(5797) > 5 are exclusively – and commonly – seen only for EW(Na i D2) < 0.2 Å. Smith et al. (2013) find a similar extreme σ-cloud behaviour towards κ Velorum (not part of our sample) at a distance of ~165 pc (EW(5780) /EW(5797) > 22 at EW(Na i D2) = 0.12 Å). This can be understood if the Local Bubble is traced by EW(Na i D2) < 0.2 Å, where harsh UV irradiation is prevalent. Conversely, we may assume EW(Na i D2) = 0.2 Å as a proxy for the boundary between the Local Bubble and surrounding ISM. The sight lines with EW(Na i D2) < 0.2 Å but EW(5780) /EW(5797) < 5 are interesting as these may identify compact cloudlets with modest column density but high volume density.
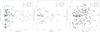 |
Fig. 7 Galactic latitude distribution vs. equivalent width of the 5780 and 5797 Å DIBs and Na i D2. Distinction is made according to distance. |
The huge scatter in the above correlation diagrams means that Na i is not a very good indicator of DIB carrier abundance (Merrill & Wilson 1938; Herbig 1995). The reason for this is partly due to the ionization potential of sodium; neutral sodium will trace weakly ionized gas as well as neutral gas. Therefore, it is not a very good discriminator between the two types of environment. DIBs, on the other hand, do discriminate between the two environments with the 5780 Å DIB favouring the weakly ionized gas and the 5797 Å DIB favouring the neutral gas. The use of the Na i D lines is further complicated by saturation effects already kicking in around EW(Na i D2) > 0.05 Å and the Na i D lines not tracing hydrogen column density in a linear fashion (Welty & Hobbs 2001). Hence, DIBs are a more discerning probe of the environment and give a more detailed picture of the diffuse ISM than Na i can, justifying our aim to map the Local Bubble in DIBs (cf. Baron et al. 2015).
3.3. Maps
The Galactic latitude distribution of equivalent widths is shown in Fig. 7 for the 5780 and 5797 Å DIBs and Na i D2. The latter shows no relation whatsoever, but the DIBs clearly are stronger towards the Galactic plane, within about | b | < 40°. The lack of dependence of Na i may be due in part to saturation though stronger Na i is seen towards more distant objects than in our survey (e.g., van Loon et al. 2009). Neither of these three tracers shows clear dependence on distance (colour-coded in the graphs). This implies that within a few hundred pc from the Sun, small-scale structure dominates the variations between different sight lines. As the DIBs do “detect” the Galactic plane they seem to be more useful tracers to map the Local Bubble than Na i.
To add a dimension, in Fig. 8 are plotted the sight lines in Galactic coordinates, i.e. projected on the sky, with EW values and distances to the Sun colour-coded and indicated by the size of the symbol, respectively. Thus we start to gain a more three-dimensional picture of the absorption. In these projections, there is a clear gap which corresponds to the northern hemisphere which is covered in Papers II and III. Also indicated are the directions towards the Magellanic Clouds, which have been studied in the past (e.g., Cox et al. 2006; van Loon et al. 2013) and is the subject of a large DIB survey presented in Bailey et al. (2015).
 |
Fig. 8 Distribution on the sky in Galactic coordinates, of the 5780 and 5797 Å DIBs and Na i D2. The EW values are colour-coded, and the distance to the Sun is indicated by the size of the symbol (smaller if farther). The directions towards the Small and Large Magellanic Clouds and Local Leo Cloud are also indicated. |
Of more immediate relevance is the location of the Local Leo Cloud, a nearby very cold cloud (T ~ 20 K) between 11.3−24.3 pc from the Sun. Hence it is well within the cavity of the Local Bubble and the closest known cold neutral gas cloud (Peek et al. 2011; Meyer et al. 2012). Our targets skirt this cloud but some sight lines from the northern hemisphere survey crossed it. In the present data set two sight lines just south of the cloud have rather strong 5780 Å DIB absorption, without detection of the 5797 Å DIB. This could be tracing the ionized skin of the cloud.
Overall, the strongest absorption is concentrated within ~± 25° of the Galactic plane (Fig. 8), but with exceptions. For instance, relatively strong absorption in both the 5780 and 5797 Å DIBs and Na i is seen around l ~ 190° and b ~ −25° to −40°. The wall of the Local Bubble may be extending farther away from the Galactic plane, possibly if it is relatively close to us. On the other hand, sight lines around l ~ 270° are more transparent despite quite long columns – especially when compared to the adjacent sight lines around l ~ 300°; perhaps the Local Bubble extends farther in the disc in the former direction.
The maps in Figs. 9 and 10 show the EW of the 5780 and 5797 Å DIBs and Na i D2, colour-coded, in two projections: onto the Galactic plane and in an orthogonal plane also crossing the Galactic centre (the “meridional” plane). In Fig. 10 non-detections are also shown, and in some cases, they would mask the detections, hence the separate plots. The Sun is marked at the coordinates (0, 0). The size of the symbols represents the distance from the projection plane, with circles representing targets that are above/in front and squares representing targets below/behind the plane, respectively.
 |
Fig. 9 Galactic maps of left to right: 5780 Å DIB, 5797 Å DIB and Na i D2 absorption, in projection top: onto the Galactic plane and bottom: in the meridional plane orthogonal to the Galactic plane. Only detections are included in these maps. |
Areas of strong 5780 and/or 5797 Å DIB absorption generally match areas of strong Na i D2 absorption and high Na0 volume density in the Welsh et al. (2010) map. There are fewer sight lines with detected 5797 Å DIB absorption, so these maps are sparser; however, if including the non-detections, Fig. 10 clearly shows the extent of the Local Bubble and, in particular, a “chimney” structure perpendicular to the Galactic plane, with 5797 Å DIB absorption confined to the plane. The 5780 Å DIB is also seen farther out along the chimney, commensurate with it being ubiquitious in the extra-planar gas (van Loon et al. 2009). The Local Bubble thus opens out into the halo in some tracers but not others. Likewise, the sight lines between l ~ 200° to 270° are transparent in the 5797 Å DIB, but absorption in the 5780 Å DIB is clearly seen along those same sight lines. This implies translucent density enhancements within the Local Bubble, or a fuzzier, extended transition rather than a sharp boundary between the Local Bubble and surrounding ISM. It is thus imperative not to ignore non-detections in mapping the ISM structure, as they clearly trace cavities but also can indicate porosity or clumpiness.
 |
Fig. 11 As in Fig. 9, but for the 5780 to 5797 Å DIB ratio. The panels on the right only show ratios derived from detections in both DIBs. |
This is emphasized in maps of the ratio of 5780 to 5797 Å DIB absorption (Fig. 11), where the paler colours trace the neutral gas in the wall of the Local Bubble and the darker colours trace the chimney. This is especially clear in the meridional plane projection, but even in the Galactic plane projection the cavity of the Local Bubble is clearly characterised by a larger 5780/5797 Å DIB ratio.
Another exciting thing revealed by this map is that within the Local Bubble cavity exist discrete regions of a low 5780/5797 Å DIB ratio; for instance towards HD 74521 at approx. (−90, −70) and (−90, + 70) pc in the Galactic plane and meridional plane, or HD 172910 at approx. (+ 130, 0) and (+ 130, −40) pc. These sight lines must be hitting clumps of cold neutral gas that somehow survive within the harsh environment of the Local Bubble.
4. Discussion
4.1. The carriers of the DIBs
DIBs are currently thought to have molecular carriers, with the DIBs representing vibronic transitions from a large number of different molecules (McCall et al. 2010). All molecules in a given sight line that give rise to a particular DIB are expected to be in their vibronic ground state, implying that two or more DIBs arising from that molecule should be part of a vibronic progression in the molecule; the relative strengths of the vibronic bands should then be exactly the same from one sight line to another (McCall et al. 2010). Therefore, a tight correlation between two DIBs is a promising, albeit insufficient, condition to identify DIBs with a common carrier (Josafatsson & Snow 1987). The problem is, of course, that these molecules may not be in the ground vibration state. Differences in excitation of low-lying energy levels might explain subtle differences between DIBs that on the whole behave concurrently.
The observations presented here of tenuous, generally exposed gas within and around the Local Bubble indicate that the 6196 and 6614 Å DIBs may not form as perfect a pair as recently suggested – McCall et al. (2010) determined a correlation coefficient of 0.99, while here we only determine r = 0.89. While our measurements are compatible with those of McCall et al., we show clear evidence of differing equivalent width ratios of these DIBs and we uncovered a statistically significant break in the relation around EW(6614) ~ 0.02−0.04 Å. Such behaviour at very low column densities may hold clues to the precise relation between the carriers of these two DIBs.
The measurements presented here show correlations between the 5780 and 5797 Å DIBs, on the one hand, and the 6196 and 6614 Å DIBs, on the other. The 5780 Å DIB correlates better with the 6196 Å DIB than with the 6614 Å DIB; the 5797 Å DIB correlates better with the 6614 Å DIB than the 5780 Å DIB does. This suggests that the carrier of the 6614 Å DIB is more closely related to that of the 5797 Å DIB than of the 5780 Å DIB. The 5797 Å DIB is also correlated with the 6196 Å DIB, even better than the 5780 Å DIB is. This suggests that the carrier of the 6196 Å DIB has similarities to those of the 5780 Å DIB and – especially – 5797 Å DIB. But, as the 5780 and 5797 Å DIB show different behaviour, the carrier of the 6196 Å DIB cannot be identical to both the carrier of the 5797 Å DIB and that of the 5780 Å DIB. In Fig. 12a the 6614/6196 Å DIB ratio is plotted against the 5780/5797 Å DIB ratio. While the 6614/6196 Å DIB ratio does vary between different sight lines, overall there is no correspondence to the behaviour of the 5780/5797 Å DIB ratio. The latter is clearly high for low Na0 column densities but the 6614/6196 Å DIB ratio is no different from that in denser columns. As in Fig. 6c, there also is a clear lower limit to the 5780/5797 Å DIB ratio ~2, and a similar lower limit is seen for the 6614/6196 Å DIB ratio.
Intriguingly, the 6203/6196 Å DIB ratio does correlate with the 5780/5797 Å DIB ratio (Fig. 12b). This is especially convincing for the denser columns, with EW(Na i D2) > 0.2 Å. The 6203/6196 Å DIB ratio seems to drop in more tenuous columns, with EW(Na i D2) < 0.2 Å (around EW(5780) /EW(5797) ≈ 5); perhaps this may be understood if the 6196 Å DIB is more readily formed than the 5797 Å DIB is (cf. Figs. 3e and 6) – as long as the radiation field is not inhibitive.
We confirm that the 5780 Å DIB favours weakly ionized environments and the 5797 Å DIB favours neutral environments, with the relation between the two breaking down above EW(5797) > 0.04 Å at high statistical significance: those denser clouds are dominated by neutral matter and the skin no longer grows in proportion. Compared to Na i, the 5780 and 5797 Å DIBs are weaker at higher Galactic latitude. This suggests that the carriers are eroded under the particularly harsh extra-planar conditions. Also, at | b | > 40° we could not detect both 6614 and 6196 Å DIBs.
 |
Fig. 12 The 6614 to 6196 Å DIB ratio vs. 5780 to 5797 Å DIB ratio. Distinction is made on the basis of the Na i D2 absorption; these four DIBs were never all detected at high Galactic latitudes (| b | > 40°). |
4.2. Implications for our understanding of the Local Bubble
The DIB maps of the Local Bubble presented in this work trace the cavity and the wall of the Local Bubble rather well. The sight lines with non-detections are of equal importance as the sight lines where DIBs are detected. In this regard the Na i map is less discriminative, as Na i absorption is nearly always detected and arises both in neutral and weakly-ionized gas. The “DIB-less” sight lines clearly reveal the extent of the cavity within the Galactic plane, as well as the vertical structure: the 5797 Å DIB map suggests a chimney opening out into the halo though the 5780 Å DIB is still detected high up in the extra-planar gas. This difference is due to the different alliance of these two DIBs to neutral and weakly-ionized gas, respectively. The “bursting’ of the Local Bubble has been noticed previously (e.g., Lallement et al. 2003; Welsh et al. 1999, 2010, 2004; Welsh & Shelton 2009; Welsh & Lallement 2012) but DIBs may indicate an extra-planar interface between the Local Bubble and halo.
Within the cavity, taking into account the distances to the targets, small neutral cloudlets are found. So even if the Local Bubble is filled with hot gas and/or the radiation field is unattenuated, denser, perhaps self-shielded structures do exist within it. On the other hand, the “wall” of the Local Bubble is porous, with some sight lines piercing through it out to large distances while adjacent sight lines encounter much absorption. This must have implications for the leakage of UV radiation – and possibly hot gas – out of the Local Bubble into the surrounding ISM, both within the halo and also the disc of the Milky Way.
5. Summary
In this first paper of a series we have presented the results from a southern hemisphere spectroscopic survey of 238 nearby early-type stars, aimed at mapping the ISM within and surrounding the Local Bubble in the 5780 and 5797 Å DIBs, and Na i. We also investigated the relationship with other DIBs detected in this spectral region, notably those at 6196 and 6614 Å, indicating subtle differences in their mutual behaviour. The DIB maps that include detections, as well as non-detections, clearly outline the extent of the Local Bubble within the Galactic plane, its vertical structure opening out into the halo, and the generally harsh conditions within the Local Bubble as indicated by a high 5780/5797 Å DIB ratio throughout. However, small more neutral cloudlets were seen close to the Sun as well, whilst the “wall” of the Local Bubble is far from impermeable. Thus we have demonstrated the viability of using DIBs to map local ISM, and we will use these data in combination with the complementary northern hemisphere survey to reconstruct a full three-dimensional map of the Local Bubble.
Acknowledgments
We wish to thank all of the staff at La Silla, and the dog. We also thank the referee for a positive report which has helped improve the presentation of our results. M.B. acknowledges an STFC studentship at Keele University. P.J.S. thanks the Leverhulme Trust for award of a Research Fellowship and the Leiden Observatory for hosting an extended visit. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
References
- Bailey, A. 2014, Ph.D. Thesis, Keele University [Google Scholar]
- Bailey, M., van Loon, J. Th., Sarre, P. J., & Beckman, J. E. 2015, MNRAS, 454, 4013 [NASA ADS] [CrossRef] [Google Scholar]
- Baron, D., Poznanski, D., Watson, D., Yao, Y., & Prochaska, J. X. 2015, MNRAS, 447, 454 [Google Scholar]
- Barstow, M. A., Boyce, D. D., Welsh, B. Y., et al. 2010, ApJ, 723, 1762 [NASA ADS] [CrossRef] [Google Scholar]
- Breitschwerdt, D., de Avillez, M. A., Fuchs, B., & Dettbarn, C. 2009, Space Sci. Rev., 143, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Cami, J., Sonnentrucker, P., Ehrenfreund, P., & Foing, B. H. 1997, A&A, 326, 822 [NASA ADS] [Google Scholar]
- Cordiner, M. A., Fossey, S. J., Smith, A. M., & Sarre, P. J. 2013, ApJ, 764, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, D. P. 2005, ARA&A, 43, 337 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Cox, D. P., & Anderson, P. R. 1982, ApJ, 253, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, N. L. J., Cordiner, M. A., Cami, J., et al. 2006, A&A, 447, 991 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farhang, A., Khosroshahi, H. G., Javadi, A., et al. 2015a, ApJ, 800, 64 (Paper II) [NASA ADS] [CrossRef] [Google Scholar]
- Farhang, A., Khosroshahi, H. G., Javadi, A., & van Loon, J.Th. 2015b, ApJS, 216, 33 (Paper III) [NASA ADS] [CrossRef] [Google Scholar]
- Fitzgerald, M. P. 1968, AJ, 73, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Friedman, S. D., York, D. G., McCallB, J., et al. 2011, ApJ, 727, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, P. C. 1981, Nature, 293, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, P. C. 1998, in The Local Bubble and Beyond, eds. D. Breitschwerdt, M. J. Freyberg, & J. Trümper, IAU Colloq. 166 (Springer-Verlag), Lect. Notes Phys., 506, 269 [Google Scholar]
- Galeazzi, M., Chiao, M., Collier, M. R., et al. 2014, Nature, 512, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, M. L. 1922, Lick Observatory Bulletin, 10, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 1975, ApJ, 196, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 1995, ARA&A, 33, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, L. M., York, D. G., Snow, T. P., et al. 2008, ApJ, 680, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurwitz, M., Sasseen, T. P., & Sirk, M. M. 2005, ApJ, 623, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., & Désert, F.-X. 1994, A&AS, 106, 39 [NASA ADS] [Google Scholar]
- Josafatsson, K., & Snow, T. P. 1987, ApJ, 319, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Kos, J., Zwitter, T., Wyse, R., et al. 2014, Science, 345, 791 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Krełowski, J., & Westerlund, B. E. 1988, A&A, 190, 339 [NASA ADS] [Google Scholar]
- Lallement, R., Welsh, B. Y., Vergely, J. L., Crifo, F., & Sfeir, D. 2003, A&A, 411, 447 [EDP Sciences] [Google Scholar]
- Lallement, R., Vergely, J.-L., Valette, B., et al. 2014a, A&A, 561, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lallement, R., Bertaux, J.-L., Quémerais, E., & Sandel, B. R. 2014b, A&A, 563, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucke, P. B. 1978, A&A, 64, 367 [NASA ADS] [Google Scholar]
- Maíz-Apellániz, J. 2001, ApJ, 560, L83 [NASA ADS] [CrossRef] [Google Scholar]
- McCall, B. J., Drosback, M. M., Thorburn, J. A., et al. 2010, ApJ, 708, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Merrill, P. W., & Wilson, O. C. 1938, ApJ, 87, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, D. M., Lauroesch, J. T., Peek, J. E. G., & Heiles, C. 2012, ApJ, 752, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Peek, J. E. G., Heiles, C., Peek, K. M. G., Meyer, D. M., & Lauroesch, J. T. 2011, ApJ, 735, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Puspitarini, L., Lallement, R., & Chen, H.-C. 2013, A&A, 555, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raimond, S., Lallement, R., Vergely, J. L., Babusiaux, C., & Eyer, L. 2012, A&A, 544, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sarre, P. J. 2006, J. Mol. Spectr., 238, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, K. T., Fossey, S. J., Cordiner, M. A., et al. 2013, MNRAS, 429, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Snowden, S. L., Egger, R., Finkbeiner, D. P., Freyberg, M. J., & Plucinsky, P. P. 1998, ApJ, 493, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Snowden, S. L., Koutroumpa, D., Kuntz, K. D., Lallement, R., & Puspitarini, L. 2015, ApJ, 806, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2014, in The Diffuse Interstellar Bands, eds. J. Cami, & N. L. J. Cox (Cambridge University Press), IAU Symp., 297, 399 [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Loon, J.Th., Smith, K. T., McDonald, I., et al. 2009, MNRAS, 399, 195 [NASA ADS] [CrossRef] [Google Scholar]
- van Loon, J.Th., Bailey, M., Tatton, B. L., et al. 2013, A&A, 550, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Welsh, B. Y., & Lallement, R. 2012, PASP, 124, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Welsh, B. Y., & Shelton, R. L. 2009, Astrophys. Space Sci., 323, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Welsh, B. Y., Sfeir, D. M., Sirk, M. M., & Lallement, R. 1999, A&A, 352, 308 [NASA ADS] [Google Scholar]
- Welsh, B. Y., Sallmen, S., & Lallement, R. 2004, A&A, 414, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Welsh, B. Y., Lallement, R., Vergely, J.-L., & Raimond, S. 2010, A&A, 510, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Welty, D. E., & Hobbs, L. M. 2001, ApJS, 133, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Westerlund, B. E., & Krełowski, J. 1988, A&A, 203, 134 [NASA ADS] [Google Scholar]
- Zasowski, G., Ménard, B., Bizyaev, D., et al. 2015, ApJ, 798, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Zirnstein, E. J., Heerikhuisen, J., & McComas, D. J. 2015, ApJ, 804, L22 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Spectral line measurements. EW stands for equivalent width, with e [ EW ] its uncertainty.
Linear regression analysis of DIB–DIB correlations of the form Y = a + bX with correlation coefficient r.
All Figures
 |
Fig. 1 Distribution on the sky of the 238 observed stars as part of the southern hemisphere DIBs survey. The size of the symbol indicates the distance from the Sun. |
| In the text | |
 |
Fig. 2 Distribution of nearest-neighbour distance, in pc, in the southern hemisphere DIBs survey. |
| In the text | |
 |
Fig. 3 Correlations between the 5780, 5797, 6196 and 6614 Å DIBs. Distinction is made on the basis of the Na i absorption. Linear regression fits are overplotted, including some from the literature. |
| In the text | |
 |
Fig. 4 The 5780 and 5797 Å DIBs in the spectra of two stars at different distance to the Sun (d) and Galactic plane (z): top: HD 169009 at d,z = 102,2.9 pc; bottom: HD 146284 at d,z = 315,102 pc. The blue spectrum is the original spectrum before removing the stellar absorption line around 5785 Å; the red and green curves are the Gaussian fits to the 5780 and 5797 Å DIBs, respectively. |
| In the text | |
 |
Fig. 5 The 5780, 5797 and 6614 Å DIBs in the spectra of HD 186500 and HD 179406; the latter is located closer to the Galactic plane. |
| In the text | |
 |
Fig. 6 Correlations between the 5780 and 5797 Å DIBs, and Na i D2. Distinction is made according to Galactic latitude. |
| In the text | |
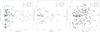 |
Fig. 7 Galactic latitude distribution vs. equivalent width of the 5780 and 5797 Å DIBs and Na i D2. Distinction is made according to distance. |
| In the text | |
 |
Fig. 8 Distribution on the sky in Galactic coordinates, of the 5780 and 5797 Å DIBs and Na i D2. The EW values are colour-coded, and the distance to the Sun is indicated by the size of the symbol (smaller if farther). The directions towards the Small and Large Magellanic Clouds and Local Leo Cloud are also indicated. |
| In the text | |
 |
Fig. 9 Galactic maps of left to right: 5780 Å DIB, 5797 Å DIB and Na i D2 absorption, in projection top: onto the Galactic plane and bottom: in the meridional plane orthogonal to the Galactic plane. Only detections are included in these maps. |
| In the text | |
 |
Fig. 10 As in Fig. 9, with non-detections included. |
| In the text | |
 |
Fig. 11 As in Fig. 9, but for the 5780 to 5797 Å DIB ratio. The panels on the right only show ratios derived from detections in both DIBs. |
| In the text | |
 |
Fig. 12 The 6614 to 6196 Å DIB ratio vs. 5780 to 5797 Å DIB ratio. Distinction is made on the basis of the Na i D2 absorption; these four DIBs were never all detected at high Galactic latitudes (| b | > 40°). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


