| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 8 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201526978 | |
| Published online | 24 November 2015 | |
Dimerization of methanimine and its charged species in the atmosphere of Titan and interstellar/cometary ice analogs
1
Scuola Normale Superiore, 56126
Pisa, Italy
2
Dipartimento di Chimica, Biologia e Biotecnologie, Università
degli Studi di Perugia, 06123
Perugia,
Italy
e-mail: nadia.balucani@unipg.it
3
Université Grenoble Alpes, IPAG, 38000
Grenoble,
France
4
Dipartimento di Ingegneria Civile e Ambientale, Università degli
Studi di Perugia, 06125
Perugia,
Italy
5
CNR-ISTM, 06123
Perugia,
Italy
Received:
16
July
2015
Accepted:
27
August
2015
Aims. We theoretically investigated the dimerization of methanimine, CH2=NH, a process that has been invoked to explain the formation of haze in the atmosphere of Titan and nitrogen organic compounds in interstellar/cometary ice analogs.
Methods. We used density functional theory to characterize the minima and transition states of the investigated processes, while we computed the energetics with the more accurate coupled cluster method. We then obtained rate coefficients via combination of capture theory and statistical calculations.
Results. The process involving two neutral molecules is characterized by significant energy barriers and cannot occur under the low temperature conditions of Titan or interstellar/cometary ices unless an external energy source is provided. On the contrary, the processes involving one molecule of either ionized or protonated methanimine are barrierless reactions and can therefore contribute to the formation of larger ions. In particular, the reaction involving ionized methanimine can also be efficient in the very low temperature conditions of the interstellar medium, leading to products of general formula C2N2H5+.
Conclusions. The present work suggests that polymerization of methanimine is not an efficient process in space unless an ionization/protonation or a significant energy source is available.
Key words: ISM: molecules / planets and satellites: individual: Titan
© ESO, 2015
1. Introduction
Methanimine, CH2=NH, is alleged to be an important species in prebiotic chemistry since it is a possible precursor of the simplest amino acid, glycine, via its subsequent reactions with HCN and H2O (Balucani 2009, 2012; Woon 2002), and it is an essential intermediate in the Strecker synthesis of aminoacetonitrile (Danger et al. 2011) and glycine (Rimola et al. 2010; Ugliengo et al. 2011; He & Smith 2014; Holtom et al. 2005; Arnaud et al. 2000). Methanimine was observed a long time ago in the interstellar medium (Godfrey et al. 1973). For a survey, the interested reader can see Dickens et al. (1997) and also Turner et al. (1999). The presence of methanimine has been inferred in the upper atmosphere of Titan, the massive moon of Saturn, from the analysis of the ion spectra recorded by Cassini Ion Neutral Mass Spectrometer (INMS), where a strong peak attributed to the protonated form of methanimine was identified (Vuitton et al. 2006). Starting from that, a mole fraction of ca. 1 × 10-5 for the neutral methanimine was retrieved at 1100 km (Vuitton et al. 2007). The atmosphere of Titan is mainly composed of dinitrogen (95−98%) and methane (2−5%) while other components (simple nitriles such as HCN, and also other small hydrocarbons, like C2H6) are present in trace amounts (Vuitton et al. 2014 and references therein). Methanimine is produced in the atmosphere of Titan through reactions involving the first electronically excited state of atomic nitrogen, N(2D), and methane or ethane, (Balucani et al. 2009, 2010), as well as through the reaction between NH and CH3 (Redondo et al. 2006) or reactions involving ionic species (Yelle et al. 2010). The photochemical model by Lavvas et al. (2008a,b) derived a larger quantity of methanimine than that inferred by the analysis of the ion spectra recorded by Cassini INMS, which is also the case for the most recent model of Loison et al. (2015), which specifically addresses the chemical pathways toward the formation of nitrogen containing organic molecules. The reason for this discrepancy is possibly due to the uncertainty associated with the loss processes of methanimine caused by a severe lack of knowledge about the chemistry of this species. CH2=NH absorbs in the UV region (Teslja et al. 2004) and its photolysis leads to HCN/HNC + H2 or H2CN + H (Larson et al. 2006). In addition, with a C=N double bond, methanimine is a highly reactive molecule that can react with atomic/radical species and with ions, which are present in the upper atmosphere of Titan. This has been recently verified by a theoretical study of the fast reaction of methanimine with CN radicals, which are also relatively abundant in the upper atmosphere of Titan (Vazart et al. 2015). Vacuum UV photons can ionize methanimine in the thermosphere of Titan or in the interstellar medium. According to the recent determination by Holzmeier et al. (2013), the adiabatic ionization energy of methanimine is 9.99 eV and at the Lyman alpha wavelength ionization of methanimine is already efficient. Also, the high proton affinity value of CH2=NH easily leads to its protonation through reactions with the major ions in the upper atmosphere of Titan (Loison et al. 2015) as well as in the interstellar medium.
Notably, imines are compounds which are well known for their capability of polymerizing under normal terrestrial conditions. Methanimine, the smallest imine, is actually considered a transient species (in spite of its being a singlet closed-shell molecule) because, once prepared, it polymerizes immediately unless kept at a very low temperature. For this reason, polymerization of methanimine has been considered to be responsible for the production of a cyclic trimer (hexahydro-1,3,5-triazine, a precursor of hexamethylenetetramine) when irradiating with a UV lamp a mixture of H2O:CH3OH:CO:NH3 at 12 K by Bernstein et al. (1995). Later, Vinogradoff et al. (2012) confirmed the importance of methanimine in the formation of 1,3,5-triazinane (an intermediate species toward hexahydro-1,3,5-triazine formation) and polymethylenimine in non-UV exposed NH2CH2OH:HCOOH ice mixtures between 290 and 330 K. Vuitton et al. (2007) suggested that a similar process could account for the missing quantitative loss process in the atmosphere of Titan, while Lavvas et al. (2008a,b) went further by suggesting that polymerization of methanimine could be an important step in the formation of the haze aerosols in the Titan upper atmosphere. Indeed, there is overwhelming evidence that the aerosols, which form the haze of Titan, are composed of organic macromolecules that are very rich in nitrogen (Israel et al. 2015; Imanaka & Smith 2010; Gu et al. 2009; Carrasco et al. 2009; Cable et al. 2012). Therefore, CH2=NH is an excellent monomer candidate to account for the nitrogen-rich aerosols of Titan through polymerization.
To explore further the role of methanimine polymerization in the formation of the Titan nitrogen-rich aerosols or interstellar/cometary ice analogs, we recently reported on a preliminary theoretical characterization of methanimine dimerization, which is the first polymerization step in a purely gaseous environment (Rosi et al. 2013). According to this preparatory work, however, the formation of a bound dimer from two CH2=NH monomers requires an amount of energy that is impossible to surmount in the low temperature environment of Titan and in that of cold interstellar objects. In this respect, the methanimine case is very similar to the case of the more widely explored HCN polymerization. HCN is known to easily polymerize in the condensed phase, forming many species of prebiotic interest (Matthews 1995) and, therefore, HCN was considered to polymerize also in the interstellar medium (Chakrabarti & Chakrabarti 2000). However, Smith et al. (2001) proved that the dimerization process in the gas phase is characterized by a very high barrier, thus precluding any significant role of HCN dimerization in space.
We have extended our electronic structure calculations to the case of the charged species of methanimine, that is, ionized methanimine and protonated methanimine. The aim is to verify whether polymerization involving charged species (which are relatively abundant in the ionosphere of Titan and can also be present in the interstellar medium) in the first dimerization step is a much more effective route. This approach is similar to that used by Yim & Choe (2012) and Jung & Choe (2013), who explored the possibility that the reaction between HCN or HNC with the protonated species HCNH+ could lead to cyanomethanimine, the dimer of HCN. According to their calculations, indeed, the presence of a proton substantially lowers the reaction barriers.
In addition to electronic structure calculations, we also determined reaction rate coefficients using a capture model and a Rice-Ramsperger-Kassel-Marcus (RRKM) method to assess the role of the open reaction channels. For the dimerization of the neutral monomers, we also repeated the electronic structure calculations at a higher level than that previously employed, but the overall picture has not changed. This paper is organized as follows: in Sect. 2 computational details of the electronic structure calculations are given; in Sect. 3 the employed capture theory and RRKM models are described; in Sect. 4 the results are discussed; and in Sect. 5 a conclusion is presented and the implications for the atmospheric models of Titan are noted.
2. Details of the electronic structure calculations
The potential energy surfaces (PESs) of the species of interest have been characterized by locating the lowest stationary points at the B3LYP (Becke 1993; Stephens et al. 1994) level of theory in conjunction with the correlation consistent valence polarized set aug-cc-pVTZ (Dunning 1989; Woon & Dunning 1993; Kendall et al. 1992). At the same level of theory, we computed the harmonic vibrational frequencies to check the nature of the stationary points, i.e., minimum, if all the frequencies are real, saddle point, if there is one (and only one) imaginary frequency. The assignment of the saddle points was performed using intrinsic reaction coordinate (IRC) calculations (Gonzalez & Schlegel 1989, 1990). The energy of the main stationary points was also computed at the higher level of calculations CCSD(T) (Bartlett 1981; Raghavachari et al. 1989; Olsen et al. 1996) using the same basis set aug-cc-pVTZ. At this level of theory, the relative energies of all the systems are expected to be computed with a precision of about ±5 kJ/mol. However, the relative energies are reported with a precision of ±1 kJ/mol to avoid excessive approximations. Both the B3LYP and the CCSD(T) energies were corrected to 0 K by adding the zero point energy correction computed using the scaled harmonic vibrational frequencies evaluated at the B3LYP/aug-cc-pVTZ level. All calculations were done using Gaussian 09 (Frisch et al. 2009) while the analysis of the vibrational frequencies was performed using Molekel (Flükiger et al. 2000).
3. Kinetics calculations
We obtained rate constants via a combination of capture theory and RRKM calculations, using the same code we developed and described in previous papers (Leonori et al. 2009, 2013; Balucani et al. 2015). The rate constant for the formation of the initial intermediate is calculated using capture theory as detailed in Vazart et al. (2015). Within this scheme, the energy is calculated for various points along the distance coordinate of the two reactants and the energy values are fitted to an equation of the form 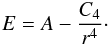 (1)Subsequently, the constant C4 and the reduced mass is used to calculate a (energy independent) capture rate constant. We prefer this approach, where C4 is derived from energy calculations for this specific system, rather than using the recently proposed general scheme for ion-polar molecule reactions (Wakelam et al. 2010). With this approach, we take the whole interaction between the two approaching units fully into account, rather than approximating it as a sum of multipole interactions (Wakelam et al. 2012).
(1)Subsequently, the constant C4 and the reduced mass is used to calculate a (energy independent) capture rate constant. We prefer this approach, where C4 is derived from energy calculations for this specific system, rather than using the recently proposed general scheme for ion-polar molecule reactions (Wakelam et al. 2010). With this approach, we take the whole interaction between the two approaching units fully into account, rather than approximating it as a sum of multipole interactions (Wakelam et al. 2012).
Enthalpy changes and barrier heights (kJ/mol, 0 K) computed at the B3LYP/aug-cc-pVTZ and CCSD(T)/aug-cc-pVTZ levels of theory for selected dissociation and isomerization processes for the systems (CH2NH)2, (CH2NH)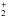 and (CH2NH)2H+.
and (CH2NH)2H+.
The microcanonical rate constant for each elementary unimolecular step is calculated using the following formula: 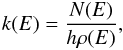 (2)where \begin{lxirformule}$N(E)$\end{lxirformule} denotes the sum of states in the transition state at energy E, ρ(E) is the reactant density of states at energy E, and h is Planck’s constant. The sum of the states N(E) is obtained by integrating the relevant density of states up to energy E and the rigid rotor/harmonic oscillator model is assumed. Both densities of states are appropriately symmetrized with respect to the number of identical configurations of the reactants and/or transition state. Where possible, we consider tunneling and quantum reflection, using the corresponding imaginary frequency of the transition state and calculating the tunneling probability for the corresponding Eckart barrier. After we calculate all microcanonical rate constants, the master equation is solved for the particular energies of interest. We set up a matrix k of the rate constants such that each off-diagonal element kij represents the rate constant from channel j to channel i, and the diagonal elements are such that the sum of each column is 0. According to this definition, the time derivative of the concentration vector, c, for all species involved is
(2)where \begin{lxirformule}$N(E)$\end{lxirformule} denotes the sum of states in the transition state at energy E, ρ(E) is the reactant density of states at energy E, and h is Planck’s constant. The sum of the states N(E) is obtained by integrating the relevant density of states up to energy E and the rigid rotor/harmonic oscillator model is assumed. Both densities of states are appropriately symmetrized with respect to the number of identical configurations of the reactants and/or transition state. Where possible, we consider tunneling and quantum reflection, using the corresponding imaginary frequency of the transition state and calculating the tunneling probability for the corresponding Eckart barrier. After we calculate all microcanonical rate constants, the master equation is solved for the particular energies of interest. We set up a matrix k of the rate constants such that each off-diagonal element kij represents the rate constant from channel j to channel i, and the diagonal elements are such that the sum of each column is 0. According to this definition, the time derivative of the concentration vector, c, for all species involved is 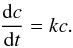 (3)In order to determine the behavior of c in the infinite future we diagonalize the matrix k and determine its eigenvectors. These eigenvectors either correspond to eigenvalues with a negative real part (vanishing in the infinite future) or 0 (stable eigenvectors). Expressing the initial concentration vector as a linear combination of these eigenvectors, we can determine the same vector in the infinite future by simply eliminating all vanishing eigenvectors from the expansion. In this matrix, the possibility of dissociation of the initial intermediate back to reactants is also taken into account. As the reactant density of states rises steeply with energy (because of the presence of multiple rotational degrees of freedom), the rate of this dissociation becomes important with increasing temperature, strongly reducing the apparent value of the capture theory rate constant. As in all RRKM calculations, efficient energy redistribution among the various degrees of freedom is assumed. Within the capture theory model, a collision is assumed to lead to a successful capture if it has enough energy to overcome the centrifugal barrier (with no tunneling).
(3)In order to determine the behavior of c in the infinite future we diagonalize the matrix k and determine its eigenvectors. These eigenvectors either correspond to eigenvalues with a negative real part (vanishing in the infinite future) or 0 (stable eigenvectors). Expressing the initial concentration vector as a linear combination of these eigenvectors, we can determine the same vector in the infinite future by simply eliminating all vanishing eigenvectors from the expansion. In this matrix, the possibility of dissociation of the initial intermediate back to reactants is also taken into account. As the reactant density of states rises steeply with energy (because of the presence of multiple rotational degrees of freedom), the rate of this dissociation becomes important with increasing temperature, strongly reducing the apparent value of the capture theory rate constant. As in all RRKM calculations, efficient energy redistribution among the various degrees of freedom is assumed. Within the capture theory model, a collision is assumed to lead to a successful capture if it has enough energy to overcome the centrifugal barrier (with no tunneling).
4. Results and discussion
Enthalpy changes and barrier heights (kJ/mol, 0 K) computed at the B3LYP/aug-cc-pVTZ and CCSD(T)/aug-cc-pVTZ levels of theory for selected dissociation and isomerization processes for the systems (CH2NH)2, (CH2NH)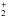 and (CH2NH)2H+ are reported in Table 1. In the following discussion, we only comment on the more accurate CCSD(T) results, while the B3LYP/aug-cc-pVTZ data are only shown for comparison between the two levels of calculations. The computed adiabatic ionization energy of methanimine at the CCSD(T) level is 9.88 eV, in good agreement with the experimental value of 9.99 eV (Holzmeier et al. 2013). The proton affinity of methanimine is 862 kJ/mol in the present calculations, which compares well with the accepted value of 853.6 kJ/mol (Vuitton et al. 2007).
and (CH2NH)2H+ are reported in Table 1. In the following discussion, we only comment on the more accurate CCSD(T) results, while the B3LYP/aug-cc-pVTZ data are only shown for comparison between the two levels of calculations. The computed adiabatic ionization energy of methanimine at the CCSD(T) level is 9.88 eV, in good agreement with the experimental value of 9.99 eV (Holzmeier et al. 2013). The proton affinity of methanimine is 862 kJ/mol in the present calculations, which compares well with the accepted value of 853.6 kJ/mol (Vuitton et al. 2007).
4.1. Dimerization of methanimine
The dimerization of methanimine leads to several minima, the structures and relative energies of which are reported in Fig. 1.
 |
Fig. 1 B3LYP optimized geometries (Å and °) and CCSD(T) relative energies (with respect to 2 × CH2NH (kJ/mol) at 0 K) of minima localized on the PES of the dimer of CH2NH. |
We find some differences between the energy values derived with the two methods (Rosi et al. 2013). This difference is due to correlation effects, which are better described at the CCSD(T) level. For this reason, we always consider CCSD(T) energies, while the B3LYP method is used for geometry optimizations where it is known to provide reliable results. In all cases, however, the general picture of the reaction does not change. The approach of two neutral methanimine molecules leads to the formation of a slightly stabilized van der Waals adduct (1) (−15 kJ/mol with respect to the energy of the two isolated methanimine molecules at the CCSD(T) level of calculations) in a barrierless process. Species (1) can isomerize to (2), which shows, instead, a real N−N bond, but it is slightly less stable than (1). The transfer of a hydrogen atom gives rise to species (3), which is much less stable than (1) and (2). The (3) intermediate, however, can give rise to species (4), which is again bound with respect to the two separated molecules of methanimine by 19 kJ/mol. All these isomerization processes, however, are characterized by very high energy barriers, ranging from ca. 200 to 360 kJ/mol. The transition states for the 1 → 2, 2 → 3, and 3 → 4 isomerization processes are reported in Fig. 2. In addition, species (1) can also isomerize to the more stable species (5) through a barrier as high as 204 kJ/mol. This species can isomerize to the less stable species (6) through a very high barrier (295 kJ/mol). Because of the very high isomerization barriers, we did not investigate this reaction channel any further.
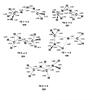 |
Fig. 2 B3LYP optimized geometries (Å and °) and CCSD(T) relative energies (with respect to 2 × CH2NH (kJ/mol) at 0 K) of saddle points localized on the PES of the dimer of CH2NH. |
In Fig. 3 we summarized these results, reporting a schematic representation of the minimum energy path leading to the dimerization of methanimine. As is clearly visible, huge isomerization barriers link the various intermediates. The presence of high barriers suggests that methanimine dimerization cannot be an important process under the conditions of Titan, i.e., a surface temperature of 94 K and a temperature of ca. 180 K in the upper layers of the atmosphere, unless a significant external energy source is provided. Because of the very unfavorable reaction profile, we have not attempted kinetics calculations as the relative rate coefficients can only be negligible.
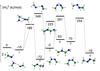 |
Fig. 3 Schematic representation of the PES of the dimer of CH2NH. We only show CCSD(T) energies (kJ/mol, 0 K), for simplicity. |
4.2. The reaction of methanimine with protonated methanimine, CH2NH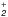
The energy profile associated with the interaction of a neutral molecule of methanimine with a protonated second molecule of methanimine is completely different. The process is barrierless and leads to a bound species, 1H+, whose structure is shown in Fig. 4. 1H+ is more stable than the separated reactants by 120 kJ/mol. However, 1H+ can only dissociate back to reactants or to five sets of products in very endothermic channels (see Fig. 5). Under the low T (≤180 K) conditions of Titan, there is not enough energy to compensate for the high endothermicity of the above mentioned channels and 1H+ dissociates back to the reactants. According to our kinetics analysis, in a collision free environment at 180 K the average lifetime of 1H+ is 7.5 × 10-12 s. In those conditions, collisional stabilization or stabilization by spontaneous emission of photons are marginal phenomena. In denser regions of the atmosphere of Titan, 1H+ could be, instead, collisionally stabilized, but its abundance is expected to be negligible because protonated methanimine is only formed significantly in the ionosphere.
 |
Fig. 4 B3LYP optimized geometry (Å and °) of the addition product of a protonated methanimine molecule to a neutral methanimine molecule. Also, the geometry of the protonated methanimine is shown. CCSD(T) relative energy with respect to CH2NH + CH2NH |
4.3. The reaction of methanimine with ionized methanimine, CH2NH+
The interaction of a neutral molecule of methanimine with an ionized second molecule of methanimine leads without a barrier to the bound (−167 kJ/mol with respect to the reactants) intermediate 1+, the structure of which is shown in Fig. 6. Its conformational isomer 1b+, also correlating with the reactants, is more stable than 1+ by 23 kJ/mol. However, species 1+ is more interesting than species 1b+ since it can isomerize, through a barrier of 137 kJ/mol, to the most stable intermediate 2+ or can directly dissociate, through a barrier of 151 kJ/mol, into CH2NHCHNH+ (trans) + H.
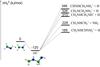 |
Fig. 5 Schematic representation of the PES of (CH2NH)2H+. Only CCSD(T) energies (kJ/mol, 0 K) are shown for simplicity. |
 |
Fig. 6 B3LYP optimized geometries (Å and °) and CCSD(T) relative energies with respect to CH2NH + CH2NH+ (kJ/mol) at 0 K of minima and saddle points localized on the PES of (CH2NH) |
The intermediate 2+ shows three low-lying dissociation pathways, as reported in Fig. 7 and Table 1, namely: (i) CH2NCHNH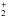 + H in an exothermic channel, by 109 kJ/mol with respect to the reactants asymptote, characterized by an exit barrier of 231 kJ/mol; (ii) CH2NHCHNH+ (trans) + H in an exothermic process, by 42 kJ/mol with respect to the reactants asymptote, characterized by an exit barrier of 284 kJ/mol; and (iii) CH2NHCHNH+ (cis) + H in an exothermic process, by 69 kJ/mol, characterized by an exit barrier of 262 kJ/mol. Other dissociation processes are very high in energy and are not reported in Fig. 7, while they are included in Table 1.
+ H in an exothermic channel, by 109 kJ/mol with respect to the reactants asymptote, characterized by an exit barrier of 231 kJ/mol; (ii) CH2NHCHNH+ (trans) + H in an exothermic process, by 42 kJ/mol with respect to the reactants asymptote, characterized by an exit barrier of 284 kJ/mol; and (iii) CH2NHCHNH+ (cis) + H in an exothermic process, by 69 kJ/mol, characterized by an exit barrier of 262 kJ/mol. Other dissociation processes are very high in energy and are not reported in Fig. 7, while they are included in Table 1.
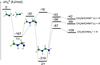 |
Fig. 7 Schematic representation of the PES of (CH2NH) |
 |
Fig. 8 Rate constants as a function of temperature: back dissociation (dashed line), CH2NCHNH |
As already mentioned, the capture process is energy independent and thus the corresponding rate constant is independent of temperature. In Fig. 8, the rate constants for the formation of CH2NCHNH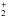 (species 1), CH2NHCHNH+ (cis) (species 2), CH2NHCHNH+ (trans) (species 3) are shown, as well as the rate constant for back dissociation to reactants. The sum of all four rate constants is equal to the temperature independent capture rate constant. For all three products, their rate constant shows a clearly decreasing trend and this is because, as can be seen, the rate of back dissociation increases very rapidly with temperature. The reason for this trend lies in the entropy of activation for the back-dissociation process and, in particular, in the presence of many rotational degrees of freedom in the reactants, which rapidly increase their density of states. According to our kinetics analysis, the formation of CH2NCHNH
(species 1), CH2NHCHNH+ (cis) (species 2), CH2NHCHNH+ (trans) (species 3) are shown, as well as the rate constant for back dissociation to reactants. The sum of all four rate constants is equal to the temperature independent capture rate constant. For all three products, their rate constant shows a clearly decreasing trend and this is because, as can be seen, the rate of back dissociation increases very rapidly with temperature. The reason for this trend lies in the entropy of activation for the back-dissociation process and, in particular, in the presence of many rotational degrees of freedom in the reactants, which rapidly increase their density of states. According to our kinetics analysis, the formation of CH2NCHNH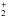 largely prevails over the other two products, despite the fact that CH2NHCHNH+ (trans) can be formed through two pathways, that is, either by the direct dissociation of the intermediate 1+ or by the dissociation of species 2+ (see Fig. 7). This can be easily rationalized in terms of the lower transition state leading from 1+ to 2+ and, then, by the lowest transition state associated with the channel leading to CH2NCHNH
largely prevails over the other two products, despite the fact that CH2NHCHNH+ (trans) can be formed through two pathways, that is, either by the direct dissociation of the intermediate 1+ or by the dissociation of species 2+ (see Fig. 7). This can be easily rationalized in terms of the lower transition state leading from 1+ to 2+ and, then, by the lowest transition state associated with the channel leading to CH2NCHNH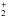 + H among those associated with the products.
+ H among those associated with the products.
An interesting effect is seen in the trends of the other two products, namely, the formation of species 2 prevails for very low temperatures and, subsequently, species 3 becomes more abundant. The reason for this lies in the fact that rearrangement of the initial intermediate has a lower energy barrier than hydrogen elimination to give species 3, and also, subsequently, the second intermediate has a lower energy barrier to form species 2. At low temperatures, energy considerations are expected to be fundamental. However, as the temperature is raised, a significant fraction of the initial intermediate gives species 3, while the fraction that rearranges to give the second intermediate goes over predominantly to species 1. The result of this is to slightly raise the rate of species 3 formation over species 2.
In the range of temperature of interest to the upper atmosphere of Titan (between 150 and 200 K), while the global capture rate coefficient is given by 1.752 × 10-9 cm3 s-1, the reactive rate coefficient for the channel leading to CH2NCHNH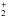 + H is expressed by 5.5 × 10-12 cm3 s-1× (T/ 300)-2.70 × exp(−40.67 /T). For the channels leading to trans and cis CH2NHCHNH+, the rate coefficient expression is 2.89 × 10-14 cm3 s-1 × (T/ 300)-2.39 × exp(−39.50 /T) and 9.17 × 10-15 cm3 s-1 × (T/ 300)-2.61 × exp(−37.50 /T), respectively (we have chosen to retain enough significant figures in our results to avoid round-off errors).
+ H is expressed by 5.5 × 10-12 cm3 s-1× (T/ 300)-2.70 × exp(−40.67 /T). For the channels leading to trans and cis CH2NHCHNH+, the rate coefficient expression is 2.89 × 10-14 cm3 s-1 × (T/ 300)-2.39 × exp(−39.50 /T) and 9.17 × 10-15 cm3 s-1 × (T/ 300)-2.61 × exp(−37.50 /T), respectively (we have chosen to retain enough significant figures in our results to avoid round-off errors).
5. Conclusion and implication for the atmospheric models of Titan and interstellar/cometary ice analogs
In this work we have analyzed the possible gas-phase reactive pathways associated with the dimerization of methanimine and with the reactions between a molecule of methanimine and its ionized or protonated forms. Those interactions can lead to the formation of new bound species. The geometry and characteristics of all these new species, many of them never characterized before to the best of our knowledge, are reported in Table 1 and shown in Fig. 9. In the low temperature conditions of Titan and in the absence of external energy sources, only the reactions involving the protonated and the ionized forms are possible because they do not exhibit a barrier in the entrance channel. However, the bound intermediate formed by the interaction between methanimine and protonated methanimine redissociates back to the reactants because product formation requires a lot of energy in very endothermic processes. The average lifetime of the gaseous addition intermediate is too small to imply a collisional stabilization in the lower density part of the atmosphere of Titan. For instance, between 800 and 1300 km the number density spans from ca. 1011 to 108 molecules cm-3 (Stevens et al. 2015) and, considering a temperature of 180 K and a typical collision cross section of 10Å2, the average collision time varies from 0.1 s to 100 s. At lower altitudes the number density increases significantly, but the mole fraction of protonated methanimine is negligible as it is formed by proton exchange with the main ions produced by electron impact and energetic photons.
 |
Fig. 9 B3LYP optimized geometries (Å and °) of the main fragments produced in the dissociation reactions reported in Table 1. |
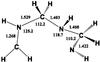 |
Fig. 10 Optimized structure of (CH2NH) |
The only gas-phase process, which is predicted to efficiently lead to products, is the process involving ionized methanimine. According to the model by Vuitton et al. (2007), the amount in the upper atmosphere of Titan of ionized methanimine is small, but not negligible. The products of the reaction CH2NH + CH2NH+ all have a mass-to-charge ratio of 57, where an important contribution is given by the abundant carbocation C4H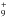 . In this condition, it is difficult to see if any of these species is present in small amounts in the ionosphere of Titan. Interestingly, we have also investigated the further reaction of 1+ with a third molecule of methanimine. The formation of the species (CH2NH)
. In this condition, it is difficult to see if any of these species is present in small amounts in the ionosphere of Titan. Interestingly, we have also investigated the further reaction of 1+ with a third molecule of methanimine. The formation of the species (CH2NH)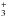 , starting from two molecules of methanimine and the ionic species CH2NH+, is a strongly exothermic reaction, being
, starting from two molecules of methanimine and the ionic species CH2NH+, is a strongly exothermic reaction, being 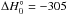 kJ/mol at CCSD(T) level. The optimized structure of (CH2NH)
kJ/mol at CCSD(T) level. The optimized structure of (CH2NH)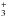 is shown in Fig. 10. We can conclude, therefore, that polymerization of methanimine in the gas-phase at low temperatures may well be initiated by the presence of an ionized molecule. As for the experiment on ice by Bernstein et al. (1995), it is well known that reaction barriers possibly present in gas-phase reactions are not significantly reduced when moving to ice-mediated reactions (see, for instance, Rimola et al. 2014). Normally, the tunneling effect is invoked to explain the observed reactivity, but in this case the reaction barriers are so high that it is difficult to think that a reaction sequence starting with dimerization of neutral methanimine molecules can account for the observed formation of hexamethylenetetramine or polymethylenimine. The reaction must start by involving a radical or an ionized species and not two neutral closed shell molecules. This was already noted by Vinogradoff et al. (2012), who suggested that the reaction between two neutral methanimine molecules is mediated by formic acid, which acts as a proton donor, and by Cottin et al. (2001), who irradiated mixed ice with protons. Notably, Vinogradoff et al. (2013) failed to see hexamethylenetetramine and polymethylenimine formation starting from pure CH2=NH ice. Since in the experiment by Bernstein et al. (1995) the ice was irradiated by VUV photons at the Lyman alpha wavelength, and we now know that methanimine can be efficiently ionized by those photons, we can also argue that ionization of several methanimine molecules can instead trigger the process in cold interstellar ices. This statement is in line with what is known for gas-phase polymerization of olefin (El-Shall 2008; Cottin et al. 2001). Alternatively, external strong energy sources that can induce local nonequilibrium conditions, could promote neutral-neutral dimerization. For instance, in a study by Zhou et al. (2010), in which acetylene ices were irradiated with energetic electrons, electronically excited acetylene molecules were invoked to account for the experimental observation of benzene formation.
is shown in Fig. 10. We can conclude, therefore, that polymerization of methanimine in the gas-phase at low temperatures may well be initiated by the presence of an ionized molecule. As for the experiment on ice by Bernstein et al. (1995), it is well known that reaction barriers possibly present in gas-phase reactions are not significantly reduced when moving to ice-mediated reactions (see, for instance, Rimola et al. 2014). Normally, the tunneling effect is invoked to explain the observed reactivity, but in this case the reaction barriers are so high that it is difficult to think that a reaction sequence starting with dimerization of neutral methanimine molecules can account for the observed formation of hexamethylenetetramine or polymethylenimine. The reaction must start by involving a radical or an ionized species and not two neutral closed shell molecules. This was already noted by Vinogradoff et al. (2012), who suggested that the reaction between two neutral methanimine molecules is mediated by formic acid, which acts as a proton donor, and by Cottin et al. (2001), who irradiated mixed ice with protons. Notably, Vinogradoff et al. (2013) failed to see hexamethylenetetramine and polymethylenimine formation starting from pure CH2=NH ice. Since in the experiment by Bernstein et al. (1995) the ice was irradiated by VUV photons at the Lyman alpha wavelength, and we now know that methanimine can be efficiently ionized by those photons, we can also argue that ionization of several methanimine molecules can instead trigger the process in cold interstellar ices. This statement is in line with what is known for gas-phase polymerization of olefin (El-Shall 2008; Cottin et al. 2001). Alternatively, external strong energy sources that can induce local nonequilibrium conditions, could promote neutral-neutral dimerization. For instance, in a study by Zhou et al. (2010), in which acetylene ices were irradiated with energetic electrons, electronically excited acetylene molecules were invoked to account for the experimental observation of benzene formation.
Acknowledgments
We acknowledge the COST Action CM1401 Our Astrochemical History for supporting a Short Term Scientific Mission of DS from SNS Pisa to IPAG Grenoble. N.B. acknowledges the financial support from the Université de Grenoble Alpes and the Observatoire des Sciences de l’Université de Grenoble.
References
- Arnaud, R., Adamo, C., Cossi, M., et al. 2000, J. Am. Chem. Soc., 122, 324 [CrossRef] [Google Scholar]
- Balucani, N. 2009, Int. J. Mol. Sci., 10, 2304 [CrossRef] [Google Scholar]
- Balucani, N. 2012, Chem. Soc. Rev., 41, 5473 [CrossRef] [Google Scholar]
- Balucani, N., Bergeat, A., Cartechini, L., et al. 2009, J. Phys. Chem. A, 113, 11138 [CrossRef] [Google Scholar]
- Balucani, N., Leonori, F., Petrucci, R., et al. 2010, Faraday Discussions, 147, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Balucani, N., Leonori, F., Petrucci, R., et al. 2015, Chem. Phys., 449, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Bartlett, R. J. 1981, Ann. Rev. Phys. Chem., 32, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Becke, A. D. 1993, J. Chem. Phys., 98, 5648 [NASA ADS] [CrossRef] [Google Scholar]
- Bernstein, M.P., Sandford, S. A., Allamaudola, L. J., et al. 1995, ApJ, 454, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Cable, M. L., Hörst, S. M., Hodyss, R., et al. 2012, Chem. Rev., 112, 1882 [CrossRef] [PubMed] [Google Scholar]
- Carrasco, N., Schmitz-Afonso, I., Bonnet, J.-Y., et al. 2009, J. Phys. Chem. A, 113, 11195 [CrossRef] [Google Scholar]
- Chakrabarti, S., & Chakrabarti, S. K. 2000, A&A, 354, L6 [NASA ADS] [Google Scholar]
- Cottin, H., Szopa, C., & Moore, M. H. 2001, ApJ, 561, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Danger, G., Borget, F., Chomat, M., et al. 2011, A&A, 535, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dickens, J. E., Irvine, W. M., DeVries, C. H., & Ohishi, M. 1997, ApJ, 479, 307 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dunning, T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- El-Shall, M. S. 2008, Accounts Chem. Res., 41, 783 [CrossRef] [Google Scholar]
- Flükiger, P., Lüthi, H. P., Portmann, S., & Weber, J. 2000, Chimia, 54, 766 [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2009, Gaussian09 Revision A.02, Gaussian Inc. Wallingford CT 2009 [Google Scholar]
- Godfrey, P. D., Brown, R. D., Robinson, B. J., & Sinclair, M. W. 1973, Astrophys. Lett., 13, 119 [NASA ADS] [Google Scholar]
- Gonzalez, C., & Schlegel, H. B. 1989, J. Chem. Phys., 90, 2154 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, C., & Schlegel, H. B. 1990, J. Phys. Chem., 94, 5523 [CrossRef] [Google Scholar]
- Gu, X., Kaiser, R. I., Mebel, A. M., et al. 2009, ApJ, 701, 1797 [NASA ADS] [CrossRef] [Google Scholar]
- He, C., & Smith, M. A. 2014, Icarus, 238, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Holtom, P. D., Bennett, C. J., Osamura, Y., Mason, N. J., & Kaiser, R. I. 2005, ApJ, 626, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Holzmeier, F., Lang, M., Hader, K., Hemberger, P., & Fischer, I. 2013, J. Chem. Phys., 138, 214310 [NASA ADS] [CrossRef] [Google Scholar]
- Imanaka, H., & Smith, M. A. 2010, Proc. National Academy of Sciences, 107, 12423 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, G., Szopa, C., Raulin, F., et al. 2015, Nature, 438, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Jung, S. H., & Choe, J. C. 2013, Astrobiology, 13, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Kendall, R. A., Dunning, T. H., & Harrison, R. J. 1992, J. Chem. Phys., 96, 6796 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, C., Ji, Y., Samartzis, P., et al. 2006, J. Chem. Phys., 125, 133302 [NASA ADS] [CrossRef] [Google Scholar]
- Lavvas, P., Coustenis, A., & Vardavas, I. 2008a, Planet. Space Sci., 56, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Lavvas, P., Coustenis, A., & Vardavas, I. 2008b, Planet. Space Sci., 56, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Leonori, F., Petrucci, R., Balucani, N., et al. 2009, J. Phys. Chem. A, 113, 4330 [CrossRef] [Google Scholar]
- Leonori, F., Skouteris, D., Petrucci, R., et al. 2013, J. Chem. Phys., 138, 024311 [NASA ADS] [CrossRef] [Google Scholar]
- Loison, J., Hébrard, E., Dobrijevic, M., et al. 2015, Icarus, 247, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, C. N. 1995, Planet. Space Sci., 43, 1365 [NASA ADS] [CrossRef] [Google Scholar]
- Olsen, J., Jörgensen, P., Koch, H., Balkova, A., & Bartlett, R. J. 1996, J. Chem. Phys., 104, 8007 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavachari, K., Trucks, G. W., Pople, J. A., & Head-Gordon, M. 1989, Chem. Phys. Lett., 157, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Redondo, P., Pauzat, F., & Ellinger, Y. 2006, Planet. Space Sci., 54, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Rimola, A., Sodupe, M., & Ugliengo, P. 2010, Phys. Chem. Chem. Phys., 12, 5285 [CrossRef] [PubMed] [Google Scholar]
- Rimola, A., Taquet, V., Ugliengo, P., Balucani, N., & Ceccarelli, C. 2014, A&A, 572, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosi, M., Falcinelli, S., Balucani, N., Casavecchia, P., & Skouteris, D. 2013, in Computational Science and Its Applications − ICCSA 2013, eds. B. Murgante, S. Misra, M. Carlini, et al. (Berlin Heidelberg: Springer), Lect. Notes Comput. Sci. 7971, 47 [Google Scholar]
- Smith, I. W. M., Talbi, D., & Herbst, E. 2001, A&A, 369, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stephens, P. J., Devlin, F. J., Chabalowski, C. F., & Frisch, M. J. 1994, J. Phys. Chem., 98, 11623 [CrossRef] [Google Scholar]
- Stevens, M. H., Evans, J. S., Lumpe, J., et al. 2015, Icarus, 247, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Teslja, A., Nizamov, B., & Dagdigian, P. J. 2004, J. Phys. Chem. A, 108, 4433 [CrossRef] [Google Scholar]
- Turner, B. E., Terzieva, R., & Herbst, E. 1999, ApJ, 518, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Ugliengo, P., Rimola, A., & Sodupe, M. 2011, Rendiconti Lincei, 22, 137 [CrossRef] [Google Scholar]
- Vazart, F., Latouche, C., Skouteris, D., Balucani, N., & Barone, V. 2015, ApJ, 810, 111 [Google Scholar]
- Vinogradoff, V., Rimola, A., Duvernay, F., et al. 2012, Phys. Chem. Chem. Phys., 14, 12309 [CrossRef] [Google Scholar]
- Vinogradoff, V., Fray, N., Duvernay, F., et al. 2013, A&A, 551, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vuitton, V., Yelle, R., & Anicich, V. 2006, ApJ, 647, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Vuitton, V., Yelle, R., & McEwan, M. 2007, Icarus, 191, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Vuitton, V., Dutuit, O., Smith, M. A., & Balucani, N. 2014, in Titan: Surface, Atmosphere and Magnetosphere, eds. I. Müller-Wodarg, C. A. Griffith, E. Lellouch, & T. E. Cravens, (Cambridge Planetary Science: Cambridge University Press) [Google Scholar]
- Wakelam, V., Smith, I., Herbst, E., et al. 2010, Space Sci. Rev., 156, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Herbst, E., Loison, J.-C., et al. 2012, ApJSS, 199, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Woon, D. E. 2002, Int. J. Quant. Chem., 88, 226 [CrossRef] [Google Scholar]
- Woon, D. E., & Dunning, T. H. 1993, J. Chem. Phys., 98, 1358 [CrossRef] [Google Scholar]
- Yelle, R. V., Vuitton, V., Lavvas, P., et al. 2010, Faraday Discussions, 147, 31 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Yim, M. K., & Choe, J. C. 2012, Chem. Phys. Lett., 538, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, L., Zheng, W., Kaiser, R. I., et al. 2010, ApJ, 718, 1243 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Enthalpy changes and barrier heights (kJ/mol, 0 K) computed at the B3LYP/aug-cc-pVTZ and CCSD(T)/aug-cc-pVTZ levels of theory for selected dissociation and isomerization processes for the systems (CH2NH)2, (CH2NH)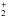 and (CH2NH)2H+.
and (CH2NH)2H+.
All Figures
 |
Fig. 1 B3LYP optimized geometries (Å and °) and CCSD(T) relative energies (with respect to 2 × CH2NH (kJ/mol) at 0 K) of minima localized on the PES of the dimer of CH2NH. |
| In the text | |
 |
Fig. 2 B3LYP optimized geometries (Å and °) and CCSD(T) relative energies (with respect to 2 × CH2NH (kJ/mol) at 0 K) of saddle points localized on the PES of the dimer of CH2NH. |
| In the text | |
 |
Fig. 3 Schematic representation of the PES of the dimer of CH2NH. We only show CCSD(T) energies (kJ/mol, 0 K), for simplicity. |
| In the text | |
 |
Fig. 4 B3LYP optimized geometry (Å and °) of the addition product of a protonated methanimine molecule to a neutral methanimine molecule. Also, the geometry of the protonated methanimine is shown. CCSD(T) relative energy with respect to CH2NH + CH2NH |
| In the text | |
 |
Fig. 5 Schematic representation of the PES of (CH2NH)2H+. Only CCSD(T) energies (kJ/mol, 0 K) are shown for simplicity. |
| In the text | |
 |
Fig. 6 B3LYP optimized geometries (Å and °) and CCSD(T) relative energies with respect to CH2NH + CH2NH+ (kJ/mol) at 0 K of minima and saddle points localized on the PES of (CH2NH) |
| In the text | |
 |
Fig. 7 Schematic representation of the PES of (CH2NH) |
| In the text | |
 |
Fig. 8 Rate constants as a function of temperature: back dissociation (dashed line), CH2NCHNH |
| In the text | |
 |
Fig. 9 B3LYP optimized geometries (Å and °) of the main fragments produced in the dissociation reactions reported in Table 1. |
| In the text | |
 |
Fig. 10 Optimized structure of (CH2NH) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


