| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | L11 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201526666 | |
| Published online | 16 October 2015 | |
The first radial velocity measurements of a microlensing event: no evidence for the predicted binary⋆,⋆⋆
1
Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de
Marseille) UMR 7326, 13388
Marseille, France
e-mail: isabelle.boisse@lam.fr
2
Instituto de Astrofísica e Ciências do Espaço, Universidade do
Porto, CAUP, Rua das
Estrelas, 4150-762
Porto,
Portugal
3
CNRS, Université Pierre et Marie Curie, UMR 7095, Institut
d’Astrophysique de Paris, 98bis
boulevard Arago, 75014
Paris,
France
4
Departamento de Física e Astronomia, Faculdade de Ciências,
Universidade do Porto, Rua do Campo
Alegre, 4169-007
Porto,
Portugal
Received: 3 June 2015
Accepted: 4 July 2015
The gravitational microlensing technique allows the discovery of exoplanets around stars distributed in the disk of the galaxy towards the bulge. The alignment of two stars that led to the discovery is unique over the timescale of a human life, however, and cannot be re-observed. Moreover, the target host is often very faint and located in a crowded region. These difficulties hamper and often make impossible the follow up of the target and study of its possible companions. A radial-velocity curve was predicted for the binary system, OGLE-2011-BLG-0417, discovered and characterised from a microlensing event. We used the UVES spectrograph mounted at the VLT, ESO to derive precise radial-velocity measurements of OGLE-2011-BLG-0417. To gather high-precision radial velocities on faint targets of microlensing events, we proposed to use the source star as a reference to measure the lens radial velocities. We obtained ten radial velocities on the putative V = 18 lens with a dispersion of ~100 m s-1, spread over one year. Our measurements do not confirm the microlensing prediction for this binary system. The most likely scenario is that the putative V = 18 mag lens is actually a blend and not the primary lens which is 2 mag fainter. Further observations and analyses are needed to understand the microlensing observation and infer on the nature and characteristics of the lens itself.
Key words: techniques: radial velocities / planets and satellites: individual: OGLE-2011-BLG-0417 / gravitational lensing: micro / methods: observational / planets and satellites: detection
Based on observations made with ESO Telescope at the Paranal Observatory under program ID 092.C-0763(A) and 093.C-0532(A).
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Different exoplanet detection methods (radial velocity, hereafter RV; stellar transits; direct imaging; pulsar timing; astrometry; and microlensing) are currently used to probe different populations of planets over a wide range of orbital radii, masses and host types. To date, around 35 exoplanets have been discovered via microlensing1. This number is relatively modest compared with that discovered by the RV method or by the Kepler satellite. However, microlensing probes a domain of the parameter space (host separation vs. planet mass) that is currently not often accessible to other methods. The detection of cold planets down to a few Earth masses (Beaulieu et al. 2006) or the observation of free floating objects of planetary mass put the planetary formation scenario to the test (Cassan et al. 2012). On the other hand, microlensing events have the characteristic of not being repeatable, and of focussing on faint stars on crowded fields that are difficult to characterise precisely. A re-observation of the system to get further parameter characterisation is often very difficult.
From the observed microlensing light curve, the first determined parameters are the mass ratio and the sky-projected angular separation of the system. Additional effects, parallax (Gould 1992; Alcock et al. 1995), xallarap (e.g. Han & Gould 1997), terrestrial (Gould & Yee 2013) or space-based parallax (Refsdal 1966), finite source effects, detection of the light coming from the lens (thanks to high angular resolution, see e.g. Kubas et al. 2012), or Bayesian analysis are used to derive the physical parameters of the different planetary systems and to proceed further in the analysis. In this context, Skowron et al. (2011) showed that the deformation of the microlensing light curve can be used to constrain all the orbital parameters of a binary lens system.
Shin et al. (2012) presented the microlensing event OGLE-2011-BLG-0417 and modelled it as due to a binary lens system. The source star is a K3 red giant located in the galactic bulge at 8 kpc with Isource = 16.74 (Vsource = 19.42). They identified the blended light as the primary lens, (Ilens = 16.30, Vlens = 18.23), which would make it one of a few case where the lens primary is significantly brighter than the source star. Gould et al. (2013) adopted the new calibration of Nataf et al. (2013) for the Bulge giant and revised the initial error budget. Located at 0.95 ± 0.06 kpc, the lens binary is composed of a primary star of 0.524 ± 0.036M⊙, orbited by a M dwarf of 0.153 ± 0.011M⊙. They showed that this event could be tested by RV measurements and published revised Keplerian parameters (reported here in Table 1). With a large expected RV amplitude, of 6.4 km s-1, and with an eccentricity of 0.69, this system can be detected using only relatively low-precision instruments, benchmarking the microlensing detection.
In this letter, we present the first radial velocity observations of this microlensing target, using the UVES spectrograph.
2. Observations
We obtained a total of 9 h of observations with the UVES cross-dispersed echelle spectrograph (Dekker et al. 2000) mounted on the VLT in P92 and P93 to measure the RV variations of the OGLE-2011-BLG-0417 binary. Ten spectra were acquired between October 2013 and September 2014.
We used the two arms of the spectrograph in parallel with a dichroic beam splinter, the standard mode DIC-1 (390+580), with a wavelength coverage of 326−445 and 476−684 nm. It probes a domain where the late-K dwarf lens emits sufficient flux and where the spectra is not strongly polluted by telluric lines. The exposure time was set to one hour to reach a signal-to-noise ratio (SNR) of ~20 at 550 nm. We used a slit of 1 arcsec which gives a spectral resolution of 40 000, sufficient to resolve the lines and calculate RV without losing too much light due to slit losses. Because of the faintness of the target, we did the guiding with the red camera, used the slow readout mode of the CCD, and we requested a seeing no larger than 1′′. Still, a slightly larger seeing than the width of the slit leads to some flux loss, but this is compensated in RV precision by a gain in the stability of the illumination of the slits of the spectrographs (Boisse et al. 2011). The log of the observations is given in Table A.2. All the measurements were kept for the analysis.
The UVES spectrograph is not stabilised in pressure and temperature. An important RV drift of the zero point is expected to be present and depend on the temporal evolution of the two parameters. To minimise this effect, a thorium-argon calibration was done before and after the scientific observation.
Because the target star is in the Galactic bulge, the field is densely crowded. We then fixed the angle of the slit with the sky as shown in the top of Fig. 1 to minimise the pollution of contaminant star inside the slit.
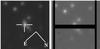 |
Fig. 1 Images of the slit-viewer camera of UVES red-arm showing the crowding of the field. The field of view is approximately 15′′ to 15′′. The black horizontal shadow is the slit opened at 1′′. On the bottom, the target is decentred (top left of the slit). On the left, the position that we chose when the slit is on the target, OGLE-2011-BLG-0417. |
3. Data reduction
We used the Reflex ESO pipeline to reduced the spectra (Freudling et al. 2013). We corrected them from cosmic rays with a 5σ-clipping process first. We then computed the weighted cross-correlation functions (CCF) of the spectra with a template K5 mask (Pepe et al. 2002). The CCF of the co-added spectrum is plotted in Fig. 2. The source and the lens are superimposed. Their RV values are different by several tens of km s-1, as expected since the lens is in the Galactic disk whereas the source is in the bulge. The observation of two significant components shows that the observed target was indeed OGLE-2011-BLG-0417.
We compared the correlations obtained for the three detectors (one in the blue and two in the red arm) to disentangle the source star from the lens. The variation as a function of wavelength of the relative contrast of the CCF is equivalent to flux ratio. So, the bluer source would show a deeper contrast in the blue wavelength domain. With a (V − I)lens = 1.93 and a (V − I)source = 2.68, the source is indeed expected to be bluer than the lens. On the contrary, the redder lens shows a higher contrast in the red. The source also presents a deepest CCF as presumed for a lower log g (giant star).
We checked with the slit-viewer camera that no other source entered the 1 arcsec slit (see bottom of Fig. 1). On three observations, however, the seeing increased or the slit drifted from the pointed target (see Table A.2). As a consequence, two of the close-by stars entered the slit. In the individual spectra, two components with low contrast appeared in the CCF profiles, however, they are well separated from the lines of the source and the lens. We tested that the CCF width of the source and the lens are constant within the error bars for our ten measurements, and hence that the measured RV are not affected by contaminant stars. We note, however, that the presence of contaminants would in principle increase the RV dispersion.
To be put in the same RV heliocentric reference, each CCF profile was corrected in wavelength from the barycentric earth radial velocity (BERV) values given by the UVES pipeline. The CCF profiles were then fitted with a two-Gaussian model to derive the RV of the lens and the source. A third and fourth Gaussians were used when contaminant stars were visible. For each observation, we calculated two RV values, one for each of the wavelength calibration secured before or after the science exposure: RVbefore and RVafter, respectively. The derived RV is the average between the two, which assumes that the instrumental drift is nearly linear between the two calibrations. We measured the spectrograph RV drift to be from 15 up to 400 m s-1, within one hour. Using the median exposure, as calculated from the photometer count of the detectors and weighted by the spectral information between the blue and red arms, does not change the result above a few m s-1. This correction of the drift allows us to reach root mean square (rms) for each of the measured stars of ~800 m s-1.
A zero-point drift of the spectrograph may have not been corrected by the thorium-argon calibrations. The RV is moreover dispersed by another source of noise due to changes in the illumination of the slit for the different spectrum (and, hence, different point spread functions). The long exposure time (one hour) was expected to average the small movement of the target in the slit, but the seeing was often significantly smaller than the slit (see Table A.2). At this stage, the main contribution to the dispersion should come from this effect, however, it is difficult to measure precisely.
We then computed a telluric mask from O2 lines (Figueira et al. 2010) and cross-correlated it with each spectra. The obtained CCF was fitted by a Gaussian to derive a zero-point RV value. Only 20 O2 lines could be fitted in the spectral domain, and the derived RV present an error of ~200 m s-1. When we further corrected the stellar RV values from the zero-point drift as calculated from the telluric lines, the rms decreases to ~250 m s-1. We plotted in Fig. 3, the RV of the source and the lens. The two stars are not gravitationally bound and their RV variations are dominated by the same instrumental systematics. The main contribution comes from the error on the telluric correction.
We then decided to use the RV from the source as a reference to measure the lens RV. This leads to the ΔRV value. This could be done because the flux of the two stars are blended in the spectra and followed the same path in the spectrograph. By doing that, the systematics observed in both stars are cancelled out.
We estimated the photon-noise uncertainty from the empirical calibration of Bouchy et al. (2005) on UVES/FLAMES (see also Loeillet et al. 2008). That leads to a mean error bar of σpn ~ 50 m s-1 on the individual targets, and we took their quadratic sum for the ΔRV photon noise error. Another source of noise comes from the drift of the instrument during the exposure. Considering this drift is linear between the calibrations and assuming that the value of the RV has a Gaussian distribution that is within the two calibrations with a probability of 99.9%, we calculated an error of σcalib = (RVbefore − RVafter)/(2 × 3). The RV of the source, the lens and the ΔRV, as well as their error bars are reported in Table A.1. The reported errors are the quadratic sum of σpn and σcalib. The mean error is ~110 m s-1 for the individuals RV and 65 m s-1 on the ΔRV.
 |
Fig. 2 CCF compute on three bandpasses of the sum of all the spectra, which allows us to identify the thinner and bluer line as the giant source and the other line, the late-K dwarf primary of the binary lens. |
4. Data analysis and results
The ten secured RV present an rms of 94 m s-1, with no significant variations. We plotted them in Fig. 4 with the best model from Gould et al. (2013). There is a clear disagreement between the observations and the predicted model. Using the PASTIS validation software (Diaz et al. 2014), we estimated the probability of the Gould et al. (2013) prediction. We modelled a Keplerian orbit with normal priors that matched the values, their uncertainties, and the correlation matrix as provided by Gould et al. (2013). This include the uncertainty in the phase that, since the observation of the microlensing event, is in fact completely lost. We used a uniform prior for the systemic RV as well as for an extra RV jitter. We ran 20 Markov chain Monte Carlo analyses of 3 × 105 iterations each. We repeated the same analyses with an opposite sign for the RV amplitude (the sign of the RV curve is not determined by the microlensing prediction) and for a no-variation scenario. After thinning and merging the chains, we ended with about 10 000 independent samples of the posterior distribution.
The best-fit model is superimposed in grey in Fig. 4. The residuals exhibit a rms of 340 m s-1, hence three times larger than the dispersion of the data. Moreover, this best-fit model departs from the prediction joint confidence interval by 3.7 sigma (a priori probability of ~2 × 10-4). We then estimated the statistical evidence of the Gould et al. (2013) prediction, using the method described in Tuomi & Jones (2012). We found a probability of 7 × 10-8 or 2 × 10-7 depending on whether we consider a RV amplitude that is positive or negative (respectively). Therefore, our spectroscopic observations unambigiously reject the microlensing prediction of Gould et al. (2013) for this binary system.
We decided to double check whether the bright blend (Iblend = 16.29, Vblend = 18.23) is the primary component of the lensing system as claimed by Gould et al. (2013). We adopt a set of isochrones (Girardi et al. 2012) with ages in the range 1−10 Gyr for a solar metallicity and the distance modulus of 950 pc. We find a G8 star with a mass of ~0.82 M⊙, almost 2 mag brighter than the primary lens. The bright blend cannot be the primary lens of the microlensing event OGLE 2011-BLG-417. We will revisit the system with high angular resolution to see if the bright blend could be a distant companion to the lensing system or a chance alignment on the line of sight of the source.
 |
Fig. 3 UVES RV of the source and the lens. The velocities of the two stars share the same instrumental systematics. |
 |
Fig. 4 UVES RV of OGLE-2011-BLG-0417 (dots) with the predicted model from Shin et al. (2012) and Gould et al. (2013; black line). The systemic was fixed to the median value of the observations. The best-fit model which departs from the prediction by 3.7 sigma, is superimposed in grey. The observations reject the modelled Keplerian at a level greater than 2 × 10-7 (see text). The insert is an enlargement around the observations. |
5. Conclusions
We used the UVES spectrograph to derive Doppler measurements of the reflex motion of the primary component of the predicted binary lens OGLE-2011-BLG-0417. The lens, composed of a late-K dwarf orbited by an M dwarf, is brighter (V = 18) than the microlensing source (V = 19.3). The huge semi-amplitude of ~6.35 km s-1 of the predicted eccentric orbit should have been easily detected with the RV precision reported here.
Our ten measurements, with a dispersion of 94 ms-1 and a mean error bar of 65 ms-1, do not confirm the microlensing analysis. These are the first published RV measurements on a microlensing target. We are led to believe that an error on the analysis of the microlensing event is the reason for the discrepancy. A quick look at the photometric data of the microlensing event seems to indicate that the brightness of the lens has been overestimated. The most likely scenario is that the bright blend of the microlensing light curve is not the light from the primary lens, which contradicts with the prediction of Gould et al. (2013). As a consequence, the RV modulation of the lensing system could not be detected because the primary is 2 mag fainter. It is not clear yet whether the bright blend is a distant companion to the OGLE 2011-BLG-417 system or a chance alignment. A more complete re-analysis of the system, taking spectroscopic and photometric data into account, will be performed in due time, but this is outside the scope of this letter.
The UVES spectrograph allowed us to reach a RV precision of 100 m s-1 on a target of 18th magnitude in V in a hour time integration. This precision was made possible thanks to the fact that the source star is observed simultaneously with the binary microlens and can serve as calibration. The technique is similar to differential photometry, but in the spectral domain.
With a modest allocation of telescope time (9 h), it would have been possible to characterise a binary system detected by microlensing with RV. This has strong implication for the modelling of the microlensing observations. This shows that spectroscopic follow-up observation of microlensing events is possible with large telescopes. Understanding the reasons for the discrepancies for this event will help to improve the characterisation of microlensing systems, which have already been detected or will be detected with the K2, WFIRST and Euclid space missions. In the coming years, using future ESO facilities such as ESPRESSO at VLT, or HIRES at E-ELT, it will be possible to perform such measurements on planetary systems detected by microlensing such as OGLE-2006-BLG-109 (Gaudi et al. 2008) and OGLE-2012-BLG-0026 (Han et al. 2013), once it has been confirmed via high angular resolution observation that there is no strong contamination by a blend, for example, thanks to high angular resolution observations. Note that, during the referee process on this letter, Yee et al. (2015) published RV measurements on another microlensing event revealing an orbit consistent with the prediction from the light-curve analysis.
Online material
Appendix A: Additional tables
RV measurements and their associated 1σ error bars.
Log of the observations.
Acknowledgments
We thanks the UVES operation astronomers that performed these observations and Christian Hummel for his help in the preparation of the p2pp process. I.B. thanks A.S. for his enthusiastic work. Between the first and last measurements, both of us became parents. What a great change! A.S. warmly thanks Rodrigo F. Díaz and José-Manuel Almenara for their substantial contribution in the development of the PASTIS software. A.S. is supported by the European Union under a Marie Curie Intra-European Fellowship for Career Development with reference FP7-PEOPLE-2013-IEF, number 627202. This work was supported by Fundação para a Ciência e a Tecnologia (FCT) through the research grant UID/FIS/04434/2013. P.F., N.C.S., and S.G.S. also acknowledge the support from FCT through Investigador FCT contracts of reference IF/01037/2013, IF/00169/2012, and IF/00028/2014, respectively, and POPH/FSE (EC) by FEDER funding through the program Programa Operacional de Factores de Competitividade – COMPETE. P.F. further acknowledges support from FCT in the form of an exploratory project of reference IF/01037/2013CP1191/CT0001.
References
- Alcock, C., Allsman, R.-A., Alves, D., et al. 1995, ApJ, 454, L125 [Google Scholar]
- Beaulieu, J.-P., Bennett, D., Fouqué, P., et al. 2006, Nature, 439, 437 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Boisse, I., Bouchy, F., Chazelas, B., et al. 2011, EPJ Web. Conf., 16, 02003 [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Pont, F., Melo, C., et al. 2005, A&A, 431, 1105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassan, A., Jubas, D., Beaulieu, J.-P., et al. 2012, Nature, 481, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., et al. 2000, Proc. SPIE, 4008, 534 [Google Scholar]
- Díaz, R. F, Almenara, J. M, Santerne, A., et al. 2014, MNRAS, 441, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Freudling, W., Romaniello, M., Ballester, P., et al. 2013, A&A, 559, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaudi, B., Bennett, D., Udalski, A., et al. 2008, Science, 319, 927 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Girardi, L., Barbieri, M., Groenewegen, M., et al. 2012, Red giants as probes of the structure and evolution of the Milky Way, Astrophys. Space Sci. Proc. (Springer), 165 [Google Scholar]
- Gould, A. 1992, ApJ, 392, 442 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gould, A., & Yee, J.-C. 2013, ApJ, 764, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A., Shin, I.-G., Han, C., et al. 2013, ApJ, 768, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C., & Gould, A. 1997, ApJ, 480, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C., Udalski, A., Choi, J.-Y., et al. 2013, ApJ, 762, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Kubas, D., Beaulieu, J.-P., Bennett, D.-P., et al. 2012, A&A, 540, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loeillet, B., Bouchy, F., Deleuil, M., et al. 2008, A&A, 479, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nataf, D., Gould, A., Fouqué, P., et al. 2013, ApJ, 769, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Refsdal, S. 1966, MNRAS, 134, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Shin, I.-G., Han, C., Choi, J.-Y., et al. 2012, ApJ, 755, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Skowron, J., Udalski, A., Gould, A., et al. 2011, ApJ, 738, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Tuomi, M., & Jones, H. R. A. 2012, A&A, 544, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yee, J.-C, Johnson, J., Skowron, J., et al. 2015, ApJ, submitted [arXiv:1506.01441] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Images of the slit-viewer camera of UVES red-arm showing the crowding of the field. The field of view is approximately 15′′ to 15′′. The black horizontal shadow is the slit opened at 1′′. On the bottom, the target is decentred (top left of the slit). On the left, the position that we chose when the slit is on the target, OGLE-2011-BLG-0417. |
| In the text | |
 |
Fig. 2 CCF compute on three bandpasses of the sum of all the spectra, which allows us to identify the thinner and bluer line as the giant source and the other line, the late-K dwarf primary of the binary lens. |
| In the text | |
 |
Fig. 3 UVES RV of the source and the lens. The velocities of the two stars share the same instrumental systematics. |
| In the text | |
 |
Fig. 4 UVES RV of OGLE-2011-BLG-0417 (dots) with the predicted model from Shin et al. (2012) and Gould et al. (2013; black line). The systemic was fixed to the median value of the observations. The best-fit model which departs from the prediction by 3.7 sigma, is superimposed in grey. The observations reject the modelled Keplerian at a level greater than 2 × 10-7 (see text). The insert is an enlargement around the observations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


