| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A108 | |
| Number of page(s) | 10 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201526550 | |
| Published online | 16 September 2015 | |
Revisiting the luminosity function of single halo white dwarfs
1
Departament de Física AplicadaUniversitat Politècnica de
Catalunya,
c/Esteve Terrades 5,
08860
Castelldefels,
Spain
e-mail:
enrique.garcia-berro@upc.edu
2
Institute for Space Studies of Catalonia,
c/Gran Capità 2–4, Edif. Nexus
201, 08034
Barcelona,
Spain
3
Facultad de Ciencias Astronómicas y Geofísicas, Universidad
Nacional de La Plata, Paseo del
Bosque s/n, 1900
La Plata,
Argentina
4
Instituto de Astrofísica de La Plata, UNLP-CONICET, Paseo del Bosque s/n,
1900
La Plata,
Argentina
5
Institut de Ciències de l’Espai (CSIC), Campus UAB, Facultat de
Ciències, Torre
C-5, 08193
Bellaterra,
Spain
Received: 18 May 2015
Accepted: 22 July 2015
Context. White dwarfs are the fossils left by the evolution of low- and intermediate-mass stars, and have very long evolutionary timescales. This allows us to use them to explore the properties of old populations, like the Galactic halo.
Aims. We present a population synthesis study of the luminosity function of halo white dwarfs, aimed at investigating which information can be derived from the currently available observed data.
Methods. We employ an up-to-date population synthesis code based on Monte Carlo techniques, which incorporates the most recent and reliable cooling sequences for metal-poor progenitors as well as an accurate modeling of the observational biases.
Results. We find that because the observed sample of halo white dwarfs is restricted to the brightest stars, only the hot branch of the white dwarf luminosity function can be used for these purposes, and that its shape function is almost insensitive to the most relevant inputs, such as the adopted cooling sequences, the initial mass function, the density profile of the stellar spheroid, or the adopted fraction of unresolved binaries. Moreover, since the cutoff of the observed luminosity has not yet been determined only the lower limits to the age of the halo population can be placed.
Conclusions. We conclude that the current observed sample of the halo white dwarf population is still too small to obtain definite conclusions about the properties of the stellar halo, and the recently computed white dwarf cooling sequences, which incorporate residual hydrogen burning, should be assessed using metal-poor globular clusters.
Key words: white dwarfs / stars: luminosity function, mass function / Galaxy: abundances / Galaxy: evolution
© ESO, 2015
1. Introduction
White dwarfs are the evolutionary remnant of stars of intermediate and low masses at the zero-age main sequence. The upper limit for a main-sequence star to evolve to a white dwarf is still the matter of some debate, but it is estimated to be ~10M⊙ (Becker & Iben 1979, 1980; Miyaji et al. 1980; Renzini & Voli 1981; Nomoto 1984; García-Berro et al. 1997; Poelarends et al. 2008). Thus, given the shape of the initial mass function (IMF) it is expected that the vast majority of the remnants of the evolution of single stars will be white dwarfs. Since white dwarfs are numerous, have well-studied properties (Althaus et al. 2010), and long evolutionary timescales, they are the most suitable tool to study the properties of old populations, like the Galactic stellar spheroid. Moreover, our knowledge of the physics controlling the evolution of white dwarfs relies on solid ground, since the basic principle of their evolution is a well understood and relatively simple cooling process. Although this basic principle of the theory of white dwarf cooling has remained unaltered in recent decades, we now have very sophisticated and accurate stellar evolutionary models that allow us to perform precise cosmochronology, and to characterize the ensemble properties of several white dwarf populations, like those of the Galactic disk; see Cojocaru et al. (2014), and references therein, for a recent work on this subject and of the system of Galactic open (García-Berro et al. 2010; Bellini et al. 2010; Bedin et al. 2010) and globular clusters (Hansen et al. 2002, 2013; García-Berro et al. 2014).
The population of white dwarfs in the Galactic stellar halo has been the subject of increased interest since the first observational and theoretical studies (Mochkovitch et al. 1990; Liebert et al. 1989). Perhaps, one of the most important reasons for this interest in halo white dwarfs is their possible contribution to the dark matter content of our Galaxy; see, for instance, Oppenheimer et al. (2001) for an observational work, and Torres et al. (2002) for a theoretical study. However, because of very low space densities and intrinsic faintness of the population of white dwarfs of the Galactic spheroid, their detection has proven to be a difficult endeavour. Moreover, as opposed to what occurs with main-sequence stars, which can be classified according to their metallicity, the atmospheres of white dwarfs are devoid of metals. This is because of their high surface gravities and long evolutionary timescales, which allow gravitational diffusion to be very efficient at settling the metals resulting from the previous evolutionary history at the base of the partially degenerate envelope. All these physical processes make halo white dwarfs indistinguishable from disk white dwarfs. Hence, the only observational method for detecting white dwarfs belonging to the Galactic spheroid, which is not hampered by relevant technical difficulties, relies on identifying them on the basis of large proper motions, as radial velocities cannot be accurately determined. This is because of the large surface gravity, which translates into a sizable gravitational redshift of the spectral features that cannot be neglected, and it is difficult to measure. Additionally, the absence of spectral lines at the very low luminosities of the coldest halo white dwarfs also prevents an accurate characterization of the faintest population of halo white dwarfs. All this, in turn, considerably reduces the size of the observational sample, since at present large volumes cannot be probed, and we are limited to studying nearby halo white dwarfs.
Nevertheless, recent observational attempts to empirically determine the luminosity function of halo white dwarfs have been successful, and we now have a reliable sample of halo white dwarfs (Harris et al. 2006; Rowell & Hambly 2011) to which the theoretical works can be compared. Comparing the results of the theoretical models with the available observed sample of halo white dwarfs is an important task, as we now also have accurate white dwarf cooling tracks for white dwarfs descending from very low-metallicity progenitors (Miller Bertolami et al. 2013; Althaus et al. 2015). These cooling tracks improve upon those used in the early and pioneering calculations of Isern et al. (1998) and García-Berro et al. (2004), and in the more recent calculation of van Oirschot et al. (2014). These evolutionary sequences have self-consistently evolved from the zero-age main sequence, through the red giant and thermally pulsing AGB phases to the white dwarf regime, and have revealed the important role of residual hydrogen burning in the atmospheres of low-mass white dwarfs, a physical process that needs verification. Finally, these kind of works are also of crucial importance to pave the road to future studies of the large population of halo white dwarfs, which the European astrometric mission Gaia will unveil in coming years (Torres et al. 2005).
Our paper aims to produce synthetic samples of the population of halo white dwarfs using the most up-to-date physical inputs and prescriptions for the Galactic spheroid and compare them with the current observational data. It is organized as follows. In Sect. 2.1 we briefly describe the numerical tools employed in this work. It is followed by Sect. 3, where we first discuss the effects of residual hydrogen burning, the adopted IMF, the assumed density profile for the Galactic halo, a population of unresolved binary white dwarfs, and star formation history. Finally, in Sect. 4, we summarize our calculations and draw our conclusions.
2. The population synthesis code
2.1. A brief description of the numerical set up
As in our previous works (García-Berro et al. 1999, 2004; Torres et al. 2002, 2005; Cojocaru et al. 2014), we use a Monte Carlo population synthesis code, in this case adapted to model the halo population. In the following, we describe the most important inputs of our standard model.
We initially produced a large number of synthetic main-sequence stars, located according to a isothermal sphere density model, 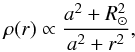 (1)where a ≈ 5 kpc is the core radius, and R⊙ = 8.5 kpc is the galactocentric distance of the Sun. We assigned to each synthetic star a value for the mass at the zero-age main sequence randomly generated from the IMF of Kroupa (2001), and a time of birth, randomly assigned within a burst of constant star formation lasting 1 Gyr. The velocities of simulated halo stars were randomly drawn from normal distributions (Binney & Tremaine 1987), i.e.,
(1)where a ≈ 5 kpc is the core radius, and R⊙ = 8.5 kpc is the galactocentric distance of the Sun. We assigned to each synthetic star a value for the mass at the zero-age main sequence randomly generated from the IMF of Kroupa (2001), and a time of birth, randomly assigned within a burst of constant star formation lasting 1 Gyr. The velocities of simulated halo stars were randomly drawn from normal distributions (Binney & Tremaine 1987), i.e., ![\begin{equation} f(v_{\rm r},v_{\rm t})=\frac{1}{(2\pi)^{3/2}}\frac{1}{\sigma_{\rm r}\sigma_{\rm t}^2} \exp\left[-\frac{1}{2}\left(\frac{v_{\rm r}^2}{\sigma_{\rm t}^2}+\frac{v_{\rm t}^2} {\sigma_{\rm t}^2}\right)\right] , \end{equation}](/articles/aa/full_html/2015/09/aa26550-15/aa26550-15-eq7.png) (2)where σr and σt – the radial and the tangential velocity dispersions, respectively, are related by the following expression:
(2)where σr and σt – the radial and the tangential velocity dispersions, respectively, are related by the following expression: ![\begin{equation} \sigma_{\rm t}^2=\frac{V_{\rm c}^2}{2}+\left[1-\frac{r^2}{a^2+r^2}\right] \sigma_{\rm r}^2+\frac{r}{2}\frac{{\rm d}(\sigma_{\rm r}^2)}{{\rm d}r} , \end{equation}](/articles/aa/full_html/2015/09/aa26550-15/aa26550-15-eq10.png) (3)which, to a first approximation, leads to
(3)which, to a first approximation, leads to 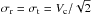 . The velocity dispersions σr and σt are those determined by Markovic & Sommer-Larsen (1997). For the calculations reported here, we adopted a circular velocity Vc = 220 km s-1. From these velocities, we obtained the heliocentric velocities of each simulated star by adding the velocity of the local standard of rest (LSR) vLSR = −220 km s-1, and the peculiar velocity of the Sun.
. The velocity dispersions σr and σt are those determined by Markovic & Sommer-Larsen (1997). For the calculations reported here, we adopted a circular velocity Vc = 220 km s-1. From these velocities, we obtained the heliocentric velocities of each simulated star by adding the velocity of the local standard of rest (LSR) vLSR = −220 km s-1, and the peculiar velocity of the Sun.
Next we computed the main-sequence lifetime for each progenitor star, adopting a set of evolutionary sequences with metallicity Z = 0.0001, which together with the age of the population (for which in our reference model we adopted 14 Gyr), and the progenitor mass, allowed us to determine which stars have had time to become white dwarfs at the time. We then obtained the corresponding masses and cooling ages for each simulated white dwarf. We employ the evolutionary sequences, that is, the progenitor and white dwarf cooling evolutionary tracks, of Althaus et al. (2015). These were obtained from fully evolutionary calculations and expand the previous calculations of Miller Bertolami et al. (2013). Hence, the main-sequence lifetimes, the relationship linking the progenitor and white dwarf masses, and the cooling ages are all self-consistently computed using an homogenous evolutionary framework. This represents a clear improvement over the most recent calculations of this kind, as we employed self-consistent evolutionary models of the right metallicity, which incorporate state-of-the-art prescriptions for all the relevant physical processes. Our calculations incorporate a fraction of 20% of non-DA white dwarfs, for which we employ theoretical cooling sequences for white dwarfs with pure helium atmospheres. We elaborate on the cooling tracks employed here in Sect. 2.2. Using these values we derived the stellar parameters of each white dwarf in the synthetic sample. Namely, we computed its luminosity, effective temperature, surface gravity, and magnitudes in the different passbands. A standard model of Galactic absorption was also used (Hakkila et al. 1997) to obtain reliable apparent magnitudes.
Our synthetic white dwarf sample is then passed through a series of filters that mimic the selection criteria employed to observationally select halo white dwarfs in a real sample. These filters are described in detail in Sect. 2.3. After this procedure is followed the white dwarf luminosity function can be computed, except for a normalization factor. We chose to normalize the theoretical results to the density of white dwarfs in the highest density bin with finite error bars of the observational luminosity function, Mbol = 15.75. This is, in fact, equivalent to normalizing the luminosity function to the total population density, given that this bin practically dominates the stellar counts. In our fiducial model only single white dwarfs were considered, however, we also explored models with a fraction of unresolved binaries in our calculations. In addition, our simulations also include a careful exploration of the effects of other inputs, which is further explained in Sect. 3.
2.2. Cooling tracks
White dwarf progenitors in the Galactic halo are characterized by a significantly low metallicity. In the solar vicinity, the halo metallicity distribution function peaks at [ Fe / H ] ~ −1.5 dex. Actually, Frebel & Norris (2013) and Carollo et al. (2010) found that the Galactic halo has a dual population. The first of these halo populations peaks at [ Fe / H ] ~ −1.6 dex, whereas the second one peaks at [ Fe / H ] ~ −2.2 dex. All in all, it is clear that to adequately capture the essential properties of this metal-poor population, a set of cooling sequences of white dwarfs with hydrogen-rich atmospheres descending from low-metallicity progenitors is needed.
We interpolate the cooling times using the set of evolutionary sequences of Althaus et al. (2015). These cooling sequences were computed considering stable, residual hydrogen shell burning in white dwarf atmospheres during the white dwarf stage, although they also provide a set of cooling tracks in which this physical mechanism is disregarded. This is an important issue, since Miller Bertolami et al. (2013) showed that although in most cases residual hydrogen burning is not a significant source of energy, for white dwarfs with hydrogen atmospheres descending from progenitors with very low metallicity it can become a dominant source of energy, and can delay significantly white dwarf cooling. This effect is more noticeable for low-mass white dwarfs with luminosities ranging from log (L/L⊙) = −2 to −4. As mentioned, we consider that the adoption of this set of sequences represents a clear improvement with respect to the most recent calculation of the luminosity of halo white dwarfs (van Oirschot et al. 2014), which employed evolutionary sequences for progenitors of solar metallicity.
Although the evolutionary sequences for white dwarfs with hydrogen-rich atmospheres that we adopt here are a clear improvement over previous attempts to model the population of single white dwarfs in the Galactic halo, a cautionary remark is in order here. There is solid evidence that old stellar systems exhibit an enhancement of α elements (Aller & Greenstein 1960; Wallerstein 1962). While this kind of enhancement has virtually no effects on the evolutionary timescales of initially low-mass stars, they can play a role in the evolution of intermediate-mass stars. In particular, the resulting total metallicity is larger than that obtained by assuming a solar-scaled composition and, because of the increase of the oxygen abundance, the global abundance of carbon, nitrogen, and oxygen is larger than the corresponding solar-scaled abundance. This, in turn, has an effect on the evolutionary timescales of the progenitor stars of typical white dwarfs. A more rigorous treatment of low-metallicity stars should require the inclusion of α-enhanced initial chemical compositions to compute the stellar sequences. Our evolutionary sequences do not take this enhancement into account, but we estimate that the effects of including it in the calculation of the white dwarf luminosity function is limited. In particular, we checked that the differences of progenitor lifetimes and resulting white dwarf masses between the solar-scaled sequences and α-enhanced ones are smaller than 1% (Pietrinferni et al. 2006) for the metallicities and progenitor masses relevant to our study. Hence, our results are almost insensitive to the adopted metal ratios.
Finally, we employed the cooling sequences of Althaus et al. (2005) and Althaus et al. (2007) for more massive oxygen-neon white dwarfs, whereas we used the cooling tracks of Bergeron et al. (2011) for white dwarfs with pure helium atmospheres. In both cases, the white dwarf evolutionary sequences correspond to progenitors of solar metallicity. This, of course, is not a self-consistent treatment, but nevertheless we judge that the effects on the computed white dwarf luminosity functions should be modest; see below for a detailed discussion.
2.3. The observational sample and its observational cuts
We compare our results with the most recent and statistically relevant observational halo white dwarf luminosity function (Rowell & Hambly 2011). This observational luminosity function was derived from a sample of 93 halo white dwarfs detected in the SuperCosmos Sky Survey (SSS). The SSS is an advanced photographic plate-digitizing machine, using plates taken with the UK Schmidt telescope (UKST), the ESO Schmidt telescope, and the Palomar Schmidt telescope. The resulting catalogs were compiled by digitizing several generations of photographic Schmidt plates. The survey uses a photometric system that has three passbands: bJ, r59F, and iN (Hambly et al. 2001). Employing data from several generations of plates, Rowell & Hambly (2011) constructed a catalog of ~10 000 white dwarfs with magnitudes down to r59F ~ 19.75, and proper motions as low as μ ~ 0.05 yr-1, covering nearly three quarters of the sky. Using strict velocity cuts, the authors isolated subsamples of white dwarfs belonging to the thin disk, thick disk, and halo populations, and presented observational white dwarf luminosity functions for each one of these populations.
In our study, we distinguish between the complete sample of synthetic halo white dwarfs and a restricted sample. The latter is obtained by replicating the observational selection criteria adopted to derive the observed halo white dwarf luminosity function of the SSS. First, a proper motion cut, depending on the bJ magnitude, is applied. This proper motion cut is given by the following expression: 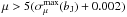 , where σμ is the standard deviation in the proper motion measurements. Also, a magnitude cut is imposed, 12 <r59F< 19.75. Next, a cut in the reduced proper motion diagram is performed, selecting only objects below and blueward of a reduced proper motion corresponding to Vtan = 30 km s-1. Lastly, to separate the halo population, a tangential velocity cut is used. Specifically, we only select stars with tangential velocities Vtan> 200 km s-1. Finally, we also impose an upper limit on the tangential velocity of 400 km s-1 to prevent selecting stars with velocities larger than the escape velocity of the Galaxy.
, where σμ is the standard deviation in the proper motion measurements. Also, a magnitude cut is imposed, 12 <r59F< 19.75. Next, a cut in the reduced proper motion diagram is performed, selecting only objects below and blueward of a reduced proper motion corresponding to Vtan = 30 km s-1. Lastly, to separate the halo population, a tangential velocity cut is used. Specifically, we only select stars with tangential velocities Vtan> 200 km s-1. Finally, we also impose an upper limit on the tangential velocity of 400 km s-1 to prevent selecting stars with velocities larger than the escape velocity of the Galaxy.
3. Results
In this section, we compare the results of our simulations to the halo luminosity function of Rowell & Hambly (2011), and we study the sensitivity of the theoretical white dwarf luminosity function to different model inputs.
To start with, we discuss how the observational selection criteria affect the size of the synthetic samples. This is done with the help of Table 1. In this table, we list for our reference model the number of white dwarfs in the original synthetic sample (first row), and in subsequent rows we list the number of white dwarfs that survive the different cuts. As is shown in Table 1, only 1.5% of the synthetic stars survive the proper motion cut. After applying the magnitude cut, we are left with 111 synthetic stars, representing about 0.02% of the original sample. For this particular realization, the reduced proper motion cut does not further decrease the number of simulated white dwarfs, whereas the filter in tangential velocities even further reduces the number of simulated stars to about 0.01% of the original sample, to 77 white dwarfs, a number comparable with that found observationally.
Number of synthetic white dwarfs that survive the different observational cuts for a typical Monte Carlo realization of our standard model.
To compare our results with those of van Oirschot et al. (2014), we only culled white dwarfs using the tangential velocity cut, as they did. Using only this selection criterion, the size of the restricted sample is much larger. In particular, when this procedure is adopted it results in a restricted sample, which is 63% of the initial sample. Obviously, the advantage of this large synthetic sample is that it is comparable to the complete sample, producing a smooth luminosity function that faithfully preserves the intricacies of the adopted model. However, the main drawback of only adopting this selection criterion is that the resulting sample is ultimately not directly comparable to the observational sample. Our sample, in contrast, is comparable to the observational sample.
The top panel of Fig. 1 shows the white dwarf luminosity function of our reference model with open circles, and the observed luminosity function of Rowell & Hambly (2011) with solid squares, while we show the corresponding residuals in the bottom panel. As is shown in the figure, the agreement between the theoretical results and the observed data is very good. Our fiducial model reproduces not only the observed slope of the white dwarf luminosity function, but also accounts for the scarcity of halo white dwarfs at very low luminosities (Mbol> 17). This indicates that our Monte Carlo code correctly reproduces the selection criteria employed by Rowell & Hambly (2011).
 |
Fig. 1 Halo white dwarf luminosity function for our fiducial Galactic model. The top panel shows the theoretical white dwarf luminosity function obtained when the cooling sequences incorporating residual hydrogen burning are employed (open circles). We also show, with solid squares, the observed halo luminosity function of Rowell & Hambly (2011). The bottom panel shows the residuals between the observed luminosity function and the theoretical calculations, Δ = 2(Nobs − Nsim) / (Nobs + Nsim). |
 |
Fig. 2 White dwarf luminosity functions when only hydrogen-rich synthetic white dwarfs are generated in the Monte Carlo simulation. The bottom panel shows, with solid squares, the residuals between our standard model, in which a fraction of 20% of non-DA white dwarfs was employed, and, with hollow circles, that in which this percentage is zero, Δ = 2(Nstd − Nno − DA) / (Nstd + Nno − DA), respectively. |
 |
Fig. 3 Same as Fig. 1 for the case in which residual hydrogen burning is not considered. The bottom panel shows the residuals between the luminosity function computed using our standard cooling sequences and that obtained when residual hydrogen burning is artifically ignored, Δ = 2(Nstd − Nno − H) / (Nstd + Nno − H). |
In a second step, we checked the sensitivity of our synthetic white dwarf luminosity function with our choice of cooling sequences for massive, oxygen-neon white dwarfs, and non-DA white dwarfs. For these stars we employed a set of cooling sequences of solar metallicity. Specifically, we assessed the final number of these white dwarfs in the restricted sample, that is, once we take observational selection criteria into account, and we found that in a typical Monte Carlo realization only one of these white dwarfs, at most, survives the successive selection cuts. The most stringent observational cut is the magnitude cut, r59F ~ 19.75. In most Monte Carlo realizations none of these white dwarfs survives this cut. Additionally, we mention that even if this cut is not employed, the proper motion cut eliminates almost 99.5% of oxygen-neon white dwarfs from the final sample. Thus, there are very few oxygen-neon white dwarfs in the final sample. The reason for this behavior is twofold. First, these white dwarfs are very scarce, since their formation is strongly inhibited by the shape of the IMF. Thus, not surprisingly, they contribute little to the white dwarf luminosity function. The second reason is that since these white dwarfs are made of oxygen and neon, their heat capacity is smaller than that of a carbon-oxygen white dwarf of the same mass (Garcia-Berro et al. 1997) and consequently cool faster. Accordingly, these white dwarfs essentially contribute to the faintest bins of the luminosity function, which is not probed by observations, because it is excluded by the magnitude cut. In summary, we conclude that the influence of adopting a set of cooling sequences of solar metallicity for oxygen-neon white dwarfs is negligible.
To assess the influence of adopting a set of cooling sequences of solar metallicity for non-DA white dwarfs, we ran an additional simulation in which the percentage of non-DA white dwarfs was set to zero, and consequently all the synthetic stars had hydrogen-rich atmospheres. We then computed the residuals between the resulting white dwarf luminosity function and that obtained with our reference model, for which the ratio of non-DA white dwarfs is 20%. The results, shown in Fig. 2, reveal that the differences are small, although not negligible. As a matter of fact, the space density of hot white dwarfs is smaller in the case in which only synthetic DA white dwarfs are generated, however, this is a consequence of the normalization procedure. Hydrogen-deficient white dwarfs have cooling sequences that resemble those of a black body, whereas the atmospheres of DA white dwarfs are more transparent. Consequently, at low temperatures non-DA white dwarfs cool faster than DA white dwarfs. Thus, the percentage of non-DA white dwarfs increases for decreasing luminosities, and therefore these white dwarfs accumulate at luminosities close to that of the peak of the theoretical luminosity function and even smaller. However, the number counts of white dwarfs in the luminosity bins close to the peak of the luminosity function dominate the total number counts of white dwarfs in the synthetic sample. Thus, since the total number of white dwarfs in any Monte Carlo realization must be kept constant and, moreover, must be close to the observed value, the hot branch of the luminosity function is depleted in the case in which non-DA white dwarfs are not generated. Nevertheless, we emphasize that because white dwarf cooling sequences of low metallicity for non-DA white dwarfs are not available, it is clear that this procedure largely overestimates the impact of adopting a set of cooling sequences of inappropriate metallicity. Thus, we conclude that the possible effect of adopting a set of cooling sequences of solar metallicity for non-DA white dwarfs is limited.
Next, we assess the sensitivity of these results to the most relevant inputs of our model. In particular, we first discuss if the adopted cooling tracks for carbon-oxygen white dwarfs with hydrogen-rich atmospheres could change this picture. In a second step, we study whether a different choice of the adopted IMF could affect our results. Later, we evaluate if a different halo model could have a noticeable influence in our calculations. Finally, we also study whether different percentages of unresolved binaries vary the shape of the white dwarf luminosity function. We conclude our assessment by comparing our theoretical results for different ages of the stellar halo.
3.1. Hydrogen burning
It has been shown (Miller Bertolami et al. 2013) that residual hydrogen burning can significantly impact the cooling process of white dwarfs with progenitors of very low metallicity, the effect being more noticeable for low-mass white dwarfs (those with masses between 0.5 and 0.6 M⊙). Since low-mass white dwarfs contribute to all the luminosity bins of the hot branch of the luminosity function, and since the shape of the luminosity function is directly related to the cooling rate, it is natural to ask ourselves whether a different choice of cooling sequences could affect the slope at moderately high luminosities. We check this using the two different sets of cooling tracks described in Althaus et al. (2015). The first of these sets is that used in our reference model, and considers residual nuclear burning, while the second set does not take nuclear reactions into account (as it occurs for white dwarf progenitors with Z> 0.001).
In Fig. 3, we present the resulting white dwarf luminosity function for the halo population when we adopt the cooling sequences in which residual hydrogen burning is artificially ignored. This luminosity function should be compared with that shown in Fig. 1. The only difference between both sets of theoretical calculations is that for the case in which the cooling sequences incorporating residual hydrogen burning are employed, there is a small plateau between Mbol = 12 and 14, which is absent in the case in which no residual hydrogen burning is considered. This plateau reflects the slow-down of cooling due to the release of energy of residual hydrogen burning. The differences between both calculations are minor, however, and the currently available observational luminosity function, which is derived using only ~100 white dwarfs, does not allow us to draw definite conclusions about the real existence of residual nuclear burning.
3.2. Initial mass function
As mentioned, we also test the influence that the adopted IMF may have on our results. Since the formation timescale of the stellar halo is short, it is straightforward to show that when a burst of negligible duration is adopted the luminosity function is given by, 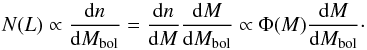 (4)In this expression, n stands for the space density, and Φ for the IMF. Thus, it is clear that the adopted IMF should influence the shape of the luminosity function.
(4)In this expression, n stands for the space density, and Φ for the IMF. Thus, it is clear that the adopted IMF should influence the shape of the luminosity function.
To test the influence of the IMF on the luminosity function, we employ three parametrizations. The first is that used in our fiducial model, namely the so-called universal mass function of Kroupa (2001). For the mass range relevant to our study this IMF is totally equivalent to a two-branch power law with exponent −α, with α = 1.3 for 0.08 ≤ M/M⊙< 0.5 and α = 2.3 for M/M⊙ ≥ 0.5. We also compute theoretical white dwarf luminosity functions adopting the classical IMF of Salpeter (1955), which is a power law with index α = 2.35. Finally we also adopt a top-heavy IMF, i.e., 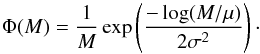 (5)In this expression μ = 10 M⊙ and σ = 0.44. This IMF was introduced by Suda et al. (2013), and is dominated by high-mass stars. It has been found that this IMF better reproduces the characteristics of metal-poor populations, namely those with [ Fe / H ] ≤ −2.
(5)In this expression μ = 10 M⊙ and σ = 0.44. This IMF was introduced by Suda et al. (2013), and is dominated by high-mass stars. It has been found that this IMF better reproduces the characteristics of metal-poor populations, namely those with [ Fe / H ] ≤ −2.
 |
Fig. 4 White dwarf luminosity functions when different IMFs are considered for the stellar spheroid. The bottom panel shows, with circles, the residuals between our standard model and, with triangles, those obtained when the Salpeter (1955) and the top-heavy IMF of Suda et al. (2013) are used, Δ = 2(Nstd − NIMF) / (Nstd + NIMF), respectively. |
The corresponding luminosity functions for these IMFs are shown in the top panel of Fig. 4, and their respective residuals with respect to our fiducial model are shown in the bottom panel of this figure. As shown in the figure, there are no noticeable differences between the calculations in which the IMF of Kroupa (2001) and that of Salpeter (1955) are employed. The reason for this is that in the relevant luminosity range the slope of both IMFs is very similar. We note, however, that when the top-heavy IMF of Suda et al. (2013) is used, the luminosity function presents a drop in the space density at large luminosities. This deficit of bright white dwarfs is quite apparent, but it is marginally consistent with the observed data.
 |
Fig. 5 White dwarf luminosity functions for different density profiles of the stellar halo. The bottom panel shows, with circles, the residuals between our standard model, and, with triangles, those obtained when the density profile of a triaxial halo (Helmi 2004) and that of Navarro et al. (1996) are employed, Δ = 2(Nstd − Nρ) / (Nstd + Nρ), respectively. |
3.3. Density profiles
Another possible concern would be the adopted density profile for the stellar halo. As explained in Sect. 2.1, in our reference model we adopted the density profile of the classical isothermal sphere, but there are other density profiles that are worth studying. Accordingly, here we study how this choice affects our results. To do this we first adopted a triaxial oblate halo model, which is based in a logarithmic dark halo potential (Helmi 2004), 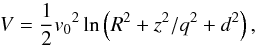 (6)which results in a density distribution:
(6)which results in a density distribution: 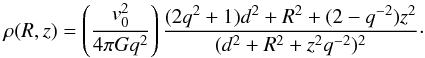 (7)In this expression, we have adopted d = 12 kpc and v0 = 131.5 km s-1, which gives a circular velocity of the Sun of 229 km s-1, and an oblateness parameter q = 0.8. Our third and last profile is the following widely used profile of Navarro et al. (1996):
(7)In this expression, we have adopted d = 12 kpc and v0 = 131.5 km s-1, which gives a circular velocity of the Sun of 229 km s-1, and an oblateness parameter q = 0.8. Our third and last profile is the following widely used profile of Navarro et al. (1996): 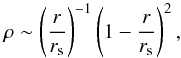 (8)with rs = 18 kpc.
(8)with rs = 18 kpc.
As Fig. 5 reveals, the differences between the luminosity functions computed, using these three different density profiles for the stellar halo, are totally negligible. This is because the sample of halo white dwarfs of Rowell & Hambly (2011) is local, whereas the differences between the three model profiles should be prominent at large distances.
3.4. Unresolved binaries
 |
Fig. 6 Same as Fig. 5, except for different fractions of unresolved binaries. The bottom panel shows, with circles, the residuals between our standard model with circles, and, with triangles, those obtained when the adopted fractions of unresolved binaries are 20% and 40%, Δ = 2(Nstd − Nbin) / (Nstd + Nbin), respectively. |
One of the potential problems when calculating the observed luminosity function for single stars are unresolved binary white dwarfs, since they compute as single stars, and hence this may modify the shape of the luminosity function. This has been proven to be the case in some Galactic clusters (Bedin et al. 2008; García-Berro et al. 2010). It is therefore interesting to check the effect that a certain fraction of unresolved binaries can have on the theoretical luminosity function. To test this, we compute a new set of simulations based on our fiducial model, increasing the fraction of unresolved binaries. As mentioned earlier, we consider no unresolved binaries in our reference model. As for the distribution of secondary masses, we adopted a model in which the masses of both components are not correlated.
Figure 6 shows the result of this numerical experiment when the fractions of unresolved binaries are, 20% and 40%, respectively. As can be observed in this figure, increasing the fraction of unresolved binaries considered in the sample does not result in any noticeable change, but results in a slight reduction of the number of white dwarfs populating the brightest luminosity bins. The reason for this can easily be explained. Since low-luminosity white dwarfs have longer evolutionary timescales the low-luminosity bins also have large space densities. Consequently, unresolved binaries also concentrate in the luminosity bins with the largest densities, and thus the bright luminosity bins are less populated. Since we normalize our theoretical luminosity function to the observed luminosity bin at Mbol = 15.75, the result is that the bright branch of the theoretical luminosity function is depleted. Nevertheless, the differences are minor even when an unrealistic percentage of 40% of the objects in the synthetic sample are unresolved binaries.
3.5. The star formation history
 |
Fig. 7 Same as Fig. 5, except for different durations of the initial burst of star formation. The bottom panel shows, with circles, the residuals between our standard model and, with triangles, those obtained when the adopted durations of the initial burst of star formation are 0.5 and 2.0 Gyr, Δ = 2(Nstd − NΔt) / (Nstd + NΔt), respectively. |
 |
Fig. 8 Same as Fig. 5, except for four various merger episodes of two strengths and at two different times. The bottom panels show the residuals between our standard model and those obtained when the impact of a merger episode is analyzed, Δ = 2(Nstd − Nmer) / (Nstd + Nmer). See text for details. |
Another point of concern is the adopted star formation history. This may also have potential effects on the morphology of the hot branch of the halo white dwarf luminosity function. To start with we discuss the effects of the duration of the initial burst of star formation. This is done with the help of Fig. 7, where we show the theoretical white dwarf luminosity functions for two burst of durations 0.5 and 2.0 Gyr, and compare them with our reference model, for which we recall that we employed a burst of duration 1.0 Gyr. This figure clearly shows that, except for the smaller space densities at moderately high luminosities, the differences between these two luminosity functions and our fiducial functions are marginal. Consequently, current observations do not allow us to discern between different durations of the initial burst of star formation.
Furthermore, a consensus about the origin of the stellar spheroid has not been reached yet. The two main competing scenarios, i.e., monolithic collpase of the protogalactic gas (Eggen et al. 1962) or formation through several merger episodes (Searle & Zinn 1978), still need to be confronted with observations. Hence, it is natural to wonder if these two scenarios leave observable imprints in the shape of the hot branch of the white dwarf luminosity function of single halo white dwarfs. To this end, we conducted an additional set of simulations in which, in addition to the initial burst of star formation, we modeled the luminosity function in which a second burst of star formation occurring some time ago is adopted. Specifically, we ran four additional simulations in which a secondary burst of star formation occurs at times 4 and 8 Gyr, varying the strength of this secondary burst. The metallicities of the secondary bursts of star formation were the same as adopted for the initial burst. This choice minimizes the effects of these merger episodes, but the effects of the different metallicity of the secondary bursts are expected to be minor. Specifically, the secondary burst was given amplitudes 20% and 40% of the initial burst. In all cases, the durations of all the bursts (that is, both the initial and the secondary ones) were kept fixed and equal to 0.1 Gyr, while we recall that in the standard model a duration of 1 Gyr was adopted. The results of this numerical experiment are shown in Fig. 8. In the left panels of this figure, we show the results from when we adopt a secondary burst with an amplitude 20% of the initial burst, whereas the right panels show the results from when the amplitude of the secondary burst is increased to 40% of the primary burst. As shown in the figure, the differences are again very small. Thus, unfortunately, the current observational database of halo white dwarfs does not allow us to distinguish the two aforementioned formation scenarios of the stellar halo.
3.6. Age of the population
Finally, we ran a set of simulations in which we varied the age of the halo population, from 11 to 13 Gyr, and we compared the results of these calculations with those obtained in our reference model, for which we adopted an age of 13.7 Gyr. We show the results of these calculations in Fig. 9. As expected, the bright branch of the white dwarf luminosity function does not depend appreciably on the adopted age of the stellar spheroid. Moreover, since the observed luminosity function does not show a cutoff, the age of the halo population cannot be yet computed using the termination of the cooling sequence of halo white dwarfs. This is a consequence of the cuts used to select the observed sample, and is specifically caused by the cut in bolometric magnitude. The only quantitative assessment about the age of the halo that can be made with the available observed data is to place a lower limit. This can be done in a simple way by imposing that the dimmest populated luminosity bin of the theoretical white dwarf luminosity function is that observationally found, at Mbol = 17.25. Using this procedure we find that, although it is not possible to fit the halo age, a lower limit for its age of 12.5 Gyr can be safely established.
4. Conclusions
In this paper, we have revisited the luminosity function of halo white dwarfs in the light of the recently computed white dwarf cooling sequences for low-metallicity progenitors. These cooling sequences (Miller Bertolami et al. 2013; Althaus et al. 2015) have been derived evolving their progenitors self-consistently from the zero-age main sequence, through the red giant and thermally pulsing AGB phases to the white dwarf regime, and have unveiled the role of residual hydrogen burning in the atmospheres of low-mass white dwarfs. In this sense, it is important to realize that these evolutionary calculations supercede those used in the early and pioneering calculations of the halo white dwarf luminosity function of Isern et al. (1998) and García-Berro et al. (2004), and in the recent work of van Oirschot et al. (2014). Moreover, in pursuing this endeavour we have employed a state-of-the-art numerical code, incorporating the most recent advances that enable an accurate description of the Galactic halo and a detailed implementation of the observational biases and restrictions. This is an issue that most theoretical calculations do not take into account, thus impeding a sought comparison with the observed sample. This is an important issue, as the observed sample of white dwarfs belonging to the Galactic spheroid suffers from small statistics. Moreover, given that the density of halo white dwarfs is low and that this population is old, hence, intrinsically faint, the detection of halo white dwarfs is hampered by observational difficulties. Consequently, the selection biases are important, and we are restricted to comparing the theoretical results of our results with an observational sample plagued with uncertainties.
 |
Fig. 9 Same as Fig. 5, except with different ages of the halo population. The bottom panel shows the residuals between our standard model and the luminosity functions obtained when the age of the stellar halo is varied, Δ = 2(Nstd − NT) / (Nstd + NT). |
Since residual hydrogen burning occurs at moderately low luminosities, say from log (L/L⊙) = −2 to −4, the halo luminosity function could eventually offer a unique possibility to test the reliability of these recent cooling sequences. This could have important consequences for our understanding of how white dwarfs are formed and how their progenitor stars evolve in low-metallicity environments, and, more specifically, it could shed light on the occurrence of the third dredge-up for metallicities ≲10-3. We have found that, unfortunately, the scarcity of halo white dwarfs at the luminosities at which residual hydrogen burning occurs prevents us from making a meaningful comparison between the sequences that incorporate this physical ingredient and those that do not. Thus, this effort will have to wait until we have larger and more reliable samples. Alternatively, this could be done using the white dwarf luminosity functions of Galactic globular clusters, of which NGC 6397 is, perhaps, the leading example.
Additionally, we have investigated whether or not the observed luminosity function of single white dwarfs can be eventually used to learn more about the stellar population of the Galactic halo. In particular, we have studied whether the observed luminosity function can be used to constrain the IMF of this population, its star formation history and age, to probe different halo density profiles, or possibly to discern the fraction of unresolved binaries that may contaminate observations. Unfortunately, our calculations show that the hot branch of the luminosity function is almost insensitive to all these input, as occurs in the disk white dwarf luminosity function (Isern et al. 2008). Consequently, unless we have a more accurate determination of the luminosity function at large bolometric magnitudes (low luminosities) there is no hope to extract all this information from the observed data. However, large space-borne surveys, like Gaia, will provide us with a large sample of halo white dwarfs (Torres et al. 2005), and hopefully a wealth of information will be extracted in the near future. Nonetheless, the lack of sensitivity of the hot branch of the luminosity function of halo white dwarfs to all these inputs can be interpreted positively since it allows us to obtain a robust statistical measure of the cooling rate of white dwarfs at low metallicities and high luminosities.
Acknowledgments
This research was partially supported by MCINN grant AYA2011–23102, by the European Union FEDER funds, by the AGAUR (Spain), by the AGENCIA through the Programa de Modernización Tecnológica BID 1728/OCAR, and by the PIP 112-200801-00940 grant from CONICET (Argentina). R.C. also acknowledges financial support from the FPI grant BES-2012-053448.
References
- Aller, L. H., & Greenstein, J. L. 1960, ApJS, 5, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., García-Berro, E., Isern, J., & Córsico, A. H. 2005, A&A, 441, 689 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., García-Berro, E., Isern, J., Córsico, A. H., & Rohrmann, R. D. 2007, A&A, 465, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Camisassa, M. E., Miller Bertolami, M. M., Córsico, A. H., & García-Berro, E. 2015, A&A, 576, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becker, S. A., & Iben, Jr., I. 1979, ApJ, 232, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, S. A., & Iben, Jr., I. 1980, ApJ, 237, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Bedin, L. R., King, I. R., Anderson, J., et al. 2008, ApJ, 678, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Bedin, L. R., Salaris, M., King, I. R., et al. 2010, ApJ, 708, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Bellini, A., Bedin, L. R., Piotto, G., et al. 2010, A&A, 513, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergeron, P., Wesemael, F., Dufour, P., et al. 2011, ApJ, 737, 28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, in Galactic dynamics (Princeton: NJ, Princeton University Press) [Google Scholar]
- Carollo, D., Beers, T. C., Chiba, M., et al. 2010, ApJ, 712, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Cojocaru, R., Torres, S., Isern, J., & García-Berro, E. 2014, A&A, 566, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggen, O. J., Lynden-Bell, D., & Sandage, A. R. 1962, ApJ, 136, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Frebel, A., & Norris, J. E. 2013, in Planets, Stars and Stellar Systems. Galactic Structure and Stellar Populations, eds. T. D. Oswalt, & G. Gilmore (Netherlands: Springer Verlag), 5, 55 [Google Scholar]
- Garcia-Berro, E., Isern, J., & Hernanz, M. 1997a, MNRAS, 289, 973 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Ritossa, C., & Iben, Jr., I. 1997b, ApJ, 485, 765 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Torres, S., Isern, J., & Burkert, A. 1999, MNRAS, 302, 173 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Torres, S., Isern, J., & Burkert, A. 2004, A&A, 418, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Berro, E., Torres, S., Althaus, L. G., et al. 2010, Nature, 465, 194 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- García-Berro, E., Torres, S., Althaus, L. G., & Miller Bertolami, M. M. 2014, A&A, 571, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hakkila, J., Myers, J. M., Stidham, B. J., & Hartmann, D. H. 1997, AJ, 114, 2043 [NASA ADS] [CrossRef] [Google Scholar]
- Hambly, N. C., MacGillivray, H. T., Read, M. A., et al. 2001, MNRAS, 326, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S., Brewer, J., Fahlman, G. G., et al. 2002, ApJ, 574, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S., Kalirai, J. S., Anderson, J., et al. 2013, Nature, 500, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, H. C., Munn, J. A., Kilic, M., et al. 2006, AJ, 131, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A. 2004, MNRAS, 351, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., García-Berro, E., Hernanz, M., Mochkovitch, R., & Torres, S. 1998, ApJ, 503, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., García-Berro, E., Torres, S., & Catalán, S. 2008, ApJ, 682, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Liebert, J., Dahn, C. C., & Monet, D. G. 1989, in Lecture Notes in Physics, IAU Colloq. 114: White Dwarfs, ed. G. Wegner (Berlin: Springer Verlag), 328, 15 [Google Scholar]
- Markovic, D., & Sommer-Larsen, J. 1997, MNRAS, 288, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., & García-Berro, E. 2013, ApJ, 775, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Miyaji, S., Nomoto, K., Yokoi, K., & Sugimoto, D. 1980, PASJ, 32, 303 [Google Scholar]
- Mochkovitch, R., Garcia-Berro, E., Hernanz, M., Isern, J., & Panis, J. F. 1990, A&A, 233, 456 [NASA ADS] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K. 1984, ApJ, 277, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Oppenheimer, B. R., Hambly, N. C., Digby, A. P., Hodgkin, S. T., & Saumon, D. 2001, Science, 292, 698 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Poelarends, A. J. T., Herwig, F., Langer, N., & Heger, A. 2008, ApJ, 675, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Renzini, A., & Voli, M. 1981, A&A, 94, 175 [NASA ADS] [Google Scholar]
- Rowell, N., & Hambly, N. C. 2011, MNRAS, 417, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Searle, L., & Zinn, R. 1978, ApJ, 225, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Suda, T., Komiya, Y., Yamada, S., et al. 2013, MNRAS, 432, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, S., García-Berro, E., Burkert, A., & Isern, J. 2002, MNRAS, 336, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, S., García-Berro, E., Isern, J., & Figueras, F. 2005, MNRAS, 360, 1381 [NASA ADS] [CrossRef] [Google Scholar]
- van Oirschot, P., Nelemans, G., Toonen, S., et al. 2014, A&A, 569, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wallerstein, G. 1962, AJ, 67, 123 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Number of synthetic white dwarfs that survive the different observational cuts for a typical Monte Carlo realization of our standard model.
All Figures
 |
Fig. 1 Halo white dwarf luminosity function for our fiducial Galactic model. The top panel shows the theoretical white dwarf luminosity function obtained when the cooling sequences incorporating residual hydrogen burning are employed (open circles). We also show, with solid squares, the observed halo luminosity function of Rowell & Hambly (2011). The bottom panel shows the residuals between the observed luminosity function and the theoretical calculations, Δ = 2(Nobs − Nsim) / (Nobs + Nsim). |
| In the text | |
 |
Fig. 2 White dwarf luminosity functions when only hydrogen-rich synthetic white dwarfs are generated in the Monte Carlo simulation. The bottom panel shows, with solid squares, the residuals between our standard model, in which a fraction of 20% of non-DA white dwarfs was employed, and, with hollow circles, that in which this percentage is zero, Δ = 2(Nstd − Nno − DA) / (Nstd + Nno − DA), respectively. |
| In the text | |
 |
Fig. 3 Same as Fig. 1 for the case in which residual hydrogen burning is not considered. The bottom panel shows the residuals between the luminosity function computed using our standard cooling sequences and that obtained when residual hydrogen burning is artifically ignored, Δ = 2(Nstd − Nno − H) / (Nstd + Nno − H). |
| In the text | |
 |
Fig. 4 White dwarf luminosity functions when different IMFs are considered for the stellar spheroid. The bottom panel shows, with circles, the residuals between our standard model and, with triangles, those obtained when the Salpeter (1955) and the top-heavy IMF of Suda et al. (2013) are used, Δ = 2(Nstd − NIMF) / (Nstd + NIMF), respectively. |
| In the text | |
 |
Fig. 5 White dwarf luminosity functions for different density profiles of the stellar halo. The bottom panel shows, with circles, the residuals between our standard model, and, with triangles, those obtained when the density profile of a triaxial halo (Helmi 2004) and that of Navarro et al. (1996) are employed, Δ = 2(Nstd − Nρ) / (Nstd + Nρ), respectively. |
| In the text | |
 |
Fig. 6 Same as Fig. 5, except for different fractions of unresolved binaries. The bottom panel shows, with circles, the residuals between our standard model with circles, and, with triangles, those obtained when the adopted fractions of unresolved binaries are 20% and 40%, Δ = 2(Nstd − Nbin) / (Nstd + Nbin), respectively. |
| In the text | |
 |
Fig. 7 Same as Fig. 5, except for different durations of the initial burst of star formation. The bottom panel shows, with circles, the residuals between our standard model and, with triangles, those obtained when the adopted durations of the initial burst of star formation are 0.5 and 2.0 Gyr, Δ = 2(Nstd − NΔt) / (Nstd + NΔt), respectively. |
| In the text | |
 |
Fig. 8 Same as Fig. 5, except for four various merger episodes of two strengths and at two different times. The bottom panels show the residuals between our standard model and those obtained when the impact of a merger episode is analyzed, Δ = 2(Nstd − Nmer) / (Nstd + Nmer). See text for details. |
| In the text | |
 |
Fig. 9 Same as Fig. 5, except with different ages of the halo population. The bottom panel shows the residuals between our standard model and the luminosity functions obtained when the age of the stellar halo is varied, Δ = 2(Nstd − NT) / (Nstd + NT). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


