| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 6 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526415 | |
| Published online | 27 August 2015 | |
Analysis of Fermi gamma-ray burst duration distribution
Astronomical Observatory, Jagiellonian University, Orla 171, 30-244 Cracow, Poland
e-mail: mariusz.tarnopolski@uj.edu.pl
Received: 26 April 2015
Accepted: 24 June 2015
Context. Two classes of gamma-ray bursts (GRBs), short and long, have been determined without any doubts, and are usually prescribed to different physical scenarios. A third class, intermediate in T90 durations has been reported in the datasets of BATSE, Swift, RHESSI, and possibly BeppoSAX. The latest release of >1500 GRBs observed by Fermi gives an opportunity to further investigate the duration distribution.
Aims. The aim of this paper is to investigate whether a third class is present in the log T90 distribution, or whether it is described by a bimodal distribution.
Methods. A standard χ2 fitting of a mixture of Gaussians was applied to 25 histograms with different binnings.
Results. Different binnings give various values of the fitting parameters, as well as the shape of the fitted curve. Among five statistically significant fits, none is trimodal.
Conclusions. Locations of the Gaussian components are in agreement with previous works. However, a trimodal distribution, understood in the sense of having three distinct peaks, is not found for any binning. It is concluded that the duration distribution in the Fermi data is well described by a mixture of three log-normal distributions, but it is intrinsically bimodal, hence no third class is present in the T90 data of Fermi. It is suggested that the log-normal fit may not be an adequate model.
Key words: gamma rays: general / methods: data analysis / methods: statistical
© ESO, 2015
1. Introduction
Gamma-ray bursts (GRBs) are most commonly classified based on their duration time T90 (time during which 90% of the burst fluence is accumulated, starting from the time at which 5% of the total fluence was detected). Mazets et al. (1981) first observed the bimodal distribution of T90 drawn for 143 events detected in the KONUS experiment. Kouveliotou et al. (1993) also found a bimodal structure in the log T90 distribution in BATSE 1B dataset; based on this data GRBs are divided into short (T90 < 2 s) and long (T90 > 2 s) classes. Horváth (1998) and Mukherjee et al. (1998) independently discovered a third peak in the duration distribution in the BATSE 3B catalog (Meegan et al. 1996), located between the short and long peaks, and the statistical existence of this intermediate class was supported (Horváth 2002) with the use of BATSE 4B data. Evidence for a third component in log T90 was also found in the Swift data (Horváth et al. 2008a,b; Zhang & Choi 2008; Huja et al. 2009; Horváth et al. 2010). Other datasets, i.e., RHESSI (Řípa et al. 2009) and BeppoSAX (Horváth 2009), are both in agreement with earlier results regarding the bimodal distribution, and the detection of a third component was established on a lower significance level (compared to BATSE and Swift) owing to less populated samples. Hence, four different satellites provided hints about the existence of a third class of GRBs. Contrary to this, the durations observed by INTEGRAL have a unimodal distribution that extends to the shortest timescales as a power law (Savchenko et al. 2012).
Only one dataset (BATSE 3B) was truly trimodal in the sense of having three peaks. In the others, a three-Gaussian distribution was found to follow the histogram better than a two-Gaussian, but those fits yielded only two peaks, so although statistical analyses support the presence of a third class, its existence is still elusive and may be due to selection and instrument effects, or might be described by a distribution that is not necessarily a mixture of Gaussians. The latest release is due to Fermi GBM observations (Gruber et al. 2014; von Kienlin et al. 2014) and consists of 1568 GRBs1 with calculated T90. This sample, to the best of the author’s knowledge, has not yet been investigated for the presence of an intermediate class; only Horváth et al. (2012) and Qin et al. (2013) conducted research on a subsample consisting of 425 bursts from the first release of the catalog.
Previous analyses, although consistent with each other (except INTEGRAL), showed variances in locations of the Gaussian components, their dispersion, relative heights, and statistical significance of a trimodal fit compared to a bimodal distribution. The aim of this article is to perform a statistical analysis of the Fermi database in order to verify the existence of the intermediate-duration GRB class. The current sample constitutes ~83% of long GRBs (T90 > 2 s), which is a larger percentage than in previous catalogs. A conventional χ2 fitting is applied. Since BATSE 4B (Horváth 2002), the maximum log-likelihood method has been used. In the case of the Swift data this was fully justified because of the small size of the population (Horváth et al. 2008a,b). However, in the first analysis of the BATSE 3B data (Horváth 1998), which consisted of 797 GRBs, three classes were detected with the χ2 method, which was later supported by the maximum log-likelihood method on a bigger dataset (Horváth 2002). Hence, the number of GRBs under consideration in this study should not be too small to conduct a conventional fitting analysis. To verify whether the χ2 fitting is applicable, the BATSE 4B data (2041 GRBs) were re-examined and results similar to those of Horváth (2002) were obtained. To be sure that the method chosen does not rule out any feature in the data under consideration, the maximum log-likelihood was also applied, but since the results were not different from those obtained using the χ2 fitting, they are not reported here or mentioned in what follows.
This article is organized as follows. Section 2 presents the χ2 fittings of different models. In Sect. 3 a comparison with previous results is discussed. Section 4 is devoted to discussion, and Sect. 5 gives concluding remarks. The computer algebra system Mathematica v10.0.2 is applied throughout this paper.
2. The χ2 fittings
2.1. Sample
In this section a dataset of 1566 GRBs is used. Two durations (the shortest and the longest) were excluded because, for every binning, they were separated from the rest of the distribution by empty bins.
2.2. Standard normal distributions
A least squares fitting of a multi-component log-normal distribution to the dataset of durations T90 is performed, i.e., a mixture of Gaussians 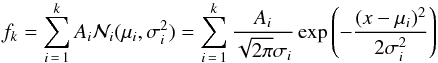 (1)is fitted to a histogram of log T90. A significance level of α = 0.05 is adopted. Twenty-five binnings are applied, defined by the bin widths w from 0.30 to 0.06 with a step of 0.01. The corresponding number of bins ranges from 15 to 69. A number of binnings is chosen rather than a neutral bin width established according to some conventional rule (e.g., Freedman-Diaconis, Scott, Knuth) because of Koen & Bere et al. (2012), who found two fits to Swift data that could not be rejected, hence restricting the analysis to only one binning might be concealing. For each binning the same fitting procedure is performed as described.
(1)is fitted to a histogram of log T90. A significance level of α = 0.05 is adopted. Twenty-five binnings are applied, defined by the bin widths w from 0.30 to 0.06 with a step of 0.01. The corresponding number of bins ranges from 15 to 69. A number of binnings is chosen rather than a neutral bin width established according to some conventional rule (e.g., Freedman-Diaconis, Scott, Knuth) because of Koen & Bere et al. (2012), who found two fits to Swift data that could not be rejected, hence restricting the analysis to only one binning might be concealing. For each binning the same fitting procedure is performed as described.
The χ2 of a fit is calculated in a standard way as 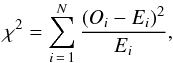 (2)where Oi is the observed ith value, Ei is the value expected based on the fit, and N is the number of bins. The number of degrees of freedom, d.o.f., of the χ2 test statistic is d.o.f. = N − m − 1, where m is the number of parameters used; for a k-Gaussian, m = 3k. First, a single-Gaussian fit is performed for all binnings. The χ2 values range from 12 180 to 54 548, with p-values being numerically equal to zero in all cases. It follows from the huge χ2 values that it is extremely unlikely that the single-Gaussian fit describes the log T90 distribution correctly.
(2)where Oi is the observed ith value, Ei is the value expected based on the fit, and N is the number of bins. The number of degrees of freedom, d.o.f., of the χ2 test statistic is d.o.f. = N − m − 1, where m is the number of parameters used; for a k-Gaussian, m = 3k. First, a single-Gaussian fit is performed for all binnings. The χ2 values range from 12 180 to 54 548, with p-values being numerically equal to zero in all cases. It follows from the huge χ2 values that it is extremely unlikely that the single-Gaussian fit describes the log T90 distribution correctly.
Next, a two-Gaussian fit is performed and the resulting χ2 are much lower; however, the majority of p-values indicates that the distributions do not follow the data well at the α = 0.05 significance level. Fitted parameters are gathered in Table 1, with p-values greater than α written in bold, while the curves are displayed in Fig. 1. The bimodal structure is well represented by a two-Gaussian fit in four out of five cases displayed in Fig. 1. The statistically unsignificant fit for w = 0.25 is also shown due to a comparison with a three-Gaussian fit to be performed further on.
Parameters of a two-Gaussian fit.
 |
Fig. 1 Two-Gaussian fits (solid black) to log T90 distributions. All except w = 0.25 are statistically significant. Colored dashed curves are the components of the mixture distribution. |
Finally, a three-Gaussian fit is performed in the same manner. The resulting χ2 are naturally lower than they were in the previous case. Again, a majority of the corresponding p-values that are smaller than α indicates that in general the duration distribution is not well described by a mixture of three log-normal components. Parameters of the five fits with p - values>α are gathered in Table 2, and the fitted curves are displayed in Fig. 2. It is important to note that these five fits are all statistically significant, including the fit for w = 0.25, for which a hypothesis that the histogram is well described by a two-Gaussian fit was rejected.
Parameters of a three-Gaussian fit.
The probability that the third component originates from statistical fluctuations may be estimated by comparing a three-Gaussian with a two-Gaussian fit, based on an observation (Band et al. 1997) that 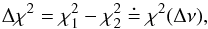 (3)where Δν = ν2 − ν1 is the difference in the degrees of freedom of fits under consideration, equal to three when Δk = 1 (compare with Eq. (1)), and
(3)where Δν = ν2 − ν1 is the difference in the degrees of freedom of fits under consideration, equal to three when Δk = 1 (compare with Eq. (1)), and  denotes equality in distribution.
denotes equality in distribution.
To elaborate to what degree a three-Gaussian fit is better than a two-Gaussian, Eq. (3) is applied and the p-values are inferred from a χ2 distribution with three degrees of freedom. A small p-value indicates a small probability that the two-Gaussian model alone describes the data in comparison with a three-Gaussian. The results, gathered in Table 3, indicate that in all binnings there is a> 20% probability (exceeding 50% for the remaining three statistically significant cases) that a three-Gaussian is a significant improvent over a two-Gaussian fit. This does not mean that the three-Gaussian models are a good description of the data, as the χ2 from Table 2 lead to rejection of the null hypothesis for only one out of five binnings with p-values greater than α in the three-Gaussian case. For this unsignificant fit, the p-value computed from Δχ2 means that a bad three-Gaussian is better than a bad two-Gaussian. For the fits that are statistically significant (when fitting both a two- and a three-Gaussian) the conclusion is that a null hypothesis cannot be rejected for both, but a three-Gaussian describes the data better with a probability >50%. Nevertheless, this probability is insufficient to claim a detection; in Horváth (2009) it was concluded that even a 96% significance level is too small to be considered evidence.
Improvements of a three-Gaussian over a two-Gaussian fit.
The Fermi distribution is dominated by long GRBs, which constitute ~83% of the sample, that is manifested through a significantly higher dispersion of the short GRB distribution. Moreover, it was proposed that the distribution for short GRBs was nearly flat for T90 ≲ 2 s (Bromberg et al. 2011, 2013) (compare with Savchenko et al. 2012); however, for smaller bin widths a statistical noise starts to dominate. This is supported by a very small p-value of ~10-4 − 10-7 for the smaller bin widths, w = 0.11 − 0.06, which indicates that at these binnings statistical noise is dominating.
Three out of five statistically significant fittings (w = 0.27, 0.25, 0.13) located the third component beyond the main peak for long GRBs. One fit (w = 0.26) showed an excess at T90 ≈ 10 s that might be assigned to an intermediate class; however, the fitted curve is very similar to a two-Gaussian. The last fit, with w = 0.20, detected two components (in addition to a peak related to short GRBs) of approximately the same height and comparable standard deviations in a region of long GRBs. For these last two fits, the dispersion of a corresponding peak of a two-Gaussian is greater than the dispersion of both the components in the three-Gaussian, hence it gives a hint toward the bimodality of the GRBs (Schilling et al. 2002). This is in agreement with a very high probability that the third group in a three-component model is a statistical fluctuation.
3. Comparison with former results
A detailed comparison between BATSE 4B and Swift catalogs has been conducted (Huja et al. 2009) and the results were found to be consistent, also in the means of differences between the instruments. The RHESSI observations were also taken into account (Řípa et al. 2009) and roughly the same distribution as in previous catalogs was reported. The BeppoSAX data were of a relatively low population and the analysis showed the presence of three components on a significance level lower than in previous catalogs, but two classes – the intermediate and long – were detected with high certainty (Horváth 2009). As short GRBs were underpopulated, the three-Gaussian fit, despite following the observations better than a two-Gaussian, consisted of a component with a high dispersion. Overall, classification analyses found three components in all four samples. Interestingly, the dataset from INTEGRAL (Savchenko et al. 2012) yields a unimodal distribution. The latest well-populated sample, based on the Fermi data, was investigated some time ago (Horváth et al. 2012) using PCA and multiclustering analysis, and a three-group structure was found in a multidimensional parameter space including duration, total fluence, hardness ratio, and peakflux256. Hence, data from five satellites supported a three-component distribution of GRBs by means of statistical significance.
In Fig. 3 all of the components’ locations found by the above-mentioned univariate analyses are plotted. Results from this work, i.e., locations of the three-Gaussian components found by a standard log-normal fitting, are consistent with previous results by means of locations as well as relative separations – mean durations of the five statistically significant fits are centered at 0.745 s, 21.61 s, and 67.05 s for short, intermediate, and long GRBs, respectively. The current sample of 1566 GRBs comprises 17% of short GRBs and 83% of long ones, based on the conventional classification ≶2 s. Because of an insufficient separation of the intermediate and long components, it is impossible to conclude what the population of intermediate class GRBs in Fermi data is, as the distribution is apparently bimodal and shows no evidence for the third class being present, and one can associate the intermediate and long groups with a single class. It is important to note that in Fermi the sensitivity at very soft and very hard GRBs was higher than in BATSE (Meegan et al. 2009). Soft GRBs are intermediate in duration, and hard GRBs have short durations. Hence, an increase in intermediate GRBs relative to long ones might be expected as a consequence of improving instruments, yet the third class remains elusive. Swift is more sensitive in soft bands than BATSE was, hence its dataset has a low fraction of short GRBs. Therefore, the group populations inferred from Fermi observations are reasonable considering the characteristics of the instruments.
 |
Fig. 3 Locations of the short (green squares), intermediate (blue crosses) and long (red triangles) GRBs from previous research and this work. |
4. Discussion
Among the 25 three-Gaussian fittings performed, five (w = 0.27, 0.26, 0.25, 0.20, 0.13) turned out to be statistically significant, with p-values exceeding the significance level α = 0.05. Locations of the respective groups for the five fits are close to each other with means μ1 = −0.128 ± 0.082 (short GRBs), μ2 = 1.335 ± 0.156 and μ3 = 1.826 ± 0.185 (long GRBs), the error being the standard deviation of the average (compare with Fig. 3). Previous works on datasets from BATSE (Horváth 1998, 2002) and Swift (Horváth et al. 2008a; Huja et al. 2009) indicated that a three-Gaussian is a better fit than a corresponding two-Gaussian. On the other hand, a three-Gaussian fit to RHESSI (Řípa et al. 2009) data yielded only a 93% probability of being correct compared to a two-Gaussian, meaning that there is a remarkable 7% probability that the log T90 is well described by a two-Gaussian, while for BeppoSAX (Horváth 2009) the goodness-of-fit was not reported (only the maximum log-likelihoods).
Moreover, the two greater means of the three-Gaussian from Fig. 2 (w = 0.20) do not satisfy the criterion of bimodality (Schilling et al. 2002) 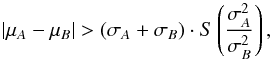 (4)with σA ≤ σB, and S(r) being the separation factor equal to 0.98 in the case of w = 0.20 (assuming equal weights; arbitrary mixtures yield an even higher value of the factor) for σ2 and σ3 from Table 2, hence long GRBs (T90> 2 s) do not have a bimodal distribution and are described by a single peak, meaning that the distribution over the whole range of available durations T90 is bimodal, with peaks corresponding to short and long GRB populations. The fit for w = 0.26 does not fulfil this condition either, where the appropriate S(r) = 1.16 is taken from (Schilling et al. 2002). The remaining three cases, although the shoulder is prominent, are also apparently bimodal.
(4)with σA ≤ σB, and S(r) being the separation factor equal to 0.98 in the case of w = 0.20 (assuming equal weights; arbitrary mixtures yield an even higher value of the factor) for σ2 and σ3 from Table 2, hence long GRBs (T90> 2 s) do not have a bimodal distribution and are described by a single peak, meaning that the distribution over the whole range of available durations T90 is bimodal, with peaks corresponding to short and long GRB populations. The fit for w = 0.26 does not fulfil this condition either, where the appropriate S(r) = 1.16 is taken from (Schilling et al. 2002). The remaining three cases, although the shoulder is prominent, are also apparently bimodal.
The relative improvements (Table 3) indicate an enourmous probability, ranging from 14% to 77%, that the third component in a three-Gaussian fit is a chance occurrence compared to a two-Gaussian.
Finally, among previous research, only the BATSE 3B data revealed a truly trimodal log T90 distribution, i.e., having three local maxima, which was not present in the following release, BATSE 4B (where only a bump was present), and is non-existent in the current BATSE catalog. Swift also observed two local maxima, although with a prominent shoulder on the left side of the long GRB peak (Horváth et al. 2008a), detected by means of the maximum log-likelihood method. Huja et al. (2009) also obtained a bimodal distribution with a bump on one side of the long GRB peak, although somewhat weaker. The explanation may be that for the sample of 388 GRBs, a maximum log-likelihood method is more robust than applying a χ2 fitting. The latter may be a drawback in undersampled populations. Fortunately, this is not a case in the Fermi data. The RHESSI distribution (Řípa et al. 2009) is also characterized by a bimodal fit with a shoulder, while in BeppoSAX clearly separated intermediate and long groups were found (Horváth 2009); however, no short GRBs were detected in the log T90 distribution there. This is most likely due to a low trigger efficiency to short GRBs, which are highly underpopulated in that sample. Interestingly, an early analysis of 222 GRBs from Swift (Horváth et al. 2008b) detected the short class, while the long GRBs were unimodal, again with a bump. Finally, the standard three-Gaussian fits passed the Anderson-Darling test, hence a mixture of log-normal distributions account well for the observed durations.
The distributions fitted in this paper are strongly dependent on the binning applied when the locations of components and their relative amplitudes are considered. No statistically significant trimodal fit was found, although a shoulder (in three out of five fits) was detected beyond the region where previous works found the intermediate class, which is a surprising result. Still, a three-Gaussian fit is a better fit than a two-Gaussian, statistically speaking. However, it is arguable whether this confirms the existence of the third class of GRBs. As the sum of two normal distributions is skewed, which is the apparent case in the Fermi sample, the underlying multimodal distribution may not necessarily be composed of Gaussians. Recently, Zitouni et al. (2015) suggested that the duration distribution corresponding to the collapsar scenario (associated with long GRBs) might not necessarily be symmetrical because of a non-symmetrical distribution of envelope masses of the progenitors.
Moreover, the more components the mixture distribution has, the more parameters are available for the curve to fit the histogram. This may be the primary reason for the calculated goodness-of-fit. On the other hand, in terms of statistical accuracy, the hypothesis that three fundamental components are needed to describe observed durations is corroborated. The true underlying form of the distribution remains obscure. Short GRBs have been underpopulated in observations ever since, and some instrument biases have been proposed to account for the emergence of a third peak. The trimodality in the BATSE 3B catalog was greatly diminished in the 4B version, which may be directly attributed to collecting a more complete sample. The Fermi database contains 75% of the number of GRBs observed in BATSE current catalog, hence further observations, as well as theoretical models that could account for the diversity of GRB events in more detail may clarify the properties of the T90 distribution and determine whether an intermediate class of GRBs is a physical or a statistical phenomenom.
Finally, a mixture of log-normal Gaussians may not be a proper model for the T90 distribution, and a mixture of intrinsically skewed distributions may be a better explanation of the observed features of the histogram. On the other hand, the duration distribution might not be a sum of components defined on (−∞, +∞), but might be a piecewise function.
5. Conclusions
-
1.
A mixture of three standard normal distributions was found tobe statistically significant in describing thelog T90 distribution for 1566 Fermi GRBs for bin widths w = 0.27, 0.26, 0.25, 0.20, 0.13. Average locations of the components are equal to 0.745 s, 21.61 s, and 67.05 s for short, intermediate, and long GRBs, respectively, or −0.128, 1.335, and 1.826 in log-scale. These results are in agreement with values obtained from previous catalogs: BATSE, Swift, RHESSI, and BeppoSAX.
-
2.
The relative improvements of a three-Gaussian fit over a two-Gaussian imply that there is a significant probability, varying from 14% to 77% among the fits, that the third component is a chance occurrence. Therefore, the third GRB class is unlikely to be present in the Fermi data.
-
3.
None of the fits is trimodal (in the sense of having three distinct peaks). Although three out of five fits show a prominent shoulder on the right side of the long GRB peak, the evidence is not sufficient to claim detection of a third class in the Fermi data. Therefore, the distribution of Fermi durations is intrinsically bimodal, hence no evidence for an intermediate class of GRBs has been found.
-
4.
The observed asymmetry may come from an underlying distribution composed of two skewed components, or it may be a piecewise function.
http://heasarc.gsfc.nasa.gov/W3Browse/fermi/fermigbrst.html, accessed on March 12, 2015.
Acknowledgments
The author acknowledges fruitful discussions with Michał Wyrȩbowski and Arkadiusz Kosior, and wishes to thank the anonymous referee for useful comments that led to significant improvements of the paper.
References
- Band, D. L., Ford, L. A., Matteson, J. L., et al. 1997, ApJ, 485, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Bromberg, O., Nakar, E., & Piran, T. 2011, ApJ, 739, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Bromberg, O., Nakar, E., Piran, T., & Sari, R. 2013, ApJ, 764, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Gruber, D., Goldstein, A., Weller von Ahlefeld, V., et al. 2014, ApJS, 211, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Horváth, I. 1998, ApJ, 508, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Horváth, I. 2002, A&A, 392, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horváth, I., Balázs, L. G., Bagoly, Z., & Veres, P. 2008a, A&A, 489, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horváth, I., Balázs, L. G., Bagoly, Z., et al. 2008b, AIP Conf. Proc., 1065, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Horváth, I., Balázs, L. G., & Bagoly, Z. 2009, Ap&SS, 323, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Horváth, I., Bagoly, Z., Balázs, L. G., et al. 2010, ApJ, 713, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Horváth, I., Balázs, L. G., Hakilla, J., Bagoly, Z., & Preece, R. D., 2012, PoS(GRB 2012)046 [Google Scholar]
- Huja, D., Mészáros, A., & Řípa, J. 2009, A&A, 504, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koen, C., & Bere, A. 2012, MNRAS, 420, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Kouveliotou, C., Meegan, C. A., Fishman, G. J., et al. 1993, ApJ, 413, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Mazets, E. P., Golenetskii, S. V., Ilinskii, V. N., et al. 1981, Ap&SS, 80, 3 [Google Scholar]
- Meegan, C. A., Pendleton, G. N., Briggs, M. S., et al. 1996, ApJS, 106, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Meegan, C. A., Lichti, G., Bhat, P. N., et al. 2009, ApJ, 702, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Mukherjee, S., Feigelson, E. D., Jogesh, B. G., et al. 1998, ApJ, 508, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, Y., Liang, E.-W., Liang, Y.-F., et al. 2013, ApJ, 763, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Řípa, J., Mészáros, A., Wigger, C., et al. 2009, A&A, 498, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savchenko, V., Neronov, A., & Courvoisier, T. J.-L. 2012, A&A, 541, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schilling, M. F., Watkins, A. E., & Watkins, W. 2002, Am. Stat., 56, 223 [CrossRef] [Google Scholar]
- von Kienlin, A., Meegan, C. A., Paciesas, W. S., et al. 2014, ApJS, 211, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Z.-B., & Choi, C.-S. 2008, A&A, 484, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zitouni, H., Guessoum, N., Azzam, W. J., & Mochkovitch, R. 2015, Ap&SS, 357, 7 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Two-Gaussian fits (solid black) to log T90 distributions. All except w = 0.25 are statistically significant. Colored dashed curves are the components of the mixture distribution. |
| In the text | |
 |
Fig. 2 Same as Fig 1, but for a three-Gaussian fit. |
| In the text | |
 |
Fig. 3 Locations of the short (green squares), intermediate (blue crosses) and long (red triangles) GRBs from previous research and this work. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


