| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 6 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201526301 | |
| Published online | 03 September 2015 | |
On the line shift and oscillator strength of Xe ii lines in the spectra of HnMn stars
1 Intituto de Física Arroyo Seco (IFAS), Centro de Investigaciones en Física e Ingeniería del Centro de la Provincia de Buenos Aires (CIFICEN), Universidad Nacional del Centro de la Provincia de Buenos Aires (UNCPBA)-Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Pinto 399, 7000 Tandil, Buenos Aires, Argentina
e-mail: hdirocco@exa.unicen.edu.ar
2 Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) 1917, Argentina
3 Facultad de Ciencias Astronómicas y Geofísicas, Univesidad Nacional de La Plata, Paseo del Bosque s/n, 1900 La Plata, Buenos Aires, Argentina
e-mail: acruzado@fcaglp.unlp.edu.ar
4 Instituto de Astrofísica de La Plata (CONICET), Paseo del Bosque s/n, 1900 La Plata, Buenos Aires, Argentina
Received: 12 April 2015
Accepted: 3 July 2015
Aims. The ultimate goal that has motivated this work is to achieve realistic oscillator strength (gf) values to find reliable values of stellar abundances. We aim to compare the gf valúes of Xe ii lines found with different theoretical and experimental methods.
Methods. We have undertaken calculations using the quasirelativistic and relativistic Hartree-Fock methods. Then we compare these results with those previously obtained from UVES spectra of HgMn stars.
Results. 1) Our theoretical gf values are more realistic than those previously obtained for most lines. When we consider only unblended, isolated, relatively noise-free lines, however, our theoretical gf values and Yuce‘s stellar values differ little from each other. 2) In a discussion of the origin of the previously observed discrepancy between the wavelengths of Xe ii lines deducted from stellar spectra and those published by National Institute of Standards and Technology (NIST), we conclude that stellar wavelengths could be considered the standard wavelengths whenever the densities in stellar atmospheres are smaller than 1 × 1016 part. cm-3.
Key words: atomic data / line: identification / stars: abundances / stars: chemically peculiar
© ESO, 2015
1. Introduction
Not long ago, Yuce et al. (2011) published a work where oscillator strengths of 100 Xe ii lines were inferred from UVES spectra of four HgMn stars: HR 6000, HD 71066, 46 Aql, and HD 175640. With the starting model parameters derived from photometry, the authors used, in turn, the codes ATLAS9, SYNTHE, ATLAS12, and WIDTH to obtain synthetic spectra and abundances of many elements and ions, among them Xe ii. In principle, this work is the more extensive source of “experimental” oscillator strength (gf) values for Xe ii, as can be verified by comparing with the National Institute of Standards and Technology (NIST) database.
In addition, Yuce et al. (2011) considered blueshifts up to 0.1 Å from the predicted wavelength of some Xe ii lines (according to the established level scheme), of a priori unidentified stellar lines. Since similar shifts are characteristic of the high current discharges used in many laboratories to obtain Xe spectra, the data of Yuce et al. (2011) provide a good standard to compare laboratory measurements affected by plasma effects (see below).
With respect to the works made about the Xe ii spectrum, since the early papers published in the ’30s by Humphreys et al. (1931), Boyce (1936), and Humphreys (1939), several works have been completed regarding energy levels and spectrum of Xe ii, transitions probabilities, line shifts, and widths. On the basis of the published material, Hansen & Persson (1987) reported a revised and complete analysis of the data. Extensive analysis of Xe spectra were performed at the Centro de Investigaciones Ópticas (CIOP, La Plata, Argentina). Some of these works (Persson et al. 1988; Gallardo et al. 1993) are related to Xe ii, and they were used as sources of data by Saloman (2004) in his critical compilation.
In particular for Xe ii, several works have been published by different authors from 1986 to date. A complete database can be found at the NIST, compiled by Kramida & Fuhr (2015).
It is important to highlight that most of the Xe ii lines analyzed in the article of Yuce et al. (2011) are weak, noised and/or blended, as it is viewed on the web page of Castelli (2011), where the UVES spectra of the stars are shown. In the last section, we analyze the behavior of some lines that are referred by the authors as without blend or noise in the stellar spectra of HR 6000 (see Table 2).
We are very interested in achieving realistic gf values to find reliable values of stellar abundances, since inaccuracies in the values of gf directly translate into inaccuracies in the calculation of stellar abundances. Therefore, we focus on analyzing and comparing the gf values of Xe ii lines obtained with different methods, both theoretical and experimental. Since the gf values of Yuce et al. (2011) disagree, in general, with other experimental and theoretical works (Di Rocco et al. 2000, and references therein), we have undertaken new calculations using the quasirelativistic Hartree-Fock and relativistic Hartree-Fock methods, which are mandatory approaches because of the relatively high Z of Xe .
We organize this paper as follows: in Sect. 2 we describe the technique we have used in obtaining the atomic Xe ii structure and spectra; in Sect. 3 we present our work methodology and our results; and in Sect. 4 we present our conclusions.
2. Obtaining the structure and spectra of Xe ii
As is well known in modern spectroscopic analysis, once a number of levels have been found by empirical spectrum analysis, the theory can be used to calculate “the best” possible wavefunctions and, from these, radiative and collisional parameters (gf values, excitation, and ionization cross sections, etc.). Of paramount importance in the theoretical calculations is the concept of configuration interaction. The “experimental” wavefunctions are expressed in terms of the Hartree-Fock orbitals, which are taken as the base functions. So, the configurations 5s5p6 and 5s2 5p4 (6s + 7s + 8s + 5d + 6d + 7d + ...), for example, can be treated together and pure designations are, many times, of little or null significance. Then, a given |γJ⟩ level is expressed as 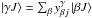 in terms of the H-F base functions |βJ⟩ (Cowan 1981). It is expected that an expansion with a manageable small set of |βJ⟩ functions can be sufficient to give reasonable gf values if the configurations are judiciously chosen (especially if the configurations have the same principal quantum number and/or the energies of the configurations are similar).
in terms of the H-F base functions |βJ⟩ (Cowan 1981). It is expected that an expansion with a manageable small set of |βJ⟩ functions can be sufficient to give reasonable gf values if the configurations are judiciously chosen (especially if the configurations have the same principal quantum number and/or the energies of the configurations are similar).
Taking into account that the empirical structure of Xe ii is well known (Hansen & Persson 1987), we have proceeded to perform calculations using the set of versatile codes from Cowan (1981). These codes are based on a quasirelativistic configuration interaction approach, allowing a least-squares fitting of the levels. With these codes, we worked in three different ways: i) We consider the electrostatic Slater parameters, F2(5p; 5p), F2(5p; nl), Gk(5p; nl), and Rk(ij;tu), and the spin-orbit parameter, φnl, from the least-squares adjustment of the levels (semi-empirical analysis) of Hansen & Persson (1987); we call this the Hansen-Persson least-squares (HPLS) approach. ii) We select the same configurations of Hansen & Persson (1987), but perform the purely ab initio calculations with proper scaling factors; we call this the Hansen-Persson Ab Initio (HPAI) approach. iii) We use an extended set of congurations judiciously chosen in a purely theoretical form; we call this the Ab Initio Many Congurations (AIMC) approach.
The theoretical results, obtained through the HPLS, HPAI, and AIMC approaches, have already been analyzed and compared, among themselves, and with the experimental approaches; e.g., Di Rocco et al. (2000). Reaffirming their conclusions, we find that the three approaches are all reasonably consistent and, therefore, some degree of quality can be conferred to all our calculations. Given this, we may choose any set of theoretical results to compare them with the results of Yuce et al. (2011), which is our aim. We may also take into consideration all of our theoretical results and obtain a final result as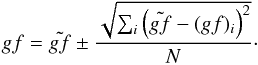 (1)Furthermore, we have used the code FAC from Gu (2008). This is a fully relativistic MultiConfiguration Dirac-Hartree-Fock (MCDHF) approach, widely used in recent years. It is important to highlight that the two sets of gf values, obtained with FAC and Cowan codes, are very similar. Clearly, we can use the gf values of different codes and generalize the Eq. (1).
(1)Furthermore, we have used the code FAC from Gu (2008). This is a fully relativistic MultiConfiguration Dirac-Hartree-Fock (MCDHF) approach, widely used in recent years. It is important to highlight that the two sets of gf values, obtained with FAC and Cowan codes, are very similar. Clearly, we can use the gf values of different codes and generalize the Eq. (1).
With that in mind, the aim of this article can be achieved by comparing the theoretical results obtained with either approach outlined above with those of Yuce et al. (2011). Therefore, to simplify and streamline our research, we use the results we obtained with the HPLS approach to work.
3. Calculations and results
3.1. The calculation of the oscillator strengths
Following Cowan’s nomenclature (1981), the calculation of transition probabilities, Aij, and related weighted oscillator strengths, gfij, are related to the calculation of line strength 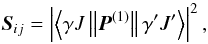 (2)where P(1) is the dipole moment of the atom measured in units of −ea0. When the energies are measured in Rydbergs, the relation between gf and S is given by
(2)where P(1) is the dipole moment of the atom measured in units of −ea0. When the energies are measured in Rydbergs, the relation between gf and S is given by 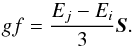 (3)The states |γJ⟩ = ∑ iaiφi and
(3)The states |γJ⟩ = ∑ iaiφi and 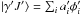 can be constructed basically in two ways: configuration interaction and multiconfiguration expansions. In the first case, the coefficients ai are fixed by the theory and the φi are optimized; in the second case, both the ai and the φi are optimized. The more useful codes using the CI approach are Cowan’s (quasirelativistic) and Gu’s (relativistic) codes; among others, the MCDHF approach is due to Froese Fischer (1997) and Grant (2007). We use the two CI treatments from Cowan and Gu because both of those are free and straightforward to use. In our opinion, the methodology of Cowan is convenient: we can use a least-squares fit of the levels and scale the radial factors (Slater integrals Fk,Gk and ζnl) in that process. Then, that scaling process indirectly takes several difficult aspects of the many atom theory (exchange, correlation, etc.) into account.
can be constructed basically in two ways: configuration interaction and multiconfiguration expansions. In the first case, the coefficients ai are fixed by the theory and the φi are optimized; in the second case, both the ai and the φi are optimized. The more useful codes using the CI approach are Cowan’s (quasirelativistic) and Gu’s (relativistic) codes; among others, the MCDHF approach is due to Froese Fischer (1997) and Grant (2007). We use the two CI treatments from Cowan and Gu because both of those are free and straightforward to use. In our opinion, the methodology of Cowan is convenient: we can use a least-squares fit of the levels and scale the radial factors (Slater integrals Fk,Gk and ζnl) in that process. Then, that scaling process indirectly takes several difficult aspects of the many atom theory (exchange, correlation, etc.) into account.
3.2. A brief about the line widths and shifts
When atoms and ions are immersed in plasma characterized by their electron temperature, Te, and electron density, Ne, the energy levels are shifted with respect to the ideal situation of the “isolated” atom (Griem 1964). Furthermore, the spectral lines are broadened because the collisions with free electrons shorten the lifetime of the excited electrons in the atoms. There are diverse mechanisms of plasma broadening but, because in the laboratory experiments the spectra of Xe ii are obtained using high current pinched discharges (Te ≈ 1 − 2 eV, Ne ≈ 1 × 1016 − 1 × 1017 cm-3), the more important mechanisms are those generically called pressure broadening (in particular, interactions with charged particles), which are treated mathematically via the impact approximation (Griem 1997; Sobelman et al. 1995).
Although we do not make explicit calculations about shifts (d) and widths (w), we recall that the calculation of both, d and w, as well as the behavior of Te and Ne, are very complex (see Sahal-Bréchot et al. 2014, as well as Peláez et al. 2009a,b). Summing up, in the semiclassical approximation both, shifts and broadenings, are basically proportional to 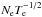 .
.
Regarding d, whereas for 6p − 6d and 6p − 7s transitions d ≈ 0.1 Å, for 6s − 6p and 5d − 6p transitions d is, in general, much lower because the initial and final levels are shifted almost the same amount. Stark parameters of some XeII lines were measured by Peláez et al. (2009a,b) for the 6p − 6d,6p − 7s,6s − 6p and 5d − 6p transitions. For the two last cases, experimental errors are, sometimes, a significant percentage of the measured Stark shifts. For comparison, it is important to establish that in the works of classical atomic spectroscopy, where the lines are measured on photographic plates, the accuracy is, typically, of the order of 0.01 Å.
3.3. Results
3.3.1. General trends
To begin with, we compare the gf values published by Yuce et al. (2011) with our theoretical gf values. From our calculations carried out, including the 5s2 5p4 6p, 5s 5p6, 5s2 5p4 6s, 5s2 5p4 7s, 5s2 5p4 8s, 5s2 5p4 5d, 5s2 5p4 6d, and 5s2 5p4 7d configurations, we have been able to identify 91 of the 98 lines for which Yuce et al. (2011) have found stellar gf values. In Table 1, third and fourth columns, the stellar gf values, obtained by Yuce et al. (2011), and the theoretical values we obtained with the Cowan Code, are shown for these 91 lines. For these 91 Xe ii lines, we analyze, at first, the ratio between our theoretical gf values and the gf values inferred by Yuce et al. (2011) from UVES spectra of HgMn stars, gfth/gfst. From this preliminary analysis, it has been apparent that some lines are too far away from the theoretical values to be adjusted. Therefore, we eliminate seven lines for which the ratio gfth/gfst> 6 from any subsequent analysis. Our intention is not to do a line-by-line comparison, but rather to assess general trends and behaviors.
We believe that, perhaps, the shift between the stellar and theoretical gf values for the remaining 84 lines could be reduced by adjusting the radial integrals entering the gf calculation. We adjusted these radial integrals for each pair of atomic configurations to achieve the best possible fit for all lines arising from the pair. In Fig. 1, panels a) and b), we show two possible fits. In both panels, the logarithm of stellar gf values are shown as a function of the theoretical values. The adjustment for the 84 Xe ii lines is shown in panel a). In an attempt to improve this adjustment, we eliminted nine lines and obtained the fit shown in panel b). In Table 1, fifth and sixth columns, the theoretical gf values are displayed for the 84 and 75 lines used in the first and second adjustment, respectively. Two important things have to be pointed out. First, adjusting the radial integrals does not significantly improve the correlation. In any case, the linear correlation coefficients take values between r = 0.61 and r = 0.63, as well as when nine lines are eliminated. Second, the factors that multiply the radial integrals range from 1.15 to 1.9 vary very little from one adjustment to another. Even if the correlation had improved, these factors that multiply the integrals are too large to account for the differences between the theoretical gf values to the stellar values.
Stellar and theoretical gf values.
 |
Fig. 1 Logarithm of stellar gf values as a function of the theoretical values. In both panels, the original data before any adjustment are indicated with circles and the data after adjusting the radial integrals are indicated with crosses. In panel a), the adjustment for 84 Xe ii lines is shown. In panel b), nine lines have been eliminated (see text). |
In order to find some general trends in the ratio gfth/gfst, in Fig. 2 this ratio is shown as a function of λ. In panel a) the 84 lines are included. In panel b) seven lines have been removed to demonstrate that a clear correlation exists between the ratio gfth/gfst and λ. From Fig. 2 it seems that some systematic source of error is affecting the results.
3.3.2. Individual behavior
We have taken 32 lines from the set of lines referred by Yuce et al. (2011) as without blend or noise; these are clearly isolated lines in the HR 6000 stellar spectrum (Castelli 2011). Wavelength, log (gfst), log (gfth), as well as | gfst − gfth | ∗ 100 /gfst, are shown in Table 2 for these 32 lines. In Fig. 3 the logarithm of stellar gf values as a function of the theoretical value is shown for these 32 lines. It is clear that the theoretical and stellar values keep a reasonable ratio for these lines (r = 0.87). We must not forget that inaccuracies in the values of gf directly translate into inaccuracies in the calculation of stellar abundances.
 |
Fig. 2 gfth/gfst as a function of λ. In panel a) 84 lines are included. In panel b) seven lines have been removed (see text). |
4. Conclusions
 |
Fig. 3 Logarithm of stellar gf values as a function of the theoretical values for 32 isolated lines (see text). Error bars as given by Yuce et al. (2011) are indicated. |
The correlation between gfth/gfst and λ, made evident in Fig. 2, can be explained. On the one hand, the weaker a line, the more uncertain its astrophysical gf value. Since the gf values have a tendency to decrease as wavelength increases, the gf values of red lines are, in general, less accurate. On the other hand, the larger the wavelength, the larger the noise and the number of telluric lines in the spectra. This also lowers the accuracy of the results, as pointed out by Yuce et al. (2011). In general, our theoretical results (Table 1, Col. 4) are nearest other authors’ theoretical or experimental results than they are to Yuce’s results. For that reason, we are able to say that our theoretical gf values are more realistic that those by Yuce el al. (2011). But, when we consider unblended, relatively noise-free, and isolated lines, our theoretical gf values and Yuce‘s stellar values differ less from each other, as we see in Fig. 3.
Note the systematic shift due to plasma effects (Griem 1964) observed in the wavelength of the lines associated with the 6d and 7s Xe ii energy levels from different spectral sources. Several works have been published on this topic by diverse authors, some as old as that by Di Rocco et al. (1986). Yuce et al. (2011) mention a discrepancy between their wavelengths measured from stellar spectra and those published by NIST, and they interpret the origin of this discrepancy as mostly due to incorrect energy levels. We establish now that, indeed, energy levels should undergo a shift in laboratory experiments. Therefore, it is clear that these lines are Xe ii lines, but shifted by plasma effects, as explained above. In fact, modeling a perturbing potential by an expression of the form Vk(r) = ∑ kCkr− k, we can infer that the energy levels and, therefore, the atomic lines are shifted when the atom is inmersed in a plasma instead of being isolated. The case k = 4 is of paramount importance in taking collisions with electrons into account. In the semiclassical approximation (Griem 1964), both shifts and broadenings are proportional to 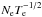 , where Ne and Te are the electron density and electron temperature, respectively. In any case, stellar wavelengths could be considered the standard wavelengths whenever the densities in stellar atmospheres are smaller than 1 × 1016 part. cm-3.
, where Ne and Te are the electron density and electron temperature, respectively. In any case, stellar wavelengths could be considered the standard wavelengths whenever the densities in stellar atmospheres are smaller than 1 × 1016 part. cm-3.
Acknowledgments
The authors sincerely appreciate the corrections and suggestions made by the referee whose contributions have greatly improved our article.
References
- Boyce, J. C. 1936, Phys. Rev., 49, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F. 2011, http://wwwuser.oats.inaf.it/castelli/stars.html [Google Scholar]
- Cowan, R. D. 1981, The Theory of Atomic Structure and Spectra (Berkeley, Los Angeles, London: University of California Press) [Google Scholar]
- Di Rocco, H. O., Bertuccelli, G., Reyna Almandos, J. G., & Gallardo, M. 1986, J. Quant. Spectr. Rad. Transf., 35, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Di Rocco, H. O., Iriarte, D. I., & Pomarico, J. A. 2000, EPJD, 10, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Froese Fischer, C., Brage, T., & Jönsson, P. 1997, Computational Atomic Structure (Bristol and Philadelphia: IOP Publishing) [Google Scholar]
- Gallardo, M., Raineri, M., & Almandos, J. G. Reyna 1993, Spectr. Lett., 26, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Grant, I. P. 2007, Relativistic Quantum Theory of Atoms and Molecules (New York: Springer) [Google Scholar]
- Griem, H. R. 1964, Plasma Spectroscopy (Berkeley, Los Angeles, London: University of California Press) [Google Scholar]
- Griem, H. R. 1997, Principles of Plasma Spectroscopy (Cambridge: Cambridge University Press) [Google Scholar]
- Gu, M. F. 2008, Can. J. Phys., 86, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, J. E., & Persson, W. 1987, Phys. Scr., 36, 602 [NASA ADS] [CrossRef] [Google Scholar]
- Humphreys, C. J. 1939, J. Res. Natl. Bur. Stand. (US), 22, 19 [Google Scholar]
- Humphreys, C. J., de Bruin, T. L., & Meggers, W. F. 1931, J. Res. Natl. Bur. Stand. (US), 6, 287 [CrossRef] [Google Scholar]
- Kramida, A., & Fuhr, J. R. 2015, http://physics.nist.gov/cgi-bin/ASBib1/TransProbBib.cgi, last updated March 2015, National Institute of Standards and Technology, Physical Measurement Laboratory, Quantum Measurement Division [Google Scholar]
- Peláez, R. J., Djurovic, S., Cirisan, N., et al. 2009a, J. Phys. B: At. Mol. Opt. Phys., 42, 12, 7 [Google Scholar]
- Peláez, R. J., Cirisan, N., Djurovic, S., et al. 2009b, A&A, 507, 1697 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Persson, W., Wahlström, C.-G., Bertuccelli, G., et al. 1988, Phys. Scr., 38, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Sahal-Bréchot, S., Dimitrijevic, M. S., & Ben Nessib, N. 2014, Atoms 2, 225 [Google Scholar]
- Saloman, E. B. 2004, J. Phys. Chem. Ref. Data, 33, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Sobelman, I.I., Vainshtein, L. A., & Yukov, E. A. 1995, Excitation of atoms and broadening of spectral lines (Springer) [Google Scholar]
- Yüce, K., Castelli, F., & Hubrig, S. 2011, A&A, 528, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Logarithm of stellar gf values as a function of the theoretical values. In both panels, the original data before any adjustment are indicated with circles and the data after adjusting the radial integrals are indicated with crosses. In panel a), the adjustment for 84 Xe ii lines is shown. In panel b), nine lines have been eliminated (see text). |
| In the text | |
 |
Fig. 2 gfth/gfst as a function of λ. In panel a) 84 lines are included. In panel b) seven lines have been removed (see text). |
| In the text | |
 |
Fig. 3 Logarithm of stellar gf values as a function of the theoretical values for 32 isolated lines (see text). Error bars as given by Yuce et al. (2011) are indicated. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


