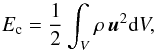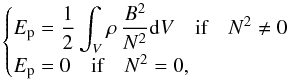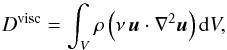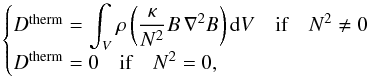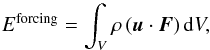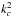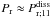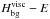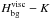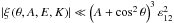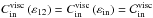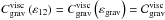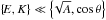| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 22 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526246 | |
| Published online | 18 September 2015 | |
Scaling laws to understand tidal dissipation in fluid planetary regions and stars I. Rotation, stratification and thermal diffusivity⋆
1
IMCCE, Observatoire de Paris, CNRS UMR 8028,
77 avenue Denfert-Rochereau,
75014
Paris,
France
e-mail:
pierre.auclair-desrotour@obspm.fr
2
Laboratoire AIM Paris-Saclay, CEA/DSM−CNRS−Université
Paris-Diderot, IRFU/SAp Centre de
Saclay, 91191
Gif-sur-Yvette,
France
3
LESIA, Observatoire de Paris, CNRS UMR 8109, UPMC, Université
Paris-Diderot, 5 place Jules
Janssen, 92195
Meudon,
France
e-mail:
stephane.mathis@cea.fr
4
SYRTE, Observatoire de Paris, CNRS UMR 8630, UPMC, LNE, 61 avenue
de l’Observatoire, 75014
Paris,
France
e-mail:
christophe.leponcin@obspm.fr
Received: 2 April 2015
Accepted: 16 June 2015
Context. Tidal dissipation in planets and stars is one of the key physical mechanisms driving the evolution of star-planet and planet-moon systems. Several signatures of its action are observed in planetary systems thanks to their orbital architecture and the rotational state of their components.
Aims. Tidal dissipation inside the fluid layers of celestial bodies is intrinsically linked to the dynamics and physical properties of those bodies. This complex dependence must be characterized.
Methods. We compute the tidal kinetic energy dissipated by viscous friction and thermal diffusion in a rotating local fluid Cartesian section of a star, planet, or moon submitted to a periodic tidal forcing. The properties of tidal gravito-inertial waves excited by the perturbation are derived analytically as explicit functions of the tidal frequency and local fluid parameters (i.e. the rotation, the buoyancy frequency characterizing the entropy stratification, viscous and thermal diffusivities) for periodic normal modes.
Results. The sensitivity of the resulting dissipation frequency-spectra, which could be highly resonant, to a control parameter of the system is either important or negligible depending on the position in the regime diagram relevant for planetary and stellar interiors. For corresponding asymptotic behaviours of tidal gravito-inertial waves dissipated by viscous friction and thermal diffusion, scaling laws for the frequencies, number, width, height, and contrast with the non-resonant background of resonances are derived to quantify these variations.
Conclusions. We characterize the strong impact of the internal physics and dynamics of fluid planetary layers and stars on the dissipation of tidal kinetic energy in their bulk. We point out the key control parameters that really play a role in tidal dissipation and demonstrate how it is now necessary to develop ab initio modelling for tidal dissipation in celestial bodies.
Key words: hydrodynamics / waves / turbulence / planet-star interactions / planets and satellites: dynamical evolution and stability
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction and context
Tides have a strong impact on the evolution of star-planet and planet-moon systems over secular timescales. Indeed, because of the dissipation of the kinetic energy of flows and displacements they induce in celestial bodies, they drive their rotational and orbital evolutions. The cases of stars and giant planets have been treated by Ogilvie (2014) and references therein, and the case of telluric planets by Correia & Laskar (2003) and Correia et al. (2008). In the case of the Earth-Moon system, their causes and effects are now strongly constrained and disentangled thanks to satellite altimeter high-precision observations of ocean tides (Egbert & Ray 2000, 2001; Ray et al. 2001). In the solar system, the actions of tides are detected and estimated from high-precision geodesic and/or astrometric observations. The reader may see the studies by Konopliv & Yoder (1996) for Venus, Williams et al. (2014) for the Moon, Lainey et al. (2007), Jacobson (2010) and Konopliv et al. (2011) for Mars, Lainey et al. (2009, 2012) for Jupiter and Saturn, and the attempt by Emelyanov & Nikonchuk (2013) for Uranus. Finally, a new extremely important astronomical laboratory to explore and constrain the physics of tides is constituted by the numerous exoplanetary systems discovered over the last 20 years (Mayor & Queloz 1995; Perryman 2011). Indeed, they are composed of a large diversity of planets (from hot Jupiters to super-Earths) and host stars, while their orbital architecture and configuration of planetary and stellar spins strongly differ from that observed in our solar system (e.g. Albrecht et al. 2012; Fabrycky et al. 2012; Valsecchi & Rasio 2014). In this context, the understanding of the tidal formation and evolution of planetary systems is one of the most important problems of modern dynamical astronomy (e.g. Laskar et al. 2012; Bolmont et al. 2012; Ferraz-Mello 2013), while the needed understanding and quantitative prediction of tidal dissipation in celestial bodies is still a challenge (e.g. Mathis & Remus 2013; Ogilvie 2014, for complete reviews).
We owe the first theoretical work about a tidally deformed body to Lord Kelvin (Kelvin 1863). Then, a physical formalism was elaborated by Love, who introduced the so-called Love numbers (Love 1911). The second-order Love number (k2) measures the inverse of the ratio between the tidal potential and the resulting linear perturbation of the gravitational potential at the surface of a body hosting a companion. It quantifies its quadripolar hydrostatic elongation along the line of centres. The introduction and estimation of tidal dissipation then became more and more important with the introduction of the tidal quality factor Q for the solar system (e.g. MacDonald 1964; Kaula 1964; Goldreich & Soter 1966). This general parameter is a simple and useful quantity that allows us to simplify the numerical simulations of planetary systems over secular timescales. In particular, the constant Q model, the so-called Kaula’s model (Kaula 1964), allows us to take internal dissipation with one parameter only into account. The factor Q is applied to rocky, or icy, and fluid bodies and correspond to a simplified Maxwell’s model, which assimilates a celestial body hosting a companion to a forced damped oscillator. It evaluates the ratio between the maximum energy stored in the tidal distortion during an orbital period and the energy dissipated by the friction. Therefore, the global response to a tidal perturbation depends on a mean elasticity, which models the restoring force acting on tidal displacements, and a friction, 1 /Q representing the damping coefficient of the system (i.e. the imaginary part of the second-order Love number; for a detailed study, see Greenberg 2009). From this approach, other models have been developed to take into account the possible dependence of Q on the main tidal frequency χ, i.e. the constant time lag model (Darwin 1879; Alexander 1973; Singer 1968; Hut 1981; Leconte et al. 2010).
As the tidal quality factor is inversely proportional to the internal dissipation in a body, it is determined by the physical properties of this body. Thus, the internal structure of stars, planets, and satellites is determinant for the study of tidal effects. In this context, recent works have derived the tidal quality factor as a function of χ and rheological parameters. Examples for rocky/icy planetary layers can be found in Efroimsky & Lainey (2007) and Henning et al. (2009; see also Tobie et al. 2005; Efroimsky 2012; Remus et al. 2012b; Correia et al. 2014). Efroimsky & Lainey (2007) illustrate the important role played by the internal properties of the perturbed host body in the orbital evolution of its system. They focus on the equilibrium tide in the case of a circular orbit, which designates the component of the strain rotating with the perturber at the frequency χ = 2(n − Ω) in the frame attached to the central body, n being the mean motion of the perturber in a non-rotating frame and Ω the spin frequency of the primary. The other components corresponding to eigenmodes of oscillation excited by tides constitute the dynamical tide. It is particularly important for fluid planetary regions and stars in which the dynamical tide can dominate the equilibrium tide. It leads to a resonant tidal dissipation that varies over several orders of magnitude as a function of their physical properties, evolutionary states, and χ (see Ogilvie 2014, and references therein). Applied to an orbital system, a tidal quality factor following this resonant behaviour makes the orbital parameters evolve erratically along secular timescales (Auclair-Desrotour et al. 2014). An interesting example is given by the case of the Earth-Moon system. Indeed, most of tidal dissipation on the Earth is due to tidal waves in oceans (Egbert & Ray 2000) where the barotropic tide is converted non-resonantly into internal waves because of non-trivial bottom topography (Pedlosky 1982). The corresponding frequency-spectrum of the dissipation is then a highly complex function of χ, while its dependence on the rotation of the planet allows us to match tidal evolution results with geological data. This important result would not be possible with constant Q or constant time lag models (Webb 1980, 1982). During the past five decades, numerous theoretical studies have been carried out to characterize and quantify the tidal energy dissipated in fluid celestial bodies (see e.g. Zahn 1966a,b,c, 1975, 1977, 1989; Ogilvie & Lin 2004, 2007; Wu 2005; Remus et al. 2012a; Cebron et al. 2012; Cébron et al. 2013). Most of these studies focussed on stars and envelopes of giant gaseous planets (see Ogilvie 2014). They concentrated on global models for tidal waves and dissipative mechanisms in fluid regions excited by a tidal perturber, which result from complex actions and couplings of rotation, stratification, viscosity, and thermal diffusion. The kinetic energy of tidal waves is thus dissipated by viscous friction and thermal diffusion. Magnetism also intervenes in stars and some planets, introducing Ohmic diffusion in addition to the two previous dissipative mechanisms.
Therefore, tidal perturbations take the form of waves in fluid regions: acoustic waves driven by compressibility, inertial waves driven by the Coriolis acceleration, gravity waves driven by the Archimedian force, and Alfvén waves driven by magnetic forces. Given their high frequencies, acoustic waves are only weakly excited by low-frequency tidal forcing, and, therefore, are ignored. Tides, however, excite gravito-inertial waves. These mixed waves combine the second and third families enumerated above. Inertial waves are caused by rotation. The Coriolis acceleration acts as a restoring force and their frequencies are smaller than the inertial one 2Ω. Gravity waves propagate in stably-stratified fluid regions, with frequencies bounded by N (the Brunt-Väisälä frequency), which depends on the gradients of the specific entropy. Their restoring force is buoyancy. Alfvén waves result from the presence of a magnetic field and propagate in stars and planets, gravito-inertial waves thus becoming magneto-gravito-inertial waves. From now on, magnetism is neglected in the present work and these waves are thus not studied.
Given the complex dynamical resonant tidal response of fluid planetary layers and stars described above and its important astrophysical consequences, it should be understood and characterized systematically. To reach this goal, two approaches can be adopted. First, global realistic models constitute an efficient tool to explore the physics of dissipation and to quantify it (e.g. Ogilvie & Lin 2004, 2007). Simultaneously, local simplified models allow us to understand in detail complex physical mechanisms in action and to explore the large domain of possible parameters in astrophysics (e.g. Ogilvie 2005; Jouve & Ogilvie 2014; Barker & Lithwick 2013, 2014). In this framework, Ogilvie & Lin (2004) proposed a reduced model based on a Cartesian fluid box in an appendix devoted to quantifying global tidal dissipation in spherical shells for planetary interiors. The objective of this simplified model was to understand the behaviour of tidal dissipation caused by the (turbulent) viscous friction acting on inertial waves in planetary and stellar convective regions. Similarly, Gerkema & Shrira (2005a) explored the complex physics of gravito-inertial waves (see also Mathis et al. 2014b). Following these previous studies, this work develops a new local Cartesian model that generalizes that by Ogilvie & Lin (2004) by taking into account the relative inclination between gravity and rotation, which is a possible stable entropy stratification or a super-adiabaticity established by convection and viscous and thermal diffusions. By studying this set-up, we answer to the following questions:
-
How does the dissipation due to the viscous friction and heat thermal diffusion depend on the fluid parameters (i.e. rotation, stratification, viscosity, and thermal diffusivity)?
-
How do the properties of the corresponding dissipation frequency spectrum vary as a function of the tidal frequency?
-
What are the asymptotical behaviours relevant for planetary and stellar interiors?
In Sect. 2, the local Cartesian model is presented. Dynamical equations are derived and solved analytically. This allows us to get the energy dissipated per unit mass in the box over a rotation period. Physical quantities are written as a series of resonant normal modes corresponding to the harmonics of the tidal forcing, allowing us to study the spectral response of the box. In Sect. 3, it is studied, on the one hand, to identify the four asymptotic regimes of tidal waves. On the other hand, we characterize the corresponding resonant dissipation frequency spectrum, i.e. the positions, width, heights, number of peaks, level of the non-resonant background, and sharpness ratio (defined as the ratio between the height of the main peak and the level of the non-resonant background). Each of these properties is expressed as a function of the fluid parameters and forcing frequency. These scaling laws give a global overview of the properties of the dissipation. In Sect. 4, we examine the particular case of super-adiabaticity in convective regions for which the square buoyancy (Brunt-Väisälä) frequency is negative. In Sect. 5, we discuss our results. Finally, in Sect. 6, we give our conclusions and highlight new questions for further studies.
2. Forced waves in stars and fluid planetary layers
2.1. The local model to be studied
Ogilvie & Lin (2004) proposed a local Cartesian model describing the behaviour of a fluid box submitted to tidal perturbations for convective regions where inertial waves propagate. This approach is of great interest because it yields an analytical expression for the viscous dissipation of the tidal kinetic energy, which is expressed as a function of the fluid properties and particularly of the Ekman number, NEk = ν/(2ΩL2), Ω being the angular velocity of the body, ν the local kinematic viscosity of the fluid, and L a characteristic length of the convective layer. Therefore, this approach allows us to understand how dissipation depends on these physical parameters. Here, in addition to inertial waves driven by the Coriolis acceleration, we take the possibility of a stable stratification, which introduces buoyancy as an additional restoring force, into account. This allows us to generalize the previous model to study the more general case of gravito-inertial waves (e.g. Gerkema & Shrira 2005a). Moreover, we also take thermal diffusion of heat, in addition to viscous friction to dissipate tidal kinetic energy, into account.
We consider a local fluid Cartesian section belonging to a planet or a star tidally perturbed at a frequency χ: a box of length L, such that L ≪ R, where R is the radius of the body. The fluid is Newtonian, of density ρ, kinematic viscosity ν, and thermal diffusivity κ. The box vertical direction (and gravity g) is inclined relatively to the spin vector of the body Ω with an angle θ. The angular velocity of the fluid (Ω) and the local gravity g are assumed to be uniform and constant. The centre of the body and of the box are denoted O and M, respectively. We use two reference frames (Fig. 1). The global frame ℛO:{O,XE,YE,ZE} rotates with the body and its natural spherical associated unit-vector basis is denoted 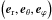 . In this frame, Ω = ΩZE and the coordinates of M are (r,θ,ϕ) in spherical geometry. Then, we introduce the frame fixed to the fluid section, ℛ:{M,ex,ey,ez} whose unit-vectors are ez = er, ey = −eθ, ex = eϕ and g = −gez. Stratification implies a new frequency, specific to gravito-inertial waves, and the Brunt-Väisälä frequency is denoted N and defined by
. In this frame, Ω = ΩZE and the coordinates of M are (r,θ,ϕ) in spherical geometry. Then, we introduce the frame fixed to the fluid section, ℛ:{M,ex,ey,ez} whose unit-vectors are ez = er, ey = −eθ, ex = eϕ and g = −gez. Stratification implies a new frequency, specific to gravito-inertial waves, and the Brunt-Väisälä frequency is denoted N and defined by ![\begin{equation} N^2 = - g \left[ \dfrac{{\rm d} \log \rho}{{\rm d}z} - \frac{1}{\gamma} \dfrac{{\rm d} \log P}{{\rm d}z } \right], \end{equation}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq37.png) (1)where γ = (∂lnP/∂lnρ)S is the adiabatic exponent (S being the specific macroscopic entropy), and P and ρ are the radial distributions of pressure and density of the background, respectively. These equilibrium quantities are supposed to vary smoothly with the radial coordinate z compared to the perturbation. For this reason, the Brunt-Väisälä frequency is taken as a constant parameter. Assuming the hydrostatic equilibrium, it becomes
(1)where γ = (∂lnP/∂lnρ)S is the adiabatic exponent (S being the specific macroscopic entropy), and P and ρ are the radial distributions of pressure and density of the background, respectively. These equilibrium quantities are supposed to vary smoothly with the radial coordinate z compared to the perturbation. For this reason, the Brunt-Väisälä frequency is taken as a constant parameter. Assuming the hydrostatic equilibrium, it becomes ![\begin{equation} N^2 = - \frac{g}{\rho} \left[ \dfrac{{\rm d} \rho }{{\rm d}z} + \frac{g \rho^2}{\gamma P} \right]\cdot \end{equation}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq43.png) (2)The regions studied are stably stratified (N2> 0) or convective (N2 ≈ 0 or N2< 0).
(2)The regions studied are stably stratified (N2> 0) or convective (N2 ≈ 0 or N2< 0).
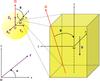 |
Fig. 1 The fluid box, its reference frame, and its position in the planet relative to the spin axis. |
2.2. Dynamical equations
Submitted to a tidal forcing force per unit mass 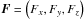 , where x ≡ (x,y,z) are the local coordinates of space, the fluid moves in the box periodically and dissipates energy through viscous friction and thermal diffusion. To obtain the equations that govern the dynamics of tidal gravito-inertial waves, we write the linearized equations of motion1 of the stratified fluid on the non-traditional f-plane assuming the Boussinesq2 and the Cowling approximations (Gerkema & Shrira 2005a; Cowling 1941). First, we introduce the wave velocity field u = (u,v,w), where u, v, and w are its components in the local azimuthal, latitudinal, and vertical directions. Next, we define the fluid buoyancy
, where x ≡ (x,y,z) are the local coordinates of space, the fluid moves in the box periodically and dissipates energy through viscous friction and thermal diffusion. To obtain the equations that govern the dynamics of tidal gravito-inertial waves, we write the linearized equations of motion1 of the stratified fluid on the non-traditional f-plane assuming the Boussinesq2 and the Cowling approximations (Gerkema & Shrira 2005a; Cowling 1941). First, we introduce the wave velocity field u = (u,v,w), where u, v, and w are its components in the local azimuthal, latitudinal, and vertical directions. Next, we define the fluid buoyancy 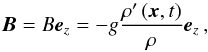 (3)where ρ′ and ρ are the density fluctuation and the reference background density, and t is the time. The three linearized components of the momentum equation are given by
(3)where ρ′ and ρ are the density fluctuation and the reference background density, and t is the time. The three linearized components of the momentum equation are given by 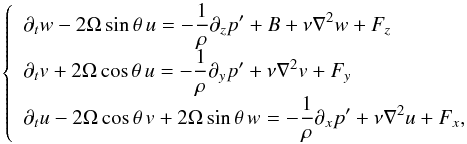 (4)where p′ is the pressure fluctuation and ∇2 ≡ ∂x,x + ∂y,y + ∂z,z. Next, we write the continuity equation in the Boussinesq approximation
(4)where p′ is the pressure fluctuation and ∇2 ≡ ∂x,x + ∂y,y + ∂z,z. Next, we write the continuity equation in the Boussinesq approximation 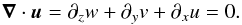 (5)Finally, we get the following equation for energy conservation:
(5)Finally, we get the following equation for energy conservation: 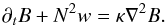 (6)By taking the scalar product of the momentum equation (Eq. (4)) with u and multiplying the heat equation (Eq. (6)) by B/N2, we obtain the energy equation for the box
(6)By taking the scalar product of the momentum equation (Eq. (4)) with u and multiplying the heat equation (Eq. (6)) by B/N2, we obtain the energy equation for the box 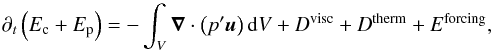 (7)where we have introduced
(7)where we have introduced
We introduce dimensionless time and space coordinates and tidal frequency, normalized buoyancy, and force per unit mass 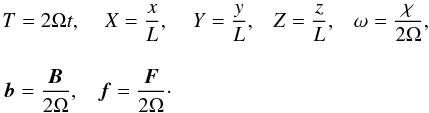 (13)The linearized Navier-Stockes equation becomes
(13)The linearized Navier-Stockes equation becomes 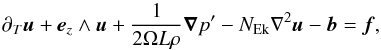 (14)where we recognize the Ekman number
(14)where we recognize the Ekman number 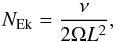 (15)which compares the strength of the viscous force to the Coriolis acceleration.
(15)which compares the strength of the viscous force to the Coriolis acceleration.
The equation of heat is written as 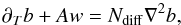 (16)where the right-hand side corresponds to thermal diffusion. We introduce the following two new control parameters:
(16)where the right-hand side corresponds to thermal diffusion. We introduce the following two new control parameters: 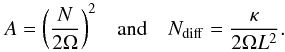 (17)A is the square ratio of the characteristic frequencies of the system (2Ω and N). This parameter is bound to the nature of tidal waves (e.g. Gerkema & Shrira 2005a,b; see also Berthomieu et al. 1978; Provost et al. 1981):
(17)A is the square ratio of the characteristic frequencies of the system (2Ω and N). This parameter is bound to the nature of tidal waves (e.g. Gerkema & Shrira 2005a,b; see also Berthomieu et al. 1978; Provost et al. 1981):
-
A ≤ 0 (i.e. N2 ≤ 0) corresponds to inertial waves;
-
0 <A< 1, corresponds to quasi-inertial waves; and
-
A ≥ 1, corresponds to gravito-inertial waves.
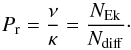 (18)Waves are damped by viscous diffusion if Pr ≥ 1; otherwise, thermal diffusion dominates.
(18)Waves are damped by viscous diffusion if Pr ≥ 1; otherwise, thermal diffusion dominates.
From now on, we assume that the unknown quantities only vary with x and z (x ∈ [0,L], z ∈ [0,L]). This assumption has no impact on qualitative results, and allows us to compare our calculations to those made by Ogilvie & Lin (2004) directly.
2.3. Velocity field and dissipation
We now solve our linearized first-order system (Eqs. (14), (5)and (16)) to get the velocity field and the energy dissipated by viscous friction and thermal diffusion. Since the tidal perturbation is periodic in time, we expand the quantities in Fourier series: ![\begin{eqnarray} \begin{array}{c c } u_x = \Re \left[ u(X,Z) {\rm e}^{-{\rm i} \omega T} \right], & u_y = \Re \left[ v(X,Z) {\rm e}^{-{\rm i} \omega T} \right], \\[1.5mm] u_z = \Re \left[ w(X,Z) {\rm e}^{-{\rm i} \omega T} \right], & p = \Re \left[ \psi (X,Z) {\rm e}^{-{\rm i} \omega T} \right], \\[1.5mm] f_x = \Re \left[ f(X,Z) {\rm e}^{-{\rm i} \omega T} \right], & f_y = \Re \left[ g (X,Z) {\rm e}^{-{\rm i} \omega T} \right], \\[1.5mm] f_z = \Re \left[ h(X,Z) {\rm e}^{-{\rm i} \omega T} \right], & b = \Re \left[ b(X,Z) {\rm e}^{-{\rm i} \omega T} \right].\\[1.5mm] \end{array} \end{eqnarray}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq89.png) (19)The spatial functions are themselves expanded in periodic spatial Fourier series in X and Z as in Ogilvie & Lin (2004):
(19)The spatial functions are themselves expanded in periodic spatial Fourier series in X and Z as in Ogilvie & Lin (2004): ![\begin{equation} \begin{array}{c c } u = \displaystyle \sum u_{mn} {\rm e}^{{\rm i} 2 \pi \left( m X + n Z \right) }, & v = \displaystyle \sum v_{mn} {\rm e}^{{\rm i} 2 \pi \left( m X + n Z \right) },\\[1mm] \vspace{0.1mm}\\[1mm] w = \displaystyle \sum w_{mn} {\rm e}^{{\rm i} 2 \pi \left( m X + n Z \right) }, & \psi = \displaystyle \sum \psi_{mn} {\rm e}^{{\rm i} 2 \pi \left( m X + n Z \right) },\\[1mm] \vspace{0.1mm}\\[1mm] f = \displaystyle \sum f_{mn} {\rm e}^{{\rm i} 2 \pi \left( m X + n Z \right) }, & g = \displaystyle \sum g_{mn} {\rm e}^{{\rm i} 2 \pi \left( m X + n Z \right) },\\[1mm] \vspace{0.1mm}\\[1mm] h = \displaystyle \sum h_{mn} {\rm e}^{{\rm i} 2 \pi \left( m X + n Z \right) }, & b = \displaystyle \sum b_{mn} {\rm e}^{{\rm i} 2 \pi \left( m X + n Z \right) }.\\[1mm] \end{array} \label{fourier} \end{equation}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq92.png) (20)For the sake of simplicity, the horizontal and vertical wave numbers (m,n) ∈ Z∗ 2 are not written under summations. By choosing periodic boundary conditions, we consider the volumetric excitation of normal modes (Wu 2005; Braviner & Ogilvie 2015). The case of periodic wave attractors can be treated by introducing reflexions on boundaries of the box (e.g. Jouve & Ogilvie 2014). The previous system becomes
(20)For the sake of simplicity, the horizontal and vertical wave numbers (m,n) ∈ Z∗ 2 are not written under summations. By choosing periodic boundary conditions, we consider the volumetric excitation of normal modes (Wu 2005; Braviner & Ogilvie 2015). The case of periodic wave attractors can be treated by introducing reflexions on boundaries of the box (e.g. Jouve & Ogilvie 2014). The previous system becomes ![\begin{eqnarray} \left\{\! \begin{array}{rcl} - {\rm i}\omega u_{mn} - \cos \theta v_{mn} + \sin \theta w_{mn} & \!\!\!\!\!\!=\!\!\!\!\!\! & - {\rm i} m \Lambda \psi_{mn} - E \left( m^2 + n^2 \right)u_{mn} \\[1mm] & & + f_{mn}\\[1mm] \vspace{0.1mm}\\ \end{array} \right. \label{systeme_eq}\!\! \end{eqnarray}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq94.png) (21)which is parametrized by the frequency ratio A, the colatitude θ and the numbers:
(21)which is parametrized by the frequency ratio A, the colatitude θ and the numbers: 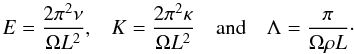 (22)The parameters E and K are both dimensionless diffusivities: E is proportional to the Ekman number NEk (Eq. (15)) of the fluid and K to its analogue Ndiff (Eq. (17)) for thermal diffusion. Similarly, we get for the Prandtl number (Eq. (18))
(22)The parameters E and K are both dimensionless diffusivities: E is proportional to the Ekman number NEk (Eq. (15)) of the fluid and K to its analogue Ndiff (Eq. (17)) for thermal diffusion. Similarly, we get for the Prandtl number (Eq. (18)) 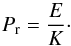 (23)Finally, Λ weights the pressure variations. This last parameter does not intervene in the expressions of the velocity field and of the perturbation of buoyancy (Eqs. (29)and (31)). Therefore, both viscous dissipation and thermal diffusion do not depend on it. The equations yield two complex dimensionless frequencies because of viscous and heat diffusion, which are functions of E and K:
(23)Finally, Λ weights the pressure variations. This last parameter does not intervene in the expressions of the velocity field and of the perturbation of buoyancy (Eqs. (29)and (31)). Therefore, both viscous dissipation and thermal diffusion do not depend on it. The equations yield two complex dimensionless frequencies because of viscous and heat diffusion, which are functions of E and K: 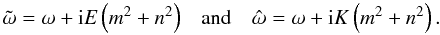 (24)Initially, assuming that f = 0, we get the dispersion relation of the viscously and thermally damped gravito-inertial modes as follows:
(24)Initially, assuming that f = 0, we get the dispersion relation of the viscously and thermally damped gravito-inertial modes as follows: 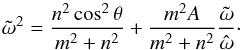 (25)For slightly damped modes (E ≪ 1 and K ≪ 1), we identify in the second member, the wave number
(25)For slightly damped modes (E ≪ 1 and K ≪ 1), we identify in the second member, the wave number 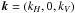 , with kH = m/L and kV = n/L (see Gerkema & Shrira 2005a). Indeed, neglecting E and K, this equation simplifies to
, with kH = m/L and kV = n/L (see Gerkema & Shrira 2005a). Indeed, neglecting E and K, this equation simplifies to 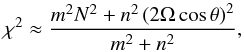 (26)which can be written
(26)which can be written 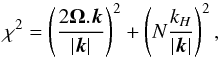 (27)where we recognize the dispersion relation of gravito-inertial waves with the respective contributions of inertial and gravity waves.
(27)where we recognize the dispersion relation of gravito-inertial waves with the respective contributions of inertial and gravity waves.
 |
Fig. 2 Gravito-inertial waves frequency range in convective and in stably stratified layers (Nc = 0 and NSLL> 0 are the corresponding buoyancy frequencies). The expressions of the boundaries χinf;SSL and χsup;SSL are explicitly given in Eq. (28). |
By letting m and n tend to infinity successively, we identify the approximative boundaries of the frequency range, χinf and χsup. When 2Ω <N (i.e. A> 1), χinf ≈ 2Ω and χsup ≈ N (see Fig. 2). The exact expressions of χinf and χsup are given by Gerkema & Shrira (2005a), as follows: ![\begin{equation} \left\{\! \begin{array}{lcl} \chi_{\rm inf} & = & \displaystyle \sqrt{ \frac{\lambda - \left[ \lambda^2 - \left( 2 \sigma N \right)^2 \right]^{1/2} }{2} }, \\ \vspace{0.1mm}\\[1.54mm] \chi_{\rm sup} & = & \displaystyle \sqrt{ \frac{\lambda + \left[ \lambda^2 - \left( 2 \sigma N \right)^2 \right]^{1/2} }{2} },\\ \end{array} \right. \label{omega_GS} \end{equation}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq125.png) (28)where
(28)where 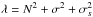 . Here, σ = 2Ωsinθ and σs = 2Ωcosθsinα, α = 0 corresponding to the propagation direction of gravito-inertial waves in the horizontal plane along the x axis (see the bottom-left panel of Fig. 1). Finally, we obtain the coefficients of the velocity field u,
. Here, σ = 2Ωsinθ and σs = 2Ωcosθsinα, α = 0 corresponding to the propagation direction of gravito-inertial waves in the horizontal plane along the x axis (see the bottom-left panel of Fig. 1). Finally, we obtain the coefficients of the velocity field u, 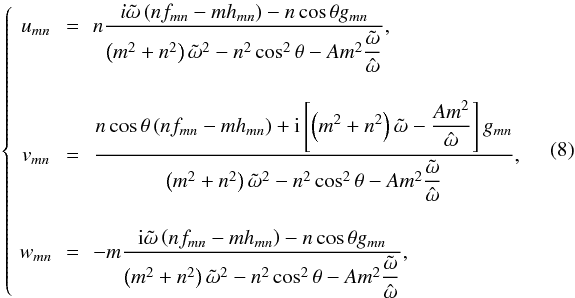 (29)of the pressure p,
(29)of the pressure p, ![\begin{equation} \begin{array}{ccl} \psi_{mn} & \!\!=\!\! & \displaystyle \frac{1}{\Lambda} \left[ \frac{ \left( \tilde{\omega} f_{mn} + i \cos \theta g_{mn} \right) \left[ n \sin \theta + {\rm i} m \left( \displaystyle \frac{A}{ \hat{\omega } } - \tilde{\omega} \right) \right] }{ \left( m^2 + n^2 \right) \tilde{\omega}^2 - n^2 \cos^2 \theta - A m^2 \displaystyle \frac{\tilde{\omega}}{\hat{\omega}}} \right.\\ & & \left. - \displaystyle \frac{ h_{mn} \left[ m \sin \theta \tilde{\omega} + {\rm i} n \left( \tilde{\omega}^2 - \cos^2 \theta \right) \right] }{ \left( m^2 + n^2 \right) \tilde{\omega}^2 - n^2 \cos^2 \theta - A m^2 \displaystyle \frac{\tilde{\omega}}{\hat{\omega}}} \right], \\ \end{array} \label{pmn} \end{equation}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq133.png) (30)and of the buoyancy b,
(30)and of the buoyancy b, 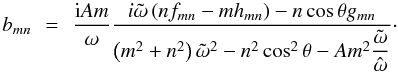 (31)Note that all the coefficients in Eqs. (29)−(31) have the same denominator. This corresponds to the left-hand side of the forced momentum equation (Eq. (14)). The tidal excitation only affects their numerators.
(31)Note that all the coefficients in Eqs. (29)−(31) have the same denominator. This corresponds to the left-hand side of the forced momentum equation (Eq. (14)). The tidal excitation only affects their numerators.
As pointed out before, the viscous dissipation of gravito-inertial waves over a tidal period (Dvisc) is deduced from the velocity field (Eq. (10)). It is provided by the quadrature of the local mean dissipation in the whole box. Using our dimensionless coordinates, we define the viscous dissipation per unit mass: 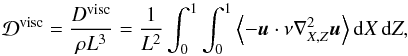 (32)where
(32)where 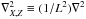 and ⟨···⟩ is the average in time. Using Fourier series expansions given in Eq. (20), this expression becomes
and ⟨···⟩ is the average in time. Using Fourier series expansions given in Eq. (20), this expression becomes 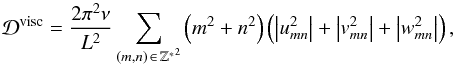 (33)as demonstrated by Ogilvie & Lin (2004). Similarly, the power dissipated by heat diffusion over a tidal period can be derived from the buoyancy perturbation (Eq. (11)). Using our dimensionless coordinates, we define the heat diffusion per unit mass
(33)as demonstrated by Ogilvie & Lin (2004). Similarly, the power dissipated by heat diffusion over a tidal period can be derived from the buoyancy perturbation (Eq. (11)). Using our dimensionless coordinates, we define the heat diffusion per unit mass 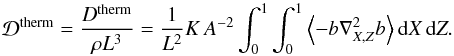 (34)Once again using Eq. (20), it becomes
(34)Once again using Eq. (20), it becomes 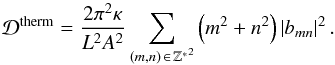 (35)The total dissipated power is the sum of both contributions, i.e.
(35)The total dissipated power is the sum of both contributions, i.e. 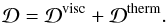 (36)Finally, we introduce the energy dissipated over a rotation period of the planet, denoted ζ,
(36)Finally, we introduce the energy dissipated over a rotation period of the planet, denoted ζ, 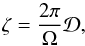 (37)and its viscous and thermal contributions,
(37)and its viscous and thermal contributions, 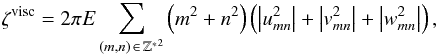 (38)
(38)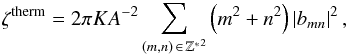 (39)which we study instead of the power (
(39)which we study instead of the power (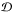 ). The energy (ζ of Eq. (37)) only depends on the control parameters A, E, and K (see Eq. (22)).
). The energy (ζ of Eq. (37)) only depends on the control parameters A, E, and K (see Eq. (22)).
 |
Fig. 3 Frequency spectra of the energy per mass unit locally dissipated by viscous friction ζvisc for inertial waves (A = 0) at the position θ = 0 for K = 0 and different Ekman numbers. In abscissa, the normalized frequency ω = χ/ 2Ω. Top left: E = 10-2. Top right: E = 10-3. Bottom left: E = 10-4. Bottom right: E = 10-5. The results obtained by Ogilvie & Lin (2004) are recovered. Note that the non-vanishing viscous dissipation at ω = 0 is the one of the geostrophic equilibrium. |
 |
Fig. 4 Frequency spectrum of the energy per mass unit dissipated in different regimes (ζ) (continuous red line), and of its viscous and thermal contributions ζvisc (dashed green line) and ζtherm (dashed blue line). The latitude is fixed at θ = 0. In abscissa, the normalized frequency ω = χ/ 2Ω. Top left: A = 1.0 × 10-2; E = 1.0 × 10-2; K = 1.0 × 10-4. Top right: A = 1.0 × 102; E = 1.0 × 10-2; K = 1.0 × 10-4. Bottom left: A = 1.0 × 10-2; E = 1.0 × 10-4; K = 1.0 × 10-2. Bottom right: A = 1.0 × 102; E = 1.0 × 10-4; K = 1.0 × 10-2. |
2.4. Spectral response
We have computed analytical formulae of the energies dissipated by viscous friction and thermal diffusion. Considering the dispersion relation Eq. (25) and the resonances involved, we know that ζ significantly varies with the tidal frequency ω. As shown by Eq. (38), its behaviour is determined by the position θ of the box and the dimensionless numbers A, E, and K. To be able to make our results comparable with the model in the appendix of Ogilvie & Lin (2004), we choose the same academic forcing, i.e. 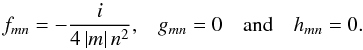 (40)We verified that the forms of the {fmn,gmn,hmn} coefficients do not affect properties of the spectra that are governed by the left-hand side of the forced momentum equation (Eq. (14)), i.e. the position and width of the resonances in the frequency-dissipation spectra. However, the spectral dependence on m and n modulate their number, their height, and the amplitude of the non-resonant background. Nevertheless, the contrast between the latter and the height of the main resonance, which is called the sharpness ratio and evaluates the relative amplitude between dynamical and equilibrium tides, are less affected. Moreover, we verified that the different main asymptotic behaviours of the system remain unchanged. In future works, it would be important to implement a more realistic treatment of the forcing term, as done by Barker & Lithwick (2013), for example, for local numerical simulations of the tidal elliptic instability.
(40)We verified that the forms of the {fmn,gmn,hmn} coefficients do not affect properties of the spectra that are governed by the left-hand side of the forced momentum equation (Eq. (14)), i.e. the position and width of the resonances in the frequency-dissipation spectra. However, the spectral dependence on m and n modulate their number, their height, and the amplitude of the non-resonant background. Nevertheless, the contrast between the latter and the height of the main resonance, which is called the sharpness ratio and evaluates the relative amplitude between dynamical and equilibrium tides, are less affected. Moreover, we verified that the different main asymptotic behaviours of the system remain unchanged. In future works, it would be important to implement a more realistic treatment of the forcing term, as done by Barker & Lithwick (2013), for example, for local numerical simulations of the tidal elliptic instability.
In Figs. 3 and 4, we plot the frequency spectra of ζvisc for various sets of parameters. The abscissa measures the dimensionless frequency ω = χ/ 2Ω, and the vertical axis the local viscous dissipation per unit mass (in logarithmic scale). Figure 3 corresponds to pure inertial waves (A = 0) in a box located at the pole (θ = 0). The plots illustrate most of the results of this section. First, the cut-off frequency for inertial modes, ωc = 1 (see the dispersion relation in Eq. (25)), clearly appears. Beyond ω = 1, the dissipation decreases by several orders of magnitude and corresponds to the non-resonant background. Second, we can observe the sharp dependence of the dissipation to the tidal frequency χ. The quantity ζ also varies with the Ekman number E. The spectrum is regular for high values of E, which correspond to waves damped by a strong viscous diffusion. In contrast, the number of resonances increases when E decreases.
Figure 4 gives an overview of the dependence of ζ, ζvisc, and ζtherm on the control parameters. Each plot corresponds to a particular regime of tidal dissipation. The number of peaks is obviously correlated to the Ekman number and we retrieve the spectra of Fig. 3 in the top-left and top-right plots where dissipation by viscous friction predominates. The ratio of the contributions, ζvisc/ζtherm, depends on the Prandtl number, the dissipation being mainly due to viscous friction for high values of Pr and to heat diffusion for low values. The cases of the bottom-left and bottom-right plots show that the critical Prandtl number, where both contributions are comparable, varies with A.
After this first qualitative approach, it is necessary to develop a quantitative physical description of the spectra taking both dissipation mechanisms into account. In a previous work, we pointed out the importance of the role played by resonances in the evolution of planetary systems. Indeed, the variations of the distance between a star or a fluid planet and its planet or satellite are directly linked to the height and width of the peaks (see Auclair-Desrotour et al. 2014). It is now possible to understand how these properties depend on the physical fluid parameters.
3. Properties of the resonances
Numerical results show that the fluid behaves like a bandpass filter with clearly identified cut-off frequencies, ωinf and ωsup; commented above (see Eq. (28)). A typical dissipation spectrum is a batch of resonances presenting a large range of positions, widths, and heights, and an apparent non-resonant background. Thanks to our analytical formulae of the viscous and thermal dissipations (Eqs. (33)and (35)), these properties can be established explicitly as functions of the colatitude θ, the ratio of squared frequencies A, the Ekman number E, and its analogue for thermal diffusion K (and the corresponding Prandtl number Pr). Thus, we treat first the eigenfrequencies ωmn and the widths lmn that do not depend on the forcing, and in a second step, the heights Hmn and the non-resonant background Hbg. Finally, we look at the number of resonances Nkc and the sharpness ratio Ξ, which is the ratio between the height of the main peak and the mean non-resonant background inside the frequency range ![\hbox{$ \left[ \omega_{\rm inf}, \omega_{\rm sup} \right] $}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq184.png) .
.
3.1. Position and population of resonances
The spectra of Fig. 3 reveal a well-organized structure. Each peak is surrounded by two others of the nearest higher orders. The fractal pattern, accentuated by the particular forcing chosen, is apparent in the bottom-right plot (E = 10-5). In this subsection, we retrieve this singular structure analytically, by studying the expression of ζ (Eq. (38)). The energy dissipated is written as an infinite sum of terms ζmn associated with the degrees m and n. As 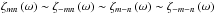 , m and n being natural integers, four terms of this series dominate all the others near a resonance. Hence, we assume the following:
, m and n being natural integers, four terms of this series dominate all the others near a resonance. Hence, we assume the following: 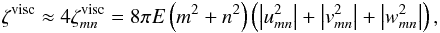 (41)
(41)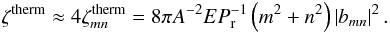 (42)ζvisc and ζtherm have the same denominator,
(42)ζvisc and ζtherm have the same denominator, 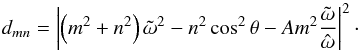 (43)Considering that the numerators vary smoothly compared to dmn, we deduce the eigenfrequencies ωmn (with (m,n) ∈ N∗ 2) from the dispersion relation (Eq. (25)). The eigenfrequencies correspond to the minima of the denominator dmn. Then, we factorize the expression given in Eq. (43) by
(43)Considering that the numerators vary smoothly compared to dmn, we deduce the eigenfrequencies ωmn (with (m,n) ∈ N∗ 2) from the dispersion relation (Eq. (25)). The eigenfrequencies correspond to the minima of the denominator dmn. Then, we factorize the expression given in Eq. (43) by 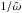 , which varies smoothly like the numerator. It yields the following polynomial P:
, which varies smoothly like the numerator. It yields the following polynomial P: 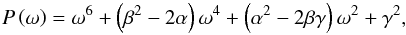 (44)where α, β and γ are positive real coefficients
(44)where α, β and γ are positive real coefficients 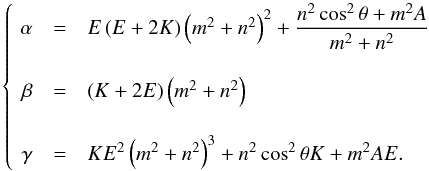 (45)
(45)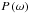 have the same minima as dmn. Hence, by differentiating
have the same minima as dmn. Hence, by differentiating 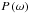 , we get:
, we get: 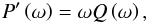 (46)Q being an even fourth degree polynomial. Thus, solutions satisfy the equation
(46)Q being an even fourth degree polynomial. Thus, solutions satisfy the equation 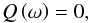 (47)and exist only if the coefficients α, β, and γ satisfy the condition
(47)and exist only if the coefficients α, β, and γ satisfy the condition 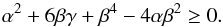 (48)Given the form of the polynomials P and Q, which involve only even terms, eigenfrequencies are symmetrical with respect to the vertical axis (ω = 0). Therefore, the domain studied can be restricted to the positive interval [ 0; + ∞ [. There is a single physical solution if 2α>β2 or α2< 2βγ,
(48)Given the form of the polynomials P and Q, which involve only even terms, eigenfrequencies are symmetrical with respect to the vertical axis (ω = 0). Therefore, the domain studied can be restricted to the positive interval [ 0; + ∞ [. There is a single physical solution if 2α>β2 or α2< 2βγ, ![\begin{equation} \omega_{mn} = \frac{1}{\sqrt{3}} \left[ 2 \alpha - \beta^2 + \sqrt{ \beta^4 + \alpha^2 - 4 \alpha \beta^2 + 6 \beta \gamma } \right]^{\frac{1}{2}}, \end{equation}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq211.png) (49)which corresponds to a minimum of P, so a maximum of ζ. We have pointed out that
(49)which corresponds to a minimum of P, so a maximum of ζ. We have pointed out that 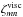 and
and 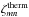 have the same denominator. Therefore, they also have the same eigenfrequencies. First, we consider the bi-parameter case of Ogilvie & Lin (2004): A = 0, K = 0 (the solution only depends on the position θ and the Ekman number E). The eigenfrequency ωmn becomes
have the same denominator. Therefore, they also have the same eigenfrequencies. First, we consider the bi-parameter case of Ogilvie & Lin (2004): A = 0, K = 0 (the solution only depends on the position θ and the Ekman number E). The eigenfrequency ωmn becomes 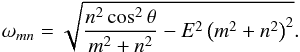 (50)Beyond a critical rank, there is no minimum any more. Only the first harmonics are resonant because they verify the condition
(50)Beyond a critical rank, there is no minimum any more. Only the first harmonics are resonant because they verify the condition 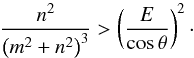 (51)Thus, there is obviously a maximum number of resonances that decreases with E and θ in the bi-parameter case. However, we see that this maximum does not correspond to the effective number of resonances. This number is actually strongly constrained by the level of the non-resonant background, which is the cause of the variations observed in Figs. 3 and 4. By plotting the analytical eigenfrequencies ωmn (Fig. 5), we retrieve the global structure of spectra. Each blue point corresponds to a mode
(51)Thus, there is obviously a maximum number of resonances that decreases with E and θ in the bi-parameter case. However, we see that this maximum does not correspond to the effective number of resonances. This number is actually strongly constrained by the level of the non-resonant background, which is the cause of the variations observed in Figs. 3 and 4. By plotting the analytical eigenfrequencies ωmn (Fig. 5), we retrieve the global structure of spectra. Each blue point corresponds to a mode 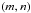 . The characteristic rank of the harmonic k = max{ | m | , | n |} is introduced to reduce the doublet
. The characteristic rank of the harmonic k = max{ | m | , | n |} is introduced to reduce the doublet 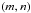 to only one index. It represents an approximative degree of the resonance. The cut-off frequency of inertial waves ωc = cosθ distinctly appears in Fig. 5 given that E ≪ 1. It can also be deduced from the simplified expression of ωmn, i.e.
to only one index. It represents an approximative degree of the resonance. The cut-off frequency of inertial waves ωc = cosθ distinctly appears in Fig. 5 given that E ≪ 1. It can also be deduced from the simplified expression of ωmn, i.e. 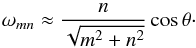 (52)The plots representing the eigenfrequencies (Fig. 5) expose the symmetries of the dispersion relation in the quasi-adiabatic approximation, which we develop from now on.
(52)The plots representing the eigenfrequencies (Fig. 5) expose the symmetries of the dispersion relation in the quasi-adiabatic approximation, which we develop from now on.
 |
Fig. 5 Structures of the frequency spectra of dissipation for inertial waves and gravito-inertial waves, with various sets of parameters. The positions of resonances (in abscissa, the normalized frequency ω = χ/ 2Ω) are indicated by blue points as functions of the characteristic rank k of the harmonics (ordinates). Top left: (θ,A,E,K) = (0,0,10-2,0). Top right: (θ,A,E,K) = (π/ 6,0,10-4,0). Bottom left: (θ,A,E,K) = (π/ 6,25,10-4,0). Bottom right: (θ,A,E,K) = (π/ 6,25,0,10-4). |
The quasi-adiabatic approximation means that the diffusivities E and K are first-order infinitesimals with respect to cosθ and 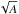 . This assumption corresponds to low viscous and thermal diffusivities (ν and κ) relevant in stellar and planetary interiors. Thus, for the main resonances (k< 10), the coefficients α, β and γ become
. This assumption corresponds to low viscous and thermal diffusivities (ν and κ) relevant in stellar and planetary interiors. Thus, for the main resonances (k< 10), the coefficients α, β and γ become 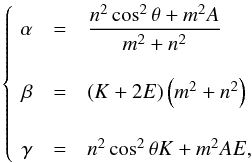 (53)and the frequency of the resonance
(53)and the frequency of the resonance 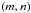 ,
, 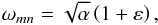 (54)where ε is a second order bias:
(54)where ε is a second order bias: 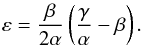 (55)Therefore, when E and K are small and can be neglected, resonances are located at the eigenfrequencies
(55)Therefore, when E and K are small and can be neglected, resonances are located at the eigenfrequencies 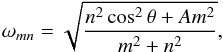 (56)which correspond to the dispersion relation of gravito-inertial waves in the adiabatic case given in Eq. (26). They give us the boundaries of the frequency range in the local model,
(56)which correspond to the dispersion relation of gravito-inertial waves in the adiabatic case given in Eq. (26). They give us the boundaries of the frequency range in the local model, 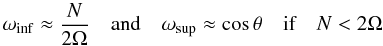 (57)or the contrary if N> 2Ω. Note that the exact expressions of ωinf and ωsup (Eq. 28) are actually a bit more complex than the previous expressions. In Figs. 4 and 5, the interval
(57)or the contrary if N> 2Ω. Note that the exact expressions of ωinf and ωsup (Eq. 28) are actually a bit more complex than the previous expressions. In Figs. 4 and 5, the interval ![\hbox{$\left[ \omega_{\rm inf}, \omega_{\rm sup} \right] $}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq245.png) delimits peaks and blue points zones. As the impact of E and K is of second order, the structure of the batch of resonances only depends on A and the colatitude θ under the quasi-adiabatic approximation. This is the reason why the plots of Fig. 5, where
delimits peaks and blue points zones. As the impact of E and K is of second order, the structure of the batch of resonances only depends on A and the colatitude θ under the quasi-adiabatic approximation. This is the reason why the plots of Fig. 5, where 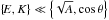 have the same appearance. By taking A = 0, we recover the expression that corresponds to pure inertial waves (see Eq. (50)).
have the same appearance. By taking A = 0, we recover the expression that corresponds to pure inertial waves (see Eq. (50)).
Moreover, Eq. (56) points out an hyper-resonant case related to quasi-inertial waves (A< 1) and characterized by the equality 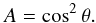 (58)When it is verified, all the peaks are superposed at the eigenfrequency
(58)When it is verified, all the peaks are superposed at the eigenfrequency 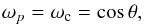 (59)and form a huge single peak. So, if N< 2Ω (quasi-inertial waves), there is a critical colatitude θ0 = arccos(N/ (2Ω)) at which the dissipation spectrum of tidal gravito-inertial waves reduces to a single resonance. The frequency range decreases when the latitude comes closer to θ0. As there is no such critical colatitude for A> 1, usual gravito-inertial waves are not affected by this effect. Their frequency range
(59)and form a huge single peak. So, if N< 2Ω (quasi-inertial waves), there is a critical colatitude θ0 = arccos(N/ (2Ω)) at which the dissipation spectrum of tidal gravito-inertial waves reduces to a single resonance. The frequency range decreases when the latitude comes closer to θ0. As there is no such critical colatitude for A> 1, usual gravito-inertial waves are not affected by this effect. Their frequency range ![\hbox{$\left[ \omega_{\rm inf}, \omega_{\rm sup} \right] $}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq245.png) is only larger at the equator than at the pole.
is only larger at the equator than at the pole.
The number of resonances constituting a spectrum can be estimated from the expressions of the eigenfrequencies ωmn (Eq. (56)). Indeed, because of the definition of k, there are 2k−1 points per line in Fig. 5, but as a result of the symmetries of ωmn some of these points have the same positions. Indeed, note that ωm′n′ = ωmn if m′ = pm and n′ = pn with p ∈ Z∗. This explains why resonances are not as numerous as modes. We denote kc the maximal rank of the harmonics dominating the background and Nkc the number of effective resonant peaks. The layer of harmonics k brings pk new peaks, i.e. 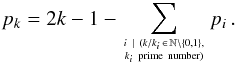 (60)So, the effective number of resonances can be computed using the following recurrence series:
(60)So, the effective number of resonances can be computed using the following recurrence series: 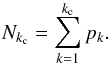 (61)The values of Nkc and
(61)The values of Nkc and 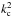 for the first orders are given in Table 1 and plotted in Fig. 6. We notice a slight difference between the two curves, the effective number of peaks growing slower than the number of modes. As a first approximation, we can consider that
for the first orders are given in Table 1 and plotted in Fig. 6. We notice a slight difference between the two curves, the effective number of peaks growing slower than the number of modes. As a first approximation, we can consider that 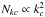 . This assumption is used to compute the scaling laws of Nkc.
. This assumption is used to compute the scaling laws of Nkc.
Numerical comparison between the number of peaks Nkc and the number of modes 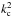 , kc being the rank of the highest harmonics, for the main resonances (1 ≤ k ≤ 10).
, kc being the rank of the highest harmonics, for the main resonances (1 ≤ k ≤ 10).
 |
Fig. 6 Real number of resonances Nkc (continuous red line) and its first order approximation |
3.2. Width of resonances
The width of a resonance is a characteristic of great interest. Indeed, in a previous
work (Auclair-Desrotour et al. 2014), we studied a
coplanar, two-body system of semi-major axis a and showed that a was submitted to rapid
changes due to resonances (see also Witte &
Savonije 1999, 2001, 2002). In this work, the system is constituted by a fluid rotating
planet and a point-like satellite. The variation Δa of the semi-major axis
a is
related to the width at mid-height lp and sharpness ratio
Ξp =
Hp/Hbg
of the pth
resonance encountered. Indeed, 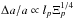 ,
i.e. the amplitude Δa varies linearly as a function of the width of the
peak that causes it, this width being the signature of the dissipation. In this section,
we compute an analytical formula of the width at mid-height lmn as a function of the
control parameters of the system. Similar to the eigenfrequencies, lmn are fully determined
by the left-hand side of Eq. (14). We
suppose that ξmn, the numerator of
ζmn in Eqs. (41) or (42),
varies smoothly compared to its denominator dmn (see Eq. (43)). Then, the width at mid-height is
computed from the relation
,
i.e. the amplitude Δa varies linearly as a function of the width of the
peak that causes it, this width being the signature of the dissipation. In this section,
we compute an analytical formula of the width at mid-height lmn as a function of the
control parameters of the system. Similar to the eigenfrequencies, lmn are fully determined
by the left-hand side of Eq. (14). We
suppose that ξmn, the numerator of
ζmn in Eqs. (41) or (42),
varies smoothly compared to its denominator dmn (see Eq. (43)). Then, the width at mid-height is
computed from the relation 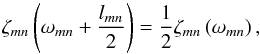 (62)which can also be
expressed as
(62)which can also be
expressed as 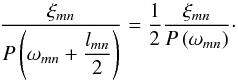 (63)Therefore, we solve the
following equation:
(63)Therefore, we solve the
following equation: 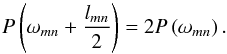 (64)Hence, the
lmn are the same for
ζvisc and ζtherm, like the
eigenfrequencies. In the context of the quasi-adiabatic approximation, we obtain
(64)Hence, the
lmn are the same for
ζvisc and ζtherm, like the
eigenfrequencies. In the context of the quasi-adiabatic approximation, we obtain
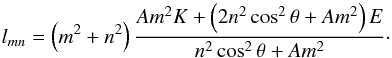 (65)Looking at the form of
this expression, we introduce two critical numbers proper to the mode
(65)Looking at the form of
this expression, we introduce two critical numbers proper to the mode
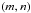 ,
,
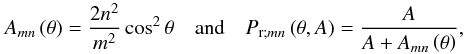 (66)which
determine asymptotical behaviours. The expression of lmn thus becomes
(66)which
determine asymptotical behaviours. The expression of lmn thus becomes
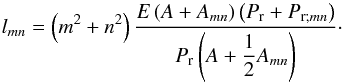 (67)A ≪
Amncharacterizes
inertial waves and A ≫
Amn gravito-inertial
waves. Similarly, if Pr ≪
Pr;mn, the resonance is
damped by thermal diffusion, and if Pr ≫
Pr;mn, it is damped by
viscous friction. We thus identify four possible regimes, summarized in Fig. 7:
(67)A ≪
Amncharacterizes
inertial waves and A ≫
Amn gravito-inertial
waves. Similarly, if Pr ≪
Pr;mn, the resonance is
damped by thermal diffusion, and if Pr ≫
Pr;mn, it is damped by
viscous friction. We thus identify four possible regimes, summarized in Fig. 7:
-
1.
A ≪ Amn and Pr ≫ Pr;mn: inertial waves damped by viscous diffusion;
-
2.
A ≫ Amn and Pr ≫ Pr;mn: gravity waves damped by viscous diffusion;
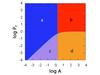
Fig. 7 Asymptotic domains. The areas on the left a) and c) correspond to inertial waves, those on the right b) and d) to gravito-inertial waves. Resonances are damped by viscosity in areas a) and b), and by thermal diffusivity in areas c) and d). The corresponding domains of parameters are a) A ≪ Amn and Pr ≫ Pr;mn; b) A ≫ Amn and Pr ≫ Pr;mn; c)A ≪ Amn and Pr ≪ Pr;mn; and d) A ≫ Amn and Pr ≪ Pr;mn.
Table 2Scaling laws of the width at mid-height lmn of the resonance associated with the doublet
 .
.
Fig. 8 Width at mid-height l11 and height
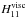 of the main resonance of ζvisc as a function of the
Ekman number E and its analogue for heat diffusion
K for different values of A (in
logarithmic scales). Top left: l11 −
E. Top right:
l11 − K.
Bottom left:
of the main resonance of ζvisc as a function of the
Ekman number E and its analogue for heat diffusion
K for different values of A (in
logarithmic scales). Top left: l11 −
E. Top right:
l11 − K.
Bottom left: 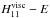 . Bottom
right:
. Bottom
right: 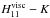 .
. -
3.
A ≪ Amn and Pr ≪ Pr;mn: inertial waves damped by thermal diffusion; and
-
4.
A ≫ Amn and Pr ≪ Pr;mn: gravity waves damped by thermal diffusion.
The scaling laws of Table 2 are directly deduced from Eq. (65). They illustrate the differences between the four identified regimes. First, we focus on inertial waves. If the viscous term overpowers the term of heat diffusion, then we have the case studied by Ogilvie & Lin (2004). The width at mid-height of resonances varies lineraly with the Ekman number. Peaks are larger for E = 10-2 than for E = 10-5 (see Fig. 3). Elsewhere, the width is proportional to K: for a given A> 0, the resonances would widen with K as they do with E in the previous case. Now, if we examine gravito-inertial waves, they behave similar to inertial waves, linearly widening with E and K in the corresponding regimes defined above. Finally, note that lmn always depends on a single parameter except in the case of inertial waves damped by thermal diffusion, for which the square frequencies ratio (A) als has a linear impact.
Assuming that the resonances all have the same qualitative behaviour, we plot the width at mid-height l11 of the main one from Eq. (65). We thus find in the plots the regimes predicted analytically as illustrated in Fig. 8, in particular, in the transition zones. In relation to the nature of the damping, the transition zones are indicated with curved lines. The transition zones correspond to the critical Prandtl number Pr;11. The parameter l11 also varies with the nature of the waves. If A ≪ 1, the Coriolis acceleration drives the dynamics and the perturbation generates quasi-inertial waves. If A>> 1, it generates quasi-gravity waves. This is the reason why we can observe two asymptotical curves on the plots. If we come back to the case of inertial waves damped by viscous diffusion (Ogilvie & Lin 2004), l11 is proportional to E and does not varies with K. Thus, the peaks become thinner when E decreases, which explains the behaviours observed in Figs. 3 and 4. Appendix B includes colour maps of the relative difference between the prediction of the analytical expression (Eq. (65)) and the real theoretical result computed from the complete formula of ζvisc (Eq. (38)). They validate the expression of l11 in asymptotical regimes and highlight transition zones where it cannot be used.
Thanks to the scaling laws of lmn, it becomes
possible to constrain the variations of orbital parameters caused by a resonance of the
internal dissipation. For instance, the amplitude Δa for the semi-major axis
a of our
two-body system (Auclair-Desrotour et al. 2014)
verifies the law 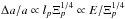 in the regime of inertial waves damped by viscous friction.
in the regime of inertial waves damped by viscous friction.
3.3. Amplitude of resonances
The height of a resonant peak also has an influence on the secular evolution of orbital parameters. Thus, we establish an analytical formula of the height Hmn of the peaks. Of course, the height of resonances depends on the tidal forcing f, which requires that we choose a form for it. Following Ogilvie & Lin (2004), we take perturbation coefficients of the form 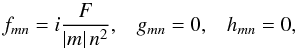 (68)and assuming
(68)and assuming 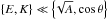 , we note that
, we note that ![\begin{equation} P \left( \omega_{mn} \right) \approx \left[ Am^2 K + \left( 2n^2 \cos^2 \theta + A m^2 \right)E \right]^2, \end{equation}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq342.png) (69)so that we can compute simple expressions for the heights of the peaks of ζvisc and ζtherm.
(69)so that we can compute simple expressions for the heights of the peaks of ζvisc and ζtherm.
3.3.1. Dissipation by viscous friction
First, we look at the resonances of ζvisc. Naming 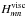 their heights, we obtain the relation
their heights, we obtain the relation ![\begin{equation} H_{mn}^{\rm visc} = \frac{8 \pi F^2 E}{m^2 n^2 \left( m^2 + n^2 \right)^2} \frac{ \left( 2 n^2 \cos^2 \theta + A m^2 \right) \left( n^2 \cos^2 \theta + A m^2 \right) }{ \left[ Am^2 K + \left( 2n^2 \cos^2 \theta + A m^2 \right)E\right]^2 }, \label{H_visc} \end{equation}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq344.png) (70)where we recognize the critical numbers Amn and Pr;mn introduced in the previous section, i.e.
(70)where we recognize the critical numbers Amn and Pr;mn introduced in the previous section, i.e. 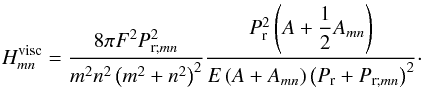 (71)Thus, the height is characterized by the same asymptotic domains as the width. The borders between them depend on Amn and Pr;mn (Table 3), but the height has different scaling laws. For example, when dissipation is led by viscosity,
(71)Thus, the height is characterized by the same asymptotic domains as the width. The borders between them depend on Amn and Pr;mn (Table 3), but the height has different scaling laws. For example, when dissipation is led by viscosity, 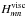 is inversely proportional to the Ekman number contrary to lmn. Therefore, the heights of the resonances increase if the Ekman number E decreases, which corroborates the plots of Fig. 3. If dissipation is led by heat diffusion, then
is inversely proportional to the Ekman number contrary to lmn. Therefore, the heights of the resonances increase if the Ekman number E decreases, which corroborates the plots of Fig. 3. If dissipation is led by heat diffusion, then 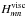 depend on both E and K. Of course, the scaling laws of
depend on both E and K. Of course, the scaling laws of 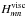 are related to the spectral decomposition of the forcing. This partly determines the decay law of the heights with the wave number k:
are related to the spectral decomposition of the forcing. This partly determines the decay law of the heights with the wave number k: 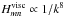 . Here, fmn ∝ 1 /k3, but if fmn did not depend on m and n, then the decay law would be
. Here, fmn ∝ 1 /k3, but if fmn did not depend on m and n, then the decay law would be 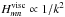 . Consequently, with the forcing chosen for this study, the height of the resonant peaks rapidly becomes comparable with the non-resonant background. Therefore, few terms
. Consequently, with the forcing chosen for this study, the height of the resonant peaks rapidly becomes comparable with the non-resonant background. Therefore, few terms 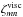 of the lowest orders are sufficient to plot the spectrum and there is no need to take into account a large number of harmonics to describe the dissipation properly.
of the lowest orders are sufficient to plot the spectrum and there is no need to take into account a large number of harmonics to describe the dissipation properly.
In the planet-satellite system studied by Auclair-Desrotour et al. (2014), we can thus write Δa/a with these new scaling laws, i.e. 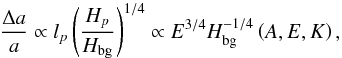 (72)in the regime of inertial waves damped by viscous friction.
(72)in the regime of inertial waves damped by viscous friction.
Asymptotic behaviours of the height 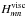 of the resonance of ζvisc associated with the doublet
of the resonance of ζvisc associated with the doublet 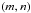 .
.
We plot the height of the main resonance 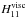 (Fig. 8) as a function of A, E, and K, using the analytical scaling laws (Eq. (70)and Table 3). The maximum of
(Fig. 8) as a function of A, E, and K, using the analytical scaling laws (Eq. (70)and Table 3). The maximum of 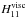 (Fig. 8, bottom-left panel) results from the inversion of the dependence on E, for Pr ~ Pr;11. Hence, it highlights the transition zone between viscous friction and thermal damping. As expected, the position of this maximum varies with A until A ≫ 1, where Pr;11 ≈ 1 asymptotically. We recall that Eq. (70) is relevant for small values of E and K (see Fig. B.1 in Appendix B).
(Fig. 8, bottom-left panel) results from the inversion of the dependence on E, for Pr ~ Pr;11. Hence, it highlights the transition zone between viscous friction and thermal damping. As expected, the position of this maximum varies with A until A ≫ 1, where Pr;11 ≈ 1 asymptotically. We recall that Eq. (70) is relevant for small values of E and K (see Fig. B.1 in Appendix B).
3.3.2. Dissipation by thermal diffusion
An expression of 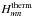 of the same form as Eq. (70) can be deduced from Eq. (39),
of the same form as Eq. (70) can be deduced from Eq. (39), ![\begin{equation} H_{mn}^{\rm therm} = \frac{8 \pi K F^2}{n^2 \left( m^2 + n^2 \right)^2} \frac{n^2 \cos^2 \theta + m^2 A}{\left[ A m^2 K + \left( 2 n^2 \cos^2 \theta + A m^2 \right)E \right]^2}, \end{equation}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq364.png) (73)which can also be written as a function of the transition parameters Amn and Pr;mn,
(73)which can also be written as a function of the transition parameters Amn and Pr;mn, 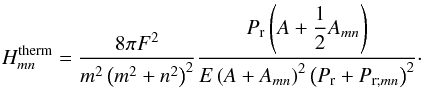 (74)Thus, the asymptotic regimes of
(74)Thus, the asymptotic regimes of 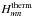 correspond to the four zones identified for lmn and
correspond to the four zones identified for lmn and 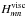 (see Fig. 7).
(see Fig. 7).
Asymptotic behaviours of the height 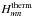 of the resonance of ζtherm associated with the doublet
of the resonance of ζtherm associated with the doublet 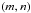 .
.
3.3.3. Total dissipation
As ζvisc and ζtherm have the same resonance eigenfrequencies, and their peaks are superposed. Therefore, when one of the dissipation mechanisms predominates at resonances, the observed peaks are all scaled by the law corresponding to this mechanism. To establish the scaling laws of the total energy, we have to delimit the domains of dissipation by viscous friction, where 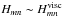 , and of dissipation by heat diffusion, where
, and of dissipation by heat diffusion, where 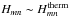 . Hence, we introduce the ratio ςmn,
. Hence, we introduce the ratio ςmn, 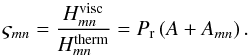 (75)The transition zone is characterized by ςmn ~ 1, or
(75)The transition zone is characterized by ςmn ~ 1, or 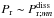 , where
, where 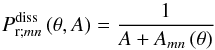 (76)is the Prandtl number indicating this transition zone. If
(76)is the Prandtl number indicating this transition zone. If 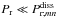 , then
, then 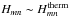 (Fig. 9, left panel); otherwise,
(Fig. 9, left panel); otherwise, 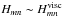 . Taking into account the new zones appearing with this condition on Pr (Fig. 9, right panel), we obtain the scaling laws for Hmn, which are the heights of resonances of the total dissipation, given in Table 5. For the sake of simplicity, we introduce a new Prandtl number,
. Taking into account the new zones appearing with this condition on Pr (Fig. 9, right panel), we obtain the scaling laws for Hmn, which are the heights of resonances of the total dissipation, given in Table 5. For the sake of simplicity, we introduce a new Prandtl number, 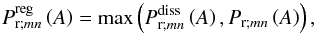 (77)which separates the regimes where Pr intervenes in scaling laws from others.
(77)which separates the regimes where Pr intervenes in scaling laws from others.
Asymptotic behaviours of the height Hmn of the resonance of ζ associated with the doublet 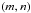 .
.
 |
Fig. 9 Left: zones of predominances for dissipative mechanisms. In the pink area b), ζtherm ≫ ζvisc: the dissipation is mainly due to thermal diffusion. In the white area a), it is led by viscous friction. The transition zone corresponds to |
3.4. The non-resonant background
The height of the non-resonant background Hbg is the magnitude of the energy dissipated inside the frequency range ![\hbox{$ \left[ \omega_{\rm inf},\omega_{\rm sup} \right] $}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq395.png) , in non-resonant areas. It only depends on the first term of the sum in the expression of ζ (Eq. 38). Indeed, each mode is related to a typical wavelength that increases when the wave numbers m and n decay. Thus, at the eigenfrequencies ω = ωmn ((m,n) ∈ N2), the perturbation presents a characteristic pattern of wavelengths λh = L/m in the x direction and λv = L/n in the z direction, but it is dominated by the lowest-order pattern m = n = 1 in the absence of resonance. If we had L ~ R, then our first mode would correspond to the large-scale hydrostatic adjustment of the flow in phase with the perturber, the equilibrium tide, or non-wave-like displacement introduced above (see e.g. Remus et al. 2012a; Ogilvie 2013).
, in non-resonant areas. It only depends on the first term of the sum in the expression of ζ (Eq. 38). Indeed, each mode is related to a typical wavelength that increases when the wave numbers m and n decay. Thus, at the eigenfrequencies ω = ωmn ((m,n) ∈ N2), the perturbation presents a characteristic pattern of wavelengths λh = L/m in the x direction and λv = L/n in the z direction, but it is dominated by the lowest-order pattern m = n = 1 in the absence of resonance. If we had L ~ R, then our first mode would correspond to the large-scale hydrostatic adjustment of the flow in phase with the perturber, the equilibrium tide, or non-wave-like displacement introduced above (see e.g. Remus et al. 2012a; Ogilvie 2013).
In this framework, the height of the non-resonant background gives us information about the mean dissipation and the smooth component of the tidal quality factor (Q). Therefore, it plays an important role in the secular evolution of planetary systems. Indeed, it is also necessary to compute the sharpness ratio Ξ ≡ H11/Hbg intervening in the expression of Δa. Thus, in this subsection, we estimate Hbg by computing the term of the main resonance, ζ11, at the frequency 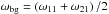 , that can be written
, that can be written 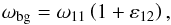 (78)with the relative distance between the two peaks,
(78)with the relative distance between the two peaks, 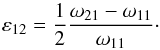 (79)Note that if A = cos2θ (critical hyper-resonant case), the characteristic level of the non-resonant background is not defined and ε12 = 0. Considering that the contributions of the main peaks are approximately the same, we write the characteristic height of the background, i.e.
(79)Note that if A = cos2θ (critical hyper-resonant case), the characteristic level of the non-resonant background is not defined and ε12 = 0. Considering that the contributions of the main peaks are approximately the same, we write the characteristic height of the background, i.e. 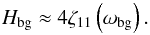 (80)
(80)
3.4.1. Dissipation by viscous friction
We first focus on the contribution of viscous friction, 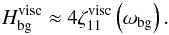 (81)Assuming
(81)Assuming 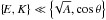 , the previous expression becomes
, the previous expression becomes ![\begin{eqnarray} \label{Hbg_visc_brut} H_{\rm bg}^{\rm visc} = 4 \pi F^2 E \varepsilon_{12}^2 \frac{ \left( A + \cos^2 \theta \right) \left[ C_{\rm grav} \left( \varepsilon_{12} \right) A +C_{\rm in} \left( \varepsilon_{12} \right) \cos^2 \theta \right] }{ \left( A + \cos^2 \theta \right)^3 \varepsilon_{12}^2 + \xi \left( \theta, A, E,K \right) } \end{eqnarray}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq414.png) (82)with
(82)with 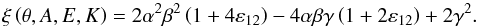 (83)The functions
(83)The functions 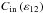 and
and 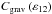 are expressed by
are expressed by 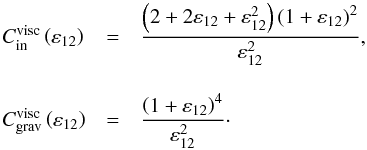 (84)The coefficients β and γ linearly depend on E and K (Eq. (53)). On the contrary, neither the Ekman number nor the dimensionless thermal diffusivity have an influence on ω11 and ε12. Therefore, the background linearly varies with the Ekman number if the condition
(84)The coefficients β and γ linearly depend on E and K (Eq. (53)). On the contrary, neither the Ekman number nor the dimensionless thermal diffusivity have an influence on ω11 and ε12. Therefore, the background linearly varies with the Ekman number if the condition 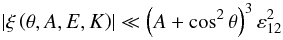 (85)is satisfied. To unravel what this implies on the physical parameters, we need to study two asymptotic cases separately:
(85)is satisfied. To unravel what this implies on the physical parameters, we need to study two asymptotic cases separately:
-
1.
A ≪ cos2θ (quasi-inertial waves),
-
2.
A ≫ cos2θ (gravito-inertial waves).
By deducing the main eigenfrequency 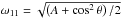 from the dispersion relation (Eq. 25), we compute the relative distance between the two main resonances,
from the dispersion relation (Eq. 25), we compute the relative distance between the two main resonances, 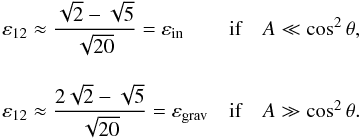 (86)Thus, the relative distance between ω11 and ωbg belongs to the interval
(86)Thus, the relative distance between ω11 and ωbg belongs to the interval ![\hbox{$ \left[ \varepsilon_{\rm in},\varepsilon_{\rm grav} \right] $}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq427.png) , εin and εgrav being the boundaries corresponding to the asymptotic cases A ≪ cos2θ (i.e. the quasi-inertial waves) and A ≫ cos2θ (i.e. the gravito-inertial waves), respectively. Numerically, εin ≈ −0.183 and εgrav ≈ 0.132 and the asymptotic values of the coefficients
, εin and εgrav being the boundaries corresponding to the asymptotic cases A ≪ cos2θ (i.e. the quasi-inertial waves) and A ≫ cos2θ (i.e. the gravito-inertial waves), respectively. Numerically, εin ≈ −0.183 and εgrav ≈ 0.132 and the asymptotic values of the coefficients 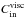 and
and 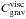 are
are 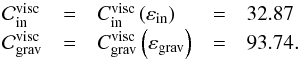 (87)From Eq. (79), we note that the dependence of the non-resonant background on E is linear only if
(87)From Eq. (79), we note that the dependence of the non-resonant background on E is linear only if 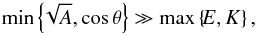 (88)which corresponds to the quasi-adiabatic approximation met before and assumed in the whole study. We thus finally obtain the expression of
(88)which corresponds to the quasi-adiabatic approximation met before and assumed in the whole study. We thus finally obtain the expression of  for inertial waves and gravity waves (Table 6),
for inertial waves and gravity waves (Table 6), 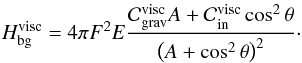 (89)The background does not depend on the Prandtl number under the quasi-adiabatic approximation. Its level is only defined by the ratio A/ cos2θ ~ A/A11. Hence, the level of the non-resonant background is completely independent of the thermal diffusivity K in both asymptotic regimes. Besides,
(89)The background does not depend on the Prandtl number under the quasi-adiabatic approximation. Its level is only defined by the ratio A/ cos2θ ~ A/A11. Hence, the level of the non-resonant background is completely independent of the thermal diffusivity K in both asymptotic regimes. Besides,  increases with E whereas
increases with E whereas 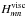 decays.
decays.
Asymptotic behaviours of the non-resonant background level  of the spectrum.
of the spectrum.
Thanks to our result for  , we now have a complete scaling law for the magnitude of the variation of the semi-major axis caused by a resonance of the dissipation spectra in the regime of inertial waves damped by viscous friction in a convective planetary or stellar region (Auclair-Desrotour et al. 2014), i.e.
, we now have a complete scaling law for the magnitude of the variation of the semi-major axis caused by a resonance of the dissipation spectra in the regime of inertial waves damped by viscous friction in a convective planetary or stellar region (Auclair-Desrotour et al. 2014), i.e. 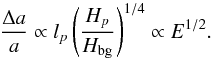 (90)Here, it is interesting to introduce a sharpness ratio Ξ corresponding to the sensitivity of dissipation to the tidal frequency ω. The parameter Ξ is defined as the ratio between the height of the resonance and the background level,
(90)Here, it is interesting to introduce a sharpness ratio Ξ corresponding to the sensitivity of dissipation to the tidal frequency ω. The parameter Ξ is defined as the ratio between the height of the resonance and the background level, 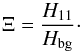 (91)Therefore, the sharpness ratio estimates the relative magnitude of the variations of the dissipation due to the main resonant peak and compares the strengths of the dynamical and equilibrium/non-wave-like tides. A high sharpness ratio characterizes a peaked spectrum, and a low sharpness ratio characterizes a smooth dependence of the dissipation on ω. As demonstrated in Auclair-Desrotour et al. (2014), this parameter is important for the dynamical evolution of planet-moon and star-planet systems. Indeed, the variation of orbital parameters is correlated to Ξ, with the evolution of these laters being smooth in absence of resonances and erratic if Ξ ≫ 1 (Auclair-Desrotour et al. 2014).
(91)Therefore, the sharpness ratio estimates the relative magnitude of the variations of the dissipation due to the main resonant peak and compares the strengths of the dynamical and equilibrium/non-wave-like tides. A high sharpness ratio characterizes a peaked spectrum, and a low sharpness ratio characterizes a smooth dependence of the dissipation on ω. As demonstrated in Auclair-Desrotour et al. (2014), this parameter is important for the dynamical evolution of planet-moon and star-planet systems. Indeed, the variation of orbital parameters is correlated to Ξ, with the evolution of these laters being smooth in absence of resonances and erratic if Ξ ≫ 1 (Auclair-Desrotour et al. 2014).
Asymptotic expressions of the sharpness ratio Ξvisc characterizing the spectrum of dissipation by viscous friction.
 |
Fig. 10 Non-resonant background level |
We can define Ξ for each of both contributions: 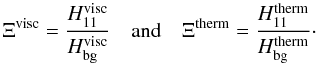 (92)The transition zones of
(92)The transition zones of 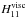 and
and  are the same. Assuming the quasi-adiabatic approximation (Eq. (88)), and considering the analytical expressions of
are the same. Assuming the quasi-adiabatic approximation (Eq. (88)), and considering the analytical expressions of 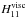 (Eq. (70)) and
(Eq. (70)) and  (Eq. (82)), we write the sharpness ratio:
(Eq. (82)), we write the sharpness ratio: ![\begin{equation} \Xi^{\rm visc} = \frac{1}{2} \frac{ \left( 2 \cos^2 + A \right) \left[ \left( A + \cos^2 \theta \right)^3 \varepsilon_{12}^2 + \xi \left( \theta, A,E, K \right) \right] }{ \varepsilon_{12}^2 \left[ A K + \left( 2 \cos^2 + A \right) E \right]^2 \left[ C_{\rm in} \cos^2 \theta + C_{\rm grav} A \right] }\cdot \label{sharpness1} \end{equation}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq463.png) (93)This expression may be simplified in asymptotic domains (see Fig. 7), where
(93)This expression may be simplified in asymptotic domains (see Fig. 7), where
Thus, the sharpness ratio becomes ![\begin{equation} \Xi^{\rm visc} = \frac{1}{2} \frac{ \left( 2 \cos^2 + A \right) \left( A + \cos^2 \theta \right)^3 }{ \left[ A K + \left( 2 \cos^2 + A \right) E \right]^2 \left[ \mathcal{C}_{\rm in}^{\rm visc} \cos^2 \theta + \mathcal{C}_{\rm grav}^{\rm visc} A \right] }\cdot \label{sharpness2} \end{equation}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq468.png) (94)Like the height of the resonances (
(94)Like the height of the resonances (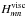 ), Ξvisc obviously presents symmetrical behaviours for gravito-inertial waves (Table 7). It is inversely proportional to the square of the dominating dimensionless diffusivity, E (for Pr ≫ Pr;11) or K (for Pr ≪ Pr;11). Hence, the sensitivity of tidal dissipation to the frequency ω increases quadratically when the diffusivities decrease (Fig. 10, bottom-left and bottom-right panels). Likewise, Ξ increases with A quadratically when A ≫ A11. If A ≪ A11, then it is related to the colatitude θ. One notices that Ξvisc does not depends on the forcing at all. Neither the amplitude F of the force, nor the form of the perturbation coefficients fmn ∝ 1 / |m|n2 intervene in the expressions of Eq. (93) and (94). Given the link existing between the sharpness ratio and the tidal quality factor Q modelling dissipation discussed above, we can deduce the qualitative evolution of orbital parameters (Eq. (90)). Indeed, if a planet is composed of a fluid with a large viscosity, the variation of the semi-major axis of its companion is smooth. In the opposite case of a low viscosity planet, it becomes strongly erratic, with intermittent rapid changes of the orbit due to resonances (e.g Auclair-Desrotour et al. 2014).
), Ξvisc obviously presents symmetrical behaviours for gravito-inertial waves (Table 7). It is inversely proportional to the square of the dominating dimensionless diffusivity, E (for Pr ≫ Pr;11) or K (for Pr ≪ Pr;11). Hence, the sensitivity of tidal dissipation to the frequency ω increases quadratically when the diffusivities decrease (Fig. 10, bottom-left and bottom-right panels). Likewise, Ξ increases with A quadratically when A ≫ A11. If A ≪ A11, then it is related to the colatitude θ. One notices that Ξvisc does not depends on the forcing at all. Neither the amplitude F of the force, nor the form of the perturbation coefficients fmn ∝ 1 / |m|n2 intervene in the expressions of Eq. (93) and (94). Given the link existing between the sharpness ratio and the tidal quality factor Q modelling dissipation discussed above, we can deduce the qualitative evolution of orbital parameters (Eq. (90)). Indeed, if a planet is composed of a fluid with a large viscosity, the variation of the semi-major axis of its companion is smooth. In the opposite case of a low viscosity planet, it becomes strongly erratic, with intermittent rapid changes of the orbit due to resonances (e.g Auclair-Desrotour et al. 2014).
3.4.2. Dissipation by thermal diffusion
Similar to  , the height of the non-resonant background of dissipation by heat diffusion is assumed to be approximately
, the height of the non-resonant background of dissipation by heat diffusion is assumed to be approximately 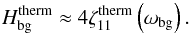 (95)Assuming the quasi-adiabatic approximation, we can write the following:
(95)Assuming the quasi-adiabatic approximation, we can write the following: 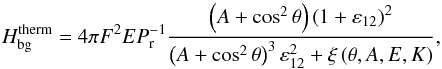 (96)where ξ has been defined above (see Eq. (83)). We introduce the function Ctherm of ε12,
(96)where ξ has been defined above (see Eq. (83)). We introduce the function Ctherm of ε12, 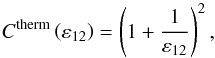 (97)which is a constant in asymptotical regimes,
(97)which is a constant in asymptotical regimes, 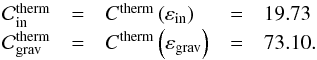 (98)When |log (A/A11)| ≫ 1, the height of the peaks can be simply expressed:
(98)When |log (A/A11)| ≫ 1, the height of the peaks can be simply expressed: 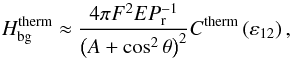 (99)or by the interpolating function, i.e.
(99)or by the interpolating function, i.e.  (100)Considering the asymptotic regimes, we obtain the scaling laws given in Table 8.
(100)Considering the asymptotic regimes, we obtain the scaling laws given in Table 8.
Asymptotic behaviours of the non-resonant background level 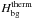 of the dissipation by heat diffusion.
of the dissipation by heat diffusion.
The sharpness ratio of dissipation by heat diffusion can be written ![\begin{equation} \Xi^{\rm therm} = \frac{1}{4} \frac{ P_{{\rm r}}^2 \left[ \left( A + \displaystyle{\frac{1}{2}} A_{11} \right)^3 \varepsilon_{12} + \xi \left( \theta, A,E,K \right) \right] }{ E^2 \left( A + A_{11} \right)^2 \left( P_{{\rm r}} + P_{{\rm r};11} \right)^2 \left( 1 + \varepsilon_{12} \right)^2 }, \end{equation}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq486.png) (101)expression, which can be simplified to
(101)expression, which can be simplified to 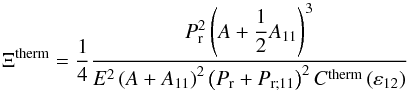 (102)in asymptotic regions where |log (A/A11)| ≫ 1, or to
(102)in asymptotic regions where |log (A/A11)| ≫ 1, or to  (103)if we use the asymptotic interpolation of the function Ctherm
(103)if we use the asymptotic interpolation of the function Ctherm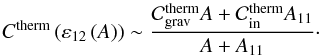 (104)Using Eq. (103), we establish the asymptotic scaling laws given in Table 9. These laws are the same as those of Table 7, which means that the variations of the energy with the tidal frequency do not depend on the dissipation mechanism in our local model. Therefore, the number of peaks, which are deduced from the sharpness ratio, have the same scaling laws in both zones of Fig. 9 (left panel).
(104)Using Eq. (103), we establish the asymptotic scaling laws given in Table 9. These laws are the same as those of Table 7, which means that the variations of the energy with the tidal frequency do not depend on the dissipation mechanism in our local model. Therefore, the number of peaks, which are deduced from the sharpness ratio, have the same scaling laws in both zones of Fig. 9 (left panel).
Asymptotic expressions of the sharpness ratio Ξtherm characterizing the spectrum of dissipation by heat diffusion.
3.4.3. Total dissipation
The background level of ζ, denoted Hbg, is the sum of  and
and 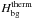 . Given that
. Given that 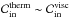 and
and 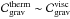 , the ratio of the backgrounds is equivalent to the one of the heights,
, the ratio of the backgrounds is equivalent to the one of the heights, 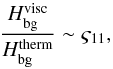 (105)and we express scaling laws of Hbg in Table 10 for the regimes identified in Fig. 9 (left panel).
(105)and we express scaling laws of Hbg in Table 10 for the regimes identified in Fig. 9 (left panel).
The asymptotic behaviours of the global sharpness ratio given in Table 11 are directly deduced from Tables 7 and 9. We notice that Ξvisc ~ Ξtherm for all regimes. Hence, Ξ ~ Ξvisc and Table 11 can be approximated by Table 7.
Asymptotic behaviours of the non-resonant background level Hbg of the total dissipation.
 |
Fig. 11 Number of resonances Nkc as a function of E (with K = 10-4) and K (with E = 10-4) for different values of A (in logarithmic scales). Left: Nkc − E. Right: Nkc − K. |
3.5. Number of resonant peaks
In spite of the theoretically large number of resonances allowed by the condition given in Eq. (48) (see also Fig. 5), the only effective resonant peaks are those that exceed the level of the non-resonant background Hbg (Figs. 3 and 4) given by Eq. (89) and (100) (see also the discussion in Rieutord & Valdettaro 2010). This tends to smooth out the variations of the quality factor Q and the resulting evolution of the orbital parameters of a star-planet/planet-satellite system. Indeed, the resonances of highest orders are absorbed in the mean dissipation level of the resonant frequency range. The harmonics thus have to match a criterion to appear in the dissipation spectrum. This criterion simply corresponds to the inequality 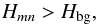 (106)where Hmn is given by Eqs. (71) and (74). The approximate wave number k introduced before allows us to compute the typical order of the smallest peaks kc. As noted before, Ξ ~ Ξvisc ~ Ξtherm, which implies that
(106)where Hmn is given by Eqs. (71) and (74). The approximate wave number k introduced before allows us to compute the typical order of the smallest peaks kc. As noted before, Ξ ~ Ξvisc ~ Ξtherm, which implies that 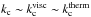 . We replace the index m and n of the height Hmn by k and use Eq. (106) to obtain
. We replace the index m and n of the height Hmn by k and use Eq. (106) to obtain ![\begin{eqnarray} k_{\rm c}^{\rm visc} \sim \left\{\! \frac{1}{2} \frac{ \left( 2 \cos^2 \theta + A \right) \left[ \left( A + \cos^2 \theta \right)^3 \varepsilon_{12}^2 + \xi \left( \theta, A,E, K \right) \right] }{ \varepsilon_{12}^2 \left[ AK + \left( 2 \cos^2 + A \right) E \right]^2 \left[ C_{\rm in} \cos^2 \theta + C_{\rm grav} A \right] } \right\}^{ \displaystyle \frac{1}{8} }\cdot \label{kc1} \end{eqnarray}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq512.png) (107)This expression can be simplified in asymptotic cases. Assuming Eq. (88), it becomes
(107)This expression can be simplified in asymptotic cases. Assuming Eq. (88), it becomes ![\begin{equation} k_{\rm c}^{\rm visc} \sim \left\{\! \frac{1}{2} \frac{ \left( 2 \cos^2 \theta + A \right) \left( A + \cos^2 \theta \right)^3 }{ \left[ AK + \left( 2 \cos^2 + A \right) E \right]^2 \left[ C_{\rm in}^{\infty} \cos^2 \theta + C_{\rm grav}^{\infty} A \right] } \right\}^{ \displaystyle \frac{1}{8} }\cdot \label{kc2} \end{equation}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq513.png) (108)In Table 12, we give the scaling laws of kc for the different asymptotic regimes. Taking resonances beyond this wave number into account does not change the global shape of the dissipation spectrum. In fact, in the situations corresponding to Figs. 3 and 4, there is no need to go beyond k ~ 10 (Fig. A.1, top-left and top-right panels). This is amply sufficient to model the dissipation realistically. The exponent 1 / 8 of kc in Eqs. (107) and (108) is related to the spectral decomposition of the perturbing force.
(108)In Table 12, we give the scaling laws of kc for the different asymptotic regimes. Taking resonances beyond this wave number into account does not change the global shape of the dissipation spectrum. In fact, in the situations corresponding to Figs. 3 and 4, there is no need to go beyond k ~ 10 (Fig. A.1, top-left and top-right panels). This is amply sufficient to model the dissipation realistically. The exponent 1 / 8 of kc in Eqs. (107) and (108) is related to the spectral decomposition of the perturbing force.
The wave number kc gives us the number of peaks Nkc (Eq. (61)), which is of great interest. As described above, we can assume 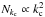 (Table 1 and Fig. 6). Thus, we immediately deduce the scaling laws of Nkc (Table 13) from those of the rank of the harmonics (Table 12) in the four asymptotic regimes (see Fig. 7). In the same way as kc,
(Table 1 and Fig. 6). Thus, we immediately deduce the scaling laws of Nkc (Table 13) from those of the rank of the harmonics (Table 12) in the four asymptotic regimes (see Fig. 7). In the same way as kc, 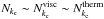 .
. 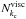 is given by the analytical expression
is given by the analytical expression ![\begin{equation} N_{k_{\rm c}}^{\rm visc} \sim \left\{\! \frac{1}{2} \frac{ \left( 2 \cos^2 \theta + A \right) \left[ \left( A + \cos^2 \theta \right)^3 \varepsilon_{12}^2 + \xi \left( \theta, A,E, K \right) \right] }{ \varepsilon_{12}^2 \left[ AK + \left( 2 \cos^2 + A \right) E \right]^2 \left[ C_{\rm in} \cos^2 \theta + C_{\rm grav} A \right] } \right\}^{ \displaystyle \frac{1}{4} }, \end{equation}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq519.png) (109)which is asymptotically equivalent to
(109)which is asymptotically equivalent to ![\begin{equation} N_{k_{\rm c}}^{\rm visc} \sim \left\{\! \frac{1}{2} \frac{ \left( 2 \cos^2 \theta + A \right) \left( A + \cos^2 \theta \right)^3 }{ \left[ AK + \left( 2 \cos^2 + A \right) E \right]^2 \left[ C_{\rm in}^{\infty} \cos^2 \theta + C_{\rm grav}^{\infty} A \right] } \right\}^{ \displaystyle \frac{1}{4} }\cdot \end{equation}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq520.png) (110)Therefore, Nkc ∝ E− 1 / 2 for inertial waves damped by viscous diffusion (see Fig. 11, left and right panels). In this regime, the number of peaks decays when the Ekman number increases as can be observed in Fig. 3. The critical degree kc, the number of resonances Nkc and the sharpness ratio Ξ are related to the others by the scaling equality
(110)Therefore, Nkc ∝ E− 1 / 2 for inertial waves damped by viscous diffusion (see Fig. 11, left and right panels). In this regime, the number of peaks decays when the Ekman number increases as can be observed in Fig. 3. The critical degree kc, the number of resonances Nkc and the sharpness ratio Ξ are related to the others by the scaling equality 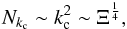 (111)in which, as pointed out above, the exponent 1 / 4 depends on the form of the coefficients of the perturbation. kc, Nkc, and Ξ all measure the smoothness of the dissipation spectrum. As the change rate of orbital parameters is proportional to the energy dissipated inside the bodies, the evolution of an orbital system is regular if they are small, and otherwise erratic.
(111)in which, as pointed out above, the exponent 1 / 4 depends on the form of the coefficients of the perturbation. kc, Nkc, and Ξ all measure the smoothness of the dissipation spectrum. As the change rate of orbital parameters is proportional to the energy dissipated inside the bodies, the evolution of an orbital system is regular if they are small, and otherwise erratic.
Asymptotic behaviours of the maximal order of noticeable resonances kc.
Asymptotic behaviours of the number of peaks 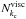 .
.
3.6. Super-adiabaticity (N2< 0)
The expression of ζdiss (Eq. (38)) allows us to compute dissipation frequency spectra if N2< 0, which corresponds to super-adiabaticity established by convection. Figure 12 shows how the spectrum of the energy dissipated by viscous friction evolves when the magnitude of an imaginary Brunt-Väisälä frequency increases. The graphs plotted correspond to pure inertial waves. We do not study the particular scaling laws describing their properties, which are obviously not the same as those found for classical configurations. Nevertheless, we can observe that strong values of |A| tend to flatten the spectrum. The height of the resonant peaks and the level of the background both decay. For example, the dissipation varies smoothly with the frequency when |A| = 102 contrary to the case of positive N2. This situation will be studied in detail in a forthcoming work.
 |
Fig. 12 Spectra of ζvisc in the case of pure inertial waves (E = 10-4 and K = 0) for A< 0. Top left: A = −0.1. Top right: A = −2. Bottom left: A = −10. Bottom right: A = −100. |
4. Discussion
Thanks to the analytical expression of the dissipated energy (Eq. (38)), we have been able to compute the hydrodynamical scaling laws that link the properties of the dissipation to the dynamics of the fluid. They are summarized in Table 14 and show that the related dependence of the dissipation onto the tidal frequency (ω) and the dimensionless characteristic numbers of the fluid (A, E and Pr) is tightly bound to the regime of tidal waves. In particular, they allow us to explain the tendencies observed in the spectra presented by Ogilvie & Lin (2004). For example, we found the number of resonances grows if the Ekman number decreases in the regime of inertial waves dissipated by viscous friction (see Fig. 3). Now, we derive laws for our local model, which demonstrate that it scales as Nkc ∝ E− 1 / 2. Likewise, the height of the peaks has been analytically proven to be inversely proportional to E, contrary to the level of the non-resonant background for which we obtain Hbg ∝ E. This explains why variations of the tidal frequency ω strongly impact the dissipation when E tends to zero. Now, to understand how the regime of the waves determines the properties of the spectra, we have focussed, for instance, on the sharpness ratio Ξ. Table 14 shows that this number always increases when the dominant dimensionless diffusivity, E or K, decreases. The difference between inertial waves and gravito-inertial waves resides in the linear dependence on the stratification parameter A. A comparison like this can be done for any other property. In the light of the scaling laws, we identify the parameters that will have a real impact on the viscous dissipation and, therefore, through the quality factor Q, on the long-term evolution of planetary systems.
Scaling laws for the properties of the energy dissipated in the different asymptotic regimes.
5. Conclusion and perspectives
Through a local approach, we have studied the physics of tidal gravito-inertial waves in stars and in fluid planetary regions. Their viscous and thermal dissipation is one of the main contributors to the secular dynamics of spins and orbits. More precisely, it determines the so-called tidal quality factor Q(χ) intervening in dynamics (Goldreich & Soter 1966; Auclair-Desrotour et al. 2014). This factor decreases when the dissipated tidal kinetic energy increases. Indeed, for an ideal elastic body, it takes very high values and the architecture of the orbital system is weakly affected by tides. In constrast, if the body is the seat of a strong dissipation, the energy dissipated becomes important, and the values of Q are smaller and systems evolve because of tides. This strong link between the secular evolution of a planetary system and tidal dissipation in their components therefore motivates studies to understand the dependence of tidal dissipation on their internal structure and dynamics.
In the case of celestial bodies constituted of fluids, previous works highlighted complex behaviour (e.g. Zahn 1975; Webb 1980; Ogilvie & Lin 2004, 2007). Indeed, liquid and gas layers do not dissipate energy like solid icy and rocky layers. The corresponding quality factor Q strongly varies as a function of forcing frequencies, fluid parameters (i.e. rotation, stratification, and diffusivities), the geometry of the fluid container and boundary conditions, and that factor can vary over several orders of magnitude. This has important consequences for the evolution of spins and orbits (e.g. Witte & Savonije 1999, Auclair-Desrotour et al. 2014). In this study, the dissipation caused by viscous friction and thermal diffusion has been estimated in a local Cartesian section of a rotating body to understand and quantify these dependences in the whole domain of parameters relevant in stars and planets; in this framework, the Cartesian fluid box complements global models (Ogilvie 2005; Jouve & Ogilvie 2014; Barker & Lithwick 2013, 2014). The equations of momentum, mass conservation, and heat transport are solved analytically with solutions expanded in periodic Fourier series. This approach yields the following conclusions:
-
Tidal dissipation resulting from viscous friction and thermal diffusion is highly resonant. Gravito-inertial waves are excited by tides at identified frequencies belonging to the interval
![\hbox{$ \left[ \chi_{\rm inf}, \chi_{\rm sup} \right] $}](/articles/aa/full_html/2015/09/aa26246-15/aa26246-15-eq575.png) , where χinf and χsup are in a first approximation the inertial (2Ω) and the Brunt-Väisälä (N) frequencies (for more precise boundaries, see Eq. 28 and Gerkema & Shrira 2005a). Thus, the fluid behaves like a bandpass filter. Inside the allowed frequency range, a batch of resonances can be excited by tides. Outside, the dissipation is weaker and varies smoothly with the forcing frequency that corresponds to the so-called equilibrium or non-wave-like tide (Remus et al. 2012a; Ogilvie 2013). In the resonant regime, a typical dissipation spectrum presents an organized structure of peaks, which have different sizes and properties. These depend, on the one hand, on the spectral form of the forcing, and in particular, on the amplitude of the harmonics, which explains the fractal pattern of the studied case. On the other hand, they are narrowly bound to the fluid parameters: rotation (Ω), stratification (N), thermal diffusivity (κ), and viscosity (ν).
, where χinf and χsup are in a first approximation the inertial (2Ω) and the Brunt-Väisälä (N) frequencies (for more precise boundaries, see Eq. 28 and Gerkema & Shrira 2005a). Thus, the fluid behaves like a bandpass filter. Inside the allowed frequency range, a batch of resonances can be excited by tides. Outside, the dissipation is weaker and varies smoothly with the forcing frequency that corresponds to the so-called equilibrium or non-wave-like tide (Remus et al. 2012a; Ogilvie 2013). In the resonant regime, a typical dissipation spectrum presents an organized structure of peaks, which have different sizes and properties. These depend, on the one hand, on the spectral form of the forcing, and in particular, on the amplitude of the harmonics, which explains the fractal pattern of the studied case. On the other hand, they are narrowly bound to the fluid parameters: rotation (Ω), stratification (N), thermal diffusivity (κ), and viscosity (ν). -
There are four asymptotic regimes for tidal waves, characterized by the frequency ratio A and the Prandtl number Pr, and the positions of the transition borders are expressed as functions of the fluid parameters. The case when A ≪ 1 corresponds to quasi-inertial waves. They are mainly driven by the Coriolis acceleration even when N2> 0. If A ≫ 1, then quasi-gravity waves are excited, the Archimedean force being predominant on the Coriolis term. Besides, depending on the value of the Prandtl number Pr, the dissipation is driven either by viscous friction (Pr ≫ Pr;11) or by thermal diffusion (Pr ≪ Pr;11).
-
For each of these asymptotic behaviours, all the properties of the dissipation spectrum can be expressed as functions of the fluid parameters: the positions, widths at mid-height, heights and number of resonances, the level of the non-resonant background, and the sharpness ratio. These scaling laws, derived analytically from the model, can be used as zero-order approaches to constrain the resulting rotational and orbital dynamics. In this context, they constitute a tool to explore the physics of dissipation and offer a first basis to validate the results obtained from direct numerical simulations and global models. For instance, they can be used to compute scaling laws for the turbulent convective dissipation of tidal inertial waves in the convective envelope of stars and giant planets as a function of their rotation (Mathis et al. 2014a).
In a near future, the method applied in this work will be extended to other dissipative systems, for example, with differential rotation (Baruteau & Rieutord 2013) or stratified convection (Leconte & Chabrier 2012). Moreover, we will include magnetic field and take into account the corresponding Ohmic dissipation in addition to viscous and thermal diffusions (e.g. Barker & Lithwick 2014). Tidal waves will become magneto-gravito-inertial waves (Mathis & de Brye 2011). This will introduce new fluid parameters (the Alfvén frequency and the Elsasser and magnetic Prandtl numbers), new asymptotic behaviours, and the corresponding scaling laws. Finally, non-linear interactions between tidal waves will be studied and characterized (e.g. Galtier 2003; Sen et al. 2012; Sen 2013; Barker & Lithwick 2013).
Online material
Appendix A: Harmonic highest degree kc
 |
Fig. A.1 Rank of the highest harmonic degree kc as a function of E (with K = 10-4) and K (with E = 10-4) for different values of A (in logarithmic scales). Left: kc − E. Right: kc − K. |
The expression of the highest harmonic degree, given in Eq. (108), is plotted as a function of the Ekman number and of the thermal diffusivity for various regimes from A ≪ 1 to A ≫ 1. It corresponds to the upper bound of harmonic degree, which is sufficient to represent all the resonances of the spectrum.
Appendix B: Relative differences ηl and ηH
The results provided by analytical expressions of Eqs. (65) and (71) have been compared to those given by the complete formula of the energy dissipated by viscous friction (Eq. (38)). The colour maps of Fig. B.1 correspond to the computation of the width at mid-height l11 and height 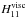 of the main resonance, which are summarized in Fig. 8. The relative differences ηl and ηH are calculated using the expressions
of the main resonance, which are summarized in Fig. 8. The relative differences ηl and ηH are calculated using the expressions 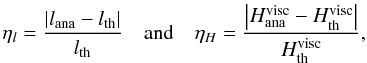 (B.1)lana and
(B.1)lana and 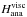 coming from Eqs. (65) and (71), and lth and
coming from Eqs. (65) and (71), and lth and 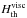 being computed with Eq. (38). The plots highlight the asymptotic domains, in dark blue, where the analytical formulae constitute a relevant approximation for the width and height of a resonance, and the critical transition zones where they cannot be applied. The light blue horizontal line corresponds to A ~ A11, the hyper-resonant case. The colour gradient in the regions near E ~ 10-2 and K ~ 10-2 indicates the values of A, E, and K for which the condition of the quasi-adiabatic approximation (Eq. (85)) is not satisfied. The same can be done with the energy dissipated by thermal diffusion.
being computed with Eq. (38). The plots highlight the asymptotic domains, in dark blue, where the analytical formulae constitute a relevant approximation for the width and height of a resonance, and the critical transition zones where they cannot be applied. The light blue horizontal line corresponds to A ~ A11, the hyper-resonant case. The colour gradient in the regions near E ~ 10-2 and K ~ 10-2 indicates the values of A, E, and K for which the condition of the quasi-adiabatic approximation (Eq. (85)) is not satisfied. The same can be done with the energy dissipated by thermal diffusion.
 |
Fig. B.1 ηl and ηH as a function of A, E, and K in logarithm scales. White contours highlight critical zones where the quasi-adiabatic assumption ( |
In this work, we do not take the non-linear interactions between tidal waves into account, while those with turbulent flows, such as convection, are treated as an effective viscosity (Goldreich & Keeley 1977; Zahn 1989; Ogilvie & Lesur 2012).
Most of the itme, tidal frequencies are small compared to the Lamb’s frequency. This allows us to filter out acoustic waves and to adopt the anelastic approximation in which ∇·(ρu) = 0. In the case where the background density ρ is uniform and constant, it reduces to the Boussinesq approximation in which ∇·u = 0.
Acknowledgments
The authors are grateful to the referee and the editor for their detailed review, which has allowed to improve the paper. This work was supported by the French Programme National de Planétologie (CNRS/INSU), the CNES-CoRoT grant at CEA-Saclay, the “Axe fédérateur Etoile” of Paris Observatory Scientific Council, and the International Space Institute (ISSI; team ENCELADE 2.0).
References
- Albrecht, S., Winn, J. N., Johnson, J. A., et al. 2012, ApJ, 757, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, M. E. 1973, Ap&SS, 23, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Auclair-Desrotour, P., Le Poncin-Lafitte, C., & Mathis, S. 2014, A&A, 561, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barker, A. J., & Lithwick, Y. 2013, MNRAS, 435, 3614 [NASA ADS] [CrossRef] [Google Scholar]
- Barker, A. J., & Lithwick, Y. 2014, MNRAS, 437, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Baruteau, C., & Rieutord, M. 2013, J. Fluid Mechanics, 719, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Berthomieu, G., Gonczi, G., Graff, P., Provost, J., & Rocca, A. 1978, A&A, 70, 597 [Google Scholar]
- Bolmont, E., Raymond, S. N., Leconte, J., & Matt, S. P. 2012, A&A, 544, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braviner, H. J., & Ogilvie, G. I. 2015, MNRAS, 447, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Cebron, D., Le Bars, M., Moutou, C., & Le Gal, P. 2012, A&A, 539, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cébron, D., Bars, M. L., Gal, P. L., et al. 2013, Icarus, 226, 1642 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., & Laskar, J. 2003, J. Geophys. Res. (Planets), 108, 5123 [Google Scholar]
- Correia, A. C. M., Levrard, B., & Laskar, J. 2008, A&A, 488, L63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Correia, A. C. M., Boué, G., Laskar, J., & Rodríguez, A. 2014, A&A, 571, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowling, T. G. 1941, MNRAS, 101, 367 [NASA ADS] [Google Scholar]
- Darwin, G. H. 1879, Roy. Soc. London Proc. Ser. I, 30, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Efroimsky, M. 2012, ApJ, 746, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Efroimsky, M., & Lainey, V. 2007, J. Geophys. Res. (Planets), 112, 12003 [Google Scholar]
- Egbert, G. D., & Ray, R. D. 2000, Nature, 405, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Egbert, G. D., & Ray, R. D. 2001, J. Geophys. Res., 106, 22475 [CrossRef] [Google Scholar]
- Emelyanov, N. V., & Nikonchuk, D. V. 2013, MNRAS, 436, 3668 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D. C., Ford, E. B., Steffen, J. H., et al. 2012, ApJ, 750, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraz-Mello, S. 2013, Celes. Mech. Dyn. Astron., 116, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Galtier, S. 2003, Phys. Rev. E, 68, 015301 [NASA ADS] [CrossRef] [Google Scholar]
- Gerkema, T., & Shrira, V. I. 2005a, J. Fluid Mech., 529, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Gerkema, T., & Shrira, V. I. 2005b, J. Geophys. Res. (Oceans), 110, 1003 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Keeley, D. A. 1977, ApJ, 212, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Soter, S. 1966, Icarus, 5, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Greenberg, R. 2009, ApJ, 698, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
- Jacobson, R. A. 2010, AJ, 139, 668 [Google Scholar]
- Jouve, L., & Ogilvie, G. I. 2014, J. Fluid Mech., 745, 223 [Google Scholar]
- Kaula, W. M. 1964, Rev. Geophys. Space Phys., 2, 661 [Google Scholar]
- Kelvin, L. 1863, Treatise on Natural Philosophy, Phil. Trans. Roy. Soc. London, 2, 837 [Google Scholar]
- Konopliv, A. S., & Yoder, C. F. 1996, Geophys. Res. Lett., 23, 1857 [NASA ADS] [CrossRef] [Google Scholar]
- Konopliv, A. S., Asmar, S. W., Folkner, W. M., et al. 2011, Icarus, 211, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Lainey, V., Dehant, V., & Pätzold, M. 2007, A&A, 465, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lainey, V., Arlot, J.-E., Karatekin, Ö., & van Hoolst, T. 2009, Nature, 459, 957 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lainey, V., Karatekin, Ö., Desmars, J., et al. 2012, ApJ, 752, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J., Boué, G., & Correia, A. C. M. 2012, A&A, 538, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leconte, J., & Chabrier, G. 2012, A&A, 540, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leconte, J., Chabrier, G., Baraffe, I., & Levrard, B. 2010, A&A, 516, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Love, A. E. H. 1911, Some Problems of Geodynamics (Cambridge University Press) [Google Scholar]
- MacDonald, G. J. F. 1964, Rev. Geophys. Space Phys., 2, 467 [Google Scholar]
- Mathis, S., & de Brye, N. 2011, A&A, 526, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & Remus, F. 2013, in Lect. Notes Phys. eds. J.-P. Rozelot, & C. . Neiner, (Berlin: Springer Verlag) 857, 111 [Google Scholar]
- Mathis, S., Auclair-Desrotour, P., Guenel, M., & Le Poncin-Lafitte, C. 2014a, in SF2A-2014: Proc. Ann. meet. French Soc. Astron. Astrophys., eds. J. Ballet, F. Martins, F. Bournaud, R. Monier, & C. Reylé, 251 [Google Scholar]
- Mathis, S., Neiner, C., & Tran Minh, N. 2014b, A&A, 565, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I. 2005, J. Fluid Mech., 543, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I. 2013, MNRAS, 429, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I. 2014, ARA&A, 52, 171 [Google Scholar]
- Ogilvie, G. I., & Lin, D. N. C. 2004, ApJ, 610, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I., & Lin, D. N. C. 2007, ApJ, 661, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I., & Lesur, G. 2012, MNRAS, 422, 1975 [NASA ADS] [CrossRef] [Google Scholar]
- Pedlosky, J. 1982, Geophysical fluid dynamics (New-York: Springer Verlag) [Google Scholar]
- Perryman, M. 2011, The Exoplanet Handbook (Cambridge University Press) [Google Scholar]
- Provost, J., Berthomieu, G., & Rocca, A. 1981, A&A, 94, 126 [NASA ADS] [Google Scholar]
- Ray, R. D., Eanes, R. J., & Lemoine, F. G. 2001, Geophys. J. Int., 144, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Remus, F., Mathis, S., & Zahn, J.-P. 2012a, A&A, 544, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remus, F., Mathis, S., Zahn, J.-P., & Lainey, V. 2012b, A&A, 541, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M., & Valdettaro, L. 2010, J. Fluid Mech., 643, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Sen, A. 2013, ArXiv e-prints [arXiv:1312.7497] [Google Scholar]
- Sen, A., Mininni, P. D., Rosenberg, D., & Pouquet, A. 2012, Phys. Rev. E, 86, 036319 [NASA ADS] [CrossRef] [Google Scholar]
- Singer, S. 1968, Geophys. J. Int., 15, 205 [Google Scholar]
- Tobie, G., Mocquet, A., & Sotin, C. 2005, Icarus, 177, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Valsecchi, F., & Rasio, F. A. 2014, ApJ, 786, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Webb, D. J. 1980, Geophys. J., 61, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Webb, D. J. 1982, Geophys. J., 70, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. G., Konopliv, A. S., Boggs, D. H., et al. 2014, J. Geophys. Res. (Planets), 119, 1546 [NASA ADS] [CrossRef] [Google Scholar]
- Witte, M. G., & Savonije, G. J. 1999, A&A, 350, 129 [NASA ADS] [Google Scholar]
- Witte, M. G., & Savonije, G. J. 2001, A&A, 366, 840 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Witte, M. G., & Savonije, G. J. 2002, A&A, 386, 222 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wu, Y. 2005, ApJ, 635, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J. P. 1966a, Annales d’Astrophysique, 29, 313 [Google Scholar]
- Zahn, J. P. 1966b, Annales d’Astrophysique, 29, 489 [Google Scholar]
- Zahn, J. P. 1966c, Annales d’Astrophysique, 29, 565 [Google Scholar]
- Zahn, J.-P. 1975, A&A, 41, 329 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 1989, A&A, 220, 112 [NASA ADS] [Google Scholar]
All Tables
Numerical comparison between the number of peaks Nkc and the number of modes 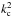 , kc being the rank of the highest harmonics, for the main resonances (1 ≤ k ≤ 10).
, kc being the rank of the highest harmonics, for the main resonances (1 ≤ k ≤ 10).
Scaling laws of the width at mid-height lmn of the
resonance associated with the doublet 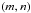 .
.
Asymptotic behaviours of the height 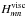 of the resonance of ζvisc associated with the doublet
of the resonance of ζvisc associated with the doublet 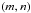 .
.
Asymptotic behaviours of the height 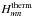 of the resonance of ζtherm associated with the doublet
of the resonance of ζtherm associated with the doublet 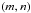 .
.
Asymptotic behaviours of the height Hmn of the resonance of ζ associated with the doublet 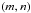 .
.
Asymptotic expressions of the sharpness ratio Ξvisc characterizing the spectrum of dissipation by viscous friction.
Asymptotic behaviours of the non-resonant background level 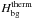 of the dissipation by heat diffusion.
of the dissipation by heat diffusion.
Asymptotic expressions of the sharpness ratio Ξtherm characterizing the spectrum of dissipation by heat diffusion.
Asymptotic behaviours of the non-resonant background level Hbg of the total dissipation.
Scaling laws for the properties of the energy dissipated in the different asymptotic regimes.
All Figures
 |
Fig. 1 The fluid box, its reference frame, and its position in the planet relative to the spin axis. |
| In the text | |
 |
Fig. 2 Gravito-inertial waves frequency range in convective and in stably stratified layers (Nc = 0 and NSLL> 0 are the corresponding buoyancy frequencies). The expressions of the boundaries χinf;SSL and χsup;SSL are explicitly given in Eq. (28). |
| In the text | |
 |
Fig. 3 Frequency spectra of the energy per mass unit locally dissipated by viscous friction ζvisc for inertial waves (A = 0) at the position θ = 0 for K = 0 and different Ekman numbers. In abscissa, the normalized frequency ω = χ/ 2Ω. Top left: E = 10-2. Top right: E = 10-3. Bottom left: E = 10-4. Bottom right: E = 10-5. The results obtained by Ogilvie & Lin (2004) are recovered. Note that the non-vanishing viscous dissipation at ω = 0 is the one of the geostrophic equilibrium. |
| In the text | |
 |
Fig. 4 Frequency spectrum of the energy per mass unit dissipated in different regimes (ζ) (continuous red line), and of its viscous and thermal contributions ζvisc (dashed green line) and ζtherm (dashed blue line). The latitude is fixed at θ = 0. In abscissa, the normalized frequency ω = χ/ 2Ω. Top left: A = 1.0 × 10-2; E = 1.0 × 10-2; K = 1.0 × 10-4. Top right: A = 1.0 × 102; E = 1.0 × 10-2; K = 1.0 × 10-4. Bottom left: A = 1.0 × 10-2; E = 1.0 × 10-4; K = 1.0 × 10-2. Bottom right: A = 1.0 × 102; E = 1.0 × 10-4; K = 1.0 × 10-2. |
| In the text | |
 |
Fig. 5 Structures of the frequency spectra of dissipation for inertial waves and gravito-inertial waves, with various sets of parameters. The positions of resonances (in abscissa, the normalized frequency ω = χ/ 2Ω) are indicated by blue points as functions of the characteristic rank k of the harmonics (ordinates). Top left: (θ,A,E,K) = (0,0,10-2,0). Top right: (θ,A,E,K) = (π/ 6,0,10-4,0). Bottom left: (θ,A,E,K) = (π/ 6,25,10-4,0). Bottom right: (θ,A,E,K) = (π/ 6,25,0,10-4). |
| In the text | |
 |
Fig. 6 Real number of resonances Nkc (continuous red line) and its first order approximation |
| In the text | |
 |
Fig. 7 Asymptotic domains. The areas on the left a) and c) correspond to inertial waves, those on the right b) and d) to gravito-inertial waves. Resonances are damped by viscosity in areas a) and b), and by thermal diffusivity in areas c) and d). The corresponding domains of parameters are a) A ≪ Amn and Pr ≫ Pr;mn; b) A ≫ Amn and Pr ≫ Pr;mn; c)A ≪ Amn and Pr ≪ Pr;mn; and d) A ≫ Amn and Pr ≪ Pr;mn. |
| In the text | |
 |
Fig. 8 Width at mid-height l11 and height
|
| In the text | |
 |
Fig. 9 Left: zones of predominances for dissipative mechanisms. In the pink area b), ζtherm ≫ ζvisc: the dissipation is mainly due to thermal diffusion. In the white area a), it is led by viscous friction. The transition zone corresponds to |
| In the text | |
 |
Fig. 10 Non-resonant background level |
| In the text | |
 |
Fig. 11 Number of resonances Nkc as a function of E (with K = 10-4) and K (with E = 10-4) for different values of A (in logarithmic scales). Left: Nkc − E. Right: Nkc − K. |
| In the text | |
 |
Fig. 12 Spectra of ζvisc in the case of pure inertial waves (E = 10-4 and K = 0) for A< 0. Top left: A = −0.1. Top right: A = −2. Bottom left: A = −10. Bottom right: A = −100. |
| In the text | |
 |
Fig. A.1 Rank of the highest harmonic degree kc as a function of E (with K = 10-4) and K (with E = 10-4) for different values of A (in logarithmic scales). Left: kc − E. Right: kc − K. |
| In the text | |
 |
Fig. B.1 ηl and ηH as a function of A, E, and K in logarithm scales. White contours highlight critical zones where the quasi-adiabatic assumption ( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.