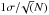| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201425379 | |
| Published online | 01 September 2015 | |
The evolving star formation rate: M⋆ relation and sSFR since z ≃ 5 from the VUDS spectroscopic survey⋆
1 Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388 Marseille, France
e-mail: lidia.tasca@lam.fr
2 Geneva Observatory, University of Geneva, Ch. des Maillettes 51, 1290 Versoix, Switzerland
3 Institut de Recherche en Astrophysique et Planétologie – IRAP, CNRS, Université de Toulouse, UPS-OMP, 14 avenue E. Belin, 31400 Toulouse, France
4 University of Bologna, Department of Physics and Astronomy (DIFA), V.le Berti Pichat, 6/2, 40127 Bologna, Italy
5 Instituto de Fisica y Astronomía, Facultad de Ciencias, Universidad de Valparaíso, 1111 Gran Bretaña, Playa Ancha Valparaíso, Chile
6 INAF–IASF Milano, via Bassini 15, 20133 Milano, Italy
7 INAF–Osservatorio Astronomico di Roma, via di Frascati 33, 00040 Monte Porzio Catone, Italy
8 University of Bologna, Department of Physics and Astronomy (DIFA), V.le Berti Pichat, 6/2, 40127 Bologna, Italy
9 Astronomy Department, University of Massachusetts, Amherst, MA 01003, USA
10 Department of Astronomy, University of Geneva, Ch. d’Écogia 16, 1290 Versoix, Switzerland
11 INAF–IASF Bologna, via Gobetti 101, 40129 Bologna, Italy
12 Department of Astronomy, California Institute of Technology, 1200 E. California Blvd., MC 249-17, Pasadena, CA 91125, USA
13 Institut d’Astrophysique de Paris, UMR 7095 CNRS, Université Pierre et Marie Curie, 98bis boulevard Arago, 75014 Paris, France
14 Institut de Recherche en Astrophysique et Planétologie – IRAP, CNRS, Université de Toulouse, UPS-OMP, 14 avenue E. Belin, 31400 Toulouse, France
15 SUPA, Institute for Astronomy, University of Edinburgh, Royal Observatory, Edinburgh, EH9 3HJ, UK
16 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
17 Centro de Estudios de Física del Cosmos de Aragón, 44001 Teruel, Spain
18 Max-Planck-Institut für Extraterrestrische Physik, Postfach 1312, 85741 Garching bei München, Germany
19 Department of Astronomy, California Institute of Technology, 1200 E. California Blvd., MC 249–17, Pasadena, CA 91125, USA
20 Research Center for Space and Cosmic Evolution, Ehime University, Bunkyo-cho 2-5, 790-8577 Matsuyama, Japan
Received: 20 November 2014
Accepted: 20 June 2015
We study the evolution of the star formation rate (SFR) – stellar mass (M⋆) relation and specific star formation rate (sSFR) of star-forming galaxies (SFGs) since a redshift z ≃ 5.5 using 2435 (4531) galaxies with highly reliable spectroscopic redshifts in the VIMOS Ultra-Deep Survey (VUDS). It is the first time that these relations can be followed over such a large redshift range from a single homogeneously selected sample of galaxies with spectroscopic redshifts. The log (SFR) − log (M⋆) relation for SFGs remains roughly linear all the way up to z = 5, but the SFR steadily increases at fixed mass with increasing redshift. We find that for stellar masses M⋆ ≥ 3.2 × 109M⊙ the SFR increases by a factor of ~13 between z = 0.4 and z = 2.3. Weextend this relation up to z = 5, finding an additional increase in SFR by a factor of 1.7 from z = 2.3 to z = 4.8 for masses M⋆ ≥ 1010M⊙. We observe a turn-off in the SFR–M⋆ relation at the highest mass end up to a redshift z ~ 3.5. We interpret this turn-off as the signature of a strong on-going quenching mechanism and rapid mass growth. The sSFR increases strongly up to z ~ 2, but it grows much less rapidly in 2 <z< 5. We find that the shape of the sSFR evolution is not well reproduced by cold gas accretion-driven models or the latest hydrodynamical models. Below z ~ 2 these models have a flatter evolution (1 + z)Φ with Φ = 2 − 2.25 compared to the data which evolves more rapidly with Φ = 2.8 ± 0.2. Above z ~ 2, the reverse is happening with the data evolving more slowly with Φ = 1.2 ± 0.1. The observed sSFR evolution over a large redshift range 0 <z< 5 and our finding of a non-linear main sequence at high mass both indicate that the evolution of SFR and M⋆ is not solely driven by gas accretion. The results presented in this paper emphasize the need to invoke a more complex mix of physical processes including major and minor merging to further understand the co-evolution of the SFR and stellar mass growth.
Key words: galaxies: evolution / galaxies: star formation / galaxies: formation / galaxies: high-redshift
© ESO, 2015
1. Introduction
Star formation is a process fundamental to galaxy evolution. Stars form from gas made available from accretion processes or that is recycled by exploding stars in their evolution cycles, different stellar populations with different histories are mixed in mergers, and they follow the dynamical evolution of galactic components forming bulges and discs ultimately leading to the spiral and elliptical galaxies observed today.
It is now well established that the star formation rate (SFR) history went through several phases (Madau & Dickinson 2014). The SFR apparently rose after the first galaxies formed (Bouwens et al. 2015), then reached a maximum plateau or peak at redshifts z ~ 1.5 − 2.5, followed by a sharp decline to the present (e.g. Bouwens et al. 2015; Cucciati et al. 2012). A main sequence in the SFR vs. stellar mass (M⋆) plane has been identified for star-forming galaxies, and it is strongly evolving with redshift (Elbaz et al. 2007; Whitaker et al. 2012; Fumagalli et al. 2014). By redshift 1 the main sequence is ~7 times higher in SFR (Elbaz et al. 2007) than the local relation (Brinchmann et al. 2004), and this becomes ~20 times higher by redshift 2 (Daddi et al. 2007). The scatter in this relation can possibly provide interesting constraints on the star formation history (SFH; Salmon et al. 2015). While a linear main sequence seems to represent the observations well at intermediate masses, claims for departure from a linear relation have been made for the massive end of the distribution (Karim et al. 2011; Whitaker et al. 2012, 2014; Schreiber et al. 2015), which may indicate faster mass growth than expected from gas accretion alone and/or star formation quenching.
The redshift evolution of the specific SFR sSFR = SFR/M⋆, M⋆ being the stellar mass, is a matter of considerable debate. While it is agreed that the mean (or median) sSFR ⟨sSFR⟩ at a given mass is steadily rising back to z ~ 2 (e.g. Whitaker et al. 2012; Fumagalli et al. 2014), the issue is far from being settled at z> 2. Over the past few years, several apparently conflicting measurements show no evolution with redshift of ⟨sSFR⟩ (Stark et al. 2009), a significant rise (Stark et al. 2013; de Barros et al. 2014; Salmon et al. 2015), or even a decrease (Bouwens et al. 2012). The ⟨sSFR⟩ was originally reported to evolve weakly over 4 <z< 6 by Stark et al. (2009), but the same authors then reported from improved spectral energy distribution (SED) fitting that the ⟨sSFR⟩ evolves more rapidly at z> 4 than previously thought (Stark et al. 2013). Their new results support up to a fivefold increase in ⟨sSFR⟩ between z ~ 2 and 7, and they claim that such a trend is much closer to expectations from cold gas accretion models (e.g. Dekel et al. 2009). The latest study from the CANDELS survey seems to agree with this picture (Salmon et al. 2015). Given the different selection functions of samples used in these calculations combined with the uncertainties in deriving M⋆ and SFR for faint galaxy samples, there needs to be a better understanding of the observations and the simulations.
On the observational side, efforts have been made to understand the limitations in computing M⋆ and SFR. The derivation of these physical parameters can be performed by a limited number of methods. At lower redshifts z< ~ 2 the SFR is often derived from the rest UV emission which needs to be corrected from dust extinction, or from the far IR luminosity assuming dust is heated by forming stars, as has been measured with the Herschel space observatory in recent years. Other important SFR indicators include spectral analysis for emission lines like [OII]3727, Hβ, or Hα. The Hα line is generally assumed to provide the most direct estimate of the SFR, now measured to z ~ 2, but at z> 1 this is done for relatively small samples of bright galaxies (e.g. Silverman et al. 2014). At higher redshifts z> 2 the sensitivity of Herschel has enabled the infrared luminosity (LIR) to be measured on samples of a few hundred galaxies (e.g. Lemaux et al. 2014; Rodighiero et al. 2014). Measuring M⋆ and SFR is most often performed by the same process along with photometric redshift determination because zphot, M⋆, and SFR may all rely on the same template fitting of the observed photometry distribution over a broad wavelength range. There are several difficulties linked to this process, including the impact on M⋆ and SFR of using different SFH, initial mass functions (IMF), or dust extinction laws. These physical parameters depend in particular on the assumed SF histories and age priors as will be discussed in a forthcoming paper (Cassará et al., in prep.). With this in mind, it is generally assumed that different methods and assumptions lead to typical uncertainties on M⋆ of ~ 0.2 − 0.3 dex (Madau & Dickinson 2014). One of the important limitations in measuring M⋆ and SFR from SED fitting was identified a number of years ago (see e.g. Ilbert et al. 2009): the photometric magnitudes in some observed bands may include flux from nebular emission lines in addition to stellar continuum, while reference templates may not include emission lines at all, requiring a specific correction when the SED fitting is performed. Emission lines can increase the observed flux in a particular band by up to 1 mag or so, particularly in the K-band and Spitzer-IRAC bands for z> 2, very important for deriving M⋆ from weighted older stellar populations, and specific protocols are implemented to address this problem (e.g. Ilbert et al. 2009; de Barros et al. 2014). Correcting for emission line contamination lowers M⋆, and hence increases the sSFR, therefore making significant differences in the measurement of the star formation main sequence at different redshifts. In de Barros et al. (2014), the effect of nebular lines, once corrected, leads to a steeper evolution of the ⟨sSFR⟩ at z> 3. Considering these limitations and using 25 different studies in the recent literature, Speagle et al. (2014) claim that there is “a remarkable consensus among MS observations” with a 0.1 dex 1σ inter-publication scatter. One should however remain cautious that the similar methods used in these studies might lead to similar results as they are affected by similar limitations and uncertainties.
The predicted evolution of ⟨sSFR⟩ from simulations has been addressed by a number of studies. Models with constant star formation from the continuous accretion of gas in cold flows along the cosmic web (Neistein & Dekel 2008; Dekel et al. 2009) show a continuously increasing M⋆ and the ⟨sSFR⟩ is expected to evolve with redshift following (1 + z)2.25 (Dekel et al. 2009; Dutton et al. 2010). Hydrodynamical simulations also predict a continuously increasing ⟨sSFR⟩ , but at levels systematically lower than the cold accretion models (Davé et al. 2011; Sparre et al. 2015). The constant ⟨sSFR⟩ as originally reported by Stark et al. (2009) at z> 2 would be puzzling in the context of these galaxy-formation models (Weinmann et al. 2011) because to reproduce such a trend would require non-trivial modifications to models, including a suppressed SFR at z> 4 in galaxies of all masses, a delayed build up of stellar mass from streamed gas, or enhanced growth of massive galaxies with a faster assembly or more efficient starbursts in mergers. Weinmann et al. (2011) conclude that a constant ⟨sSFR⟩ at high z would make it difficult to form enough massive galaxies at z ~ 1 − 3 in SAM, unless the rate of mass assembly due to mergers and the associated starbursts are pushed to the model limits. Finding a rising ⟨sSFR⟩ with redshift then seems much more acceptable from a model point of view.
The most recent data seem to indicate that the ⟨sSFR⟩ continues rising beyond redshift z ~ 2 (Stark et al. 2013; de Barros et al. 2014; Salmon et al. 2015). However, large uncertainties remain in the determination of this relation up to high redshifts (z ~ 6), resulting from both the determination of the physical parameters SFR and M⋆ and from the small fields observed leading to significant cosmic variance. Further exploration of these relations from new independent datasets is therefore in order.
In this paper we use 4531 galaxies with spectroscopic redshifts in the VIMOS Ultra Deep Survey (VUDS), the largest spectroscopic survey available at 2 <z< 6 (Le Fèvre et al. 2015), to investigate the evolution of the SFR–M⋆ relation and of the mean sSFR over this redshift range. The VUDS survey covers 1 square degree in three different fields, minimizing cosmic variance effects. We use the Le Phare code for SED fitting, including emission line treatment as described in Ilbert et al. (2009). We describe the VUDS spectroscopic data and associated photometric data used in the SED fitting in Sect. 2. The methodology to measure M⋆ and SFR from SED fitting is described in Sect. 3. We present the evolution of the SFR–M⋆ relation from redshift z = 0.5 to z = 5 in Sect. 4. The evolution of the ⟨sSFR⟩ is discussed in Sect. 5. We conclude in Sect. 6.
We use a cosmology with H0 = 100 h km s-1 Mpc-1, h = 0.7, Ω0,Λ = 0.7 and Ω0,m = 0.3. All magnitudes are given in the AB system, and we keep the AB notation apparent throughout the paper.
2. The VUDS spectroscopic sample
The VIMOS Ultra Deep Survey (VUDS) is a spectroscopic survey of ≈10 000 galaxies used to study galaxy evolution in the redshift range 2 <z< 6 +, as described in Le Fèvre et al. (2015). Galaxies in this redshift range are selected from a combination of photometric redshifts, with the first or second peaks in the zphot probability distribution function satisfying zphot + 1σ> 2.4, as well as from colour selection criteria like LBG, combined with a flux limit 22.5 ≤ iAB ≤ 25. A random purely flux selected sample with iAB = 25 is added to the spectroscopic multi-slit masks, geometry permitting. Spectra are obtained with the VIMOS spectrograph on the ESO-VLT (Le Fèvre et al. 2003), covering a wavelength range 3650 <λ< 9350 Å at a resolution R ≃ 230, with integration times of ~14 h. Redshifts are measured from these spectra in a well-controlled process delivering a reliability flag for each measurement (Le Fèvre et al. 2015). This is the largest spectroscopic sample at this depth and in this redshift range available today.
The redshift distribution of the VUDS sample extends from z ~ 2 to higher than z ~ 6 (median z = 3), and a lower redshift sample is also assembled from z ~ 0 to z ~ 2 (median z = 0.9) coming from the random flux-selected sample. For this study we use a total sample of 4531 galaxies with a reliable spectroscopic redshift measurement over the whole redshift range 0 <z< 6 (which represents about two-thirds of the final sample as data processing is in progress for the last third).
For this study we use the 2435 galaxies in VUDS with the highest spectroscopic redshift reliability, flags 3 and 4. This is the core sample used in the main analyses of the SFR–M⋆ and sSFR(z) relations presented below. We also use flags 2 and 9 objects, which are ~70 − 75% reliable (as measured from repeated observations), to augment the size of the sample in the highest redshift bin z> 4.5.
The VUDS survey is conducted in three fields, COSMOS, ECDFS, and VVDS-02h (also known as CFHTLS-D1). Each of these fields has extensive very deep multi-band photometry ranging at minima from broadband u to Spitzer-IRAC 4.5 μm band. The COSMOS field has the most extensive photometric set, with 30 bands including standard broadband as well as medium-band photometry (see Ilbert et al. 2013, and references therein). The ECDFS and CFHTLS-D1 have accumulated exceptional deep broadband photometric datasets, as described in Cardamone et al. (2010) and Le Fèvre et al. (2015), respectively.
 |
Fig. 1 SFR–M⋆ relation for VUDS star-forming galaxies. Points are colour-coded depending on the spectroscopic redshift of each galaxy as indicated in the inset. A clear evolution of the SFG main sequence is observed in the VUDS sample up to the highest redshifts z ≃ 5. This is confirmed to z ~ 2 when comparing VUDS data to the main sequence measured from the SDSS at z ~ 0.2 (Peng et al. 2010; full line), the MS at z ~ 1 by Elbaz et al. (2007; dashed line), and the MS of Daddi et al. (2007; dotted line) at z ~ 2. At z> 2 the VUDS data appear to lie significantly above the Daddi et al. (2007) main sequence. |
3. Spectral energy distribution fitting: M⋆ and SFR
We measure M⋆ and SFR for each galaxy from fitting the full SED produced from all available multi-wavelength data. The knowledge of accurate spectroscopic redshifts is an important advantage in the SED fitting process as it minimizes the occurrence of possible degeneracies when trying to measure both a photometric redshift and a set of physical parameters from the same SED fitting process. We therefore perform the SED fitting for each galaxy using the spectroscopic redshifts of our sample. Spectral energy distribution fitting is performed using the code Le Phare (Arnouts et al. 1999; Ilbert et al. 2006). The core engine for Le Phare is template fitting to the photometric dataset of each galaxy using a range of templates coming from Bruzual & Charlot (2003, hereafter BC03) models and is using a Chabrier (2003) IMF. We use exponentially declining star formation histories SFR ∝ e− t/τ (τ in the range 0.1 Gyr to 30 Gyr), and two delayed SFH models with peaks at 1 and 3 Gyr. The SEDs are generated for a grid of 51 ages (in the range 0.1 Gyr to 14.5 Gyr). A Calzetti et al. (2000) dust extinction law was applied to the templates with E(B − V) in the range 0 to 0.5. We used models with two different metallicities. The best fit is obtained by means of the best χ2 between the observed SED and the set of templates. A key feature of Le Phare is the realistic addition of emission lines to the templates, as extensively described in Ilbert et al. (2009). In short this is performed using the SFR of each template: the SFR is transformed into line equivalent widths using a standard set of transformations issued from case B line recombination and these lines are then added to the stellar population models. A constant ratio is set between emission lines (before correcting them for extinction), and the flux of the emission lines is allowed to vary within a factor of 2. In the redshift range considered here several emission lines can reach high enough equivalent widths to significantly modify near-IR broadband magnitudes, most notably Hβ–4861 Å, the [OIII]4959–5007 Å doublet, and the Hα–6562 Å line. When these lines are in emission they can change the magnitude in one of the redder bands of our photometric dataset, the K-band for z ≃ 3 up to the IRAC 3.6 and 4.5 μm bands for z ~ 4 to 6, altering the computation of, for example, stellar masses and SFR if the SED fitting is using only stellar continuum templates. In the redshift range 2 <z< 6 the K-band and IRAC 3.6 and 4.5 μm bands cover a wavelength from ~4000 Å to 1 μm, a most important domain for deriving the stellar mass, as M⋆ is roughly proportional to the observed flux at these rest wavelengths in the SED fitting process. Including emission lines may change the observed flux in the affected bands by more than one magnitude, which in turn may change a SED-derived stellar mass by 0.1−0.2 dex compared to standard SED fitting without emission lines included (see e.g. Salmon et al. 2015; de Barros et al. 2014). This was originally discussed in Ilbert et al. (2009), and further studied recently (Stark et al. 2013; de Barros et al. 2014; Salmon et al. 2015) when it was realized that emission lines may significantly bias SFR and sSFR measurements at redshifts z> 2 if not properly taken into account of in the SED fitting. The process of adding emission lines to templates is not likely to be fully controlled beyond the first principles, because the exact strength of each line is not known a priori for each galaxy, and it may therefore introduce some uncertainties leading to a larger dispersion in the distribution of measured parameters. One important point is the dispersion in the relation between line strength and SFR, and the evolution of this relation with redshift. While recent studies have provided some complex means of taking into account the main emission lines (e.g. de Barros et al. 2014), the simple approach used by Le Phare significantly limits the sensitivity of the derived stellar mass and SFR to the presence of emission lines in the most important rest-frame bands.
 |
Fig. 2 SFR–M⋆ relation for VUDS star-forming galaxies per redshift bins from z ~ 0.5 to z ~ 5. In each panel coloured data points represent individual galaxies, while contours show the density of galaxies. VUDS galaxies with redshifts ~100% reliable (flags 3 and 4, see Le Fèvre et al. 2014) are plotted with filled (coloured) heavy symbols, while galaxies with redshifts ~70−75% reliable (flag 2) are indicated with light grey open symbols. The black squares in each panel represent the median SFR in increasing mass bins obtained from the individual galaxies. The main sequence observed locally by the SDSS (Peng et al. 2010) and at z ~ 1 by Elbaz et al. (2007) is indicated in the 0 <z< 0.7 panel by the dotted and dashed lines, respectively. At higher redshifts the contiguous line indicates the MS of Schreiber et al. (2015), including the high-mass turn-off observed in their study, and the Elbaz et al. (2007)z = 1 relation is added as the dashed line in the 0.7 <z< 1.5 panel. Horizontal dot-dashed lines in each panel indicate the limit in SFR above which our data are statistically complete, as imposed by the iAB ≤ 25 limit of our sample. |
4. The evolution of the SFR–M⋆ relation
4.1. The star-forming main sequence up to z ~ 5
As a unique feature, the VUDS survey covers the whole redshift range from the local universe up to z = 5.5 using spectroscopically confirmed galaxies. The derivation of the SFR and M⋆ parameters is performed following the same methods and input data, making the relative comparison of the SFR–M⋆ relations at different redshifts less prone to systematics.
We plot the SFR–M⋆ relation for all VUDS galaxies in Fig. 1, colour-coded as a function of redshift. It is immediately visible that the distribution of VUDS galaxies over this large redshift range does not follow a single main-sequence relation. On average, our sample galaxies are more than 1 dex above the local main sequence (MS) of star-forming galaxies in the SDSS (Peng et al. 2010) at any redshift considered in this study. A significant fraction of our data also lie above the Daddi et al. (2007) MS at z ~ 2.
The evolution of the MS location with redshift is best seen when plotting the SFR vs. M⋆ in several redshift bins as presented in Fig. 2 with single galaxy points as well as median values in stellar mass bins. In the lowest redshift bin of our sample at z< 0.7 the galaxies with very small masses down to M⋆ ~ 107M⊙ lie quite high in SFR, on the MS of z ~ 1Elbaz et al. (2007), while intermediate mass galaxies 8.5 < log (M⋆) < 9.5 are in between the MS from SDSS (Brinchmann et al. 2004; Peng et al. 2010) and the z ~ 1 MS of Elbaz et al. (2007) as expected in this redshift bin. At z ~ 1 our data are slightly above in SFR (or less massive) than in the Elbaz et al. (2007) relation. The difference between our data and data in the literature is ~0.1 dex and could be the result of different systematics between our study and other studies in the literature. Going to higher redshifts where the bulk of VUDS galaxies are identified, we find that our galaxies are reaching strong SFRs SFR> 100 M⊙/yr, with the sample still containing high-mass galaxies up to a few 1011M⊙, thanks to the large volume covered. In the redshift bin z = [ 1.5,2.5 ] VUDS galaxies with log (M⋆) < 10.25 are above the z ~ 2 MS relation of Schreiber et al. (2015) likely due in part to the median redshift of our data z = 2.37 (resulting from the photometric redshift selection of the VUDS sample). For z = [ 2.5,3.5 ] lower mass galaxies are also above the Schreiber et al. (2015) relation, while at z> 3.5 the VUDS data are quite well centred on this relation up to z ~ 5.5. Over the redshift range z = [ 1.5,3.5 ] it can be clearly seen that a significant fraction the most massive galaxies in our sample with log(M⋆) > 10.25 are below the Schreiber et al. (2015) relation. This is further discussed in the next section.
Prior to discussing the SFR–M⋆ relation it is important to take into account that the VUDS selection function includes a 22.5 ≤ iAB ≤ 25 magnitude selection which implies a low SFR limit, in effect a Malmquist bias evolving with redshift (see e.g. Reddy et al. 2012). The high magnitude cutoff iAB = 22.5 limits the detection of massive and star-forming galaxies at z< ~ 1, but it is not expected to exclude any massive galaxies at higher redshifts as was verified from the VVDS survey (Le Fèvre et al. 2013). We use the semi-analytic model of Wang et al. (2008) applied to the COSMOS field to better identify the statistical completeness of our data with this selection limit (here we use the term statistical completeness as the ability to identify galaxies with a certain property in the VUDS fields). Applying the VUDS magnitude selection to the simulation we find that the magnitude limit restricts the sample to galaxies with higher SFR as redshift increases, as indicated in Fig. 2. The VUDS is essentially statistically complete in the SFR–M⋆ plane up to M⋆ ~ 5 × 109M⊙ and − 2 < log (SFR) < 1.8 for z< 0.7. It is statistically complete for log (SFR) > − 0.4,0.5,0.6,0.8, and 1 at z ~ 1, 2, 3, 4, and 5, respectively. We further note that if trying to fit a linear main sequence log (SFR) = log (M⋆)α, the slope α would then be artificially flattened at lower masses by the magnitude selection, and we do not attempt in this paper to quantify the MS slope at stellar masses for which this effect is at work.
To further analyse the behaviour of the SFR as a function of mass at different epochs, we compute median SFRs in increasing mass bins, imposing the SFR limits quoted above, as plotted in Fig. 2. From the median values we see departure from a linear main sequence relation at both the lowest and the highest masses. These observed trends are the consequence of two effects: the bias against low SFR and low M⋆ galaxies due to the VUDS selection function as described above, and a turn-off of the SFR–M⋆ relation at high masses, as is further discussed in Sect. 4.2 below.
4.2. A turn-off in the SFR–M⋆ relation: evolution with redshift
As the VUDS survey is conducted in a 1 sq. deg area, it is picking up more of the rarer galaxies at the high-mass end of the M⋆ distribution. This is a key advantage compared to most other surveys probing smaller areas, and allows the behaviour of the SFR–M⋆ relation to be studied reliably at the highest masses.
We observe a significant departure from a linear main sequence at high masses and at all redshifts z< 3.5 probed by this study, which seems to indicate a physical dependency of the SFR on M⋆. In the redshift bin 0.7 <z< 1.5, our data indicate a turn-off at a mass M⋆ ~ 1010M⊙. Going to higher redshifts, we observe a significant turn-off of the SFR–M⋆ relation in both of the 1.5 <z< 2.5 and 2.5 <z< 3.5 redshift bins, occurring at M⋆ ~ 1.5 and ~2.5 × 1010M⊙, respectively. In 1.5 <z< 2.5 our median SFR measurements stay almost constant from log(M⋆) = 10.2 to 11.2 at log(SFR) = 1.6 ± 0.1, and so present a deficit in SFR of ~ 1 dex compared to the SFR expected by extrapolating the SFR at log(M⋆) = 10.2 if SFR ∝ M⋆. Similarly in 2.5 <z< 3.5, extrapolating from log(M⋆) = 10.2 would lead to log(SFR) = 2.5 while we measure log(SFR) = 1.9 ± 0.1. In the redshift bin 3.5 <z< 4.5 a turn-off may be happening at around M⋆ ~ 3 × 1010M⊙, but it is not significant at less than 1.5σ. At z ~ 5 we do not observe a turn-off and the SFR–M⋆ relation seems to be linear over the mass range probed except at the low-mass end as is expected due to the sample selection function described in Sect. 4.1.
The VUDS data selection ensures that most of the strongest SFGs at high masses are included in the sample, unless there is a substantial population of high-mass, high SFR, heavily obscured galaxies at z> 1.5. If any bias is present at high masses in VUDS, it would be against a population of low star-forming galaxies with SFR< 3 M⊙/yr at z> ~ 2.5. Such a population has been identified at z ~ 2 − 3 as claimed by Whitaker et al. (2013), and remains elusive at z> 3. A large low SFR population at these redshifts might indicate galaxies that have already quenched, pushing the onset of star formation to even higher redshifts, and it remains possible that a low SFR and high M⋆ population could exist in small numbers at these redshifts. However, such a population would only lower the average SFR at high M⋆ in the SFR–M⋆ relation and therefore further amplify the turn-off in the main sequence reported here, and our results remain qualitatively robust to any putative low SFR – high M⋆ population. What we observe is a small population of galaxies with intermediate SFR, which might represent galaxies on their way to the passive population observed at lower redshifts. While these objects are star-forming with SFR> 3 M⊙/yr at z> ~ 2.5 and cannot be excluded from the analysis of a star-forming population, they are definitely off the MS extrapolation to high mass and are driving median SFR values down. This population deserves a closer look (Tasca et al., in prep.). Another population, which is likely missed by VUDS, are galaxies that are heavily star-forming but strongly obscured by dust. As shown by Rodighiero et al. (2014) and Whitaker et al. (2012) comparing UV-selected and IR-selected samples, we expect to have missed less than 7% of high-mass high-SFR galaxies lying mostly above the MS. This fraction of possibly missed galaxies is not high enough to produce the trend we observe in our data.
Departure from a linear MS has been reported in the literature. From a radio stacking analysis, Karim et al. (2011) found tentative evidence for curvature of the star formation sequence. Up to z ~ 2.5 our data are in agreement with the results by Whitaker et al. (2012) who find that the SFR–M⋆ relation follows a power-law 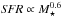 rather than a linear relation. Whitaker et al. (2014) bring further evidence for a mass-dependent behaviour of the SFR–M⋆ relation with a steep slope for low-mass galaxies, and a shallower slope at high mass from the 3D-HST survey using photometry from CANDELS. Furthermore, our results identify for the first time a similar behaviour at z> 2.5. We find that for massive galaxies with M⋆> 1010M⊙, the rise in median SFR with mass is slower than for galaxies at lower masses, and this property seems to hold to z ~ 3.5. To understand the behaviour at the massive end, Whitaker et al. (2012, 2014) compare UV-selected and infrared luminosity selected samples and conclude that the linear MS relation observed from UV rest-frame data is the result of the selection function truncating galaxies with high stellar mass and high SFR but with a lot of dust extinction, and that without the UV selection the relation would show downward curvature. The VUDS selection function is, in effect, UV-selected because of the iAB ≤ 25 cutoff, although we do not see a continuous linear SFR–M⋆ relation; instead, we observe a high-mass turn-off. We therefore infer that the observed turn-off is not only related to dust-obscured galaxies, but also to a general lack of strongly star-forming galaxies at high masses, at least in the redshift range 1 <z< 3.5.
rather than a linear relation. Whitaker et al. (2014) bring further evidence for a mass-dependent behaviour of the SFR–M⋆ relation with a steep slope for low-mass galaxies, and a shallower slope at high mass from the 3D-HST survey using photometry from CANDELS. Furthermore, our results identify for the first time a similar behaviour at z> 2.5. We find that for massive galaxies with M⋆> 1010M⊙, the rise in median SFR with mass is slower than for galaxies at lower masses, and this property seems to hold to z ~ 3.5. To understand the behaviour at the massive end, Whitaker et al. (2012, 2014) compare UV-selected and infrared luminosity selected samples and conclude that the linear MS relation observed from UV rest-frame data is the result of the selection function truncating galaxies with high stellar mass and high SFR but with a lot of dust extinction, and that without the UV selection the relation would show downward curvature. The VUDS selection function is, in effect, UV-selected because of the iAB ≤ 25 cutoff, although we do not see a continuous linear SFR–M⋆ relation; instead, we observe a high-mass turn-off. We therefore infer that the observed turn-off is not only related to dust-obscured galaxies, but also to a general lack of strongly star-forming galaxies at high masses, at least in the redshift range 1 <z< 3.5.
 |
Fig. 3 Distribution of sSFR vs. M⋆ for VUDS galaxies in several redshift bins with medians ranging from z ~ 0.4 to z ~ 5. VUDS galaxies with redshifts ~ 100% reliable (flags 3 and 4, see Le Fèvre et al. 2014) are plotted with filled (coloured) heavy symbols, while galaxies with redshifts ~ 70 − 75% reliable (flag 2) are indicated with light grey open symbols. The stellar mass limit above which the median sSFR is computed is indicated by the vertical dashed lines in this panel, chosen to be M⋆ ≥ 5 × 109M⊙ for z ≤ 1.5 and M⋆ ≥ 1010M⊙ for z> 1.5. The limit in the data as imposed by the VUDS selection function is indicated by the dot-dash line in each panel, as validated imposing a similar selection function on the Wang et al. (2008) SAM. The median sSFRs above the mass limits are indicated by the large coloured squares. The error bars represent the |
 |
Fig. 4 Evolution of the sSFR with redshift for VUDS star-forming galaxies, obtained by computing the median sSFR value for M⋆ ≥ 5 × 109M⊙ when z ≤ 1.5 and M⋆ ≥ 1010M⊙ for z> 1.5. Error bars on each VUDS data point indicate the 1σ error on the median of the observed sSFR distribution and are generally smaller than the size of the data points. For the points at z = 3.9 and z = 4.8 flags 2, 3, 4, and 9 have been included to increase the sample size, and we also indicate the median values for flags 3 and 4 only, represented by the coloured squares that lie at only slightly lower values (almost undistinguishable for z = 3.9). At z< 2.4 we find that the sSFR evolution follows (1 + z)2.8, while the evolution is slower at 2.4 <z< 5 following (1 + z)1.2 (dotted line). The ± 1σ of the sSFR distribution is represented by the light grey short dash – long dash lines below and above the median values. Several other datasets from the literature are plotted as discussed in the text (Reddy et al. 2012; Bouwens et al. 2012; SFGs from Fumagalli et al. 2013; Stark et al. 2013; Gonzalez et al. 2014); some of these points have been slightly shifted to avoid overlap with the VUDS data points, see the exact values in these papers. Several models predicting the evolution of the sSFR are indicated, including galaxy growth dominated by cold gas accretion (Dekel et al. 2009, dashed line, normalized to sSFR(z = 0) = 0.1), the hydrodynamical simulation of Davé et al. (2011, dot-dashed line), and the latest results from the Illustris hydrodynamical simulation (Sparre et al. 2014, long-dashed line). |
Median redshifts and specific SFRs from the VUDS sample in 0 <z< 5.
A departure from a linear MS relation from lack of strongly star-forming galaxies can be interpreted as the result of star-formation quenching. Quenching could be produced either because the gas supply is reduced (e.g. if the rate of gas accretion is reduced) or because stars cannot form as efficiently (e.g. because of feedback or environment effects). Galaxy mergers would have the effect of bringing galaxies out of the MS even if the SFR increased during the merger event (Peng et al. 2010). Interestingly, we find that the turn-off mass where departure from a linear main sequence seems to occur decreases with decreasing redshift, going from M⋆ ~ 2.5 × 1010M⊙ at z ~ 3 to M⋆ ~ 1010M⊙ at z ~ 1 and M⋆ ~ 8 × 108M⊙ at z ~ 0.4. This downsizing trend echoes downsizing in other properties (Cowie et al. 1996) and is expected in models relating quenching to the fast evolution of the SFR density (e.g. Peng et al. 2010).
At the highest redshifts of our sample z> 4.5, we find that the SFR follows a linear 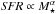 , without an apparent turn-off at high mass. Although our sample may not be large enough to identify a turn-off, this result is comparable to Steinhardt et al. (2014). Assuming that the fraction of high-mass, high SFR, dust-obscured galaxies is not higher at these redshifts than for z< 4.5, a possible interpretation is that at these high redshifts the SFR quenching mechanisms are not yet fully in place. As the SFRD is in a strongly increasing phase (Bouwens et al. 2015), the number of SNe capable of driving strong winds may not yet be sufficient for feedback to be strong enough to lower star formation. Similarly, the number and mass of central massive black holes may not bring AGN feedback to sufficient levels to quench star formation. From our data we therefore argue that star formation quenching mechanisms may become most efficient starting at z< ~ 4. The downsizing in the mass turn-off may also indicate that this quenching progresses steadily to lower masses as redshift decreases.
, without an apparent turn-off at high mass. Although our sample may not be large enough to identify a turn-off, this result is comparable to Steinhardt et al. (2014). Assuming that the fraction of high-mass, high SFR, dust-obscured galaxies is not higher at these redshifts than for z< 4.5, a possible interpretation is that at these high redshifts the SFR quenching mechanisms are not yet fully in place. As the SFRD is in a strongly increasing phase (Bouwens et al. 2015), the number of SNe capable of driving strong winds may not yet be sufficient for feedback to be strong enough to lower star formation. Similarly, the number and mass of central massive black holes may not bring AGN feedback to sufficient levels to quench star formation. From our data we therefore argue that star formation quenching mechanisms may become most efficient starting at z< ~ 4. The downsizing in the mass turn-off may also indicate that this quenching progresses steadily to lower masses as redshift decreases.
5. The evolution of the specific star formation rate since z ≃ 5
In this section we explore the evolution with redshift of the median value of the sSFR.
The distribution of sSFR as a function of stellar mass is shown in Fig. 3 for different redshift bins. The VUDS selection function implies some restrictions in probing the sSFR-M⋆ plane, and we plot the empirical limits on the sSFR–M⋆ resulting from the VUDS selection in Fig. 3. Below z = 1.5 the VUDS sample is statistically complete in sSFR and mass above M⋆ = 5 × 109M⊙. Above z = 1.5 we use a low-mass cutoff of M⋆ = 1010M⊙ to compute the median sSFR. Above these mass limits, we find a wide range in sSFR of more than 2 dex: in z = [ 1.5,3.5 ] we observe sSFR as low as ~0.3, and going up to ~30. At z> 3.5 the lowest sSFR are ~1, and go beyond ~30. The median value in sSFR and M⋆ is indicated in each panel, and discussed below. The sSFR decreases with M⋆ as expected from the lower SFR for high M⋆ (see Sect. 4, and Whitaker et al. 2012, 2014). It is important to note that because of the large 1 deg2 field and corresponding large volume surveyed by VUDS compared to the smaller ~170 arcmin2 of CANDELS (Salmon et al. 2015), ~55 arcmin2 of González et al. (2014) in ERS and HUDF, or ~300 arcmin2 of Stark et al. (2013) in GOODS, our sample includes a larger number of galaxies with high masses M⋆> 1010M⊙. Samples in smaller fields than explored in VUDS are likely missing the highest mass galaxies and therefore may not sample enough galaxies to identify the high-mass behaviour of the sSFR.
The evolution of the median sSFR with redshift is presented in Fig. 4, and median sSFR measurements are listed in Table 1. We compute the error on the median value as 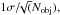 where σ is the standard deviation in the sSFR distribution and Nobj is the number of galaxies in the redshift bin considered. We compute the median sSFR above a stellar mass lower limit of M⋆ = 5 × 109M⊙ for 0 <z< 1.5 and M⋆ ≥ 1010M⊙ for z> 1.5. At z< 1.5 our data are fully consistent with the results presented in Fumagalli et al. (2014) from the 3D-HST survey, and somewhat higher than Ilbert et al. (2015) likely due to the difference in the mass range sampled. At redshifts z ~ 2 − 3 our data is in excellent agreement with the data presented in Reddy et al. (2012) using BM, BX, and LBG galaxies (Steidel et al. 2003). At redshifts z ~ 3 − 5 our median sSFR measurements compare well with González et al. (2014), but are a factor ~1.4 lower than Stark et al. (2013) or Bouwens et al. (2012).
where σ is the standard deviation in the sSFR distribution and Nobj is the number of galaxies in the redshift bin considered. We compute the median sSFR above a stellar mass lower limit of M⋆ = 5 × 109M⊙ for 0 <z< 1.5 and M⋆ ≥ 1010M⊙ for z> 1.5. At z< 1.5 our data are fully consistent with the results presented in Fumagalli et al. (2014) from the 3D-HST survey, and somewhat higher than Ilbert et al. (2015) likely due to the difference in the mass range sampled. At redshifts z ~ 2 − 3 our data is in excellent agreement with the data presented in Reddy et al. (2012) using BM, BX, and LBG galaxies (Steidel et al. 2003). At redshifts z ~ 3 − 5 our median sSFR measurements compare well with González et al. (2014), but are a factor ~1.4 lower than Stark et al. (2013) or Bouwens et al. (2012).
From our data we observe a strong evolution of the median sSFR from z ~ 0.4 to z ~ 2.3: the observed sSFR evolution in the VUDS dataset is very steep, decreasing by a factor ~ 13 from z = 2.3 to z = 0.4. At z ~ 2.3 we find a median sSFR sSFR(z = 2.3) = 2.3 ± 0.16 Gyr-1. Parametrizing the sSFR evolution as log (sSFRz) = A + Φ × log (1 + z) we find A = − 10.1 ± 0.03 and Φ = 2.8 ± 0.2 for z< 2.3, somewhat less steep than discussed by Fumagalli et al. (2014) who report a slope of Φ ~ 3. At z> 2.3 the sSFR continues to rise and reaches sSFR(z = 4.8) = 3.9 ± 0.5 Gyr-1. We find that in our data the evolution between z ~ 5 and z ~ 2 is slower than for z< 2, and is best parametrized with A = − 9.3 ± 0.02 and Φ = 1.2 ± 0.1. This trend does not change if we impose a lower cut in sSFR (e.g. log (sSFR) > − 9.2 and − 9 in z = [ 2.5,3.5 ] and z = [ 3.5,4.5 ], respectively). This is discussed further in Sect. 6.
6. Discussion and summary
We use a spectroscopic sample of 2435 star-forming galaxies with highly reliable spectroscopic redshifts (flags 3 and 4) from the VUDS survey to study the evolution with redshift of the SFR–M⋆ relation and of the sSFR, up to a redshift z ~ 5. We use an additional sample of 2096 galaxies with reliable spectroscopic redshifts (flags 2 and 9) to consolidate statistical analysis when necessary. Spectral energy distribution fitting using the code Le Phare is performed on the extensive photometric data at the spectroscopic redshift of each galaxy and taking into account the contributions from nebular emission lines. The knowledge of the spectroscopic redshift enables us to limit degeneracies in computing the SFR and M⋆. Our data cover a range of M⋆ from 109 to 1011M⊙ at z ~ 2, as enabled by the large 1 square degree field surveyed, while at our highest redshifts 4.5 <z< 5.5 we observe galaxies with M⋆> 109.4M⊙. We then discuss the observed SFR–M⋆ relations as well as the evolution of the sSFR with redshift. The VUDS data used in this study cover a wide redshift range 0 <z< ~ 5 with a large number of galaxies at z> 2, which allows for the first time a consistent study of evolution from a single survey with the same selection function, avoiding the difficulties in comparing inhomogeneous samples.
The SFR–M⋆ relation strongly evolves with redshift. We clearly identify a main sequence along which galaxies lie, and the position of the main sequence evolves with redshift. We observe that a main sequence holds above z ~ 2 and up to the highest redshifts z ~ 5 in our sample, as observed in other datasets (e.g. Stark et al. 2013; Salmon et al. 2015). We find that for redshifts z< 3.5 the SFR–M⋆ relation at high masses is not a linear extrapolation of the relation at the lower masses in agreement with Whitaker et al. (2012, 2014). Furthermore, we find that the mass at which the main sequence becomes non-linear decreases with decreasing redshift from M⋆ ~ 2.5 × 1010M⊙ at z ~ 3 down to M⋆ ~ 1010M⊙ at z ~ 1 and M⋆ ~ 8 × 108M⊙ at z ~ 0.4. Interpreting the turn-off at high masses as the effect of star formation quenching, this downsizing pattern may indicate that this quenching is gradually progressing from high masses at high redshifts to low masses at low redshifts. At z> 3.5 the main sequence seems to become more linear. This may indicate that quenching processes are not yet fully active at these redshifts, and that possible quenching processes like SNe or AGN feedback would only bring-up sufficient energy release to significantly quench star-formation at redshifts below z ~ 3.5.
We compute the sSFR from z ~ 0.1 all the way up to z ~ 5. We find that the dependence on redshift of the median sSFR is different at low redshifts (z< 2.3) or at high redshifts 2.5 <z< 5. At the lower redshifts, we observe a strong rise in sSFR by a factor of ~13 from z = 0.4 to z = 2.3 reaching a sSFR(z = 2.3) = 2.3 Gyr-1 following an evolution ∝(1 + z)Φ with Φ = 2.8 ± 0.2 similar to that reported in the literature (e.g. SFGs in Fumagalli et al. 2014). From z = 2.3 to z = 4.8 the sSFR continues to increase but at a slower rate. At redshifts 2 <z< 3 our data are in excellent agreement with Reddy et al. (2012). At the highest redshift end of our dataset 3 <z< 5 our data are broadly consistent with data in the literature (Bouwens et al. 2012; Stark et al. 2013; González et al. 2014) when considering systematics in computing the sSFR. At redshift z ~ 4 we find that the VUDS median sSFR is the same as González et al. (2014), ~1.7 times lower than Bouwens et al. (2012), and ~2 times lower than Stark et al. (2013). Our highest redshift measurement at z ~ 5 is about 20% higher than González et al. (2014) and ~ 30% lower than Bouwens et al. (2012) or Stark et al. (2013). From z = 2 to z = 5 we find sSFR ∝ (1 + z)Φ with Φ = 1.2 ± 0.1 for galaxies selected above a mass limit M⋆ = 1010M⊙. The observed evolution at z> 2.3 in our data is somewhat flatter than the evolution ∝(1 + z)3.4 as reported in (Salmon et al. 2015) but for galaxies selected at a smaller mass M⋆ = 109M⊙ ~ 0.5 dex lower than ours.
The flattening of the sSFR evolution beyond redshift z ~ 2 in our data is compared to models in Fig. 4. Models based on cold accretion-driven galaxy growth are expected to follow sSFR ∝ (1 + z)Φ with Φ = 2.25 (Dekel et al. 2009). The sSFR at a given mass in these models is lower than our data and other data in the literature for z< ~ 2. The VUDS data and other observational results are located at significantly higher sSFR than hydrodynamical simulations incorporating parametrised galactic outflows (Davé et al. 2011), as well as above the latest Illustris hydrodynamical moving-mesh simulation (Sparre et al. 2015), as shown in Fig. 4. At higher redshifts these hydrodynamical simulations intersect the observed data at z ~ 4 but with a steeper slope than in observational data. The comparison of observed data with current models therefore seems to indicate that the sSFR evolution does not follow a pure accretion driven galaxy mass growth.
Several important physical processes are known to be at play that could well alter the simplified cold-accretion growth picture. We presented observational evidence in Sect. 4.2 supporting a picture where star formation quenching starts to be efficient below z ~ 3.5, in effect reducing the increase in SFR expected from cold accretion alone. Mergers are ubiquitous at all redshifts, reaching a major merger fraction of ~20% at z ~ 1.5 (López-Sanjuan et al. 2013) and staying high to beyond z ~ 3 (Tasca et al. 2014) driving the mass growth in a different way than cold gas accretion does. The effect of merging on the SFR vs. M⋆ relation can be viewed as a straight shift in M⋆ at fixed SFR, with equal mass (major) mergers doubling M⋆. Repeated minor merger events would also participate in this trend of increasing M⋆ with only a modest increase in SFR if the merging galaxies are of lower SFR than the primary galaxy, leading to a further flattening of the sSFR evolution with redshift. Mergers produce a mass increase from stars formed beyond the immediate environment of the galaxy adding to the stars formed in the galaxy breaking the SFR ∝ M⋆ relation. It is then likely that these processes combine with cold gas accretion to modulate the SFR and mass growth to produce the observed sSFR evolution.
Despite remarkable improvements in the observational data, the main limitations to the study of the sSFR remain the uncertainties and systematics errors associated with the computation of SFR and M⋆. Progress in measuring SFR on individual galaxies beyond z ~ 2.5 will require a significant improvement in observing capabilities such as what is expected from the JWST, able to follow direct SFR tracers like the Hα line to z ~ 6.6 and beyond. Improvements on M⋆ estimates will be even harder to obtain because of current unknowns on the IMF evolution with redshift or more complex SFH than in current models. It is nevertheless clear, and perhaps not surprising, that the sSFR evolution now becoming clear from the VUDS observational results presented in this paper and others in the literature requires models with a more balanced mix of physical processes than the models dominated by cold gas accretion that have been developed so far. This new generation of observations and models will in turn help to better understand the SFH and galaxy stellar mass assembly.
Acknowledgments
We thank the ESO staff for their continuous support for the VUDS survey, particularly the Paranal staff conducting the observations and Marina Rejkuba and the ESO user support group in Garching. This work is supported by funding from the European Research Council Advanced Grant ERC-2010-AdG-268107-EARLY and by INAF Grants PRIN 2010, PRIN 2012 and PICS 2013. A.C., O.C., M.T. and V.S. acknowledge the grant MIUR PRIN 2010–2011. This work is based on data products made available at the CESAM data center, Laboratoire d’Astrophysique de Marseille. This work partly uses observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS.
References
- Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2012, ApJ, 754, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2015, ApJ, 803, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cardamone, C. N., van Dokkum, P. G., Urry, C. M., et al. 2010, ApJS, 189, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., Songaila, A., Hu, E. M., & Cohen, J. G. 1996, AJ, 112, 839 [Google Scholar]
- Cucciati, O., Tresse, L., Ilbert, O., et al. 2012, A&A, 539, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., Oppenheimer, B. D., & Finlator, K. 2011, MNRAS, 415, 11 [NASA ADS] [CrossRef] [Google Scholar]
- de Barros, S., Schaerer, D., & Stark, D. P. 2014, A&A, 563, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dekel, A., Birnboim, Y., Engel, G., et al. 2009, Nature, 457, 451 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dutton, A. A., van den Bosch, F. C., & Dekel, A. 2010, MNRAS, 405, 1690 [NASA ADS] [Google Scholar]
- Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fumagalli, M., Labbé, I., Patel, S. G., et al. 2014, ApJ, 796, 35 [NASA ADS] [CrossRef] [Google Scholar]
- González, V., Bouwens, R., Illingworth, G., et al. 2014, ApJ, 781, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Arnouts, S., Le Floc’h, E., et al. 2015, A&A, 579, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karim, A., Schinnerer, E., Martínez-Sansigre, A., et al. 2011, ApJ, 730, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Saisse, M., & Mancini, D. 2003, in SPIE Conf. Ser. 4841, eds. M. Iye, & A. F. M. Moorwood, 1670 [Google Scholar]
- Le Fèvre, O., Cassata, P., Cucciati, O., et al. 2013, A&A, 559, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Fèvre, O., Tasca, L. A. M., Cassata, P., et al. 2015, A&A, 576, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemaux, B. C., Le Floc’h, E., Le Fèvre, O., et al. 2014, A&A, 572, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Neistein, E., & Dekel, A. 2008, MNRAS, 383, 615 [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Pettini, M., Steidel, C. C., et al. 2012, ApJ, 754, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Rodighiero, G., Renzini, A., Daddi, E., et al. 2014, MNRAS, 443, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Salmon, B., Papovich, C., Finkelstein, S. L., et al. 2015, ApJ, 799, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silverman, J. D., Kashino, D., Arimoto, N., et al. 2014, ApJS, submitted [arXiv:1409.0447] [Google Scholar]
- Sparre, M., Hayward, C. C., Springel, V., et al. 2015, MNRAS, 447, 3548 [Google Scholar]
- Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S., Bunker, A., et al. 2009, ApJ, 697, 1493 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Schenker, M. A., Ellis, R., et al. 2013, ApJ, 763, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Adelberger, K. L., Shapley, A. E., et al. 2003, ApJ, 592, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Steinhardt, C. L., Speagle, J. S., Capak, P., et al. 2014, ApJ, 791, L25 [Google Scholar]
- Tasca, L. A. M., Le Fèvre, O., López-Sanjuan, C., et al. 2014, A&A, 565, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, J., De Lucia, G., Kitzbichler, M. G., & White, S. D. M. 2008, MNRAS, 384, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Weinmann, S. M., Neistein, E., & Dekel, A. 2011, MNRAS, 417, 2737 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., van Dokkum, P. G., Brammer, G., & Franx, M. 2012, ApJ, 754, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., van Dokkum, P. G., Brammer, G., et al. 2013, ApJ, 770, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Franx, M., Leja, J., et al. 2014, ApJ, 795, 104 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 SFR–M⋆ relation for VUDS star-forming galaxies. Points are colour-coded depending on the spectroscopic redshift of each galaxy as indicated in the inset. A clear evolution of the SFG main sequence is observed in the VUDS sample up to the highest redshifts z ≃ 5. This is confirmed to z ~ 2 when comparing VUDS data to the main sequence measured from the SDSS at z ~ 0.2 (Peng et al. 2010; full line), the MS at z ~ 1 by Elbaz et al. (2007; dashed line), and the MS of Daddi et al. (2007; dotted line) at z ~ 2. At z> 2 the VUDS data appear to lie significantly above the Daddi et al. (2007) main sequence. |
| In the text | |
 |
Fig. 2 SFR–M⋆ relation for VUDS star-forming galaxies per redshift bins from z ~ 0.5 to z ~ 5. In each panel coloured data points represent individual galaxies, while contours show the density of galaxies. VUDS galaxies with redshifts ~100% reliable (flags 3 and 4, see Le Fèvre et al. 2014) are plotted with filled (coloured) heavy symbols, while galaxies with redshifts ~70−75% reliable (flag 2) are indicated with light grey open symbols. The black squares in each panel represent the median SFR in increasing mass bins obtained from the individual galaxies. The main sequence observed locally by the SDSS (Peng et al. 2010) and at z ~ 1 by Elbaz et al. (2007) is indicated in the 0 <z< 0.7 panel by the dotted and dashed lines, respectively. At higher redshifts the contiguous line indicates the MS of Schreiber et al. (2015), including the high-mass turn-off observed in their study, and the Elbaz et al. (2007)z = 1 relation is added as the dashed line in the 0.7 <z< 1.5 panel. Horizontal dot-dashed lines in each panel indicate the limit in SFR above which our data are statistically complete, as imposed by the iAB ≤ 25 limit of our sample. |
| In the text | |
 |
Fig. 3 Distribution of sSFR vs. M⋆ for VUDS galaxies in several redshift bins with medians ranging from z ~ 0.4 to z ~ 5. VUDS galaxies with redshifts ~ 100% reliable (flags 3 and 4, see Le Fèvre et al. 2014) are plotted with filled (coloured) heavy symbols, while galaxies with redshifts ~ 70 − 75% reliable (flag 2) are indicated with light grey open symbols. The stellar mass limit above which the median sSFR is computed is indicated by the vertical dashed lines in this panel, chosen to be M⋆ ≥ 5 × 109M⊙ for z ≤ 1.5 and M⋆ ≥ 1010M⊙ for z> 1.5. The limit in the data as imposed by the VUDS selection function is indicated by the dot-dash line in each panel, as validated imposing a similar selection function on the Wang et al. (2008) SAM. The median sSFRs above the mass limits are indicated by the large coloured squares. The error bars represent the |
| In the text | |
 |
Fig. 4 Evolution of the sSFR with redshift for VUDS star-forming galaxies, obtained by computing the median sSFR value for M⋆ ≥ 5 × 109M⊙ when z ≤ 1.5 and M⋆ ≥ 1010M⊙ for z> 1.5. Error bars on each VUDS data point indicate the 1σ error on the median of the observed sSFR distribution and are generally smaller than the size of the data points. For the points at z = 3.9 and z = 4.8 flags 2, 3, 4, and 9 have been included to increase the sample size, and we also indicate the median values for flags 3 and 4 only, represented by the coloured squares that lie at only slightly lower values (almost undistinguishable for z = 3.9). At z< 2.4 we find that the sSFR evolution follows (1 + z)2.8, while the evolution is slower at 2.4 <z< 5 following (1 + z)1.2 (dotted line). The ± 1σ of the sSFR distribution is represented by the light grey short dash – long dash lines below and above the median values. Several other datasets from the literature are plotted as discussed in the text (Reddy et al. 2012; Bouwens et al. 2012; SFGs from Fumagalli et al. 2013; Stark et al. 2013; Gonzalez et al. 2014); some of these points have been slightly shifted to avoid overlap with the VUDS data points, see the exact values in these papers. Several models predicting the evolution of the sSFR are indicated, including galaxy growth dominated by cold gas accretion (Dekel et al. 2009, dashed line, normalized to sSFR(z = 0) = 0.1), the hydrodynamical simulation of Davé et al. (2011, dot-dashed line), and the latest results from the Illustris hydrodynamical simulation (Sparre et al. 2014, long-dashed line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.