| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 5 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201526294 | |
| Published online | 31 July 2015 | |
Toward a consistent use of overshooting parametrizations in 1D stellar evolution codes
1
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Str. 1,
85748
Garching,
Germany
e-mail:
mviallet@mpa-garching.mpg.de
2
Steward Observatory, 933 N. Cherry Ave., Tucson, AZ
85721,
USA
3
New Mexico Consortium, Los Alamos, NM
87544,
USA
4
Theoretical Division, Los Alamos National
Laboratory, Los Alamos,
NM
87545,
USA
Received: 10 April 2015
Accepted: 8 June 2015
Several parametrizations for overshooting in 1D stellar evolution calculations coexist in the literature. These parametrizations are used somewhat arbitrarily in stellar evolution codes, based on what works best for a given problem or even for the historical reasons related to the development of each code. We point out that these different parametrizations correspond to different physical regimes of overshooting, depending on whether the effects of radiation are dominant, marginal, or negligible. Our analysis is based on previously published theoretical results, as well as on multidimensional hydrodynamical simulations of stellar convection where the interaction between the convective region and a stably stratified region is observed. Although the underlying hydrodynamical processes are the same, the outcome of the overshooting process is profoundly affected by radiative effects. Using a simple picture of the scales involved in the overshooting process, we show how three regimes are obtained, depending on the importance of radiative effects. These three regimes correspond to the different behaviors observed in hydrodynamical simulations so far and to the three types of parametrizations used in 1D codes. We suggest that the existing parametrizations for overshooting should coexist in 1D stellar evolution codes and should be applied consistently at convective boundaries depending on the local physical conditions.
Key words: stars: evolution / stars: interiors / hydrodynamics / convection / turbulence
© ESO, 2015
1. Introduction
For more than 50 years, convection has been described in 1D stellar evolution codes by the mixing-length theory (MLT, Böhm-Vitense 1958). It is well known that one of the shortcomings of MLT is its inability, by construction, to describe the boundary layer between the convective region and a neighboring stably stratified region. In the MLT picture, the flow simply stops at the boundary. This contradicts basic physics, because inertia allows the flow to penetrate the stably stratified region, inducing mixing beyond the boundary of the convective region (see, e.g., Arnett et al. 2015).
Such an extra mixing at convective boundaries is routinely added in stellar evolution calculations, since it is required to reproduce well-established observational features across the Hertzsprung-Russel diagram (e.g., Maeder 1975; Matraka et al. 1982; Schroder et al. 1997; Herwig 2005; Pace et al. 2012; Montalbán et al. 2013). Currently, this extra mixing is parametrized in very crude ways in stellar evolution codes, and it relies on free parameters that need to be calibrated. This situation is very similar to the one of convection itself, with MLT relying on the mixing length parameter. In fact, overshooting is one aspect of convection, and a better description of overshooting should eventually rely on a better description of turbulent convection. A lot of effort has been devoted to the development of a non-local theory of convection, which, in principle, should allow for a consistent description of overshooting (Gough 1977; Stellingwerf 1982; Xiong 1986; Kuhfuss 1986; Canuto & Mazzitelli 1991; Canuto 1992; Gehmeyr & Winkler 1992; Wuchterl & Feuchtinger 1998; Deng et al. 2006). Usually, this is done by looking for a working closure in the framework of Reynolds-Averaged Navier-Stokes (RANS) equations (see e.g. Canuto 1997; Xiong et al. 1997; Canuto & Dubovikov 1998; Deng et al. 2006; Canuto 2011, and references therein).
Although RANS is the appropriate mathematical framework for improving the description of hydrodynamical processes in stellar evolution, one should abandon the idea of finding the “ultimate” parametrization that would describe overshooting correctly in any physical situations. Although the word “overshooting” is widely used to describe extra mixing at convective boundaries (and we adopt this terminology as well), it is misleading because the mixing cannot be seen simply as resulting from a unique, basic, physical process. Mixing at convective boundaries likely results from the interplay of several physical processes (shear instabilities, g-modes, etc.), the usual picture of plume penetration being only one aspect of the problem. A better description of convective boundary mixing requires first of all a better understanding of the nature and efficiency of the mixing processes that are taking place in the boundary layer and how they are affected by the local physical conditions. This work takes a first step in this direction by looking specifically at the effect of thermal diffusion.
In Sect. 2, we describe the three types of parametrization for overshooting that are used in stellar evolution calculations. Currently, these parametrizations are used somewhat arbitrarily. In Sect. 3, we develop a physical picture for the effects of radiation on the overshooting process that leads us to define three distinctive regimes of overshooting. Hydrodynamical simulations support our picture and are discussed. Furthermore, we show that the different parametrizations that are used currently correspond to these different thermal regimes of overshooting. We conclude in Sect. 4 that the description of overshooting in stellar evolution codes could be already improved by using existing parametrizations in a more physically consistent way. In case such a better practice leads to theoretical predictions contradicting observations for some specific cases, this would point to shortcomings in the current descriptions and provide valuable information for improving them.
2. Existing parametrizations of overshooting
2.1. Chemical mixing
In this approach, it is assumed that overshooting does not affect the thermal structure. In terms of the logarithmic temperature gradients, one has ∇ = ∇rad in the overshooting layer. Regarding the mixing of chemical elements, two approaches are possible. In the simplest approach, the composition is assumed to be mixed instantaneously over a distance lov beyond the limit of the convective region, with lov typically parametrized in terms of the pressure scale height. This is the approach taken in BaSTI (Pietrinferni et al. 2004), TGEC (Théado et al. 2012), and DSEP (Dotter et al. 2008). Another possibility is to treat this mixing as a diffusive process with a prescribed diffusion coefficient Dov. Originally, this approach was suggested by Freytag et al. (1996) based on radiative hydrodynamical simulations of near-surface convection. Following Freytag et al. (1996), Dov is usually parametrized as 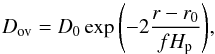 (1)with r0 the location of the convective boundary, which is typically given by the Schwarzschild or Ledoux criteria, D0, which is a reference diffusivity (typically the mixing-length diffusivity DMLT evaluated close to the boundary1), and f a free parameter. This “diffusive mixing” approach is the one taken in MESA (Paxton et al. 2011) and GARSTEC (Weiss & Schlattl 2008).
(1)with r0 the location of the convective boundary, which is typically given by the Schwarzschild or Ledoux criteria, D0, which is a reference diffusivity (typically the mixing-length diffusivity DMLT evaluated close to the boundary1), and f a free parameter. This “diffusive mixing” approach is the one taken in MESA (Paxton et al. 2011) and GARSTEC (Weiss & Schlattl 2008).
2.2. Penetrative convection
Zahn (1991) showed that when the convective boundary is located deep inside the star, the overshooting material is able to change the entropy stratification and induce a nearly adiabatic (yet subadiabatic) region (see also Schmitt et al. 1984). Zahn (1991) coined this “penetrative convection”. In stellar evolution codes, this is implemented by artificially increasing the size of the adiabatic region on a distance lov, which is typically parametrized in terms of the pressure scale height2. The major difference from chemical mixing is that the thermal structure of the star is modified: ∇ = ∇ad in the overshooting region. In addition, the chemical composition is assumed to be mixed instantaneously in this region. This treatment of overshooting is the one implemented in GENEC (Eggenberger et al. 2008).
2.3. Turbulent entrainment
Turbulent entrainment is a process that is well-known in geophysics, because it is observed both in the atmosphere and in the oceans. Entrainment is the physical process by which turbulent eddies entrain mass at the convective boundary, inducing a steady growth in the size of the convective region as long as energy is supplied to the system. Turbulent entrainment is observed in the simulations of the oxygen-burning shell presented in Meakin & Arnett (2007), showing that the relevance of this process for stellar evolution has been overlooked. To our knowledge, only Staritsin (2013, 2014) has published stellar evolution models that include turbulent entrainment at convective boundaries. His approach follows “bulk” entrainment models in which the boundary layer is collapsed to a discontinuity separating the well-mixed region from the stably stratified region (see, e.g., Fernando 1991). The velocity Ve at which this boundary moves as a result of entrainment can be parametrized as 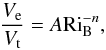 (2)where Vt is the typical turbulent velocity at the boundary, A and n are parameters that characterize the entrainment (see below), and RiB is the so-called bulk Richardson number, which characterizes the “stiffness” of the boundary. It is defined as
(2)where Vt is the typical turbulent velocity at the boundary, A and n are parameters that characterize the entrainment (see below), and RiB is the so-called bulk Richardson number, which characterizes the “stiffness” of the boundary. It is defined as 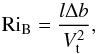 (3)where l is the typical size of the turbulent eddies doing the entrainment, and
(3)where l is the typical size of the turbulent eddies doing the entrainment, and 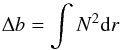 (4)is the buoyancy jump across the interface (N is the Brunt-Väisälä frequency). The spatial integration is performed on a region that contains the convective boundary. Once Ve is determined, the size by which the convective region is extended because of entrainment during one time step is given by d = VeΔt.
(4)is the buoyancy jump across the interface (N is the Brunt-Väisälä frequency). The spatial integration is performed on a region that contains the convective boundary. Once Ve is determined, the size by which the convective region is extended because of entrainment during one time step is given by d = VeΔt.
The entrainment law (2) is well-established in fluid dynamics (see, e.g., Fernando 1991). The values of A and n were measured in different experimental setups and geophysical environments. Meakin & Arnett (2007) found that their simulations correspond to n ~ 1.05 and A ~ 0.027, which are the values used in Staritsin (2013, 2014).
3. Impact of radiation on overshooting
3.1. Measure of radiative effects in stellar hydrodynamics
A characteristic of stellar hydrodynamics is that, at the typical temperature and density of stellar plasma, photons are very efficient in transporting heat. A measure of the effect of radiation on the flow is given by the Péclet number Pe, defined as 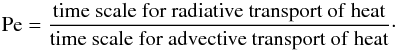 (5)When Pe ≫ 1, radiation has a negligible impact and the flow can be considered as evolving adiabatically. When Pe ≪ 1, radiation dominates. In the optically thick interior, heat transport by radiation can be described as a diffusion process, and the corresponding thermal diffusivity χ (units: cm2/s) is given by
(5)When Pe ≫ 1, radiation has a negligible impact and the flow can be considered as evolving adiabatically. When Pe ≪ 1, radiation dominates. In the optically thick interior, heat transport by radiation can be described as a diffusion process, and the corresponding thermal diffusivity χ (units: cm2/s) is given by 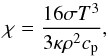 (6)where T is the temperature, ρ the density, κ the Rossland opacity, cp the heat capacity at constant pressure (see, e.g., Kippenhahn et al. 2012). In this case, the Péclet number can be defined as
(6)where T is the temperature, ρ the density, κ the Rossland opacity, cp the heat capacity at constant pressure (see, e.g., Kippenhahn et al. 2012). In this case, the Péclet number can be defined as 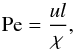 (7)where u (resp. l) is a typical velocity (resp. length) scale of the flow. The Prandtl number, defined as the ratio of viscosity to thermal diffusion Pr = ν/χ, takes very low values in stellar plasma, typically Pr = 10-9 − 10-6. The situation is very different in geophysical flows, where Prandtl numbers are of order unity. In fact, many insights from geophysical studies can be generalized to the stellar case by introducing the effects of thermal diffusion.
(7)where u (resp. l) is a typical velocity (resp. length) scale of the flow. The Prandtl number, defined as the ratio of viscosity to thermal diffusion Pr = ν/χ, takes very low values in stellar plasma, typically Pr = 10-9 − 10-6. The situation is very different in geophysical flows, where Prandtl numbers are of order unity. In fact, many insights from geophysical studies can be generalized to the stellar case by introducing the effects of thermal diffusion.
 |
Fig. 1 Sketch of the different scales of eddies present in the flow. η and Λ are the Kolmogorov and integral scales, respectively. The scales contributing to overshooting are those between lmin and lmax. Depending on the location of the transition scale ld where Pe ~ 1, one can define three different regimes of overshooting (see text). |
3.2. Scales involved in the overshooting process
Stellar convection is characterized by very high values of the Reynolds number, implying that the flow is highly turbulent: motion extends over a wide range of scales (see, e.g., Arnett et al. 2014). An important characteristic of turbulent convection is that transport properties in the bulk of the convective region are dominated by large-scale, coherent structures usually described as “convective plumes” (e.g., Stein & Nordlund 1989; Cattaneo et al. 1991; Porter & Woodward 2000; Murphy & Meakin 2011; Viallet et al. 2013).
As convective plumes approach the boundary of the convective region, they are deflected sideways. At the same time, inertia allows a plume to penetrate the stably stratified region, where it undergoes “buoyancy braking”, which is the process in which kinetic energy is converted into potential energy due to the work done against gravity in the stably stratified region. Although buoyancy braking reduces the kinetic energy of the overshooting material, the flow comes to a rest mostly due to the turbulent dissipation that arises as it breaks apart and forms a turbulent cascade through pressure-strain effects resulting from the interaction with the stable region. We coin this process “buoyancy breaking”.
If we adopt the picture of a turbulent flow extending from the integral scale Λ down to the Kolmogorov dissipation scale η, it is sound to assume that overshooting is effectively achieved by a certain subrange of scales comprised between lmin and lmax (see Fig. 1). Here, lmax is the typical length scale of plumes, while lmin is the length scale of the smallest eddies that are able to contribute significantly to mixing at the boundary. We can expect that these scales are distributed spatially: the smallest scales are found deeper in the overshooting region. This physical picture of the scales involved in overshooting is the basis for the interpretation of radiative effects outlined in the next section.
3.3. Regimes of overshooting depending on the importance of radiative effects
A turbulent flow is characterized by a wide range of eddies with velocity scale u and length scale l. Although the proper definition of a “turbulent Péclet number” is not trivial, we can consider Eq. (7) as a qualitative definition of a scale-dependent Péclet number. A critical scale is the scale ld that corresponds to Pe ~ 1. Below this scale, eddies are strongly affected by thermal diffusion, above this scale, eddies evolve adiabatically. The assumption that the transition occurs exactly at Pe = 1 is a simplification, but it is sufficient for the picture presented in this work. Given the range of scales [ lmin,lmax ] that contribute to overshooting, we define three different regimes of overshooting depending on the location of the transition Pe ~ 1, as summarized in Fig. 1 and detailed below.
3.3.1. Case 1: lmax<ld – Diffusion-dominated regime
In this case, all the scales participating in the overshooting process have Pe ≲ 1 and are strongly affected by thermal diffusion. Turbulent eddies are only able to mix composition, without affecting the entropy structure significantly (see Zahn 1991). This is the spirit of the “chemical mixing” parametrization presented in Sect. 2.1. This parametrization was first proposed in Freytag et al. (1996). Freytag (1995) presents radial profiles of the Péclet number for the A-type star and white dwarf models published in Freytag et al. (1996; see their Figs. 11 and 12). They show that Pe ≲ 10 across the convective and overshooting region, which is consistent with our picture.
3.3.2. Case 2: l l
l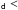 lmax – Penetrative regime
lmax – Penetrative regime
In this case, there is a transition within the boundary layer: scales that have Pe ≳ 1 mix entropy and composition, whereas scales that have Pe ≲ 1 are only able to mix composition. This structures the boundary layer in two parts: a nearly adiabatic, well-mixed sublayer, and a “diffusion-dominated” sublayer where only the composition is mixed (see Zahn 1991). This picture is supported by the structure of the boundary layer at the bottom of the convective envelope of the red giant model described in Viallet et al. (2013). Studying the mean-field budget equation for internal energy, the authors find that the boundary layer is in a thermal balance in which the heat advected by entropy-rich material into the layer is counterbalanced by the cooling by radiative diffusion. This results locally in a “super-stellar” radiative flux (Lrad>L⋆).
 |
Fig. 2 Radial profiles of the length scales LO, Lχ, and the Péclet number in the boundary layer of the red giant model of Viallet et al. (2013). The thick dashed lines denote the extent of the boundary layer, defined as the region of buoyancy braking. The x-axis is normalized by the radius of the star R = 4.1 × 1012 cm. |
We now show that the boundary layer is indeed characterized by a transition in the turbulent Péclet number, consistent with the picture outlined above. We first introduce the so-called Ozmidov scale: 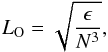 (8)where ϵ is the turbulent dissipation rate of kinetic energy, N the Brunt-Väisälä frequency, and LO is the length scale of the smallest eddies that are affected by buoyancy (e.g., Ozmidov 1965; Smyth & Moum 2000). We then introduce the length scale resulting from equating the thermal diffusion time scale to the buoyancy time scale:
(8)where ϵ is the turbulent dissipation rate of kinetic energy, N the Brunt-Väisälä frequency, and LO is the length scale of the smallest eddies that are affected by buoyancy (e.g., Ozmidov 1965; Smyth & Moum 2000). We then introduce the length scale resulting from equating the thermal diffusion time scale to the buoyancy time scale: 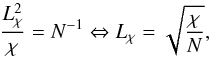 (9)where Lχ can be interpreted as the scale below which thermal diffusion “erases” the effect of buoyancy. Inspired by the literature on turbulent mixing (Ozmidov 1965; Osborn 1980; Brethouwer & Lindborg 2009), we take ϵ/N2 as a proxy for the turbulent transport of heat. One therefore has
(9)where Lχ can be interpreted as the scale below which thermal diffusion “erases” the effect of buoyancy. Inspired by the literature on turbulent mixing (Ozmidov 1965; Osborn 1980; Brethouwer & Lindborg 2009), we take ϵ/N2 as a proxy for the turbulent transport of heat. One therefore has 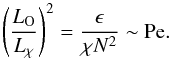 (10)Figure 2 shows the profiles of LO, Lχ, and Pe in the boundary layer of the red giant model of Viallet et al. (2013). There is indeed a transition in the Péclet number in the boundary layer from ~ 103 to ~ 10-1, where the length scales LO and Lχ cross each other.
(10)Figure 2 shows the profiles of LO, Lχ, and Pe in the boundary layer of the red giant model of Viallet et al. (2013). There is indeed a transition in the Péclet number in the boundary layer from ~ 103 to ~ 10-1, where the length scales LO and Lχ cross each other.
The existence of such a transition is key because it allows a balance to be reached: overshooting extends the size of the adiabatic region until radiative effects inhibit the process3. We are currently not able to predict the depth at which this boundary layer develops, since it would require a model for the turbulent dissipation of plumes. Theoretical predictions for the extent of the penetration region exist (e.g., Schmitt et al. 1984; Zahn 1991; Hurlburt et al. 1994; Rempel 2004), but they are based on the rather laminar picture of plumes decelerating due to buoyancy braking alone. For the moment, one can rely on the parametrization for “penetrative convection” described in Sect. 2.2. This parametrization does not include the diffusion-dominated layer in which composition is mixed. Zahn (1991) argues that this layer is very thin (see, however, Rempel 2004). In the red-giant model of Viallet et al. (2013), it occupies roughly one third of the boundary layer. This could result from the limited resolution inherent to numerical simulations of stellar interiors and requires further investigation.
Finally, it should be mentioned that Brummell et al. (2002) do not find any evidence of penetrative convection in their 3D simulations. This could be due to their somewhat artificial setup, in which the profile of thermal conductivity is fixed and/or to the fact that their direct numerical simulations probe a different dynamical regime given the values of the dimensionless numbers (Prandtl, Reynolds, Rayleigh numbers) that they could afford in their investigation (Rempel 2004).
3.3.3. Case 3: ld<lmin – Entrainment regime
In this case, all relevant scales have Pe ≫ 1, and the overshooting process can be considered to be completely adiabatic. The process of mass entrainment results in a growth of the well-mixed (entropy + composition) region. The key difference with the previous case is that there is nothing that can counterbalance the process: entrainment proceeds as long as energy is injected into the system.
This regime is observed by Meakin & Arnett (2007) in their calculations of the convection in the oxygen-burning shell of a massive star. The reason is that late phases of stellar evolution are driven by neutrino cooling, which acts on a time scale shorter than photon cooling (Arnett 1996). As a result, radiative diffusion becomes negligible and does not affect overshooting. Although their boundary layers have finite thickness with a non-trivial internal structure, the authors have shown that their data is described well by the parametrization of “bulk” entrainment presented in Sect. 2.3.
Turbulent entrainment is also observed in hydrodynamical simulations of the He-flash by Mocák et al. (2009, 2010, 2011). This specific phase of stellar evolution is strongly out of thermal equilibrium owing to the ignition of helium in a degenerate environment. The large release of nuclear energy drives convection on a time scale that is much shorter than the radiative time scale. Radiative diffusion becomes negligible and turbulent entrainment is obtained, as in the previous case.
4. Conclusion
Based on previous theoretical and numerical work, this paper presents a simple physical picture of the effects of radiation on overshooting. Other non-adiabatic effects exist in stars (nuclear burning, neutrino losses), but from current simulations we do not see any evidence of a direct role for these effects on overshooting. We show that the three existing parametrizations for overshooting correspond to different regimes, depending on the importance of radiative effects. As a result, we suggest that these three different parametrizations should coexist in 1D stellar evolution codes and be applied consistently depending on the local physical conditions. Ideally, the selection of the adequate parametrization should be based on the value of the Péclet number in the boundary layer. However, one faces two difficulties:
-
1.
How do we estimate the Péclet number? According to our work,the quantity that allows distinguishing between the differentthermal regimes is given by Eq. (10). However, thisquantity cannot be computed in the framework of MLT, whichhas, by construction, ϵ = 0 (no flow) when N2> 0. The Péclet number within the convective region can be estimated easily with the formula
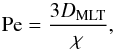 (11)where
(11)where 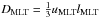 is the usual diffusion coefficient computed from MLT. In a first approach, this quantity could be used to extrapolate the value of the Péclet number in the boundary layer.
is the usual diffusion coefficient computed from MLT. In a first approach, this quantity could be used to extrapolate the value of the Péclet number in the boundary layer. -
2.
Given a definition of the Péclet number at the boundary, what are the range of values that define each regime? The simple picture developed in this work allows us to distinguish between three thermal regimes of overshooting, depending on whether the effect of radiation are dominant, marginal, or negligible. However, it does not make any prediction about the transition between these regimes, whether in terms of the values of the Péclet number at with such transitions occur or in terms of how sharp such transitions are.
Therefore, we are not yet able to give a practical criterion that would allow automatic selection of the appropriate description during a stellar evolution calculation. However, as a rule of thumb, we suggest:
-
1.
applying “chemical mixing” near the surface of stars, whereradiative effects become important (inefficient convection);
-
2.
applying “penetrative convection” in the deep interior of stars (efficient convection) for the phases which are photon-cooled (core-overshooting on the main-sequence, convective envelope undershooting, etc.);
-
3.
applying “turbulent entrainment” in the deep interior when the evolution is driven by neutrino losses (late stages of stellar evolution) or in phases that are in strong thermal imbalance (e.g., He-flash in low-mass stars).
It should be stressed that we do not claim that the current parametrizations describe each regime accurately. In particular, the calibration of free parameters is still required. However, a good starting point is to use the relevant parametrization for each regime. For instance, it is very likely incorrect to apply turbulent entrainment to describe convective cores on the main sequence as done in Staritsin (2013), since in this phase the time scales are long enough for radiative diffusion to affect overshooting. Likewise, considering our current understanding, it is inconsistent to use the “chemical mixing” description deep inside the stellar interior; this may contribute to the errors found by Schindler et al. (2015).
Failure to reproduce observational trends should then point to flaws in the parametrizations of these different regimes, such as those due to missing physics. For instance, the effects of composition are currently taken into account very poorly, mainly because of the (arbitrary) choice of using the Schwarzschild or the Ledoux criteria and the ad hoc use of thermohaline mixing. In fact, like radiation, composition probably affects the regime of overshooting and could drastically change the simple picture of the three regimes defined in this work. Likewise, rotation and magnetic field could also affect the nature and the efficiency of mixing at convective boundaries.
Here as well, insight from multidimensional simulations should help us to understand which are the relevant parameters that characterize these processes and how the parameter space is split into different regimes of overshooting. This work was a first step toward this goal, and it was focused on thermal diffusion. Applying this strategy to other physical processes should bring us closer to a physically consistent description of convective boundary mixing in 1D stellar evolution codes.
Acknowledgments
This work is supported by the European Research Council through grant ERC-AdG No. 341157-COCO2CASA. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number OCI-1053575. C.M. and WDA acknowledge support from NSF grant 1107445 at the University of Arizona. M.V. and V.P. thank Francois Lignières for enlightening discussions. We thank Marcelo Miller Bertolami, Achim Weiss, and Simon Campbell for useful comments on an earlier draft, and Bernd Freytag for pointing out the relevant figures in his thesis.
References
- Arnett, D. 1996, Supernovae and Nucleosynthesis, 1nd edn. (Princeton University Press) [Google Scholar]
- Arnett, W. D., Meakin, C., & Viallet, M. 2014, AIP Advances, 4, 041010 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, W. D., Meakin, C., Viallet, M., et al. 2015, ApJ, submitted [arXiv:1503.00342] [Google Scholar]
- Böhm-Vitense, E. 1958, ZA, 46, 108 [Google Scholar]
- Brethouwer, G., & Lindborg, E. 2009, J. Fluid Mech., 631, 149 [CrossRef] [Google Scholar]
- Brummell, N. H., Clune, T. L., & Toomre, J. 2002, ApJ, 570, 825 [Google Scholar]
- Canuto, V. M. 1992, ApJ, 392, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M. 1997, ApJ, 482, 827 [Google Scholar]
- Canuto, V. M. 2011, A&A, 528, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Canuto, V. M., & Dubovikov, M. 1998, ApJ, 493, 834 [Google Scholar]
- Canuto, V. M., & Mazzitelli, I. 1991, ApJ, 370, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, F., Brummell, N. H., Toomre, J., Malagoli, A., & Hurlburt, N. E. 1991, ApJ, 370, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Deng, L., Xiong, D. R., & Chan, K. L. 2006, ApJ, 643, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Ap&SS, 316, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Fernando, H. J. S. 1991, Ann. Rev. Fluid Mech., 23, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B. 1995, Ph.D. Thesis, Christian-Albrechts-Universität [Google Scholar]
- Freytag, B., Ludwig, H.-G., & Steffen, M. 1996, A&A, 313, 497 [Google Scholar]
- Gehmeyr, M., & Winkler, K.-H. A. 1992, A&A, 253, 92 [NASA ADS] [Google Scholar]
- Gough, D. O. 1977, ApJ, 214, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F. 2005, ARA&A, 43, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Hurlburt, N. E., Toomre, J., Massaguer, J. M., & Zahn, J.-P. 1994, ApJ, 421, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., Weigert, A., & Weiss, A. 2012, Stellar Structure and Evolution (Berlin Heidelberg: Springer-Verlag) [Google Scholar]
- Kuhfuss, R. 1986, A&A, 160, 116 [NASA ADS] [Google Scholar]
- Maeder, A. 1975, A&A, 43, 61 [NASA ADS] [Google Scholar]
- Matraka, B., Wassermann, C., & Weigert, A. 1982, A&A, 107, 283 [NASA ADS] [Google Scholar]
- Meakin, C. A., & Arnett, D. 2007, ApJ, 667, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Mocák, M., Müller, E., Weiss, A., & Kifonidis, K. 2009, A&A, 501, 659 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mocák, M., Campbell, S. W., Müller, E., & Kifonidis, K. 2010, A&A, 520, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mocák, M., Siess, L., & Müller, E. 2011, A&A, 533, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montalbán, J., Miglio, A., Noels, A., et al. 2013, ApJ, 766, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, J. W., & Meakin, C. 2011, ApJ, 742, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Osborn, T. R. 1980, J. Phys. Oceanogr., 10, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Ozmidov, R. V. 1965, Atmos. Ocean Phys., 8, 853 [Google Scholar]
- Pace, G., Castro, M., Meléndez, J., Théado, S., & do Nascimento, J.-D. 2012, A&A, 541, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Porter, D. H., & Woodward, P. R. 2000, ApJS, 127, 159 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Rempel, M. 2004, ApJ, 607, 1046 [NASA ADS] [CrossRef] [Google Scholar]
- Schindler, J.-T., Green, E. M., & Arnett, W. D. 2015, ApJ, 806, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, J. H. M. M., Rosner, R., & Bohn, H. U. 1984, ApJ, 282, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Schroder, K.-P., Pols, O. R., & Eggleton, P. P. 1997, MNRAS, 285, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Smyth, W. D., & Moum, J. N. 2000, Physics of Fluids, 12, 1327 [NASA ADS] [CrossRef] [Google Scholar]
- Staritsin, E. I. 2013, Astron. Rep., 57, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Staritsin, E. I. 2014, Astron. Rep., 58, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., & Nordlund, A. 1989, ApJ, 342, L95 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stellingwerf, R. F. 1982, ApJ, 262, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Théado, S., Alecian, G., LeBlanc, F., & Vauclair, S. 2012, A&A, 546, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viallet, M., Meakin, C., Arnett, D., & Mocák, M. 2013, ApJ, 769, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, A., & Schlattl, H. 2008, Ap&SS, 316, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Wuchterl, G., & Feuchtinger, M. U. 1998, A&A, 340, 419 [NASA ADS] [Google Scholar]
- Xiong, D.-R. 1986, A&A, 167, 239 [NASA ADS] [Google Scholar]
- Xiong, D. R., Cheng, Q. L., & Deng, L. 1997, ApJS, 108, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 1991, A&A, 252, 179 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Sketch of the different scales of eddies present in the flow. η and Λ are the Kolmogorov and integral scales, respectively. The scales contributing to overshooting are those between lmin and lmax. Depending on the location of the transition scale ld where Pe ~ 1, one can define three different regimes of overshooting (see text). |
| In the text | |
 |
Fig. 2 Radial profiles of the length scales LO, Lχ, and the Péclet number in the boundary layer of the red giant model of Viallet et al. (2013). The thick dashed lines denote the extent of the boundary layer, defined as the region of buoyancy braking. The x-axis is normalized by the radius of the star R = 4.1 × 1012 cm. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


