| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A5 | |
| Number of page(s) | 16 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201525950 | |
| Published online | 20 July 2015 | |
[C ii] emission from galactic nuclei in the presence of X-rays
Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, CA 91109-8099, USA
e-mail: William.Langer@jpl.nasa.gov
Received: 24 February 2015
Accepted: 27 May 2015
Context. The luminosity of [C ii] is used as a probe of the star formation rate in galaxies, but the correlation breaks down in some active galactic nuclei (AGNs). Models of the [C ii] emission from galactic nuclei do not include the influence of X-rays on the carbon ionization balance, which may be a factor in reducing the [C ii] luminosity.
Aims. We aim to determine the properties of the ionized carbon and its distribution among highly ionized states in the interstellar gas in galactic nuclei under the influence of X-ray sources. We calculate the [C ii] luminosity in galactic nuclei under the influence of bright sources of soft X-rays.
Methods. We solve the balance equation of the ionization states of carbon as a function of X-ray flux, electron, atomic hydrogen, and molecular hydrogen density. These are input to models of [C ii] emission from the interstellar medium (ISM) in galactic nuclei representing conditions in the Galactic central molecular zone and a higher density AGN model. The behavior of the [C ii] luminosity is calculated as a function of the X-ray luminosity. We also solve the distribution of the ionization states of oxygen and nitrogen in highly ionized regions.
Results. We find that the dense warm ionized medium (WIM) and dense photon dominated regions (PDRs) dominate the [C ii] emission when no X-rays are present. The X-rays in galactic nuclei can affect strongly the C+ abundance in the WIM, converting some fraction to C2+ and higher ionization states and thus reducing its [C ii] luminosity. For an X-ray luminosity L(X-ray) ≳ 1043 erg s-1 the [C ii] luminosity can be suppressed by a factor of a few, and for very strong sources, L(X-ray) >1044 erg s-1 such as found for many AGNs, the [C ii] luminosity is significantly depressed. Comparison of the model with several extragalactic sources shows that the [C ii] to far-infrared ratio declines for L(X-ray) ≳ 1043 erg s-1, in reasonable agreement with our model.
Conclusions. We conclude that X-rays can suppress the C+ abundance and, therefore, the [C ii] luminosity of the ISM in active galactic nuclei with a large X-ray flux. The X-ray flux can arise from a central massive accreting black hole and/or from many smaller discrete sources distributed throughout the nuclei. We also find that the lower ionization states of nitrogen and oxygen are also suppressed at high X-ray fluxes in warm ionized gas.
Key words: Galaxy: center / X-rays: ISM / ISM: general / atomic processes
© ESO, 2015
1. Introduction
The fine structure line of ionized carbon, [C ii], at 158 μm is widely used to trace the galactic star formation rate (SFR; Stacey et al. 2010; de Looze et al. 2011, 2014; Pineda et al. 2014), as is the far-infrared (FIR) dust emission (e.g. Malhotra et al. 1997; Luhman et al. 1998; Stacey et al. 2010; de Looze et al. 2014). In principle the energy output of bright young stars is transferred to the gas and dust and reemitted either in the important FIR cooling lines such as [C ii] or as continuum dust emission. In extragalactic sources the luminosity of [C ii] is often correlated with the FIR dust emission thus reinforcing the suggestion that these trace the SFR. However there are some notable exceptions in which the luminosity of [C ii] is significantly suppressed with respect to the infrared luminosity. The relationship between the intensity of [C ii] and other star formation tracers appears to work in the Galactic disk (Pineda et al. 2014) and most extragalactic sources (de Looze et al. 2014), however it breaks down somewhat in many luminous infrared galaxies (LIRGs; Díaz-Santos et al. 2014) and ultra luminous infrared galaxies (ULIRGs; Malhotra et al. 1997; Luhman et al. 1998; Rigopoulou et al. 2014) and even more so in many active galactic nuclei (AGN; Stacey et al. 2010, Sargsyan et al. 2014, Gullberg et al. 2015). The assumption is that there is a deficit in [C ii] luminosity in these sources and in particular in their central regions (Malhotra et al. 1997; Luhman et al. 1998; Rigopoulou et al. 2014; Gullberg et al. 2015).
Several explanations have been offered for the decrease in the [C ii] to FIR luminosity (e.g. Nakagawa et al. 1995; Malhotra et al. 1997; Luhman et al. 1998; Stacey et al. 2010; Gullberg et al. 2015), including: 1) the [C ii] emission is optically thick and saturated, if it arises from very dense photon dominated regions (PDRs), where the excitation temperature of the 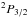 –
–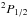 transition is thermalized and does not radiate as efficiently as the dust with increasing energy input; 2) for high ratios of UV flux to density the dust grains are positively charged and are less efficient at heating the gas via photoejected electrons, thus the
transition is thermalized and does not radiate as efficiently as the dust with increasing energy input; 2) for high ratios of UV flux to density the dust grains are positively charged and are less efficient at heating the gas via photoejected electrons, thus the 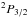 level is less populated (Wolfire et al. 1990; Kaufman et al. 1998); and 3) a reduction in the column density of ionized carbon in the PDRs due to a soft ultraviolet radiation field that can heat the dust but not maintain a large layer of C+. However, detailed models of the source of [C ii] are lacking and none of the proposed mechanisms appear to explain the reduction in all sources.
level is less populated (Wolfire et al. 1990; Kaufman et al. 1998); and 3) a reduction in the column density of ionized carbon in the PDRs due to a soft ultraviolet radiation field that can heat the dust but not maintain a large layer of C+. However, detailed models of the source of [C ii] are lacking and none of the proposed mechanisms appear to explain the reduction in all sources.
In this paper we propose that X-rays can also produce a deficiency in the [C ii] to FIR luminosity ratio in the presence of a large X-ray flux at energies above ~1 keV. Under these conditions, a significant fraction of carbon is in higher ionization states (C2+, C3+, etc.) in some of the regions responsible for [C ii] emission, in particular the highly ionized interstellar medium (ISM) gas components. We also propose that X-ray photoionization from strong X-ray sources can reduce the abundance of the lower ionization states of nitrogen and oxygen in the ionized gas and therefore the emission from their FIR fine-structure lines. For example, the [N iii] 57 μm line is observed to be comparable to the [N ii] 122 μm line in extragalactic sources (Graciá-Carpio et al. 2011). The abundance of N++ will be comparable to or greater than that for N+ because the critical density for exciting the N++ fine-structure levels is much higher than that of those for N+(Madden et al. 2013). Previous work on the effects of X-rays on chemistry have focused on the X-ray dissociation regions (XDRs) of molecular clouds (e.g. Langer 1978; Krolik & Kallman 1983; Maloney et al. 1996; Meijerink & Spaans 2005) or YSOs (Bruderer et al. 2009) and protoplanetary disks (Ádámkovics et al. 2011)1.
Here we consider the effects of high X-ray fluxes on the interstellar gas environments that emit in [C ii]. These include primarily the highly ionized gas, which is composed of several components including the warm ionized medium (WIM), hot ionized medium (HIM), the dense ionized skins surrounding clouds (DIS), and H ii regions. A large X-ray flux will also affect the [C ii] emission from diffuse atomic hydrogen clouds and, to a much lesser extent, the PDRs surrounding molecular clouds. We also consider the ionization balance of nitrogen and oxygen in the WIM. The emphasis in this paper is different from that in the XDR models (Maloney et al. 1996; Meijerink & Spaans 2005) in that we do not evaluate the molecular abundances in the dense UV shielded molecular clouds, but focus instead on the abundance of the carbon ionization state in the major ISM components. Whether X-rays play a significant role in reducing the abundance of C+ (and other gas tracers such as N+, N2+, O0 and O2+) in the ISM and, thus, [C ii] emission will depend on details of the distribution of X-ray sources, their luminosity, and the properties of the ISM. In addition, a high flux of X-rays can compete with UV heating resulting in an increase in the FIR luminosity (Voit 1991) and therefore further reducing the [C ii] to FIR ratio.
We will show that the X-ray flux can reduce the abundance of C+ primarily in highly ionized regions and that, under the right conditions, will reduce the [C ii] emission significantly in galactic nuclei. In the Galactic disk the WIM contributes about 20% to 30% of the [C ii] luminosity (Pineda et al. 2013; Velusamy & Langer 2014) using the scale heights derived from [C ii] (Langer et al. 2014a; Velusamy & Langer 2014). In the Galactic central molecular zone (CMZ) the WIM densities are much higher and may contribute an even larger percentage of the [C ii] luminosity. We conclude that this mechanism is important in some active galactic environments with large X-ray luminosity and must be included along with the previously suggested mechanisms to explain the reduction in the [C ii] to FIR luminosity in galaxies.
X-rays are an important radiation component of active galactic nuclei (AGNs) composing up to 40% of of the total luminosity (Mushotzky et al. 1993). Ebrero et al. (2009) summarize the soft (0.5–2 keV) X-ray luminosities in a large sample (>1000) of AGNs (reproduced in Fig. 1) which have luminosities in the range 1040 erg s-1 to 2 × 1047 erg s-1. Iwasawa et al. (2011) in a recent study of LIRGs found that 43 out of 44 sources had X-rays luminosities ranging from ~1040 erg s-1 to ~1043 erg s-1 in the 0.5 to 10 keV range. The mean radius of the soft X-ray emission in their sample was 5.3 kpc and so represents emission throughout the LIRG, however they found that the distribution of the hard X-ray emission is much more compact. X-ray luminosities greater than 1040 erg s-1 represent an important ionization source that must be taken into account in understanding the conditions of the ISM and the corresponding emission in FIR lines from ions.
 |
Fig. 1 Soft X-ray (0.5–2.0 keV) luminosity for a sample of 1009 AGNs as a function of red shift z reproduced from Fig. 1 in Ebrero et al. (2009). The insert key identifies the X-ray survey used to compile the data (see Ebrero et al. (2009) for their definitions). The soft X-ray luminosities for this sample of AGNs range from ~1040 to ~2 × 1047 erg s-1. |
Even in more quiescent galaxies X-rays are important in the nucleus. For example, the Galactic CMZ is observed to have extended diffuse X-ray emission as well as numerous X-ray point sources (Muno et al. 2009), including an accreting stellar black hole (Heindl et al. 1993). In addition, the massive black hole near Sgr A is a potential X-ray source. It has been suggested that X-rays could provide the >10-15 s-1 ionization rate of hydrogen needed to explain the H3+ observations of Goto et al. (2014). The cross section for ionization of heavy atoms by X-rays is orders of magnitude larger than hydrogen, primarily due to K shell ionization at X-ray energies greater than a few hundred eV. In addition, X-ray photoionization of hydrogen produces energetic photoejected electrons which produce secondary ionization of carbon (Maloney et al. 1996; Meijerink & Spaans 2005). Thus, X-rays can play an important role in ionizing carbon and other metals. The penetration depth of 1 keV X-rays in the diffuse ionized gas in the CMZ is a column density N(H+) > few × 1022 cm-2 and in the neutral gas, is N(H+2H2) ~ several ×1021 cm-2. Thus X-rays suffuse galactic nuclei and X-ray photoionization needs to be considered in the ionization balance of metals in the ISM.
Our paper is organized as follows. In Sect. 2 we develop the reactions and ionization balance model, while in Sect. 3 we present sample model calculations of the distribution of ionization states of C, N, and O. In Sect. 4 we model the [C ii] luminosity as a function of X-ray luminosity, and discuss the consequences and implications of X-ray photoionization on the [C ii] emission from AGNs. In Sect. 4 we also validate our [C ii] emissivity model for galactic nuclei by calculating the luminosity from the CMZ and comparing it to observations. Finally, we summarize our results in Sect. 5.
2. X-ray ionization model for carbon
In this section we develop the X-ray photoionization balance equations for the ionization states of carbon. Multiply ionized carbon can be produced by L- and K-shell photoionization by X-rays. K-shell photoionization dominates L-shell photoionization at energies above its threshold, EK ~ 0.3–0.4 keV for carbon. Furthermore, these higher energy X-rays penetrate further in the ISM than the low energy X-rays that dominate L-shell photoionization because the L-shell photoionization cross sections are large for hydrogen and carbon near their thresholds ~11 to 15 eV. We consider only X-rays with energies ≳1 keV because they have large enough cross sections to influence the ionization balance but not so large that they cannot penetrate large column densities.
2.1. Carbon ion balance equations
Here we describe the reduced set of reactions that dominate the ionization balance of carbon in the presence of X-rays. The X-ray photoionization processes are: 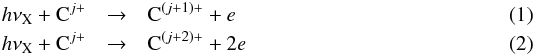 where j labels the initial ionization state, Cj, and ranges from 0 to 5 for L-shell ionization (Eq. (1)) and 0 to 4 for Auger K-shell ionization (Eq. (2)). The X-ray photoionization rate from Cj is designated
where j labels the initial ionization state, Cj, and ranges from 0 to 5 for L-shell ionization (Eq. (1)) and 0 to 4 for Auger K-shell ionization (Eq. (2)). The X-ray photoionization rate from Cj is designated 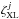 and
and 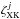 for L-shell and K-shell, respectively.
for L-shell and K-shell, respectively.
The electron recombination reactions are, 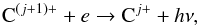 (3)where the reaction rate coefficient from j + 1 to j is labeled
(3)where the reaction rate coefficient from j + 1 to j is labeled 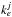 Ions can charge exchange with atomic hydrogen,
Ions can charge exchange with atomic hydrogen, 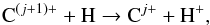 (4)where the reaction rate coefficient from j + 1 to j is labeled
(4)where the reaction rate coefficient from j + 1 to j is labeled 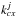 . In regions with molecular hydrogen Cj+ generally reacts rapidly via ion-molecule reactions,
. In regions with molecular hydrogen Cj+ generally reacts rapidly via ion-molecule reactions, 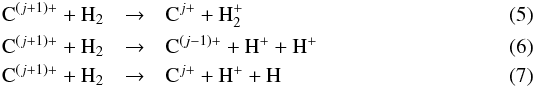 except for C+ which reacts slowly with H2 via radiative association,
except for C+ which reacts slowly with H2 via radiative association, 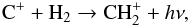 (8)we label these ion molecule reactions
(8)we label these ion molecule reactions 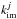 . To calculate the number density of carbon ions we need to solve a set of balance equations,
. To calculate the number density of carbon ions we need to solve a set of balance equations, 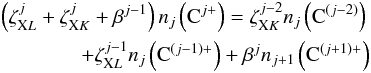 (9)where
(9)where 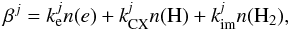 (10)for j = 0 to jmax–1 (note that ζjmax = 0 and βjmax = 0 in Eq. (9) because there is no ionization out of and no recombination into the maximum charge state, respectively, and that β-1 = 0 because there is no recombination from the lowest charge state). In addition we need the number density conservation equation,
(10)for j = 0 to jmax–1 (note that ζjmax = 0 and βjmax = 0 in Eq. (9) because there is no ionization out of and no recombination into the maximum charge state, respectively, and that β-1 = 0 because there is no recombination from the lowest charge state). In addition we need the number density conservation equation, 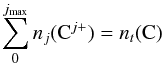 (11)where nt(C) is the total number density of all carbon charge states. For the galactic center ISM the X-ray energy range of interest is greater than 1 keV and we can neglect the L-shell photoionization rate (see Sect. 3.1). These equations can be solved analytically and used to calculate the fractional ionization of each species, fi = ni/nt, where i labels the ionization state, and
(11)where nt(C) is the total number density of all carbon charge states. For the galactic center ISM the X-ray energy range of interest is greater than 1 keV and we can neglect the L-shell photoionization rate (see Sect. 3.1). These equations can be solved analytically and used to calculate the fractional ionization of each species, fi = ni/nt, where i labels the ionization state, and 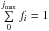 .
.
2.2. X-ray photoionization cross sections
Verner et al. (1993) provide fits for X-ray photoionization cross sections for C0 to C4+ for the 1s-shell (K-shell), C0 to C+3 for the 2s-shell (L-shell), and C0 and C+ for the 2-p shell (L-shell). The 2s- and 2p-shell cross sections contribute less than 5% to the total cross section above 0.4 keV. To facilitate solving for fi we fit the cross sections for X-ray photoionization of C0, C+, C2+, C3+, and C4+ from Verner et al. (1993) and Verner & Yakovlev (1995) with a power law fit above 0.4 keV. The fits are very similar for all the K-shell reactions Cj+→ C(j+2)+, and have a form, 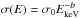 , and for simplicity we adopt an average value, σ0 = 4.1 × 10-20 cm2 and b = 2.8. In Sect. 3 we will combine σ(E) with the X-ray photon flux to calculate the X-ray photoionization rates. As we are only interested in solving for the effects of X-rays on the carbon ionization balance in regions where neutral carbon is readily ionized by UV we will neglect the balance equations for C0. This assumption is valid in the presence of UV which ionizes neutral carbon rapidly in unshielded regions in the ISM, otherwise there would not be any C+ and it would recombine to C0. Furthermore, the ionization of C0 by UV is generally orders of magnitude larger than that by X-rays.
, and for simplicity we adopt an average value, σ0 = 4.1 × 10-20 cm2 and b = 2.8. In Sect. 3 we will combine σ(E) with the X-ray photon flux to calculate the X-ray photoionization rates. As we are only interested in solving for the effects of X-rays on the carbon ionization balance in regions where neutral carbon is readily ionized by UV we will neglect the balance equations for C0. This assumption is valid in the presence of UV which ionizes neutral carbon rapidly in unshielded regions in the ISM, otherwise there would not be any C+ and it would recombine to C0. Furthermore, the ionization of C0 by UV is generally orders of magnitude larger than that by X-rays.
2.3. Electron recombination reaction rate coefficients
The reaction rate coefficients for radiative and dielectronic recombination of electrons with carbon ions up to C6+ have been calculated by Nahar & Pradhan (1997) and Badnell et al. (2003) and Badnell (2006) with radiative recombination dominating at low temperatures (as in diffuse clouds) but dielectronic recombination becoming more important at the higher temperatures found in the WIM and DIS. We use the values for the total recombination rate coefficients published in Table 5 of Nahar & Pradhan (1997) in our model calculations. The reactions are given in Table 1 and we list the reaction rate coefficients for two characteristic gas temperatures, 100 K and 8000 K.
Electron recombination reactions.
2.4. Charge exchange with atomic hydrogen
Reaction rate coefficients for charge transfer between carbon ions and atomic hydrogen have been summarized for C+ to C4+ by Kingdon & Ferland (1996) along with fits in the form, ![\begin{equation} k_{\rm CX}(T_4) = aT_{4}^{b}[1 + c \rm{e}^{{\rm d}{\it T_4}}]~\rm{cm^3\,s^{-1}} \end{equation}](/articles/aa/full_html/2015/08/aa25950-15/aa25950-15-eq76.png) (12)where T4 is the kinetic temperature in units of 104 K, and the fitting coefficients are given in their Table 1. The charge exchange of C+ with H is very small owing to the large endothermic barrier, ΔE ~ 2.5 eV (due to the different ionization potentials of C and H). Typically most exothermic charge exchange reactions of highly ionized metals proceed rapidly under ISM conditions with a reaction rate coefficient of order 10-9 cm3 s-1, but that is not the case for doubly ionized carbon. Although charge exchange of C2+ with H is energetically favorable, its cross section is small owing to the nature of the crossings in the intermediate molecular potential (McCarroll & Valiron 1975; Kingdon & Ferland 1996). However, the higher ionization states of carbon do charge exchange rapidly. In Table 2 we list the reaction rate coefficients for carbon ions at 8000 K and 100 K, typical of temperatures found in the WIM and diffuse atomic hydrogen gas, respectively.
(12)where T4 is the kinetic temperature in units of 104 K, and the fitting coefficients are given in their Table 1. The charge exchange of C+ with H is very small owing to the large endothermic barrier, ΔE ~ 2.5 eV (due to the different ionization potentials of C and H). Typically most exothermic charge exchange reactions of highly ionized metals proceed rapidly under ISM conditions with a reaction rate coefficient of order 10-9 cm3 s-1, but that is not the case for doubly ionized carbon. Although charge exchange of C2+ with H is energetically favorable, its cross section is small owing to the nature of the crossings in the intermediate molecular potential (McCarroll & Valiron 1975; Kingdon & Ferland 1996). However, the higher ionization states of carbon do charge exchange rapidly. In Table 2 we list the reaction rate coefficients for carbon ions at 8000 K and 100 K, typical of temperatures found in the WIM and diffuse atomic hydrogen gas, respectively.
Charge exchange with H reaction rate coefficients.
2.5. C+ ion molecule reactions with H2
C+ reacts slowly with molecular hydrogen via associative recombination, C+ + H2 → CH + hν (McElroy et al. 2013), and this reaction does not play a significant role in the carbon ionization balance outside of dense PDRs. In contrast, the reactions of Cn+ with H2 for n ≥ 2 are likely to be fast, ~10-10 to 10-9 cm3 s-1 for most cases (Langer 1978). Thus the admixture of a small amount of molecular hydrogen can have a large effect on the carbon X-ray photoionization balance. The only multiply charged carbon ion molecule reaction that has been measured in the lab is, C2+ + H2 (Smith & Adams 1981) and it has a reaction rate coefficient of ~1.2 × 10-10 cm3 s-1 with the dominant channel → H+ + H+ + C comprising ~90% of the total. We assume that higher charge states have the same reaction rate coefficient and end products, although the actual product channel is not critical for the model, and these are listed in Table 3.
+ hν (McElroy et al. 2013), and this reaction does not play a significant role in the carbon ionization balance outside of dense PDRs. In contrast, the reactions of Cn+ with H2 for n ≥ 2 are likely to be fast, ~10-10 to 10-9 cm3 s-1 for most cases (Langer 1978). Thus the admixture of a small amount of molecular hydrogen can have a large effect on the carbon X-ray photoionization balance. The only multiply charged carbon ion molecule reaction that has been measured in the lab is, C2+ + H2 (Smith & Adams 1981) and it has a reaction rate coefficient of ~1.2 × 10-10 cm3 s-1 with the dominant channel → H+ + H+ + C comprising ~90% of the total. We assume that higher charge states have the same reaction rate coefficient and end products, although the actual product channel is not critical for the model, and these are listed in Table 3.
Reaction rate coefficients of Cn+ with H2.
3. Results
The gas in galactic nuclei is exposed to a different radiation environment than that in the galactic disks with intense UV and X-ray radiation fields due to the presence of young O-type stars, supernovae, stellar black holes, and a massive black hole at the center. In AGNs this environment reaches an extreme with X-ray luminosities, L(X-ray), in excess of 1040 erg s-1 and up to ~2 × 1047 erg s-1 (e.g. Ebrero et al. 2009). These large luminosities are sufficient to influence the distribution of higher ionized states of carbon in galactic nuclei and depends on the flux of soft X-rays with energies above the K-shell ionization threshold (~0.3–0.4 keV). If the source of X-rays in the galactic center is due to an accreting black hole the X-ray luminosity flux, 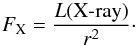 (13)In the notation of Maloney et al. (1996),
(13)In the notation of Maloney et al. (1996), 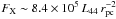 erg cm-2 s-1, where L44 = LX/ 1044 erg s-1 and rpc is the distance to the X-ray source in pc. Thus, neglecting absorption above 1 keV, FX can be very large throughout most of a galactic nucleus and these X-rays will have a major impact on the properties of the neutral and ionized gas. While X-ray emission from massive black holes can effect the ionization balance, chemistry, and thermal properties over large volumes of the galactic center, other weaker sources can have comparable influence on nearby clouds. For example, strong supernova shocks can produce luminosities LX ~ 1036 to 1040 erg s-1 and stellar black holes can produce ~1037–1038 erg s-1 (Heindl et al. 1993).
erg cm-2 s-1, where L44 = LX/ 1044 erg s-1 and rpc is the distance to the X-ray source in pc. Thus, neglecting absorption above 1 keV, FX can be very large throughout most of a galactic nucleus and these X-rays will have a major impact on the properties of the neutral and ionized gas. While X-ray emission from massive black holes can effect the ionization balance, chemistry, and thermal properties over large volumes of the galactic center, other weaker sources can have comparable influence on nearby clouds. For example, strong supernova shocks can produce luminosities LX ~ 1036 to 1040 erg s-1 and stellar black holes can produce ~1037–1038 erg s-1 (Heindl et al. 1993).
Maloney et al. (1996) modeled the effects of enhanced UV and X-ray fluxes on the thermal and chemical balance of molecular gas in galactic nuclei, generating a grid of XDR models that covered a range of X-ray radiation field energy fluxes FX = 0.1 to 106 erg cm-2 s-1. They set a lower limit of 1 keV to guarantee that the X-rays will penetrate sufficient depth into the molecular cloud to affect the chemical and thermal balance. Meijerink et al. (2007) also modeled the effects of enhanced UV and X-rays on molecular gas in galactic nuclei, but covered a narrower range of energy flux, FX = 1.6 × 10-2 to 1.6 × 102 erg cm-2 s-1. Here we consider the effects of large X-ray fluxes on the carbon balance in the ionized ISM, the diffuse atomic hydrogen clouds, and the PDRs of dense molecular clouds in galactic nuclei. We begin by calculating the X-ray photoionization rates.
3.1. X-ray photoionization rates
Here we calculate the X-ray ionization rates for carbon ions parameterized in terms of the X-ray energy flux, FX. The X-ray photoionization rate for carbon ions of charge state j is 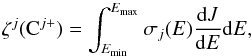 (14)where dJ/ dE is the photon spectral distribution of X-rays as a function of energy in units of photons cm-2 s-1 keV-1, and Emin and Emax are the minimum and maximum X-ray energies, respectively. The spectral distribution is usually expressed as a power law distribution,
(14)where dJ/ dE is the photon spectral distribution of X-rays as a function of energy in units of photons cm-2 s-1 keV-1, and Emin and Emax are the minimum and maximum X-ray energies, respectively. The spectral distribution is usually expressed as a power law distribution, 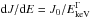 . For Seyfert galaxies Γ is typically in the range 1.4 to 2.0 below 100 keV with a distribution average ~1.7 (Mushotzky et al. 1993). However, the spectral index can vary with energy, for example (Iwasawa et al. 2011) found different spectral slopes for hard and soft X-rays in a sample of LIRGs. For AGNs (Maloney et al. 1996) adopted Γ ~ 2 for AGNs and Meijerink et al. (2007)Γ = 1.9 for the X-ray spectrum of an accreting massive black hole. Here we will adopt Γ = 1.9. We will set Emin = 1 keV because, as discussed above, lower energy X-rays can be neglected except very near the X-ray source, and Emax is usually taken to be 100 keV.
. For Seyfert galaxies Γ is typically in the range 1.4 to 2.0 below 100 keV with a distribution average ~1.7 (Mushotzky et al. 1993). However, the spectral index can vary with energy, for example (Iwasawa et al. 2011) found different spectral slopes for hard and soft X-rays in a sample of LIRGs. For AGNs (Maloney et al. 1996) adopted Γ ~ 2 for AGNs and Meijerink et al. (2007)Γ = 1.9 for the X-ray spectrum of an accreting massive black hole. Here we will adopt Γ = 1.9. We will set Emin = 1 keV because, as discussed above, lower energy X-rays can be neglected except very near the X-ray source, and Emax is usually taken to be 100 keV.
To calculate the photoionization rate as a function of the energy flux we will vary J0 to represent different X-ray fluxes. We rewrite the spectral energy distribution as, 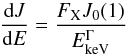 (15)where J0(1) is the value that produces a luminosity flux of 1 erg cm-2 s-1 for a given spectral index Γ. We find J0(1) by solving
(15)where J0(1) is the value that produces a luminosity flux of 1 erg cm-2 s-1 for a given spectral index Γ. We find J0(1) by solving 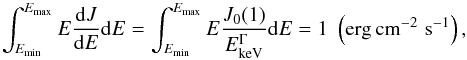 (16)substituting Γ = 1.9, integrating from 1 to 100 keV, and converting units from keV to erg. This conversion yields, J0(1) = 1.1 × 108 photons cm-2 s -1 keV-1. We now express dJ/ dE = 1.1 × 108FX/E1.9 where FX is in units of erg cm-2 s-1. Substituting dJ/ dE and σ(EkeV) into Eq. (14) yields
(16)substituting Γ = 1.9, integrating from 1 to 100 keV, and converting units from keV to erg. This conversion yields, J0(1) = 1.1 × 108 photons cm-2 s -1 keV-1. We now express dJ/ dE = 1.1 × 108FX/E1.9 where FX is in units of erg cm-2 s-1. Substituting dJ/ dE and σ(EkeV) into Eq. (14) yields 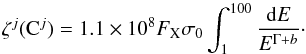 (17)This equation is valid at the boundary of the cloud as long as we can neglect absorption of the X-rays. For 1 keV, our assumed lower threshold, where most of the ionization occurs, the absorption opacity is less than one for a hydrogen column density ≲(5−10) × 1021 cm-2, depending on the metallicity. Only the giant molecular clouds (GMCs) have sufficient column density to absorb X-rays at this energy, however, as discussed the X-ray ionization has little effect on the [C ii] emission from the molecular hydrogen boundaries of the cloud and therefore we neglect the attenuation of X-rays in determining the luminosity from this layer. Substituting σ0, Γ, and b into Eq. (17) and integrating from 1 to 100 keV yields, ζj(Cj) ≃ 1.2 × 10-12FX s-1.
(17)This equation is valid at the boundary of the cloud as long as we can neglect absorption of the X-rays. For 1 keV, our assumed lower threshold, where most of the ionization occurs, the absorption opacity is less than one for a hydrogen column density ≲(5−10) × 1021 cm-2, depending on the metallicity. Only the giant molecular clouds (GMCs) have sufficient column density to absorb X-rays at this energy, however, as discussed the X-ray ionization has little effect on the [C ii] emission from the molecular hydrogen boundaries of the cloud and therefore we neglect the attenuation of X-rays in determining the luminosity from this layer. Substituting σ0, Γ, and b into Eq. (17) and integrating from 1 to 100 keV yields, ζj(Cj) ≃ 1.2 × 10-12FX s-1.
In the neutral gas clouds the electrons ejected by X-ray photoionization, primarily of hydrogen, produce secondary ionization. The multiplicative effects of these secondary ionizations of metals is of order a few and here we adopt a factor of two for carbon (see Maloney et al. 1996; Meijerink & Spaans 2005). However, in the ionized WIM and DIS the photoejected electrons scatter via Coulomb interactions off the ambient electrons. This scattering is large compared with the electron ionization cross sections for Cn+ (cf. Suno & Kato 2006) and the photoejected electrons are rapidly thermalized. Therefore above a fractional ionization of a couple of percent, thermalization is so rapid (Maloney et al. 1996) that the probability of secondary ionization of carbon can be neglected in the WIM and DIS.
The X-ray photoionization rate of carbon ions can be quite large in galactic nuclei and this process will result in the conversion of C+ to higher ionization states in diffuse ionized regions. Meijerink et al. (2007) considered FX = 1.6 × 10-2 to 1.6 × 102 erg cm-2 s-1 in their XDR models of dense gas in galaxy nuclei and Maloney et al. (1996) studied a range of 0.1 to 106 erg cm-2 s-1. In this section, for illustrative purposes, we will usually consider an X-ray flux of FX = 10-3 to 104 erg cm-2 s-1, but sometimes consider higher values. The lower limit reflects an ionization rate at which X-rays are unimportant in the ion balance. In the following subsections we present the distribution of ionized states of carbon as a function of X-ray flux, under different conditions of electron, atomic hydrogen, and molecular hydrogen abundances, corresponding to different AGN ISM environments. To simplify the solution we include an ionization state only up to C4+, as our main purpose is to study the conversion of C+ to higher states. Thus the fractional abundance f(C4+) represents all charge states z ≥ 4.
3.2. Highly ionized regions
There are several environments in which hydrogen is completely ionized. One is the WIM, where the densities in the disk are usually low, n(e) ~ few × 10-2 cm-3 (Haffner et al. 2009), but are much higher in galactic nuclei. In the CMZ, the average electron density, ⟨ n(e) ⟩ ~ 10 cm-3 (Cordes & Lazio 2003; Roy 2013), but may be higher in AGNs. Other highly ionized regions are those associated with H ii sources and H ii-like dense ionized skins (DIS) around dense molecular clouds, where the electron densities may be high, n(e) ~1–100 cm-3 (Oberst et al. 2011; Langer et al. 2015). Finally, there is the HIM which is detected via thermal X-ray emission and where hydrogen and helium are completely ionized. The HIM would have Tkin ~ 105−few × 106 K and n(e) < few × 10-3 cm-3 (Cox 2005; Ferrière et al. 2007). In general the densities for the HIM are too small for this component to contribute much to the [C ii] emission from galactic nuclei and we neglect it here.
In Fig. 2a we show the solutions for a low density completely ionized gas, n(e) = 0.01 cm-3 (fully ionized, n(H) = n(H2) = 0 cm-3) and Tkin = 8000 K. It can be seen that as the X-ray energy flux increases the C+ is first converted to C2+, then C3+, and at FX ~ 10-1 erg cm-2 s-1 C+ becomes negligible and all the carbon is in the higher ionization states. For FX> 1 erg cm-2 s-1 carbon is essentially in the highest charge state considered here, C4+. For galactic centers and H ii-like regions where the electron densities are higher, we show results for n(e) = 1 cm-3 and 10 cm-3 in Figs. 2b and c, respectively. Increasing the electron density shifts the transition from C+ to higher ionization states to larger FX as a larger X-ray radiation flux is needed to offset the more rapid electron recombination to lower ionization states. For all the electron densities considered here there is a threshold in FX where C+ goes to zero in the highly ionized gas. Adding a small amount of atomic hydrogen, n(H) ~ 0.01 cm-3, does not have much of an effect on the distribution of ionization states of carbon (not shown). For the HIM the combination of a lower electron recombination rate coefficient at the higher temperatures and the lower electron density pushes the transition from C+ to Cj+ to low values of FX; for example, for Tkin = 105 K and n(e) = 0.003 cm-3 we find f(C+) < 0.1 for the lowest flux considered here FX = 10-3 erg cm-2 s-1.
 |
Fig. 2 Fractional ionization state of C+ to C4+ versus X-ray luminosity flux, FX, for n(e) = 0.01 cm-3(top), 1.0 cm-3(middle), and 10.0 cm-3(bottom) at Tkin = 8000 K, assuming a fully ionized region (n(H) = n(H2) = 0 cm-3). |
3.3. Atomic hydrogen clouds
We next address the question whether a large flux of X-rays will modify the distribution of C+ in low density diffuse atomic hydrogen clouds. The presence of even modest amounts of atomic hydrogen will keep carbon from reaching highly ionized states because of the efficiency of charge exchange, except for C2+ which does not charge exchange efficiently. In Fig. 3a we show the fraction of C+ and higher ionization states for conditions in a diffuse atomic hydrogen cloud with Tkin = 100 K, a hydrogen density n(H) = 25 cm-3, a small admixture of electrons, and no molecular hydrogen. As can be seen in this figure only the two lowest carbon ionization states are present, and the higher charge states have very small fractional abundances because they charge exchange rapidly with H to lower ionization states. For FX ≲ 10 erg cm-2 s-1 carbon is mainly singly ionized, however in the presence of an X-ray energy flux FX ≳ 10 erg cm-2 s-1 X-ray K-shell photoionization converts C+ rapidly into C3+, which then charge exchanges to C2+. Thus under high X-ray flux conditions low density atomic hydrogen clouds would have a low fraction of C+ but a high fraction of C2+ and [C ii] emission would be reduced. In Fig. 3b we show the same calculation for a hydrogen density n(H) = 100 cm-3 and we see it has the same behavior as the lower n(H) case but the transition occurs at a higher flux FX.
The results in Fig. 3 assume a very small, but non-neglible, electron abundance because it will be present in atomic clouds due to ionization of hydrogen by cosmic rays and X-rays. Under typical ISM conditions found in the Galactic disk the electron fraction in diffuse atomic clouds is small (n(e) /n(H) < 10-3). However, the electron fraction increases with increasing X-ray flux. We can estimate the electron fraction by balancing X-ray ionization with electron recombination. We find a fractional electron abundance ~10-2 for FX = 103 erg cm-2 s-1 in a cloud with n(H) = 102 cm-3. However, the addition of a small fractional abundance of electrons (<0.1) does not change the distribution of Cn+ in the diffuse clouds. Finally, we note that for very large X-ray energy fluxes, FX> 105 erg cm-2 s-1 and for n(H) < 100 cm-3 that the fractional abundance of H+, f(H+) > 0.1 and the assumption of a neutral atomic hydrogen cloud is no longer valid.
 |
Fig. 3 Fractional ionization state of C+ through C4+ versus X-ray luminosity flux, FX, for a diffuse atomic hydrogen cloud with n(H) = 25 cm-3 (panel a)) and 100 cm-3 (panel b)), assuming n(e) = 0.1 cm-3, and Tkin = 100 K and no H2, panel c) includes a 10% admixture of H2. |
3.4. Molecular hydrogen clouds
Highly ionized states of carbon react rapidly with molecular hydrogen and so the main reservoirs of carbon in molecular cloud PDR and XDR regions is C+. Meijerink & Spaans (2005) and Meijerink et al. (2007) included the production of C2+ by X-ray photoionization in their XDR models (see Meijerink & Spaans 2005, Appendix D.3.1). However, as discussed above, the rapid reaction with H2 reduces the C2+ abundance to very low values in their models, even at their maximum energy flux, FX = 160 erg cm-2 s-1. We illustrate the influence of a small admixture of molecular hydrogen, n(H2) = 10 cm-3, or a 10% admixture, on the carbon ionization balance in a diffuse hydrogen cloud with n(H) = 100 cm-3 and Tkin = 100 K. As seen in Fig. 3c the crossover from C+ to C2+ occurs at a higher value of FX than in a cloud with only atomic hydrogen (Fig. 3b).
The rapid charge transfer with molecular hydrogen has a more profound effect in dense PDRs where the H2 suppresses significantly the population of higher carbon ionization states as is illustrated in Fig. 4 for n(H2) = 103 cm-3, where the hydrogen density is held constant (which may not be valid at high X-ray fluxes as discussed below). In the XDR models of Maloney et al. (1996, 1997) and Meijerink & Spaans (2005), Meijerink et al. (2007) the molecular hydrogen density n(H2) ≥ 103 cm-3 and molecular hydrogen is efficient at suppressing the highly ionized states of carbon to such an extent that is necessary to go to very large X-ray fluxes, FX> 103 erg cm-2 s-1 to see any significant decrease in C+. The results are relatively insensitive to the choice of kinetic temperature because the charge exchange reactions with H2 dominate the ionization balance in the PDRs.
In Fig. 4 the hydrogen density was held constant to illustrate the effects of the reactions of the multiply ionized carbon with the ambient gas. However, the X-rays not only ionize carbon but also ionize the hydrogen molecules, producing H which can subsequently be destroyed in reactions with H2 leading to atomic hydrogen (H
which can subsequently be destroyed in reactions with H2 leading to atomic hydrogen (H + H2 → H
+ H2 → H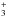 + H, followed by reactions of H
+ H, followed by reactions of H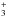 with atoms, trace molecules and electrons that lead to additional production of H atoms). Maloney et al. (1996) estimate that every direct ionization of H2 leads to three H atoms. The formation of H2 takes place on grain surfaces and the formation rate depends on the grain cross section, sticking coefficients, and recombination efficiency as summarized in Appendix D.1 of Meijerink & Spaans (2005). Typical formation rates are of order (1−3) × 10-17n(H)ntot, where ntot is the total number of hydrogen nucleons (=n(H) + 2n(H2)). Thus the PDR layers of dense molecular clouds become atomic hydrogen (and eventually H+) above a threshold FX. We estimate that for dense PDR layers the fraction of H, f(H) is of order one for FX ≳ 102 erg cm-2 s-1. Detailed models of PDR/XDR layers show this transition (see Maloney et al. 1996; Meijerink & Spaans 2005). Thus, although X-rays can, in principle, produce multiply ionized carbon ions in the H2 gas, under realistic conditions in dense molecular clouds this situation is unlikely to be maintained as the molecular hydrogen is dissociated at a lower energy flux than needed to sustain highly ionized states of carbon. As discussed below this process results in the PDR/XDR layers occurring deeper in the cloud where the X-ray flux has been attenuated.
with atoms, trace molecules and electrons that lead to additional production of H atoms). Maloney et al. (1996) estimate that every direct ionization of H2 leads to three H atoms. The formation of H2 takes place on grain surfaces and the formation rate depends on the grain cross section, sticking coefficients, and recombination efficiency as summarized in Appendix D.1 of Meijerink & Spaans (2005). Typical formation rates are of order (1−3) × 10-17n(H)ntot, where ntot is the total number of hydrogen nucleons (=n(H) + 2n(H2)). Thus the PDR layers of dense molecular clouds become atomic hydrogen (and eventually H+) above a threshold FX. We estimate that for dense PDR layers the fraction of H, f(H) is of order one for FX ≳ 102 erg cm-2 s-1. Detailed models of PDR/XDR layers show this transition (see Maloney et al. 1996; Meijerink & Spaans 2005). Thus, although X-rays can, in principle, produce multiply ionized carbon ions in the H2 gas, under realistic conditions in dense molecular clouds this situation is unlikely to be maintained as the molecular hydrogen is dissociated at a lower energy flux than needed to sustain highly ionized states of carbon. As discussed below this process results in the PDR/XDR layers occurring deeper in the cloud where the X-ray flux has been attenuated.
 |
Fig. 4 Fraction of carbon ionization states versus X-ray luminosity flux, FX, for a dense molecular hydrogen gas, n(H2) = 103 cm-3 and Tkin = 100 K, with an admixture n(H) = 1 cm-3 and n(e) = 0.1 cm-3. Carbon remains in the singly ionized state, C+, up to FX ~ 5 × 103 erg cm-2 s-1. |
3.5. X-ray ionization of nitrogen and oxygen
In addition to carbon, atomic oxygen, and nitrogen and oxygen ions have fine-structure transitions that are important diagnostics of the ISM in galaxies and are used as tracers of the SFR (see, for example de Looze et al. 2014). These atoms and ions also play an important role in the thermal balance of the galactic gas. The O and N atomic and ionic lines also show intensity deficits (e.g. Luhman et al. 1998; Dale et al. 2004; Graciá-Carpio et al. 2011).
In this paper we do not model the complete ionization distribution of these species and their FIR emission but instead focus on a few key differences in their chemistry in highly ionized gas as it is likely that much of the emission from galaxies come from these ISM components. These differences alter the distribution of their higher ionization states as compared with carbon2. First, the ionization potential of N (14.534 eV) is significantly greater than hydrogen (13.598 eV) so photoionization occurs only for EUV photons somewhat beyond the Lyman limit (911.8 Ångström). In contrast the ionization potential of oxygen, 13.6181 eV, is only slightly above that of hydrogen but still beyond the Lyman limit. In the WIM charge exchange reactions with protons are able to sustain a significant fraction of O+ and N+ even in the absence of EUV or X-rays. In the case of oxygen the energy difference is small (in temperature units ~224 K) such that the protons in the warm and hot ISM can efficiently charge exchange with O, but in the case of nitrogen the energy difference is so large (~10 980 K) that the ionized gas must be ≳few × 103 K for efficient ionization of N. Furthermore, calculations of the cross sections for H+ + N → N+ + H differ (Kingdon & Ferland 1996; Lin et al. 2005) resulting in somewhat different reaction rates at the temperatures of interest in the WIM (Langer et al. 2015).
In ISM gas with atomic hydrogen, the ions will neutralized by charge exchange with H because the reaction rate coefficient for O+ + H is fast, ~10-9 cm3 s-1, and, while that for N+ + H is slow, ~10-12 cm3 s-1 at 8000 K, it is still faster than that for C+. Furthermore, in contrast to C2+, the charge exchange cross sections for N2+ and O2+ with H are fast, ~10-9 cm3 s-1 at 8000 K, so higher ionization states of N and O will be difficult to sustain in gas containing atomic hydrogen. It will be even more difficult to have an abundance of N+ and O+ in molecular hydrogen gas as their reaction rate coefficients with H2 are very large and, indeed, are primary pathways to forming oxygen- and nitrogen-bearing molecules in shielded regions. Therefore, highly ionized states of nitrogen and oxygen are likely to be found only in the warm highly ionized gas.
We have modeled the distribution of the ionized states of nitrogen and oxygen under conditions of a warm dense ionized medium, similar to the model for carbon in Sect. 3.2. We use the photoionization cross-sections in Verner et al. (1993), charge exchange reaction rate coefficients from McElroy et al. (2013), Lin et al. (2005), and Kingdon & Ferland (1996), and electron recombination rate coefficients from Nahar & Pradhan (1997), Badnell et al. (2003) and Badnell (2006). We show in Fig. 5 results for nitrogen and oxygen in a dense ionized gas with n(e) = 10 cm-3 and n(H+) = n(e). Figure 5a is a plot of the fractional abundances of oxygen ions, O0 to O4+. It can be seen that proton charge exchange keeps oxygen ionized even in the absence of X-rays and that neutral oxygen is essentially absent. As the X-ray flux increases O2+ increases at the expense of O+ and for FX> few × 102 erg cm-2 s-1 all the oxygen is in the highest ionization state considered here, O4+. Figure 5b and c plot the distribution of nitrogen ions, N0 to N4+, using the charge exchange rate coefficients of Lin et al. (2005) and Kingdon & Ferland (1996), respectively. Their distribution is somewhat different than oxygen at low X-ray fluxes because the temperature is not high enough for efficient charge exchange by H+ to keep all the nitrogen ionized. Instead the nitrogen is only partially ionized, but more so using the results of Kingdon & Ferland (1996). As the X-ray flux increases it ionizes the nitrogen and N+ increases, and then at larger fluxes the distribution starts to resemble those of carbon and oxygen. For FX> few × 102 erg cm-2 s-1 all the nitrogen is essentially in the form of N4+ (the highest ionization state included in our models).
 |
Fig. 5 Fraction of oxygen ionization states a) and nitrogen ionization states (b) and c)) versus X-ray luminosity flux, FX, for a dense WIM with n(e) = 10 cm-3 and Tk = 8000 K. Panel b) assumes the charge transfer rates of Lin et al. (2005) and panel c) those of Kingdon & Ferland (1996) – see text. |
We expect the fine-structure FIR lines from N+, O0, and O2+ to come primarily from the WIM or H ii regions because their abundances will be much smaller in neutral clouds because of the rapid charge exchange and ion molecule reactions of N+ and O+ with H and H2. In the WIM, if the dominant processes are proton charge exchange, X-ray photoionization, and electron radiative and dielectronic recombination, then the distribution of lower ionized states of nitrogen and oxygen in the WIM will be shifted towards higher ionization states for large X-ray fluxes. We expect that the emission from lines such as [O iii] at 52 μm and 88 μm, [N ii] at 122 μm and 205 μm, and [N iii] at 57 μm, will also be suppressed in the presence of a strong X-ray flux, as is observed in a number of starburst and active galactic sources.
4. Discussion
The solutions in Sect. 3 show that it is possible for a high X-ray flux in galactic nuclei to alter the carbon ionization balance and reduce the C+ abundance and correspondingly the [C ii] luminosity. In the presence of a high flux of soft X-rays above 1 keV, a condition encountered in many AGNs (Stacey et al. 2010; Ebrero et al. 2009), the abundance of singly ionized carbon is reduced and converted into higher ionization states. This reduction occurs primarily in the hot highly ionized gas that fills most of the galactic central zone, to some degree in the dense ionized skins surrounding molecular clouds, less so in diffuse atomic hydrogen clouds, and very little, if at all, in the dense PDRs at the edge of the CO molecular cores. Furthermore, in galactic nuclei with a high X-ray flux we would expect to see an increase in the dust temperature and infrared luminosity (Voit 1991). Therefore in galactic nuclei, and in particular in AGNs, we expect a reduction in [C ii] emission relative to FIR/IR emission depending on the relative contribution of different ISM components to the [C ii] luminosity. Unfortunately the next most abundant ion, C2+, does not have fine structure FIR emission lines as its 2s2 ground state has spin zero, and C3+, although it has spin angular momentum due to its unpaired electron in the 2S level, does not have a nuclear spin or orbital angular momentum to break the degeneracy of the two electron spin states. Instead to test the effect of X-ray ionization on the carbon balance we would need studies of their UV emission. For example the [C iv] UV resonance lines are detected in extragalactic sources and have been used to trace the formation rate of massive stars (Leitherer & Lamers 1991; Robert et al. 1993). [C iv] UV absorption lines have also been used to study the properties of the Galactic Halo (Savage et al. 2000) where carbon is presumed to be collisionally ionized in hot coronal gas (Gnat & Sternberg 2007).
To illustrate the potential effects of X-rays in reducing [C ii] emission we have run a number of simple models of [C ii] luminosity as a function of X-ray luminosity. One model uses the ISM conditions of the CMZ and the other the higher densities appropriate to AGNs. To model any actual nucleus we would need to know many parameters including the properties of various ISM components – their densities, temperatures and filling factors, and the distribution and luminosities of the X-ray sources. As will be seen below the primary effect of the X-rays is to reduce the [C ii] emission from the ionized gas. Thus whether X-ray photoionization plays an important role or not depends on the relative contribution of the WIM and PDR components in galactic nuclei. In the remainder of this section we present simple models for the contribution to [C ii] emission from the ISM components in galactic nuclei and parameterize the effects of X-ray ionization on the reduction in [C ii] emission. In one we will be guided by the properties of the ISM in the CMZ, but consider much larger X-ray luminosities than found there. In the other we consider much higher electron densities for the WIM and H2 densities in PDRs, as well as a larger volume. Our intent is not to model any particular galactic nucleus but to highlight the general behavior of the [C ii] emissivity in AGNs and similar active nuclei as a function of X-ray luminosity.
4.1. [C ii] emissivity from X-ray dominated nuclei
We can estimate the [C ii] luminosity by summing the contributions of the different ISM components over their respective volumes. To simplify our model calculations we assume that the physical parameters within each of these components are uniform and represent typical gas conditions. The total galactic luminosity is 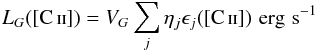 (18)where VG is the total volume of all [C ii] emitting regions, ηj is the fractional volume occupied by each ISM component j, and ϵj([C ii]) is the [C ii] emissivity in erg cm-3 s-1 of component j. The emissivity for optically thin lines,
(18)where VG is the total volume of all [C ii] emitting regions, ηj is the fractional volume occupied by each ISM component j, and ϵj([C ii]) is the [C ii] emissivity in erg cm-3 s-1 of component j. The emissivity for optically thin lines, 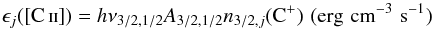 (19)where A3/2,1/2 is the Einstein spontaneous radiation coefficient, ν3/2 /,1/2 is the transition frequency, and n3/2,j(C+) is the number density of the upper
(19)where A3/2,1/2 is the Einstein spontaneous radiation coefficient, ν3/2 /,1/2 is the transition frequency, and n3/2,j(C+) is the number density of the upper 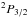 state in ISM component j. In the optically thin limit one can solve exactly for the density of the
state in ISM component j. In the optically thin limit one can solve exactly for the density of the 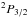 state as a function of the density and temperature of the collision partner (see Goldsmith et al. 2012, Langer et al. 2014b),
state as a function of the density and temperature of the collision partner (see Goldsmith et al. 2012, Langer et al. 2014b), 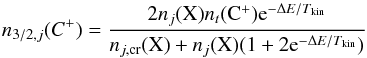 (20)where ΔE = 91.25 K, nj(X) is the density of the dominant collision partner X (=e, H, H2) in each ISM component j, and nj,cr(X) is the corresponding critical density (see Goldsmith et al. 2012, Wiesenfeld & Goldsmith 2014). In this paper we use the exact solution, but note that in the limit where the density of the collision partner, n(X), is much less than the critical density, ncr(X), Eq. (20) can be simplified to n3/2(C+) ≃ 2(n(X) /ncr(X))e− 91.25 /Tkin.
(20)where ΔE = 91.25 K, nj(X) is the density of the dominant collision partner X (=e, H, H2) in each ISM component j, and nj,cr(X) is the corresponding critical density (see Goldsmith et al. 2012, Wiesenfeld & Goldsmith 2014). In this paper we use the exact solution, but note that in the limit where the density of the collision partner, n(X), is much less than the critical density, ncr(X), Eq. (20) can be simplified to n3/2(C+) ≃ 2(n(X) /ncr(X))e− 91.25 /Tkin.
We define the average emissivity as ⟨ ϵ( [C ii] ) ⟩ = LG([C ii])/VG, which upon substituting the line parameters for [C ii] yields, 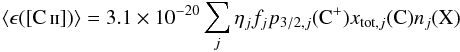 (21)where fj is the fractional abundance of C+ with respect to all the charge states of ionized carbon for ISM component j, p3/2,j(C+) = n3/2,j(C+) /nt(C+) is the fractional population of the
(21)where fj is the fractional abundance of C+ with respect to all the charge states of ionized carbon for ISM component j, p3/2,j(C+) = n3/2,j(C+) /nt(C+) is the fractional population of the 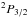 state, xtot,j(C) is the total fractional abundance of carbon in all charge states with respect to the total hydrogen density (nt = n(H) + 2n(H2) + n(H+)), and nj(X) is the dominant collision partner in component j.
state, xtot,j(C) is the total fractional abundance of carbon in all charge states with respect to the total hydrogen density (nt = n(H) + 2n(H2) + n(H+)), and nj(X) is the dominant collision partner in component j.
4.2. Galactic nucleus with CMZ model parameters
In this section we set up a model galactic nucleus to study the [C ii] emissivity as a function of X-ray luminosity based on ISM parameters of the CMZ. To model the [C ii] emissivity from galactic nuclei we need to know the filling factor, density, temperature, and fractional abundance of C+ for each ISM component. We will use the conditions of the ISM in the CMZ as a guide for many, but not all components, and will consider a much wider range of X-ray luminosity than is found there. The dominant ISM components in the nucleus are: 1) a dense WIM; 2) a low density HIM; 3) cold diffuse atomic hydrogen clouds CNM; 4) a dense ionized skin (DIS) surrounding molecular clouds; 5) the dense PDRs of GMCs; and 6) compact H ii regions. We will neglect the contribution from the HIM because its densities are too low, n(e) ~few × 10-3 cm-3 and the compact H ii regions which, while bright, have too small a filling factor, to contribute to the bulk of the [C ii] emission. We consider the galactic nucleus to be a disk with a size similar to the CMZ. We assume a radius r = 200 pc which is the boundary of massive GMCs at l ~ 358.̊7 in the CMZ as traced by CO (Oka et al. 1998) and a scale height z = 30 pc (disk thickness of 60 pc) slightly larger than the scale height of the dense WIM (Ferrière et al. 2007)3.
We adopt the following densities and temperatures for the key ISM components that contribute to the [C ii] emission from galactic nuclei: 1) the low density WIM is assumed to have Tkin = 8000 K and an average density n(e) ~ 10 cm-3 (Cordes & Lazio 2003; Roy 2013); 2) diffuse atomic hydrogen clouds with n(H) = 100 cm-3 and Tkin = 100 K, 3) dense PDRs with n(H2) = 103 cm-3 and Tkin = 100 K, and for the dense ionized skins we adopt n(e) = 20 cm-3 from the study of two clouds at the edge of the CMZ (Langer et al. 2015). These values are summarized in Table 4. We also assume a fractional abundance of carbon appropriate to the inner Galaxy, xtot,j(C) = 5 × 10-4, which is an extrapolation of the metal abundance profile in the disk to inside 3 kpc (see Wolfire et al. 2003, Pineda et al. 2013).
We estimate the filling factor, η, of each component from the mass and density of the components. The mass of the GMCs in the CMZ is estimated to lie in the range (2−6) × 107M⊙ (Oka et al. 1998; Ferrière et al. 2007) and we adopt the intermediate value 4 × 107M⊙ . Their average H2 densities are in the range 104–105 cm-3. We estimate the volume filled by the GMCs by dividing the total mass in GMCs, by the density. For n(H2) ~ 104 cm-3, the volume filled by clouds is ~8 × 104 pc3, which yields a filling factor ηH2 about 1.1% of the volume of the CMZ, for 105 cm-3 the volume is only ~8 × 103 pc3, or ηH2 ~ 0.11% of the CMZ volume. The [C ii] emission from the dense PDR layer outside the CO cloud can be estimated from models of massive GMCs (Wolfire et al. 2010) who find that the PDR layers lie in the range 1 to 1.5 mag thick regardless of the cloud mass, UV radiation field, or hydrogen density. Therefore the fractional volume filled by the PDR is just the difference between the volume occupied by the cloud out to the edge of the PDR minus that of the dense CO core. For example, assuming a typical cloud mass of 105M⊙ and a core density of 104 cm-3 and PDR density of 103 cm-3, the PDR occupies ~30 percent of the total cloud volume, which corresponds to ~3 × 10-3 of the volume of the CMZ. For more massive clouds, 106M⊙ , and interior and PDR densities, 105 cm-3 and 104 cm-3, respectively, the PDRs occupy only ~7 × 10-4 of the CMZ.
Here we will consider a range of PDR filling factors, η (PDR) = 1 × 10-3 to 3 × 10-3. The choice of PDR filling factor has an influence on the models for two reasons, first, as shown above, it takes a very large X-ray flux to alter the carbon ionization balance in H2 gas, and second, if the X-ray flux is large enough to alter the carbon ion abundance it is also large enough to destroy H2. Thus increasing the X-ray flux only pushes the PDR-like layer deeper into the cloud, but does not destroy it. To simulate this situation in our model we assume that X-ray photoionization does not alter the C+ abundance in the PDR component.
The dense ionized skins occupy about 30% of the volume of the CO core of the GMCs, for a filling factor η(DIS) ~2 × 10-3, if the size of this region is similar to that derived for clouds in the region of Sgr E (Langer et al. 2015). The diffuse atomic clouds have an estimated mass ~5 × 105M⊙ (Ferrière et al. 2007) which corresponds to a filling factor ~0.03 at a density n(H) = 100 cm-3. The ionized gas fills roughly 95% of the volume of the galactic nucleus, of which 80% is the dense WIM and ~15% the HIM (see Ferrière et al. 2007) with negligible [C ii] emission.
Galactic nucleus model parameters.
4.2.1. [C ii] luminosity in the central X-ray model
To demonstrate the effects of X-ray photoionization on the [C ii] emission we calculate the [C ii] luminosity as a function of X-ray luminosity for a central X-ray source, such as might be generated by a massive accreting black hole using the ISM parameters in Table 4. We calculate the X-ray flux as a function of radius assuming no attenuation and r-2. Figure 6 shows the total [C ii] luminosity, L([C ii]) in units of solar luminosity, L⊙, as a function of X-ray luminosity, L(X-ray), ranging from 1038 to 1048 erg s-1 (the upper limit is a factor of a few beyond what is observed in AGNs). Results are shown for three different choices of filling factor η (PDR) = 1, 2, and 3 × 10-3, and it can be seen that it takes an X-ray luminosity ≥1042 erg s-1 to have a measurable effect on the C+ balance and decrease the [C ii] luminosity in the galactic nucleus, and >1043 erg s-1 to have a significant effect. At the highest X-ray luminosities it is possible to suppress, by an order of magnitude or more, the [C ii] emission from the X-ray region of an AGN. The asymptotic value is the contribution mainly from the PDRs.
For a central X-ray source the contributions to the total luminosity will change as a function of galactic radius. In Fig. 7 we plot the contribution of the individual ISM components to L([C ii]) as a function of distance from the central source, r(pc), for two values of the central X-ray luminosity, L(X - ray) = 1042 and 1044 erg s-1, adopting the intermediate filling factor η(PDR) = 2 × 10-3. We chose these luminosities as examples because it is in this range of L(X-ray) that the photoionization of the WIM begins to make a difference in the relative contributions of the PDRs and the WIM. For L (X - ray) = 1042 erg s-1 (Fig. 7 top panel) the WIM dominates the contribution to [C ii] throughout the nucleus, followed by emission from the dense PDRs, while the diffuse H i clouds and dense ionized skins (DIS) around the GMCs make negligible contributions to L([C ii]). At higher luminosities the X-rays have a more profound effect on the total emission, as shown in Fig. 7 (bottom panel), and there is a different mix of ISM components contributing to L([C ii]). For L(X-ray) = 1044 erg s-1 PDRs dominate the [C ii] luminosity for r ≲ 100 pc, while the WIM dominates [C ii] luminosity outside 100 pc, and the H i and DIS components are, again, negligible. Overall, the total [C ii] luminosity decreases with increasing L(X-ray) as was shown in Fig. 6. The ISM physical conditions in the WIM, DIS, dense PDRs, and atomic hydrogen clouds may be different in the AGNs, LIRGs, or ULIRGs from those found in the CMZ, but the general dependence of the [C ii] luminosity on X-ray luminosity will be similar.
 |
Fig. 6 [C ii] luminosity in units of solar luminosity as a function of the luminosity of a central X-ray source. The assumed ISM parameters and dimensions of the nucleus are given in the text. The three curves represent different values of the filling factor for PDR and PDR-like conditions in the nucleus. |
 |
Fig. 7 [C ii] luminosities of the individual ISM components are plotted as a function of radius in a galactic nucleus with a central X-ray source with L(X-ray) = 1042 (top panel) and 1044 erg s-1 (bottom panel) with a filling factor η(PDR) = 2 × 10-3. The assumed ISM parameters and dimensions of the nucleus are given in the text. The dense WIM dominates the [C ii] emission at L(X-ray) =1040 erg s-1 but is increasingly suppressed with increasing L(X-ray) until the PDRs dominate the emission. |
4.2.2. [C ii] luminosity in the uniform X-ray flux model
Whereas in some galactic nuclei the X-ray luminosity is dominated by a central source, in others the luminosity may result from diffuse emission and/or numerous discrete sources spread throughout. To model this situation we assume a uniform flux throughout the nucleus and calculate the luminosity, L(X-ray) = FXA, where A is the area of the boundary of the galactic nucleus. We adopt the same disk model with a radius of 200 pc and 60 pc thick used in the CMZ model with a central X-ray source. The exact dimensions are not critical because the results can be extended to galaxies with X-ray regions of different size through the relationship between flux, emissivity, and luminosity for a uniform environment. The ISM parameters are again given in Table 4 and we adopt the intermediate value η(PDR) = 2 × 10-3. The X-ray luminosity for a uniform flux is just proportional to the area of the outermost volume, L(X-ray) = FXAAGN, where AAGN is the area of the AGN’s uniform X-ray source, while the [C ii] luminosity is proportional to the emissivity times the volume, L([C ii]) = ϵ([C ii])VAGN, where VAGN is the corresponding volume of the uniform X-ray source. Therefore, the results plotted below using the dimensions of the CMZ can be converted to different AGN volumes as follows, 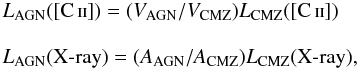 (22)in which one scales a given AGN X-ray luminosity by the ratio of areas to the CMZ and then determines the CMZ [C ii] luminosity and scales it by the ratio of the volumes to derive the AGN [C ii] luminosity. In Fig. 8 we plot the [C ii] luminosity arising from a galactic nucleus with uniform X-ray source. The luminosities of the individual ISM components are plotted as a function of X-ray luminosity. The dense WIM dominates the [C ii] luminosity up to L(X-ray) ~ 1044 erg s-1, after which PDRs, with a filling factor η(PDR) = 2 × 10-3, dominate the emission. Finally, in Fig. 9 we compare the [C ii] luminosity of the central and uniform X-ray models as a function of L(X-ray) assuming the same CMZ ISM conditions and n(e) = 10 cm-3 for the WIM and the same value for η(PDR) = 2 × 10-3. The two solutions for L([C ii]) are very similar. At low X-ray luminosity the flux is too low to influence the C+ abundance and the emissivities are independent of L(X-ray), while high luminosities the C+ abundances are reduced in the WIM throughout the volume and the PDRs dominate the emission. At intermediate X-ray luminosities the solutions for the central source reduces the C+ abundance primarily in the interior (smaller r) while having less of an effect near the outer part of the nucleus, and this tends to average out to a solution close to that of having a uniform flux.
(22)in which one scales a given AGN X-ray luminosity by the ratio of areas to the CMZ and then determines the CMZ [C ii] luminosity and scales it by the ratio of the volumes to derive the AGN [C ii] luminosity. In Fig. 8 we plot the [C ii] luminosity arising from a galactic nucleus with uniform X-ray source. The luminosities of the individual ISM components are plotted as a function of X-ray luminosity. The dense WIM dominates the [C ii] luminosity up to L(X-ray) ~ 1044 erg s-1, after which PDRs, with a filling factor η(PDR) = 2 × 10-3, dominate the emission. Finally, in Fig. 9 we compare the [C ii] luminosity of the central and uniform X-ray models as a function of L(X-ray) assuming the same CMZ ISM conditions and n(e) = 10 cm-3 for the WIM and the same value for η(PDR) = 2 × 10-3. The two solutions for L([C ii]) are very similar. At low X-ray luminosity the flux is too low to influence the C+ abundance and the emissivities are independent of L(X-ray), while high luminosities the C+ abundances are reduced in the WIM throughout the volume and the PDRs dominate the emission. At intermediate X-ray luminosities the solutions for the central source reduces the C+ abundance primarily in the interior (smaller r) while having less of an effect near the outer part of the nucleus, and this tends to average out to a solution close to that of having a uniform flux.
 |
Fig. 8 Luminosities of the individual ISM components arising from a galactic nucleus with a uniform X-ray source, and physical parameters given in the text and Table 4 are plotted as a function of X-ray luminosity. |
 |
Fig. 9 [C ii] luminosity for the central X-ray source (black line) compared to that of the uniform flux model (red line). The ISM properties are the same in both models. |
4.3. AGN representative model of [C ii] emission
In the CMZ model we adopted an average electron density n(e) = 10 cm-3, but the most central region has been estimated to have a much higher density (cf. Ferrière et al. 2007). For example, Mezger & Pauls (1979) used thermal radio continuum radio observations to derive a central n(e) ~26 cm-3 while Mehringer et al. (1992, 1993) derive even higher electron densities outside compact HII regions near Sgr B1 and B2 and derive an average electron density of ~60 and 80 cm-3 over two regions ~700 and 170 pc2, respectively. The conditions encountered in the most energetic region of the CMZ is likely to prevail over a much larger volume in AGNs. In addition, the [N iii] luminosity in some galactic nuclei is comparable to that of [N ii] but requires higher electron densities to excite its 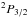 level. Thus it is reasonable to consider a model for AGNs with much higher WIM densities than the CMZ. In addition, the PDR densities are also likely higher (Stacey et al. 2010). To illustrate the impact of higher electron densities we first demonstrate the sensitivity of the WIM [C ii] luminosity as a function of n(e) on a stand alone basis and then in a simple model of AGNs.
level. Thus it is reasonable to consider a model for AGNs with much higher WIM densities than the CMZ. In addition, the PDR densities are also likely higher (Stacey et al. 2010). To illustrate the impact of higher electron densities we first demonstrate the sensitivity of the WIM [C ii] luminosity as a function of n(e) on a stand alone basis and then in a simple model of AGNs.
4.3.1. [C ii] luminosity from the WIM
In the model adopted here for the [C ii] luminosity from AGNs the WIM dominates the emission of [C ii] over a wide range of X-ray luminosities. However, the model adopts a fixed electron density in the WIM, n(e) = 10 cm-3. To understand better the sensitivity to the choice of this parameter we have also calculated the luminosity from the WIM, LWIM([C ii]), versus the electron density. Figure 10 shows the fraction of singly ionized carbon in the WIM as a function of X-ray luminosity for a range of WIM electron abundances, n(e) = 1 to 25 cm-3. As expected, the smaller the electron abundance the more profound is the effect of X-rays on f(C+) for a given X-ray luminosity, because the electron recombination rate of C+ cannot as efficiently offset the X-ray photoionization rate. In the absence of X-rays the luminosity from the WIM would be expected to decrease roughly like n(e)-2 below the electron critical density (ncr(e) ~ 40 cm-3). However, we expect that the [C ii] luminosity from the WIM decreases faster than the density n(e) in the presence of a large X-ray flux because not only does the collisional excitation rate decrease, but so does the fraction of available C+. This nonlinear effect can be seen in Fig. 11, which plots LWIM as a function of L(X-ray) for the range of n(e) plotted in Fig. 10. In Fig. 12 we plot the total [C ii] luminosity, Ltot as a function of L(X-ray) for a range of n(e) in the WIM, and it can be seen that the drop in [C ii] luminosity can be quite large if the WIM electron density is higher, such as might be expected in AGNs.
 |
Fig. 10 Fraction of singly ionized carbon in the WIM versus X-ray luminosity in the uniform X-ray flux model, for a range of WIM electron densities. |
 |
Fig. 11 [C ii] luminosity arising from the WIM versus X-ray luminosity, for a range of electron densities in the WIM. The remaining ISM parameters are the same as that for the uniform model. |
 |
Fig. 12 Total [C ii] luminosity (all ISM components) versus X-ray luminosity, for a range of electron densities in the WIM. The remaining ISM parameters are the same as that for the uniform model. |
4.3.2. [C ii] luminosity from an AGN
We model a hypothetical AGN assuming a disk geometry with a central X-ray source. The WIM electron density is n(e) = 50 cm-3 and the PDR has n(H2) = 5 × 103 cm-3. The molecular mass in AGNs is larger than the CMZ but as the density of the GMCs is an order of magnitude higher the filling factor is not much different from what we calculated for the CMZ and we assume η = 0.002. One other difference is the scale height of the gas which is likely to be higher than in the CMZ due to a higher pressure and we adopt a scale height for CO clouds and the WIM of 100 pc and 200 pc, respectively. The [C ii] luminosity for this AGN model is plotted in Fig. 13 as a function of galactic radius from the central source for a range of L(X-ray). The X-ray flux close to the central accretion hole ionizes the C+ and reduces the luminosity of the WIM as can be seen in the decrease in the luminosity as a function of X-ray luminosity. As one goes further from the central source the WIM increases and contributes to the total. At a few hundred pc there is roughly an order of magnitude difference in the total luminosity. The L([C ii]) dependence on L(X-ray) is similar to the CMZ example except that the luminosity is larger due to higher electron and H2 densities.
 |
Fig. 13 Total [C ii] luminosity of a hypothetical AGN versus galactic radius for a range of X-ray luminosities. The key labels the log of the X-ray luminosity and ranges from LogL(X-ray) = 40 to 48. The decrease in [C ii] luminosity with increasing L(X-ray) is due to the destruction of C+ in the WIM close to the source of X-rays. The radius over which the X-rays photoionize C+ increases with increasing X-ray luminosity. |
4.4. Observational test case
In Fig. 14, we compare our model calculations to a sample of six extragalactic sources for which the [C ii], FIR, and X-ray luminosities have been measured (Stacey et al. 2010 and references therein). We also include two high-redshift AGNs compiled by Gullberg et al. (2015) in [C ii] and FIR, and in X-rays by Vignali et al. (2005) and Law et al. (2004). We calculated the model [C ii]/FIR ratio by dividing the predicted [C ii] luminosity for different PDR filling factors (Fig. 6) by the FIR luminosity of the CMZ, LFIR = 4 × 108L⊙ (Launhardt et al. 2002). The observed X-ray luminosities cover 2 to 10 keV and, because the spectral energy distribution increases at lower energies the actual luminosity would be a factor ~3.8 larger for E> 1 keV assuming the spectral energy distribution in Eq. (15) with Γ = 1.9. Thus the data points would shift slightly to the right by ~0.59 on the log scale, which is still consistent with our model calculation. We see that for this sample of AGNs the [C ii]/FIR luminosity ratio is in good agreement with our model predictions, showing significantly lower [C ii]/FIR ratios for L(X - ray) > 1043 erg s-1.
 |
Fig. 14 Predicted [C ii]/FIR luminosity ratio versus X-ray luminosity for different PDR filling factors (see Fig. 6). Also plotted are data points for six AGNs (red bullets) observed in [C ii], FIR, and X-rays (Stacey et al. 2010) and two high-redshift AGNs (black squares) observed in [C ii] (as compiled in Gullberg et al. 2015), FIR by Vignali et al. (2005), and X-rays by Law et al. (2004). We assumed 30% uncertainties for the [C ii]/FIR ratios from Stacey et al. (2010) and for the X-ray luminosities. |
4.5. Central molecular zone [C ii] luminosity
The Galactic CMZ provides the best opportunity to check our model of [C ii] luminosity in the presence of X-rays because we have the best information about the state of its ISM components, at least as compared to external galaxies. However, in practice the uncertainties in its ISM conditions are too large to allow more than an estimate of the [C ii] luminosity.
Unfortunately, the Galactic CMZ is not a strong source of X-ray luminosity. Chandra has detected ≳9000 discrete stellar sources in the innermost CMZ (Muno et al. 2009), but most of these have luminosities in the range L(X - ray) = 1031 and 1033 erg s-1 with a few having maximum values ~few × 1034 erg s-1. Adopting an average luminosity per source of 1032 erg s-1 yields a maximum extended luminosity of order 1036 erg s-1, which is too low to have much of an effect on the [C ii] luminosity based on the results in Fig. 8. The strongest point source in the CMZ, 1E 1740.7–2942, is believed to be an accreting stellar black hole and has a luminosity, L(X-ray) ~few × 1037 erg s-1 (see Maloney et al. 1997). The black hole assumed associated with Sgr A at the Galactic Center has a current luminosity ~1033 erg s-1 (Baganoff et al. 2001), but may have been brighter in the recent past. Thus X-rays likely have little effect on the [C ii] luminosity of the CMZ. and so it is not a good source for testing the effects of X-rays on [C ii] luminosity. Nonetheless, the CMZ [C ii] luminosity does provide an opportunity to validate whether our model predicts the right order of magnitude for the [C ii] luminosity.
To calculate the [C ii] luminosity for the CMZ we use the CMZ physical dimensions adopted in Sect. 4.2 and ISM parameters in Table 4 for the atomic clouds, PDRs, and DIS components, but modify the WIM model to fit with the WIM electron profile (Ferrière et al. 2007), as discussed below. The atomic, molecular, and ionized gas in the CMZ is concentrated at the center and decreases with radius and distance above and below the plane. We are interested in calculating the [C ii] luminosity arising from the volume of the CMZ so the distribution of the atomic clouds and the PDRs and DISs associated with the GMCs is not important under the assumption that the clouds have the same characteristics throughout the CMZ volume, as assumed here, and as long as the X-ray flux has a minimal impact on the C+ abundance. The WIM density, in contrast, does change throughout the CMZ. Ferrière et al. (2007) summarizes the results from Lazio & Cordes (1998) and Cordes & Lazio (2002, 2003) and expresses the electron space averaged density as the sum of three terms, one of which, ⟨ n(e) ⟩ 3(r,z), dominates in the CMZ with a profile that decreases as a Gaussian in r and z (the other two terms are smaller in absolute value but have much larger scale factors and so decrease very slowly in the CMZ). We have simplified this expression by neglecting the offset terms in ⟨ n(e) ⟩ and setting ⟨ n(e) ⟩ 1 and ⟨ n(e) ⟩ 2 constant in the CMZ, which yields 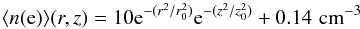 (23)where the peak density is ~10 cm-3 at the center and decreases with Gaussian parameters r0 = 145 pc and z0 = 26 pc.
(23)where the peak density is ~10 cm-3 at the center and decreases with Gaussian parameters r0 = 145 pc and z0 = 26 pc.
We have calculated the [C ii] emissivity throughout the CMZ disk (r ≤ 200 pc and | z | ≤ 30 pc) using the model of the CMZ discussed above and assuming a central source with X-ray luminosity 1037 erg s-1. We integrate the emissivity over the volume of the CMZ to derive an emergent [C ii] luminosity, L([C ii]) ~7–9 × 105L⊙, for η(PDR) = (1−3) × 10-3. This luminosity hardly differs from that without an X-ray source because, as shown earlier, the X-ray luminosity is too low to modify the C+ distribution in the ISM components. For comparison we have calculated the [C ii] luminosity measured by BICE using the line intensity contours in Fig. 8 of Nakagawa et al. (1998) integrated over the area of the CMZ. We estimate that BICE observes L([C ii]) ~ 4.5 × 105 erg s-1. Our L([C ii]) model of the CMZ and the BICE observations agree within a factor of two or better which is probably about the best that we can expect given the uncertainties in ISM parameters assumed in our model calculation. In summary, the reasonable agreement of our [C ii] emissivity model and the observed [C ii] luminosity of the CMZ lends confidence to the approach presented here.
5. Summary
We have explored the influence of X-rays on the ionization balance of carbon and [C ii] luminosity in the ISM with a focus on its effect in galactic nuclei with large X-ray luminosity. In the presence of a large X-ray flux we find that C+ can be converted to higher ionization states, Cj+ with j ≥ 2. The effect of X-rays on the [C ii] luminosity of galactic nuclei depends on the X-ray luminosity and the details of the properties of the ISM, namely the density, temperature, and filling factors for each of the ISM components. The biggest impact is on the ionization distribution in the WIM, where C+ is more readily converted to C2+, C3+, etc., thus reducing its contribution to the [C ii] luminosity.
Thus X-ray photoionization is another mechanism to consider in understanding the reduction of the [C ii] to FIR luminosity ratio in AGNs. It appears that, on average, it requires a soft X-ray luminosity greater than about 1042–1043 erg s-1 to have a noticeable effect on the [C ii] luminosity. Our Galaxy does not fall into this category, but many others do, in particular some LIRGs and ULIRGs, and many AGNs. If the primary X-ray source is an accreting black hole then the [C ii] will be suppressed in its vicinity but not necessarily throughout the entire galactic nucleus. However, as discussed above, AGNs have, on average, considerably larger X-ray luminosities with L(X-ray) ranging up to a few × 1047 erg s-3 (Ebrero et al. 2009). In the AGNs with L(X-ray) ≳ 1043 erg s-1, depending on the details of the ISM parameters, X-rays can suppress the [C ii] luminosity. It is precisely these sources that consistently have a much lower [C ii] luminosity compared to their FIR dust luminosity (see summary by Gullberg et al. 2015) which may be due, in part, to the influence of X-rays on the C+ photoionization into higher ionization states.
We have also briefly considered the ionization balance of nitrogen and oxygen in the dense WIM under the influence of X-rays. We find that the lower ionization states of nitrogen and oxygen are suppressed at high X-ray fluxes and at the highest flux values these elements are essentially in the highest ionization state. We did not calculate detailed models of the emission from the FIR lines of the lower ionization states, but it is apparent, by comparison with the results for carbon, then the emission from these tracers will be suppressed at high fluxes. [N iii] is observed to be strong in some galaxies which requires an ionization source for N and N+. The usual explanation invokes an EUV flux, but X-rays are an alternative explanation and have the advantage of being present throughout galactic nuclei. Thus X-ray photoionization may explain some of the decrease in emission from carbon, nitrogen, and oxygen ions and the increase in emission of higher ionization states, such as [N iii] and [O iii], in AGNs.
We have been guided by conditions in the Galactic CMZ, but AGNs will have different ISM parameters of density, temperature, and filling factor for the various gas components and each one would need to be analyzed on a case by case basis. For comparison we adopted a model of an AGN with higher WIM and PDR densities. We also compared our [C ii] luminosity models with a small data set of extrgalactic sources with high X-ray luminosities. We find that their [C ii] to FIR ratio decreases significantly at an X-ray luminosity consistent with our model calculations. Finally, to confirm that the [C ii] emissivity model we use is reasonable we calculated the [C ii] luminosity for the CMZ where conditions are reasonably well known, at least in comparison to extragalactic sources. The Galactic CMZ model produces a [C ii] luminosity ~7–9 × 105L⊙, depending on the details of parameters chosen for the WIM and PDRs. This [C ii] luminosity compares reasonably well, given all the uncertainties in the ISM conditions, to the [C ii] luminosity of ~ 4.5 × 105L⊙ we estimate from the BICE observations.
In conclusion, X-ray photoionzation can alter the ionization balance of the ionization states of carbon, nitrogen, and oxygen primarily in the ionized ISM, resulting in a significant fraction of their abundance shifting to highly ionized states in AGNs. Therefore the effects of X-rays on the ionization balance needs to be included in any modeling and interpretation of carbon, nitrogen, and oxygen FIR line emission in AGNs.
There is also a body of work on the carbon ionization balance in very hot diffuse ionized gas due to electron collisional ionization of carbon (e.g. Gnat & Sternberg 2007).
An example of the differences in the distribution of C, N, and O ionization states in the presence of X-rays can be seen in the models of Ádámkovics et al. (2011) for protoplanetary disks.
The scale height of the WIM adopted for the CMZ is less than that derived from [C ii] for the Galactic disk where the density is much lower (Langer et al. 2014a; Velusamy & Langer 2014).
Acknowledgments
We would like to thank an anonymous referee for a careful reading of our manuscript and several suggestions that improved the models and discussion. We would also like to thank Dr. P. F. Goldsmith for useful comments on the text and Dr. B. Drouin for discussions regarding the spin states of [C iii] and [C iv]. This work was performed at the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Ádámkovics, M., Glassgold, A. E., & Meijerink, R. 2011, ApJ, 736, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R. 2006, A&A, 447, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Badnell, N. R., O’Mullane, M. G., Summers, H. P., et al. 2003, A&A, 406, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baganoff, F. K., Bautz, M. W., Brandt, W. N., et al. 2001, Nature, 413, 45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bruderer, S., Doty, S. D., & Benz, A. O. 2009, ApJS, 183, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002, unpublished [arXiv:astro-ph/0207156v3] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2003, unpublished [arXiv:astro-ph/0301598] [Google Scholar]
- Cox, D. P. 2005, ARA&A, 43, 337 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Dale, D. A., Helou, G., Brauher, J. R., et al. 2004, ApJ, 604, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Looze, I., Baes, M., Bendo, G. J., Cortese, L., & Fritz, J. 2011, MNRAS, 416, 2712 [Google Scholar]
- de Looze, I., Cormier, D., Lebouteiller, V., et al. 2014, A&A, 568, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz-Santos, T., Armus, L., Charmandaris, V., et al. 2014, ApJ, 788, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Ebrero, J., Carrera, F. J., Page, M. J., et al. 2009, A&A, 493, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrière, K., Gillard, W., & Jean, P. 2007, A&A, 467, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gnat, O., & Sternberg, A. 2007, ApJS, 168, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., Langer, W. D., Pineda, J. L., & Velusamy, T. 2012, ApJS, 203, 13 [Google Scholar]
- Goto, M., Geballe, T. R., Indriolo, N., et al. 2014, ApJ, 786, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Graciá-Carpio, J., Sturm, E., Hailey-Dunsheath, S., et al. 2011, ApJ, 728, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Gullberg, B., De Breuck, C., Vieira, J. D., et al. 2015, MNRAS, 449, 2883 [NASA ADS] [CrossRef] [Google Scholar]
- Haffner, L. M., Dettmar, R.-J., Beckman, J. E., et al. 2009, Rev. Mod. Phys., 81, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Heindl, W. A., Cook, W. R., Grunsfeld, J. M., et al. 1993, ApJ, 408, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Iwasawa, K., Sanders, D. B., Teng, S. H., et al. 2011, A&A, 529, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaufman, M. J., Hollenbach, D. J., & Tielens, A. G. G. M. 1998, ApJ, 497, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Kingdon, J. B., & Ferland, G. J. 1996, ApJS, 106, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Krolik, J. H., & Kallman, T. R. 1983, ApJ, 267, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D. 1978, ApJ, 225, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D., Pineda, J. L., & Velusamy, T. 2014a, A&A, 564, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langer, W. D., Velusamy, T., Pineda, J. L., Willacy, K., & Goldsmith, P. F. 2014b, A&A, 561, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langer, W. D., Goldsmith, P. F., Pineda, J. L., et al. 2015, A&A, 576, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Launhardt, R., Zylka, R., & Mezger, P. G. 2002, A&A, 384, 112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Law, N. M., Rutledge, R. E., & Kulkarni, S. R. 2004, MNRAS, 350, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Lazio, T. J. W., & Cordes, J. M. 1998, ApJ, 505, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., & Lamers, H. J. G. L. 1991, ApJ, 373, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, C. Y., Stancil, P. C., Gu, J. P., Buenker, R. J., & Kimura, M. 2005, Phys. Rev. A, 71, 062708 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, M. L., Satyapal, S., Fischer, J., et al. 1998, ApJ, 504, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C., Rémy, A., Galliano, F., et al. 2013, IAU Symp., 292, 127 [NASA ADS] [Google Scholar]
- Malhotra, S., Helou, G., Stacey, G., et al. 1997, ApJ, 491, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Maloney, P. R., Hollenbach, D. J., & Tielens, A. G. G. M. 1996, ApJ, 466, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Maloney, P. R., Colgan, S. W. J., & Hollenbach, D. J. 1997, ApJ, 482, L41 [NASA ADS] [CrossRef] [Google Scholar]
- McCarroll, H., & Valiron, P. 1975, A&A, 44, 465 [NASA ADS] [Google Scholar]
- McElroy, D., Walsh, C., Markwick, A. J., et al. 2013, A&A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mehringer, D. M., Yusef-Zadeh, F., Palmer, P., & Goss, W. M. 1992, ApJ, 401, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Mehringer, D. M., Palmer, P., Goss, W. M., & Yusef-Zadeh, F. 1993, ApJ, 412, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Meijerink, R., & Spaans, M. 2005, A&A, 436, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meijerink, R., Spaans, M., & Israel, F. P. 2007, A&A, 461, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mezger, P. G., & Pauls, T. 1979, in The Large-Scale Characteristics of the Galaxy, ed. W. B. Burton, IAU Symp., 84, 357 [Google Scholar]
- Muno, M. P., Bauer, F. E., Baganoff, F. K., et al. 2009, ApJS, 181, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Mushotzky, R. F., Done, C., & Pounds, K. A. 1993, ARA&A, 31, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Nahar, S. N., & Pradhan, A. K. 1997, ApJS, 111, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Nakagawa, T., Doi, Y., Yui, Y. Y., et al. 1995, ApJ, 455, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Nakagawa, T., Yui, Y. Y., Doi, Y., et al. 1998, ApJS, 115, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Oberst, T. E., Parshley, S. C., Nikola, T., et al. 2011, ApJ, 739, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, T., Hasegawa, T., Sato, F., Tsuboi, M., & Miyazaki, A. 1998, ApJS, 118, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Pineda, J. L., Langer, W. D., Velusamy, T., & Goldsmith, P. F. 2013, A&A, 554, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pineda, J. L., Langer, W. D., & Goldsmith, P. F. 2014, A&A, 570, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rigopoulou, D., Hopwood, R., Magdis, G. E., et al. 2014, ApJ, 781, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Robert, C., Leitherer, C., & Heckman, T. M. 1993, ApJ, 418, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, S. 2013, ApJ, 773, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Sargsyan, L., Samsonyan, A., Lebouteiller, V., et al. 2014, ApJ, 790, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., Wakker, B., Jannuzi, B. T., et al. 2000, ApJS, 129, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D., & Adams, N. G. 1981, MNRAS, 197, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Stacey, G. J., Hailey-Dunsheath, S., Ferkinhoff, C., et al. 2010, ApJ, 724, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Suno, H., & Kato, T. 2006, Atom. Data Nucl. Data Tables, 92, 407 [Google Scholar]
- Velusamy, T., & Langer, W. D. 2014, A&A, 572, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verner, D. A., & Yakovlev, D. G. 1995, A&AS, 109, 125 [NASA ADS] [Google Scholar]
- Verner, D. A., Yakovlev, D. G., Band, I. M., & Trzhaskovskaya, M. B. 1993, Atom. Data Nucl. Data Tables, 55, 233 [Google Scholar]
- Vignali, C., Brandt, W. N., Schneider, D. P., & Kaspi, S. 2005, AJ, 129, 2519 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, G. M. 1991, ApJ, 379, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Wiesenfeld, L., & Goldsmith, P. F. 2014, ApJ, 780, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., Tielens, A. G. G. M., & Hollenbach, D. 1990, ApJ, 358, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003, ApJ, 587, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., & McKee, C. F. 2010, ApJ, 716, 1191 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Soft X-ray (0.5–2.0 keV) luminosity for a sample of 1009 AGNs as a function of red shift z reproduced from Fig. 1 in Ebrero et al. (2009). The insert key identifies the X-ray survey used to compile the data (see Ebrero et al. (2009) for their definitions). The soft X-ray luminosities for this sample of AGNs range from ~1040 to ~2 × 1047 erg s-1. |
| In the text | |
 |
Fig. 2 Fractional ionization state of C+ to C4+ versus X-ray luminosity flux, FX, for n(e) = 0.01 cm-3(top), 1.0 cm-3(middle), and 10.0 cm-3(bottom) at Tkin = 8000 K, assuming a fully ionized region (n(H) = n(H2) = 0 cm-3). |
| In the text | |
 |
Fig. 3 Fractional ionization state of C+ through C4+ versus X-ray luminosity flux, FX, for a diffuse atomic hydrogen cloud with n(H) = 25 cm-3 (panel a)) and 100 cm-3 (panel b)), assuming n(e) = 0.1 cm-3, and Tkin = 100 K and no H2, panel c) includes a 10% admixture of H2. |
| In the text | |
 |
Fig. 4 Fraction of carbon ionization states versus X-ray luminosity flux, FX, for a dense molecular hydrogen gas, n(H2) = 103 cm-3 and Tkin = 100 K, with an admixture n(H) = 1 cm-3 and n(e) = 0.1 cm-3. Carbon remains in the singly ionized state, C+, up to FX ~ 5 × 103 erg cm-2 s-1. |
| In the text | |
 |
Fig. 5 Fraction of oxygen ionization states a) and nitrogen ionization states (b) and c)) versus X-ray luminosity flux, FX, for a dense WIM with n(e) = 10 cm-3 and Tk = 8000 K. Panel b) assumes the charge transfer rates of Lin et al. (2005) and panel c) those of Kingdon & Ferland (1996) – see text. |
| In the text | |
 |
Fig. 6 [C ii] luminosity in units of solar luminosity as a function of the luminosity of a central X-ray source. The assumed ISM parameters and dimensions of the nucleus are given in the text. The three curves represent different values of the filling factor for PDR and PDR-like conditions in the nucleus. |
| In the text | |
 |
Fig. 7 [C ii] luminosities of the individual ISM components are plotted as a function of radius in a galactic nucleus with a central X-ray source with L(X-ray) = 1042 (top panel) and 1044 erg s-1 (bottom panel) with a filling factor η(PDR) = 2 × 10-3. The assumed ISM parameters and dimensions of the nucleus are given in the text. The dense WIM dominates the [C ii] emission at L(X-ray) =1040 erg s-1 but is increasingly suppressed with increasing L(X-ray) until the PDRs dominate the emission. |
| In the text | |
 |
Fig. 8 Luminosities of the individual ISM components arising from a galactic nucleus with a uniform X-ray source, and physical parameters given in the text and Table 4 are plotted as a function of X-ray luminosity. |
| In the text | |
 |
Fig. 9 [C ii] luminosity for the central X-ray source (black line) compared to that of the uniform flux model (red line). The ISM properties are the same in both models. |
| In the text | |
 |
Fig. 10 Fraction of singly ionized carbon in the WIM versus X-ray luminosity in the uniform X-ray flux model, for a range of WIM electron densities. |
| In the text | |
 |
Fig. 11 [C ii] luminosity arising from the WIM versus X-ray luminosity, for a range of electron densities in the WIM. The remaining ISM parameters are the same as that for the uniform model. |
| In the text | |
 |
Fig. 12 Total [C ii] luminosity (all ISM components) versus X-ray luminosity, for a range of electron densities in the WIM. The remaining ISM parameters are the same as that for the uniform model. |
| In the text | |
 |
Fig. 13 Total [C ii] luminosity of a hypothetical AGN versus galactic radius for a range of X-ray luminosities. The key labels the log of the X-ray luminosity and ranges from LogL(X-ray) = 40 to 48. The decrease in [C ii] luminosity with increasing L(X-ray) is due to the destruction of C+ in the WIM close to the source of X-rays. The radius over which the X-rays photoionize C+ increases with increasing X-ray luminosity. |
| In the text | |
 |
Fig. 14 Predicted [C ii]/FIR luminosity ratio versus X-ray luminosity for different PDR filling factors (see Fig. 6). Also plotted are data points for six AGNs (red bullets) observed in [C ii], FIR, and X-rays (Stacey et al. 2010) and two high-redshift AGNs (black squares) observed in [C ii] (as compiled in Gullberg et al. 2015), FIR by Vignali et al. (2005), and X-rays by Law et al. (2004). We assumed 30% uncertainties for the [C ii]/FIR ratios from Stacey et al. (2010) and for the X-ray luminosities. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


