| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | L5 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201526421 | |
| Published online | 26 June 2015 | |
The changing rotation period of comet 67P/Churyumov-Gerasimenko controlled by its activity
1 Deutsches Zentrum für Luft- und Raumfahrt (DLR), Institut für Planetenforschung, Rutherfordstraße 2, 12489 Berlin, Germany
e-mail: keller@mps.mpg.de
2 Institut für Geophysik und extraterrestrische Physik, TU Braunschweig, 38106 Braunschweig, Germany
3 Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg, 3, 37077 Göttingen, Germany
4 Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388 Marseille, France
Received: 27 April 2015
Accepted: 4 June 2015
Context. The ESA Rosetta spacecraft has been orbiting the nucleus of comet 67P/Churyumov-Gerasimenko since August 2014. The rotation axis of the irregularly shaped nucleus has a large obliquity (52°) and is oriented such that the southern hemisphere is insolated during perihelion.
Aims. We calculate the change in the rotation period as a function of the cometary orbital position due to forces exerted by cometary activity.
Methods. We used a detailed shape model of 67P with >105 facets. We calculated the efficiency of the facets to exert a torque based on their radial distance from the center of mass and their orientation. We applied our thermal model to calculate the diurnal water-ice sublimation rate from each facet. The reaction force per facet combined with its torque efficiency creates a torque and changes the angular momentum. The component of the torque parallel to the spin axis changes the rotation period.
Results. Our model shows that the rotation period increases slightly during the approach of the comet to the Sun. It reaches a maximum shortly before equinox and drops rapidly during perihelion passage. The magnitude of the change depends on the actual sublimation rates. The change in sign mainly depends on the shape of the nucleus and not much on the sublimation variation. The roughness of the nucleus has little influence.
Conclusions. For the given geometry of the rotation axis, the change in the rotation period is mainly influenced by the sublimation activity of the irregular shape of the nucleus. The rotation period increases until shortly before equinox in early May 2015, in good agreement with observations, and will then become shorter rapidly.
Key words: comets: general / comets: individual: 67P/Churyumov-Gerasimenko / space vehicles / methods: numerical
© ESO, 2015
1. Introduction
Interest in the physical properties of 67P/Churyumov-Gerasimenko (hereafter 67P) strongly increased when European Space Agency (ESA) selected this comet as a backup target for the Rosetta comet rendezvous mission (Glassmeier et al. 2007). Only two apparitions of 67P were available for detailed observations before the spacecraft reached its target in 2014. Hubble Space Telescope observations taken after 67P’s perihelion passage on Sep. 18, 2002 revealed a rotation period of the nucleus between 12 and 12.8 h (Lamy et al. 2006). Lowry et al. (2012) revisited all light curve observations (Lowry et al. 2006; Tubiana et al. 2008, 2011) and determined the sidereal rotation period of the nucleus P = 12.76137 ± 0.00006 h. The high-accuracy observations using the OSIRIS science cameras onboard Rosetta, starting after hibernation of the spacecraft and its commissioning in March 2014, yielded P = 12.4043 ± 0.0007 h. The combination of all observations led to the suggestion that the period changed if compared before and after perihelion in 2009. A slightly refined determination of the pre-perihelion period to P = 12.76129 ± 0.00005 h leads to a decrease in the period by 1285 s (Mottola et al. 2014). The obliquity of the rotation axis (52°) and its orientation cause strong seasonal effects.
A change in the spin period was observed for comet 10P/Tempel 2 for the first time (Mueller 1996). Gutiérrez et al. (2003) found a change in the spin period of comet 6P/d’Arrest. The spin-up of cometary nuclei is probably the most plausible reason for cometary splitting (Jewitt 1997). Belton et al. (2011) determined the variation in the rotation rate of comet 9P/Tempel 1 from thousands of ground-based and spacecraft observations. They could even determine the variation in the spin acceleration. The spin rate slowed down on approach to perihelion, passed through a minimum, and then accelerated rapidly as the comet passed through perihelion, eventually reaching a maximum post-perihelion. This knowledge was used to coordinate the arrival of the Stardust NEXT mission spacecraft during the next apparition in 2011.
The spin acceleration of 67P could well be attributed to sublimation-induced torque during the 2009 perihelion passage. Gutiérrez et al. (2005) investigated the outgassing-induced effects for a range of possible models of 67P. The rotation period of 67P is closely monitored by the Rosetta operations team and reported biweekly. Somewhat surprising was that the rotation period increased from the beginning of the rendezvous at 3.7 au in August 2014 slowly by ca. 60 s when the comet reached 2 au preperihelion in March 2015. No significant change in the rotation axis itself has been detected, although the bi-lobate nucleus is very ragged. It is expected that the rotation period will rapidly drop during the perihelion passage, in agreement with the previous perihelion passage, which is behavior similar to what was derived for Comet 9P/Tempel 1 (Belton et al. 2011).
Keller et al. (2015) calculated the water production rate variation of 67P using the detailed SHAP4 shape model of the nucleus (Preusker et al. 2015) derived from images taken by the scientific imager OSIRIS onboard Rosetta (Keller et al. 2007). The surface of the nucleus is described by more than 105 facets with a typical resolution of about 25 m. The program calculates the illumination conditions and hence the energy input of all facets during each time step. A sublimation model determines the gas production and the temperature, hence the instantaneous force acting on each facet. This extension of the model can then be used to determine the non-gravitational forces acting on the nucleus as they vary with heliocentric distance and insolation. These forces will exert a net torque on the rotation if the resulting chirality of the axis is not zero. For the first time, such calculations are based on the known shape, mass, and density of a cometary nucleus.
In the following section we briefly describe our model extension. Then in Sect. 3 we calculate the chirality of 67P’s rotation axis under different illumination conditions and discuss its implication for the variation in the rotation period. We demonstrate that the currently observed slowdown of the period can be accounted for by the shape of 67P and predict that the torque will change sign before the equinox on May 11, 2015. From there on the spin rate of the nucleus will strongly increase (its rotation period decreases).
2. Model
To study the effect of sublimation-induced reaction on the comet’s spin rate, we modeled the sublimation process as reported in Keller et al. (2015). Basically, 67P is described as a polyhedron with triangular facets, for which we adopted the SHAP4 shape model by Preusker et al. (2015), down-sampled to approximately 108 000 facets. We assume that sublimation is driven by solar energy input (direct, reflected, and re-emitted), and that, owing to the low thermal inertia of the cometary material (Gulkis et al. 2015), local thermal equilibrium is reached very rapidly with respect to the typical time of changes in illumination. Under those assumptions, the equilibrium temperature of the surface or of a sublimating subsurface layer depends only on the instantaneous solar energy input and not on the insolation history. For the purpose of this study, we used a two-layer thermal model (Skorov et al. 2011), where a porous, refractory dust layer is superposed on a sublimating water-ice or a dust layer. The properties of the body are assumed to be constant across the surface, and a net torque arises as a consequence of varying illumination over an irregular body. The net torque due to sublimation can be written as 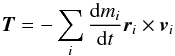 (1)where vi is a vector describing the gas ejection velocity, with orientation parallel to the facet’s normal; ri is the vector from the center of mass to the center of the facet; and the index i runs over all facets. The term dmi/ dt is the mass sublimation rate, whereas −vi dmi/ dt is the reaction force for facet i. The magnitude of the gas ejection velocity is computed as
(1)where vi is a vector describing the gas ejection velocity, with orientation parallel to the facet’s normal; ri is the vector from the center of mass to the center of the facet; and the index i runs over all facets. The term dmi/ dt is the mass sublimation rate, whereas −vi dmi/ dt is the reaction force for facet i. The magnitude of the gas ejection velocity is computed as  (2)where m is the molar mass of water, R the gas constant, and Tg the gas temperature. The constant η represents the efficiency of impulse transfer and is essentially a measure of the collimation of the gas beam. For this study we fixed the value of η to 0.77 (Gutiérrez et al. 2005). The gas temperature Tg can be estimated by linear interpolation between the surface and the sublimation temperatures provided by the sublimation model. This approximation introduces only a small error because vi is proportional to
(2)where m is the molar mass of water, R the gas constant, and Tg the gas temperature. The constant η represents the efficiency of impulse transfer and is essentially a measure of the collimation of the gas beam. For this study we fixed the value of η to 0.77 (Gutiérrez et al. 2005). The gas temperature Tg can be estimated by linear interpolation between the surface and the sublimation temperatures provided by the sublimation model. This approximation introduces only a small error because vi is proportional to 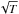 . The net torque will cause a change in the angular momentum L according to
. The net torque will cause a change in the angular momentum L according to 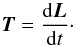 (3)In general, the resulting motion will be an excited rotation with forced precession of the spin axis. The full rotation can be modeled by integrating the Euler equations of motion. In the case of 67P, however, no precession of the spin axis larger than 0.3° has been observed so far (Preusker et al. 2015), showing that the comet finds itself close to a relaxed rotational state. This does not seem to be very rare (Samarasinha et al. 2004). We therefore adopted a simplified approach, where we consider the angular momentum vector to always be parallel to the spin vector, and where both are parallel to the Z axis of a body-fixed reference system. We then considered only the Z component of the torque, which mainly contributes to the change in the spin rate, according to
(3)In general, the resulting motion will be an excited rotation with forced precession of the spin axis. The full rotation can be modeled by integrating the Euler equations of motion. In the case of 67P, however, no precession of the spin axis larger than 0.3° has been observed so far (Preusker et al. 2015), showing that the comet finds itself close to a relaxed rotational state. This does not seem to be very rare (Samarasinha et al. 2004). We therefore adopted a simplified approach, where we consider the angular momentum vector to always be parallel to the spin vector, and where both are parallel to the Z axis of a body-fixed reference system. We then considered only the Z component of the torque, which mainly contributes to the change in the spin rate, according to 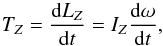 (4)with IZ being the largest moment of inertia of the body and ω its spin rate. In this approximation we also neglect the small changes to the inertia moment due to mass loss. By integrating Eq. (4) over time, we can therefore compute the evolution of the spin rate (and of the rotation period). The inertia axes and moments, body volume, and mass are computed by using the method by Dobrovolskis (1996), when assuming a uniform bulk density of 460 kg/m3. The resulting largest moment of inertia is IZ = 1.67 × 1019 kg m2.
(4)with IZ being the largest moment of inertia of the body and ω its spin rate. In this approximation we also neglect the small changes to the inertia moment due to mass loss. By integrating Eq. (4) over time, we can therefore compute the evolution of the spin rate (and of the rotation period). The inertia axes and moments, body volume, and mass are computed by using the method by Dobrovolskis (1996), when assuming a uniform bulk density of 460 kg/m3. The resulting largest moment of inertia is IZ = 1.67 × 1019 kg m2.
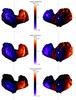 |
Fig. 1 Two different views of the shape model seen in the equatorial plane. The rotation (Z) axis points up. The color indicates the magnitude of the Z component of the torque. Blue increases and red decreases the rotation period, respectively. Top: torque distribution on Jan. 20, 2015. Middle: torque efficiency distribution. Bottom: torque distribution at perihelion. The torque distribution has dimensions of a torque per unit area [kg s-2]. The torque efficiency has dimensions of a length [km]. |
 |
Fig. 2 Change in period (ΔP) and heliocentric distance versus time around perihelion for Model B normalized to match observations on Apr. 13, 2015 when the observed ΔP was + 80.5 s. The observed values for the rotation period are listed in Table 1. The ΔP that is equivalent to the change during the last apparition is −1285 s. |
3. Results, discussions, and prediction
Torque efficiency of facets We calculate, as a first step, the efficiency of the facets to exert a torque that changes the Z component of the angular momentum (LZ). This efficiency depends on the position and orientation of a facet i. The cross product of the radius vector ri and the unit normal of the facet 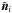 forms a vector. Its component parallel to the rotation axis is given by the dot product
forms a vector. Its component parallel to the rotation axis is given by the dot product 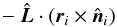 (5)where
(5)where 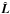 is a unit vector parallel to the angular momentum vector. The farther the facet is away from the rotation axis, the stronger its influence (efficiency) if its normal deviates from the plane defined by the rotation axis and the position of the facet. Multiplying the torque efficiency by the magnitude of the local force normal to the surface yields the relevant torque component. After summing over all facets, it yields
is a unit vector parallel to the angular momentum vector. The farther the facet is away from the rotation axis, the stronger its influence (efficiency) if its normal deviates from the plane defined by the rotation axis and the position of the facet. Multiplying the torque efficiency by the magnitude of the local force normal to the surface yields the relevant torque component. After summing over all facets, it yields 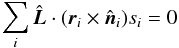 (6)for the closed surface of the nucleus, where si is the surface area of the ith facet.
(6)for the closed surface of the nucleus, where si is the surface area of the ith facet.
Figure 1 shows two equatorial views of the nucleus where facets that can increase the rotation period (decrease the rotation rate) are colored to show the contrasting effects. The images in the middle row show the torque efficiency. Since they are far away from the rotation axis, the boundaries of the Seth and Ash regions on the big lobe and the Bastet region on the small lobe can yield the strongest retarding influence on the rotation rate if illuminated and active (see Thomas et al. 2015 and El-Maarry et al. 2015 for the naming and location of the geomorphological regions). Looking down on the nucleus from the north (like the Sun during northern summer), the blue color of the big lobe prevails. We calculated the distribution of activity over the surface by applying our Model B (Keller et al. 2015), which assumes homogeneous activity controlled by instantaneous insolation. The integration over one spin was performed for the situation on Jan. 20, 2015 when the comet is 2.5 au from the Sun and the subsolar latitude is 28° (north) (see Fig. 1 upper row). By then the rotation period had already increased by 15 s. The solar distance keeps decreasing and the activity increasing, and as long as these efficient areas are illuminated, the retarding torque on the rotation axis increases. In contrast, the large cliff on Anuktet near the boundary to Serqet and further south to Maftet shows a strong potential to increase the rotation rate (here the torque efficiency is bright red) because the normals of the facets point almost perpendicularly to the connection lines between the facets and the rotation axis (Fig. 1 middle left). The red color starts to dominate for facets located in the equatorial region and inn the southern hemisphere. Similarly, looking at the nucleus from the opposite side (Fig. 1 right column) the “mountainous” eastern parts of Imhotep near Ash and Apis also appear bright red. When these areas are illuminated and active, accelerating forces will dominate. We expect the rotation period to decrease once the subsolar latitude is near the equator or more southern around perihelion (Fig. 1 lower right). Rotation period variation and comparison with observations Around Rh = 3.5 au, the negative dLz/ dt starts to lead to an increase in the rotation period as observed. Once Rh becomes smaller than about 1.8 au and the subsolar latitude crosses the equator, the torque changes its sign. Then the torque increases rapidly, and the change in the Z component of the angular momentum peaks at perihelion (Fig. 3). The positive excursion of the angular momentum change is slightly asymmetric relative to perihelion caused by the asymmetry of the sublimation rate due to the subsolar latitude variation. The rotation period starts to drop shortly before perihelion and reaches its strongest gradient around perihelion. It reaches its initial (former) value of 12.4043 h again when the comet’s heliocentric distance decreases below 1.4 au shortly before perihelion and the subsolar latitude falls below −18° (Fig. 2). The rotation period will approach its final post perihelion value at a heliocentric distance beyond Rh> 2.5 au when the subsolar latitude becomes positive (north) again.
 |
Fig. 3 Change of angular momentum (Z direction) and heliocentric distance as function of time around perihelion. |
The effective torque acting on the rotation of a more symmetric (spherical) body depends on the roughness of its surface. Basically, the effects of sublimation act similarly to the forces considered for YORP. We artificially smoothed the vertices of the shape model of 67P to investigate the importance of the roughness for the rotation changes. Surprisingly, the calculations show less than a 10% difference. The magnitude of the resulting torque is mainly determined by the global features of the shape discussed previously.
The idealized assumption of homogeneous activity overestimates the overall sublimation rate of water strongly. Taken at face value the model predicts a decrease of ΔP = − 7300 s. This value is a factor of 5.7 higher than what is expected by comparison to the previous period. Scaling so that ΔP = − 1285 s is reached after perihelion reduces the maximum positive ΔP from +960 s to +140 s. The Rosetta Flight Dynamics Team have published values for the rotation period starting on Jan. 1, 2015 where ΔP = + 9.5 s was found. Table 1 lists the rotation periods taken from the Rosetta mission operational products (CATT) released by ESA. The latest observation on Apr. 15, 2015 resulted in +80.5 s. By scaling our model to this value, a minimum ΔP = − 750 s will be reached after perihelion. The variation in the model ΔP is much shallower starting at larger distances from perihelion than what is found by the observations (see Fig. 2). This agrees with the fact that Model B overestimates early water sublimation of 67P. We have to keep in mind that the water production across the southern hemisphere may not be uniform, as already suggested by Keller et al. (2015), and that the real topography of the southern hemisphere is not yet known because the south pole is still not illuminated. A more detailed comparison will have to await forthcoming observations.
Regardless of the details of the production rate normalization, in our model the sign of the Z component of the torque, TZ, (Eq. (4)) changes after April 15, 2015 when the comet’s heliocentric distance is <1.9 au and the subsolar latitude is 14° (north).
4. Summary and conclusions
In a first step we transformed a high-resolution shape model of 67P into a model that reflects the efficiency of the facets to influence the Z component of the angular momentum based on their position and orientation. In a second step we calculated the varying pressure on the facets caused by sublimation of water ice according to Model B of Keller et al. (2015) and determined the change in the rotation period along the orbit of 67P. The effective torque that changes the rotation period depends on the distribution of the active facets and their efficiency. The model predicts an increase (positive ΔP) in the rotation period until shortly before the equinox in early May 2015 followed by a steep decrease around perihelion to a relatively large negative ΔP that is expected if the comet behaves similarly to its last perihelion passage. We notice that we cannot achieve both the positive and negative observed ΔP with a single normalization constant. To achieve the corresponding negative ΔP = −1285 s, the effective torque after perihelion has to increase by strengthening torque-efficient facets either by nonuniform activity and/or by topography. Once the production rate of water as a function of the heliocentric distance is available, the modeling of the rotation period will provide additional information on the distribution of activity. The global shape and topography of 67P’s nucleus determines the rotation properties and their variation. Its surface roughness is of minor importance. We predict that the presently observed lengthening of the rotation period will be reversed once the comet nears its perihelion. The actual final value of the negative ΔP will depend on the topography of the still unknown southern hemisphere. We plan to calculate the effects of the sublimation on the full angular momentum of the nucleus. Our model can also be used to calculate the non-gravitational effects on the orbital motion of the comet.
Observed rotation periods of comet 67P.
Acknowledgments
We acknowledge the support of the ESA Rosetta Flight Dynamics Team.
References
- Belton, M. J., Meech, K. J., Chesley, S., et al. 2011, Icarus, 213, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Dobrovolskis, A. R. 1996, Icarus, 124, 698 [NASA ADS] [CrossRef] [Google Scholar]
- El-Maarry, M. R., Thomas, N., Gioacomini, L., et al. 2015, A&A, in press DOI:10.1051/0004-6361/201525723 [Google Scholar]
- Glassmeier, K.-H., Boehnhardt, H., Koschny, D., Kührt, E., & Richter, I. 2007, SSR, 128, 1 [NASA ADS] [Google Scholar]
- Gulkis, S., Allen, M., von Allmen, P., et al. 2015, Science, 347, 0709 [Google Scholar]
- Gutiérrez, P. J., de Léon, J., Jorda, L., et al. 2003, A&A, 407, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gutiérrez, P. J., Jorda, L., Samarasinha, N. H., & Lamy, P. 2005, Planet. Space Sci., 53, 1135 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. 1997, Earth, Moon, and Planets, 79, 35 [Google Scholar]
- Keller, H., Barbieri, C., Lamy, P., et al. 2007, Space Sci. Rev., 128, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, H., Mottola, S., Davidsson, B., et al. 2015, A&A, accepted [Google Scholar]
- Lamy, P. L., Toth, I., Weaver, H. A., et al. 2006, A&A, 458, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lowry, S. C., Fitzsimmons, A., Jorda, L., et al. 2006, in BAAS, 38, AAS/Division for Planetary Sciences Meeting Abstracts #38, 492 [Google Scholar]
- Lowry, S., Duddy, S. R., Rozitis, B., et al. 2012, A&A, 548, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mottola, S., Lowry, S., Snodgrass, C., et al. 2014, A&A, 569, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mueller, B. 1996, Icarus, 123, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Preusker, F., Scholten, F., Matz, K.-D., et al. 2015, A&A, submitted [Google Scholar]
- Samarasinha, N. H., Mueller, B. E., Belton, M. J., & Jorda, L. 2004, Comets II, 1, 281 [NASA ADS] [Google Scholar]
- Skorov, Y. V., Lieshout, R. V., Blum, J., & Keller, H. U. 2011, Icarus, 212, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thomas, N., Sierks, H., Barbieri, C., et al. 2015, Science, 347, 440 [Google Scholar]
- Tubiana, C., Barrera, L., Drahus, M., & Boehnhardt, H. 2008, A&A, 490, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tubiana, C., Böhnhardt, H., Agarwal, J., et al. 2011, A&A, 527, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Two different views of the shape model seen in the equatorial plane. The rotation (Z) axis points up. The color indicates the magnitude of the Z component of the torque. Blue increases and red decreases the rotation period, respectively. Top: torque distribution on Jan. 20, 2015. Middle: torque efficiency distribution. Bottom: torque distribution at perihelion. The torque distribution has dimensions of a torque per unit area [kg s-2]. The torque efficiency has dimensions of a length [km]. |
| In the text | |
 |
Fig. 2 Change in period (ΔP) and heliocentric distance versus time around perihelion for Model B normalized to match observations on Apr. 13, 2015 when the observed ΔP was + 80.5 s. The observed values for the rotation period are listed in Table 1. The ΔP that is equivalent to the change during the last apparition is −1285 s. |
| In the text | |
 |
Fig. 3 Change of angular momentum (Z direction) and heliocentric distance as function of time around perihelion. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


