| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 7 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526145 | |
| Published online | 11 June 2015 | |
The formation of regular interarm magnetic fields in spiral galaxies
1 School of Mathematics, University of Manchester, Oxford Road, Manchester, M13 9PL, UK
e-mail: moss@ma.man.ac.uk
2 Institute of Continuous Media Mechanics, Koroleva, 1, 614013 Perm, Russia
3 MPI für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
4 Department of Physics, Moscow State University, 119991 Moscow, Russia
Received: 20 March 2015
Accepted: 27 April 2015
Context. Observations of regular magnetic fields in several nearby galaxies reveal magnetic arms situated between the material arms. The nature of these magnetic arms is a topic of active debate. Previously, we found a hint that taking into account the effects of injections of small-scale magnetic fields (e.g. generated by turbulent dynamo action) into the large-scale galactic dynamo can result in magnetic arm formation.
Aims. We now investigate the joint roles of an arm/interarm turbulent diffusivity contrast and injections of small-scale magnetic field on the formation of large-scale magnetic field (“magnetic arms”) in the interarm region.
Methods. We use the relatively simple “no-z” model for the galactic dynamo. This involves projection onto the galactic equatorial plane of the azimuthal and radial magnetic field components; the field component orthogonal to the galactic plane is estimated from the solenoidality condition.
Results. We find that the addition of diffusivity gradients to the effects of magnetic field injections makes the magnetic arms much more pronounced. In particular, the regular magnetic field component becomes larger in the interarm space than that within the material arms.
Conclusions. The joint action of the turbulent diffusivity contrast and small-scale magnetic field injections (with the possible participation of other effects previously suggested) appears to be a plausible explanation for the phenomenon of magnetic arms.
Key words: galaxies: spiral / galaxies: magnetic fields / dynamo / ISM: magnetic fields / Galaxy: disk
© ESO, 2015
1. Introduction
Dynamo modelling of galactic magnetic fields has a long history, being particularly intensive over the last 30 years. We do not intend to give a comprehensive review here, but Ruzmaikin et al. (1988) can be mentioned as a seminal work, and comprehensive reviews were given by Beck et al. (1996), Brandenburg (2015); see also Beck et al. (2015) for more recent developments. Substantial progress has been made towards understanding the basic mechanisms of dynamo excitation, including both detailed direct numerical simulations in “boxes”, and also some more detailed models for global field structure.
A conspicuous feature of some “grand design” spiral galaxies (e.g. M 81, NGC 6946) is the presence in the regular (large-scale) magnetic field of prominent magnetic arms, situated in the interarm regions between the material arms, as delineated by regions of active star formation. Such arms are not always well pronounced or complete, and may include a number of filaments, as in IC 342 (Beck 2015). The origin of magnetic arms has attracted significant attention, but so far there is no completely satisfactory explanation of their origin. Early studies include Moss (1998) and Shukurov (1998) who in the context of simple mean field dynamo models appealed to variations in the alpha coefficient and turbulent resistivity (η) that were modulated by the location of the material arms; specifically, it can be expected that η will be enhanced by the additional turbulence associated with star forming regions (SFRs).
Later relevant studies include Chamandy et al. (2013, 2014, 2015) who use a sophisticated mean field dynamo model and argue that enhanced vertical outflows within the arms regions will preferentially remove large-scale fields from there. Small-scale helicity is also removed by the vertical flows, preventing catastrophic quenching. Additionally, they include modulations of the alpha term. These models do produce some of the observed properties, but possibly are not completely satisfactory. For example, these models require dynamo numbers that are close to marginal to generate magnetic arms efficiently, and the outflows cannot be too strong. Gradients of turbulent diffusivity are ignored and pitch angles of the fields are rather small compared to those of typical galaxies.
Moss et al. (2013) took a somewhat different approach, modelling the effects of SFRs in the material arms by stochastic injection of small-scale magnetic field within the arms, supposedly the result of small-scale dynamo action in the SFRs. Their model produces (maybe unsurprisingly) a satisfactory enhancement of small-scale fields in the arms, but no significant enhancement of interarm regular (large-scale) fields.
Summary of models.
A significant omission from the last paper, for perceived technical reasons, was an enhanced turbulent diffusivity in the arms associated with the assumed turbulence driven by the star formation. The authors speculated that this might be a significant omission. The presence of such variations in the turbulent diffusivity cannot be verified directly by observations, but given our understanding of the physical processes operating, it appears a plausible assumption. Accordingly, we here present similar models to those in Moss et al. (2013), but now including the terms associated with inhomogeneities in η in the dynamo equations (including the diamagnetic terms), and we demonstrate that regular magnetic arms located between the material arms are indeed produced. We note in passing that contrasts in diffusivity between disc and halo regions have been included in dynamo models for at least 25 years (see e.g. Brandenburg et al. 1992).
 |
Fig. 1 Field vectors at dimensionless times t ≈ 3.0 and 17.0 (2.3 and 13.3 Gyr), for Model 2 with the diffusivity contrast parameter ηa = 4. Here, and in subsequent similar figures, the vectors give the magnetic field direction, with lengths proportional to the magnetic field strengths, and the contours delineate the arms. The corotation radius is approximately 0.7R. |
2. The model
2.1. The dynamo setup
The dynamo equation is 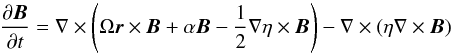 (1)in the standard notation. Note the presence of gradients of diffusivity, both in the diamagnetic term and the diffusion term. The model is basically the thin disc model (“no-z” approximation) described in Moss et al. (2012, 2013). In these earlier papers it had not been possible to include terms corresponding to gradients of η. The relevant part of the algorithm was reorganized slightly, and a typo in the code corrected, after which the code ran smoothly with gradients of η included. (The typo did not affect the part of the code used in earlier papers.) The novel feature of the models of Moss et al. (2012, 2013) is the continual stochastic injection of small-scale field at discrete locations, to simulate the effects of SFRs in introducing small-scale field into the interstellar medium (ISM). In short, random fields Binj = Binj0f(r,t) are added at approx nspot = 75 randomly chosen discrete locations in the material arms (defined below) with re-randomization (i.e. changing the location of the injection sites and the distribution of field strengths over them by choosing a new independent set of random numbers) at intervals dtinj ≈ 10 Myr. nspot and Binj0 are free parameters in the model, which are regarded as a proxies for unmodelled processes in the SFRs. Another key point is that the seed field at time zero is random, in discrete patches, and of approximately equilibrium strength. This is envisaged as being the result of small-scale dynamo action within very early SFRs. (Note that the no-z approximation implicitly preserves the solenoidality condition ∇·B = 0 for both the dynamo generated and injected fields.) Full details are in Moss et al. (2012). The disc can be flared or flat, noting that there is currently some uncertainty as to whether galactic discs are substantially flat or flared (cf. Lazio & Cordes 1998); further investigation of this point is needed, but the results are not sensitive to this assumption. The HI disc of the Milky Way does flare, but it is unclear whether the ionized gas disc does so, and the observational data for external galaxies are inconclusive. This issue appears unimportant for our modelling – see Sect. 3.1 and also Moss et al. (2012).
(1)in the standard notation. Note the presence of gradients of diffusivity, both in the diamagnetic term and the diffusion term. The model is basically the thin disc model (“no-z” approximation) described in Moss et al. (2012, 2013). In these earlier papers it had not been possible to include terms corresponding to gradients of η. The relevant part of the algorithm was reorganized slightly, and a typo in the code corrected, after which the code ran smoothly with gradients of η included. (The typo did not affect the part of the code used in earlier papers.) The novel feature of the models of Moss et al. (2012, 2013) is the continual stochastic injection of small-scale field at discrete locations, to simulate the effects of SFRs in introducing small-scale field into the interstellar medium (ISM). In short, random fields Binj = Binj0f(r,t) are added at approx nspot = 75 randomly chosen discrete locations in the material arms (defined below) with re-randomization (i.e. changing the location of the injection sites and the distribution of field strengths over them by choosing a new independent set of random numbers) at intervals dtinj ≈ 10 Myr. nspot and Binj0 are free parameters in the model, which are regarded as a proxies for unmodelled processes in the SFRs. Another key point is that the seed field at time zero is random, in discrete patches, and of approximately equilibrium strength. This is envisaged as being the result of small-scale dynamo action within very early SFRs. (Note that the no-z approximation implicitly preserves the solenoidality condition ∇·B = 0 for both the dynamo generated and injected fields.) Full details are in Moss et al. (2012). The disc can be flared or flat, noting that there is currently some uncertainty as to whether galactic discs are substantially flat or flared (cf. Lazio & Cordes 1998); further investigation of this point is needed, but the results are not sensitive to this assumption. The HI disc of the Milky Way does flare, but it is unclear whether the ionized gas disc does so, and the observational data for external galaxies are inconclusive. This issue appears unimportant for our modelling – see Sect. 3.1 and also Moss et al. (2012).
Non-dimensional time τ is measured in units of h2/η. When η = 1026 cm2 s-1 and h = 500 pc, this is approximately 0.78 Gyr. Radius r is measured in units of the galactic radius R, taken as 10 kpc.
 |
Fig. 2 Model 2. Intensity of the large-scale magnetic field at times 2.34, 3.9, 7.8, 11.7, 12.48 and 13.26 Gyr (left to right, top to bottom). Contours shows isolines of large-scale field intensity (darker corresponds to a larger value). The first and last panels can be compared with the panels of Fig. 1. |
The code was implemented on a Cartesian grid with 537 × 537 points, equally spaced, extended to beyond the galactic radius to about 1.17R, i.e. over −1.17R ≲ R ≲ 1.17R. In this outer region beyond r = R, there is no alpha-effect and the diffusivity retains its global background value. This enables satisfactory treatment of the boundary conditions – see Moss et al. (2012). The timestep is fixed at approximately 0.04 Myr.
2.2. The arm generation algorithm
We define a function
 where ra,b are arbitrary values and φ0 = ωpτ, where ωp is the dimensionless pattern speed.
where ra,b are arbitrary values and φ0 = ωpτ, where ωp is the dimensionless pattern speed.
Then we put
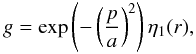 where η1 = 1, r> 0.4, and goes smoothly to zero as r → 0. Then
where η1 = 1, r> 0.4, and goes smoothly to zero as r → 0. Then
 where m is an arbitrary number. The diffusivity contrast is defined as Δηa = 1 + η10.
where m is an arbitrary number. The diffusivity contrast is defined as Δηa = 1 + η10.
This algorithm is rather arbitrary, but gives satisfactory results with the values ra = 1,a = π/ 4,b = 4 (as in Moss et al. 2012). In the illustrative computations described below m = 4.
The arms rotate rigidly with pattern speed ωp, chosen to give corotation radii 0.5R ≲ rcorr ≲ 0.7R – see Table 1.
3. Results
3.1. Main computations
A number of models were computed, with both flat and flared discs. The essential features of the results were the same for each class of model, and so only results for flat discs are presented here. Salient parameters are shown in Table 1. The underlying models are in general similar to Model 75 of Moss et al. (2013), for example, but here with a flat disc. We take h0 = 500 pc and a slightly larger value Rα = 5 is taken to compensate for the increased value of the diffusivity η in the arms. Plots of field vectors at dimensionless times τ = 3 and 17 are shown in Fig. 1, with the diffusivity contrast parameter Δηa = 4. The strong visual impression is that the large-scale field is reduced in the arms, and that there are pronounced large-scale magnetic structures (corresponding to regular field) between the material arms. Moreover, these effects are seen at very early times. This impression is reinforced (in a somewhat different representation) by Fig. 2, showing maps of the large-scale field at dimensionless times between τ = 3 and 17 approximately 2.3 and 13.3 Gyr. This figure can be compared to Fig. 4 of Moss et al. (2013). Additionally, Fig. 3 shows the global amplitudes of large-and small-scale fields in the arms and interarm regions. This figure can be compared to Fig. 8 of Moss et al. (2013), and clearly demonstrates the effects of the assumed η-gradients, in that in the interarm region the large-scale (regular) field is now two or three times larger than in the arms.
Model 2 has corotation radius at approximately 0.7R. We computed models with different corotation radii, and it appears that the results are quite insensitive to such changes. For example, Fig. 5 shows field vector plots at τ = 17 for a model with corotation at approximately 0.5R. (The anomalously large vectors in Fig. 5 (and 9c below) are attributable to a field injection soon before plotting.)
The value taken for the diffusivity contrast parameter Δηa is rather arbitrary, so the computation of Model 2 (Fig. 1) was repeated with Δηa = 6, see Fig. 6. The magnetic arms are more marked and the interarm magnetic structures are somewhat narrower. Further increase in Δηa can give more filamentary magnetic “arms”.
3.2. Field reversals
Large-scale field reversals are a common feature of the models and were also present in the models of Moss et al. (2012, 2013) see also Poezd et al. (1993). Moss & Sokoloff (2013) showed that when the seed field is inhomogeneous and of near equipartition strength, whether or not reversals appeared in the statistically steady field (and indeed the details of this configuration more generally) depends quite sensitively on the details of the initial field distribution. Several models were run with the same parameters as Model 2, but using different sequences of the (pseudo-)random numbers that define the initial field distribution and subsequent field injections. The field configurations at the end of the runs were generically similar, several with reversals but one (Fig. 7) with only a very weak feature near the outer radius.
We also made an experiment in which the seed field was weak and smooth, and the model was allowed to evolve without injections until the dynamo was saturated, with a “standard” looking smooth spiral structure. At τ = 8 the injections were turned on and evolution proceeded as in the other cases. The field at τ = 17 is shown in Fig. 8. Now there are no large-scale reversals, but other features of the field are similar to those in other models. This clearly demonstrates that the occurrence of large-scale reversals is a consequence of the form of the seed field and the injection history.
The models presented above all have a more or less homogeneous inner ring of field, with a reversal between the ring and the outer arms. A field reversal has been observed in the Milky Way, but it is unclear whether it is a global or local feature. Reversals have not (so far) been detected in external galaxies. In some ways the presence of the ring is a consequence of the way the model is set up, as the arms are only distinctly defined outside of the central regions (see Moss et al. 2013).
 |
Fig. 3 Model 2, showing global amplitudes of large- and small-scale field in the arms (respectively thick and thin red dashed) and large- and small-scale field in the interarm regions (respectively thick and thin blue curves). |
 |
Fig. 4 Model 7. Computation starting from a random seed field (as Model 2), but with no ongoing small-scale field injections. Δηa = 4. |
3.3. Additional computations
Simulations strongly suggest that spiral arms are not permanent structures, but dissolve and reform over comparatively short intervals (see the review by Dobbs & Baba 2014). It is also possible that arms may disappear altogether for intervals and then reappear. We also conducted two experiments to test how such changes in the structure of the material arms might influence our results. In the first (Model 10), the position of the spiral arms jumps randomly at time intervals [t] ≈ 5 × 108 yr. In the second (Model 6 – see Fig. 9), the spiral arms are removed altogether for two intervals of about 1.6 × 109 Gyr before reappearing. The conclusion from these computations is that the magnetic interarm structures are present soon after the material arms reappear. Model 6 has the same parameters as Model 2 described above, but the arms (and associated diffusivity inhomogeneities) are removed for 8.5 ≤ τ ≤ 10.5 and 13.0 ≤ τ ≤ 15.0. Figure 9 shows field vectors at times τ = 8.4 (i.e. just before the arms are “turned off”), τ = 9.9, and τ = 10.6 (i.e. soon after restoring the arms). At τ = 8.4 field structures are as in Fig. 1. These disappear almost immediately the arms are removed, and a near-circular field is present (Fig. 9b at τ = 9.9). When the arms are turned back “on” structures similar to those seen in Fig. 1 rapidly reappear – see field plots at τ = 10.6 in Fig. 9c.
Additionally, when the arms jump randomly (Model 10), similar structures quickly adjust to the new positions of the arms. Field vectors are not shown for this case. These idealized experiments suggest that magnetic field structures are not very dependent on the evolutionary history of the material arms.
 |
Fig. 5 Field vectors at dimensionless time τ = 17.0 (13.3 Gyr), for model 3 with diffusivity contrast parameter ηa = 4. The corotation radius is approximately 0.5R. |
 |
Fig. 6 Field vectors at dimensionless time τ = 17.0 (13.3 Gyr), for Model 8 with the larger diffusivity contrast parameter ηa = 6. The corotation radius is approximately 0.7R. |
 |
Fig. 7 Field vectors at dimensionless time τ = 17.0 (13.3 Gyr), for Model 9 with parameters as Model 2, but a different sequence of random numbers defining the initial field and subsequent injections. |
 |
Fig. 8 Field vectors at dimensionless time τ = 17.0 (13.3 Gyr), for Model 19. Here the seed field was weak and smooth, and there were no random injections until τ = 8. The corotation radius is approximately 0.7R. |
3.4. Roles of small-scale field injections and diffusivity gradients
In order to separate the role of diffusivity gradients alone in producing the magnetic structures discussed above, Model 7 shows the result of a computation with parameters as Model 2, except that there are no ongoing field injections. The field rapidly (by τ ≲ 3) becomes steady. Figure 4 shows the field structure (nominally at 13.26 Gyr, i.e, τ = 17). Enhanced interarm fields (magnetic arms) are clearly visible (we note that there is only “regular” field in this computation). In Fig. 10 the contrast between the global amplitudes of the regular field in the arm and interarm regions is clearly visible.
 |
Fig. 9 Field vectors at dimensionless times a) t ≈ 8.4, b) 9.9 and c) 10.6, for Model 6 with the diffusivity contrast parameter ηa = 4. The arms are removed between τ = 8.5 and 10.5, and panel c) shows that the interarm regular fields appear almost immediately after the arms reappear. The anomalously long vectors are the result of a field injection just before τ = 10.6. |
This suggests strongly (and consistently with the suggestion of Moss et al. 2012 – and even Moss 1998) – that the diffusivity gradients postulated can be largely responsible for the formation of (regular field) magnetic arms. The small-scale field injections provide (unsurprisingly) the observed enhanced small-scale field within the material arms. These injections form a consistent part of the model in that they are a direct consequence of the strong star formation in the arms, that in turn drives the turbulence that is responsible for the increased diffusivity there.
 |
Fig. 10 Model 7, showing global amplitudes of large- and small-scale field in the arms (respectively thick and thin red dashed) and large- and small-scale field in the interarm regions (respectively thick and thin blue curves). |
4. Discussion and conclusions
We have presented a mechanism for magnetic arm formation based on the joint action of turbulent diffusivity contrasts and small-scale magnetic field injections from small-scale dynamo action, plausibly associated with supernovae complexes and HII regions, although we cannot use this energy input to the ISM directly to calibrate our parameter Binj0. This mechanism produces quite marked large-scale magnetic structures situated mainly between the material arms (see, e.g., Fig. 1). However, from time to time a magnetic arm can intersect somewhere a material arm, e.g. Figs. 1 (right hand panel) and 6. The magnetic arms obtained are quite robust structures and do not require fine tuning of the dynamo governing parameters.
In general, the effect of introducing the diffusivity contrast is to increase the global mean diffusivity and to reduce the global mean large-scale field. However the increased localization of the large-scale field could result in local enhancements, but in practice this effect seems smaller. The much increased local diffusivity in the arms results in a more rapid decay of the injected small-scale field, and so a greater contrast between large- and small-scale fields, as suggested by the figures. A test case omitting the term indicates that the turbulent diamagnetic velocity 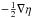 appearing in Eq. (1) plays only a minor role.
appearing in Eq. (1) plays only a minor role.
Our model reproduces the main feature of the effect, but no attempt has been made to reproduce all details of magnetic arm formation. In particular, small-scale dynamo action is represented only by magnetic field injections. The statistical properties of injections are obviously simplified, e.g. injections occur at regular prescribed instants rather than being distributed more or less homogeneously in time. Presumably, this statistical inhomogeneity is responsible for a sharp peak in evolution of the small-scale field in arms shown in Fig. 3. Development of the model in order to obtain a more realistic description of small-scale dynamo action seems to be an important undertaking.
The pitch angles of the field structures are generally smaller than those of the spiral arms (similarly to those of Chamandy et al. 2013, obtained using a quite different mechanism), but locally have more realistic values, especially in the model (Fig. 6) with larger diffusivity contrast. Additionally, their B-structures are not aligned along the structures, again differing from most observations – small deviations are possibly occasionally present. In some cases the interarm structures are rather broad compared to those observed, but M 81, for example, does have broad interarm structures (e.g. Krause et al. 1989). Larger diffusivity contrasts than illustrated can give narrower and more filamentary arms. Our model assumes a link between star formation and magnetic arms. Indeed, stronger star formation gives larger diffusivity contrast which in turn gives more pronounced magnetic arms – compare Figs. 1 and 6. Isolation of a correlation between star formation and magnetic arms as well as verification of other possible consequences of the model requires a richer observational basis for investigation of the magnetic arms. At the moment it is not very clear how much can be deduced from observations of several nearby galaxies (NGC 6946 appears likely to yield initial results). Although our models are restricted to the no-z approximation, this does seem to be quite robust when applied to disc galaxies (e.g. Chamandy et al. 2014).
We recognize that our assumed diffusivity gradients are a theoretical (but plausible) assumption and are not based directly on observational evidence, and that there are several other mechanisms that can contribute to formation of magnetic arms. In particular, modulation of the alpha effect and time delay between the distributions of dynamo drivers and dynamo suppression, the treatment of helicity fluxes including enhanced outflow in the interarm regions, etc, can all play a role (e.g. Chamandy et al. 2013, 2014, 2015). We believe however that the mechanism described here, based on joint action of the turbulent diffusivity contrast and small-scale magnetic field injections, gives a natural basis for explaining the phenomenon within classical mean-field dynamo theory.
Acknowledgments
R.S. and D.S. are grateful to MPIfR for financial support and hospitality during visits to Bonn. D.S. acknowledges financial support from RFBR under grant 15-02-01407. R.B. acknowledges support by DFG Research Unit FOR1254.
References
- Beck, R. 2015, A&A, in press, DOI: 10.1051/0004-6361/201425572 [Google Scholar]
- Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Bomans, D., Colafrancesco, et al. 2015, PoS(AASKA14)094 [Google Scholar]
- Brandenburg, A. 2015, Astrophys. Space Sci. Lib., 407, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Donner, K.-J., Moss, D., et al. 1992, A&A, 259, 453 [NASA ADS] [Google Scholar]
- Chamandy, L., Shukurov, A., & Subramanian, K. 2013, MNRAS, 428, 3569 [NASA ADS] [CrossRef] [Google Scholar]
- Chamandy, L., Shukurov, A., Subramanian, K., & Stoker, K. 2014, MNRAS, 443, 1867 [NASA ADS] [CrossRef] [Google Scholar]
- Chamandy, L., Shukurov, A., & Subramanian, K. 2015, MNRAS, 446, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C., & Baba, J. D. 2014, PASA, 31, 35 [Google Scholar]
- Krause, M., Beck, R., & Hummel, E. 1989, A&A 217, 17 [NASA ADS] [Google Scholar]
- Lazio, T. J. W., & Cordes, J. M. 1998, in Radio Emission from Galactic and Extragalactic Compact Sources, IAU Colloq. 164, eds. J. A. Zensus, G. B. Taylor, & J. M. Wrobel, ASP Conf. Ser., 144, 329 [Google Scholar]
- Moss, D. 1998, MNRAS, 297, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D., & Sokoloff, D. 2013, Geophys. Astrophys. Fluid Dyn., 107, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D., Stepanov, R., Arshakian, T. G., et al. 2012, A&A, 537, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Beck, R., Sokoloff, D., et al. 2013, A&A, 556, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poezd, A., Shukurov, A., & Sokoloff, D. 1993, MNRAS, 264, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Ruzmaikin, A., Shukurov, A., & Sokoloff, D. 1988, Magnetic Fields of Galaxies, (Dordrecht: Kluwer) [Google Scholar]
- Shukurov, A. 1998, MNRAS, 299, L21 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Field vectors at dimensionless times t ≈ 3.0 and 17.0 (2.3 and 13.3 Gyr), for Model 2 with the diffusivity contrast parameter ηa = 4. Here, and in subsequent similar figures, the vectors give the magnetic field direction, with lengths proportional to the magnetic field strengths, and the contours delineate the arms. The corotation radius is approximately 0.7R. |
| In the text | |
 |
Fig. 2 Model 2. Intensity of the large-scale magnetic field at times 2.34, 3.9, 7.8, 11.7, 12.48 and 13.26 Gyr (left to right, top to bottom). Contours shows isolines of large-scale field intensity (darker corresponds to a larger value). The first and last panels can be compared with the panels of Fig. 1. |
| In the text | |
 |
Fig. 3 Model 2, showing global amplitudes of large- and small-scale field in the arms (respectively thick and thin red dashed) and large- and small-scale field in the interarm regions (respectively thick and thin blue curves). |
| In the text | |
 |
Fig. 4 Model 7. Computation starting from a random seed field (as Model 2), but with no ongoing small-scale field injections. Δηa = 4. |
| In the text | |
 |
Fig. 5 Field vectors at dimensionless time τ = 17.0 (13.3 Gyr), for model 3 with diffusivity contrast parameter ηa = 4. The corotation radius is approximately 0.5R. |
| In the text | |
 |
Fig. 6 Field vectors at dimensionless time τ = 17.0 (13.3 Gyr), for Model 8 with the larger diffusivity contrast parameter ηa = 6. The corotation radius is approximately 0.7R. |
| In the text | |
 |
Fig. 7 Field vectors at dimensionless time τ = 17.0 (13.3 Gyr), for Model 9 with parameters as Model 2, but a different sequence of random numbers defining the initial field and subsequent injections. |
| In the text | |
 |
Fig. 8 Field vectors at dimensionless time τ = 17.0 (13.3 Gyr), for Model 19. Here the seed field was weak and smooth, and there were no random injections until τ = 8. The corotation radius is approximately 0.7R. |
| In the text | |
 |
Fig. 9 Field vectors at dimensionless times a) t ≈ 8.4, b) 9.9 and c) 10.6, for Model 6 with the diffusivity contrast parameter ηa = 4. The arms are removed between τ = 8.5 and 10.5, and panel c) shows that the interarm regular fields appear almost immediately after the arms reappear. The anomalously long vectors are the result of a field injection just before τ = 10.6. |
| In the text | |
 |
Fig. 10 Model 7, showing global amplitudes of large- and small-scale field in the arms (respectively thick and thin red dashed) and large- and small-scale field in the interarm regions (respectively thick and thin blue curves). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


