EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 578 (June 2015) A&A, 578 (2015) A62 Full HTML
Free Access
Issue
A&A
Volume 578, June 2015
Article Number A62
Number of page(s) 7
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201526044
Published online 05 June 2015

© ESO, 2015

1. Introduction

Almost 200 molecules have been detected in space1, as well as several of their isomers. For several years (e.g., Hollis et al. 2006), the variations between isomers have been thought to provide important clues to the routes of formation and destruction of the corresponding species. We previously reported a study of 32 isomeric forms detected in several sources, and, surprisingly, we noticed that on average the most stable isomer is also the most abundant and that isomers with the lowest energy difference also have the largest relative abundances (Lattelais et al. 2009). We called it the minimum energy principle (MEP). Although it is not clear yet why the MEP works in the interstellar medium (ISM), perhaps isomerization at the moment of the molecule formation or cosmic-rays induced UV photolysis as suggested by Puletti et al. (2010), it has a notable predictive power. For example, based on the MEP, we predicted that glycine is difficult to detect because it is not the most stable isomer in its family (Lattelais et al. 2011a), and that acetamide and formamide are the most stable isomers in their respective families (Lattelais et al. 2010). The latter prediction has been confirmed by the recent works by Mendoza et al. (2014) and Lopèz-Sepulcre et al. (2015), who detected formamide in a dozen sources. This example is particularly important as it demonstrates that the peptide bond (N–C = O), crucial for terrestrial life, is the most stable bond in its family. In addition, a recent study shows that formamide could be a crucial molecule in the synthesis of genetic and metabolic species (e.g., Saladino et al. 2012; Ferus et al. 2015).

There are, however, some notable exceptions to the MEP, already mentioned by Lattelais et al. (2009): the cases of C4H3N and C2H4O2. For example, in the C2H4O2 case, acetic acid (CH3COOH) is more stable than methyl formate (HCOOCH3), but observations (in hot cores or corinos) show that methyl formate is more abundant (by about a factor 10) than acetic acid. A possible explanation for these exceptions is that adsorption on the grain surfaces plays a crucial role. In particular, Lattelais et al. (2011b) carried out a study of the adsorption of the couple methyl formate and acetic acid and found that the relative adsorption energies may be at the origin of the exception to the MEP. Alternatively, isomerization by UV photolysis may have timescales that induce the observed MEP exception for the acetic acid – methyl formate couple (Puletti et al. 2010).

In this context, the case of the four isomers of the CHON generic formula – isocyanic acid (HNCO), cyanic acid (HOCN), fulminic acid (HCNO) and isofulminic acid (HONC) – may provide additional information to understand the validity of the MEP and its limitations. The CHON isomers present the largest energy difference between the most stable and the successive isomer (e.g., Fig. 1 in Lattelais et al. 2009). The four different isomers are all closed-shell molecules whose relative stabilities range on the energy scale in the order HNCO > HOCN > HCNO > HONC. The first systematic calculations using density functional theory (DFT) in the B3LYP formulation showed HOCN, HCNO, and HONC energetically higher than HNCO by 28.7, 67.9, and 87.1 kcal/mol, respectively (Mebel et al. 1996). The most accurate ab initio calculations using full coupled cluster through triple excitations (CCSDT) with large basis sets refined these energy differences to subchemical accuracy as 24.65, 70.67, and 84.12 kcal/mol, respectively (Schuurman et al. 2004).

This article focuses on the CHON family and the relative adsorption energies on a variety of surfaces. We note that we are not concerned with the mechanisms coupling the adsorption and the formation of the CHON isomers on the grain surfaces. In view of their very weak abundances, we focus only on the adsorption of a single molecule. Considering multiple adsorptions or the formation of a monolayer is clearly irrelevant.

The article is organized as follows. We review the available observations in Sect. 2, describe the considered grain surface models in Sect. 3, and present the theoretical approach in Sect. 4 starting with a brief outline of the methods used in which we discuss the main features of the calculations. The theoretical adsorption energies obtained are given in Sect. 5, and the possible implications on the observed abundances are discussed in Sect. 6.

2. Previous observations of the CHON isomers

The most stable isomer, HNCO, was detected in Sgr B2 more than forty years ago (Snyder & Buhl 1972). Following this detection, which was seen as the first example of a peptide bond, a systematic search was carried out in a wide variety of environments. Thus, HNCO was detected in cold dense cores (Brown 1981; Marcelino et al. 2009, 2010; Lopéz- Sepulcre et al. 2015), in hot cores (Snyder & Buhl 1972; Churchwell et al. 1986; Martin et al. 2008) and hot corinos (Lopéz-Sepulcre et al. 2015), in photon-dominated regions (Jansen et al. 1995), in diffuse clouds (Turner et al. 1999), in the direction of the Galactic center (Kuan & Snyder 1996; Cummins et al. 1986; Turner 1991; Martin et al. 2008), in molecular shocks (Mendoza et al. 2014), and in external galaxies (Meier & Turner 2005; Martin et al. 2008).

The second most stable isomer, HOCN, was detected in Sgr B2 (OH), the estimated abundance with respect to HNCO being ~0.005 (Brünken et al. 2009). Observations towards different regions of Sgr B2 and towards several sources showed the same trend with HOCN/HNCO varying in the range of 0.003 to 0.03 (Brünken et al. 2010; Marcelino et al. 2010). Specifically, a difference is observed between the cold and hot sources, with the former having on average an abundance ratio HNCO/HOCN smaller than the latter.

The third isomer on the energy scale, HCNO, was detected in dark cloud cores and in a lukewarm corino, but remains undetected towards Sgr B2 and molecular shocks (Marcelino et al. 2009, 2010; Mendoza et al. 2014). The same dichotomy, even more pronounced (by one order of magnitude) is observed for the abundance ratio HNCO/HCNO between cold and warm sources.

The fourth isomer, HONC, the highest in energy in the series of CHON species, has been characterized in the laboratory (Mladenovic et al. 2009), but its detection has not yet been reported.

3. Considered grain surfaces

Several grain models were originally proposed such as ices and/or carbonaceous coatings on mineral particles (Greenberg 1976) and refractory minerals such as silicates and metal oxides possibly mixed with graphitic carbon (Mathis et al. 1977). Following these lines, various components were identified according to the environment by means of mid-IR spectroscopy, from the polycyclic aromatic hydrocarbon (PAH) molecules that are present in the spectra of almost all objects (Léger & Puget 1984; Allamandola et al. 1985), carbonates (Kemper et al. 2002; Ceccarelli et al. 2002; Chiavassa et al. 2005), and silicates (Molster et al. 2002) to complex interstellar ices (Schutte 1999; Gibb et al. 2004; Watanabe & Kouchi 2008; Boogert et al. 2015). Hence, three types of surfaces presented below appear chemically relevant to the distribution of the species between the gas phase and the grains.

The structure of the grains in which a silicate core is coated with ice is the most commonly used. Experimentally, the temperatures at which various species desorb from the ice have been characterized using the temperature programmed desorption (TPD) technique (see, e.g., Collings et al. 2004). Recently, we reported a joint theory/TPD experiment (Lattelais et al. 2011b) focused on the adsorption of two couples of isomers: acetic acid (AA)/methyl formate (MF) and ethanol (EtOH)/di-methyl ether (DME). Comparison between the theoretical adsorption energies Eads on ice with those derived from the TPD experiments showed that both agree whenever measurement is possible.

However, ice is not the only surface to be considered. Following Weingartner & Draine (2001), grains could also be composed of a mixture of amorphous silicate and carbonaceous matter including PAHs with up to ~2500 atoms. In this model, the larger PAH molecules close to graphene are assumed to contain ~10–15% of the cosmic carbon abundance. Other evaluations find values up to 20% (Joblin et al. 2004; Tielens 2005). The same grain model suggests that a silicate surface could also be a support for molecular adsorption, which was tested recently (Noble et al. 2012) on the thermal desorption of CO, O2, and CO2. Here, two model surfaces were used, namely a graphene sheet, which proved reliable in previous studies of the adsorption of molecular hydrogen (Pauzat et al. 2011), and a surface of hydroxylated silica that had been used previously to investigate the adsorption of chiral prebiotic species (Downs & Hazen 2004; Pauzat et al. 2015).

To the best of our knowledge, the adsorption of the four CHNO isomers on the three types of surfaces has never been considered. For the modeling of the icy grains, only the top layer of the ice is generally considered in the description of the chemical processes. Alternative options are represented by the recent models by Garrod & Pauly (2011) and Taquet et al. (2012), and the subsequent works from those authors. The surface reactions are described within the standard Langmuir-Hinschelwood model and the reactions are treated by rate equations (Hasegawa et al. 1992). In the gas-grain modeling of the CHNO isomers abundances by Quan et al. (2010), the crucial values of the adsorption energies were a priori set equal for all four isomers and estimated to 5.6 kcal/mol i.e., 2800 K.

4. Computational background

The Vienna ab initio simulation package (VASP; Kresse & Hafner 1993, 1994) was used to carry out all the calculations. The core electrons are kept frozen and replaced by pseudopotentials generated by the plane augmented wave method (PAW), and plane wave basis sets were used in the calculations. The Brillouin zone was integrated with the Monkhorst-Pack sets of k-points centered at the Γ point with an optimized 500 eV energy cutoff. The grid was adapted to provide an equivalent treatment for all the unit cells considered.

As in a previous work (Lattelais et al. 2011b) we used the generalized gradient approximation (GGA) in the form of the Perdew and Wang exchange-correlation functional (PW91) for geometry optimization and in the computation of adsorption energies on the ice and silicate surfaces. The interactions between the HNCO isomers and the water ice and silicate surfaces are pure hydrogen bonding. Generalized gradient approximation extension is crucial for the accurate treatment of the hydrogen bonds and water structures, and the PW91 form has been tested extensively for a variety of intermolecular interactions including H bonding (Yang 2005; Meng 2002, 2004). On the other hand, the interactions of HNCO isomers with graphene are more complex, mixing dispersion, electrostatic interaction, and hydrogen bonding. The long-range van der Waals interactions in these systems were considered by employing the semiempirical approach proposed by Grimme (PBE+D2; Grimme et al. 2010). This method relies on corrections added to the DFT total energy and forces, based on a damped atom-pairwise potential C6R-6, where C6 represents the dispersion coefficient for a given atom and R is the distance between the atoms.

Taking into account that periodic calculations are based on the replication of the unit cell along the three directions in space, the size of the unit cell is a critical parameter that has to be determined in order to avoid any spurious interaction. The basal and the vertical dimensions have been checked according to the procedure detailed in the following paragraphs.

The interaction energy with the surface, hereafter referred to as adsorption energy, is obtained as Eads = (Esurf + ECHON) − E, where E is the energy of the optimized [surface + CHON molecule] complex, Esurf is the energy of the pristine surface, and ECHON is the energy of a single molecule optimized in a cell large enough so that there is no interaction with the periodic replicas.

4.1. Graphene model

Since graphene is a model for a grain surface, it is not supposed to be accessible on both sides as it should be for hydrogen storage purposes (Heine et al. 2004; Chan et al. 2004). The graphene surface, i.e., the top layer of graphite, is composed of benzene rings. It is planar and assumed to remain planar contrary to some models that include five-membered cycles to force a curvature more appropriate to hydrogen storage (Okamoto & Miyamoto 2001). Such a planar constraint, valid here for adsorption, would not be justified if chemisorption were to be considered as it is, for example, in the first step of H2 synthesis (see Jeloaica & Sidis 1996).

In our model, the carbon-carbon bond was set to 1.42 Å, which is the experimental bond length for graphite. No further optimization of the geometry of the graphene surface has been done. We have considered different cells with increasing size to study the influence of the distance between molecular replicas of the CHON isomers on the adsorption energy, as we did in our study of the adsorption of H2 on graphene (Pauzat et al. 2011). In the biggest cell used here, i.e., the (4√3 × 4√3) graphene cell, the closest neighbor is ~17 Å away (Fig. 1).

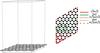thumbnail Fig. 1

Views of the graphene sheet. Left: side view of the (4√3 × 4√3) graphene cell with a height of 30 Å. Right: scheme of the different cells considered in this work: the green solid line represents the (2 × 2) unit cell; the green dotted line the (4 × 4) unit cell; the red solid line the (√3 × √3) cell, which is rotated 30° from the unit cell; the red short-dotted line the (2√3 × 2√3) cell; and the long-dotted line the (4√3 × 4√3) cell.

4.2. The ice model

The modeling of bulk and surface ice structure and reactivity has attracted some attention in the past (Hirsch & Ojamae 2004; Kuo & Singer 2003; Casassa & Pisani 2002). It provides, together with our own experience (Casassa et al. 2005; Calatayud et al. 2003), the basis for the present study. Levering on the preceding results, we took a periodic representation of solid water in the form of hexagonal ice composed of bi-layers of water molecules. Among the different structures possible, we considered only the apolar variety. On the one hand, it seems the most plausible arrangement according to the crystallization conditions in the ISM; on the other hand, it is computationally justified because only apolar structures can generate slabs that are stable (Bussolin et al. 1998), reproduce the bulk properties, and have a balanced distribution of alternate hydrogen and oxygen sites at their surfaces (for a complete discussion, see Casassa et al. 2005). The model unit (Cell 1) contains two bilayers (Fig. 2), i.e., an elementary volume whose replication in three spatial directions creates a series of ice surfaces of infinite dimensions. This volume is defined by three structural parameters a, b, and c. Here, the basal plane dimensions (corresponding to the surface interacting with the adsorbate) are a = 7.145 Å and b = 8.73 Å. The third dimension of the cell was determined so that there is no interaction between molecules generated by a translation perpendicular to the ice surface.

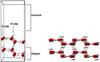thumbnail Fig. 2

Side views of hexagonal apolar ice: unit cells 1G (left) and 2G (right) with two bi-layers.

However, the interactions generated by lateral translations between the adsorbed species are not fully eliminated in these conditions. An intermolecular distance larger than 14 Å is necessary, which led us to double the dimensions of the cell in the two directions of the plane, i.e., a = 14.29 Å and b = 17.46 Å while retaining the height of 30 Å ((2 × 2) cell).

thumbnail Fig. 3

Views of the (4 × 4) silica slabs: (upper panels) (0001) silica slab; (lower panels) (10\hbox{$\bar{1}$}0) silica slab. Left: side views; right: top views.

4.3. The silica model

The presence of silica in the ISM had been disputed for a long time until its recent identification in the envelope of T Tauri stars (Sargent et al. 2009). In the same way as ice and graphite, well-defined surfaces of silica can be obtained from single crystals in view of laboratory experiments. Because of the abundance of hydrogen in space, the grain surfaces are supposed to be hydroxylated, which means that there are no free oxygen atoms left on the surface. This assumption is consistent with the DFT calculations by Goumans et al. (2007), which showed that the hydroxylated form of the quartz (0001) surface was more stable than the raw surface obtained by the simple cut of a single crystal. In this study, we kept the same hydroxylated mineral, but investigate the possibilities for adsorption created not only by the (0001) surface, but also by the (10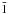\hbox{$\bar{1}$}0) surface, which is supposed to be more responsive to adsorption according to Downs & Hazen (2004).

The model surfaces were obtained by an appropriate cut of the top three silicon layers of the experimental crystal structure. The reactive surface dangling bonds of the oxygen atoms were saturated with hydrogen atoms whose positions were optimized. The silicon atoms on the bottom of the slab (nonreactive surface) are saturated by hydrogen atoms positioned in the direction of the missing oxygens at a distance SiH of 1.5 Å. To be safe from any unwanted interaction between the silica sheets generated by the 3D periodic treatment, a height of 30 Å was taken for the unit cell.

The (0001) silica unit cell is hexagonal, with a = b = 4.916 Å and γ = 120° while the (10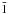\hbox{$\bar{1}$}0) silica unit cell is orthorhombic, with a = 4.916 Å, b = 5.405 Å, and γ = 90°. In order to remove the lateral interactions, we had to consider a (4 × 4) cell for each silica surface, reaching a (19.664 × 21.62) Å2 and a (19.664 × 19.664) Å2 surfaces for the (10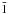\hbox{$\bar{1}$}0) and (0001) surfaces, respectively, in all adsorption calculations.

5. Adsorption energies

5.1. Adsorption on graphene

After the first screening, we discarded all the CHON arrangements parallel to the surface that were found higher in energy than the perpendicular ones. The most stable situations are found when the hydrogen atom of the CHON isomer is on top of a carbon atom of graphene, the bond involving the hydrogen atom in the molecule being perpendicular to the graphene surface, and the CHON molecule in a plane including the carbon atom of graphene and the center of a benzene ring (see Table 1).

Table 1

Views of the most stable geometries of the adsorbed CHON isomers on graphene.

For each molecule, we calculated the adsorption energy (as described above) for every cell described in Fig. 1. As the size of the unit cell increases, the distance between molecular replicas increases accordingly. Figure 4 shows the adsorption energy2 as a function of the distance between replicas. The most remote point corresponds to the (4√3 × 4√3) unit cell with a distance of 17 Å. The adsorption energies, extrapolated (with a linear function of 1 /d2) beyond this point to an infinite distance between molecular replicas are 3.7, 4.4, 7.8, and 8.1 kcal/mol for HCNO, HNCO, HONC, and HOCN, respectively.

thumbnail Fig. 4

Adsorption on graphene. Adsorption energy Eads (kcal/mol) as a function of the cell parameter that is also the distance between molecular replicas. The dotted lines represent the fit made with a linear function of 1 /d2 (d being the distance between replicas).

We can see in Fig. 4 that the differences between the adsorption energies of any two CHON isomers are almost constant from this point, which means that the lateral interactions between replicas are now negligible at that distance (and beyond). The hydrogen bond length is 2.36, 2.30, 2.06, and 2.03 Å, respectively. The greater the difference, the shorter the bond length. The attachment to the surface is stronger when an OH group of the molecule is involved. Without dispersion correction, we found the same energetic trend, but the values are half those given above.

5.2. Adsorption on ice

Table 2

Views of the most stable geometries of the adsorbed CHON isomers on apolar ice.

Table 3

Views of the geometry of the adsorbed CHON molecules on silica.

Table 4

Relative energies (eV) and adsorption energies (eV) of CHON isomers on interstellar model surfaces.

It can be seen in Table 2 that all four CHON isomers adsorb on the surface by two hydrogen bonds: one between an oxygen atom from the ice surface and the H atom from the adsorbed isomer; the other between an H atom from the surface and the atom at the other extremity of the molecule. However, the CHON isomers have adsorption energies that vary from one to another. To help in the discussion, the atoms belonging to the adsorbates will be in italics.

  • i)

    Isocyanic acid (HNCO), the most abundant isomer, is adsorbedby means of a hydrogen bond (NH··· Oice) between the NH group of HNCO and an oxygen site of the ice, and another (O··· HOice) between the oxygen of HNCO and a hydrogen site of the ice. The adsorption energy of 13.8 kcal/mol, equivalent to that of H2O on the ice shows that HNCO does not desorb before the ice sublimates.

  • ii)

    Cyanic acid (HOCN), the second most abundant isomer, is also adsorbed by means of two hydrogen bonds, but the structure of the interactions changes from (NH··· Oice) to (OH··· Oice). This hydrogen shift results in the stronger adsorption energy of the four isomers (30.0 kcal/mol), twice as much as that of the most abundant isomer.

  • iii)

    Fulminic acid (HCNO), the last observed isomer, also has two hydrogen bonds with the ice. One (O··· HOice) is comparable to the one in HNCO, but the other (CH··· Oice) is much weaker than any other hydrogen bond possible in the present context. The total interaction amounts to 10.6 kcal/mol, which means that HCNO would be released to the gas phase before the ice sublimates.

  • iv)

    Isofulminic acid (HONC), not yet observed, is almost as strongly bound to the ice (26.5 kcal/mol) as HOCN. The two molecules share a similar bond with the ice (OH··· Oice) but the second link is (C··· HOice), whereas for HOCN it is (N··· HOice). The hydrogen bond between a carbon atom and an HO fragment of ice is weaker than the one between a nitrogen atom and the HO fragment of ice.

5.3. Adsorption on silica

As shown above for the ice, the four CHON isomers have varying adsorption energies on silica. These adsorption energies also vary from one surface to another, although they are in the same energetic order. The fact that smaller adsorption energies are found for the (0001) surface than for (10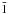\hbox{$\bar{1}$}0) confirms the statement by Downs & Hazen (2004) that the latter surface is more responsive to adsorption. However, even for the “best” silica surface, the adsorption energies are still less than half those on the ice, as shown in Table 3. As in the preceding discussion, the atoms belonging to the adsorbates will be in italics.

The strength of the hydrogen bonds is systematically weaker than for the ice surface because of the smaller charge separation between the oxygen and the silicon atom.

  • i)

    HCNO adsorbs on both (0001) and (10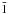\hbox{$\bar{1}$}0) surfaces with onehydrogen bond (CH···Osil). The position of the molecule with respect to the two surfaces does not change enough to induce a significant variation of the adsorption energy (Table 3) as shown by the close values found for the two surfaces, i.e., ~3.5 kcal/mol.

  • ii)

    HNCO adsorbs on silica by means of two hydrogen bonds. For both surfaces there is a (NH···Osil) hydrogen bond. However, the second link to the surface is structurally different. For the (0001) surface, the bonding also originates from the nitrogen atom as (N···Hsil), whereas it implies (O···Hsil) for the (10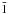\hbox{$\bar{1}$}0) surface. The final result is that, with two hydrogen bonds for both surfaces, we find a similar adsorption energy even if the position of HNCO with respect to the surfaces is different.

  • iii)

    HOCN adsorbs more on the (10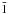\hbox{$\bar{1}$}0) surface than on the (0001) surface. It makes two hydrogen bonds with the (10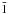\hbox{$\bar{1}$}0) surface ((OH···Osil) and (N···Hsil)), whereas it only makes one with the (0001) surface, (OH···Osil). The main reason is that the (10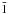\hbox{$\bar{1}$}0) surface allows a better match between the adsorption points and the length of the OCN/ONC skeleton.

  • iv)

    As is true for HOCN, HONC has a larger adsorption energy on the (10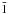\hbox{$\bar{1}$}0) surface than on the (0001) surface because it adsorbs by means of two hydrogen bonds on the (10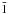\hbox{$\bar{1}$}0) surface, (OH···Osil) and (C···Hsil), whereas it adsorbs by means of only one hydrogen bond on the (0001) surface, (OH···Osil). The reason is the same as above.

In all cases, the general trend along the series of isomers is the same as for the water ice surface, with the adsorption energies in the order HOCN > HONC > HNCO > HCNO.

6. Discussion and conclusion

Table 4 summarizes the results of our computations. The aim of the present study was to determine how strongly the four isomers of the CHON generic formula would adsorb at the surfaces of interstellar grains of different types. Three model surfaces were used for this purpose, graphene, water ice, and silica, which were found to provide interaction energies of different magnitudes to be ranked in the same order for all isomers:

water ice > silica > graphene.

Considering the different isomers, the ordering of the adsorption energies is the same, independent of the substrate: 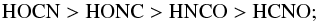HOCN>HONC>HNCO>HCNO;\begin{eqnarray*} \rm HOCN > HONC > HNCO > HCNO; \end{eqnarray*}and totally disconnected of their energy ordering: 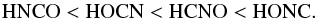HNCO<HOCN<HCNO<HONC.\begin{eqnarray*} \rm HNCO < HOCN < HCNO < HONC. \end{eqnarray*}For example, on graphene and ice the lowest adsorbing energies are obtained for HCNO and HNCO, while they are about two times larger for HOCN and HONC (because of the OH bond). An analogous behavior is observed for the silicate substrates where the difference is even larger and the HCNO possesses the lowest adsorption energy. The critical point is the possibility of forming strong hydrogen bonding, and the stronger bonding is obtained when a -OH bond of a CHON isomer interacts with an oxygen atom at the surface of the solid substrate.

In summary, in any of the studied substrates, the least surface-bound isomer is HCNO, shortly followed by HNCO, and then HONC and HOCN. This implies that HCNO is released from the grain surface into the gas phase at almost the same dust temperature at which HNCO is released. On the contrary, HOCN is released at higher temperatures. Since the largest difference in the abundance ratio between cold and warm sources is observed in HNCO/HCNO rather than HNCO/HOCN (Sect. 2), we are forced to conclude that, in the case of the CHON isomer family, the adsorption does not seem to directly influence the abundance ratio. On the contrary, the relative energy (lower for HOCN than HCNO) seems to play a major role. Supporting this conclusion, when the two couples (HNCO/HCNO and HNCO/HOCN) are considered in the MEP framework, the measured ratios approximately fit with it (Fig. 1 in Lattelais et al. 2009).

Of course, it is possible that the differences in the CHON isomer abundances are totally set by the gas phase and/or grain surface formation and destruction routes, as discussed by Marcelino et al. (2010) and Quan et al. (2010). Nonetheless, while the models seem to reproduce fairly well the abundances and isomer abundance ratios in cold gas, they have trouble reproducing the observations towards the hot gas. It is then tempting to suggest that the MEP might indeed be at work in the sublimated CHON isomers, as the relative abundances also follow the relative stability energies (see also Fig. 1 in Lattelais et al. 2009). This might also suggest that some partial isomerization occurs during the ice sublimation.

It will be interesting, on the one hand, to have more observations of HNCO, HOCN, and HCNO in well-defined zones for a larger body of different objects and, on the other hand, to see how the predictions of the chemical models change with the specific values of the adsorption energies provided in the present work.

2

For convenience: 1 kcal/mol = 350 cm-1 = 500 K.

Acknowledgments

This work was supported by CNRS national program PCMI (Physics and Chemistry of the Interstellar Medium), COST Action CM 805, “The Chemical Cosmos”, and the Agence Nationale pour la Recherche (ANR), France (contract ANR-08-BLAN-0225, project FORCOMS). Part of the calculations were performed using HPC resources from GENCI-CINES (Grant 2013-085128).

References

  1. Boogert, A., Gerakines, P., & Whittet, D. 2015, ARA&A, 53, in press [arXiv:1501.05317] [Google Scholar]
  2. Brown, R. D. 1981, ApJ, 248, L119 [NASA ADS] [CrossRef] [Google Scholar]
  3. Brünken, S., Gottlieb, C. A., McCarthy, M. C., & Thaddeus, P. 2009, ApJ, 697, 880 [NASA ADS] [CrossRef] [Google Scholar]
  4. Brünken, S., Belloche, A., Martin, S., & Menten, K. M. 2010, A&A, 516, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bussolin, G., Casassa, S., Pisani, C., & Ugliengo, P., 1998, J. Chem. Phys., 108, 9516 [NASA ADS] [CrossRef] [Google Scholar]
  6. Calatayud, M., Courmier, D., & Minot, C., 2003, Chem. Phys. Lett., 369, 287 [NASA ADS] [CrossRef] [Google Scholar]
  7. Casassa, S., & Pisani, C., 2002, J. Chem. Phys., 116, 9864 [NASA ADS] [CrossRef] [Google Scholar]
  8. Casassa, S., Calatayud, M., Doll, K., Minot, C., & Pisani, C., 2005, Chem. Phys. Lett., 409, 110 [NASA ADS] [CrossRef] [Google Scholar]
  9. Ceccarelli, C., Caux, E., Tielens, A. G. G. M., et al. 2002, A&A, 395, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Chan, S. P., Ji, M., Gong, X. G., & Liu, Z. F. 2004, Phys. Rev. B, 69, 092101 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chiavassa, A., Ceccarelli, C., Tielens, A. G., Caux, E., & Maret, S. 2005, A&A, 431, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Churchwell, E., Wood, D., Myers, P. C., & Myers, R. V. 1986, ApJ, 305, 405 [NASA ADS] [CrossRef] [Google Scholar]
  13. Collings, M. P., Anderson, M. A., Chen, R., et al. 2004, MNRAS, 354, 1133 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cummins, S. E., Linke, R. A., & Cronin, P. 1986, ApJS, 60, 819 [NASA ADS] [CrossRef] [Google Scholar]
  15. Downs, R. T., & Hazen, R. M., 2004, J. Mol. Catal., 216, 273 [CrossRef] [Google Scholar]
  16. Ferus, M., Nesvorny, D., Sponer, J., et al. 2015, PNAS, 112, 657 [Google Scholar]
  17. Garrod, R. T., & Pauly, T. 2011, ApJ, 735, A15 [NASA ADS] [CrossRef] [Google Scholar]
  18. Gibb, E., Whittet, D., Boogert, A., & Tielens, A. G., 2004, ApJS, 151, 35 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  19. Goumans, T. P. M., Wander, A., Brown, W. A., & Catlow, C. R. A. 2007, Phys. Chem. Chem. Phys., 9, 2146 [CrossRef] [Google Scholar]
  20. Greenberg, J. M. 1976, Astrophys. Space Sci., 39, 9 [NASA ADS] [CrossRef] [Google Scholar]
  21. Grimme, S., Antony, J., Ehrlich, S., & Krieg, H. 2010, J. Chem. Phys., 132, 154104 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  22. Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef] [Google Scholar]
  23. Heine, T., Zhechkov, L., & Seifert, G., 2004, Phys. Chem. Chem. Phys., 6, 980 [CrossRef] [Google Scholar]
  24. Hirsch, T. K., & Ojamae, L., 2004, J. Phys. Chem. B, 108, 15856 [CrossRef] [Google Scholar]
  25. Hollis, J. M., Lovas, F. J.,Remijan, A. J., et al. 2006, ApJ, 643, L25 [Google Scholar]
  26. Jansen, D. J., Spaans, M., Hogerheijde, M. R., & van Dishoeck, E. F. 1995, A&A, 303, 541 [NASA ADS] [Google Scholar]
  27. Jeloaica, L., & Sidis, V., 1996, Chem. Phys. Lett., 300, 157 [Google Scholar]
  28. Joblin, C., Léger, A., & Martin, P. 2004, ApJ, 393, L79 [Google Scholar]
  29. Kemper, F., Jäger, C., Waters, L. B. M. F., et al. 2002, Nature, 414, 295 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  30. Kresse, G., & Hafner, J. 1993, Phys. Rev. B, 48, 13115 [NASA ADS] [CrossRef] [Google Scholar]
  31. Kresse, G., & Hafner, J. 1994, Phys. Rev. B, 49, 14251 [Google Scholar]
  32. Kuan, Y.-J., & Snyder, L. E. 1996, ApJ, 470, 981 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kuo, J. L., & Singer, S. L. 2003, Phys. Rev. E, 67, 016114 [NASA ADS] [CrossRef] [Google Scholar]
  34. Lattelais, M., Pauzat, F., Ellinger, Y., & Ceccarelli, C. 2009, ApJ, 696, L133 [Google Scholar]
  35. Lattelais, M., Pauzat, F., Ellinger, Y., & Ceccarelli, C. 2010, A&A, 519, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Lattelais, M., Pauzat, F., Pilmé, J., Ellinger, Y., & Ceccarelli, C. 2011a, A&A, 532, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Lattelais, M., Bertin, M., Mokrane, H., et al. 2011b, A&A, 532, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Lopèz-Sepulcre, A., Jaber, A., Mendoza, B., et al. 2015, MNRAS, 449, 2438 [NASA ADS] [CrossRef] [Google Scholar]
  39. Marcelino, N., Cernicharo, J., Tercero, B., & Roueff, E. 2009, ApJ, 690, L27 [NASA ADS] [CrossRef] [Google Scholar]
  40. Marcelino, N., Brünken, S., Cernicharo, J., et al. 2010, A&A, 516, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Martin, S., Requena-Torres, M. A., Martin-Pintado, J., & Mauersberger, R. 2008, ApJ, 678, 245 [NASA ADS] [CrossRef] [Google Scholar]
  42. Mathis, J. S., Rumpl, W., & Nordsieck, K. H., 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
  43. Mebel, A. M., Luna, A., Lin, M. C., & Morokuma, K. 1996, J. Chem. Phys., 105, 6439 [NASA ADS] [CrossRef] [Google Scholar]
  44. Meier, D. S., & Turner, J. L. 2005, ApJ, 618, 259 [NASA ADS] [CrossRef] [Google Scholar]
  45. Mendoza, E., Lefloch, B., López-Sepulcre, A., et al. 2014, MNRAS, 445, 151 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  46. Meng, S., Xu, L. F., Wang, E. G., & Gao, S. 2002, Phys. Rev. Lett., 89, 176104 [NASA ADS] [CrossRef] [Google Scholar]
  47. Meng, S., Wang, E. G., & Gao, S. 2004, Phys. Rev. B, 69, 195404 [NASA ADS] [CrossRef] [Google Scholar]
  48. Mladenovic, M., Lewerenz, M., McCarthy, M. C., & Thaddeus, P. 2009, J. Chem. Phys., 131, 174308 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  49. Molster, F. J., Yamamura, I., Waters, L. B. M. F., et al. 2002, Nature, 401, 563 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  50. Noble, J. A., Congiu, E., Dulieu, F., & Fraser, H. J. 2012, MNRAS, 421, 768 [NASA ADS] [Google Scholar]
  51. Okamoto, Y., & Miyamoto, Y. 2001, J. Phys. Chem. B, 105, 3470 [CrossRef] [Google Scholar]
  52. Pauzat, F., Lattelais, M., Ellinger, Y., & Minot, C. 2011, MNRAS, 412, 2729 [NASA ADS] [CrossRef] [Google Scholar]
  53. Pauzat, F., Marloie, G., Markovits, A., & Ellinger, Y. 2015, Int. J. Astrobiol., available on CJO2015, DOI: 10.1017/S1473550415000087 [Google Scholar]
  54. Puletti, F., Malloci, G., Mulas, G., & Cecchi-Pestellini, C. 2010, MNRAS, 402, 1667 [NASA ADS] [CrossRef] [Google Scholar]
  55. Quan, D. H., Herbst, E., Osamura, Y., & Roueff, E. 2010, ApJ, 725, 2101 [NASA ADS] [CrossRef] [Google Scholar]
  56. Saladino, R., Botta, G., Pino, S., Costanzo, G., & Di Mauro, E. 2012, Chem. Soc. Rev., 41, 5526 [CrossRef] [Google Scholar]
  57. Sargent, B. A., Forrest, W. J., Tayrien, C., et al. 2009, ApJ, 690, 1193 [NASA ADS] [CrossRef] [Google Scholar]
  58. Schutte, W. A. 1999, in Solid Interstellar Matter: the ISO Revolution, eds. L. d’Hendecourt, C. Joblin, & A. Jones (Paris: EDP Sciences, Berlin: Springer-Verlag), 183 [Google Scholar]
  59. Schuurman, M. S., Muir, S. R., Allen, W. D., & Schaefer III, H. F. 2004, J. Chem. Phys., 120, 11586 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  60. Snyder, L. E., & Buhl, D. 1972, ApJ, 177, 619 [NASA ADS] [CrossRef] [Google Scholar]
  61. Taquet, V., Ceccarelli, C., & Kahane, C. 2012, ApJ, 538, A42 [Google Scholar]
  62. Tielens, A. G. G. M. 2005, in Proc. Dusty and Molecular Universe: a prelude to Herschel and Alma, ed. A. Wilson, ESA SP, 577, 245 [Google Scholar]
  63. Turner, B. E., Terzieva, R., & Herbst, E. 1999, ApJ, 518, 699 [NASA ADS] [CrossRef] [Google Scholar]
  64. Watanabe, N., & Kouchi, A., 2008, Progress in Surface Science, 83, 439 [NASA ADS] [CrossRef] [Google Scholar]
  65. Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
  66. Yang, J., Meng, S., Xu, L. F., & Wang, E. G., 2005, Phys. Rev. B, 71, 035413 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Views of the most stable geometries of the adsorbed CHON isomers on graphene.

In the text
Table 2

Views of the most stable geometries of the adsorbed CHON isomers on apolar ice.

In the text
Table 3

Views of the geometry of the adsorbed CHON molecules on silica.

In the text
Table 4

Relative energies (eV) and adsorption energies (eV) of CHON isomers on interstellar model surfaces.

In the text

All Figures

thumbnail Fig. 1

Views of the graphene sheet. Left: side view of the (4√3 × 4√3) graphene cell with a height of 30 Å. Right: scheme of the different cells considered in this work: the green solid line represents the (2 × 2) unit cell; the green dotted line the (4 × 4) unit cell; the red solid line the (√3 × √3) cell, which is rotated 30° from the unit cell; the red short-dotted line the (2√3 × 2√3) cell; and the long-dotted line the (4√3 × 4√3) cell.
In the text
thumbnail Fig. 2

Side views of hexagonal apolar ice: unit cells 1G (left) and 2G (right) with two bi-layers.

In the text
thumbnail Fig. 3

Views of the (4 × 4) silica slabs: (upper panels) (0001) silica slab; (lower panels) (10\hbox{$\bar{1}$}0) silica slab. Left: side views; right: top views.
In the text
thumbnail Fig. 4

Adsorption on graphene. Adsorption energy Eads (kcal/mol) as a function of the cell parameter that is also the distance between molecular replicas. The dotted lines represent the fit made with a linear function of 1 /d2 (d being the distance between replicas).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.