| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 12 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201525855 | |
| Published online | 15 June 2015 | |
The formation of supermassive black holes in rapidly rotating disks
1 Sorbonne Universités, UPMC Univ Paris 06, UMR 7095, Institut d’Astrophysique de Paris, 75014 Paris, France
e-mail: latif@iap.fr
2 CNRS, UMR 7095, Institut d’Astrophysique de Paris, 75014 Paris, France
3 Departamento de Astronomía, Facultad Ciencias Físicas y Matemáticas, Universidad de Concepción, Av. Esteban Iturra s/n Barrio Universitario, Casilla 160-C, Chile
4 Scuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy
Received: 10 February 2015
Accepted: 13 April 2015
Massive primordial halos exposed to moderate UV backgrounds are the potential birthplaces of supermassive black holes. In these halos, an initially isothermal collapse will occur, leading to high accretion rates of ~0.1 M⊙ yr-1. During the collapse, the gas in the interior will turn into a molecular state, and will form accretion disk in order to conserve angular momentum. We consider here the structure of such an accretion disk and the role of viscous heating in the presence of high accretion rates for a central star of 10, 100, and 104 M⊙. Our results show that the temperature in the disk increases considerably due to viscous heating, leading to a transition from the molecular to the atomic cooling phase. We found that the atomic cooling regime may extend out to several 100 AU for a 104 M⊙ central star and that it provides substantial support to stabilize the disk. It therefore favors the formation of a massive central object. The comparison of clump migration and contraction time scales shows that stellar feedback from these clumps may occur during the later stages of the evolution. Overall, viscous heating provides an important pathway to obtain an atomic gas phase within the center of the halo, and helps in the formation of very massive objects. The massive object may collapse to form a massive black hole of about ≥104 M⊙.
Key words: black hole physics / methods: analytical / early Universe / quasars: supermassive black holes / cosmology: theory / accretion, accretion disks
© ESO, 2015
1. Introduction
Self-gravitating accretion disks are common around astrophysical objects ranging from protoplanetary disks around stars to the disks in massive spiral galaxies like our Milky Way. They are formed as a consequence of gravitational collapse owing to the conservation of the angular momentum. The size of these disks varies from a few astronomical units (AU) to kiloparsec (kpc) scales. In the context of early structure formation, disks with sizes of a few hundred AU to pc scales are expected to form (Abel et al. 2000; Bromm et al. 2002). Numerical simulations show the formation of such disks both in minihalos of 105−106 M⊙ (Clark et al. 2011; Greif et al. 2012; Latif et al. 2013b) and in massive primordial halos of ~ 107 M⊙ (Regan & Haehnelt 2009; Latif et al. 2012, 2013a; Becerra et al. 2015) forming in the early Universe at about z = 15; however, the long term evolution and stability of such disks are not well understood. Particularly, they have not been explored in the presence of a central massive object because of the computational costs required for a simulation pursuing a long time-evolution.
The observations of high redshift quasars reveal that black holes of a billion solar masses were assembled within the first billion years after the Big Bang (Fan et al. 2003, 2006; Mortlock et al. 2011; Venemans et al. 2013). The potential pathways for the formation of the earliest supermassive blacks holes include the seeds from stellar remnants, the direct collapse of a massive protogalactic gas cloud referred to as the direct collapse, and stellar dynamical processes in dense stellar clusters (see dedicated reviews for the details of these processes; Volonteri 2010; Natarajan 2011; Haiman 2013). The direct collapse scenario has emerged as the most feasible way to assemble massive black holes in a short time and is the focus of this work. It mandates that gas must be of a primordial composition and the molecular hydrogen cooling must remain suppressed. The massive primordial halos of 107−108 M⊙ forming around z = 15−20 are the potential birthplaces of the direct collapse black holes. It has been shown that supermassive stars of 104−106 M⊙ can form as a result of direct collapse in massive primordial halos if the cooling mainly proceeds via atomic lines (Begelman et al. 2006; Volonteri et al. 2008; Latif et al. 2013c; Schleicher et al. 2013; Hosokawa et al. 2013). Ferrara et al. (2014) have estimated the initial mass function of the resulting direct collapse black holes and found that previous UV feedback can play a central role in determining its shape. The molecular hydrogen cooling can be quenched in the ubiquity of UV flux emitted from the stellar populations. In particular, the photons with energies between 11.2−13.6 eV, known as the Lyman-Werner radiation, can travel long distances and dissociate the molecular hydrogen over large scales. The strength of such a flux has been investigated in numerous studies (Omukai 2001; Shang et al. 2010; Latif et al. 2014a).
It has recently been shown that keeping the collapse completely isothermal with cooling only due to atomic hydrogen is difficult because of the combined effect of considering realistic spectra emitted from Pop II stars where the H− photodissociation is disfavored (Sugimura et al. 2014; Agarwal & Khochfar 2015) and the more realistic initial conditions in 3D simulations (Latif et al. 2015), where the degree of ionization is enhanced by the virialization shocks. Hence, it stimulates H2 formation via the H− route and increases the required strength of the radiation background. Considering both effects, the critical value of the UV flux is now a few times 104 in units of J21 (Latif et al. 2015). This is about two orders of magnitude higher than previous estimates, and the formation sites of direct collapse black holes become exceedingly rare once such thresholds are adopted (Dijkstra et al. 2008, 2014; Agarwal et al. 2012). It is therefore important to explore whether direct collapse only occurs under isothermal conditions or if additional processes can also help to build up a massive central object.
Indeed, recent simulations suggest that massive to supermassive stars may form even in the presence of a moderate UV flux. In this case, an initially isothermal collapse in the presence of atomic cooling may still yield a significant mass supply to the center of the halo where stars of 103−104 M⊙ can efficiently form (Latif et al. 2014b). In such a scenario, large accretion rates of 0.1−1 M⊙/yr occur on a spatial scale of 1 pc and the core of the halo is cooled by the molecular hydrogen. In the presence of such rapid accretion, the central part of the disk can potentially form a massive star and fragmentation may occur on larger scales. We expect the formation of a rapidly rotating disk surrounding such stars as a result of angular momentum conservation as proposed by Oh & Haiman (2002) and Volonteri & Rees (2005). The properties and the stability of the disk forming in massive primordial halos were first explored by Lodato & Natarajan (2006), who found that the mass of the central object depends on halo properties such as mass, spin, and its ability to cool. They also suggested that low spin halos are more efficient in forming a massive central object. While the detailed properties of rapidly rotating disks are currently unknown, their thermal and dynamical properties will be highly relevant once the central star becomes massive and dominates the gravitational potential. Even in the presence of moderate accretion rates, viscous heating can raise the gas temperature and help stabilize the disk against fragmentation (Latif & Schleicher 2015). This effect will be considerably enhanced in the presence of larger accretion rates and more massive central objects. This may have important implications for the formation of massive central objects.
In this study, we therefore consider an atomic cooling halo exposed to a moderate UV background, implying an initially isothermal collapse with high accretion rates, as expected from numerical simulations (Latif et al. 2014b). Because of the conservation of angular momentum, we assume that a self-gravitating disk forms in the central region, and we expect most of the disk to be initially molecular owing to the self-shielding against the radiation background. Using a simple analytical model, we investigate the properties of these disks in the presence of central massive objects, and explore the impact of viscous heating on the thermal evolution. Particularly, we demonstrate that viscous heating can dissociate the molecular hydrogen and leads to a transition toward an atomic cooling regime. Various stages of the disk evolution with a central object of 10, 100, and 104 M⊙ are investigated. They are considered to represent a time evolution due to the growth of the central object. We study the stability of the disk by computing the viscous parameter α. The masses of the clumps forming inside the disk are estimated and their fates are determined by comparing their migration and collapse time scales.
This article is organized in the following way. In Sect. 2, we discuss our theoretical framework and its main assumptions. In Sect. 3, we present our main results. In Sect. 3.1, we discuss the properties of the disk in the presence of a 10 solar mass star. We further describe the intermediate and late stages of the disk evolution when the central object becomes more massive in Sects. 3.2 and 3.3. The potential caveats in our model are discussed in Sect. 3.4. In Sect. 4, we summarize the main conclusions and discuss future perspectives.
2. Theoretical framework
In massive primordial halos, a disk is expected to form as a consequence of gravitational collapse owing to the conservation of angular momentum (Oh & Haiman 2002; Volonteri & Rees 2005; Lodato & Natarajan 2006). It is confirmed from 3D cosmological simulations that a rotationally supported disk forms in halos of 107−108 M⊙ illuminated by a moderate UV flux emitted by Pop II stars at z ~ 15 (Regan et al. 2014; Latif & Volonteri 2015). It is found that the rotational support is enhanced in the presence of H2 cooling compared to the atomic line cooling case. Under these conditions, an initially isothermal collapse occurs but the central core is cooled by the molecular hydrogen. Mass inflow rates of ~ 0.1 M⊙/yr are observed in the presence of a moderate UV flux and can be maintained for at least 30 000 years after the initial collapse (Latif et al. 2014b; Latif & Volonteri 2015).
Motivated by these studies, we employ here an analytical model to investigate the properties of a self-gravitating accretion disk embedded in large accretion flows (Inayoshi & Haiman 2014; Latif & Schleicher 2015). The disk is formed in massive primordial halos irradiated by a background UV flux of strengths 100−1000 (in units of J21 = 10-21 erg / cm2/ s / Hz / sr) at z = 15. The stability of a self-gravitating accretion disk can be measured with the Toomre Q parameter (Toomre 1964) given by 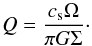 (1)Here Ω and cs are the orbital frequency and the sound speed of the disk; G is the gravitational constant and Σ is the surface density of the disk, which is given as
(1)Here Ω and cs are the orbital frequency and the sound speed of the disk; G is the gravitational constant and Σ is the surface density of the disk, which is given as 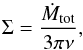 (2)where Ṁtot is the mass accretion rate and ν is the viscosity in the disk resulting from the gravitational stresses. We presume that the disk is marginally stable with Toomre Q = 1 and its scale-height can be estimated assuming that the disk is in hydrostatic equilibrium in the vertical direction via
(2)where Ṁtot is the mass accretion rate and ν is the viscosity in the disk resulting from the gravitational stresses. We presume that the disk is marginally stable with Toomre Q = 1 and its scale-height can be estimated assuming that the disk is in hydrostatic equilibrium in the vertical direction via 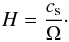 (3)The temperature of the disk is computed by assuming that the viscous heating rate is approximately equal to the disk cooling rate. The viscous heating rate for a self-gravitating disk can be estimated by solving Eq. (50) given in Lodato (2007). They provide the heating rate per surface area given as
(3)The temperature of the disk is computed by assuming that the viscous heating rate is approximately equal to the disk cooling rate. The viscous heating rate for a self-gravitating disk can be estimated by solving Eq. (50) given in Lodato (2007). They provide the heating rate per surface area given as 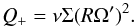 (4)In the case of Keplarian rotation,
(4)In the case of Keplarian rotation, 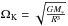 . As realistic disks are at least partially supported also via turbulent and thermal pressure, we assume here that the rotation is not entirely Keplerian, but adopt an efficiency parameter ϵK = Ω / ΩK ~ 0.5, which describes the deviations of the angular velocity Ω from the Keplerian rotation. Using such a rotational profile, the viscous heating rate can be evaluated as
. As realistic disks are at least partially supported also via turbulent and thermal pressure, we assume here that the rotation is not entirely Keplerian, but adopt an efficiency parameter ϵK = Ω / ΩK ~ 0.5, which describes the deviations of the angular velocity Ω from the Keplerian rotation. Using such a rotational profile, the viscous heating rate can be evaluated as 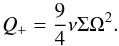 (5)It should also be noted that similar expressions for the viscous heating rate are given by Pringle (1981) and Balbus & Hawley (1998)1. The cooling rate per surface area of the disk can be computed as
(5)It should also be noted that similar expressions for the viscous heating rate are given by Pringle (1981) and Balbus & Hawley (1998)1. The cooling rate per surface area of the disk can be computed as 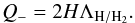 (6)Here ΛH / H2 is the atomic or molecular cooling rate in units of erg / cm3/ s and H is the height of the disk. To compute the viscosity of the disk, we adopt the standard formalism given by Shakura & Sunyaev (1973) as
(6)Here ΛH / H2 is the atomic or molecular cooling rate in units of erg / cm3/ s and H is the height of the disk. To compute the viscosity of the disk, we adopt the standard formalism given by Shakura & Sunyaev (1973) as 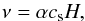 (7)where α is the viscous parameter and is calculated by combining Eqs. (1)−(3), and (7) as
(7)where α is the viscous parameter and is calculated by combining Eqs. (1)−(3), and (7) as 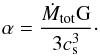 (8)Solving the thermal balance equation (i.e., Q+ = Q−) with respect to Ω in the case of molecular cooling, we get the following expression:
(8)Solving the thermal balance equation (i.e., Q+ = Q−) with respect to Ω in the case of molecular cooling, we get the following expression: 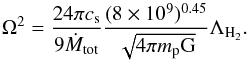 (9)For the densities given in the disk (>108 cm-3), we use the optically thick H2 line cooling by employing the opacity factor min [ 1,(nH2/ (8 × 109 cm-3))-0.45 ] given by Ripamonti & Abel (2004). We use the high density limit for H2 cooling given by Galli & Palla (1998) adopted from Hollenbach & McKee (1979). We further assume that the transition from the molecular to the atomic cooling regime occurs once the gas temperature reaches a value of ≥4000 K. For atomic cooling regime, solving the thermal balance equation yields the relation
(9)For the densities given in the disk (>108 cm-3), we use the optically thick H2 line cooling by employing the opacity factor min [ 1,(nH2/ (8 × 109 cm-3))-0.45 ] given by Ripamonti & Abel (2004). We use the high density limit for H2 cooling given by Galli & Palla (1998) adopted from Hollenbach & McKee (1979). We further assume that the transition from the molecular to the atomic cooling regime occurs once the gas temperature reaches a value of ≥4000 K. For atomic cooling regime, solving the thermal balance equation yields the relation 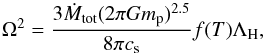 (10)where f(T) is given as (Omukai 2001; Inayoshi & Haiman 2014)
(10)where f(T) is given as (Omukai 2001; Inayoshi & Haiman 2014) 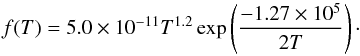 (11)Here ΛH is the atomic cooling function. We use the expression given in Appendix B of Anninos et al. (1997) originally computed by Cen (1992) to take into account the cooling due to the collisional excitation of hydrogen atoms (known as atomic line cooling). We have checked using a one-zone model that atomic line cooling actually yields the dominant contribution in this regime (Grassi et al. 2014). We note that the differences between Eqs. (9) and (10) arise as a result of the multiplication with the species abundances, and the correction factor due to the optical depth. As we are considering a case with a large inflow rate onto the disk, the central star will form and grow via rapid accretion, and the central star will also dominate the gravitational potential at least on the scales considered here. The surface density of the disk can be computed as
(11)Here ΛH is the atomic cooling function. We use the expression given in Appendix B of Anninos et al. (1997) originally computed by Cen (1992) to take into account the cooling due to the collisional excitation of hydrogen atoms (known as atomic line cooling). We have checked using a one-zone model that atomic line cooling actually yields the dominant contribution in this regime (Grassi et al. 2014). We note that the differences between Eqs. (9) and (10) arise as a result of the multiplication with the species abundances, and the correction factor due to the optical depth. As we are considering a case with a large inflow rate onto the disk, the central star will form and grow via rapid accretion, and the central star will also dominate the gravitational potential at least on the scales considered here. The surface density of the disk can be computed as 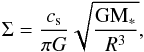 (12)and density inside the disk is
(12)and density inside the disk is 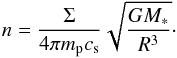 (13)We estimate the initial masses of the clumps as
(13)We estimate the initial masses of the clumps as 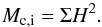 (14)These clumps can grow via accretion and we compute the maximum clump mass, the so-called gap-opening mass, by using the relation given in Levin (2007):
(14)These clumps can grow via accretion and we compute the maximum clump mass, the so-called gap-opening mass, by using the relation given in Levin (2007): ![\begin{equation} M_{\rm c} = M_{\rm c,i} \left[12 \pi \frac{\alpha}{0.3}\right]^{1/2} \left(\frac{R}{H}\right)^{1/2}\cdot \label{eq14} \end{equation}](/articles/aa/full_html/2015/06/aa25855-15/aa25855-15-eq60.png) (15)The mass accretion rate onto the clumps (Ṁc) is estimated as
(15)The mass accretion rate onto the clumps (Ṁc) is estimated as 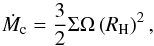 (16)where RH is the Hill radius given as
(16)where RH is the Hill radius given as 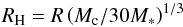 (17)and M∗ is the mass of the central star. The Kelvin-Helmholtz (KH) contraction time scale is estimated as
(17)and M∗ is the mass of the central star. The Kelvin-Helmholtz (KH) contraction time scale is estimated as ![\begin{equation} t_{\rm KH} = \frac{M_{\rm c}}{\dot{M}_{\rm c}} \sim 10^4 \left(\frac{M_{\rm c}}{30~ M_{\odot}}\right) \left[\frac{\dot{M}_{\rm c}}{3\times 10^{-3}~ M_{\odot}\,{\rm yr}^{-1}}\right]^{-1}~{\rm yr}. \label{eq151} \end{equation}](/articles/aa/full_html/2015/06/aa25855-15/aa25855-15-eq66.png) (18)The Kelvin-Helmholtz (KH) contraction time scale given above is equivalent to the mass accretion time scale and is valid in the presence of high accretion rates (0.1 M⊙/yr), which remain in the stage of adiabatic evolution as long as the accretion rate is high. In the case of accretion rates below 10-2 M⊙/yr, we compute the KH time scale using the expression (Hosokawa et al. 2012)
(18)The Kelvin-Helmholtz (KH) contraction time scale given above is equivalent to the mass accretion time scale and is valid in the presence of high accretion rates (0.1 M⊙/yr), which remain in the stage of adiabatic evolution as long as the accretion rate is high. In the case of accretion rates below 10-2 M⊙/yr, we compute the KH time scale using the expression (Hosokawa et al. 2012) 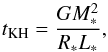 (19)where M∗ is the mass, R∗ is the radius, and L∗ is the luminosity of the protostar. We use Eq. (4) of Hosokawa et al. (2012) to compute the luminosity and their Fig. 5 to estimate the radius of the star. The clumps formed inside the disk will migrate inward provided that the migration time scale is shorter than the time for the clumps to contract and form a protostar. The migration of clumps forming in self-gravitating disks has been investigated in detail in the context of planet formation as a result of gravitational instabilities (Rafikov 2002, 2009). In the theory of planet-disk interactions, the idealized migration time scales are well known. If the mass of the planet is small and the perturbations induced by the clumps are in the linear regime, one speaks of Type I migration. On the other hand, if the planet becomes massive enough to open a gap in the disk, it migrates inward roughly on the viscous time scale. This is called Type II migration and its time scale can be estimated as (Lin & Papaloizou 1986)
(19)where M∗ is the mass, R∗ is the radius, and L∗ is the luminosity of the protostar. We use Eq. (4) of Hosokawa et al. (2012) to compute the luminosity and their Fig. 5 to estimate the radius of the star. The clumps formed inside the disk will migrate inward provided that the migration time scale is shorter than the time for the clumps to contract and form a protostar. The migration of clumps forming in self-gravitating disks has been investigated in detail in the context of planet formation as a result of gravitational instabilities (Rafikov 2002, 2009). In the theory of planet-disk interactions, the idealized migration time scales are well known. If the mass of the planet is small and the perturbations induced by the clumps are in the linear regime, one speaks of Type I migration. On the other hand, if the planet becomes massive enough to open a gap in the disk, it migrates inward roughly on the viscous time scale. This is called Type II migration and its time scale can be estimated as (Lin & Papaloizou 1986) 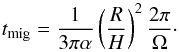 (20)The migration time scales are usually derived assuming that the planet acts like a point mass in the disk and the density profile in the disk is smooth. Nonetheless, the results from the numerical simulations are in good agreement with these estimates (Baruteau et al. 2011; Zhu et al. 2012). We use the expression given in Eq. (20) to compute the clump migration time scale. Our choice of the migration time scale is rather conservative as the time for Type II migration is slower than for Type I migrations. We note that this time scale may be even shorter for clumpy disks, therefore potentially enhancing the importance of migration.
(20)The migration time scales are usually derived assuming that the planet acts like a point mass in the disk and the density profile in the disk is smooth. Nonetheless, the results from the numerical simulations are in good agreement with these estimates (Baruteau et al. 2011; Zhu et al. 2012). We use the expression given in Eq. (20) to compute the clump migration time scale. Our choice of the migration time scale is rather conservative as the time for Type II migration is slower than for Type I migrations. We note that this time scale may be even shorter for clumpy disks, therefore potentially enhancing the importance of migration.
To quantify the impact of tidal forces due to the central star, we compute the Roche limit given as 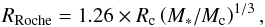 (21)where Rc and Mc are the radius and the mass of the secondary clumps, and M∗ is the mass of the central star.
(21)where Rc and Mc are the radius and the mass of the secondary clumps, and M∗ is the mass of the central star.
We estimate the photoevaporation of the disk by the central star in the following way. For high accretion rates (i.e., ≥0.01 M⊙/yr), the stellar radius almost linearly increases with mass and consequently these stars have large radii with low surface temperatures of about 5000 K (Schleicher et al. 2013; Hosokawa et al. 2013). They emit close to the Eddington luminosity given as (Ferrara et al. 2014) 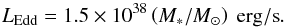 (22)To obtain an upper limit on the number of ionizing photons per second, we assume here that all photons are emitted at a frequency of 13.6 eV. The mass evaporation rate of the disk is computed using the expression given by Hollenbach et al. (1994):
(22)To obtain an upper limit on the number of ionizing photons per second, we assume here that all photons are emitted at a frequency of 13.6 eV. The mass evaporation rate of the disk is computed using the expression given by Hollenbach et al. (1994): 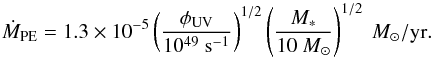 (23)Dividing the disk mass by the photoevaporation rate, we estimate the disk photoevaporation time as
(23)Dividing the disk mass by the photoevaporation rate, we estimate the disk photoevaporation time as 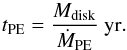 (24)The expression given here is only a lower limit because we assume peak emission at 13.6 eV. As rapidly accreting supermassive stars are expected to have cool atmospheres with a temperature of 5000 K, the UV emission may be considerably suppressed, reducing the potential effect of photoevaporation (Schleicher et al. 2013; Hosokawa et al. 2013). We expect the photoevaporation time of individual gravitationally bound clumps to be even longer owing to their enhanced surface and column densities.
(24)The expression given here is only a lower limit because we assume peak emission at 13.6 eV. As rapidly accreting supermassive stars are expected to have cool atmospheres with a temperature of 5000 K, the UV emission may be considerably suppressed, reducing the potential effect of photoevaporation (Schleicher et al. 2013; Hosokawa et al. 2013). We expect the photoevaporation time of individual gravitationally bound clumps to be even longer owing to their enhanced surface and column densities.
 |
Fig. 1 Disk properties for the central star of 10M⊙. Temperature, surface density, viscous parameter α, and clump masses are shown. Left panel: atomic cooling regime; right panel: H2 cooling regime. |
 |
Fig. 2 Disk properties for the central star of 10M⊙. Migration, Kelvin-Helmholtz, orbital and viscous time scales, as well as accretion rates onto the clumps are shown. Left panel: atomic cooling regime; right panel: H2 cooling regime. |
3. Results
We present here the results from our model described in the previous section. The properties of the disk forming inside a massive primordial halo of 107−108 M⊙ illuminated by a moderate Lyman-Werner flux are investigated here. We presume that the gas inflow rate to the disk is 0.1 M⊙/yr (unless stated otherwise), as found in numerical simulations investigating such conditions (Latif et al. 2014b). In the presence of such accretion rates, the central star is expected to be on the Hayashi track, implying a cool atmosphere with ~5000 K where radiative feedback is inefficient (Hosokawa et al. 2012; Schleicher et al. 2013). The gas in the disk is of a primordial composition and we consider the gas to be fully molecular in the initial stage. We examine the disk properties over a range of evolutionary stages considering a central star of 10, 100, and 104 M⊙. Particularly, we explore how the viscous heating in the presence of the central star influences the thermal properties of the disk. We note that a very similar evolution is expected if the central object is not a protostar, but already a massive black hole. In this case, the viscous heating would be the same, while the self-shielding of the disk would prevent a strong impact of the radiation onto the disk. The results for the various cases are discussed in the following subsections.
3.1. Early stage of disk evolution with 10 M⊙ central star
The thermal properties of the disk with a central star of 10 M⊙ are shown in Fig. 1. It is found that above 20 AU the disk is cooled by molecular hydrogen and the temperature in the disk varies from about 300 K to 4500 K. At this point, the viscous heating becomes dominant, molecular hydrogen gets collisionally dissociated and is no longer able to cool the gas. At radii below 20 AU, atomic line cooling starts to become effective and keeps the gas temperature above 4000 K. It shows that in the presence of high accretion rates, the molecular hydrogen is collisionally dissociated and a transition from the molecular to the atomic line cooling takes place. The surface density in the disk varies from 1 to 106 g / cm2. For comparison, we show a profile with R-1 as expected for a Mestel disk (Mestel 1963). The profile for the surface density is steeper than for the Mestel disk owing to the non-isothermal evolution.
To assess the stability of the disk, we compute the viscous parameter α for both the molecular and the atomic cooling regime, which is shown in Fig. 1. Our choice for the critical value of α is 1 (see discussion in Sect. 3.4), which is motivated by numerical simulations including a detailed model for thermal processes showing that disks fragment at α = 1 (Zhu et al. 2012; see also Gammie 2001). The results from our model show that the disk is stable within 20 AU, hereafter called the stable radius (α ≤ 1), and becomes unstable at larger radii (α> 1). Our estimates for the clump masses in the unstable regime show that clumps with masses between 0.1−1 M⊙ are expected to form. We further estimate the gap opening mass (i.e., the mass obtained by the clumps after opening a gap in the disk) and find that it can reach up to a few solar masses. The mass accretion rates onto the clumps range from 0.01 M⊙/yr in the interior of the disk to 0.001 M⊙/yr in its outskirts. This can be understood from the fact that the gas density in the inner part of the disk is higher than at the outer radii which leads to higher accretion rates.
To determine whether clumps will be able to survive or migrate inward, we have estimated the migration (Tmig) and the Kelvin-Helmholtz (TKH) time scales. The ratio of TKH to Tmig is shown in Fig. 2. We find that this ratio remains larger than one in the unstable region. Therefore, clumps are expected to migrate inward on the viscous time scale. For comparison with other time scales in the problem, we have also computed the viscous heating time, the orbital time, and the photoevaporation time, and compared them with Tmig and TKH. We note that the Kelvin-Helmholtz time for the clumps remains larger than all other time scales in the H2 cooling regime because of the lower accretion rates and gets inverted within the 10 AU owing to the higher accretion rates. In the atomic cooling regime, TKH seems to drop in the interior. However, because of the rather low clump masses in this regime, we expect no significant impact on the further accretion. Overall, we show that the orbital time scale is comparable to TKH in the atomic cooling regime and scales with radius in the H2 cooling regime. It is also noted that the viscous heating time scale is shorter than orbital time scale which means that significant heating can occur within one orbital period. The photoevaporation time scale of the disk is on the order of 105 years, much longer than the migration and the viscous time scales. It is comparable to the Kelvin-Helmholtz time scale in the outer parts of the disk. Therefore, we expect that the impact of photoevaporation will be negligible during the time scales considered here.
3.2. Intermediate stage with 100 M⊙ central star
Because of the short migration time and the stability in the inner part of the disk, the central star is expected to rapidly grow in mass. We have computed the state of the disk for a central star of 100 M⊙. The properties of the disk are very similar to the case with a central star of 10 M⊙; in the presence of an accretion rate of 0.1 M⊙/yr, initially the disk is cooled by the molecular hydrogen. Because of the strong viscous heating, H2 cooling becomes inefficient and eventually H2 gets collisionally dissociated. It is found that in this case, the range for atomic cooling increases up to a scale of 40 AU, which is about twice the size of the case with M∗ = 10 M⊙. In general, the disk is hotter and denser in comparison with the 10 M⊙ central star. The disk surface density is about a factor of three higher and reaches a few times 105 g / cm2 at 4 AU. The stable radius is shifted farther outward and extends up to 63 AU. No large differences are observed in the clump masses. The mass accretion rates onto the clumps are about an order of magnitude higher and range from about 0.02−0.1 M⊙/yr.
The comparison of Tmig and TKH shows that the clumps forming beyond the stable radius are expected to migrate inward. The Kelvin-Helmholtz time is shorter than the previous case because of the higher accretion rates onto the clumps. The viscous heating time is again much shorter than all other time scales. It is about one year and further declines in the disk interior. The photoevaporation time scale for the disk is about 10 000 years. It is longer than all other time scales and thus its effect on the mass accretion of the central star is minor.
3.3. Late stage with 104 M⊙ central star
The analysis of the early and the intermediate stages of the disk evolution shows that the stable radius of the disk continually grows outward and clumps forming outside this radius are expected to migrate inward. As a result, the central star may reach 104 M⊙ in about 100 000 years assuming a constant mass supply of 0.1 M⊙/yr. The stellar radius of such a star can be about 40 AU (Hosokawa et al. 2013). Therefore, we adopt this value as the inner edge of our disk. We have computed the disk properties for a central star of 104 M⊙ and show the results in Fig. 3. We found that the temperature of the disk is increased due to the presence of a very massive central star. The temperature in the disk varies from 1000−4000 K and the atomic cooling regime extends up to a few 100 AU. Overall, the surface density of the disk is about an order of magnitude higher than in the 10 M⊙ case. Our criterion for the stability of the disk shows that the stable radius is about 250 AU.
The masses of the clumps are comparable to the previous cases. The mass accretion rates onto the clumps are almost equivalent to the gas inflow rate onto the disk and even become higher in local regions. In such a case, the accretion onto the clumps will be limited by the gas mass supply to the disk. Our estimates therefore provide an upper limit on the clump accretion rates. The comparison of the migration and the Kelvin-Helmholtz time scales is shown in Fig. 4. The ratio of TKH to Tmig drops below one in the unstable regime. It suggests that the clumps may contract toward the main sequence as the Kelvin-Helmholtz time becomes shorter owing to the higher accretion rates onto the clumps. The comparison of the time scales shows that the viscous heating time again remains shorter than the other time scales. We also expect a clumpy mode of accretion in the disk interior due to the migration and disruption of the clumps. For αcrit = 1, the central star is expected to grow further and may reach 105 M⊙ because of a continuous gas supply from the stable part of the disk. Our lower limit of the disk photoevaporation time is about 1000 years, comparable to the migration time scale and much longer than the viscous heating time. It is almost equivalent to the disk accretion time scale. However, this time represents only a lower limit, and the photoevaporation may actually take considerably longer, in particular as rapidly accreting supermassive stars are expected to have cool atmospheres with a temperature of about 5000 K (Hosokawa et al. 2013; Schleicher et al. 2013). Even if that changes at later stages of the evolution, the emission is unlikely to peak exactly at 13.6 eV which will decrease the number of produced ionizing photons. We will therefore assume that photoionization will not be relevant during the evolution considered here, but may become relevant at later stages, in particular after the formation of a central black hole.
 |
Fig. 3 Disk properties for the central star of 104 M⊙. Temperature, surface density, viscous parameter α, and clump masses are shown. Left panel: atomic cooling regime, right panel: H2 cooling regime. |
 |
Fig. 4 Disk properties for the central star of 104 M⊙. Migration, Kelvin-Helmholtz, orbital and viscous time scales, as well as accretion rates onto the clumps are shown. Left panel: atomic cooling regime, right panel: H2 cooling regime. |
 |
Fig. 5 Disk properties for the central star of 104 M⊙ and the accretion rate of 1 M⊙/yr. Temperature, surface density, viscous parameter α, and clump masses are shown. Left panel: atomic cooling regime, right panel: H2 cooling regime. |
 |
Fig. 6 Disk properties for the central star of 104 M⊙ and accretion rate of 1 M⊙/yr. Migration, Kelvin-Helmholtz, orbital and viscous time scales, as well as accretion rates onto the clumps are shown. Left panel: atomic cooling regime, right panel: H2 cooling regime. |
We further explored the case with a mass accretion rate of 1 M⊙/yr, as the presence of a very massive central object is expected to increase the accretion rate owing to its gravitational attraction, and similar effects have also been found in numerical simulations (e.g., Latif et al. 2013c). The properties of the disk in this case are shown in Fig. 5. A notable difference compared to the lower accretion rate is that the disk is even hotter and denser. It is completely unstable, i.e., the value of α is always larger than 1. The masses of the clumps are further increased by a factor of a few and clumps of about 10 M⊙ are expected to form. The mass accretion onto the clumps is comparable to the gas inflow rate to the disk and even increases locally for the reasons outlined above. The comparison of the time scales is shown in Fig. 6. The ratio of the migration to the Kelvin-Helmholtz time scales remains smaller than one similar to the lower accretion rate case (i.e., 0.1 M⊙/yr). In such a case, the disk is highly unstable and vigorous fragmentation will occur. The detailed evolution is difficult to predict in this framework because the clumps are still exposed to significant accretion, potentially leading to an inward migration. Such a scenario, however, requires further exploration via numerical simulations.
3.4. Caveats in our model
We have assumed the critical value of the viscous parameter to be αcrit = 1 based on the numerical simulations of Zhu et al. (2012) who employed a detailed treatment of the cooling. However, some studies suggest a critical value of αcrit = 0.06 (Rice et al. 2005), even though their simulations did not consider the detailed modeling of thermal processes. In such a case, the disk in our model will be unstable throughout its evolution and will fragment into multiple clumps. However, the clumps will migrate inward because the migration time remains shorter than the Kelvin-Helmholtz time. During the later stages of the disk evolution in the presence of a very massive (~ 104 M⊙) central star, the migration time becomes longer than the Kelvin-Helmholtz time in the interior of the disk and clumps may survive. To improve our current understanding, detailed studies should be pursued to determine the value of αcrit under primordial conditions both in the atomic and the molecular cooling regimes.
Our estimate for the Roche limit shows that clumps within the central 10 AU will be tidally disrupted, but the clumps forming beyond this can exist. If the clumps are able to contract and reach the main sequence, they may emit UV radiation and can inhibit the further inflow of the gas to the center. Our model does not take into account in situ star formation and its impact on the structure of the disk expected at the later stages of the evolution. Estimates by Inayoshi & Haiman (2014) have shown that the UV feedback from such stars will not be important in the atomic cooling regime, but a further exploration of such processes will be necessary in the future. From the current estimates, it appears very likely that the disk fragments into multiple clumps at least on larger scales, leading to the formation of a starburst ring surrounding the central object. The accretion onto the central source may nevertheless continue if enough material falls onto the central parts of the disk, for instance owing to the enhanced gravitational potential. In some cases, it is conceivable that very massive central objects may form.
We note that chemical heating and cooling may play an additional role in realistic disk models, in particular at the transition from the molecular to the atomic regime. While this may delay the transition, we also note that the viscous heating rate steeply increases with decreasing radius, so that eventually the molecular hydrogen will be completely dissociated. While this may shift the radius where the transition occurs, we expect its impact to be minor owing to the steep radial dependence of the viscous heating rate.
Our model is only valid up to the central 1000 AU of the disk as the assumption of fully molecular disk breaks down on larger scales. If the gas is not fully molecular, the cooling will be somewhat less efficient, and it will be more straightforward for viscous heating to stabilize the gas even on larger scales. In general, the densities in the disk beyond 1000 AU will be lower and we expect mass accretion rates onto the clumps of about 10-2−10-3 M⊙/yr. This will result in a Kelvin-Helmholtz time of about 105 yr, and 104 M⊙ can be accreted before feedback on these scales becomes relevant.
Finally, the clump migration presents an additional uncertainty in the disks considered here, and it can be potentially enhanced if the disks are very clumpy. The clumpy disks may increase the effects of migration, in particular at the late stages of the evolution. At the same time, three-body effects may play a role and lead to the ejection of some of the clumps, thus reducing the accretion onto the central source.
4. Discussion and conclusions
We present here a simple model for a disk forming in a massive primordial halo of 107−108 M⊙. The halo is irradiated by a moderate Lyman-Werner flux and high accretion rates of about 0.1 M⊙/yr are expected to occur. We explore various stages of the disk evolution with a central object of 10, 100, and 104 M⊙. It is presumed that the disk is fully molecular, in a steady-state condition and metal free. The properties of the disk are computed assuming that the disk is in thermal equilibrium, i.e., the cooling is balanced by the viscous heating due to the turbulence and spiral shocks. We presume that the disk becomes unstable for the critical value of the viscous parameter α = 1. This study enables us to quantify the effect of viscous heating and helps us to understand the formation of a massive central object in such a disk. These considerations hold both in the presence of a massive central star as well as in the presence of a massive black hole.
Our results show that the disk is initially cooled by molecular hydrogen, which later gets dissociated as viscous heating dominates and a transition from the molecular to the atomic cooling takes place. The temperature in the disk interior remains about 3000−4000 K. The role of viscous heating becomes more important during the later stages of the disk evolution as the central star becomes more massive. In this case, the range of the atomic cooling extends outward. For the case of a central star of 104 M⊙, the size of the atomic cooling regime is about 200 AU. Overall, as the central star becomes more massive, the disk becomes denser and hotter. Our criterion for the stability of the disk (i.e., αcrit = 1) shows that the disk remains stable in the interior and becomes unstable in the outskirts. For a central star of 10 M⊙, the size of the stable radius is 30 AU. It extends to 300 AU for a central star of 104 M⊙. The disk is expected to fragment beyond the stable radius. Clumps with masses of a few M⊙ are expected to form in the unstable regime. The accretion rates onto the clumps become higher as the central star becomes more massive.
To assess the fate of these clumps, we have computed the migration and the Kelvin-Helmholtz time scales. The comparison of the time scales shows that the migration time remains much shorter than the Kelvin-Helmholtz time during the early stages of the disk evolution and that the clumps forming in the unstable regime migrate inward. However, as the central star becomes more massive (~ 104 M⊙), an inversion of the time scales takes place outside the stable radius. The Kelvin-Helmholtz time then becomes shorter than the migration time scale. In this case, the clumps will contract and evolve toward the main sequence. The estimates of the Roche limit show that in this case the clumps forming within the central 10 AU will be tidally disrupted. Therefore, the central clump may reach 105 M⊙ for αcrit = 1 if there is still a sufficient gas supply to the stable disk, for instance because of a more direct infall, which can be enhanced by the mass of the central object. For 0.06 <αcrit< 1, the disk becomes unstable on all scales, therefore enhancing fragmentation. In this case, maintaining the accretion onto the central clump may be more difficult. An accurate determination of αcrit is therefore important, particularly in this regime.
We also investigated a case with an accretion rate of 1 M⊙/yr for a central star of 104 M⊙. We find that the disk becomes highly unstable in this case and the migration time scale also remains longer than the Kelvin-Helmholtz time scale. In such a case, strong fragmentation may occur. A final conclusion for this scenario is however not straightforward, because of the continuing fragmentation and ongoing accretion. It will therefore be important to assess the evolution of the late phases of such disks also with numerical simulations. A potential concern for models of accretion disks is the presence of outflows, which may reduce the accretion onto the central object. Such outflows may be driven either via radiative feedback, or as a result of magnetic processes in the accretion disk. Supermassive stars forming via rapid mass accretion on the order of ≥ 0.01 M⊙/yr do not produce strong UV feedback owing to their low surface temperatures. Thus, no strong outflow powered by radiation feedback is expected from these stars. However, it is conceivable that the inner part of the disk is efficiently magnetized via dynamos, potentially leading to the formation of jets and outflows (Tan & Blackman 2004; Latif & Schleicher, in prep.).
We have also assumed that the disk is metal free, but this may not always be the case. The halos irradiated by UV flux may also get polluted by supernova winds. If there are trace amount of dust and metals, they can cool the gas to lower temperatures (Omukai et al. 2005; Cazaux & Spaans 2009; Latif et al. 2012; Bovino et al. 2014). Although we still expect the viscous heating to be dominant within the disk interior, metals and dust are likely to enhance the instability on larger scales. In such a case, a stellar cluster or a starburst ring may form on larger scales surrounding the central object, and its evolution in the presence of ongoing inflows needs to be explored in future studies.
Overall, our results suggest that very massive objects may form even in the presence of a moderate UV background, and that viscous heating may play a central role in stabilizing the disks surrounding these stars. Therefore, massive black holes of about 105 M⊙ may form in rapidly rotating metal free accretion disks exposed to a large inflow rate of 0.1 M⊙/yr. Our study further confirms the hypothesis that a complete isothermal collapse is not necessary in order to form a direct collapse black hole, and that it alleviates the need for an extremely strong radiation background in this scenario. We conclude that a moderate background may be sufficient to maintain high accretion rates on large scales, while viscous heating in the center may stabilize the gas in the center during the formation of massive objects. As a result, the proposed mechanism will considerably enhance the abundance of massive black holes at z ~ 10. This has important implications for the expected number density of direct collapse black holes observed at z ≥ 6.
There is a factor of two differences between the expressions given by Pringle (1981) and Lodato (2007) depending on whether one considers one side of the disk or both sides. We do not distinguish here between both sides of the disk and therefore use the expression given by Lodato (2007).
Acknowledgments
We thank Marta Volonteri and Stefano Bovino for interesting discussions and helpful suggestions. The research leading to these results has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007−2013 Grant Agreement no. 614199, project “BLACK”). DRGS is indebted to the Scuola Normale Superiore (SNS) in Pisa for an invitation as a “Distinguished Scientist”, which has stimulated the research described in this manuscript.
References
- Abel, T., Bryan, G. L., & Norman, M. L. 2000, ApJ, 540, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Agarwal, B., & Khochfar, S. 2015, MNRAS, 446, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Agarwal, B., Khochfar, S., Johnson, J. L., et al. 2012, MNRAS, 425, 2854 [NASA ADS] [CrossRef] [Google Scholar]
- Anninos, P., Zhang, Y., Abel, T., & Norman, M. L. 1997, New Astron., 2, 209 [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]
- Baruteau, C., Meru, F., & Paardekooper, S.-J. 2011, MNRAS, 416, 1971 [NASA ADS] [CrossRef] [Google Scholar]
- Becerra, F., Greif, T. H., Springel, V., & Hernquist, L. 2015, MNRAS, 446, 2380 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., Volonteri, M., & Rees, M. J. 2006, MNRAS, 370, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Bovino, S., Grassi, T., Schleicher, D. R. G., & Latif, M. A. 2014, ApJ, 790, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Bromm, V., Coppi, P. S., & Larson, R. B. 2002, ApJ, 564, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., & Spaans, M. 2009, A&A, 496, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cen, R. 1992, ApJS, 78, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, P. C., Glover, S. C. O., Smith, R. J., et al. 2011, Science, 331, 1040 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dijkstra, M., Haiman, Z., Mesinger, A., & Wyithe, J. S. B. 2008, MNRAS, 391, 1961 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M., Ferrara, A., & Mesinger, A. 2014, MNRAS, 442, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X., Strauss, M. A., Schneider, D. P., et al. 2003, AJ, 125, 1649 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X., Strauss, M. A., Richards, G. T., et al. 2006, AJ, 131, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrara, A., Salvadori, S., Yue, B., & Schleicher, D. 2014, MNRAS, 443, 2410 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, D., & Palla, F. 1998, A&A, 335, 403 [NASA ADS] [Google Scholar]
- Gammie, C. F. 2001, ApJ, 553, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Grassi, T., Bovino, S., Schleicher, D. R. G., et al. 2014, MNRAS, 439, 2386 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Greif, T. H., Bromm, V., Clark, P. C., et al. 2012, MNRAS, 424, 399 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Haiman, Z. 2013, The First Galaxies (Berlin; Heidelberg: Springer-Verlag), Astrophys. Space Sci. Lib., 396, 293 [Google Scholar]
- Hollenbach, D., & McKee, C. F. 1979, ApJS, 41, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D., Johnstone, D., Lizano, S., & Shu, F. 1994, ApJ, 428, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Hosokawa, T., Omukai, K., & Yorke, H. W. 2012, ApJ, 756, 93 [Google Scholar]
- Hosokawa, T., Yorke, H. W., Inayoshi, K., Omukai, K., & Yoshida, N. 2013, ApJ, 778, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Inayoshi, K., & Haiman, Z. 2014, MNRAS, 445, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., & Schleicher, D. R. G. 2015, MNRAS, 449, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., & Volonteri, M. 2015, ArXiv e-prints [arXiv:1504.00263] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., & Spaans, M. 2012, A&A, 540, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013a, MNRAS, 433, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013b, ApJ, 772, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. C. 2013c, MNRAS, 436, 2989 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Bovino, S., Van Borm, C., et al. 2014a, MNRAS, 443, 1979 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Bovino, S., Grassi, T., & Spaans, M. 2014b, ApJ, 792, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Bovino, S., Grassi, T., Schleicher, D. R. G., & Spaans, M. 2015, MNRAS, 446, 3163 [NASA ADS] [CrossRef] [Google Scholar]
- Levin, Y. 2007, MNRAS, 374, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1986, ApJ, 309, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Lodato, G. 2007, Nuovo Cimento Rivista Serie, 30, 293 [Google Scholar]
- Lodato, G., & Natarajan, P. 2006, MNRAS, 371, 1813 [NASA ADS] [CrossRef] [Google Scholar]
- Mestel, L. 1963, MNRAS, 126, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Mortlock, D. J., Warren, S. J., Venemans, B. P., et al. 2011, Nature, 474, 616 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Natarajan, P. 2011, Bulletin of the Astronomical Society of India, 39, 145 [NASA ADS] [Google Scholar]
- Oh, S. P., & Haiman, Z. 2002, ApJ, 569, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Omukai, K. 2001, ApJ, 546, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Omukai, K., Tsuribe, T., Schneider, R., & Ferrara, A. 2005, ApJ, 626, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2002, ApJ, 572, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2009, ApJ, 704, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Regan, J. A., & Haehnelt, M. G. 2009, MNRAS, 393, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Regan, J. A., Johansson, P. H., & Wise, J. H. 2014, ApJ, 795, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, W. K. M., Lodato, G., & Armitage, P. J. 2005, MNRAS, 364, L56 [NASA ADS] [CrossRef] [Google Scholar]
- Ripamonti, E., & Abel, T. 2004, MNRAS, 348, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. R. G., Palla, F., Ferrara, A., Galli, D., & Latif, M. 2013, A&A, 558, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shang, C., Bryan, G. L., & Haiman, Z. 2010, MNRAS, 402, 1249 [NASA ADS] [CrossRef] [Google Scholar]
- Sugimura, K., Omukai, K., & Inoue, A. K. 2014, MNRAS, 445, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, J. C., & Blackman, E. G. 2004, ApJ, 603, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Venemans, B. P., Findlay, J. R., Sutherland, W. J., et al. 2013, ApJ, 779, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M. 2010, A&ARv, 18, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M., & Rees, M. J. 2005, ApJ, 633, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M., Lodato, G., & Natarajan, P. 2008, MNRAS, 383, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Hartmann, L., Nelson, R. P., & Gammie, C. F. 2012, ApJ, 746, 110 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Disk properties for the central star of 10M⊙. Temperature, surface density, viscous parameter α, and clump masses are shown. Left panel: atomic cooling regime; right panel: H2 cooling regime. |
| In the text | |
 |
Fig. 2 Disk properties for the central star of 10M⊙. Migration, Kelvin-Helmholtz, orbital and viscous time scales, as well as accretion rates onto the clumps are shown. Left panel: atomic cooling regime; right panel: H2 cooling regime. |
| In the text | |
 |
Fig. 3 Disk properties for the central star of 104 M⊙. Temperature, surface density, viscous parameter α, and clump masses are shown. Left panel: atomic cooling regime, right panel: H2 cooling regime. |
| In the text | |
 |
Fig. 4 Disk properties for the central star of 104 M⊙. Migration, Kelvin-Helmholtz, orbital and viscous time scales, as well as accretion rates onto the clumps are shown. Left panel: atomic cooling regime, right panel: H2 cooling regime. |
| In the text | |
 |
Fig. 5 Disk properties for the central star of 104 M⊙ and the accretion rate of 1 M⊙/yr. Temperature, surface density, viscous parameter α, and clump masses are shown. Left panel: atomic cooling regime, right panel: H2 cooling regime. |
| In the text | |
 |
Fig. 6 Disk properties for the central star of 104 M⊙ and accretion rate of 1 M⊙/yr. Migration, Kelvin-Helmholtz, orbital and viscous time scales, as well as accretion rates onto the clumps are shown. Left panel: atomic cooling regime, right panel: H2 cooling regime. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


