| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201525785 | |
| Published online | 12 June 2015 | |
Onset of the Kelvin-Helmholtz instability in partially ionized magnetic flux tubes
Departament de Física, Universitat de les Illes Balears, 07122 Palma de Mallorca, Spain
e-mail: david.martinez@uib.es
Received: 2 February 2015
Accepted: 18 April 2015
Context. Recent observations of solar prominences show the presence of turbulent flows that may be caused by Kelvin-Helmholtz instabilites (KHI). However, the observed flow velocities are below the classical threshold for the onset of KHI in fully ionized plasmas.
Aims. We investigate the effect of partial ionization on the onset of KHI in dense and cool cylindrical magnetic flux tubes surrounded by a hotter and lighter environment.
Methods. The linearized governing equations of a partially ionized two-fluid plasma were used to describe the behavior of small-amplitude perturbations superimposed on a magnetic tube with longitudinal mass flow. A normal mode analysis was performed to obtain the dispersion relation for linear incompressible waves. We focused on the appearance of unstable solutions and studied the dependence of their growth rates on various physical parameters. We obtained an analytical approximation of the KHI linear growth rate for slow flows and strong ion-neutral coupling. We applied this to solar prominence threads.
Results. The presence of a neutral component in a plasma may contribute to the onset of the KHI even for sub-Alfvénic longitudinal shear flows. Collisions between ions and neutrals reduce the growth rates of the unstable perturbations, but cannot completely suppress the instability.
Conclusions. Turbulent flows in solar prominences with sub-Alfvénic flow velocities may be interpreted as consequences of KHI in partially ionized plasmas.
Key words: magnetohydrodynamics (MHD) / waves / instabilities / Sun: corona / Sun: filaments, prominences
© ESO, 2015
1. Introduction
Recent observations of the solar atmosphere have shown the presence of turbulent flows in quiescent prominences (see Berger et al. 2010; Ryutova et al. 2010). These phenomena have been interpreted in terms of the Rayleigh-Taylor instability (RTI) and the Kelvin-Helmhotz instability (KHI). The latter is a well-known hydrodynamic instability caused by a shear flow velocity at the interface between two fluids (see Chandrasekhar 1961). A great number of papers have been devoted to the study of this instability in many astrophysical environments, such as Earth’s aurora (Hallinan & Davis 1970), protoplanetary disks (Michikoshi & Inutsuka 2006), the magnetopause (Guo et al. 2010), or planetary magnetospheres (Ogilvie & Fitzenreiter 1989). In solar coronal plasmas this instability has been observed in coronal mass ejections, for instance (Foullon et al. 2011).
Classical magnetohydrodynamic studies (see, e.g., Chandrasekhar 1961) have shown that as a result of the effect of a magnetic field, fully ionized incompressible plasmas are stable to small amplitude perturbations if the velocity of the shear flow is sub-Alfvénic. Accordingly, the magnetohydrodynamic KHI can only be triggered by super-Alfvénic shear flows. Some turbulent flows detected in quiescent prominences exhibit a behavior that resembles the nonlinear stage of the KHI, but the measured velocities, lower than 30 km s-1 (Zirker et al. 1998; Berger et al. 2010), are below the threshold, ≳100 kms-1 (see Terradas et al. 2008), for triggering this instability. Therefore it might appear as if these turbulences cannot be interpreted as consequences of KH instabilities. However, the condition mentioned in the previous lines only applies to fully ionized plasmas, and quiescent prominences are not fully ionized, but are partially ionized, that is, they are also composed of neutral particles that do not feel the magnetic field and therefore ignore its stabilizing effect. The existence of this neutral component may modify the criterion for the appearance of the KHI, allowing the onset of the instability even for sub-Alfvénic velocities.
The KHI in partially ionized incompressible plasmas has been studied, for example, by Watson et al. (2004) and Soler et al. (2012), and it has been found that neutrals are unstable even for sub-Alfvénic flows. Therefore, in the absence of certain stabilizing factors such as surface tension, partially ionized incompressible plasmas are always unstable in the presence of a velocity shear. But these results have been obtained for the case of a Cartesian interface. However, the magnetic field in the solar atmosphere is better represented by means of flux tubes. Properties of waves in a fully ionized magnetic flux tube have been investigated by Edwin & Roberts (1983) and Goossens et al. (2009), for instance. The effect of partial ionization in a cylindrical geometry has been studied by Soler et al. (2009, 2013). However, mass flow was not included in the works by Soler et al. (2009, 2013), but it is a necessary feature for the possible appearance of a KHI. Hence, the logical step forward is to include this previously ignored effect.
In the present work we use a multifluid theory to examine the influence of partial ionization on the onset of KHI in magnetic flux tubes cooler and denser than their environment. More precisely, we use a two-fluid approximation (see Priest 1982; Zaqarashvili et al. 2011) that treats electrons and ions as a single fluid that interacts with the other component of the plasma, the neutral fluid, by means of collisions. We include a mass flow in the longitudinal direction of the flux tube that has a discontinuity at the interface that separates the two media of different densities. To avoid further complexity in the model, we ignore effects like the surface tension of the fluids and compressibility. Restricting ourselves to the linear regime, we superimpose small-amplitude perturbations to the equilibrium state and derive a dispersion relation for the incompressible waves generated by these perturbations. This dispersion relation is a generalization of the formulas found in Edwin & Roberts (1983) for the fully ionized case.
This paper is organized as follows: in Sect. 2 we describe our model and then present the basic governing equations. In Sect. 3 we derive the dispersion relation for linear incompressible waves and obtain an analytical approximation to the unstable solution for slow, sub-Alfvénic flows, and strong ion-neutral coupling. In Sect. 4 we perform a parametric study of the solutions to the dispersion relation and obtain the dependence of the KHI growth rate on the model parameters. In Sect. 5 we apply the theory to a solar prominence thread. Finally, we conclude in Sect. 6.
2. Model and equations
2.1. Equilibrium state
The equilibrium state is a partially ionized cylindrical magnetic flux tube of radius a embedded in an unbounded medium. We used cylindrical coordinates, namely r, ϕ, and z, for the radial, azimuthal, and longitudinal coordinates, respectively. A sketch of the model can be found in Fig. 1. The subscripts “0” and “ex” denote quantities related to the internal and external plasma. The densities of ions and neutrals are ρi and ρn and only depend on the radial direction as 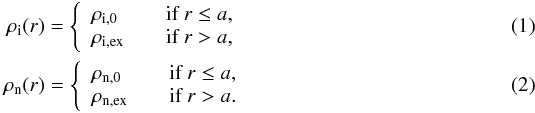 Hence, there is an abrupt jump in density between the internal and external plasmas. We have chosen the particular case when the internal plasma is denser than the external one. The magnetic field, denoted by B, is constant and pointing along the flux tube axis, with the same value in both media, that is, B0 = Bex. In addition, we considered a longitudinal mass flow with constant velocity denoted by U. The flow velocity is discontinuous at the boundary of the flux tube.
Hence, there is an abrupt jump in density between the internal and external plasmas. We have chosen the particular case when the internal plasma is denser than the external one. The magnetic field, denoted by B, is constant and pointing along the flux tube axis, with the same value in both media, that is, B0 = Bex. In addition, we considered a longitudinal mass flow with constant velocity denoted by U. The flow velocity is discontinuous at the boundary of the flux tube.
 |
Fig. 1 Sketch of the model. |
2.2. Governing equations
We studied the behavior of a partially ionized plasma using a two-fluid theory. We assumed that the plasma is composed of an ionized fluid made of ions and electrons and of a neutral fluid made of neutral particles. The two fluids interact by means of ion-neutral collisions. The general two-fluid equations can be found in Priest (1982), Zaqarashvili et al. (2011), and Khomenko et al. (2014), for instance. Here, we restricted ourselves to the linearized version of those equations, which describe the evolution of small-amplitude perturbations. Hence, the set of two-fluid equations that describe the behavior of linear incompressible perturbations superimposed on the equilibrium state are
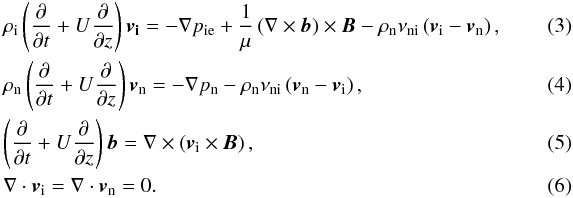 In these equations, vi and vn are the velocities of ions and neutrals, pie and pn are the pressure perturbations of ion-electrons and neutrals, b is the magnetic field perturbation, μ is the magnetic permeability, γ is the adiabatic index, and νni is the neutral-ion collision frequency. In addition, we defined the ionization fraction as χ = ρn/ρi.
In these equations, vi and vn are the velocities of ions and neutrals, pie and pn are the pressure perturbations of ion-electrons and neutrals, b is the magnetic field perturbation, μ is the magnetic permeability, γ is the adiabatic index, and νni is the neutral-ion collision frequency. In addition, we defined the ionization fraction as χ = ρn/ρi.
In the following calculations, we replaced the velocities of ions and neutrals by their corresponding Lagrangian displacements, ξi and ξn, given by
 In addition, we defined the total (thermal + magnetic) pressure perturbation of the ionized fluid, P′, as
In addition, we defined the total (thermal + magnetic) pressure perturbation of the ionized fluid, P′, as 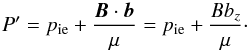 (9)
(9)
3. Normal mode analysis
From here on, we followed the same procedure as in Soler et al. (2013) and performed a normal mode analysis. Since the equilibrium is uniform in the azimuthal and longitudinal directions, we expressed the perturbations as proportional to exp(imϕ + ikzz), where m and kz are the azimuthal and longitudinal wavenumbers, respectively. We only retained the dependence of the perturbations on the radial direction. Furthermore, the temporal dependence was set as exp( − iωt), where ω is the angular frequency. By combining Eqs. (3)−(5), we derive a system of four coupled equations for the radial components of the Lagrangian displacements, ξr,i and ξr,n, and the pressures, P′ and pn, namely ![\begin{eqnarray} \label{eq:pre_tot} && \frac{\partial P'}{\partial r}=\rho_{\rm{i}}\left( \Omega^2-\omega_{\rm A}^2+{\rm i}\chi \nu_{\rm{ni}}\Omega \right) \xi_{\rm{r,i}}-{\rm i}\rho_{\rm{n}}\nu_{\rm{ni}}\Omega \xi_{\rm{r,n}}, \\ \label{eq:pre_n} && \frac{\partial p_{\rm{n}}}{\partial r}=-{\rm i}\rho_{\rm{n}}\nu_{\rm{ni}}\Omega \xi_{\rm{r,i}}+\rho_{\rm{n}} \Omega(\Omega+{\rm i} \nu_{\rm{ni}})\xi_{\rm{r,n}}, \\ \label{eq:xi_ri} && \rho_{\rm{i}}\left(\widetilde{\Omega}^2-\omega_{\rm{A}}^2\right)\frac1{r}\frac{\partial(r\xi_{\rm{r,i}})}{\partial r}=\left(\frac{m^2}{r^2}+k_{z}^2\right)\left(P'+{\rm i}\frac{\nu_{\rm{ni}}}{\Omega+{\rm i} \nu_{\rm{ni}}}p_{\rm{n}}\right), \\ \label{eq:xi_rn} && \rho_{\rm{n}}\rho_{\rm{i}}\left(\widetilde{\Omega}^2-\omega_{\rm{A}}^2\right)\frac1{r}\frac{\partial(r\xi_{\rm{r,n}})}{\partial r}={\rm i}\frac{\nu_{\rm{ni}}} {\Omega+{\rm i}\nu_{\rm{ni}}}\rho_{\rm{n}}\left(\frac{m^2}{r^2}+k_{z}^2\right) P' \nonumber \\ &&\qquad \qquad-\left(\frac{m^2}{r^2}+k_{z}^2\right)\left[\frac{\rho_{\rm{n}}\nu_{\rm{ni}}^2}{(\Omega+{\rm i}\nu_{\rm{ni}})^2}- \frac{\rho_{\rm{i}}\left(\widetilde{\Omega}^2-\omega_{\rm{A}}^2\right)}{\Omega(\Omega+{\rm i}\nu_{\rm{ni}})}\right]p_{\rm{n}},~~~~~~~~~~~ \end{eqnarray}](/articles/aa/full_html/2015/06/aa25785-15/aa25785-15-eq40.png) where Ω = ω − Ukz is the Doppler-shifted frequency. Other parameters that appear in the equations are the square of the modified frequency,
where Ω = ω − Ukz is the Doppler-shifted frequency. Other parameters that appear in the equations are the square of the modified frequency, 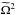 , and the square of the Alfvén frequency,
, and the square of the Alfvén frequency, 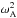 , defined as
, defined as 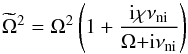 (14)and
(14)and 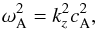 (15)where
(15)where 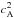 is the square of the Alfvén speed, computed as
is the square of the Alfvén speed, computed as 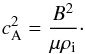 (16)Now we combined Eqs. (10)−(13)and obtained two uncoupled equations for the pressures, namely
(16)Now we combined Eqs. (10)−(13)and obtained two uncoupled equations for the pressures, namely 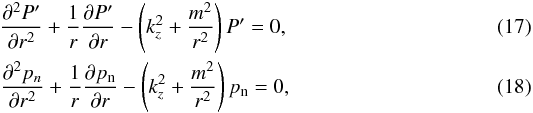 whose solutions are combinations of modified Bessel functions of the first and second kind, Im(kzr) and Km(kzr), respectively. We required the solutions to be regular at r = 0 and vanishing at r → ∞. Hence,
whose solutions are combinations of modified Bessel functions of the first and second kind, Im(kzr) and Km(kzr), respectively. We required the solutions to be regular at r = 0 and vanishing at r → ∞. Hence,
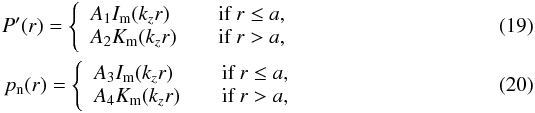 where A1–A4 are arbitrary constants. In turn, the radial components of the Lagrangian displacements of the two fluids are related to P′ and pn as
where A1–A4 are arbitrary constants. In turn, the radial components of the Lagrangian displacements of the two fluids are related to P′ and pn as 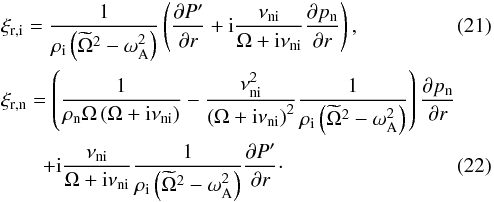
3.1. Dispersion relation and approximate KHI growth rate
To find the dispersion relation that describes the behavior of the waves in this system, we need to impose that P′, pn, ξr,i and ξr,n are continuous at r = a, that is, at the boundary of the tube. After applying the boundary conditions, we obtain a system of algebraic equations for the constants A1–A4. The non-trivial solution to the system provides the dispersion relation, namely ![\begin{eqnarray} \left[\frac{I_{\rm{m}}'(k_{z}a)}{I_{\rm{m}}(k_{z}a)}\rho_{\rm{n,ex}}\Omega_{\rm{ex}}\left(\Omega_{\rm{ex}}+{\rm i}\nu_{\rm{ni,ex}} \right)-\frac{K_{\rm{m}}'(k_{z}a)}{K_{\rm{m}}(k_{z}a)}\rho_{\rm{n,0}}\Omega_{\rm{0}}\left(\Omega_{\rm{0}}+{\rm i}\nu_{\rm{ni,0}}\right) \right] \nonumber \\ \qquad \times \left[\frac{I_{\rm{m}}'(k_{z}a)}{I_{\rm{m}}(k_{z}a)}\rho_{\rm{i,ex}}\left(\widetilde{\Omega}_{\rm{ex}}^2- \omega_{\rm{A,ex}}^2\right)-\frac{K_{\rm{m}}'(k_{z}a)}{K_{\rm{m}}(k_{z}a)}\rho_{\rm{i,0}}\left(\widetilde{\Omega}_{\rm{0}}^2- \omega_{\rm{A,0}}^2\right)\right] \nonumber \\ \qquad +\frac{I_{\rm{m}}'(k_{z}a)}{I_{\rm{m}}(k_{z}a)}\frac{K_{\rm{m}}'(k_{z}a)}{K_{\rm{m}}(k_{z}a)}\frac{\rho_{\rm{n,0}}\rho_{\rm{n,ex}}\Omega_{\rm{0}}\Omega{\rm{ex}}}{\left(\Omega_{\rm{0}}+{\rm i}\nu_{\rm{ni,0}}\right)\left(\Omega_{\rm{ex}}+i\nu_{\rm{ni,ex}}\right)} \nonumber \\ \qquad \times \left[\nu_{\rm{ni,0}}\left(\Omega_{\rm{ex}}+{\rm i}\nu_{\rm{ni,ex}}\right)-\nu_{\rm{ni,ex}}\left(\Omega_{\rm{0}}+{\rm i}\nu_{\rm{ni,0}}\right)\right]^2=0, \label{eq:dis_rel} \end{eqnarray}](/articles/aa/full_html/2015/06/aa25785-15/aa25785-15-eq58.png) (23)
(23)
where the prime denotes the derivative of the modified Bessel function with respect to its argument.
To simplify Eq. (23), we used the so-called thin tube (TT) approximation, that is, we assumed kza ≪ 1. We performed an asymptotic expansion of the modified Bessel functions for small arguments and m ≠ 0 and only kept the first term in the expansion. The resulting TT dispersion relation is ![\begin{eqnarray} \left[\rho_{\rm{i,0}}\left(\Omega_{\rm{0}}\left(\Omega_{\rm{0}}\!+\!{\rm i}\chi_{\rm{0}}\nu_{\rm{ni,0}}\right)\!-\!\omega_{\rm{A,0}}^2\right) \! +\!\rho_{\rm{i,ex}}\left(\Omega_{\rm{ex}}\left(\Omega_{\rm{ex}}\!+\!{\rm i}\chi_{\rm{ex}}\nu_{\rm{ni,ex}}\right)\!-\!\omega_{\rm{A,ex}}^2\right) \right] \nonumber \\ \qquad\times \left[\rho_{\rm{n,0}}\Omega_{\rm{0}}\left(\Omega_{\rm{0}}+{\rm i}\nu_{\rm{ni,0}}\right)+\rho_{\rm{n,ex}}\Omega_{\rm{ex}}\left( \Omega_{\rm{ex}}+{\rm i}\nu_{\rm{ni,ex}}\right)\right] \nonumber \\ \qquad +\left[\rho_{\rm{n,0}}\Omega_{\rm{0}}\nu_{\rm{ni,0}}+\rho_{\rm{n,ex}}\Omega_{\rm{ex}}\nu_{\rm{ni,ex}}\right]^2=0, \label{eq:TT_rel} \end{eqnarray}](/articles/aa/full_html/2015/06/aa25785-15/aa25785-15-eq61.png) (24)which is the same expression, with a slightly different notation, as Eq. (37) of Soler et al. (2012), obtained for the case of a Cartesian interface. Hence, the geometrical effect associated with the cylindrical magnetic tube disappears in the TT limit.
(24)which is the same expression, with a slightly different notation, as Eq. (37) of Soler et al. (2012), obtained for the case of a Cartesian interface. Hence, the geometrical effect associated with the cylindrical magnetic tube disappears in the TT limit.
We considered the limit when the collision frequencies go to zero, that is, when the two fluids are uncoupled and show a completely independent behavior. If we neglect the terms associated with the ion-neutral collisions, we can recover from Eq. (24)the dispersion relations for the classical hydrodynamic and magnetohydrodynamic KHI (Chandrasekhar 1961). In that case, the dispersion relation for our model is given by ![\begin{equation} \label{eq:TT_rel2} \left[\rho_{\rm{i,0}}\left(\Omega_{\rm{0}}^2-\omega_{\rm{A,0}}^2\right)\!+\!\rho_{\rm{i,ex}}\left(\Omega_{\rm{ex}}^2-\omega_{\rm{A,ex}}^2\right)\right]\left[\rho_{\rm{n,0}}\Omega_{\rm{0}}^2+\rho_{\rm{n,ex}}\Omega_{\rm{ex}}^2\right]\!=\!0, \end{equation}](/articles/aa/full_html/2015/06/aa25785-15/aa25785-15-eq62.png) (25)from which we can obtain separated solutions for the ionized and the neutral plasma component. On the one hand, the solutions for the neutral fluid are given by
(25)from which we can obtain separated solutions for the ionized and the neutral plasma component. On the one hand, the solutions for the neutral fluid are given by 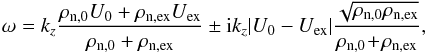 (26)where the branch with a positive imaginary part implies that the amplitudes of the perturbations grow with time. This growing solution exists for any value of the shear flow velocity. Therefore, the neutral fluid is always unstable in the presence of a shear flow.
(26)where the branch with a positive imaginary part implies that the amplitudes of the perturbations grow with time. This growing solution exists for any value of the shear flow velocity. Therefore, the neutral fluid is always unstable in the presence of a shear flow.
On the other hand, for the ionized component we have the following solutions: ![\begin{eqnarray} \label{eq:sol_ion} \omega&=&k_{z}\frac{\rho_{\rm{i,0}}U_{\rm{0}}+\rho_{\rm{i,ex}}U_{\rm{ex}}}{\rho_{\rm{i,0}}+\rho_{\rm{i,ex}}} \nonumber \\ &&\pm k_{z}\left[\frac{B_{\rm{0}}^2+B_{\rm{ex}}^2}{\mu(\rho_{\rm{i,0}}+\rho_{\rm{i,ex}})}-(U_{\rm{0}}-U_{\rm{ex}})^2\frac{\rho_{\rm{i,0}}\rho_{\rm{i,ex}}}{(\rho_{\rm{i,0}}+\rho_{\rm{i,ex}})^2}\right]^{1/2}, \end{eqnarray}](/articles/aa/full_html/2015/06/aa25785-15/aa25785-15-eq64.png) (27)
(27)
from which it can be seen that the magnetohydrodynamic KHI only appears when 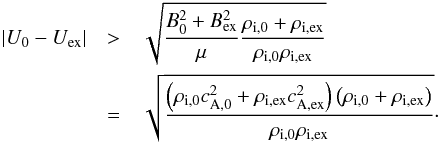 (28)This velocity threshold is caused by the effect of the longitudinal magnetic field on the ionized fluid. The velocity threshold is super-Alfvénic, which indicates that the typically observed flows along prominence threads or spicules, for example, cannot trigger a KHI if the plasma is fully ionized. This same criterion for the velocity threshold can be found in other works devoted to the study of waves in fully ionized plasmas with longitudinal mass flows. For instance, Eq. (28)is equivalent (if we assume cA,ex = 0) to Eq. (5) of Ryutova (1988).
(28)This velocity threshold is caused by the effect of the longitudinal magnetic field on the ionized fluid. The velocity threshold is super-Alfvénic, which indicates that the typically observed flows along prominence threads or spicules, for example, cannot trigger a KHI if the plasma is fully ionized. This same criterion for the velocity threshold can be found in other works devoted to the study of waves in fully ionized plasmas with longitudinal mass flows. For instance, Eq. (28)is equivalent (if we assume cA,ex = 0) to Eq. (5) of Ryutova (1988).
In addition, according to Ryutova (1988) and Ryutova et al. (2010), a fully ionized plasma may be subject to an explosive instability if the shear flow velocity, ΔU, fulfills the following condition: 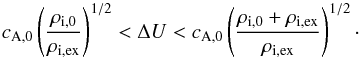 (29)Therefore, taking into account the suggested existence of the explosive instability, three unstable branches would be expected to appear in the set of solutions to the dispersion relation: the first one, associated with the neutrals, would be present for any value of the shear flow velocity; the second one, the explosive instability, would appear between the shear flow velocity thresholds given by Eq. (29); and the third one, associated with the ions, would follow the criterion of Eq. (28). (Note that if Bex ≠ 0 but Bex = B0, as in our model, the lower and upper limits of Eq. (29)need to be multiplied by the factor
(29)Therefore, taking into account the suggested existence of the explosive instability, three unstable branches would be expected to appear in the set of solutions to the dispersion relation: the first one, associated with the neutrals, would be present for any value of the shear flow velocity; the second one, the explosive instability, would appear between the shear flow velocity thresholds given by Eq. (29); and the third one, associated with the ions, would follow the criterion of Eq. (28). (Note that if Bex ≠ 0 but Bex = B0, as in our model, the lower and upper limits of Eq. (29)need to be multiplied by the factor 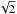 ).
).
We return to the coupled case. The full dispersion relation, Eq. (23), must be solved numerically when ion-neutral collisions are at work. However, it is possible to find an approximate solution when the ion-neutral coupling is strong and sub-Alfvénic flows are considered. For simplicity, we also assumed that the external flow velocity is zero, that is, Uex = 0. For sub-Alfvénic flows, the only unstable solution we obtain from the dispersion relation in the uncoupled case is that associated with neutrals, Eq. (26), since the magnetic field is able to stabilize ions, Eq. (27). Hence, we tried to find a correction to the neutrals-related solution due to ion-neutral collisions. To do so, we write ω = ω0 + iγ, where ω0 is the neutrals’ unstable solution given in Eq. (26)and γ is a small correction. We inserted this expression for ω into the TT dispersion relation, Eq. (24), and only kept up to first-order terms in γ and second-order terms in U0. After some algebraic manipulations, we found a solution for γ. We omit the details for the sake of simplicity. Finally, the following approximate solution for the frequency was obtained, 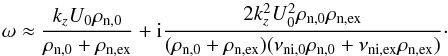 (30)The approximated growth rate, that is, the imaginary part of ω, is quadratic in the flow velocity and inversely proportional to the collision frequencies. Hence, if the same parameters are considered, the value of the growth rate is lower in the strongly coupled case than in the uncoupled case (compare with Eq. (26)). This means that ion-neutral collisions have a stabilizing effect.
(30)The approximated growth rate, that is, the imaginary part of ω, is quadratic in the flow velocity and inversely proportional to the collision frequencies. Hence, if the same parameters are considered, the value of the growth rate is lower in the strongly coupled case than in the uncoupled case (compare with Eq. (26)). This means that ion-neutral collisions have a stabilizing effect.
4. Exploring the parameter space
Because of its complexity, Eq. (23)must be solved numerically. In this section we study the dependence of the solutions of the dispersion relation with respect to various physical parameters. We also compare the full results with the analytical approximation shown in the previous section.
Throughout this section we use dimensionless parameters. Unless otherwise stated, we use ρi,0/ρi,ex = 2, ρn,0/ρn,ex = 2, cA,0 = 1 and kza = 0.1. For simplicity, we assumed that the collision frequency has the same value in both internal and external plasmas, so we dropped the subscripts from νni. In addition, we now focus on the kink mode, the only mode that causes displacements of the axis of the cylinder, so we used m = 1. All frequencies were normalized with respect to the kink frequency, ωk, which is the frequency of the kink wave in the TT limit in the fully ionized case (see, e.g., Ryutov & Ryutova 1976; Spruit 1981). The kink frequency is given by 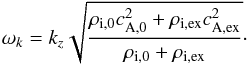 (31)To begin with, we studied the dependence of the solutions of the dispersion relation with respect to the shear flow velocity. Hence, we took ΔU ≡ U0 − Uex as a free variable. We considered three different values for the collision frequency, which allowed us to investigate the behavior of the solutions depending on the strength of the ion-neutral coupling. Figure 2 displays the real and imaginary parts of the frequency as functions of the normalized shear flow velocity for a) weak coupling (νni/ωk = 0.1), b) intermediate coupling (νni/ωk = 1); and c) strong coupling (νni/ωk = 10). The red symbols represent the solutions obtained numerically from the complete dispersion relation, Eq. (23). The full numerical results are compared with the analytical solutions in the strongly coupled limit (shown as blue solid lines) and in the uncoupled case (shown as blue dashed lines). In addition, the classical shear flow velocity threshold for the KHI in a fully ionized fluid (Eq. (28)) is denoted by the vertical dotted lines.
(31)To begin with, we studied the dependence of the solutions of the dispersion relation with respect to the shear flow velocity. Hence, we took ΔU ≡ U0 − Uex as a free variable. We considered three different values for the collision frequency, which allowed us to investigate the behavior of the solutions depending on the strength of the ion-neutral coupling. Figure 2 displays the real and imaginary parts of the frequency as functions of the normalized shear flow velocity for a) weak coupling (νni/ωk = 0.1), b) intermediate coupling (νni/ωk = 1); and c) strong coupling (νni/ωk = 10). The red symbols represent the solutions obtained numerically from the complete dispersion relation, Eq. (23). The full numerical results are compared with the analytical solutions in the strongly coupled limit (shown as blue solid lines) and in the uncoupled case (shown as blue dashed lines). In addition, the classical shear flow velocity threshold for the KHI in a fully ionized fluid (Eq. (28)) is denoted by the vertical dotted lines.
 |
Fig. 2 Upper panels: ωR/ωk as a function of the normalized shear flow velocity, ΔU/cA,0, for kza = 0.1, m = 1, and three different collision frequencies (a) νni/ωk = 0.1; b) νni/ωk = 1 and c) νni/ωk = 10). Lower panels: ωI/ωk as a function of ΔU/cA,0 for the same set of parameters as above. The red symbols represent the solutions of the full dispersion relation, i.e., Eq. (23); the blue solid lines correspond to the analytical approximation given by Eq. (30), and the blue dashed lines show the unstable branch of the neutral fluid when there is no coupling (Eq. (26)). |
The upper panels of Fig. 2 display the real part of the frequency. We observe a very similar behavior for the three studied cases. Initially, when the shear flow velocity is zero, we find two solutions with nonzero ωR. These solutions are associated with the ionized fluid and correspond to the usual kink magnetohydrodynamic wave found in fully ionized tubes (Edwin & Roberts 1983). The solution with ωR> 0 is the forward-propagating kink wave, while the solution with ωR< 0 is the backward-propagating kink wave. A third solution with ωR> 0 emerges when the shear flow velocity increases from zero. The new solution is associated with the neutral component of the plasma in the sense that this solution only appears in the presence of neutrals. However, note that such simple associations between solutions and fluids cannot be made when the coupling is high and ions and neutrals behave as a single fluid. As the flow velocity continues to increase, the three solutions converge for a critical flow velocity that depends on the collision frequency. The stronger the ion-neutral coupling, the lower the critical flow. From that point on, the real part of the frequency is proportional to ΔU and is well described by the real part of Eq. (26)or, equivalently, Eq. (30).
The lower panels of Fig. 2 display the imaginary part of the frequency. The differences between the panels are much more remarkable than before, meaning that the value of the collision frequency has a strong effect on the imaginary part of the frequency. The shaded zone denotes the region of instability, ωI> 0. In this case, perturbations exponentially grow with time (in the opposite case perturbations are damped). We observe that for low shear flow velocities there is only one unstable solution, corresponding to that originally associated with the neutral component of the plasma. A second unstable branch (originally associated with ions) appears for higher flow velocities above the classical super-Alfvénic threshold (Eq. (28)). Importantly, the only instability present for slow, sub-Alfvénic speeds is that originally associated with the neutral component of the plasma regardless of the collisional coupling between ions and neutrals. Ion-neutral collisions reduce the growth rate of that instability to a great extent, but collisions are not able to completely suppress the instability (Watson et al. 2004; Soler et al. 2012). We overplot with a blue solid line the analytical approximation to the growth rate (Eq. (30)). The approximation shows that the growth rate is directly proportional to the square of the shear flow velocity and inversely proportional to the ion-neutral collision frequency. As expected, the approximation agrees well with the numerical results for low shear flow velocities. For weak coupling, the approximation is reasonably good for flow velocities up to 40% the internal Alfvén speed. When the collision frequency is increased, the range of agreement between the numerical results and the approximation is greatly extended to super-Alfvénic speeds. Finally, note that the stable solution in the left panel that is absent from the other two panels (see the lowest curve). The reason for this absence is that for high collision frequencies this solution moves beyond the vertical scale used in the plots. We are not interested in this solution because it is always stable.
The explosive instability described by Ryutova (1988) would for our set of parameters appear in the range  (when νni = 0; the existence of collisions between ions and neutrals would modify this criterion). The lower panels of Fig. 2 show that the only solution with a positive imaginary part of the angular frequency is the one associated with the neutrals. Thus, we observe no evidence of the explosive instability. The only additional remarkable feature in that range is found in the upper panels of the same figure: the real part of the angular frequency of one of the solutions associated with ions changes from being negative to being positive, meaning a change in the direction of the wave propagation.
(when νni = 0; the existence of collisions between ions and neutrals would modify this criterion). The lower panels of Fig. 2 show that the only solution with a positive imaginary part of the angular frequency is the one associated with the neutrals. Thus, we observe no evidence of the explosive instability. The only additional remarkable feature in that range is found in the upper panels of the same figure: the real part of the angular frequency of one of the solutions associated with ions changes from being negative to being positive, meaning a change in the direction of the wave propagation.
To investigate in more detail the effect of ion-neutral collisions on the instability for slow flows, we performed the following study. We fixed the shear flow velocity to ΔU/cA,0 = 1 and computed the frequencies as a function of the ion-neutral collision frequency, νni. The chosen flow velocity is below the classical threshold for the KHI in fully ionized plasmas (Chandrasekhar 1961), so that only the neutral component is unstable in this configuration. The results are displayed in Fig. 3, where the solutions originally associated with ions are shown as red diamonds and those originally associated with neutrals are plotted with blue crosses. There is always one unstable solution for any value of νni, but its growth rate decreases when the collision frequency increases. The growth rate is reduced because neutrals feel indirectly, through the collisions with ions, the stabilizing effect of the magnetic field. In addition, as discussed before, the analytical approximation for the growth rate, Eq. (30), agrees well with the numerical results for high values of the collision frequencies, as is consistent with the assumptions behind the approximation. For the real part of the frequency, we note that the frequency of solutions associated with ions decreases until it reaches a plateau for νni/ωk> 1 (Soler et al. 2013), while the frequency of the solution associated with the neutrals stays constant all over the range.
 |
Fig. 3 a) ωR/ωk and b) ωI/ωk for the kink mode (m = 1) as a function of νni/ωk, with ΔU/cA,0 = 1 and kza = 0.1. The red diamonds are the solutions originally associated with the ions when there is no coupling, while the blue crosses are the solutions for neutrals. The solid line is the analytical approximation given by Eq. (30). In b) the shaded area denotes the region of instability. |
For the sake of completeness, we also studied the behavior of the solutions depending on m. The mode with m = 0 is known as the sausage mode and produces expansions and contractions of the plasma tube, without displacing its axis (Edwin & Roberts 1983). Modes with m> 1 are known as fluting modes (Edwin & Roberts 1983). As can be seen in Eq. (24), the TT limit is independent of the value of m for m ≠ 0; this fact implies that in the range of applicability of that approximation there will not be substantial variations in the behavior of the different modes. To observe some dissimilarities, we need to choose parameters beyond the TT case. We therefore kept the values of the parameters used in the previous section, but changed the dimensionless longitudinal wavenumber to a higher value, namely, kza = 2, and took νni/ωk = 1. The results show that there are minor differences for each solution: the solutions weakly depend on m and, for large m, they become independent of this parameter.
We also repeated the calculations made in this section for higher values of the longitudinal wavenumber, kz. We did not include the results here because they are not significantly different from what we have already explained. When kz is increased, the system moves away from the regime of the TT approximation, but this only produces a slight variation in the real part of the normalized angular frequencies, while the imaginary part, that is, the growth rates, remains almost unaltered.
 |
Fig. 4 Application to solar prominence threads. Growth rates as functions of the shear flow velocity for the following set of parameters: ρi,0 + ρn,0 = 10-9 kg m-3, ρi,ex + ρn,ex = 2 × 10-10 kg m-3, B0 = Bex = 10-3 T, a = 100 km, T0 = 7000 K and Tex = 35 000 K; in the left panel the wavenumber is kz = 2π/λ = 2π × 10-5 m-1 and in the right panel it is kz = 2π × 10-6 m-1. The red dashed lines correspond to a fully ionized plasma (χ = 0), the blue crosses to a partially ionized case (χ = 4), and the black diamonds to a weakly ionized case (χ = 100). The solid lines represent the solutions given by the analytical approximation in Eq. (30). The shaded zone denotes the region of flow velocity values that have been frequently measured in solar prominences. |
5. Application to solar prominence threads
In this section we perform a specific application to solar prominence plasmas. We solved the full dispersion relation, Eq. (23), with values representative of a quiescent prominence. Therefore, the internal medium represents a prominence thread with densities of ions and neutrals such that ρi,0 + ρn,0 = 10-9 kg m-3, a temperature of T0 = 7000 K and radius of a = 100 km; the external medium is composed of inter-thread plasma with ρi,ex + ρn,ex = 2 × 10-10 kg m-3 and Tex = 35 000 K, which corresponds to the regime of prominence-corona transition region (PCTR). Densities and temperatures were chosen for the equilibrium condition of the total pressure (thermal plus magnetic) to be fulfilled, that is, the total pressure is the same in both media. The magnetic fields are B0 = Bex = 10 G. We focused on the kink mode, so we took m = 1. The neutral-ion collision frequencies depend on the temperatures and densities and were computed using the following expression (see Braginskii 1965) 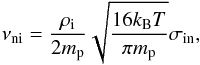 (32)where mp is the proton mass, kB is the Boltzmann constant, σin ≈ 5 × 10-19 m2 is the collisional cross section for a hydrogen plasma.
(32)where mp is the proton mass, kB is the Boltzmann constant, σin ≈ 5 × 10-19 m2 is the collisional cross section for a hydrogen plasma.
Figure 4 displays the most unstable solution of Eq. (23)as a function of the shear flow velocity for three different values of the ionization fraction: the red dashed lines represent the fully ionized case (χ = 0), the blue crosses represent a partially ionized situation (χ = 4), and the black diamonds depict a weakly ionized case (χ = 100). The left panel shows the results for a wavelength λ = 100 km, which corresponds to a longitudinal wavenumber kz = 2π/λ = 2π × 10-5 m-1. In the right panel the wavelength used is λ = 1000 km, so kz = 2π × 10-6 m-1. The shaded zone of Fig. 4 denotes a range of typical velocities (from 10 km s-1 to 30 km s-1) that have been measured in quiescent prominences (Zirker et al. 1998; Berger et al. 2010). The limits of this zone could slightly vary depending on the observations that are chosen as reference, but this variation is not significant for our analysis. We see that for a fully ionized case the instability only appears for shear flow velocities far from the detected values. In contrast, the cases with a neutral component show instabilities for the entire range of velocities. Hence, partial ionization may explain the occurrence of KHI in solar prominence plasmas even when the observed flows are below the classical threshold.
If we compare the two panels in Fig. 4, we note that in the right panel the growth rates are lower than in the left. More precisely, they are about one order of magnitude smaller when the shear flow velocities are high. Since the wavenumber in the right panel is one order of magnitude smaller than in the left panfel, this behavior agrees with Eq. (26). On the other hand, when the velocities are low, the growth rates on the right are two orders of magnitude smaller, which is consistent with what it is derived from Eq. (30).
In addition, in Fig. 4 we overplot with solid lines the approximate analytical solutions given by the imaginary part of Eq. (30). The growth rates obtained from the analytical approximation are within the same order of magnitude; thus, Eq. (30)may be used to calculate estimates of the growth rates of KHI in a real prominence thread without the need of solving the much more complex full dispersion relation.
Our analysis has demonstrated that KHI may be present in quiescent prominences as a result of the effect of partial ionization. However, we are not yet allowed to state that this magnetohydrodynamic instability may explain the observed turbulent flows. Before we may do this, it is necessary to check whether the growth rates given by the theory are consistent with an instability that can be actually observed. Estimated lifetimes of prominence threads are about 20 minutes (Lin et al. 2005). For the region of highest observed velocities we computed the following growth times of the instability (τ ≡ 1 /ωI): a) λ = 100 km ⇒ τ ~ 100 s for the weakly ionized case (χ = 100) and τ ~ 1000 s for χ = 4; b) λ = 1000 km ⇒ τ ~ 104 s(~2.8 h) for χ = 100 and τ ~ 105 s(~28 h) for χ = 4. The growth times obtained for λ = 1000 km are longer than the typical lifetime of a thread; therefore, an instability originated by a perturbation with this wavelength cannot be the cause of the observed turbulent flows. Conversely, the growth times for the shortest wavelength are of the same order of magnitude or lower than the detected lifetimes. This means that during the life of a prominence thread there is enough time for the development of a KHI caused by a perturbation with that wavelength.
In addition, the analytical approximation we have derived in Sect. 3.1, that is, Eq. (30), may be a useful tool in the field of prominence seismology (Ballester 2014). We introduce a new parameter 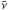 , called mean collision frequency of the plasma, that is defined through the following relation
, called mean collision frequency of the plasma, that is defined through the following relation 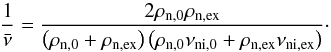 (33)Thus, the imaginary part of Eq. (30)can be now written as
(33)Thus, the imaginary part of Eq. (30)can be now written as 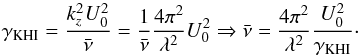 (34)Values of the three parameters that appear in the right-hand side of Eq. (34), namely the flow velocity, the perturbation wavelength, and the KHI growth rate, could be estimated from observations. Consequently, through this formula, we could estimate the coupling degree between the two components of the plasma.
(34)Values of the three parameters that appear in the right-hand side of Eq. (34), namely the flow velocity, the perturbation wavelength, and the KHI growth rate, could be estimated from observations. Consequently, through this formula, we could estimate the coupling degree between the two components of the plasma.
6. Conclusions
Although they may not embrace all the physics of the considered system, simple models like the one developed in this paper allow focusing on a particular effect and facilitate interpreting the results.
Here, we have studied how the existence of a neutral component in a plasma affects the propagation of waves and the possible occurrence of KHI in a cylindrical magnetic flux tube. We used a two-fluid theory to obtain the dispersion relation for linear incompressible waves. Then, we studied the dependence of the solutions on several physical parameters, namely the shear flow velocity, the collision frequency between ions and neutrals, the longitudinal wavenumber, and the azimuthal wavenumber. We have found that perturbations at an interface separating two partially ionized plasmas are unstable for any velocity shear, contrary to what occurs in fully ionized plasmas, in which the effect of the magnetic field only allows the onset of the KHI for super-Alfvénic shear flows. Perturbations with large longitudinal wavenumbers have higher growth rates than those with lower values of that parameter. The two constituent fluids of the plasma, that is, neutral and ionized, are coupled through collisions. This coupling exerts a significant influence: increasing the ion-neutral collision frequency reduces the growth rates of the unstable perturbations, although it is not possible to avoid the onset of the KHI. These results are consistent with previous works like the ones developed in simpler configurations by Watson et al. (2004) and Soler et al. (2012), for example. Equation (23)of the present paper reduces to Eq. (37) of Soler et al. (2012) or Eq. (26) of Watson et al. (2004) in the TT limit, that is, when the product of the longitudinal wavenumber by the radius of the tube is much lower than one. Moreover, in the absence of an equilibrium flow and when the densities of neutrals go to zero, we can recover from our dispersion relation the incompressible limit of Eq. (8a) of Edwin & Roberts (1983), corresponding to a fully ionized cylindrical flux tube.
We have also found that the solutions of the dispersion relation slightly depend on the azimuthal wavenumber. Modes with a higher azimuthal wavenumber are more unstable, but this variation is only appreciable beyond the TT limit and has not a great significance.
Then, we applied our model to a thread of a quiescent prominence by choosing values for the densities and temperatures typical of those coronal features and solving the dispersion relation for several degrees of ionization and wavelengths. We concluded that for a certain combination of parameters, the turbulent flows detected in quiescent prominences may be interpreted as consequences of KHI in partially ionized plasmas. The growth rates of the instability increase when the ionization fraction increases, that is, when the relative densities of neutrals increase.
Furthermore, we have provided an analytical approximation of the KHI growth rates for slow shear flows and strong ion-neutral collisional coupling. This formula, Eq. (30), is easier to handle than the full dispersion relation and thus easier to interpret: growth rates of the KHI show a quadratic dependence on the longitudinal wavenumber and the shear flow velocity and are inversely proportional to the ion-neutral collision frequency. The analytical approximation may be useful in the field of prominence seismology. From it we can define a mean collision frequency, 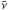 (given by Eq. (33)), that provides an estimate of the coupling degree of the plasmas. Values of this parameter may be computed from observational data.
(given by Eq. (33)), that provides an estimate of the coupling degree of the plasmas. Values of this parameter may be computed from observational data.
And even though we have used a model where the magnetic field is equal in both media, the conclusions extracted from its analysis may also be valid when the magnetic field inside the flux tube differs from that outside.
For the sake of simplicity, we ignored effects like gravity, compressibility, or surface tension. We also chose a particular alignment between the mass flow and the magnetic field: they are parallel, a configuration that gives a higher stability to the system. In future investigations the model used here can be improved by including these effects, which may have affect the KHI. Moreover, we only focused on the linear phase of the instability, while the nonlinear regime would likewise be of interest. Moreover, we assumed that the plasma is only composed of hydrogen, while more elements with several states of ionization are involved, of course. A much more complex model that incorporates various of these refinements would be needed to fully understand the KHI in prominences, but such a model could not be studied analytically, and numerical simulations would be required. Our paper is an improvement from previous investigations, but there is space for much future work in this field.
Acknowledgments
We thank the anonymous referee for helpful remarks and suggestions. We acknowledge the financial support from the Spanish MINECO through project AYA2011-22846, from CAIB through the “Grups Competitius” program, and from FEDER funds. D.M. acknowledges support from MINECO through a “FPI” grant and through funding for a short stay at KU Leuven. In addition, D.M. acknowledges the hospitality of the Centre for mathematical-Plasma Astrophysics of KU Leuven, and specially thanks Tom Van Doorsselaere and Marcel Goossens for their supervision and advice during his short stay. R.S. acknowledges discussion with the ISSI teams on “Partially ionized plasmas in astrophysics” and “Implications for coronal heating and magnetic fields from coronal rain observations and modelling” and thanks ISSI for their support. R.S. also acknowledges support from MINECO through a “Juan de la Cierva” grant, from MECD through project CEF11-0012, and from the “Vicerectorat d’Investigació i Postgrau” of the UIB. J.T. acknowledges support from the Spanish Ministerio de Educación y Ciencia through a “Ramón y Cajal” grant.
References
- Ballester, J. L. 2014, in IAU Symp. 300, eds. B. Schmieder, J.-M. Malherbe, & S. T. Wu, 30 [Google Scholar]
- Berger, T. E., Slater, G., Hurlburt, N., et al. 2010, ApJ, 716, 1288 [NASA ADS] [CrossRef] [Google Scholar]
- Braginskii, S. I. 1965, Rev. Plasma Phys., 1, 205 [NASA ADS] [Google Scholar]
- Chandrasekhar, S. 1961, Hydrodynamic and hydromagnetic stability (Oxford: Clarendon) [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Foullon, C., Verwichte, E., Nakariakov, V. M., Nykyri, K., & Farrugia, C. J. 2011, ApJ, 729, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Goossens, M., Terradas, J., Andries, J., Arregui, I., & Ballester, J. L. 2009, A&A, 503, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guo, X. C., Wang, C., & Hu, Y. Q. 2010, J. Geophys. Res., 115, 10218 [CrossRef] [Google Scholar]
- Hallinan, T. J., & Davis, T. N. 1970, Planet. Space Sci., 18, 1735 [NASA ADS] [CrossRef] [Google Scholar]
- Khomenko, E., Collados, M., Díaz, A., & Vitas, N. 2014, Phys. Plasmas, 21, 092901 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Engvold, O., der Voort, L., Wiik, J., & Berger, T. 2005, Sol. Phys., 226, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Michikoshi, S., & Inutsuka, S.-I. 2006, ApJ, 641, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, K. W., & Fitzenreiter, R. J. 1989, J. Geophys. Res., 94, 15113 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R. 1982, in Solar magneto-hydrodynamics Geophys. Astrophys. Manager (Dordrecht: D. Reidel), 21 [Google Scholar]
- Ryutov, D. A., & Ryutova, M. P. 1976, Sov. J. Exp. Theor. Phys., 43, 491 [NASA ADS] [Google Scholar]
- Ryutova, M. P. 1988, Sov. Phys. JETP, 67, 1594 [Google Scholar]
- Ryutova, M., Berger, T., Frank, Z., Tarbell, T., & Title, A. 2010, Sol. Phys., 267, 75 [Google Scholar]
- Soler, R., Oliver, R., & Ballester, J. L. 2009, ApJ, 699, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Díaz, A. J., Ballester, J. L., & Goossens, M. 2012, ApJ, 749, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Díaz, A. J., Ballester, J. L., & Goossens, M. 2013, A&A, 551, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spruit, H. C. 1981, A&A, 98, 155 [NASA ADS] [Google Scholar]
- Terradas, J., Arregui, I., Oliver, R., & Ballester, J. L. 2008, ApJ, 678, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, C., Zweibel, E. G., Heitsch, F., & Churchwell, E. 2004, ApJ, 608, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Zaqarashvili, T. V., Khodachenko, M. L., & Rucker, H. O. 2011, A&A, 529, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zirker, J. B., Engvold, O., & Martin, S. F. 1998, Nature, 396, 440 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Sketch of the model. |
| In the text | |
 |
Fig. 2 Upper panels: ωR/ωk as a function of the normalized shear flow velocity, ΔU/cA,0, for kza = 0.1, m = 1, and three different collision frequencies (a) νni/ωk = 0.1; b) νni/ωk = 1 and c) νni/ωk = 10). Lower panels: ωI/ωk as a function of ΔU/cA,0 for the same set of parameters as above. The red symbols represent the solutions of the full dispersion relation, i.e., Eq. (23); the blue solid lines correspond to the analytical approximation given by Eq. (30), and the blue dashed lines show the unstable branch of the neutral fluid when there is no coupling (Eq. (26)). |
| In the text | |
 |
Fig. 3 a) ωR/ωk and b) ωI/ωk for the kink mode (m = 1) as a function of νni/ωk, with ΔU/cA,0 = 1 and kza = 0.1. The red diamonds are the solutions originally associated with the ions when there is no coupling, while the blue crosses are the solutions for neutrals. The solid line is the analytical approximation given by Eq. (30). In b) the shaded area denotes the region of instability. |
| In the text | |
 |
Fig. 4 Application to solar prominence threads. Growth rates as functions of the shear flow velocity for the following set of parameters: ρi,0 + ρn,0 = 10-9 kg m-3, ρi,ex + ρn,ex = 2 × 10-10 kg m-3, B0 = Bex = 10-3 T, a = 100 km, T0 = 7000 K and Tex = 35 000 K; in the left panel the wavenumber is kz = 2π/λ = 2π × 10-5 m-1 and in the right panel it is kz = 2π × 10-6 m-1. The red dashed lines correspond to a fully ionized plasma (χ = 0), the blue crosses to a partially ionized case (χ = 4), and the black diamonds to a weakly ionized case (χ = 100). The solid lines represent the solutions given by the analytical approximation in Eq. (30). The shaded zone denotes the region of flow velocity values that have been frequently measured in solar prominences. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


