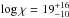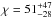| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201525720 | |
| Published online | 16 June 2015 | |
Model comparison for the density structure along solar prominence threads
1
Instituto de Astrofísica de Canarias,
38205
La Laguna, Tenerife
Spain
e-mail:
iarregui@iac.es
2
Departamento de Astrofísica, Universidad de La
Laguna, 38206, La
Laguna, Tenerife,
Spain
3
Departament de Física, Universitat de les Illes
Balears, 07122
Palma de Mallorca,
Spain
e-mail:
roberto.soler@uib.es
Received: 22 January 2015
Accepted: 13 May 2015
Context. Quiescent solar prominence fine structures are typically modelled as density enhancements, called threads, which occupy a fraction of a longer magnetic flux tube. This is justified from the spatial distribution of the imaged plasma emission or absorption of prominences at small spatial scales. The profile of the mass density along the magnetic field is unknown, however, and several arbitrary alternatives are employed in prominence wave studies. The identification and measurement of period ratios from multiple harmonics in standing transverse thread oscillations offer a remote diagnostics method to probe the density variation of these structures.
Aims. We present a comparison of theoretical models for the field-aligned density along prominence fine structures. They aim to imitate density distributions in which the plasma is more or less concentrated around the centre of the magnetic flux tube. We consider Lorentzian, Gaussian, and parabolic profiles. We compare theoretical predictions based on these profiles for the period ratio between the fundamental transverse kink mode and the first overtone to obtain estimates for the density ratios between the central part of the tube and its foot-points and to assess which one would better explain observed period ratio data.
Methods. Bayesian parameter inference and model comparison techniques were developed and applied. To infer the parameters, we computed the posterior distribution for the density gradient parameter that depends on the observable period ratio. The model comparison involved computing the marginal likelihood as a function of the period ratio to obtain the plausibility of each density model as a function of the observable. We also computed the Bayes factors to quantify the relative evidence for each model, given a period ratio observation.
Results. A Lorentzian density profile, with plasma density concentrated around the centre of the tube, seems to offer the most plausible inversion result. A Gaussian profile would require unrealistically high values of the density gradient parameter, and a parabolic density distribution does not enable us to obtain well-constrained posterior probability distributions. However, our model comparison results indicate that the evidence points to the Gaussian and parabolic profiles for period ratios in between 2 and 3, while the Lorentzian profile is preferred for higher period ratio values. The method we present can be used to obtain information on the plasma structure along threads, provided period ratio measurements become widely available.
Key words: magnetohydrodynamics (MHD) / methods: statistical / Sun: filaments, prominences / Sun: oscillations
© ESO, 2015
1. Introduction
When observed with high spatial resolution instrumentation, the fine structure of solar prominences appears to be distributed in the form of fine strands of plasma that is presumably aligned with the local magnetic field. This strands become visible as bright or dark filamentary structures in emission or absorption when observing prominences in the limb or on the disk. As described by Heinzel (2007), the fine structure of prominences is manifested differently in limb observations and on disk filaments, which makes it difficult to identify the same structures as seen on the limb and on the disk. When observed on the limb, the fine structure is composed by horizontal and vertical threads and knots of prominence plasma that exhibit a significant dynamical behaviour (see e.g., Heinzel 2007; Berger et al. 2008; Mein & Mein 1991; Schmieder et al. 2010, 2013, 2014). On the disk, the high-resolution Hα images show fine-structure fibrils, visible along the spine of quiescent filaments, with average widths of the order of 0.3′′, while their length is in between 5′′ and 40′′ (Lin et al. 2005; Lin 2011). Filament threads are thought to be made of relatively cold and dense plasma, with chromospheric properties, occupying a fraction of a longer invisible magnetic flux tube and surrounded by hot plasma with coronal properties.
In the past years, the analysis of spectra and images of prominence plasmas and the improvement of non-local thermodynamic equilibrium (non-LTE) radiative transfer models have enabled the development of inversion- and forward-modelling techniques to infer plasma parameters in solar prominences (see Labrosse et al. 2010, for a review). Tandberg-Hanssen (1995) and Patsourakos & Vial (2002) compiled various density determinations in prominences and showed that this parameter varies by at least two orders of magnitude, from 109 to 1011 cm-3. Magnetic fields show a similar variability, with field strengths that range from a few G to 20–30 G in quiescent prominences (e.g., Bommier et al. 1994; Merenda et al. 2006; Gunár et al. 2007) to higher values in active region prominences. Spectro-polarimetric observations are now able to offer information on the prominence magnetic field, although individual flux tubes cannot yet be resolved (López Ariste & Casini 2002; López Ariste et al. 2005; Orozco Suárez et al. 2014). These studies have provided a wealth of knowledge on the physical quantities and dynamics of prominences (Heinzel & Anzer 2006; Heinzel 2007; Mackay et al. 2010; Labrosse et al. 2010; Parenti 2014; Vial & Engvold 2015).
To obtain information about the value of physical quantities, such as the temperature, density, and magnetic field strength and their spatial variation along and across the magnetic field is of fundamental importance to understand the physical properties and dynamical processes operating in solar prominences. A widely followed approach is the 1D and 2D non-LTE modelling of prominences and filaments, including their fine structures, and the comparison between the observed spectral line properties with the synthetic line characteristics (e.g., Heinzel 1995, 2015; Paletou 1995; Gouttebroze & Labrosse 2000; Gunár et al. 2007, 2013, 2014). An alternative approach is the theoretical modelling of magnetohydrodynamic (MHD) waves in fine-structure equilibrium models and the comparison of the observed waves with the theoretical MHD wave properties, a diagnostic tool known as prominence seismology (Ballester 2005, 2006, 2014; Oliver 2009).
The method of prominence seismology relies on the comparison between observed and theoretical properties of waves and oscillations. The analysis of imaging and spectroscopic data has clearly shown the presence of small amplitude oscillations in prominence fine structures (see Arregui et al. 2012, for a review). Some of these oscillations produce the transverse displacement of the threads and have been interpreted in terms of MHD transverse kink waves (Lin et al. 2009; Lin 2011). The observed disturbances have characteristic periods of a few minutes and velocity amplitudes of a few km s-1. By measuring the oscillation properties and comparing them to theoretical predictions, information on the unknown parameters can be obtained. Because of the relatively simple structure of prominence threads in comparison to the full prominence structure, seismology studies approximate their magnetic and plasma configuration using simplified magnetic flux tube models in cylindrical geometry. By adopting the zero plasma-β approximation, models that study linear tube oscillations are then constructed by specifying a particular density structure that defines the thread inside the tube. Following this approach, models have been used to analyse the oscillatory properties of standing transverse thread oscillations. Díaz et al. (2002) used a piece-wise constant density profile along and across the thread to model a cold thread embedded in a hotter coronal gas. Soler et al. (2010) extended this model by considering a smooth variation of density across the field to study damped transverse oscillations, and Arregui et al. (2011) further increased the complexity of the modelling by adopting fully non-uniform density models with a smooth variation of the density along and across the magnetic field. In all these studies, the density structuring along and across the field was arbitrarily prescribed.
In a recent study, Soler et al. (2015) have considered three alternative models for the density profile along threads and have computed period ratios between the fundamental kink mode and the first overtone of transverse thread oscillations. Period ratios are sensitive to the details of the density variation along the magnetic field, hence the inversion of observed period ratios using longitudinally non-uniform density models provides information on the density profile of prominence threads (see e.g., Díaz et al. 2010). Following this approach, and using their theoretical predictions, Soler et al. (2015) obtained estimates of the magnitude of the density gradient along the thread.
Because any inference is model dependent, their results are conditional on the specific models that have been assumed to explain observations. A second level of inference consist of presenting the same data to different models to assess in a quantitative manner which one is favoured. This paper presents the solution to that problem, which necessarily demands the Bayesian solution to the model comparison problem. The Bayesian formalism for inference and model comparison is the only fully correct way we have to obtain information about physical parameters and the plausibility of hypotheses from observations under incomplete and uncertain information (see e.g., Trotta 2008; von Toussaint 2011). The three density models adopted by Soler et al. (2015) are considered to devise a method by which their relative plausibility in explaining period ratio data for transverse thread oscillations can be obtained, hence inferring the degree of evidence for each one. The method thus developed can be applied to the analysis of future period ratio measurements in prominence threads.
The layout of the paper is as follows. Section 2 describes the considered prominence thread density models. In Sect. 3 the solutions to the forward problem for transverse thread oscillations are discussed. Seismology results for the inference of the density gradient along threads are shown in Sect. 4. In Sect. 5, the three models are compared to evaluate which one would better explain observed period ratios. Section 6 presents our conclusions.
2. Thread density models
Because of the apparent filamentary structure of prominence plasmas at small spatial scales, individual threads are commonly modelled by means of magnetic flux tube models in which a density enhancement, surrounded by plasma in coronal conditions, occupies a fraction of a longer magnetic flux tube. Although prominences are formed by many threads, observations often show that individual threads oscillate independently. We neglected the interaction between neighbouring structures and considered a model for an individual and isolated structure. Following Soler et al. (2015), we considered such a prominence thread model consisting of a straight cylindrically symmetric magnetic flux tube of radius R and length L, with the magnetic field directed along the longitudinal coordinate, z (see Fig. 1 in Soler et al. 2015). The ends of the tube are located at z = ± L/ 2. The magnetic field strength, B0, is uniform and under the plasma-β = 0 approximation the spatial distribution of the mass density, ρ0, can be chosen arbitrarily. This fact was used to consider three alternative density distributions along the equilibrium magnetic field that were compared in our study.
Prominence threads are denser near the tube centre than at the foot-points. By denoting the internal density at the centre as ρi(0) = ρi,0 and that at the foot-point as ρi(L/ 2) = ρi,L/ 2, the ratio of densities is given by χ = ρi,0/ρi,L/ 2 with χ ≥ 1. For χ = 1, the thread is homogeneous. The density variation is stronger for higher values of χ.
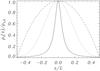 |
Fig. 1 Spatial variation of the equilibrium mass density along the magnetic flux tube for prominence thread models with a Lorentzian profile (solid line), a Gaussian profile (dotted line), and a parabolic profile (dashed line). The ratio of centre to foot-point densities is χ = 100. |
Using these definitions, Soler et al. (2015) constructed three alternative density models for longitudinally inhomogeneous prominence threads: a Lorentzian profile with 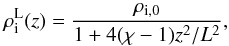 (1)a Gaussian profile with
(1)a Gaussian profile with 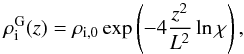 (2)and a parabolic profile with
(2)and a parabolic profile with 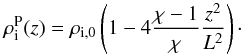 (3)Figure 1 shows the spatial variation of the density distribution for the three considered profiles. For the Lorentzian profile, the dense plasma is located in a narrow fraction of the tube around its centre, and the density decreases significantly as soon as we move towards the foot-points of the tube. For the parabolic profile, the density is broadly distributed along the tube. These profiles represent two extreme cases. The intermediate case is given by the Gaussian profile for which the dense plasma is also located around the centre of the tube, but the gradient is smoother that in the Lorentzian case and sharper than in the parabolic case.
(3)Figure 1 shows the spatial variation of the density distribution for the three considered profiles. For the Lorentzian profile, the dense plasma is located in a narrow fraction of the tube around its centre, and the density decreases significantly as soon as we move towards the foot-points of the tube. For the parabolic profile, the density is broadly distributed along the tube. These profiles represent two extreme cases. The intermediate case is given by the Gaussian profile for which the dense plasma is also located around the centre of the tube, but the gradient is smoother that in the Lorentzian case and sharper than in the parabolic case.
None of the specifically assumed density profiles is expected to be an accurate quantitative representation of the real density variation along solar prominence threads, but they provide a means to model alternative cases which, by means of the model comparison technique presented in this paper, can offer information about whether the density is more or less distributed around the denser central part of the magnetic flux tube.
3. Period ratio of inhomogeneous threads
Each of the assumed equilibrium density profiles produces distinct transverse wave signatures. In particular, the ratio of periods between the fundamental transverse kink mode and its first overtone is known to be sensitive to the longitudinal variation of the density along the magnetic flux tube. This is known since the study by Andries et al. (2005b) in the context of coronal loop oscillations. Andries et al. (2005a) were the first to use this fact to perform a seismic inversion of the longitudinal density structuring from observations of period ratios of transverse loop oscillations, an approach that has been frequently employed since then (see Andries et al. 2009, for a review). Period ratio measurements are scarce in prominence oscillations, but Díaz et al. (2010) employed the same technique to investigate the dependence of the period ratio on the equilibrium parameters to find that for prominence plasmas the period ratio is higher than two, and to obtain an estimate of the length of the supporting magnetic tube.
For the particular three density profiles described above, Soler et al. (2015) obtained analytical and numerical approximations to the period ratio of transverse oscillations of individual threads. The obtained period ratios are functions of a single parameter, the ratio of the central density to the foot-point density. Soler et al. (2015) computed period ratios as a function of the increasing density gradient parameter χ by reducing the foot-point density while keeping the density at the central part of the tube and found that the period ratio r = P0/P1 is higher than 2. They noted, however, that by doing so, the total mass in the thread is different for different profiles, which prevents a direct comparison between the results from different profiles. To solve this problem, Soler et al. (2015) considered the same average density in the thread by defining an average internal density, which keeps the period ratio variation as a function of the average density equal for the three profiles. The relevant expression is Eq. (17) in Soler et al. (2015), which was empirically obtained after analysing their numerical computations. The important result behind this equation is that the period ratio is only a function of the ratio of the average density to the central density. This property enables expressing the period ratio as a function of χ, although the functional dependence on this parameter is different for each considered density profile. The relevant forward solutions for each adopted density profile are obtained upon substitution of their expressions (18)–(20) for the average density as a function of χ into their Eq. (17) for the period ratio as a function of the average density (see Soler et al. 2015). These expressions are ![\begin{eqnarray} \label{rl} r^{\rm L}&=&\left(\frac{P_0}{P_1}\right)^{\rm L}=1+\left(\frac{\sqrt{\chi-1}}{\arctan\sqrt{\chi-1}}\right)^{1/2}, \\[2mm] \label{rg} r^{\rm G}&=&\left(\frac{P_0}{P_1}\right)^{\rm G}=1+\left(\frac{2\ln\chi}{\sqrt{\pi}\ \mathrm{erf\sqrt{\ln\chi}}}\right)^{1/2}, \end{eqnarray}](/articles/aa/full_html/2015/06/aa25720-15/aa25720-15-eq26.png) and
and 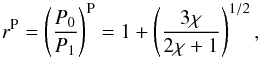 (6)where the superscripts of the period ratio indicate that the solution of the forward problem corresponds to the Lorentzian, Gaussian, and parabolic density profiles, respectively.
(6)where the superscripts of the period ratio indicate that the solution of the forward problem corresponds to the Lorentzian, Gaussian, and parabolic density profiles, respectively.
The three solutions for the period ratio as a function of the density variation along the thread are displayed in Fig. 2. When χ = 1, the three curves obtain the period ratio r = 2 for longitudinally homogeneous thread models (Soler et al. 2015). As the density variation increases, the period ratio increases in the three cases. This increase is more marked for the Lorentzian profile and is very subtle in the case of the parabolic profile. For the Gaussian profile an intermediate result is obtained for the rate of the period ratio increase.
 |
Fig. 2 Dependence of the period ratio between the fundamental mode and the first overtone as a function of the density gradient parameter, χ, for a Lorentzian profile (solid line), a Gaussian profile (dotted line), and a parabolic profile (dashed line). |
4. Parameter inference
Using the solutions to the forward problem for the three density profiles, we now devised a method for infering the parameter. This can be used to obtain information on the density gradient along the threads from period ratio measurements. To this end, we used Bayes’ theorem (Bayes & Price 1763), 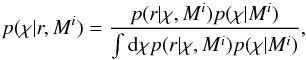 (7)to perform the inversion of parameter χ from data r, assuming density models Mi, where we chose upper scripts P, G, L in model names MP,G,L as representations of the parabolic, Gaussian, and Lorentzian profiles, respectively. Bayes’ theorem states that the posterior probability distribution of the unknown parameter given the period ratio data, p(χ | r,Mi), is proportional to the likelihood function, p(r | χ,Mi) and the prior probability, p(χ | Mi). The posterior encodes all the information about the parameter χ and quantifies the degree of belief on its values conditional on the observed data and the assumed model.
(7)to perform the inversion of parameter χ from data r, assuming density models Mi, where we chose upper scripts P, G, L in model names MP,G,L as representations of the parabolic, Gaussian, and Lorentzian profiles, respectively. Bayes’ theorem states that the posterior probability distribution of the unknown parameter given the period ratio data, p(χ | r,Mi), is proportional to the likelihood function, p(r | χ,Mi) and the prior probability, p(χ | Mi). The posterior encodes all the information about the parameter χ and quantifies the degree of belief on its values conditional on the observed data and the assumed model.
The forward solutions to the period ratio are given by Eqs. (4)–(6) for the Lorentzian, Gaussian, and parabolic profiles, respectively. To evaluate the likelihood for each profile, we assumed that the model is true. Then, the period ratio measurement (r) will differ from the prediction, for instance, rL for the Lorentzian profile, because of measurement uncertainties (e), so that r = rL ± e. The probability of obtaining the measured value is equal to the probability of the error. Assuming Gaussian errors, the likelihood for the three models is then expressed in the following manner: ![\begin{equation} \label{like1} p(r | \chi,M^i)=\frac{1}{\sqrt{2\pi}\sigma}\exp \left[-\frac{[r-r^i(\chi)]^2}{2\sigma^2}\right], \end{equation}](/articles/aa/full_html/2015/06/aa25720-15/aa25720-15-eq39.png) (8)with i = P, G, L depending on the model under consideration and σ2 the variance associated with the observed period ratio. We have explicitly stated in this expression that the likelihood is conditional on the parameter χ. In the following we assign observed period ratio errors to the standard deviation σ.
(8)with i = P, G, L depending on the model under consideration and σ2 the variance associated with the observed period ratio. We have explicitly stated in this expression that the likelihood is conditional on the parameter χ. In the following we assign observed period ratio errors to the standard deviation σ.
 |
Fig. 3 a) Posterior probability distribution for log χ under the Gaussian density gradient model, MG, for a period ratio of r = 3.0 and uncertainty given by σ = 0.2 (dashed); σ = 0.4 (solid); σ = 0.8 (dotted) and considering log χ ∈ [ 1,60 ] in the prior range. For σ = 0.4, the inferred median of the distribution is |
The prior indicates our level of knowledge (ignorance) on the model before considering the observed data. This is translated into the level of knowledge (ignorance) on the possible values of the parameter χ. We have adopted a uniform prior distribution for this parameter upon which the three model depend over a given range, so that we can write 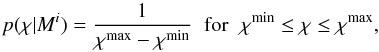 (9)and zero otherwise. We only considered models with a positive density gradient from foot-point to tube centre, hence χ ≥ 1. In the following, we adopt χmin = 2 and χmax = 500 unless otherwise stated.
(9)and zero otherwise. We only considered models with a positive density gradient from foot-point to tube centre, hence χ ≥ 1. In the following, we adopt χmin = 2 and χmax = 500 unless otherwise stated.
The Bayesian framework enables us to perform the inference making use of all the available information in a consistent manner and with a correct propagation of errors in the observations to uncertainty on inferred parameters. Figure 3 shows posterior probability distributions for the density gradient along the thread computed using Eq. (7) with the likelihood and prior given by Eqs. (8) and (9) for a hypothetical period ratio measurement, r = 3, for three values of the period ratio measurement error and two out of the three density models, the Gaussian and Lorentzian profiles. The values of σ were chosen so as to be representative of period ratio measurements in which a relative error on both periods of about 10% is assumed, which leads to Δr = 0.4 for a value of r = 3. For these cases, well-constrained distribution are obtained that enable us to say something about the most plausible value of χ. We call attention to the markedly asymmetric distributions in both cases, with larger upper error bars. The higher the value of σ, the less constrained the obtained distributions. For the Gaussian profile (Fig. 3a) the inversion is more conveniently made for the logarithm of χ. Equation (5) for this profile leads to a very slowly increasing period ratio as a function of χ (see dotted line in Fig. 2). For σ = 0.4, the posterior distribution has a median of log χ ~ 19, which seems unrealistically large. For the Lorentzian profile (Fig. 3b) the inversion leads to a posterior with a median of χ ~ 51, considering the same observational error. For the parabolic profile the inversion does not lead to a well-constrained posterior distribution. The reason is that the forward solution, given by Eq. (6), predicts a constant period ratio of r = 2.22 for χ ≫ 1. The fact that the inference for the parabolic profile fails to constrain the density gradient or that the inversion with the Gaussian profiles leads to unrealistically high values of χ does not mean that models MP and MG must be discarded, as we show below in the model comparison analysis.
5. Model comparison
The Bayesian framework also enables us to present different models to the same data and assess in a quantitative manner which one is favoured by them. To develop the method for performing this comparison, we followed a procedure similar to the one employed by Arregui et al. (2013) for coronal loop oscillations in expanding and/or stratified loops. We rewrote Bayes’ theorem in terms of the probability of a given model, conditional on the observed data, as 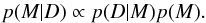 (10)To determine the relative plausibility of two competing models, we need to evaluate their posterior probabilities to ascertain their relative merits. We considered two such models, Mi and Mj. By applying Eq. (10) to them, the relative plausibility of one model against the other is given by the posterior ratio (Jeffreys 1961)
(10)To determine the relative plausibility of two competing models, we need to evaluate their posterior probabilities to ascertain their relative merits. We considered two such models, Mi and Mj. By applying Eq. (10) to them, the relative plausibility of one model against the other is given by the posterior ratio (Jeffreys 1961) 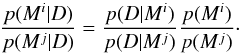 (11)The first ratio on the right-hand side expresses how well the observed data are predicted by model Mi compared to model Mj. The second ratio, the prior odds ratio, measures how much our initial assumptions favoured Mi over Mj before considering the data. As we have no particular a priori preference for any of the three models compared in this study, we considered p(Mi) = p(Mj) = 1 / 2 in all our model comparisons. Our assessment of the plausibility of models is then based on the computation of the so-called Bayes factor of Mi against Mj given by
(11)The first ratio on the right-hand side expresses how well the observed data are predicted by model Mi compared to model Mj. The second ratio, the prior odds ratio, measures how much our initial assumptions favoured Mi over Mj before considering the data. As we have no particular a priori preference for any of the three models compared in this study, we considered p(Mi) = p(Mj) = 1 / 2 in all our model comparisons. Our assessment of the plausibility of models is then based on the computation of the so-called Bayes factor of Mi against Mj given by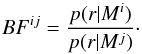 (12)We computed Bayes factors to assess which model of the three proposed density profiles better explains a given period ratio measurement.
(12)We computed Bayes factors to assess which model of the three proposed density profiles better explains a given period ratio measurement.
Before computing Bayes factors, we obtained relevant information concerning the plausibility of each model by first computing their marginal likelihood, which informed us on how well a given model performs in explaining data on period ratios. This is so because in the model comparison, we are interested in the most probable model, independently of the parameters, which means that we should marginalise out all parameters. This was achieved by performing an integral of the likelihood over the full parameter space. In our particular one-dimensional problem, the marginal likelihood for a given model Mi can be written as 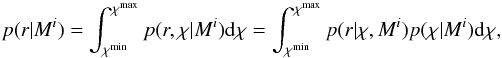 (13)where χ ∈ [ χmin,χmax ] represents the range in the parameter of the models, and we used the product rule to expand the probability of r and χ, given model Mi. Figure 4 displays marginal likelihoods for the three models. They were computed using expressions (13) and using the forward models (4)–(6) for period ratios in the range 2 to 6. In Figs. 4a–c, three different values of σ are considered to show the influence of different measurement errors on the distribution of the plausibility for each model. Figure 4d compares the marginal likelihood for the three models for a fixed period ratio measurement error. The magnitude of each of the curves provides the plausibility of each model for a given observed period ratio.
(13)where χ ∈ [ χmin,χmax ] represents the range in the parameter of the models, and we used the product rule to expand the probability of r and χ, given model Mi. Figure 4 displays marginal likelihoods for the three models. They were computed using expressions (13) and using the forward models (4)–(6) for period ratios in the range 2 to 6. In Figs. 4a–c, three different values of σ are considered to show the influence of different measurement errors on the distribution of the plausibility for each model. Figure 4d compares the marginal likelihood for the three models for a fixed period ratio measurement error. The magnitude of each of the curves provides the plausibility of each model for a given observed period ratio.
 |
Fig. 4 a)–c) Marginal likelihoods computed using Eq. (13) for models MP, ML, and MG as a function of the period ratio for different values of the uncertainty, with σ = 0.2 (dashed), σ = 0.4 (solid), and σ = 0.8 (dotted). d) The three marginal likelihoods computed for a fixed value of σ = 0.4: p(r | MP) as a dashed line, p(r | MG) as a dotted line, and p(r | ML) as a solid line. In all plots, χ ∈ [ 2,500 ]. |
From Figs. 4a–c, it is easy to see that by increasing the value of σ, related to the uncertainty on the measured period ratio, the magnitude of the three marginal likelihoods decreases and the distributions spread out over a wider range of values of r, thus decreasing the amount of evidence for or against any of the considered models. When comparing the marginal likelihood for the three models in Fig. 4d, we see that the parabolic and Gaussian profiles are likely to produce period ratios in the lower half of the considered period ratios range, from 2 to 4. Beyond that, their likelihood decreases significantly. According to Eq. (6), see also Fig. 2, the parabolic profile predicts period ratios that approach the value r = 2.2 and then keep this constant value for increasing values of χ. The integrated marginal likelihood, dashed line in Fig. 4d, peaks at that value but could also explain slightly lower and higher period ratios, hence spreads both sides of the peak because of the considered uncertainty on the measured period ratio. The Gaussian profile produces a similar marginal likelihood, shifted towards higher values of the period ratio. This means that the Gaussian profile is likely to reproduce period ratio values similar to those reproduced by the parabolic profile. Hence, if our observed period ratio is in the range between 2 and 4, it can be difficult to obtain significant evidence for one model to be preferred over the other. The Lorentzian profile predicts period ratios as given by Eq. (4). The corresponding marginal likelihood distribution shows that this model is more likely to reproduce values of the period ratio higher than those that can be reproduced by the parabolic and the Gaussian profiles. The distribution peaks at about 4.4, but is rather extended and covers almost all values of the considered range for the period ratio.
To state the relative plausibility of one model over another based on quantitative calculations, we computed the Bayes factors using Eq. (12). They are functions of the marginal likelihood ratios and provide quantitative information on the magnitude of the evidence for one model to be preferred over another. To assign different levels of evidence to the values of the Bayes factors, we used the empirical table by Kass & Raftery (1995), which assigns evidence for model Mi against model Mj that is minimal evidence to values of 2log (BFij) in between 0 and 2, positive evidence to values in between 2 and 6, strong evidence to values in between 6 and 10, and very strong evidence to values of 2log (BFij) higher than 10.
 |
Fig. 5 Bayes factors computed using Eq. (12) for the model comparisons between a) the parabolic, MP, and the Gaussian, MG, density models; b) the parabolic, MP, and the Lorentzian, ML, density models; and c) the Gaussian, MG, and the Lorentzian, ML, density models, as a function of the period ratio. A value of σ = 0.4 has been considered and χ ∈ [ 2,500 ] in all computations. |
5.1. Parabolic versus Gaussian profile
Figure 5a shows the Bayes factors corresponding to the comparison between the parabolic and the Gaussian density models (BFPG as a solid line and BFGP as a dashed line) as a function of the observable period ratio. Different shades of grey limit ranges in period ratio with different levels of evidence for one model being preferred against the alternative, depending on the magnitude of the Bayes factors and following the scale described above. White regions indicate values of period ratio for which there is minimal evidence for any of the models that are being compared. Different shades of grey indicate regions with positive, strong, and very strong evidence, with the level of evidence being higher for darker regions.
The marginal likelihoods for the two models (see Fig. 4d) tell us that the Gaussian and parabolic profiles have a significant likelihood for reproducing period ratio values on a similar range, with the likelihood for the parabolic profile being slightly shifted towards lower values of the period ratio. Bayes factors quantify and locate exactly where and to which degree the plausibility for one model is higher than the alternative. We first consider regions where BFPG is positive, meaning that the evidence for the parabolic profile is stronger than that for the Gaussian profile. The evidence for MP instead of MG is minimal since BFPG never reaches values above 2. The region where both Bayes factors are too small to provide positive evidence for any of the models corresponds to the values r = [ 2.0−2.84 ] (white region). The regions where BFGP is positive, meaning that the evidence for the Gaussian profile is stronger than that for the parabolic profile, show positive evidence for MG instead of MP for period ratios in the range r = [ 2.84−3.64 ], strong evidence in the range r = [ 3.64−4.41 ], and very strong evidence for r> 4.41.
In summary, the evidence in favour of MP instead of MG or vice versa is minimal until we reach a period ratio of r = 2.84. Period ratios higher than this value imply positive, strong, and very strong support for the Gaussian profile instead of the parabolic profile, for which no supporting evidence can be found in the considered period ratio range.
5.2. Parabolic versus Lorentzian profile
Figure 5b shows the Bayes factors corresponding to the comparison between the parabolic and the Lorentzian density models (BFPL as a solid line and BFLP as a dashed line) as a function of the observable period ratio. As before, the different shades of grey limit ranges in period ratio with different levels of evidence for one model being preferred against the alternative.
The marginal likelihoods for the two models (see Fig. 4d) show that the regions in the measured period ratio for which each of the two models better predicts the observable are quite different, with the marginal likelihood for the parabolic profile concentrated in between 2 and 4 and the marginal likelihood for the Lorentzian profile being significant for higher values of the period ratio. To which extend the observed period ratios would support one model against the alternative is assessed by the magnitude of the Bayes factors. We first consider regions where BFPL is positive, meaning that the evidence for the parabolic profile is stronger than that for the Lorentzian profile. Strong evidence is found for MP instead of ML for period ratios in the range r = [ 2.0−2.34 ] and positive evidence in the range r = [ 2.34−2.81 ]. Then, a region appears in white, with r = [ 2.81−3.14 ], where the evidence in favour of any of the two models is minimal because of the low values of both Bayes factors. The regions where BFLP is positive, meaning that the evidence for the Lorentzian profile is stronger than that for the parabolic profile, show positive evidence for ML instead of MP for period ratios in the range r = [ 3.14−3.40 ], strong evidence in the range r = [ 3.40−3.62 ], and very strong evidence for r> 3.62.
The evidence for data supporting any of the competing models is inconclusive in a small range of period ratio values around r ~ 3, where both marginal likelihoods have similar magnitude. A measured period ratio with a value to the left of that region would support the parabolic profile, the stronger the lower the value of the measured period ratio. A measured period ratio with a value to the right of that region would support the Lorentzian profile, the stronger the higher the value of the measured period ratio.
5.3. Gaussian versus Lorentzian profile
Finally, Fig. 5c shows the Bayes factors corresponding to the comparison between the Gaussian and the Lorentzian density models (BFGL as a solid line and BFLG as a dashed line) as a function of the observable period ratio.
The marginal likelihoods for the two models (see Fig. 4d) indicate that, as in the previous comparisons, the regions in the measured period ratio for which each of the two models better predicts the observable are clearly different. We first consider the values of the Bayes factors in regions where BFGL is positive, meaning that the evidence for the Gaussian profile is stronger than that for the Lorentzian profile. They show positive evidence for MG instead of ML for period ratios in the range r = [ 2.0−3.08 ]. The evidence is minimal in the region r = [ 3.08−3.46 ] because of the low values of the Bayes factors. The regions where BFLG is positive, meaning that the evidence for the Lorentzian profile is stronger than that for the Gaussian profile, show positive evidence for ML instead of MG for period ratios in the range r = [ 3.46−3.74 ], strong evidence in the range r = [ 3.74−3.97 ], and very strong evidence for r> 3.97.
Similarly to what we found with the comparison between MP and ML, the evidence in favour of MG instead of ML or vice versa is inconclusive in a small range of period ratio values around r ~ 3.25, for which their marginal likelihoods have similar magnitude. A measured period ratio with a value to the left of that region would support the Gaussian profile. A measured period ratio with a value to the right of that region would support the Lorentzian profile, the stronger the higher the value of the measured period ratio.
5.4. Discussion of results
A Bayesian model comparison enables only comparing face to face the performance of two models at a time. However, we summarise our results as follows. When the period ratio is roughly in between 2 and 3, the evidence for the Lorentzian profile is lower than that for the parabolic and Gaussian profiles. However, the latter two profiles show evidence that is minimal. Hence the question cannot be settled as to which model among MP and MG is more plausible. When the period ratio is roughly in between 3 and 4, the evidence for the Gaussian profile and for the Lorentzian profile is both times stronger than that for the parabolic profile. In turn, the Lorentzian profile has stronger evidence than the Gaussian for period ratios beyond ~3.5. Finally, for higher period ratios, the Gaussian profile has stronger evidence than the parabolic profile, but the Lorentzian profile clearly shows the strongest evidence in comparison to both the Gaussian and parabolic profiles. This means that the Lorentzian profile, with the mass density occupying a narrow extension around the central part of the flux tube, offers the most plausible explanation for the density profile of prominence threads along the magnetic field if measured period ratios are higher than ~3.5.
Soler et al. (2015) noted that no reliable simultaneous measurements of the two periods are available yet in observations of prominence thread oscillations. Lin et al. (2007) reported a possible case, with a measured period ratio of r = 4.44. Soler et al. (2015) performed a seismology application using this observed ratio, which led to χ ~ 347 when the Lorentzian profile was used and χ ~ 1048 when the Gaussian profile was used. This led Soler et al. (2015) to conclude that the measured period ratio would be compatible with the Lorentzian profile, since the inversion offers a more realistic value for the density gradient parameter. The Bayesian model comparison presented in this paper enables us to confirm this conclusion on the basis of the computed Bayes factors. For instance, for r = 4.44, the BFGP = 10.16 leads to very strong evidence supporting model MG instead of model MP. However, the BFLP = 29.73 and BFLG = 19.56 leave ML as the most plausible model, and with very strong evidence.
It must be noted that these particular numbers were obtained assuming an uncertainty on the data with σ = 0.4. The marginal likelihoods in Fig. 4 and the Bayes factors in Fig. 5 depend on the uncertainty on the data. Measured errors corresponding to these events, which were not provided by Lin et al. (2007), need to be used to properly confirm this result. When we repeat the calculations for the same value of r = 4.41, but doubling the error to σ = 0.8, we obtain BFGP = 2.41; BFLP = 7.03 and BFLG = 4.61. We would have positive evidence for MG instead of MP, strong evidence for ML instead of MP, and positive evidence for ML instead of MG. The conclusion would therefore be similar, with the evidence supporting the Lorentzian profile, but to a lesser extent.
6. Conclusions
Observed and theoretically modelled wave dynamics offer an alternative way to infer information about physical parameters in prominence fine structures. This seismology approach works by proposing a given model for which wave properties are computed and by inferring the unknown plasma and field conditions from a comparison with observed wave properties. Alternative models are usually proposed and might lead to different inversion results. This necessitates obtaining information about which of the alternative models better explains the observed data.
Bayesian analysis techniques offer the only self-consistent method to compare theoretical models and observations and to propagate uncertainty from measured quantities to the inferred parameters or to the amount of evidence supporting a given model. We have applied Bayesian inference and model comparison techniques to obtain information on the density structure along solar prominence threads and to assess which of the three alternative models for the density variation along prominence threads would better explain given observed values for the period ratio.
The three density models offer different results for the inversion of the density gradient parameter. A Lorentzian density profile, with plasma density concentrated around the centre of the tube, seems to offer the most realistic inversion result. A Gaussian profile, with the mass spread over a larger portion of the tube, would require unrealistically high values of the density gradient parameter. A parabolic density distribution does not enable us to obtain well-constrained posterior probability distributions for the density gradient. However, this does not imply that the parabolic and Gaussian models can be disregarded.
Our model comparison results indicate that for period ratios roughly in between 2 and 3, the parabolic and Gaussian profiles lead to the highest marginal likelihoods. By computing Bayes factors, we obtained a full quantitative assessment of the plausibility of each model as a function of the observed parameter considering all the information available on data, their uncertainty, and the model parameters. The different levels of evidence for different ranges of the observable were obtained on the basis of the magnitude of the Bayes factors. They depend on the specific models and the uncertainty on the data and are, therefore, by no means presented as general limits. The procedure needs to be repeated for every observation. Our results indicate that a Lorentzian profile, with the mass density concentrated around the centre of the magnetic flux tube, would offer the most plausible explanation for measurements in which the period ratio deviates significantly from its value of 2 in homogeneous thread models. For period ratio measurements roughly in between 2 and 3, the evidence would be inconclusive and insufficient for deciding between the Gaussian and the parabolic profiles.
The models we used considered static threads and did not take into account the flow effects. Results from Soler & Goossens (2011) on flowing threads suggest that the period ratio may change as the dense part of the thread flows along the magnetic flux tube.
Although no observations of the period ratio in prominence threads are currently available, the framework developed in this article has the potential to infer information about the spatial variation of density along threads if observations of the period ratio are eventually reported.
Acknowledgments
We are grateful to the referee for comments that improved the manuscript. We acknowledge financial support from the Spanish Ministry of Economy and Competitiveness (MINECO) through projects AYA2011–22846 (Dynamics and Seismology of Solar Coronal Structures) and AYA2014-55456-P (Bayesian Analysis of the Solar Corona), from FEDER funds, and from CAIB through the “Grups Competitius” program. I.A. acknowledges financial support through a Ramón y Cajal fellowship. R.S. acknowledges support from MINECO through a Juan de la Cierva grant, from MECD through project CEF11-0012, and from the “Vicerectorat d’Investigació i Postgrau” of the Universitat de les Illes Balears.
References
- Andries, J., Arregui, I., & Goossens, M. 2005a, ApJ, 624, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Andries, J., Goossens, M., Hollweg, J. V., Arregui, I., & Van Doorsselaere, T. 2005b, A&A, 430, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andries, J., van Doorsselaere, T., Roberts, B., et al. 2009, Space Sci. Rev., 149, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Arregui, I., Soler, R., Ballester, J. L., & Wright, A. N. 2011, A&A, 533, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arregui, I., Oliver, R., & Ballester, J. L. 2012, Liv. Rev. Sol. Phys., 9, 2 [Google Scholar]
- Arregui, I., Asensio Ramos, A., & Díaz, A. J. 2013, ApJ, 765, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Ballester, J. L. 2005, Space Sci. Rev., 121, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Ballester, J. L. 2006, Roy. Soc. London Philos. Trans. Ser. A, 364, 405 [Google Scholar]
- Ballester, J. L. 2014, in IAU Symp. 300, eds. B. Schmieder, J.-M. Malherbe, & S. T. Wu, 30 [Google Scholar]
- Bayes, M., & Price, M. 1763, Roy. Soc. London Philos. Trans. Ser. I, 53, 370 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, T. E., Shine, R. A., Slater, G. L., et al. 2008, ApJ, 676, L89 [Google Scholar]
- Bommier, V., Landi Degl’Innocenti, E., Leroy, J.-L., & Sahal-Bréchot, S. 1994, Sol. Phys., 154, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz, A. J., Oliver, R., & Ballester, J. L. 2002, ApJ, 580, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz, A., Oliver, R., & Ballester, J. 2010, ApJ, 725, 1742 [NASA ADS] [CrossRef] [Google Scholar]
- Gouttebroze, P., & Labrosse, N. 2000, Sol. Phys., 196, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Gunár, S., Heinzel, P., Schmieder, B., Schwartz, P., & Anzer, U. 2007, A&A, 472, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunár, S., Heinzel, P., Anzer, U., & Mackay, D. H. 2013, J. Phys. Conf. Ser., 440, 012035 [NASA ADS] [CrossRef] [Google Scholar]
- Gunár, S., Schwartz, P., Dudík, J., et al. 2014, A&A, 567, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P. 1995, A&A, 299, 563 [NASA ADS] [Google Scholar]
- Heinzel, P. 2007, in The Physics of Chromospheric Plasmas, eds. P. Heinzel, I. Dorotovič, & R. J. Rutten, ASP Conf. Ser., 368, 271 [Google Scholar]
- Heinzel, P. 2015, in Astrophys. Space Sci. Lib. 415, eds. J.-C. Vial, & O. Engvold, 103 [Google Scholar]
- Heinzel, P., & Anzer, U. 2006, ApJ, 643, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffreys, H. 1961, in Theory of Probability, 3rd edn. (Oxford University Press) [Google Scholar]
- Kass, R. E., & Raftery, A. E. 1995, JASA, 90, 773 [Google Scholar]
- Labrosse, N., Heinzel, P., Vial, J.-C., et al. 2010, Space Sci. Rev., 151, 243 [Google Scholar]
- Lin, Y. 2011, Space Sci. Rev., 158, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Engvold, O., Rouppe van der Voort, L., Wiik, J. E., & Berger, T. E. 2005, Sol. Phys., 226, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Engvold, O., Rouppe van der Voort, L. H. M., & van Noort, M. 2007, Sol. Phys., 246, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Soler, R., Engvold, O., et al. 2009, ApJ, 704, 870 [NASA ADS] [CrossRef] [Google Scholar]
- López Ariste, A., & Casini, R. 2002, ApJ, 575, 529 [NASA ADS] [CrossRef] [Google Scholar]
- López Ariste, A., Casini, R., Paletou, F., et al. 2005, ApJ, 621, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D., Karpen, J., Ballester, J., Schmieder, B., & Aulanier, G. 2010, Space Sci. Rev., 151, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Mein, P., & Mein, N. 1991, Sol. Phys., 136, 317 [Google Scholar]
- Merenda, L., Trujillo Bueno, J., Landi Degl’ Innocenti, E., & Collados, M. 2006, ApJ, 642, 554 [Google Scholar]
- Oliver, R. 2009, Space Sci. Rev., 149, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Orozco Suárez, D., Asensio Ramos, A., & TrujilloBueno, J. 2014, A&A, 566, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paletou, F. 1995, A&A, 302, 587 [NASA ADS] [Google Scholar]
- Parenti, S. 2014, Liv. Rev. Sol. Phys., 11, 1 [Google Scholar]
- Patsourakos, S., & Vial, J.-C. 2002, Sol. Phys., 208, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Chandra, R., Berlicki, A., & Mein, P. 2010, A&A, 514, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmieder, B., Kucera, T. A., Knizhnik, K., et al. 2013, ApJ, 777, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Tian, H., Kucera, T., et al. 2014, A&A, 569, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soler, R., & Goossens, M. 2011, A&A, 531, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soler, R., Arregui, I., Oliver, R., & Ballester, J. 2010, ApJ, 722, 1778 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Goossens, M., & Ballester, J. L. 2015, A&A, 575, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tandberg-Hanssen, E. 1995, The Nature of Solar Prominences (Dordrecht, Boston: Kluwer), Astrophys. Space Sci. Lib., 199 [Google Scholar]
- Trotta, R. 2008, Contemporary Physics, 49, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Vial, J.-C., & Engvold, O. 2015, Solar Prominences, Astrophys. Space Sci. Lib., 415 [Google Scholar]
- von Toussaint, U. 2011, Rev. Mod. Phys., 83, 943 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Spatial variation of the equilibrium mass density along the magnetic flux tube for prominence thread models with a Lorentzian profile (solid line), a Gaussian profile (dotted line), and a parabolic profile (dashed line). The ratio of centre to foot-point densities is χ = 100. |
| In the text | |
 |
Fig. 2 Dependence of the period ratio between the fundamental mode and the first overtone as a function of the density gradient parameter, χ, for a Lorentzian profile (solid line), a Gaussian profile (dotted line), and a parabolic profile (dashed line). |
| In the text | |
 |
Fig. 3 a) Posterior probability distribution for log χ under the Gaussian density gradient model, MG, for a period ratio of r = 3.0 and uncertainty given by σ = 0.2 (dashed); σ = 0.4 (solid); σ = 0.8 (dotted) and considering log χ ∈ [ 1,60 ] in the prior range. For σ = 0.4, the inferred median of the distribution is |
| In the text | |
 |
Fig. 4 a)–c) Marginal likelihoods computed using Eq. (13) for models MP, ML, and MG as a function of the period ratio for different values of the uncertainty, with σ = 0.2 (dashed), σ = 0.4 (solid), and σ = 0.8 (dotted). d) The three marginal likelihoods computed for a fixed value of σ = 0.4: p(r | MP) as a dashed line, p(r | MG) as a dotted line, and p(r | ML) as a solid line. In all plots, χ ∈ [ 2,500 ]. |
| In the text | |
 |
Fig. 5 Bayes factors computed using Eq. (12) for the model comparisons between a) the parabolic, MP, and the Gaussian, MG, density models; b) the parabolic, MP, and the Lorentzian, ML, density models; and c) the Gaussian, MG, and the Lorentzian, ML, density models, as a function of the period ratio. A value of σ = 0.4 has been considered and χ ∈ [ 2,500 ] in all computations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.