| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201425318 | |
| Published online | 29 April 2015 | |
A new quark-hadron hybrid equation of state for astrophysics
I. High-mass twin compact stars
1
Physics DepartmentFaculty of Science, University of Zagreb,
Bijenička c. 32, 10000
Zagreb, Croatia
e-mail:
sanjinb@phy.hr
2
Department of Physics, The University of Tokyo,
7-3-1 Hongo, Bunkyo-ku,
113-0033
Tokyo,
Japan
3
Institute for Theoretical Physics, University of
Wrocław, Pl. M. Borna
9, 50-204
Wroclaw,
Poland
4
Bogoliubov Laboratory for Theoretical Physics, Joint Institute for
Nuclear Research, 141980
Dubna,
Russia
5
Instituto de Física, Universidad Autónoma de San Luis Potosí,
S.L.P., 78290
México,
Mexico
6
GSI Helmholtzzentrum für Schwerionenforschung GmbH,
Planckstraße 1, 64291
Darmstadt,
Germany
Received: 11 November 2014
Accepted: 3 March 2015
Aims. We present a new microscopic hadron-quark hybrid equation of state model for astrophysical applications, from which compact hybrid star configurations are constructed. These are composed of a quark core and a hadronic shell with a first-order phase transition at their interface. The resulting mass-radius relations are in accordance with the latest astrophysical constraints.
Methods. The quark matter description is based on a quantum chromodynamics (QCD) motivated chiral approach with higher-order quark interactions in the Dirac scalar and vector coupling channels. For hadronic matter we select a relativistic mean-field equation of state with density-dependent couplings. Since the nucleons are treated in the quasi-particle framework, an excluded volume correction has been included for the nuclear equation of state at suprasaturation density which takes into account the finite size of the nucleons.
Results. These novel aspects, excluded volume in the hadronic phase and the higher-order repulsive interactions in the quark phase, lead to a strong first-order phase transition with large latent heat, i.e. the energy-density jump at the phase transition, which fulfils a criterion for a disconnected third-family branch of compact stars in the mass-radius relationship. These twin stars appear at high masses (~2 M⊙) that are relevant for current observations of high-mass pulsars.
Conclusions. This analysis offers a unique possibility by radius observations of compact stars to probe the QCD phase diagram at zero temperature and large chemical potential and even to support the existence of a critical point in the QCD phase diagram.
Key words: stars: neutron / stars: interiors / dense matter / equation of state
© ESO, 2015
1. Introduction
The physics of compact stars is an active subject of modern nuclear astrophysics research since it allows the state of matter to be probed at conditions that are currently inaccessible in high-energy collider facilities: extremes of baryon density at low temperature. It provides one of the strongest observational constraints on the zero-temperature equation of state (EoS) by recent high-precision mass measurement of high-mass pulsars by Demorest et al. (2010) and Antoniadis et al. (2013). Any scenarios for the existence of exotic matter and a phase transition at high density that tend to soften the EoS may be abandoned unless they provide stable compact star configurations with a mass not less than 2 M⊙. There are still several possibilities for which it is hard or impossible to detect quark matter in compact stars, namely when a) the phase transition occurs at densities that are too high, exceeding the central density of the maximum mass configuration; b) the transition only occurs very close to the maximum mass, beyond the limit of masses for observed high-mass pulsars; or when c) the transition is a crossover (or very close to it) so that the hybrid star characteristics is indistinguishable from that of pure neutron stars. The last case has been dubbed the “masquerade” problem Alford et al. (2005). This case seems to be characteristic of the use of modern chiral quark models with vector meson interactions Bratovic et al. (2013) which are very similar in their behaviour to standard nuclear EoS like APR (Akmal et al. 1998) or DBHF (Fuchs 2006) in the transition region (see e.g. Klähn et al. 2007, 2013). However, the opposite case is also possible: when the phase transition to quark matter is accompanied by a large enough binding energy release, corresponding to a jump in density and thus compactness of the star, an instability may be triggered that will eventually result in the emergence of a third family of compact stellar objects, in addition to white dwarfs and neutron stars. The existence of such a branch of supercompact stellar objects that is disconnected from the neutron star sequence has long been speculated in different contexts related to phase transitions in dense matter (cf. Gerlach 1968; Kämpfer 1981; Schertler et al. 2000; Glendenning & Kettner 2000). This phenomenon has been studied as a consequence of the appearance of pion and kaon condensates by Kämpfer (1981) and Banik & Bandyopadhyay (2001), respectively; hyperons have been studied by Schaffner-Bielich et al. (2002); and quark matter has been studied by Glendenning & Kettner (2000), Schertler et al. (2000), Fraga et al. (2002), Banik & Bandyopadhyay (2003), Agrawal & Dhiman (2009), and Agrawal (2010). All the results of these early studies, however, could be ruled out by the recent observation of high-mass pulsars. The question arose whether the twin star phenomenon as an indicator for a first-order phase transition could also concern compact stars with masses as high as 2 M⊙. If answered positively, the observation of significantly different radii for high-mass pulsars of the same mass would also allow conclusions for isospin symmetric matter as probed in heavy-ion collisions.
The ongoing heavy-ion programs at the collider facilities at RHIC (US) and LHC at CERN in Geneva (Switzerland), combined with the success of modern lattice quantum chromodynamics (QCD), did lead to the result that the nature of the QCD transition at vanishing chemical potential and finite temperature is a crossover. The physics of the QCD phase diagram at finite chemical potential and finite temperatures will be the subject of research within the future high-energy facilities at FAIR in Darmstadt (Germany) and NICA in Dubna (Russia). One of their main goals is to find a critical endpoint (CEP) of first-order transitions or indications for a first-order phase transition at high baryon density like signatures for a quark-hadron mixed phase. In general, a phase transition in isospin asymmetric stellar matter is directly related to the corresponding phase transition in symmetric matter, and therefore relevant to the understanding of the QCD phase diagram (cf. Fukushima & Sasaki 2013; Fukushima 2014). Since increasing the isospin asymmetry would result in lowering the temperature of the CEP to zero (Ohnishi et al. 2011) the detection of first-order phase transition signals in zero temperature asymmetric compact star matter like the mass twin phenomenon would thus prove the existence of at least one CEP in the QCD phase diagram Alvarez-Castillo & Blaschke (2013), Blaschke et al. (2013a). Unfortunately, heavy-ion collision experiments probe matter with only slight isospin asymmetry of about 60% neutron excess and hence cannot provide constraints for larger isospin asymmetry or even β-equilibrium (>90 % neutron excess) relevant for compact star phenomenology.
The major ingredient of compact star physics is the zero-temperature EoS in β-equilibrium (for recent works, cf. Steiner et al. 2013; Masuda et al. 2013; Orsaria et al. 2013; Alford et al. 2013; Hebeler et al. 2013; Inoue et al. 2013; Klähn et al. 2013; Fraga et al. 2013; Yasutake et al. 2014; Yamamoto et al. 2014). More precisely, hybrid EoS can be decomposed into three parts: (a) low-density nuclear matter; (b) high-density exotic matter such as hyperons or quarks; (c) the phase transition region between low- and high-density parts. The conditions for the transition depend on details of the underlying microscopic descriptions of matter. For the EoS to yield a third family and/or the twin phenomenon, the following two conditions should be fulfilled (for details, see Haensel et al. 2007; Read et al. 2009; Zdunik & Haensel 2013; Alford et al. 2013):
-
(1)
The latent heat of the phase transition should fulfil a constraint Δε > Δεmin (Haensel et al. 2007; Zdunik & Haensel 2013; Alford et al. 2013), where Δεmin ~ 0.6εcrit for the schematic hybrid EoS investigated in Alford et al. (2013) and Alvarez-Castillo & Blaschke (2013) with εcrit being the critical energy density for the onset of the transition.
-
(2)
The high-density part of the EoS should be sufficiently stiff.
The third family of compact objects is attained via an unstable branch, which can be realized by a soft EoS in the transition region, ensured by condition (1). Condition (2) is necessary for the core matter to withstand the pressure from the hadronic shell and thus to provide stability for the new, disconnected hybrid star branch.
Confirming the existence of high-mass twins represents an outstanding challenge for observational campaigns to develop precise radius measurements for compact stellar objects (cf. Mignani et al. 2012; Gendreau et al. 2012; Miller 2013). If detected, the twin phenomenon would be a compelling astrophysical signature of a strong first-order phase transition in the QCD phase diagram at zero temperature and thus strong evidence for the presence of at least one critical end point. By invoking that the high-mass pulsars PSR J1614-2230 by Demorest et al. (2010) and PSR J0348+0432 Antoniadis et al. (2013), with their precisely measured masses 1.97 ± 0.04 M⊙ and 2.01 ± 0.04 M⊙, respectively, could be such twin stars, we predict in this work that their radii should differ at least by about 1 km (depending on the model details). It remains to be shown whether these values are within the capabilities of future experimental X-ray satellite missions like the Neutron Star Interior Composition Explorer (NICER)1, the Nuclear Spectroscopic Telescope Array (NUSTAR)2, and/or the Square Kilometer Array (SKA)3.
In this work we present a microscopically founded example for the class of hybrid EoS that fulfil criteria (1) and (2) for the occurrence of a third family of compact stars based on a first-order phase transition from hadronic matter to quark matter. In our case, the nuclear matter phase is described by a relativistic mean-field (RMF) model with density-dependent meson-nucleon couplings introduced in Typel & Wolter (1999) using the DD2 parametrization from Typel et al. (2010) with finite-volume modifications. The quark matter phase is given by a Nambu-Jona-Lasinio model (NJL) with higher-order quark interactions, as introduced in Benic (2014). For the phase transition between hadronic and quark matter phases we apply a Maxwell construction. The resulting quark-hadron hybrid EoS allows for massive twin star configurations for which their gravitational masses are in agreement with the present 2 M⊙ constraint set by Demorest et al. (2010) and Antoniadis et al. (2013).
The paper is organized as follows. In Sect. 2 we introduce our new quark-hadron hybrid EoS and in Sect. 3 we discuss its characteristic features such as excluded volume, mass-radius relations, and twin configurations. The paper closes with the summary in Sect. 4.
2. Model equation of state for massive twin phenomenon
For quark matter at high densities we employ the recently proposed NJL-based model of Benic (2014). For the low-density region we use the nuclear RMF EoS (Typel & Wolter 1999) with the well-calibrated DD2 parametrization of Typel et al. (2010). In order to maximize the latent heat at the phase transition, we correct the standard DD2 EoS by accounting for an excluded volume of the nucleons that results from Pauli blocking due their quark substructure. The latter aspect will be introduced in the following section.
2.1. Excluded nucleon volume in the hadronic equation of state
The composite nature of nucleons can be modelled by the excluded-volume mechanism as discussed by e.g. Rischke et al. (1991) in the context of RMF models. Considering nucleons as hard spheres of volume Vnuc, the available volume Vav for the motion of nucleons is only a fraction Φ = Vav/V of the total volume V of the system. The available volume fraction can be written as 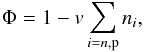 (1)with the nucleon number densities ni and the volume parameter
(1)with the nucleon number densities ni and the volume parameter 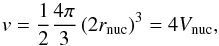 (2)if we assume identical radii rnuc = rn = rp of neutrons and protons. The total hadronic pressure and energy density are given by the relations
(2)if we assume identical radii rnuc = rn = rp of neutrons and protons. The total hadronic pressure and energy density are given by the relations 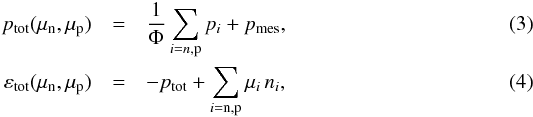 with contributions from nucleons and mesons. They depend on the nucleon chemical potentials μn and μp. The nucleonic pressures are given by
with contributions from nucleons and mesons. They depend on the nucleon chemical potentials μn and μp. The nucleonic pressures are given by 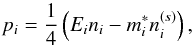 (5)with the nucleon number densities and scalar densities
(5)with the nucleon number densities and scalar densities ![\begin{eqnarray} n_{i} &=& \frac{\Phi}{3\pi^{3}} k_{i}^{3}, \\ n_{i}^{(s)} &=& \frac{\Phi m_{i}^{\ast}}{2\pi^{2}} \left[ E_{i} k_{i} - \left( m_{i}^{\ast} \right)^{2} \ln \frac{k_{i}+E_{i}}{m_{i}^{\ast}}\right], \end{eqnarray}](/articles/aa/full_html/2015/05/aa25318-14/aa25318-14-eq23.png) that contain the energies
that contain the energies 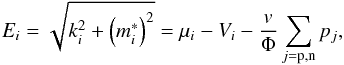 (8)as well as Fermi momenta ki and effective masses
(8)as well as Fermi momenta ki and effective masses 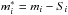 . The vector potentials Vi, scalar potentials Si and the mesonic contribution pmes to the total pressure have the usual form of RMF models with density-dependent couplings (for more details, see Typel & Wolter 1999).
. The vector potentials Vi, scalar potentials Si and the mesonic contribution pmes to the total pressure have the usual form of RMF models with density-dependent couplings (for more details, see Typel & Wolter 1999).
In conventional RMF models the in-medium nucleon-nucleon interaction is modelled by the exchange of (σ, ω, and ρ) mesons between pointlike nucleons. The excluded volume causes an additional effective repulsion between the nucleons. Hence, the parameters of the RMF model have to be refitted in order to retain the characteristic properties of nuclear matter. The parameters of the nucleon-meson couplings in the DD2 RMF model were determined by fitting to properties of finite nuclei (for details, see Typel et al. 2010). This approach leads to very satisfactory results all over the nuclear chart and gives nuclear matter parameters that are consistent with current experimental constraints. In Table 1 the parameters of the new parametrization DD2-EV with excluded-volume effects are given assuming a volume parameter v = (1 / 0.35) fm3. This corresponds to a nucleon radius of rnuc ≈ 0.55 fm. See Typel et al. (2010) for the definition of the quantities in the table and their relation to the coupling functions. The saturation density nsat and the particle masses are not changed compared to the original DD2 parametrization. The DD2-EV parameters were determined such that the binding energy per nucleon E/A, the compressibility K, the symmetry energy J, and the symmetry energy slope parameter L are also identical to that of the DD2 effective interaction. For the hadronic EoS we use the original DD2 parametrization without excluded-volume effects at baryon densities below the saturation density nsat of the model since these densities are well tested in finite-nucleus calculations. At densities above nsat we replace the DD2 model by the DD2-EV parametrization with excluded-volume corrections. The maximum baryon density that can be described by this model is nmax = 1 /v = 0.35 fm-3 owing to the choice of the volume parameter v. At this density the pressure diverges and the transition to quark matter has to start below nmax. In stellar matter the usual contributions to the pressure and energy density of the electrons are added to the hadronic part. Requiring charge neutrality, i.e. ne = np and β equilibrium, where μn = μp + μe, the pressure and energy density become functions of a single quantity, the baryon chemical potential μB = μn.
The expected transition from hadronic to quark matter at zero temperature with increasing density is still lacking a full microscopic theoretical description from first principles. In particular, reliable models with both hadronic and quark degrees of freedom are not available. Thus, a phase transition construction with separate models for both phases has to be employed. The critical chemical potential, the type of phase transition, and the extension of a possible mixed phase are not known. The aim of our approach for the EoS is to provide a reasonable microscopic model that allows for an extended mixed phase of hadrons and quarks with a large latent heat. This condition governs the choice of the volume parameter v and corresponding small maximum density nmax. It does not mean that nucleons cannot be found at higher densities. They exist up to a density of 0.404 fm-3 in beta equilibrium in the mixed phase. It is not possible to identify the relevant degrees of freedom unambiguously in a dense medium. From a more fundamental point of view, the quark substructure of nucleons has to be considered. It leads to strong repulsion at high densities due to the action of the Pauli exclusion principle on the quark level.
Parameters of the DD2-EV model.
2.2. NJL model with 8-quark interactions
In order to describe cold quark matter that is significantly stiffer than the ideal gas, we employ the recently developed generalization of the NJL model by Benic (2014), which includes 8-quark interactions in both Dirac scalar and vector channels (NJL8). The mean-field thermodynamic potential of the two-flavor NJL8 model is given as ![\begin{eqnarray} \Omega &=& U -2 N_{\rm c}\sum_{f={\rm u,d}} \left[\frac{1}{2\pi^2}\int_0^\Lambda {\rm d} p\, p^2 E_f -\frac{1}{48\pi^2}\left\{\left(2\tilde{\mu}_f^3-5M_f^2\tilde{\mu}_f\right) \phantom{\left(\frac{\sqrt{\tilde{\mu}_f^2-M_f^2}+\tilde{\mu}_f}{M_f}\right)} \right.\right. \nonumber\\ &&\left. \left. \times\sqrt{\tilde{\mu}_f^2-M_f^2}+3M_f^4\ln\left(\frac{\sqrt{\tilde{\mu}_f^2-M_f^2}+\tilde{\mu}_f}{M_f}\right)\right\} \right]-\Omega_0 , \label{eq:pot} \end{eqnarray}](/articles/aa/full_html/2015/05/aa25318-14/aa25318-14-eq66.png) (9)with
(9)with 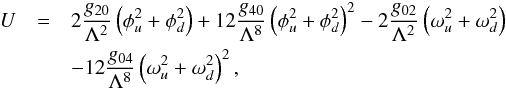 (10)and energy-momentum relation,
(10)and energy-momentum relation, 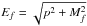 , with
, with 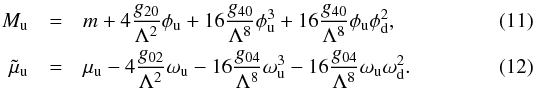 Expressions for Md and
Expressions for Md and 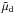 are obtained by cyclic permutation of indices in (11)and (12), respectively. The model parameters are the 4-quark scalar and vector couplings g20 and g02, the 8-quark scalar and vector couplings g40 and g04, as well as the current quark mass m and the momentum cutoff Λ, which is placed on the divergent vacuum energy. The constant Ω0 ensures zero pressure in the vacuum.
are obtained by cyclic permutation of indices in (11)and (12), respectively. The model parameters are the 4-quark scalar and vector couplings g20 and g02, the 8-quark scalar and vector couplings g40 and g04, as well as the current quark mass m and the momentum cutoff Λ, which is placed on the divergent vacuum energy. The constant Ω0 ensures zero pressure in the vacuum.
The model is solved by means of finding the extremum value of the thermodynamic potential (9)with respect to the mean-fields (X = φu,φd,ωu,ωd), i.e. 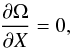 (13)and the pressure is obtained from the relation p = −Ω.
(13)and the pressure is obtained from the relation p = −Ω.
In this work we use the parameter set of Kashiwa et al. (2007), g20 = 2.104, g40 = 3.069, m = 5.5 MeV, and Λ = 631.5 MeV. Furthermore, the vector channel strengths are quantified by the ratios  (14)Here, we will concentrate on the parameter space where η2 is small and use η4 to control the stiffness of the EoS. We note that small η2 ensures an early onset of quark matter, i.e. it refers to low densities for the onset of quark matter (depending on the stiffness of the nuclear EoS at corresponding densities).
(14)Here, we will concentrate on the parameter space where η2 is small and use η4 to control the stiffness of the EoS. We note that small η2 ensures an early onset of quark matter, i.e. it refers to low densities for the onset of quark matter (depending on the stiffness of the nuclear EoS at corresponding densities).
Within this approach we can calculate the partial pressures pf and densities nf = ∂pf/∂μf for f = (u,d). In neutron stars, neutrino-less β-equilibrium is typically fulfilled, i.e. the corresponding equilibrium weak process in nuclear matter is the nuclear β-decay: 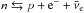 . In quark matter, it is replaced by
. In quark matter, it is replaced by 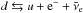 , and hence here the following relation holds between the contributing chemical potentials, μd = μu + μe (neutrino escapes from the star, so its chemical potential is set to zero). Moreover, the following condition,
, and hence here the following relation holds between the contributing chemical potentials, μd = μu + μe (neutrino escapes from the star, so its chemical potential is set to zero). Moreover, the following condition, 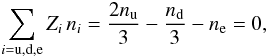 (15)ensures local charge neutrality. The total pressure in the quark phase is then given by the sum of the partial pressures, p = pu + pd + pe, with electron pressure pe. The latter is calculated based on the relativistic and degenerate Fermi gas. Moreover, the baryon chemical potential and the baryon density in the quark phase (Q) and hadronic phase (H) are obtained as
(15)ensures local charge neutrality. The total pressure in the quark phase is then given by the sum of the partial pressures, p = pu + pd + pe, with electron pressure pe. The latter is calculated based on the relativistic and degenerate Fermi gas. Moreover, the baryon chemical potential and the baryon density in the quark phase (Q) and hadronic phase (H) are obtained as 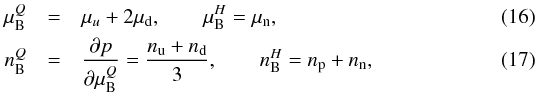 with neutron and proton chemical potentials (μn,μp) and densities (nn,np). When no confusion arises, indices Q and H will be omitted for simplicity.
with neutron and proton chemical potentials (μn,μp) and densities (nn,np). When no confusion arises, indices Q and H will be omitted for simplicity.
For the construction of the phase transition, we apply Maxwell’s condition in the pressure-chemical potential plane, i.e. pressures in quark and hadronic phases must be equal 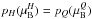 at coexistence
at coexistence 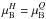 , in order to ensure thermodynamic consistency. This approach is tantamount to assuming a large surface tension at the hadron-quark interface. The critical baryon chemical potential is obtained by matching the pressures from the hadronic (DD2-EV) and quark (NJL8) EOSs. With this setup, a first-order phase transition is obtained by construction with a significant jump in baryon density and energy density as illustrated in Fig. 1. It will be discussed further in Sect. 3.
, in order to ensure thermodynamic consistency. This approach is tantamount to assuming a large surface tension at the hadron-quark interface. The critical baryon chemical potential is obtained by matching the pressures from the hadronic (DD2-EV) and quark (NJL8) EOSs. With this setup, a first-order phase transition is obtained by construction with a significant jump in baryon density and energy density as illustrated in Fig. 1. It will be discussed further in Sect. 3.
 |
Fig. 1 Upper panel: Maxwell construction in the P − μB plane for the DD2 EoS (brown solid line) and the NJL8 EoS (red dashed line) for η2 = 0.08, η4 = 0.0, as well as the DD2-EV EoS (violet solid line) and the same NJL8 EoS parametrization. Lower panel: same construction as in the upper panel for the corresponding ε − μB plane. (Colour online.) |
3. Results
The model parameters used to calculate the hybrid EoS are as follows. We modify the DD2 EoS with the excluded volume mechanism as described in Sect. 2.1 (DD2-EV). The high-density part is given by the NJL8 EoS (9), where we use η2 = 0.08 and consider η4 as a free parameter.
The rationale behind our choice of a low value for η2 and the particular value for v is at this stage purely phenomenological. The parameter η2 controls both the onset of quark matter and the stiffness of the quark EoS. We note that a measure for the stiffness (or softness) of the EoS is the speed of sound cs defined via 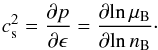 (18)When comparing two EoS, the stiffer one has the steeper slope of p(ε), while the slope of n(μB) is lower. In the present model, a larger value for η2 would result in more similar quark and hadronic EoS, and hence disfavour the anticipated condition of maximized latent heat at the phase transition. Since a small value of η2 ensures a low onset of quark matter, the nuclear EoS is insensitive to the detailed behaviour of the Φ function close to the maximum density nmax. Thus we use the traditional linear dependence (1)on the nucleon densities.
(18)When comparing two EoS, the stiffer one has the steeper slope of p(ε), while the slope of n(μB) is lower. In the present model, a larger value for η2 would result in more similar quark and hadronic EoS, and hence disfavour the anticipated condition of maximized latent heat at the phase transition. Since a small value of η2 ensures a low onset of quark matter, the nuclear EoS is insensitive to the detailed behaviour of the Φ function close to the maximum density nmax. Thus we use the traditional linear dependence (1)on the nucleon densities.
 |
Fig. 2 Upper panel: hybrid EoS built from DD2-EV and NJL8 with phase transition via the Maxwell construction, for the NJL8 parameter η2 = 0.08 and varying η4 from 0.0–30. Lower panel: squared speed of sound for these hybrid EoS. For comparison, in both panels the hadronic EoS DD2 is shown (solid brown line). (Colour online.) |
3.1. Hybrid equation of state
The new quark-hadron hybrid EoS, based on DD2-EV and NJL8, is shown in the upper panel of Fig. 2 illustrating the pressure-energy density plane, for fixed η2 = 0.08 and varying vector-coupling parameters η4. We note that with increasing vector coupling parameters, η2 and η4, the sound speed rises (see lower panel of Fig. 2). We also note that the different mass-dimension of the 4-quark and 8-quark vector operators separates the region in density in which the respective operator influences the speed of sound. In particular, while η2 controls the stiffness of the EoS in the low-density region, η4 stiffens the EoS in the high-density region. This can be seen from Fig. 2 where η2 = 0.08 and η4 is varied from η4 = 0.0 (red dashed line) to η4 = 30.0 (violet solid line). In addition to the selected values shown in Fig. 2, we explored the total parameter range η4 = 0.0−30.0 in steps of Δη4 = 1.0. Above the maximum value of η4 = 30.0 the transition from DD2-EV to NJL8 violates the requirement of causality (Fig. 2), which takes place at ϵ ≃ 240 MeV fm-3. We have checked that in all our cases the causality limit is reached only at energy densities beyond which the mass-radius sequences turn unstable.
Exploring the available parameter spaces in both hadronic and quark matter phases, we have found the maximized latent heat in the combination of two aspects: (a) taking into account finite-sized effects of the nucleons using the excluded volume and (b) applying small values of η2 for the NJL8 quark-matter model. This is illustrated in Fig. 1 where we compare the phase transition constructions from DD2 and DD2-EV to NJL8 with η2 = 0.08 and η4 = 0.0. The upper panel of Fig. 1 shows pressure vs. chemical potential, from which it becomes clear that our excluded volume approach reduced the critical chemical potential for the onset of quark matter. Furthermore, it also increases the differences between the slopes of the pressure curves for hadronic and quark EoS at the phase transition. The excluded volume results in an increased latent heat, Δε, which is shown in the bottom panel of Fig. 1. For the NJL8 parameters explored here (η2 = 0.08, η4 = 0.0), we find Δε ≃ 0.34εcrit for the transition with DD2 and Δε ≃ 0.81εcrit for the transition with DD2-EV.
With the given choice of nuclear matter parameters, the excluded volume correction generates a stiff nuclear EoS at suprasaturation densities, close to the limit of causality, i.e. 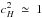 . Furthermore, the choice of small η4 ensures a soft quark matter EoS at the phase transition densities, i.e.
. Furthermore, the choice of small η4 ensures a soft quark matter EoS at the phase transition densities, i.e. 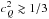 . The resulting maximized jump in energy density at the phase transition from DD2-EV to NJL8 is illustrated in Fig. 2 for the parameter range η4 = 0.0−30.0, for which we obtain Δε ≃ (0.81−0.70)εcrit.
. The resulting maximized jump in energy density at the phase transition from DD2-EV to NJL8 is illustrated in Fig. 2 for the parameter range η4 = 0.0−30.0, for which we obtain Δε ≃ (0.81−0.70)εcrit.
Our approach for the construction of a quark-hadron phase transition with large latent heat extends beyond the phenomenological model of Zdunik & Haensel (2013) and Alford et al. (2013), known as ZHAHP. In their approach, the latent heat Δε is a free parameter and the quark EoS is defined by a constant speed of sound 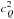 . Nevertheless, in providing as one of the major requirements for the existence of the third family the rule of thumb that the latent heat is around Δε ≃ 0.6, the ZHAHP approach proves to be extremely practical (see e.g. Alvarez-Castillo & Blaschke 2013). However, it is unphysical to treat
. Nevertheless, in providing as one of the major requirements for the existence of the third family the rule of thumb that the latent heat is around Δε ≃ 0.6, the ZHAHP approach proves to be extremely practical (see e.g. Alvarez-Castillo & Blaschke 2013). However, it is unphysical to treat 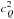 and Δε as mutually independent parameters. Within a microscopic description for the EoS both quantities are always correlated, for example, the relative stiffness of the EoS between hadronic and quark phases defines the latent heat
and Δε as mutually independent parameters. Within a microscopic description for the EoS both quantities are always correlated, for example, the relative stiffness of the EoS between hadronic and quark phases defines the latent heat 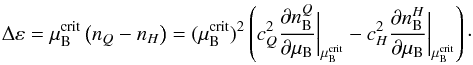 (19)In the above formula all the quantities are evaluated at the critical chemical potential of the transition
(19)In the above formula all the quantities are evaluated at the critical chemical potential of the transition 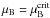 .
.
3.2. Mass-radius relationship
 |
Fig. 3 Mass-radius relations for our hybrid DD2-EV NJL8 EoSs for constant η2 = 0.08 and varying η4 = 0.0−30.0. Horizontal colour bands mark the current 2 M⊙ constraints from high-precision mass measurement of high-mass pulsars, PSR J1614–2230 (red) by Demorest et al. (2010) and PSR J0348+0432 (blue) by Antoniadis et al. (2013). For comparison with DD2-EV, the mass-radius curve for the hadronic EoS DD2 is also shown (solid brown line). Furthermore, we show results from the mass-radius analysis of the millisecond pulsar PSR J0437–4715 by Bogdanov (2013), and constraints from the X-ray spectroscopic study of the thermally emitting isolated neutron star RX J1856.5–3754 by Hambaryan et al. (2014). (Colour online.) |
Based on our novel quark-hadron hybrid EoS we calculate the mass-radius relations from solutions of the Tolman-Oppenheimer-Volkoff (TOV) equations. For a selection of quark matter parameters, i.e. constant η2 = 0.08 and varying η4 = 0.0−30.0, we show the resulting mass-radius curves in Fig. 3. Horizontal coloured bands mark the constraints from high-precision mass measurements of the high-mass pulsars PSR J1614-2230 and PSR J0348+0432 by Demorest et al. (2010) and Antoniadis et al. (2013), respectively. In Fig. 3, the green shaded vertical bands mark the results of the mass-radius analysis of the millisecond pulsar PSR J0437-4715 by Bogdanov (2013), with 1σ, 2σ, and 3σ confidence level assuming a mass of 1.76 M⊙. These data form the basis of a new Bayesian analysis of constraints for hybrid EoS parametrizations Alvarez-Castillo et al. (2014) which ought to supersede the first study of this kind by Steiner et al. (2010). In addition, we show data from the X-ray spin phase-resolved spectroscopic study of the thermally emitting isolated neutron star RX J1856.5-3754 by Hambaryan et al. (2014), indicating potential compactness constraints. The solid brown line in Fig. 3 corresponds to the purely hadronic EoS DD2, i.e. without excluded volume corrections, for comparison with DD2-EV.
The excluded volume approach introduced here results in large neutron star radii, R ≃ 14.75 km for M = 1.5 M⊙ in comparison to DD2 (R ≃ 13 km). It can be understood in terms of the significant stiffening of the nuclear EoS above saturation density (nsat = 0.149 fm-3). At the phase transition the stellar configuration proceeds from the stable hadronic branch to an unstable branch, marked by dotted lines in Fig. 3. The mass-radius coordinates where this happens are defined by the critical chemical potential 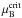 , or density
, or density 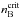 , of the corresponding hybrid EoS. We note that for all hybrid EoS explored in this study, the critical density is
, of the corresponding hybrid EoS. We note that for all hybrid EoS explored in this study, the critical density is 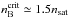 . Specifically, the initially stable hadronic configuration at
. Specifically, the initially stable hadronic configuration at 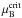 grows by a tiny amount of mass (~5 × 10-4 M⊙) while the radius remains constant and becomes a still stable hybrid branch. We estimate the size of the resulting quark core to be ~80 cm with significantly increased density. Only after that, the configuration turns to the unstable branch during which the quark core grows. The unstable branch reverts to another stable branch due to the strong repulsive force 8-quark interaction of the NJL8 EoS at high densities.
grows by a tiny amount of mass (~5 × 10-4 M⊙) while the radius remains constant and becomes a still stable hybrid branch. We estimate the size of the resulting quark core to be ~80 cm with significantly increased density. Only after that, the configuration turns to the unstable branch during which the quark core grows. The unstable branch reverts to another stable branch due to the strong repulsive force 8-quark interaction of the NJL8 EoS at high densities.
Our selection of nuclear and quark matter parameters allows not only for high-mass hadronic and quark configurations, in agreement with the 2 M⊙ pulsar data from Demorest et al. (2010) and Antoniadis et al. (2013), but also for the consistent transition from the hadronic branch to the quark-hadron hybrid branch. Here we identify the latter as the third family of compact stellar objects, with maximum masses in the range Mmax = 1.92−2.30 M⊙, which are above those of the underlying hadronic model DD2-EV. Moreover, we confirm that all hybrid EoS fulfil the condition of causality, i.e. the maximum speed of sound of the hybrid star configurations is in the range 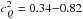 . In addition, our results are in agreement with the mass-radius analysis of the millisecond pulsar PSR J0437−4715 by Bogdanov (2013) within 3σ confidence level (see the green vertical bands in Fig. 3), and with the compactness study of the isolated neutron star RX J1856.5–3754 by Hambaryan et al. (2014; see the yellow box in Fig. 3) where a radius of around 14−18 km at a mass range of 1.5−1.8 M⊙ was found within the 1σ confidence level (see also Trümper 2011).
. In addition, our results are in agreement with the mass-radius analysis of the millisecond pulsar PSR J0437−4715 by Bogdanov (2013) within 3σ confidence level (see the green vertical bands in Fig. 3), and with the compactness study of the isolated neutron star RX J1856.5–3754 by Hambaryan et al. (2014; see the yellow box in Fig. 3) where a radius of around 14−18 km at a mass range of 1.5−1.8 M⊙ was found within the 1σ confidence level (see also Trümper 2011).
3.3. Radii difference of the high-mass twins
The most striking consequence of a strong first-order phase transition in compact star matter is the possible existence of a third family of compact stars, a branch of stable hybrid star configurations in the mass-radius diagram disconnected from the second family branch of ordinary hadronic stars entailing the twin phenomenon: for a certain range of masses there are pairs of stars (twins) with the same gravitational mass but different internal structure. In order to quantify the unlikeness of the twins as a measure of the pronouncedness of the phase transition we consider the radii difference δR = Rmax − Rtwin between the radius at the maximum mass Mmax on the hadronic branch and that of the corresponding mass twin on the third family branch of hybrid star configurations. In Table 2, we list δR at fixed η2 = 0.08 for selected values of the dimensionless 8-quark interaction strength η4 in the range where it allows for the twin phenomenon (see also Fig. 3 for comparison).
Parameters of high-mass twin neutron star configurations for the relevant range of dimensionless 8-quark interaction couplings η4 in the vector meson channel at fixed η2 = 0.08.
The largest radii difference we obtain for η4 = 0.0, however, is for M below the current maximum mass constraint of Demorest et al. (2010) and Antoniadis et al. (2013). In agreement with these latter constraints are the parametrizations η4 = 5.0−30.0, with δR = 1.16−0.13 km. The reduced radii difference for increasing η4 can be understood not only from the stiffening of the quark matter EoS at high densities, but also from the reduced latent heat Δε, i.e. the reduced jump in energy density going from the hadronic EoS to the hybrid EoS (see Fig. 2), also listed in Table 2. From the required condition Δε> 0.6εcrit, it becomes clear from Table 2 that twin configurations are only obtained for η4 = 0.0−30.0. For η4 ≳ 30.0 the phase transition to quark matter proceeds without developing a disconnected third family branch; all configurations on this sequence up to the maximum mass are stable (see also Fig. 3).
4. Conclusions
Compact stars harbour central densities in excess of nuclear saturation density, conditions that are currently inaccessible in nuclear high-energy experiments. Their study contributes to a key direction of research in nuclear and hadron physics, i.e. the possible transition from a state of matter with nuclear degrees of freedom to a deconfined state with quark and gluon degrees of freedom. Despite the success of lattice QCD at vanishing chemical potential and high temperatures identifying the nature of the transition as crossover, for finite chemical potentials only phenomenological models can be used (cf. Lattimer & Prakash 2010; Klähn et al. 2013; Buballa et al. 2014, and references therein). Such models, in particular with the phase transition from nuclear to quark matter, have also been very useful in astrophysical applications, e.g. in simulations of protoneutron star cooling (cf. Pons et al. 2001; Popov et al. 2006; Blaschke et al. 2013b) and simulations of core-collapse supernovae (cf. Sagert et al. 2009; Fischer et al. 2011; Nakazato et al. 2014). It is therefore of paramount interest to develop quark-hadron hybrid models from which it is possible to deduce observables that allow us to further constrain the as yet highly uncertain QCD phase diagram, e.g. the possible existence of a critical point. This identification will be possible with the discovery of a first-order phase transition at low temperatures and large chemical potential, conditions which refer to the state of matter at compact star interiors in β-equilibrium.
In this paper, we took on this challenge and developed a novel quark-hadron hybrid EoS. It is based on the nuclear EoS DD2, which is a relativistic mean-field model with density-dependent couplings. While such models treat nucleons as point-like quasi-particles, here we also take finite size effects of the nucleons into account via an excluded-volume approach above nuclear saturation density. The excluded volume correction introduced here is an attempt to account for the Pauli blocking at the quark level. In Blaschke & Röpke (1988) the authors considered Pauli quenching of nucleons as quark substructure effects on the basis of which the strong isospin-dependence has been evaluated (see also Di Toro et al. 2006, for the isospin dependence of the phase transition) and applied to obtain stable massive hybrid star solutions (see also Blaschke et al. 1990). At the current status our excluded volume approach is still quite basic and will be improved in upcoming studies. For the quark matter EoS we apply the NJL model formalism, including higher-order repulsive quark interactions. This become dominant in particular at high densities. We note that the current status of research for the vector interactions in quark matter remains unsettled (for details, see e.g. Steinheimer & Schramm 2014; Sugano et al. 2014) and its impact on the possible existence of the CEP remains an open question (see Bratovic et al. 2013; Contrera et al. 2014; Hell et al. 2013, and references therein). The quark-hadron phase transition has been constructed applying the Maxwell criterion, which results in a strong first-order phase transition. The excluded volume on the hadronic side in combination with the stiff quark EoS results not only in an early onset of quark matter, but also in a large latent heat at the phase transition.
From our novel hybrid EoS which we provide to the community for different values of the higher-order quark interaction strength, we have constructed the mass-radius relations based on TOV solutions. Our main findings can be summarized as follows:
The excluded volume for the high-density nuclear EoS results in large radii for intermediate-mass neutron stars.
The transition to quark matter results in a first stable hybrid configuration with a tiny quark core, which then turns to the unstable branch.
The unstable branch reverts to a stable hybrid branch owing to the strong repulsive higher-order quark interactions, which we identity as third family of compact stars.
For all configurations explored in this study, we find that the maximum masses belong to the stable hybrid branch and that all EoS remain causal. Moreover, most of our parameter choices fulfil a variety of current constraints on mass-radius relations, such as large maximum masses around 2 M⊙ (Demorest et al. 2010; Antoniadis et al. 2013) and radii in the range of 14–17 km for canonical compact objects of M ≃ 1.7 M⊙ (Bogdanov 2013; Hambaryan et al. 2014).
From an observational perspective, a particularly interesting consequence of a third family of compact objects is the twin phenomenon, where two stars of the same mass have different radii. In the present paper, we even found high-mass twins with M ≃ 2 M⊙ with radius differences of the order of about 1 km. It remains to be shown whether future surveys that are devoted to neutron star radii determinations, such as the X-ray satellite missions NICER, SKA, and NUSTAR, will have the required sensitivity of less than 1 km and will be able to resolve the twin phenomenon. It would, in turn, provide a unique signature of a first-order phase transition to exotic superdense matter in compact star interiors.
We note that in addition to the size of the emitting region, the main issue of the radius analyses using X-ray burst sources such as Steiner et al. (2010) and Steiner et al. (2013), is the question of the atmosphere composition. If the assumption of a hydrogen atmosphere made by Guillot & Rutledge (2014) is not correct and a helium atmosphere should instead be assumed, then the extracted radius will increase by at least 2 km, see Fig. 3 of Servillat et al. (2012). This would then be compatible with stiff neutron star EoS while the mass-radius relation extracted for the hydrogen atmosphere assumption would practically be compatible only with strange quark matter EoS models. For further details we refer to the reviews by Miller (2013) and Trümper (2011).
The aspects discussed in this paper may have important consequences when taken into account consistently in dynamical simulations of supernova collapse and explosions, binary mergers, and so on, where during the phase transition the gain in gravitational binding energy will be available to the system as heat, which in turn can trigger the local production of neutrinos as a result of the different β-equilibrium condition obtained. Furthermore, the current work improves on the previous phenomenological studies of Alford et al. (2013) and Alvarez-Castillo & Blaschke (2013), where the latent heat and the speed of sound were considered as mutually independent parameters.
Acknowledgments
We gratefully acknowledge numerous discussions and collaboration work on the topic addressed in this contribution with our colleagues, in particular with A. Ayriyan, G.A. Contrera, H. Grigorian, O. Kaczmarek, T. Klähn, E. Laermann, R. Łastowiecki, M.C. Miller, G. Poghosyan, S.B. Popov, M. Sokolowski, J. Trümper, D.N. Voskresensky and F. Weber. This research has been supported by Narodowe Centrum Nauki (NCN) within the “Maestro” programme under contract number DEC-2011/02/A/ST2/00306. The visits of S.B. and D.E.A.-C. at the University of Wroclaw were supported by the COST Action MP1304 “NewCompStar” within the STSM programme. S. B. acknowledges partial support by the Croatian Science Foundation under Project No. 8799. D.B. acknowledges support by the Polish Ministry for Science and Higher Education under grant number 1009/S/IFT/14. D.E.A.-C. is grateful for support by the Heisenberg-Landau programme for collaboration between JINR Dubna and German Universities and Institutes. T.F. is supported by the NCN within the “Sonata” programme under contract number UMO-2013/11/D/ST2/02645. S.T. acknowledges support by the Helmholtz Association (HGF) through the Nuclear Astrophysics Virtual Institute (VH-VI-417), and by the Heisenberg-Landau programme.
References
- Agrawal, B. K. 2010, Phys. Rev. D, 81, 023009 [NASA ADS] [CrossRef] [Google Scholar]
- Agrawal, B. K., & Dhiman, S. K. 2009, Phys. Rev. D, 79, 103006 [NASA ADS] [CrossRef] [Google Scholar]
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M., Braby, M., Paris, M. W., & Reddy, S. 2005, ApJ, 629, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M. G., Han, S., & Prakash, M. 2013, Phys. Rev. D, 88, 083013 [NASA ADS] [CrossRef] [Google Scholar]
- Alvarez-Castillo, D., Ayriyan, A., Blaschke, D., & Grigorian, H. 2014, ArXiv e-prints [arXiv:1408.4449] [Google Scholar]
- Alvarez-Castillo, D. E., & Blaschke, D. 2013, Proc. of 17th Conference of Young Scientists and Specialists, Dubna, April 8−12, 22, ArXiv e-prints [arXiv:1304.7758] [Google Scholar]
- Antoniadis, J., Freire, Paulo C. C., Wex, N., et al. 2013, Science, 340, 6131 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Banik, S., & Bandyopadhyay, D. 2001, Phys. Rev. C, 64, 055805 [NASA ADS] [CrossRef] [Google Scholar]
- Banik, S., & Bandyopadhyay, D. 2003, Phys. Rev. D, 67, 123003 [NASA ADS] [CrossRef] [Google Scholar]
- Benić, S. 2014, EPJ A, 50, 111 [Google Scholar]
- Blaschke, D., & Röpke, G. 1988, JINR Dubna preprint, JINR-E2-88-77 [Google Scholar]
- Blaschke, D., Kämpfer, B., & Towmasjan, T. 1990, Sov. J. Nucl. Phys., 52, 675 [Google Scholar]
- Blaschke, D., Alvarez-Castillo, D. E., & Benic, S. 2013a, PoS CPOD, 063 [Google Scholar]
- Blaschke, D., Grigorian, H., & Voskresensky, D. N. 2013b, Phys. Rev. C, 88, 065805 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bogdanov, S. 2013, ApJ, 762, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Bratovic, N., Hatsuda, T., & Weise, W. 2013, Phys. Lett. B, 719, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Buballa, M., Dexheimer, V., Drago, A., et al. 2014, J. Phys. G, 41, 123001 [NASA ADS] [CrossRef] [Google Scholar]
- Contrera, G. A., Grunfeld, A. G., & Blaschke, D. B. 2014, Phys. Part. Nucl. Lett., 11, 342 [CrossRef] [Google Scholar]
- Demorest, P., Pennucci, T., Ransom, S. M., Roberts, M. S. E., & Hessels, J. W. T. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fischer, T., Sagert, I., Pagliara, G., et al. 2011, ApJS, 194, 28 [Google Scholar]
- Fraga, E. S., Pisarski, R. D., & Schaffner-Bielich, J. 2002, Nucl. Phys. A, 702, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Fraga, E. S., Kurkela, A., & Vuorinen, A. 2014, ApJ, 781, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Fuchs, C. 2006, Prog. Part. Nucl. Phys., 56, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fukushima, K. 2014, Nucl. Phys. A, 931, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Fukushima, K., & Sasaki, C. 2013, Prog. Part. Nucl. Phys., 72, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Gendreau, K. C., et al. 2012, Proc. SPIE Space Telescopes and Instrumentation, 8443, 844313 [Google Scholar]
- Gerlach, U. H. 1968, Phys. Rev., 172, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Glendenning, N. K., & Kettner, C. 2000, A&A, 353, 795 [Google Scholar]
- Guillot, S., & Rutledge, R. E. 2014, ApJ, 796, L3 [Google Scholar]
- Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, Neutron stars 1: equation of state and structure (Heidelberg: Springer) [Google Scholar]
- Hambaryan, V., Neuhäuser, R., Suleimanov, V., & Werner, K. 2014, J. Phys. Conf. Ser., 496, 012015 [Google Scholar]
- Hebeler, K., Lattimer, J. M., Pethick, C. J., & Schwenk, A. 2013, ApJ, 773, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Hell, T., Kashiwa, K., & Weise, W. 2013, J. Mod. Phys., 4, 644 [CrossRef] [Google Scholar]
- Inoue, T., Aoki, S., Doi, T., et al. 2013, Phys. Rev. Lett., 111, 112503 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kämpfer, B. 1981, J. Phys. A, 14, L471 [CrossRef] [Google Scholar]
- Kashiwa, K., Kouno, H., Sakaguchi, T., Matsuzaki, M., & Yahiro, M. 2007, Phys. Lett. B, 647, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Klähn, T., Blaschke, D., Sandin, F., et al. 2007, Phys. Lett. B, 654, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Klähn, T., Łastowiecki, R., & Blaschke, D. 2013, Phys. Rev. D, 88, 085001 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J. M., & Prakash, M. 2010, ArXiv e-prints [arXiv:1012.3208] [Google Scholar]
- Masuda, K., Hatsuda, T., & Takatsuka, T. 2013, Prog. Theor. Phys., 073D01 [Google Scholar]
- Mignani, R. P., Zane, S., Walton, D., et al. 2012, IAU Symp., 285, 372 [NASA ADS] [Google Scholar]
- Miller, M. C. 2013, ArXiv e-prints [arXiv:1312.0029] [Google Scholar]
- Nakazato, K., Sumiyoshi, K., & Yamada, S. 2014, A&A, 558, A5 [Google Scholar]
- Ohnishi, A., Ueda, H., Nakano, T., Ruggieri, M., & Sumiyoshi, K. 2011, Phys. Lett. B, 704, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Orsaria, M., Rodrigues, H., Weber, F., & Contrera, G. A. 2013, Phys. Rev. D, 87, 023001 [NASA ADS] [CrossRef] [Google Scholar]
- Pons, J. A., Steiner, A. W., Prakash, M., & Lattimer, J. M. 2001, Phys. Rev. Lett., 86, 5223 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Popov, S. B., Grigorian, H., & Blaschke, D. 2006, Phys. Rev. C, 74, 025803 [NASA ADS] [CrossRef] [Google Scholar]
- Read, J. S., Lackey, B. D., Owen, B. J., & Friedman, J. L. 2009, Phys. Rev. D, 79, 124032 [NASA ADS] [CrossRef] [Google Scholar]
- Rischke, D. H., Gorenstein, M. I., Stoecker, H., & Greiner, W. 1991, Z. Phys. C, 51, 485 [Google Scholar]
- Sagert, I., Fischer, T., Hempel, M., et al. 2009, Phys. Rev. Lett., 102, 081101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schaffner-Bielich, J., Hanauske, M., Stöcker, H., & Greiner, W. 2002, Phys. Rev. Lett., 89, 171101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schertler, K., Greiner, C., Schaffner-Bielich, J., & Thoma, M. H. 2000, Nucl. Phys. A, 677, 463 [CrossRef] [Google Scholar]
- Servillat, M., Heinke, C. O., Ho, W. C. G., et al. 2012, MNRAS, 423, 1556 [Google Scholar]
- Steiner, A. W., Lattimer, J. M., & Brown, E. F. 2010, ApJ, 722, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, A. W., Lattimer, J. M., & Brown, E. F. 2013, ApJ, 765, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Steinheimer, J., & Schramm, S. 2014, Phys. Lett. B, 736, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Sugano, J., Takahashi, J., Ishii, M., Kouno, H., & Yahiro, M. 2014, Phys. Rev. D, 90, 037901 [NASA ADS] [CrossRef] [Google Scholar]
- Di Toro, M., Drago, A., Gaitanos, T., Greco, V., & Lavagno, A. 2006, Nucl. Phys. A, 775, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Trümper, J. E. 2011, Prog. Part. Nucl. Phys., 66, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Typel, S., & Wolter, H. H. 1999, Nucl. Phys. A, 656, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Typel, S., Röpke, G., Klähn, T., Blaschke, D., & Wolter, H. H. 2010, Phys. Rev. C, 81, 015803 [NASA ADS] [CrossRef] [Google Scholar]
- Yamamoto, Y., Furumoto, T., Yasutake, N., & Rijken, T. A. 2014, Phys. Rev. C, 90, 045805 [NASA ADS] [CrossRef] [Google Scholar]
- Yasutake, N., Łastowiecki, R., Benić, S., et al. 2014, Phys. Rev. C, 89, 065803 [NASA ADS] [CrossRef] [Google Scholar]
- Zdunik, J. L., & Haensel, P. 2013, A&A, 551, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Parameters of high-mass twin neutron star configurations for the relevant range of dimensionless 8-quark interaction couplings η4 in the vector meson channel at fixed η2 = 0.08.
All Figures
 |
Fig. 1 Upper panel: Maxwell construction in the P − μB plane for the DD2 EoS (brown solid line) and the NJL8 EoS (red dashed line) for η2 = 0.08, η4 = 0.0, as well as the DD2-EV EoS (violet solid line) and the same NJL8 EoS parametrization. Lower panel: same construction as in the upper panel for the corresponding ε − μB plane. (Colour online.) |
| In the text | |
 |
Fig. 2 Upper panel: hybrid EoS built from DD2-EV and NJL8 with phase transition via the Maxwell construction, for the NJL8 parameter η2 = 0.08 and varying η4 from 0.0–30. Lower panel: squared speed of sound for these hybrid EoS. For comparison, in both panels the hadronic EoS DD2 is shown (solid brown line). (Colour online.) |
| In the text | |
 |
Fig. 3 Mass-radius relations for our hybrid DD2-EV NJL8 EoSs for constant η2 = 0.08 and varying η4 = 0.0−30.0. Horizontal colour bands mark the current 2 M⊙ constraints from high-precision mass measurement of high-mass pulsars, PSR J1614–2230 (red) by Demorest et al. (2010) and PSR J0348+0432 (blue) by Antoniadis et al. (2013). For comparison with DD2-EV, the mass-radius curve for the hadronic EoS DD2 is also shown (solid brown line). Furthermore, we show results from the mass-radius analysis of the millisecond pulsar PSR J0437–4715 by Bogdanov (2013), and constraints from the X-ray spectroscopic study of the thermally emitting isolated neutron star RX J1856.5–3754 by Hambaryan et al. (2014). (Colour online.) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


