| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201424684 | |
| Published online | 17 March 2015 | |
New analytical and numerical models of a solar coronal loop
I. Application to forced vertical kink oscillations⋆
1 Group of Astrophysics, University of Maria Curie-Skłodowska, ul. Radziszewskiego 10, 20-031 Lublin, Poland
e-mail: kmur@kft.umcs.lublin.pl
2 Central (Pulkovo) Astronomical Observatory, Russian Academy of Sciences, St. Petersburg, Russia
3 Department of Physics, Indian Institute of Technology (Banaras Hindu University), 221005 Varanasi, India
Received: 26 July 2014
Accepted: 22 January 2015
Aims. We construct a new analytical model of a solar coronal loop that is embedded in a gravitationally stratified and magnetically confined atmosphere. On the basis of this analytical model, we devise a numerical model of solar coronal loops. We adopt this model to perform the numerical simulations of its vertical kink oscillations excited by an external driver.
Methods. Our model of the solar atmosphere is constructed by adopting a realistic temperature distribution and specifying the curved magnetic field lines that constitute a coronal loop. This loop is described by 2D, ideal magnetohydrodynamic equations that are numerically solved by the FLASH code.
Results. The vertical kink oscillations are excited by a periodic driver in the vertical component of velocity, which is acting at the top of the photosphere. For this forced driver with its amplitude 3 km s-1, the excited oscillations exhibit about 1.2 km s-1 amplitude in their velocity and the loop apex oscillates with an amplitude in displacement of about 100 km.
Conclusions. The newly devised analytical model of the coronal loops is utilized for the numerical simulations of the vertical kink oscillations, which match well with the recent observations of decayless kink oscillations excited in solar loops. The model will have further implications on the study of waves and plasma dynamics in coronal loops, revealing physics of energy and mass transport mechanisms in the localized solar atmosphere.
Key words: Sun: atmosphere / Sun: chromosphere / Sun: corona / Sun: oscillations
A movie associated to Fig. 4 is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The solar corona is a magnetically dominated and gravitationally stratified medium that can alter the scenario of magnetohydrodynamic (MHD) waves (e.g., Pascoe 2014). Among a number of magnetic structures present there, magnetic loops are considered to be major building blocks of the solar corona. They are outlined by curved and closed magnetic field lines, which are rooted in the deep atmospheric layers and are built of denser and hot plasma.
Coronal loops act as a wave guide for various kinds of MHD waves and oscillations. Among various modes, the standing, large-amplitude magnetoacoustic kink waves were detected in solar coronal loops (e.g., Aschwanden et al. 1999, 2000; Wang & Solanki 2004; Wang et al. 2008; Verwichte et al. 2009; Aschwanden & Schrijver 2011; White et al. 2012; Srivastava & Goossens 2013, and references therein). These transverse (horizontally and vertically polarized) kink waves are modeled by a number of authors (e.g., Gruszecki et al. 2006; Ofman & Wang 2008; Ofman 2009; Luna et al. 2010; Selwa et al. 2011; Antolin et al. 2014, and references therein) who confirmed the observational data by revealing that these waves decay on a timescale comparable to the oscillation wave period. Recently, small amplitude transverse waves were reported by De Moortel & Nakariakov (2012); Nisticó et al. (2013), and Anfinogentov et al. (2013) who found decayless oscillations with velocity amplitude of a few km s-1, displacement amplitude less than 1 Mm, and wave periods within the range of 2.5 to 11 min.
The wave and plasma dynamics of coronal loops are highly dependent upon their plasma and magnetic field structuring. In most of the theoretical studies thus far, analytical models of coronal loops were devised for a gravity-free medium and loop oscillations were triggered by impulsive sources. Our aim here is to construct, for the first time, an analytical model of a coronal loop in a gravitationally stratified solar atmosphere. As the problem is formidable, we limit ourselves to the simplest conceivable case of a two-dimensional (2D) model of a coronal arcade loop. As a result of very long analytical expressions consisting of a few thousand lines, which constitute the analytical model for the equilibrium mass density and gas pressure, we focus on the modest case of a loop. On the basis of our analytical model, we develop a numerical model of a loop. The newly developed coronal loop model will have several applications in studies of the properties of excited MHD waves and plasma dynamics in these loops. With some modification, the model can be adopted to a coronal loop to reveal its wave and dynamical processes. However, as its first application, we study the vertical kink oscillations evolved into the model loop. These oscillations are excited by a forced periodic driver in the vertical component of velocity, which acts at the top of the photosphere.
This paper is organized as follows. The analytical model of a coronal loop is introduced in Sect. 2. A numerical model and the results are described in Sect. 3. This paper is concluded by a short summary in Sect. 4.
2. The analytical model of a coronal loop
2.1. MHD equations
We consider a coronal plasma that is described by the ideal MHD equations 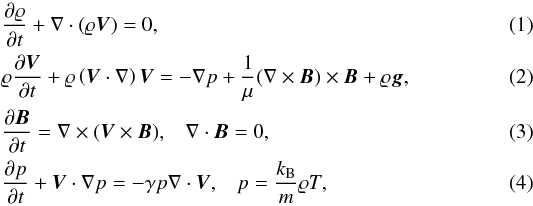 where ϱ is mass density, V represents the plasma velocity, p is a gas pressure, B is the magnetic field, T is a temperature, kB is Boltzmann’s constant, γ = 5/3 is the adiabatic index, m is a particle mass that is specified by mean molecular weight of 0.6, and g = (0, − g,0) is the gravitational acceleration. The value of g is equal to 274 m s-2.
where ϱ is mass density, V represents the plasma velocity, p is a gas pressure, B is the magnetic field, T is a temperature, kB is Boltzmann’s constant, γ = 5/3 is the adiabatic index, m is a particle mass that is specified by mean molecular weight of 0.6, and g = (0, − g,0) is the gravitational acceleration. The value of g is equal to 274 m s-2.
2.2. Equilibrium conditions
We assume that the above system is invariant along the horizontal coordinate, z (∂/∂z = 0) and set the z-components of the velocity, Vz, and magnetic field, Bz, to zero.
In this 2D model, the solar atmosphere is in static equilibrium (V = 0) with the Lorentz force balanced by the pressure gradient and gravity forces, and the divergence-free magnetic field, 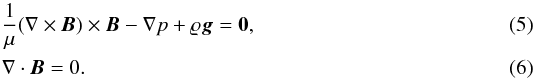
2.2.1. Hydrostatic atmosphere
A hydrostatic atmosphere corresponds to the magnetic-free (B = 0) case in which the gas pressure gradient is balanced by the gravity force 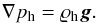 (7)With the use of the ideal gas law given by Eq. (4) and the vertical y-component of Eq. (7), we express the hydrostatic gas pressure and mass density as
(7)With the use of the ideal gas law given by Eq. (4) and the vertical y-component of Eq. (7), we express the hydrostatic gas pressure and mass density as 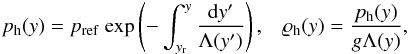 (8)where
(8)where 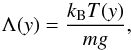 (9)is the pressure scale-height, and pref denotes the gas pressure at the reference level yr which we set and hold fixed at yr = 10 Mm.
(9)is the pressure scale-height, and pref denotes the gas pressure at the reference level yr which we set and hold fixed at yr = 10 Mm.
 |
Fig. 1 Profile of hydrostatic solar atmospheric temperature vs. height y. |
We adopt a realistic plasma temperature profile given by the semiempirical model of Avrett & Loeser (2008), which is extrapolated into the solar corona (Fig. 1). In this model, the temperature attains a value of about 4300 K at the bottom of the chromosphere (y ≈ 0.6 Mm), and 7 × 103 K at the top of the chromosphere (y ≈ 2.0 Mm). At the transition region, which is located at y ≃ 2.1 Mm, T exhibits an abrupt jump (Fig. 1), and it enhances up to about 0.7 × 106 K in the solar corona at y = 8 Mm. Higher in the solar corona, the temperature grows very slowly, tending to its asymptotic value of about 1.6 MK. The temperature profile uniquely determines the equilibrium mass density and gas pressure profiles, which fall off with the height (not shown here).
2.2.2. Magnetic atmosphere
The solenoidal condition of Eq. (6) is automatically satisfied if we express the equilibrium magnetic field with the use of magnetic flux-function (A(x,y)) as 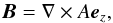 (10)where ez is a unit vector along z-direction. Setting
(10)where ez is a unit vector along z-direction. Setting  (11)from Eqs. (5) and (10), we get
(11)from Eqs. (5) and (10), we get  (12)Hence we infer the hydrostatic condition along the magnetic field line, which is specified by the equation A = const. From the x- and y-components of Eq. (5), we obtain the equilibrium equation for a system with translational symmetry (Low 1975; Priest 1982),
(12)Hence we infer the hydrostatic condition along the magnetic field line, which is specified by the equation A = const. From the x- and y-components of Eq. (5), we obtain the equilibrium equation for a system with translational symmetry (Low 1975; Priest 1982), 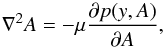 (13)where
(13)where 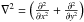 is the Laplacian.
is the Laplacian.
We assume now that the flux-function A(x,y) is known. Therefore, from Eqs. (12) and (13), we find the following expressions for ϱ and p (Solov’ev 2010; Kraśkiewicz et al. 2015; Kuźma et al. 2015): ![\begin{eqnarray} \varrho &=& \varrho_{\rm h} +\frac{1}{\mu g} \left[\frac{\partial}{\partial y} \left( \int \frac{\partial ^{2} A}{\partial y^{2}} \frac{\partial A}{\partial x} {\rm d}x + \frac{1}{2} \left(\frac{\partial A}{\partial x}\right)^{2} \right) - \frac{\partial A}{\partial y} \nabla ^{2} A \right] , \label{eq:B3} \\ p &=& p_{\rm h} -\frac{1}{2\mu } \left(\frac{\partial A}{\partial x}\right)^{2} - \frac{1}{\mu} \int \frac{\partial ^{2} A}{\partial y^{2}} \frac{\partial A}{\partial x} {\rm d}x . \label{eq:B2} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24684-14/aa24684-14-eq55.png)
2.3. A coronal loop
For a coronal loop, we make the following choice: ![\begin{eqnarray} \nonumber A(x,y)& =& S_{\rm 1} \log\left[k^2x^2 + k^2(y+y_{\rm 00})^2\right] \\ &&\quad +\varepsilon S_{\rm 1} \frac{k^2x^2}{1\!+\!\{k^2[x^2 + a(y+y_{\rm 00})^2 \!-\!x_{\rm 0}^2-b(y_{\rm 0}\!+\!y_{\rm 00})^2] \}^2} , \label{eq:B4} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24684-14/aa24684-14-eq56.png) (16)where k is the inverse scale-length, −y00 is the vertical coordinate of the singularity in the magnetic field, and a, b, ε, x0, y0, and y00 are dimensionless parameters. We set them as a = b = 0.85, k = 1 Mm-1, x0 = y0 = 4 Mm, y00 = 1 Mm, S1 ≈ 11.4 Gauss Mm, and hold them constant. These loop parameters are chosen to have a small-size loop (averaged radius ≈ 5 Mm), which significantly simplifies numerical simulations. Vectors of magnetic field, resulting from Eq. (16) are illustrated in Fig. 2 (top). As a result of the symmetry, the right-hand side of the system is displayed only, and the magnetic field vectors consist the arcade with a singularity at (x = 0, y = −y00) Mm.
(16)where k is the inverse scale-length, −y00 is the vertical coordinate of the singularity in the magnetic field, and a, b, ε, x0, y0, and y00 are dimensionless parameters. We set them as a = b = 0.85, k = 1 Mm-1, x0 = y0 = 4 Mm, y00 = 1 Mm, S1 ≈ 11.4 Gauss Mm, and hold them constant. These loop parameters are chosen to have a small-size loop (averaged radius ≈ 5 Mm), which significantly simplifies numerical simulations. Vectors of magnetic field, resulting from Eq. (16) are illustrated in Fig. 2 (top). As a result of the symmetry, the right-hand side of the system is displayed only, and the magnetic field vectors consist the arcade with a singularity at (x = 0, y = −y00) Mm.
 |
Fig. 2 Top panel: vectors of equilibrium magnetic field, expressed in units of ≈ 11.4 Gauss, and log (ϱ) (color maps). The mass density, ϱ, is given in units of 10-12 kg m-3. Bottom panel: logarithm of temperature (expressed in units of 1 MK) profile. Only the right-hand side of the system (which is symmetric about the vertical x = 0 axis) is displayed. |
The first term on the right side of Eq. (16) corresponds to the potential magnetic arcade in which the magnetic field varies as 1 /r, where r is a radial distance from the axis of symmetry, placed beneath the photosphere, at the location of the singularity. This potential magnetic field does not alter the hydrostatic state of the solar atmosphere and the equilibrium mass density and a gas pressure remain equal to ϱh(y) and ph(y), respectively.
Since a purely potential arcade does not lead to any loop structure, we implement the small, nonpotential correction (second) term in Eq. (16), which highlights in the body of the magnetic arcade a narrow loop of its radius 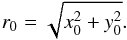 (17)This correction term is chosen to have the integral in Eq. (15) evaluated analytically. However, the analytical expressions for the equilibrium mass density, ϱ(x,y), and a gas pressure, p(x,y), derived by the symbolic package MAXIMA from Eqs. (14) and (15), are too long to be displayed here.
(17)This correction term is chosen to have the integral in Eq. (15) evaluated analytically. However, the analytical expressions for the equilibrium mass density, ϱ(x,y), and a gas pressure, p(x,y), derived by the symbolic package MAXIMA from Eqs. (14) and (15), are too long to be displayed here.
Within the coronal loop, the plasma parameters are significantly different from those in the ambient corona. The correction results in mass density enhancement within the loop. The mass density (ϱ) within the loop is about twice as large at the loop apex and ten times as large at the loop footpoint as the ambient coronal mass density (Fig. 2). This loop is about four times warmer at its apex and ten times hotter at x ≈ 3 Mm and y ≈ 3.5 Mm than the ambient plasma (Fig. 2, bottom). Below the denser strandlike structure, which occupies the top layer of the loop, there is the layer of rarefied strandlike plasma at the lower side (Fig. 2, top). The whole strandlike structure is about 500 km wide and the loop is about 15 Mm long with its major radius of about 5 Mm. It should be noted that loop length, width, and major axis, etc., are the free parameters, and the model can yield the range of loop morphology. We can simply mimic the various kinds of coronal loops with different radius of curvature and height, with different magnetic field strength, and confined plasma with given density and temperature. However, here we only choose the small size of the model loop to avoid computationally extensive numerical calculations. Our main aim is to introduce our new coronal loop model with a simple example of vertical kink oscillations. Its various applications and other parametric studies will be taken up in future projects.
3. Numerical model for vertical kink oscillations
To solve the 2D, ideal MHD equations numerically, we use the FLASH code (Fryxell et al. 2000; Lee & Deane 2009; Lee 2013), in which a third-order, unsplit Godunov-type solver with various slope limiters and Riemann solvers as well as adaptive mesh refinement (AMR; MacNeice et al. 1999) are implemented. Among a number of options, we choose the minmod slope limiter and the Roe Riemann solver (e.g., Tóth 2000).
 |
Fig. 3 Blocks system used in the numerical simulations. |
 |
Fig. 4 Temporal evolution of ϱ(x,y) at t = 550 s (top) and t = 700 s (bottom), expressed in units of 10-12 kg m-3. Arrows represent plasma velocity, given in units of 1 km s-1. (Online movie) |
We set the simulation box as (− 7.5 Mm,7.5 Mm) × (0.5 Mm,8.0 Mm) and impose time-dependent boundary conditions for all plasma quantities at all four boundaries; at these boundaries we set all plasma quantities to their equilibrium values; the only exception is the bottom boundary, where we additionally place the periodic driver as ![\begin{equation} \label{eq:Btwist} V_{y}(x,y,t) = A_{V}\, \exp\left[-\frac{x^{2} + (y-y_{\rm d})^{2}}{w ^{2}} \right] \sin\left(\frac{2\pi}{P_{\rm d}}t\right), \end{equation}](/articles/aa/full_html/2015/04/aa24684-14/aa24684-14-eq92.png) (18)where AV is the amplitude of the driver, (0,yd) is its spatial position, w denotes its width, and Pd is its period. We set AV = 3 km s-1, yd = 0.5 Mm, w = 1 Mm, Pd = 300 s, and hold them fixed. The driving period Pd = 300 s corresponds to the average lifetime of a solar granule, as the granules (together with a random coronal flows, which we do not explore here) can be regarded as a real physical driver of decayless coronal loop oscillations (Valery Nakariakov, priv. comm.).
(18)where AV is the amplitude of the driver, (0,yd) is its spatial position, w denotes its width, and Pd is its period. We set AV = 3 km s-1, yd = 0.5 Mm, w = 1 Mm, Pd = 300 s, and hold them fixed. The driving period Pd = 300 s corresponds to the average lifetime of a solar granule, as the granules (together with a random coronal flows, which we do not explore here) can be regarded as a real physical driver of decayless coronal loop oscillations (Valery Nakariakov, priv. comm.).
 |
Fig. 5 Time-signatures of ϱ (top) and Vy (bottom) collected at (x = 0,y = 4.5) Mm, and their wavelet spectra with 5.0 min global period. |
In our present work, we use an AMR grid with a minimum (maximum) level of refinement set to 3 (8). We performed the grid convergence studies by refining the grid by a factor of two. As the numerical results remained essentially same for the grid of maximum block levels 7 and 8, we adopted the latter levels to obtain our results.
Note that small-size blocks of numerical grid occupy the altitude up to y ≈ 5 Mm, below the solar transition region and in the neighborhood of the loop (Fig. 3), and every numerical block consists of 8 × 8 identical numerical cells. This results in an excellent resolution of steep spatial profiles, and greatly reduces the numerical diffusion in these regions.
Figure 4 shows the spatial profiles of ϱ(x,y) at two timespans. We only display the right-hand part of the simulation region. As a result of the driver, essentially fast magnetoacoustic-gravity waves are excited in the system. The fast magnetoacoustic waves are quasi-isotropic and they propagate upward across the curved magnetic field lines. At t = 550 s (top) and t = 700 s (bottom), the plasma is moving downward (upward) and the apex of the loop attains approximately its lowest (highest) position of ≈ 4.6 Mm (≈ 4.7 Mm), oscillating with the amplitude of about 100 km. It should be noted that the vertical kink oscillations of a curved coronal loop are fundamentally different from horizontal kink modes, since they are confined to the loop plane and can lead to the change of its length. These oscillations are seen in Fig. 5, which illustrates the time signature of ϱ (top) and Vy (bottom) collected at the point (x = 0, y = 4.5) Mm, settled just below the apex. From this figure, we clearly see that the quasi-periodic oscillations are present in the system, and the wave period of these oscillations is equal to the driving period, Pd = 300 s. Indeed, from wavelet spectra of these time signatures, we infer that the velocity time signature is a combination of globally distributed 5 min and 3 min wave periods, but the 5 min wave period is predominant. The periodogram analyses (Scargle 1982; bottom-panels) also show that the presence of significant (>99%) power peaks around 5 min wave period in both mass density as well as velocity time profiles, which do match with the wavelet power spectral analyses. The amplitude of these oscillations in Vy is about 1.1 km s-1 (Fig. 5, bottom). The phase difference between velocity and density variations with o is π/4 (quarter period), which is a typical property of the fundamental kink oscillations excited in a loop.
4. Summary
In the present paper, we have presented for the first time the analytical and numerical models of a solar coronal loop, which is embedded in a gravitationally stratified solar corona. These models are based on the analytical models of Solov’ev (2010). The Kraśkiewicz et al. (2015) and Kuźma et al. (2015) reports can also be referred for detailed mathematical formulation of the analytical and numerical models. Using these models, we performed the 2D numerical simulations of the vertical kink oscillations of this loop excited by the forced periodic driver that acts at the top of the photosphere, centrally below the apex of the loop.
The numerical simulations adapt the realistic model of the hydrostatic solar atmosphere in the FLASH code and a slightly modified potential magnetic field. Our model exhibits the formation of the quasi-periodic vertical oscillations of their wave period equal to the driving wave period of 300 s and their velocity amplitude is about 1.2 km s-1, while the loop apex oscillates with its amplitude of 100 km. These values match the recent observational findings of Nisticó et al. (2013) and Anfinogentov et al. (2013).
The implemented driver mimics a downdraft associated with a solar granule as the driving period is set to the lifetime of a granule, which is 300 s, and its amplitude is 3 km s-1. However, the value of 3 km s-1 seems to be larger by a factor of about 3 than the downdraft speed. We have verified by numerical experiments that a lower amplitude of the driver resulted in fewer pronounced oscillations (not shown). Moreover, to simplify numerical simulations we have chosen the coronal loop to be only about 15 Mm long, which is at least an order of magnitude shorter than a typical coronal loop. In the case of a typical loop, the fast magnetoacoustic waves would experience more spatial spreading while propagating from the launching place upward toward the typical loop apex and covering a long distance. As a result, this apex would be affected by a less energetic signal and it would experience lower amplitude oscillations. In this case, a larger amplitude of the periodic driver would be required or a driver can be set higher up, somewhere in the solar corona, modeling its random velocity field. Qualitatively, we can state that the oscillation amplitude should decline with the loop length and it should grow with the amplitude of the forced driver. These parametric studies would be important for impulsively excited waves with the non-forced drivers, which will be the subject of a future study using the newly developed coronal loop model.
Online material
Movie of Fig. 4 Access here
Acknowledgments
We thank the referee for his/her valuable comments, which improved the manuscript considerably. A.S. would like to express his gratitude to K.M. for hospitality during his visits to Lublin in May of 2013 and 2014, and for the support in the frame of Marie Curie International Research Staff Exchange Scheme Fellowship within the 7th European Community Framework Program. A.K.S. thanks K.M. and UMCS, Lublin, for providing a visit fund during September-October 2014 during which he contributed to the project. The work has also been supported by a Marie Curie International Research Staff Exchange Scheme Fellowship within the 7th European Community Framework Program. A.S.’s contribution to this article was partially supported by the Presidium of the Russian Academy of Sciences (project P9) and the Russian Foundation for Basic Research, project 13-02-00714. The software used in this work was in part developed by the DOE-supported ASCI/Alliance Center for Astrophysical Thermonuclear Flashes at the University of Chicago. The visualizations of the simulation variables have been carried out using the IDL (Interactive Data Language) software package.
References
- Anfinogentov, S., Nisticò, G., & Nakariakov, V. M. 2013, A&A, 560, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antolin, P., Yokoyama, T., & Van Doorsselaere, T. 2014, ApJ, 787, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., & Schrijver, C. J. 2011, ApJ, 736, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Nightingale, R. W., & Alexander, D. 2000, ApJ, 541, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Avrett, E. H., & Loeser, R. 2008, ApJS, 175, 229 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., & Nakariakov, V. M. 2012, Roy. Soc. London Philos. Trans. Ser. A, 370, 3193 [Google Scholar]
- Fryxell, B., Olson, K., Ricker, P., et al. 2000, ApJS, 131, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Gruszecki, M., Murawski, K., Selwa, M., & Ofman, L. 2006, A&A, 460, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraśkiewicz, J., Murawski, K., Solov’ev, A., & Srivastava, A. K. 2015, Sol. Phys., submitted [Google Scholar]
- Kuźma, B., Murawski, K., & Solov’ev, A. 2015, A&A, submitted [Google Scholar]
- Lee, D. 2013, J. Comput. Phys., 243, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, D., & Deane, A. E. 2009, J. Comput. Phys., 228, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Low, B. C. 1975, ApJ, 197, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, M., Terradas, J., Oliver, R., & Ballester, J. L. 2010, ApJ, 716, 1371 [NASA ADS] [CrossRef] [Google Scholar]
- MacNeice, P., Spicer, D. S., & Antiochos, S. 1999, 8th SOHO Workshop: Plasma Dynamics and Diagnostics in the Solar Transition Region and Corona, 446, 457 [Google Scholar]
- Nisticò, G., Nakariakov, V. M., & Verwichte, E. 2013, A&A, 552, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofman, L. 2009, ApJ, 694, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., & Wang, T. J. 2008, A&A, 482, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J. 2014, Res. Astron. Astrophys., 14, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R. 1982, Solar magneto-hydrodynamics (Dordrecht: D. Reidel Pub. Co.) [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Selwa, M., Solanki, S. K., & Ofman, L. 2011, ApJ, 728, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Solov’ev, A. A. 2010, Astron. Rep., 54, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Srivastava, A. K., & Goossens, M. 2013, ApJ, 777, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Tóth, G. 2000, J. Comput. Phys., 161, 605 [Google Scholar]
- Verwichte, E., Aschwanden, M. J., Van Doorsselaere, T., Foullon, C., & Nakariakov, V. M. 2009, ApJ, 698, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T. J., & Solanki, S. K. 2004, A&A, 421, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T. J., Solanki, S. K., & Selwa, M. 2008, A&A, 489, 1307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, R. S., Verwichte, E., & Foullon, C. 2012, A&A, 545, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Profile of hydrostatic solar atmospheric temperature vs. height y. |
| In the text | |
 |
Fig. 2 Top panel: vectors of equilibrium magnetic field, expressed in units of ≈ 11.4 Gauss, and log (ϱ) (color maps). The mass density, ϱ, is given in units of 10-12 kg m-3. Bottom panel: logarithm of temperature (expressed in units of 1 MK) profile. Only the right-hand side of the system (which is symmetric about the vertical x = 0 axis) is displayed. |
| In the text | |
 |
Fig. 3 Blocks system used in the numerical simulations. |
| In the text | |
 |
Fig. 4 Temporal evolution of ϱ(x,y) at t = 550 s (top) and t = 700 s (bottom), expressed in units of 10-12 kg m-3. Arrows represent plasma velocity, given in units of 1 km s-1. (Online movie) |
| In the text | |
 |
Fig. 5 Time-signatures of ϱ (top) and Vy (bottom) collected at (x = 0,y = 4.5) Mm, and their wavelet spectra with 5.0 min global period. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


