| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201424324 | |
| Published online | 11 February 2015 | |
Dissipative effects on the sustainment of a magnetorotational dynamo in Keplerian shear flow
1
Université de Toulouse, UPS-OMP, IRAP
Toulouse, France
e-mail:
antoine.riols@irap.omp.eu
2
CNRS, IRAP, 14
avenue Edouard Belin, 31400
Toulouse,
France
3
CNRS, Institut de Mécanique des Fluides de Toulouse
(IMFT), Allée du Professeur Camille
Soula, 31400
Toulouse,
France
4
Univ. Grenoble Alpes, IPAG, 38000
Grenoble,
France
5
CNRS, IPAG, 38000
Grenoble,
France
6
Department of Applied Mathematics and Theoretical Physics,
University of Cambridge, Centre for
Mathematical Sciences, Wilberforce Road, Cambridge
CB3 0WA,
UK
Received: 2 June 2014
Accepted: 4 October 2014
The magnetorotational (MRI) dynamo has long been considered one of the possible drivers of turbulent angular momentum transport in astrophysical accretion disks. However, various numerical results suggest that this dynamo may be difficult to excite in the astrophysically relevant regime of magnetic Prandtl number (Pm) significantly smaller than unity, for reasons currently not well understood. The aim of this article is to present the first results of an ongoing numerical investigation of the role of both linear and nonlinear dissipative effects in this problem. Combining a parametric exploration and an energy analysis of incompressible nonlinear MRI dynamo cycles representative of the transitional dynamics in large aspect ratio shearing boxes, we find that turbulent magnetic diffusion makes the excitation and sustainment of this dynamo at moderate magnetic Reynolds number (Rm) increasingly difficult for decreasing Pm. This results in an increase in the critical Rm of the dynamo for increasing kinematic Reynolds number (Re), in agreement with earlier numerical results. Given its very generic nature, we argue that turbulent magnetic diffusion could be an important determinant of MRI dynamo excitation in disks, and may also limit the efficiency of angular momentum transport by MRI turbulence in low Pm regimes.
Key words: accretion, accretion disks / dynamo / instabilities / magnetohydrodynamics (MHD) / turbulence
© ESO, 2015
1. Introduction
Magnetorotational instability (MRI) occurs in differentially rotating flows whose angular velocity decreases with distance to the rotation axis (Velikhov 1959; Chandrasekhar 1960; Balbus & Hawley 1991) and is the most commonly invoked excitation mechanism of angular momentum-transporting turbulence in accretion disks (Balbus & Hawley 1998). In a uniform magnetic field B, the MRI amplifies arbitrarily small perturbations exponentially and breaks down nonlinearly into MHD turbulence (e.g. Hawley et al. 1995). The transport efficiency of MRI turbulence continues to be debated, and may be reduced in the astrophysically relevant regime of low magnetic Prandtl number (Pm), the ratio between kinematic viscosity and magnetic diffusivity (Lesur & Longaretti 2007; Balbus & Henri 2008).
Another question in this context is that of the origin of the MRI-supporting magnetic field. In some cases, this field may be generated by an internal disk dynamo process which could bootstrap MHD turbulence in the disk independently of its magnetic environment (Balbus & Hawley 1998; Donati et al. 2005). Early simulations by Hawley et al. (1996) in the so-called zero net flux configuration appropriate to this problem showed that such a dynamo is indeed possible and is intimately coupled to the MRI (see also Brandenburg et al. 1995), but its viability in disks has since been questioned by numerical studies suggesting that it may be impossible to excite at low Pm (Fromang et al. 2007), although the physical reasons for this are not yet clear (Bodo et al. 2011; Käpylä & Korpi 2011; Oishi & Mac Low 2011; Simon et al. 2011).
The aim of this article is to seek a physical explanation for this behaviour by exploiting recently discovered dynamical properties of this subcritical dynamo mechanism (Rincon et al. 2007, 2008; Lesur & Ogilvie 2008), whose principles are otherwise rather simple: starting from a zero net-flux axisymmetric weak poloidal field, a larger toroidal field is generated through the Ω effect. This field is MRI-unstable to non-axisymmetric MHD perturbations, whose growth results in a nonlinear electromotive force (EMF) that sustains (and can also reverse) the axisymmetric field. Recent work suggests that three-dimensional cyclic nonlinear solutions provide the first germs of excitation of the dynamo in shearing box simulations (Herault et al. 2011; Riols et al. 2013) and possibly form the backbone of the ensuing self-sustained MHD turbulence. Parametric studies of cycles representative of the transitional dynamics, complemented with an analysis of their energetics, may therefore prove useful to understand how dissipative effects affect the dynamo transition as a whole. Here, we present the first results of an ongoing numerical investigation of this kind. We focus on the simpler case of incompressible dynamics in large aspect ratio shearing boxes, which includes most of the fundamental physical complexity of the problem, except for stratification and boundary effects. An exhaustive study of different configurations will be presented in a subsequent paper.
The equations and numerical framework used in this article are presented in Sect. 2. In Sect. 3, we study the characteristics of the transition in elongated shearing boxes using generic incompressible numerical simulations, in order to check if the results of Fromang et al. (2007) on the Pm-dependence of the transition extend to such configurations. We also investigate whether cycles still provide the first germs of MRI dynamo chaos at kinematic Reynolds number (Re) larger than studied by Riols et al. (2013). In Sect. 4, we compute the existence boundaries of several cycles in the magnetic versus kinematic Reynolds number parameter plane and analyse their energy budget to identify physical effects affecting the dynamics in the vicinity of Pm ~ 1. Additional numerical experiments aiming at investigating the conditions of excitation of the dynamo, and why it appears harder to excite at low Pm, are presented in Sect. 5. A short discussion concludes the paper.
2. Equations and numerical framework
2.1. Model
The equations and numerical framework are the same as in the work of Herault et al. (2011) and Riols et al. (2013) and have already been described in detail in these papers. We use the cartesian local shearing sheet description of differentially rotating flows (Goldreich & Lynden-Bell 1965), whereby the axisymmetric differential rotation is approximated locally by a linear shear flow Ux = −Sxey, and a uniform rotation rate Ω = Ω ez, with Ω = (2/3)S for a Keplerian equilibrium. Here (x,y,z) are respectively the shearwise, streamwise and spanwise directions, corresponding to the radial, azimuthal and vertical directions in accretion disks. We refer to the (x,z) projection of vector fields as their poloidal component and to the y direction as their toroidal component. Stratification and compressibility effects are ignored for simplicity. The evolution of the three-dimensional velocity field perturbations u and magnetic field B is governed by the three-dimensional incompressible, dissipative MHD equations: 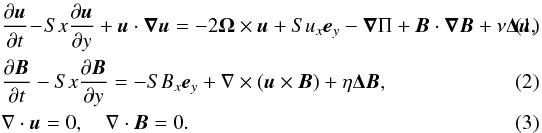 The kinematic and magnetic Reynolds numbers are defined by Re = SL2/ν and Rm = SL2/η, where ν and η are the constant kinematic viscosity and magnetic diffusivity, L is a typical scale of the spatial domain and time is measured with respect to S-1. The magnetic Prandtl number is Pm = ν/η = Rm/Re. Π is the total of fluid plus magnetic pressure divided by the uniform density. B is expressed in terms of an alfvénic velocity. Both u and B are measured in units of SL.
The kinematic and magnetic Reynolds numbers are defined by Re = SL2/ν and Rm = SL2/η, where ν and η are the constant kinematic viscosity and magnetic diffusivity, L is a typical scale of the spatial domain and time is measured with respect to S-1. The magnetic Prandtl number is Pm = ν/η = Rm/Re. Π is the total of fluid plus magnetic pressure divided by the uniform density. B is expressed in terms of an alfvénic velocity. Both u and B are measured in units of SL.
2.2. Numerical methods
We use the SNOOPY code (Lesur & Longaretti 2007) to perform direct numerical simulations (DNS) of Eqs. (1)−(3). This code provides a spectral implementation of the so-called numerical shearing box model of the shearing sheet, in a finite domain of size (Lx,Ly,Lz), at numerical resolution (Nx,Ny,Nz). The x and y directions are taken as periodic while shear-periodicity is imposed in x. A discrete spectral basis of shearing waves with constant ky and kz wavenumbers and constant shearwise Lagrangian wavenumber kx0 is used to represent the fields in the sheared Lagrangian frame. The shearing of nonaxisymmetric perturbations in this model (ky ≠ 0) is described using time-dependent Eulerian shearwise wavenumbers, kx(t) = kx0 + Skyt. Shearing waves are “leading” when kxky< 0 and “trailing” when kxky> 0.
Nonlinear periodic solutions are computed with the Newton-Krylov solver PEANUTS interfaced to SNOOPY, and followed in parameter space using arclength continuation. Almost all the results presented in the paper are for a maximum resolution of (48,48,72), ensuring convergence for all parameters considered, except for some of the results of Sect. 3.1 which required a higher resolution.
2.3. Symmetries and aspect ratio choice
The dynamics in the transitional regimes typical of simulations displaying recurrent dynamics (Re and Rm of a few hundreds to thousands) is already quite complex and clearly involves a large number of cyclic solutions. Given the current state of understanding of the dependence of the MRI dynamo transition on dissipative effects, our strategy to make progress on this problem is to simplify the dynamics as much as possible and focus on a few simple dynamo cycles which encapsulate the basic physics of the dynamo. To achieve this, we enforce that the dynamics takes place in a symmetric subspace to facilitate the analysis (this does not compromise the underlying dynamical complexity, see Sect. 3 of Riols et al. 2013), and notably monitor the axisymmetric MRI-supporting field  (y-average of B), more specifically its energetically dominant Fourier mode
(y-average of B), more specifically its energetically dominant Fourier mode 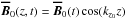 with kz0 = 2π/Lz. We also restrict our study to the large aspect ratio configuration (Lx,Ly,Lz) = (0.7,20,2) already employed by Herault et al. (2011) and Riols et al. (2013), and Re and Rm values in the range of a few hundred, which effectively guarantees that only a small number of simple nonlinear cyclic solutions are excited (see Sect. III. D of Herault et al. (2011) for a detailed explanation). Different aspect ratio configurations will be explored in a future paper.
with kz0 = 2π/Lz. We also restrict our study to the large aspect ratio configuration (Lx,Ly,Lz) = (0.7,20,2) already employed by Herault et al. (2011) and Riols et al. (2013), and Re and Rm values in the range of a few hundred, which effectively guarantees that only a small number of simple nonlinear cyclic solutions are excited (see Sect. III. D of Herault et al. (2011) for a detailed explanation). Different aspect ratio configurations will be explored in a future paper.
3. Numerical exploration of the dynamo transition
3.1. Dynamical lifetime of DNS in the (Re, Rm) plane
As mentioned in the introduction, the numerical study of Fromang et al. (2007), for a single box size (π,2π,π), in a compressible isothermal case, suggests that zero net flux MRI turbulence cannot be sustained for Pm below some critical Pmc. The transitional dynamics in this box involves very intricate nonlinear interactions between many shearing waves and is therefore particularly difficult to analyse. As explained previously, we found it more convenient here to use an elongated box in which fewer shearing waves are active to address the problem of the nature of the Pm-dependence of the transition.
 |
Fig. 1 Maps of the dynamical lifetime in generic DNS, as a function of Re and Rm (Lx = 0.7, Ly = 20, Lz = 2). Each row is for a different random initial condition. The second and third maps (from top to bottom) use the same noise realization (see text) but different amplitudes (A = 5 for the second case and A = 2.5 for the third case). The maps on the left are for simulations at mild Re and Rm that can be conducted at moderate numerical resolution (48 × 48 × 72). The maps on the right are for higher Re and Rm, requiring a higher resolution (96 × 96 × 128). The dashed line corresponds to Pm = 1. |
As a preliminary step, we first ensured that the results obtained by Fromang et al. (2007) pertain to our large aspect ratio configuration. For this purpose, we used a cartography procedure similar to that described in Riols et al. (2013). We performed a series of DNS for different Reand Rm, using the same random initial condition. The latter was generated as follows: for each field component, we generated a set of random complex Fourier modes and normalized the total energy density to obtain a particular white noise incompressible “realization”. For u and B, a given zero net-flux initial condition is obtained by multiplying this particular noise realization by an amplitude factor A (see Riols et al. (2013) for details). The typical dynamical lifetime measured in each DNS was then plotted on a two dimensional map covering the (Re,Rm) grid. To check whether the results were generic, we performed the same experiment for three different initial conditions. The first and second ones were constructed from different noise realizations but the same amplitude A = 5. The third one used the same noise realization as the second one but with A = 2.5 (shooting along the same direction in phase space but at different distances from the laminar state).
Figure 1 (left) shows the corresponding dynamical lifetime maps for Reand Rmbetween 100 and 1000, computed for a numerical resolution 48 × 48 × 72. The maps on the right are for the same initial conditions, but extend to higher Reand Rm(from 500 to 3000). They required a larger numerical resolution (128 × 128 × 96). All the DNS whose dynamical lifetime exceeds 600 S-1 are systematically on or above the Pm ~ 1 line. At low Re, the dynamics seems to be sustained only for Rmlarger than some critical Rmc. At higher Re, the transition border visually follows a Pm ≃ Pmc line, with Pmc of the order of unity. This behaviour suggests that the transition border is indeed similar to that obtained by Fromang et al. (2007), and does not depend on the shearing box aspect ratio or compressibility of the fluid, at least on the qualitative level.
 |
Fig. 2 Maps of dynamical lifetimes as a function of Rm and initial perturbation amplitude A, for a fixed noise realization (see text) and six different Re. The resolution is (δA = 0.04,δRm = 2) except for Re = 70 where (δA = 0.02,δRm = 1) and for Re = 550 where δRm = 5. |
3.2. Transition maps
To justify our interest in cycles, we then attempted to check whether the conclusion of Riols et al. (2013), that chaotic dynamo action at Re = 70 results from their global bifurcations, extends to larger Re. The simplest signature of this effect is in the form of fractal-like sets of initial perturbations for which the dynamics is long-lived. To check this, we performed several series of DNS spanning a range of Rm and initial conditions, each of them generated from a unique noise realization (using the same procedure as in Sect. 3.1) and varying the perturbation amplitude A. We constructed maps of the dynamical lifetimes for each run as a function of Rm and A, for Re = (70,85,100,150,200,550).
Figure 2 shows that the boundary separating the regions in phase space where the dynamics is long-lived from those where perturbations decay rapidly has the same qualitative fractal-like structure for all Re. Long-lived simulations are characterized by recurrent dynamics reminiscent of nonlinear cycles, suggesting that the excitation of the MRI dynamo is indeed tied to that of cycles.
At the largest Re considered though, the fractal-like features appear to be smoothed out, and the correspondence between recurrent dynamics and chaotic flows less pronounced. We also note that at Re = 550, the transition border seems to be at higher Rm than at Re = 70, in line with the results of Fromang et al. (2007) and the results ofSect. 3.1.
Overall, the previous results suggest that the excitation of self-sustaining MHD turbulence in this problem is related to the existence of MRI dynamo cycles and their global bifurcations. This vindicates the idea that studying how the dynamics of simple nonlinear cycles is affected by changes in Re and Rm may be useful to identify the physical mechanisms responsible for the Pm-dependence of the transition.
4. Parametric study of MRI dynamo cycles
4.1. Existence boundaries in the (Re, Rm) plane
 |
Fig. 3 Existence boundaries of three cycle pairs (dashed lines) in the (Re,Rm) plane and critical Rec(Rm), Rmc(Re) of saddle nodes obtained by continuation (symbols). Black arrows indicate the regions in which the cycles exist. For SN1, dark blue/black bullets correspond to low resolution results (24 × 12 × 36), and light blue/grey bullets are for double resolution (48 × 24 × 72). Inset: selected continuation curves of SN1 at fixed Rm. |
Motivated by the previous results, we investigated the domains of existence in parameter space of three pairs of cycles SN1, SN2, and SN3 born out of saddle node bifurcations at pair-specific critical Rmc(Re). SN1 and SN2 have already been documented by Riols et al. (2013) (see their Figs. 7, 8), while SN3 was found more recently.
Continuation with respect to Re at fixed Rm of the lower and upper branches LB1 and UB1 of SN1 (Fig. 3, inset) shows that they only exist in a finite range of Re, whose extent widens as Rm increases. SN2 and SN3 behave similarly (not shown). The existence boundaries of all cycle pairs in the (Re,Rm) plane were constructed by combining all critical Rmc(Re) and Rec(Rm) obtained by continuation (Fig. 3). For Rm in the 300−500 range, all cycles disappear at low enough Pm and their Rmc increases with Re. This behaviour, reminiscent of the results of Fromang et al. (2007), is investigated below (the seemingly large differences between their transitional Re, Rm and ours are essentially due to aspect ratio differences and do not reflect fundamental physical differences). For SN1, we plotted the critical points obtained for both low resolution simulations (24 × 12 × 36) and at higher resolution (48 × 24 × 72). The boundary appears to be almost independent of resolution. Note that we found it very difficult to explore the strongly nonlinear regime Rm > 500 at the maximum resolution considered. Tentative results at this resolution (not shown) suggest that SN1 may have an upper boundary in Rm in this regime.
4.2. Magnetic energy budgets of MRI dynamo cycles
As the MRI dynamo rests on the sustainment of the axisymmetric MRI-supporting field  against dissipative processes through nonlinear interactions of non-axisymmetric modes, analysing the magnetic energy budget of dynamo cycles, most importantly transitional lower branch saddles such as LB1, may give useful physical insights into the Pm ≤ 1 regime. To do this, we write
against dissipative processes through nonlinear interactions of non-axisymmetric modes, analysing the magnetic energy budget of dynamo cycles, most importantly transitional lower branch saddles such as LB1, may give useful physical insights into the Pm ≤ 1 regime. To do this, we write  (4)where u1 and b1 stand for non-axisymmetric “MRI wave” perturbations supported by shearing waves with wavenumbers | ky | = ky0 = 2π/Ly, kx(t) = Skyt, | kz | = kz0 for u1 and kz = 0 for b1.
(4)where u1 and b1 stand for non-axisymmetric “MRI wave” perturbations supported by shearing waves with wavenumbers | ky | = ky0 = 2π/Ly, kx(t) = Skyt, | kz | = kz0 for u1 and kz = 0 for b1.
The sum over j ≥ 2 stands for all other (smaller-scale) fluctuations.
We first integrate the energy equation for 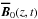 over the volume and half cycle period T/2 = S-1Ly/Lx. Denoting this operation by ⟨⟩ and taking into account that cyclic magnetic reversals change
over the volume and half cycle period T/2 = S-1Ly/Lx. Denoting this operation by ⟨⟩ and taking into account that cyclic magnetic reversals change  into
into  , we obtain the energy budget for
, we obtain the energy budget for  ,
,  and ° is the Hadamard (entrywise) product; Ω0 is the energy provided by the linear stretching of
and ° is the Hadamard (entrywise) product; Ω0 is the energy provided by the linear stretching of  by the shear (Ω effect) and I0 is a nonlinear induction term; A0 is the magnetic energy exchanged with other modes through nonlinear advection and D0 is the ohmic dissipation; A01 is the energy exchanged with the MRI-unstable waves and A02+ is the energy exchanged with all j ≥ 2 modes. Figure 4a,b (left) display the x and y projections of Eq. (5) for LB1 as a function of Re, at fixed Rm (UB1 is more energetic but behaves similarly). The MRI-supporting azimuthal field
by the shear (Ω effect) and I0 is a nonlinear induction term; A0 is the magnetic energy exchanged with other modes through nonlinear advection and D0 is the ohmic dissipation; A01 is the energy exchanged with the MRI-unstable waves and A02+ is the energy exchanged with all j ≥ 2 modes. Figure 4a,b (left) display the x and y projections of Eq. (5) for LB1 as a function of Re, at fixed Rm (UB1 is more energetic but behaves similarly). The MRI-supporting azimuthal field 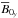 loses energy through laminar dissipation D0y, but also through a nonlinear advective transfer to other modes A0y< 0, which therefore acts as a weakly nonlinear (“turbulent”) diffusion. The Ω effect is the only net source term for
loses energy through laminar dissipation D0y, but also through a nonlinear advective transfer to other modes A0y< 0, which therefore acts as a weakly nonlinear (“turbulent”) diffusion. The Ω effect is the only net source term for 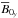 , therefore the sustainment of
, therefore the sustainment of 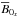 is critical for the dynamo. Figure 4a (left) shows that
is critical for the dynamo. Figure 4a (left) shows that 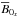 gains energy from the nonlinear term A01x> 0, which is the product of the MRI correlation of u1 and b1, and loses energy via D0x and
gains energy from the nonlinear term A01x> 0, which is the product of the MRI correlation of u1 and b1, and loses energy via D0x and 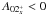 , so that
, so that 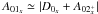 .
. 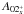 transfers energy to smaller scales (where it is dissipated), and can again be interpreted as a nonlinear diffusion of
transfers energy to smaller scales (where it is dissipated), and can again be interpreted as a nonlinear diffusion of 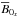 .
.
 |
Fig. 4 Magnetic energy budgets as a function of Re: a) x projection of the budgets for |
To understand how energy is injected into the MRI wave and transferred to  , we now consider the energy budget for b1,
, we now consider the energy budget for b1, 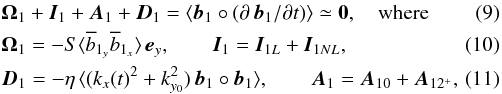
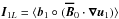 and I1NL is a nonlinear induction term;
and I1NL is a nonlinear induction term;  is the energy exchanged through advection between the MRI wave and
is the energy exchanged through advection between the MRI wave and  , and A12+ accounts for a similar exchange with smaller scales (Eq. (9) is almost zero because the wave carries a negligible amount of energy at both t = 0 and t = T/2). Figure 4a,b (right) shows that the x and y components of the MRI perturbation b1 are fed by induction (respectively by I1x and Ω1y, with I1NLx ≪ I1Lx). As expected, some of the energy injected via the MRI is transferred back nonlinearly to
, and A12+ accounts for a similar exchange with smaller scales (Eq. (9) is almost zero because the wave carries a negligible amount of energy at both t = 0 and t = T/2). Figure 4a,b (right) shows that the x and y components of the MRI perturbation b1 are fed by induction (respectively by I1x and Ω1y, with I1NLx ≪ I1Lx). As expected, some of the energy injected via the MRI is transferred back nonlinearly to 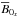 through A10x = −A01x, and some of it is lost through laminar dissipation D1x. The rest
through A10x = −A01x, and some of it is lost through laminar dissipation D1x. The rest  is transferred to smaller scales and can be regarded as a nonlinear diffusion of MRI-unstable perturbations. Using a similar analysis, we checked that j ≥ 2 perturbations are mostly excited via nonlinear interactions, and not by the MRI, for all cases studied here. Summing Eqs. (5) and (9) to eliminate A01x, we obtain
is transferred to smaller scales and can be regarded as a nonlinear diffusion of MRI-unstable perturbations. Using a similar analysis, we checked that j ≥ 2 perturbations are mostly excited via nonlinear interactions, and not by the MRI, for all cases studied here. Summing Eqs. (5) and (9) to eliminate A01x, we obtain  (12)which translates that the energy injected via the MRI as I1x must balance the total of “laminar” ohmic dissipation | D0x + D1x | and nonlinear dissipation
(12)which translates that the energy injected via the MRI as I1x must balance the total of “laminar” ohmic dissipation | D0x + D1x | and nonlinear dissipation 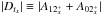 for the dynamo to be sustained (I0x ≪ I1x in all cases studied here).
for the dynamo to be sustained (I0x ≪ I1x in all cases studied here).
 |
Fig. 5 Ratio between nonlinear dissipation Dtx and injected energy I0x + I1x for LB1 and UB1 and two different Rm. |
To understand how Eq. (12) is satisfied in different regimes, we show in Fig. 5 the ratio | Dtx | /(I0x + I1x) for LB1 and UB1 as a function of Re, for two values of Rm. This ratio is always significantly larger for UB1 than for LB1, which is consistent with the standard picture of upper branches being more nonlinear than lower branches. The amplitude of  is larger on UB1 (Fig. 3, inset), which results in a stronger MRI driving (the MRI is always in the regime
is larger on UB1 (Fig. 3, inset), which results in a stronger MRI driving (the MRI is always in the regime 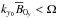 here, so the stronger the field, the larger the growth rate). The most important observation, however, is the significant increase of | Dtx | /(I0x + I1x) with Re for the saddle solution LB1, which shows that a larger fraction of the energy injected in
here, so the stronger the field, the larger the growth rate). The most important observation, however, is the significant increase of | Dtx | /(I0x + I1x) with Re for the saddle solution LB1, which shows that a larger fraction of the energy injected in  and b1 is lost through nonlinear dissipation
and b1 is lost through nonlinear dissipation 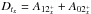 as Re increases. Our interpretation is that this relative enhancement of “turbulent” magnetic diffusion is tied to the facilitated excitation of velocity fluctuations at large Re.
as Re increases. Our interpretation is that this relative enhancement of “turbulent” magnetic diffusion is tied to the facilitated excitation of velocity fluctuations at large Re.
5. Disappearance of the dynamo
The previous results provide qualitative clues to understand the conditions of excitation of the dynamo. We note that the amplitude of  on LB1 seems to asymptote to a constant at large Re and fixed Rm (Fig. 3 (inset)), and therefore so should the MRI growth rate for this branch. This suggests that the MRI may not be able to sustain
on LB1 seems to asymptote to a constant at large Re and fixed Rm (Fig. 3 (inset)), and therefore so should the MRI growth rate for this branch. This suggests that the MRI may not be able to sustain  , b1 and therefore the dynamo against the total effective magnetic diffusion beyond some critical Re, as observed in Figs. 3 and 5. To investigate more precisely how the energy balance of Eq. (12) may be broken, we prepared a family of initial conditions resembling LB1 at t = 0, consisting of an axisymmetric field
, b1 and therefore the dynamo against the total effective magnetic diffusion beyond some critical Re, as observed in Figs. 3 and 5. To investigate more precisely how the energy balance of Eq. (12) may be broken, we prepared a family of initial conditions resembling LB1 at t = 0, consisting of an axisymmetric field 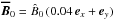 parametrized by
parametrized by 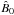 , plus non-axisymmetric perturbations in the form of a given packet of shearing waves (| ky | = ky0, kx(t = 0) = 0 and multiple kz) with weak but random amplitudes (
, plus non-axisymmetric perturbations in the form of a given packet of shearing waves (| ky | = ky0, kx(t = 0) = 0 and multiple kz) with weak but random amplitudes (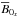 /
/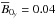 is representative of LB1 and ensures that Ω0y is of the order of D0y). This set of initial conditions was then integrated by DNS during half a cycle period typical of a reversal of
is representative of LB1 and ensures that Ω0y is of the order of D0y). This set of initial conditions was then integrated by DNS during half a cycle period typical of a reversal of  , for a range of Re and
, for a range of Re and 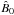 . The results were used to construct a map of the net energy Δℰm = I0x + I1x − | D0x + D1x + Dtx | gained or lost by the active magnetic modes during the reversal, as a function of Re and
. The results were used to construct a map of the net energy Δℰm = I0x + I1x − | D0x + D1x + Dtx | gained or lost by the active magnetic modes during the reversal, as a function of Re and 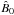 , for several Rm (Fig. 6 (left)). The isolines Δℰm = 0 are reminiscent of the continuation curves of SN1 (Fig. 3 (inset)). The range of Re in which the system gains more energy from the MRI than it dissipates (Δℰm> 0) widens significantly at larger Rm.
, for several Rm (Fig. 6 (left)). The isolines Δℰm = 0 are reminiscent of the continuation curves of SN1 (Fig. 3 (inset)). The range of Re in which the system gains more energy from the MRI than it dissipates (Δℰm> 0) widens significantly at larger Rm.
 |
Fig. 6 Energy budget of simulations integrated over St = Ly/Lx for three values of Rm. Left: net energy gain Δℰm as a function of Re and |
Figure 6 (right) shows plots of the different terms in Eq. (12) normalized by (I0x + I1x) as a function of Re, for 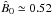 . At Rm = 280, the system loses energy for all Re after a reversal. At Rm = 350, there is a range of Re in which more energy is pumped in by the MRI than dissipated. This range widens at even larger Rm = 400. The transition from a sustained to a decaying regime at large Re occurs because | D0x + D1x | /(I0x + I1x) tends to a constant at large Re, while | Dtx | /(I0x + I1x) increases slowly. The reason why the dynamo can be sustained at larger Re as Rm increases is that the MRI growth rate is not asymptotic in Rm in the transitional 300−500Rm range. Laminar dissipation is reduced relative to energy injection as Rm increases, which partially offsets the increase in “turbulent” diffusion at large Re. Equivalently, we may conclude that this increase at large Re requires to go to larger Rm to recover the dynamo, as observed in Figs. 2 and 3 and reported by Fromang et al. (2007).
. At Rm = 280, the system loses energy for all Re after a reversal. At Rm = 350, there is a range of Re in which more energy is pumped in by the MRI than dissipated. This range widens at even larger Rm = 400. The transition from a sustained to a decaying regime at large Re occurs because | D0x + D1x | /(I0x + I1x) tends to a constant at large Re, while | Dtx | /(I0x + I1x) increases slowly. The reason why the dynamo can be sustained at larger Re as Rm increases is that the MRI growth rate is not asymptotic in Rm in the transitional 300−500Rm range. Laminar dissipation is reduced relative to energy injection as Rm increases, which partially offsets the increase in “turbulent” diffusion at large Re. Equivalently, we may conclude that this increase at large Re requires to go to larger Rm to recover the dynamo, as observed in Figs. 2 and 3 and reported by Fromang et al. (2007).
6. Discussion
Why is the MRI dynamo in Keplerian flow harder to excite at low Pm? Using a simple numerical setup, we have found that weakly nonlinear “turbulent” diffusion (in a qualitative, not strictly mean-field theoretical sense) of large-scale magnetic modes makes it increasingly difficult to sustain the dynamo at moderate Rm as Re increases. The significant advective transfers of magnetic energy to small scales reported by Fromang et al. (2007) in smaller aspect ratio simulations at large Re corroborate this conclusion. A subtle point is that the velocity fluctuations behind turbulent magnetic diffusion in this subcritical problem are not externally prescribed but are indirectly transiently excited by the MRI.
Turbulent diffusion has also been measured in turbulent flows of low Pm liquid metals (Frick et al. 2010; Rahbarnia et al. 2012), in which it is strongly suspected of raising (kinematic) dynamo thresholds (Miralles et al. 2013). Given the very generic nature of this effect, we therefore argue that it could be an important determinant of MRI dynamo excitation in low Pm rotating shear flows, such as occur in parts of some accretion disks (some of which also have low Rm). Besides, the fact that it also affects MRI-active modes suggests that it may be linked to the drop in angular momentum transport reported in net-flux (imposed field) MRI simulations at (moderately) low Pm.
More work is clearly required to connect these results to the full diversity of simulated and astrophysical regimes, most importantly the numerically challenging limit Re ≫ Rm ≫ 1, and to study to which extent the conclusions pertain to numerical configurations with different aspect ratio. A similar preliminary study in smaller aspect ratio boxes suggests that the same qualitative conclusions apply in this case. These results will be presented in a future paper. Other nonlinear effects, some of which may qualitatively relate to the mean-field theoretical α effect with vertical stratification, are also probably very important in the disk dynamo problem (Brandenburg et al. 1995; Gressel 2010; Davis et al. 2010; Käpylä & Korpi 2011; Oishi & Mac Low 2011; Simon et al. 2011; Blackman 2012) and will be worthwhile of investigation along the same lines.
Acknowledgments
This research was supported by the University Paul Sabatier of Toulouse under an AO3 grant, by the Midi-Pyrénées region and by the French National Program for Stellar Physics (PNPS). Numerical calculations were carried out on the CALMIP platform (CICT, University of Toulouse), whose assistance is gratefully acknowledged.
References
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]
- Balbus, S. A., & Henri, P. 2008, ApJ, 674, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Blackman, E. G. 2012, Phys. Scr., 86, 058202 [NASA ADS] [CrossRef] [Google Scholar]
- Bodo, G., Cattaneo, F., Ferrari, A., Mignone, A., & Rossi, P. 2011, ApJ, 739, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Nordlund, A., Stein, R. F., & Torkelsson, U., 1995, ApJ, 446, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1960, Proc. Natl. Acad. Sci., 46, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, S. W., Stone, J. M., & Pessah, M. E. 2010, ApJ, 713, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Paletou, F., Bouvier, J., & Ferreira, J. 2005, Nature, 438, 466 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Frick, P. A., Noskov, V. I., Denisov, S. A., & Stepanov, V. A. 2010, Phys. Rev. Lett., 105, 184502 [NASA ADS] [CrossRef] [Google Scholar]
- Fromang, S., Papaloizou, J., Lesur, G., & Heinemann, T. 2007, A&A, 476, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., & Lynden-Bell, D. 1965, MNRAS, 130, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Gressel, O. 2010, MNRAS, 405, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1995, ApJ, 440, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 464, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Herault, J., Rincon, F., Cossu, C., et al. 2011, Phys. Rev. E, 84, 036321 [NASA ADS] [CrossRef] [Google Scholar]
- Käpylä, P. J., & Korpi, M. J. 2011, MNRAS, 413, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Longaretti, P.-Y. 2007, MNRAS, 378, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Ogilvie, G. I. 2008, A&A, 488, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miralles, S., Bonnefoy, N., Bourgoin, M., et al. 2013, Phys. Rev. E, 88, 013002 [NASA ADS] [CrossRef] [Google Scholar]
- Oishi, J. S., & Mac Low, M.-M. 2011, ApJ, 740, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Rahbarnia, K., Brown, B. P., Clark, M. M., et al. 2012, ApJ, 759, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Rincon, F., Ogilvie, G. I., & Proctor, M. R. E. 2007, Phys. Rev. Lett., 98, 254502 [NASA ADS] [CrossRef] [Google Scholar]
- Rincon, F., Ogilvie, G. I., Proctor, M. R. E., & Cossu, C. 2008, Astron. Nachr., 329, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Riols, A., Rincon, F., Cossu, C., et al. 2013, J. Fluid Mech., 731, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. B., Hawley, J. F., & Beckwith, K. 2011, ApJ, 730, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Velikhov, E. P. 1959, Sov. Phys. JETP, 36, 1398 [Google Scholar]
All Figures
 |
Fig. 1 Maps of the dynamical lifetime in generic DNS, as a function of Re and Rm (Lx = 0.7, Ly = 20, Lz = 2). Each row is for a different random initial condition. The second and third maps (from top to bottom) use the same noise realization (see text) but different amplitudes (A = 5 for the second case and A = 2.5 for the third case). The maps on the left are for simulations at mild Re and Rm that can be conducted at moderate numerical resolution (48 × 48 × 72). The maps on the right are for higher Re and Rm, requiring a higher resolution (96 × 96 × 128). The dashed line corresponds to Pm = 1. |
| In the text | |
 |
Fig. 2 Maps of dynamical lifetimes as a function of Rm and initial perturbation amplitude A, for a fixed noise realization (see text) and six different Re. The resolution is (δA = 0.04,δRm = 2) except for Re = 70 where (δA = 0.02,δRm = 1) and for Re = 550 where δRm = 5. |
| In the text | |
 |
Fig. 3 Existence boundaries of three cycle pairs (dashed lines) in the (Re,Rm) plane and critical Rec(Rm), Rmc(Re) of saddle nodes obtained by continuation (symbols). Black arrows indicate the regions in which the cycles exist. For SN1, dark blue/black bullets correspond to low resolution results (24 × 12 × 36), and light blue/grey bullets are for double resolution (48 × 24 × 72). Inset: selected continuation curves of SN1 at fixed Rm. |
| In the text | |
 |
Fig. 4 Magnetic energy budgets as a function of Re: a) x projection of the budgets for |
| In the text | |
 |
Fig. 5 Ratio between nonlinear dissipation Dtx and injected energy I0x + I1x for LB1 and UB1 and two different Rm. |
| In the text | |
 |
Fig. 6 Energy budget of simulations integrated over St = Ly/Lx for three values of Rm. Left: net energy gain Δℰm as a function of Re and |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


