| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201423713 | |
| Published online | 10 February 2015 | |
A two-mode planetary nebula luminosity function
1 Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México, Ap. 70-543, 04510 D.F., México Mexico
e-mail: ary@nucleares.unam.mx
2 Instituto Nacional de Astrofísica, Óptica y Electrónica, Ap. 51, 72000 Puebla, México, Mexico
3 Instituto de Astronomía, Universidad Nacional Autónoma de México, Ap. 70-264, 04510 D.F., México, Mexico
4 LUTH, Observatoire de Meudon, 92195 Meudon Cedex, France
Received: 26 February 2014
Accepted: 4 November 2014
Context. We propose a new planetary nebula luminosity function (PNLF) that includes two populations in the distribution. Our PNLF is a direct extension of the canonical function proposed by Jacoby et al. (1987), in order to avoid problems related with the histogram construction, it is cast in terms of cumulative functions.
Aims. We are interested in recovering the shape of the faint part of the PNLF in a consistent manner, for galaxies with and without a dip in their PNLFs.
Methods. The parameters for the two-mode PNLF are obtained with a genetic algorithm, which obtains a best fit to the PNLF varying all of the parameters simultaneously in a broad parameter space.
Results. We explore a sample of nine galaxies with various Hubble types and construct their PNLF. All of the irregular galaxies, except one, are found to be consistent with a two-mode population, while the situation is less clear for ellipticals and spirals.For the case of NGC 6822, we show that the two-mode PNLF is consistent with previous studies of the star formation history within that galaxy. Our results support two episodes of star formation, in which the second episode is significantly stronger.
Key words: planetary nebulae: general / galaxies: luminosity function, mass function
© ESO, 2015
1. Introduction
More than two decades ago, several authors reported that the bright end of the distribution function of planetary nebula (PN), as a function of their magnitude in the [O iii] 5007 line, was remarkably similar in a large sample of galaxies (Jacoby et al. 1990a,b; Ciardullo 2012, and references therein). The galaxies studied were mainly ellipticals, irregulars, and a few spirals. In particular, they found that the bright cutoff of the planetary nebula luminosity function (PNLF) is consistent with a universal absolute magnitude 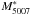 , from which a distance modulus can be calculated, and thus PNLFs have been used as standard candles to estimate the distance to galaxies where PNe are observed.
, from which a distance modulus can be calculated, and thus PNLFs have been used as standard candles to estimate the distance to galaxies where PNe are observed.
Among such studies are those by Jacoby et al. (1989) for M 81, Ciardullo et al. (1989b) for the Leo I group, Jacoby et al. (1990a) for the Virgo Cluster, Pottasch (1990) for the galactic center, Jacoby et al. (1990b) for the Magellanic Clouds, Ciardullo et al. (1991) for the NGC 1023 group, McMillan et al. (1993) for the Fornax Cluster, Jacoby et al. (1996) for the Coma I region, Feldmeier et al. (1997) for several spiral galaxies, Peña et al. (2007 for NGC 3109, Herrmann et al. (2008) for several face-on spiral galaxies, Hernández-Martínez & Peña (2009) for NGC 6822, and Peña et al. (2012) for NGC 300.
A number of studies attempted to understand how, why, or in what type of galaxies the PNLF cutoff can be used as a standard candle for distance estimates (Dopita et al. 1992; Méndez et al. 1993; Ciardullo et al. 1989a,b); however, the physical mechanism responsible for such universality in the 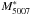 , especially across galaxies of different Hubble types, is still not clear.
, especially across galaxies of different Hubble types, is still not clear.
Theoretical attempts to model the PNLF of an old stellar population, corresponding to what we expect to find in elliptical galaxies, assuming single-star post-AGB evolution, have not been successful (Marigo et al. 2004; Ciardullo 2006). A possible explanation could involve massive central stars in old populations produced through binary evolution (i.e., Ciardullo et al. 2005). More recently, using fully hydrodynamical simulations of the evolution of PNe, Schönberner et al. (2007) argue that there is no need to invoke central stars with masses over 0.7 M⊙ to account for the bright end of the PNLF. At present the invariance of 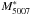 in all Hubble-type galaxies is still an open question.
in all Hubble-type galaxies is still an open question.
Henize & Westerlund (1963) were the first to compute a PNLF. They assumed that PNe are objects of constant mass and are subject to uniform expansion velocity, so that they fade as a result of expansion. The number of PNe between magnitudes M and M + dM is proportional to the time spent in that magnitude range. Jacoby (1980) showed that observations of the faint PNe in the LMC fit well the luminosity function proposed by HW63. In general, the faint part of the observational PNLF follows the HW63 model, while the brightest part decreases more steeply.
On the other hand, Ciardullo et al. (1989a, hereafter C89) showed that the brightest part of the PNLF can be reproduced by an exponential cutoff. Using the magnitudes of [O iii] 5007, C89 found a good agreement between their theoretical PNLF and observations of PNe in 24 spiral and elliptical galaxies. Fitting the exponential cutoff in combination with the HW63 luminosity function, C89 suggested that PNe could be used as standard candles.
While the upper end of the PNLF is invariant among galaxies, its global shape may vary from one galaxy to another. Some galaxies, like the Small Magellanic Cloud (SMC, Jacoby & de Marco 2002, hereafter JM02) present a dip in the PNLF, others do not. The details of the interpretation of this dip vary among authors, but in essence it is considered to be a result of the rapid decline in luminosity of the most massive central stars descending the white dwarf cooling track not being compensated by the presence of PNe with less massive central stars (Jacoby & de Marco 2002; Marigo et al. 2004; Méndez et al. 2008). Thus, the presence or absence of a dip in the PNLF can be a signature of the star formation history of those stellar populations that give rise to the PNe detected at present in the galaxies. However, since the canonical PNLF does not account for the presence of such a dip, it is customary to restrict the data used to derive the PNLF parameters to the brightest end when it shows evidence of a decrease in number of PNe towards larger magnitudes.
Hernández-Martínez & Peña (2009, hereafter HMP09) constructed the PNLF of the dwarf irregular NGC 6822 and found a statistically significant dip in the luminosity function. In both the SMC and NGC 6822 the PNLF dip is ~2.5 mag fainter than the brightest PNe. Carigi et al. (2006) and Hernández-Martínez et al. (2009) presented a study of the star formation history of NGC 6822, showing evidence of two important star forming episodes, which could be related to a dip seen in the PNLF (see Sect. 6). A similar dip is seen in the PNLF of other galaxies which are known to have more than one star formation episode (the SMC for instance, see Nöel et al. 2008).
If the PNe sample is large, obtaining the LF via the traditional χ2 approach is relatively simple because one could fit the PNLF to a histogram built with the data (i.e., Méndez et al. 2001; Teodorescu et al. 2005; Johnson et al. 2009). However, if the sample of PNe is small, this procedure becomes very sensitive to the parameters used to construct the histogram (i.e., bin size, number of bins, range of values used). For instance the presence of a dip can be missed by a slight change in bin size or position. In order to minimize these uncertainties C89, based on Hanes & Whittaker (1987), perform a maximum likelihood analysis, from which they obtain the fitting parameters of the function. Alternatively, Peña et al. (2007) fitted small samples of PNe to a cumulative luminosity function. The cumulative luminosity function is also insensitive to the histogram parameters, but some important features of the canonical PNLF could be masked (for instance the dip).
Another problem with the PNLF is that the sample can be incomplete at the faint end. In fact, since the most important parameter used in the canonical PLNF is the magnitude of the brightest PN (see the following section), usually only the brightest PNe in the analysis. However, it is not clear what is the appropriate range, and by restricting the sample, the incompleteness could lead to misidentifying a dip.
We built a cumulative PNLF in order to use small or large samples. We only restrict the data at the faint end when incompleteness of the sample is obvious, even if there is evidence of a dip in the sample.
An important goal of this paper is to recover the shape of the faint part of the PNLF in a consistent manner, for galaxies with and without a dip in their PNLFs. The proposed PNLF is based on the function by Ciardullo et al. (1989a).
The paper is organized as follows:
In Sect. 2 we review the properties of the canonical PNLF and its cumulative form. A two-mode PNLF is described in Sect. 3, and in Sect. 4 we present the results of the PNLF for a sample of nine galaxies. In Sect. 5 we show that the two-mode function can be consistent with other observational data. A summary is provided in Sect. 6.
2. Cumulative and non-cumulative PNLFs
Usually, larger samples allow smaller bins to form a histogram with more detail without losing its general shape (see Hogg 2008). Some studies with large samples suggest that the bin size should be related to the dispersion and the total number of data points (Scott 1979). For instance, for normally distributed samples it has been proposed that a bin size 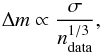 (1)is appropiate, where σ is the standard deviation and ndata is the number of data points in the sample.
(1)is appropiate, where σ is the standard deviation and ndata is the number of data points in the sample.
For the PNLF this is not the case, the optimal bin size to present it as a histogram can be chosen after the data has been fit, for instance by a maximum likelihood analysis (see C89). However, it does not correlate simply with the sample size.
More recently, Herrmann et al. (2008) presented the PNLFs for several spiral galaxies. All of the observational PNLFs constructed therein used a uniform bin size (~0.3 mag), regardless of the number of PNe in each galaxy (ranging from 20 to 150 objects). Reid & Parker (2010) added 80 PNe to the luminosity function of the LMC, with 584 objects and a bin size of 0.2 mag.
We note that the bin size is not the only parameter that determines a histogram; also the maximum and minimum magnitude, as well as the center of the bins are also important. The selection of the position of the bin center can also be important to find a dip in the PNLF. If a histogram is used to restrict the data to be fit, the presence of a dip can be confused with sample incompleteness and indirectly affect the fit.
One way to avoid potential binning issues (which has been adopted in some studies) is to use cumulative distribution functions. For instance, the cumulative function of the PNLF was recently fitted to a sample of ~20 PNe in NGC 3109 by Peña et al. (2007). From their estimate of 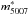 , the authors obtained a distance modulus from the PNLF in good agreement with the value obtained from Cepheid stars. As we will show in the next section, the fitting of the observational data with cumulative functions is not affected by the histogram considerations, such as the bin size, limits, or the position of the first bin.
, the authors obtained a distance modulus from the PNLF in good agreement with the value obtained from Cepheid stars. As we will show in the next section, the fitting of the observational data with cumulative functions is not affected by the histogram considerations, such as the bin size, limits, or the position of the first bin.
The canonical form of the PNLF (based on the function of HW63, with the exponential cutoff suggested by C89) is ![\begin{equation} \label{eq:pnlf} N(m_{5007})=n\,{\rm{e}}^{-0.307\mu}{\rm{e}}^{0.307m_{5007}}\left[1-{\rm{e}}^{3(m^*_{5007}-m_{5007})}\right], \end{equation}](/articles/aa/full_html/2015/03/aa23713-14/aa23713-14-eq12.png) (2)where n is a normalization constant,
(2)where n is a normalization constant, 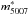 is the apparent λ5007 magnitude of the brightest PN that can exist in a given galaxy, μ = 5log d − 5 + A5007 is the distance modulus, and A5007 is the extinction. In order to simplify the notation we will substitute NT = n e− 0.307μ in Eq. (2)and drop the 5007 subindices to obtain
is the apparent λ5007 magnitude of the brightest PN that can exist in a given galaxy, μ = 5log d − 5 + A5007 is the distance modulus, and A5007 is the extinction. In order to simplify the notation we will substitute NT = n e− 0.307μ in Eq. (2)and drop the 5007 subindices to obtain ![\begin{equation} \label{eq:pnlf2} N(m;N_T,m^*)=N_T {\rm{e}}^{0.307m}\left[1-{\rm{e}}^{3(m^*-m)}\right]. \end{equation}](/articles/aa/full_html/2015/03/aa23713-14/aa23713-14-eq19.png) (3)As discussed above, empirical evidence suggests that the absolute magnitude
(3)As discussed above, empirical evidence suggests that the absolute magnitude 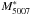 is the same for all galaxies. Ciardullo et al. (2002) derived different
is the same for all galaxies. Ciardullo et al. (2002) derived different 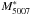 for different metallicities; the difference is not very significant so PNe have been regarded as standard candles and are widely used in the so-called cosmic ladder as a distance indicator.
for different metallicities; the difference is not very significant so PNe have been regarded as standard candles and are widely used in the so-called cosmic ladder as a distance indicator.
Several observations of the PNLF in nearby galaxies (IC 342, M 74, M 83, M 94, see also Herrmann et al. 2008), in which the canonical luminosity function of Jacoby et al. (1990) is in good agreement with the observed function at least in the brightest 1.5 mag, support the use of this portion of the PNLF as a distance indicator. However, the faintest part cannot always be reproduced by the exponential shape, and almost all such studies blame it on the incompleteness of the sample.
As we have mentioned before, the observed PNLFs for two irregular galaxies, i.e., SMC, NGC 6822 (see JM02, HMP09), show a dip at about 2.5 mag after which the PNLF rises again and then drops at the end of the sample. This decrease in the number of PNe could be considered as evidence of an additional stellar population or a different evolutionary scenario for the central stars in the PNe. In these cases, the authors have also focused only on the brightest PNe observed to estimate distances.
One of the techniques used to estimate the PNLF is to build a histogram of the apparent magnitudes of the PNe and fit the brightest portion of this histogram to the functional form of the PNLF to estimate m∗ and NT. This procedure is particularly tricky because the number of bins, the bin size and the initial position of the first bin are treated as free parameters, and they are commonly determined arbitrarily. In fact, the choice of bin size and position of the first bin can determine whether a dip in the PNLF is present or not.
The already limited number of PNe available for a given galaxy often results in a problem of small statistics. At the same time, the binning procedure reduces the data to only a few points, of which only those corresponding to the brightest PNe are used for the fit, and thus the issue of small number statistics is only aggravated.
A cumulative PNLF has the advantage of improving the statistics by using more points to do the fit, while the assumptions about the histogram bins (i.e., size and number) are no longer necessary.
The cumulative PNLF can be obtained as 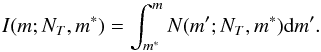 (4)Using Eqs. (3) and (4) one obtains,
(4)Using Eqs. (3) and (4) one obtains, ![\begin{eqnarray} I(m;N_T,m^*)&=&N_T\left[{\rm{A}}\,{\rm{e}}^{3m^*-B m}+C\,{\rm{e}}^{0.307m} \nonumber\right. \\ & & \left. -(A+C)\,{\rm{e}}^{0.307m^*}\right], \label{eq:cumulative} \end{eqnarray}](/articles/aa/full_html/2015/03/aa23713-14/aa23713-14-eq23.png) (5)where, A = 0.37 133, B = 2.693 and C = 3.25 733. An example of this cumulative PNLF can be found in Peña et al. (2007), where it was obtained for a sample of 20 PNe from NGC 3109.
(5)where, A = 0.37 133, B = 2.693 and C = 3.25 733. An example of this cumulative PNLF can be found in Peña et al. (2007), where it was obtained for a sample of 20 PNe from NGC 3109.
If the cumulative PNLF is used, the uncertainties introduced by the binning procedure are eliminated, however there is still the issue of restricting the fit to the brightest PNe in the sample. Certainly at the faintest end the PNe sample is incomplete, and the luminosity function will have a drop in number (a plateau if the cumulative function is considered).
In star-forming galaxies where a dip is present, it is not easy to fit the PNLF (standard or cumulative), and what is usually done is to restrict the fit to the brightest PNe, before the dip in the luminosity function. Results obtained for these galaxies agree (within the error bars) with the canonical value of 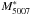 . If the dip is due to a second stellar population, the underlying assumption is that this second one does not overlap with the first population of the bright end of the PNLF, at least in the portion used to fit the data.
. If the dip is due to a second stellar population, the underlying assumption is that this second one does not overlap with the first population of the bright end of the PNLF, at least in the portion used to fit the data.
3. The two-mode planetary nebula luminosity function
Since the number of observable PNe in extragalactic sources is rather limited, we would like to use as many objects as possible to characterize their luminosity function. In this regard the cumulative PNLF seems the most natural choice. Instead of restricting the analysis to the brightest PNe in the sample, we propose to explicitly include a second mode in the fitted luminosity function. Of course, any new two-mode luminosity function must have the same properties as the canonical PNLF in order to reproduce the results for galaxies with a single mode. One should point out that using a cumulative function, the data fit may have some inconsistencies due to lack of statistical independence of the cumulative data.
Thus, the proposed two-mode PNLF is: 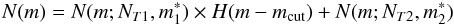 (6)where, H(m − mcut) is the Heaviside step function, defined as
(6)where, H(m − mcut) is the Heaviside step function, defined as 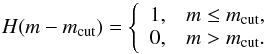 (7)The proposed function is the sum of two standard PNLFs, allowing each mode to have a different NT, and m∗. One of the two-modes is truncated abruptly at a magnitude (mcut); this is a simple mathematical artifact, certainly, and one could introduce another cutoff for the second population, or extend the function to three or more modes. However, in the spirit of having as few free parameters as possible we will adopt the form in Eq. (6).
(7)The proposed function is the sum of two standard PNLFs, allowing each mode to have a different NT, and m∗. One of the two-modes is truncated abruptly at a magnitude (mcut); this is a simple mathematical artifact, certainly, and one could introduce another cutoff for the second population, or extend the function to three or more modes. However, in the spirit of having as few free parameters as possible we will adopt the form in Eq. (6).
A cumulative function of the two-mode luminosity function of Eq. (6) can be obtained by integrating over the magnitude. Integration of the first mode gives ![\begin{eqnarray} I_1(m;N_{T1},m^*_1,m_{\rm cut}) & = &\int^{m_{\rm up}}_{m_1^*}N(m';N_{T1},m^*_1){\rm{d}}m', \label{eq:I1a} \\ & = & N_{T1}\left[A\,{\rm{e}}^{3m^*_1-B m_{\rm up}}+C\,{\rm{e}}^{0.307 m_{\rm up}}\nonumber \right.\\ & & \left.-(A+C)\,{\rm{e}}^{0.307m^*_1}\right], \end{eqnarray}](/articles/aa/full_html/2015/03/aa23713-14/aa23713-14-eq31.png) where the integration is stopped at mcut by virtue of
where the integration is stopped at mcut by virtue of 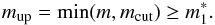 (10)We note that after the cutoff magnitude mcut the first luminosity function drops to zero, but the cumulative remains at a constant value. The integration of the second mode is analogous to the sample population case (for
(10)We note that after the cutoff magnitude mcut the first luminosity function drops to zero, but the cumulative remains at a constant value. The integration of the second mode is analogous to the sample population case (for 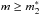 ),
), ![\begin{eqnarray} \label{eq:I2} I_2(m;N_{T2},m^*_2)&= & N_{T2}\left[A\,{\rm{e}}^{3m^*_2-B m}+C\,{\rm{e}}^{0.307 m}\right.\nonumber \\ & &\left.-(A+C)\,{\rm{e}}^{0.307m^*_2}\right]. \end{eqnarray}](/articles/aa/full_html/2015/03/aa23713-14/aa23713-14-eq34.png) (11)The total cumulative luminosity function is then the sum of the two-modes:
(11)The total cumulative luminosity function is then the sum of the two-modes: 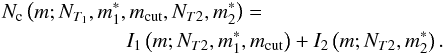 (12)
(12)
4. Results
We have used observations of nine galaxies described below and constructed their cumulative PNLFs (Table 1). We then use the aga-v1 code (Rodríguez-González et al. 2012) for each galaxy to obtain the best fit of one- and two-mode cumulative PNLFs. The aga-v1 code uses the Asexual Genetic Algorithm described in Cantó et al. (2009), and allows us to find the best fit exploring a wide parameter range in order to minimize a merit function, in this case a χ2. The code varies simultaneously and independently all the parameters of the fit in such a space.
To estimate the uncertainty in our fitting procedure, we perform 100 realizations for every PNLF in each galaxy presented in this paper. Each realization is obtained by varying the original data as follows: 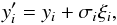 (13)where
(13)where 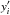 represents the ith data point of the new set, yi and σi are the original data and its associated errors, which are assumed to follow a Poisson distribution,
represents the ith data point of the new set, yi and σi are the original data and its associated errors, which are assumed to follow a Poisson distribution, 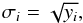 (14)and ξi is a uniformly distributed random deviate. Each data set constructed is fed to the aga-v1 code and yields a set of fitting parameters that minimize the χ2 merit function. We allow the code to find
(14)and ξi is a uniformly distributed random deviate. Each data set constructed is fed to the aga-v1 code and yields a set of fitting parameters that minimize the χ2 merit function. We allow the code to find 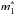 ,
, 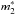 , and mcut anywhere from half a magnitude below the minimum in the sample to half a magnitude above the maximum in the sample; the range covered for NT,1 and NT,2 is from 10-7 to 102. An additional constraint that we have enforced is that
, and mcut anywhere from half a magnitude below the minimum in the sample to half a magnitude above the maximum in the sample; the range covered for NT,1 and NT,2 is from 10-7 to 102. An additional constraint that we have enforced is that 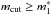 , otherwise the results are unphysical. It is important, however, to mention that
, otherwise the results are unphysical. It is important, however, to mention that 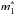 and
and 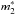 are allowed to be smaller or larger than each other.
are allowed to be smaller or larger than each other.
The aga-v1 code is similar to many Monte Carlo methods, where an ensemble average is used to obtain the average values and the dispersion of the parameters of the fit. Thus, from the 100 realizations for each galaxy we obtain the fit parameters from the average value of each of the parameters (NT1, m ∗ 1, mcut, m ∗ 2, and NT2); and an estimate of the uncertainty (from standard deviation).
Sample of galaxies with Hubble-type, number of PNe and some previous fit values.
In addition we compute a Kolmogorov-Smirnov (K-S) test, in order to asses the likelihood of the data and the proposed function (Eq. (12)) to arise from the same distribution.
 |
Fig. 1 Cumulative PNLF of the Large Magellanic Cloud. The triangles are the data from Reid & Parker (2010) and the solid line is our two-mode fit. |
The K-S test gives two measures of the goodness of the fit: a significance level with a value between 0 and 1, listed simply as K-S in Table 10 (a value close to 0 means that the data and the function are significantly different), and the maximum departure (listed as D) between the cumulative function of the data and the function provided. Ciardullo et al. (1989a), Feldmeier et al. (1997), and Herrmann et al. (2008) also used a K-S test to compare their fits (from a maximum likelihood method) to observations.
Our best fits are presented in Table 2, where we named the galaxies, and describe for each of them the best fit parameters (NT,1, 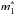 , mcutNT,2 and
, mcutNT,2 and 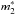 ) for the cumulative PNLF. In Table 2 we show the results of these tests in our best fits (presented in Table 2), the number of the galaxy, the total number of PNe and the number of PNe used for each fit, the K-S and D values for the test, and the number of modes in the cumulative PNLF.
) for the cumulative PNLF. In Table 2 we show the results of these tests in our best fits (presented in Table 2), the number of the galaxy, the total number of PNe and the number of PNe used for each fit, the K-S and D values for the test, and the number of modes in the cumulative PNLF.
4.1. The sample of galaxies
In order to explore the PNLF for galaxies of differents Hubble-types, we selected nine galaxies: four irregulars (SMC, LMC, NGC 6822, NGC3109), three spirals (NGC 300, M 31 and M 33), a dwarf elliptical (NGC 205), and an elliptical galaxy (NGC 4697).
In Table 1, we describe the sample by name, Hubble-type of the galaxy, number of PNe observed, and two fit parameters of the PNLF (Nexp( − 0.307μ) and 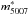 ). For some galaxies, we show two fit parameter values, because the authors that present de PNe sample do not fit a PNLF. For NGC 205, we take the inside sample of PNe, since Corradi et al. (2005) find that the other ones are very faint.
). For some galaxies, we show two fit parameter values, because the authors that present de PNe sample do not fit a PNLF. For NGC 205, we take the inside sample of PNe, since Corradi et al. (2005) find that the other ones are very faint.
Cumulative PN luminosity function fits.
For LMC, we take the sample of Reid & Parker (2010); in Fig. 1 we show the observations and the fit to the cumulative PNLF in the LMC. The triangles are the observational data presented by Reid & Parker (2010) and the solid line is our best fit using the two-mode cumulative PNLF (Eq. 12, hereafter 2mc-PNLF).
Our best fit yields 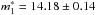 , NT1 = (1.71 ± 0.04) × 10-1, mcut = 15.95 ± 0.4, NT2 = (1.19 ± 0.01) × 10-1, and
, NT1 = (1.71 ± 0.04) × 10-1, mcut = 15.95 ± 0.4, NT2 = (1.19 ± 0.01) × 10-1, and 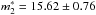 . A Kolmogorov-Smirnov test shows that the 2mc-PNLF is not inconsistent with the data (the value of the K-S paramters are also listed in Table 3). The value of
. A Kolmogorov-Smirnov test shows that the 2mc-PNLF is not inconsistent with the data (the value of the K-S paramters are also listed in Table 3). The value of 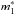 is in very good agreement with that reported by Peña et al. (2007) for
is in very good agreement with that reported by Peña et al. (2007) for 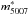 , while the NT1 obtained by the 2mc-PNLF is lower than the NT for the simple cumulative PNLF. Naturally, the reason for this is that the total population of PNe is divided into two populations as proposed in Eq. (12): NT is related to the number of PN expected at a certain magnitude m, and NT1 and NT2 are related to the number of PNe in the first and in the second mode (or population), respectively. From the values of
, while the NT1 obtained by the 2mc-PNLF is lower than the NT for the simple cumulative PNLF. Naturally, the reason for this is that the total population of PNe is divided into two populations as proposed in Eq. (12): NT is related to the number of PN expected at a certain magnitude m, and NT1 and NT2 are related to the number of PNe in the first and in the second mode (or population), respectively. From the values of 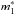 ,
, 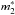 , and mcut, we know that the PNe for the first mode of the function (the brightest one) the second mode overlap in the ~14.56 to ~15.87 mag range. Therefore, NT includes a contribution from the second population. Thus, one should not expect NT and NT1 to coincide in general, but rather NT1 ≤ NT.
, and mcut, we know that the PNe for the first mode of the function (the brightest one) the second mode overlap in the ~14.56 to ~15.87 mag range. Therefore, NT includes a contribution from the second population. Thus, one should not expect NT and NT1 to coincide in general, but rather NT1 ≤ NT.
Kolmogorov-Smirnov test results.
For the SMC, Jacoby & De Marco (2002) obtained a statistically complete PNLF in 10 mag (from 14 to 24). Their Fig. 6 shows a dip, starting at a magnitude of 17, and ending at 20 mag. The cumulative PNLF is shown in Fig. 2 with the crosses. The best fit using our 2mc-PNLF (continuous line) gives NT1 = 3.97 × 10-2, 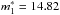 , and mcut = 17.29 for the first mode and NT2 = 1.46 × 10-2 and
, and mcut = 17.29 for the first mode and NT2 = 1.46 × 10-2 and 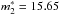 for the second one. Our mcut( = 17.29) fits very well with the dip seen in the observed PNLF.
for the second one. Our mcut( = 17.29) fits very well with the dip seen in the observed PNLF.
 |
Fig. 2 Cumulative PNLF of the Small Magellanic Cloud. The plus symbols are the data from Jacoby & De Marco (2002), the solid is our two-mode fit. |
 |
Fig. 3 Cumulative PNLF of NGC 6822. The plus signs and the dashed line are the data and the fit of HMP09, respectively. The solid line is our two-mode fit. |
 |
Fig. 4 PNLF (non-cumulative) of NGC 6822. The thin solid line and the dashed line are the histogram of the observational data and the fit of HMP09, respectively. The dotted and dashed-dotted lines are the first and the second mode of our fitted function and the thick solid line is our two-mode fit. |
Figure 3 shows the cumulative luminosity function of the PNe in NGC 6822. The plus symbols and the dashed lines are the observational data and the empirical PNLF presented by HMP09. Their best fit is given by NT = 5 × 10-3, m∗ = 20.43, and a break in the PNLF distribution at a magnitude of ~22.65. They related the break (dip in the non-cumulative PNLF) with a second population in this galaxy. The best fit using the 2mc-PNLF yields NT1 = 3.01 × 10-3, 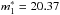 , mcut = 20.6, NT2 = 3.21 × 10-3, and
, mcut = 20.6, NT2 = 3.21 × 10-3, and 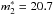 . In Fig. 4 we show the non-cumulative luminosity functions for the same galaxy, the dashed line is the empirical PNLF and the solid line is the non-cumulative PNLF obtained with the parameters of the PNLF fit. The dotted and dash-dotted lines are the individual modes of the PNLF. The PNLF fits well the observational data of NGC 6822. We note that the locus and the depth of the dip are reproduced with our fit.
. In Fig. 4 we show the non-cumulative luminosity functions for the same galaxy, the dashed line is the empirical PNLF and the solid line is the non-cumulative PNLF obtained with the parameters of the PNLF fit. The dotted and dash-dotted lines are the individual modes of the PNLF. The PNLF fits well the observational data of NGC 6822. We note that the locus and the depth of the dip are reproduced with our fit.
NGC 3109 has a peculiar PNLF, which is shown in Fig. 5. What is particular about this galaxy is the void in its luminosity function around mOIII ~ 25, which could be identified as the signature of a second PN population. However, the fitting algorithm applied to the PNLF of NGC 3109 yielded a solution consistent with a single mode. The algorithm yielded a second mode with 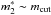 ; the fit parameters are given in Table 2. This effective single mode was somewhat worrisome since there is a noticeable plateau in the cumulative function at mOIII ~ 25. For this reason we re-ran the fitting algorithm, first with a single population, and then with two-modes, but arbitrarily restricting mcut to lie in the range of 23.5−25.5 mag.
; the fit parameters are given in Table 2. This effective single mode was somewhat worrisome since there is a noticeable plateau in the cumulative function at mOIII ~ 25. For this reason we re-ran the fitting algorithm, first with a single population, and then with two-modes, but arbitrarily restricting mcut to lie in the range of 23.5−25.5 mag.
 |
Fig. 5 Cumulative PNLF of NGC 3109. The plus signs and the dashed line are the observational data and the single mode fitted in Peña et al. (2007). The solid line and the dotted lines are the one- and two-mode best fits, respectively, obtained with our genetic algorithm. |
In order to explore possible correlations between the fitting parameters, we calculate the covariance matrix (see Feigelson & Babu 2012), 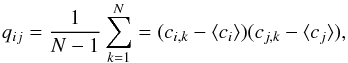 (15)where ci and cj are the fitting parameters (i.e., NT1, m ∗ 1, mcut, NT2,
(15)where ci and cj are the fitting parameters (i.e., NT1, m ∗ 1, mcut, NT2, 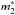 ) and the sum is carried out over 100 realizations (N = 100); ⟨ ci ⟩ and ⟨ cj ⟩ are the mean values obtained over the realizations (see Table 2). Using the mean values of the fitting parameters presented in row 5 of Table 2 and the fitting parameters obtained for each of the realizations we calculated the covariance matrix PNLF of NGC 3109,
) and the sum is carried out over 100 realizations (N = 100); ⟨ ci ⟩ and ⟨ cj ⟩ are the mean values obtained over the realizations (see Table 2). Using the mean values of the fitting parameters presented in row 5 of Table 2 and the fitting parameters obtained for each of the realizations we calculated the covariance matrix PNLF of NGC 3109,  One can see that the covariance matrix has cross-correlations close to zero (given by the off-diagonal matrix coefficients). These small values indicate that pairs of fitting parameters are not linearly correlated. Moreover, orthogonality tests for the fitting parameters show that NT1 and NT2 are orthogonal and all pairs of fitting parameters have angles close to 90°.
One can see that the covariance matrix has cross-correlations close to zero (given by the off-diagonal matrix coefficients). These small values indicate that pairs of fitting parameters are not linearly correlated. Moreover, orthogonality tests for the fitting parameters show that NT1 and NT2 are orthogonal and all pairs of fitting parameters have angles close to 90°.
Figures 6–8 show the cumulative PNLF for the spiral galaxies M 31, M 33, and NGC 300, respectively. For M 31 and M 33 the PNLF is consistent with two modes, but the shape of the luminosity function for these two galaxies is somewhat different. For M 31, the PNLF has a noticeable steepening of the slope after a magnitude ~22.5. The cutoff magnitude of the first population obtained for this galaxy is 22.29, while the second mode starts off at 22.17. Thus, in these galaxies the overlap of the two populations is marginal.
 |
Fig. 6 Cumulative PNLF of M 31. |
For M 33, the PNLF (Fig. 7) has a distinct break at a magnitude ~22.8. This is possible if the two populations do not overlap, as found from the fit, in which 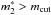 . For instance in Fig. 6 of Ciardullo et al. (2004) one could see evidence of two dips in their PNLF. In the present work we only confirm one dip at 22.9 mag, in accordance with their second dip, which is the sharper.
. For instance in Fig. 6 of Ciardullo et al. (2004) one could see evidence of two dips in their PNLF. In the present work we only confirm one dip at 22.9 mag, in accordance with their second dip, which is the sharper.
 |
Fig. 7 Cumulative PNLF of M 33. |
Figure 8 shows the PNLF of NGC 300 (a spiral galaxy). In our best fit the second mode of the PNLF starts very close to the completeness limit of the observational data, meaning that it is consistent with a single mode PNLF. However, the NT fit by Peña et al. (2012) is different from the value obtained using the present form of the PNLF. Again, as in the case of NGC 3109, NGC 300 has to be analyzed and the sample improved, basically by completing the whole galaxy, in order to explore the shape of the PNLF in more detail.
 |
Fig. 8 Cumulative PNLF of NGC 300. |
 |
Fig. 9 Cumulative PNLF of NGC 205. |
 |
Fig. 10 Cumulative PNLF of NGC 4697. |
In Fig. 9 the PNLF for the dwarf elliptical galaxy is shown. NGC 205 has a similar behavior to NGC 300, in which a second population was found to begin at a magnitude well within the region in which the sample is incomplete. Therefore, it can be considered as consistent with a single-mode PNLF.
Finally, Fig. 10 shows the PNLF for the elliptical galaxy NGC 4697. This data were obtained from Méndez et al. (2001); they argued the possibility of a dip, but with our method we do not support that idea. We clearly see only a one-mode PNLF.
As far as we can say from our study, it is not clear if the number of modes correlates directly with the Hubble type of the galaxy, but we can see that in most of the galaxies with recent star formation that a dip is present.
5. Are two-modes reasonable?
In most of the galaxies in our sample, in particular irregulars and spirals, we have shown that the PNLF can be fitted with two modes, Eq. (12). At the same time many studies have shown that the value of the absolute magnitude of the brightest PN is fairly uniform in a large sample of galaxies (C89). This could be explained if PNe are initially formed at a similar brightness M∗. The maximum brightness is attained for PNe with central stars having evolved from stars with initial masses around 2.5 solar masses (see Fig. 10 in Marigo et al. 2004). If galaxies with old stellar populations have the same M∗ as star forming galaxies, this means that their brightest PNe should have progenitors of equal masses. This is contrary to canonical stellar evolution, unless galaxies with old stellar populations have all experienced a recent star formation burst and there is no evidence for this. One way out of this problem is the scenario proposed by Ciardullo et al. (2005) in which the brightest PNe arise from the coalescence of two intermediate-mass stars.
The expansion of a PN will produce a drop in density, thus reducing its brightness. The decrease in brightness, in the case of ionization bounded PNe is also due to the decrease in the luminosity of the central star when it enters the white dwarf cooling track. As time proceeds, new bright PNe will be produced in the galaxy (from less massive stars) to replace those that have become fainter, and eventually the entire PNe distribution function will shift to larger magnitudes (Marigo et al. 2004).
In order to study the two-population PNLF one can consider the lifetime of a PN ~ 103 − 105 yr, which is small compared to the star progenitor lifetime. Thus, to some extent, the PNe that we observe are being produced by stars dying at the present time.
We assume a stellar initial mass function defined by Kroupa et al. (1993), 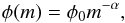 (16)where φ0 is a normalization constant, and
(16)where φ0 is a normalization constant, and 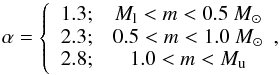 (17)where Ml = 0.1 M⊙ and Mu = 100 M⊙ are the lower and upper limits of the initial mass function. The number of stars or PN observed nowadays can be related to the star formation history ψ(t) (mass per unit time turned into stars at a given time t) as
(17)where Ml = 0.1 M⊙ and Mu = 100 M⊙ are the lower and upper limits of the initial mass function. The number of stars or PN observed nowadays can be related to the star formation history ψ(t) (mass per unit time turned into stars at a given time t) as 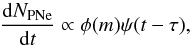 (18)where τ is the time elapsed since the last busrt.
(18)where τ is the time elapsed since the last busrt.
Therefore, the total number of PNe for two populations (labeled 1 and 2) can be estimated by,  where t1 and t2 are the time since the formation of each stellar population, assumed to have happened in bursts of width Δt. These equations also assume that populations 1 and 2 have PNe with the same lifetimes.
where t1 and t2 are the time since the formation of each stellar population, assumed to have happened in bursts of width Δt. These equations also assume that populations 1 and 2 have PNe with the same lifetimes.
Since PNe are formed by stars within a range of masses from ~1 to 8 M⊙, we should restrict the initial mass function to this range 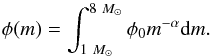 (21)Taking the lifetime of the stars to be a function of their mass, τ(m), we can estimate the age of the stars dying now for each population,
(21)Taking the lifetime of the stars to be a function of their mass, τ(m), we can estimate the age of the stars dying now for each population, 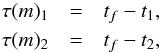 (22)where tf is the age of the host galaxy. The main sequence lifetime τMS(m) can be obtained, for instance, from stellar evolution models (i.e., Maeder & Meynet 1989). One can, however, invert the equation and obtain the mass of the stars that are progenitors of the PNe seen at the present time for each population. The ratio between the number of PNe from the first and the second population is given by (Eqs. (19)and (20)),
(22)where tf is the age of the host galaxy. The main sequence lifetime τMS(m) can be obtained, for instance, from stellar evolution models (i.e., Maeder & Meynet 1989). One can, however, invert the equation and obtain the mass of the stars that are progenitors of the PNe seen at the present time for each population. The ratio between the number of PNe from the first and the second population is given by (Eqs. (19)and (20)), 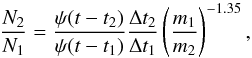 (23)Carigi et al. (2006), based on the spectrophotometric study of Wyder (2001; 2003), obtained the star formation history of NGC 6822 and found evidence for two separate events of star formation. From their results we can estimate the N1/N2 ratio of the two stellar populations. The NGC 6822 estimated age is ~13.5 Gyr, and the peak of each starburst of this galaxy (see Fig. 4 in Carigi et al. 2006), occurred at t1 = 8 Gyr and t2 = 11.5 Gyr. Using these values in Eq. (22), we obtain τ(m)1 = 5.5 Gyr and τ(m)2 = 2 Gyr. From the models of Maeder & Meynet (1989) we can estimate the mass of the stars dying at the present time to be m1 ~ 1.45 M⊙ and m2 ~ 1.8 M⊙.
(23)Carigi et al. (2006), based on the spectrophotometric study of Wyder (2001; 2003), obtained the star formation history of NGC 6822 and found evidence for two separate events of star formation. From their results we can estimate the N1/N2 ratio of the two stellar populations. The NGC 6822 estimated age is ~13.5 Gyr, and the peak of each starburst of this galaxy (see Fig. 4 in Carigi et al. 2006), occurred at t1 = 8 Gyr and t2 = 11.5 Gyr. Using these values in Eq. (22), we obtain τ(m)1 = 5.5 Gyr and τ(m)2 = 2 Gyr. From the models of Maeder & Meynet (1989) we can estimate the mass of the stars dying at the present time to be m1 ~ 1.45 M⊙ and m2 ~ 1.8 M⊙.
For the two bursts of star formation derived by Carigi et al. (2006) we then have
-
burst 1: t1 = 5 Gyr ago. The stars from this burst which are producing PNe today have a mass of m1 ≈ 1.4 M⊙;
-
burst 2: t2 = 0.74 Gyr ago. The stars from this burst which are producing PNe today have a mass of m2 ≈ 2.5 M⊙.
For each of the two bursts, we will have PNe corresponding to stars of masses M1 and M2, respectively, at all stages of their evolution since the nebulae evolve and dissipate in timescales of ~104 yr, which are much smaller than the duration of the bursts. In Fig. 11 we show the [O III] magnitude M5007 as a function of evolutionary time tev (from the beginning of the PNe phase) of the nebula produced by stars of masses M1 and M2, taken from Fig. 10 in Marigo et al. (2004).
 |
Fig. 11 M5007 (absolute magnitude of the 5007 line) versus PN age for two progenitor masses, 2.5 (dashed line) and 1.4 (solid line) M⊙ (taken from Fig. 10 in Marigo et al. 2004). |
 |
Fig. 12 Frequency rate for the PNe of the two bursts versus M50007. The short-dashed line shows the normalized frequency for the second burst, and the long-dashed line shows the normalized frequency (multiplied by 0.3) for the first burst. The solid line is the sum. |
If we assume that the star formation rate was uniform within the ~104 yr total evolutionary time of the observed PNe, from the M5007(tev) curves in Fig. 11 we can obtain the frequency distribution of the nebula as ![\begin{equation} f(M_{5007})=A\,\left[\left(\frac{{\rm{d}}t_{\rm ev}}{{\rm{d}}_{M_5007}}\right)_{t_a}+\left(\frac{{\rm{d}}t_{\rm ev}}{{\rm{d}}_{M_5007}}\right)_{t_b}\right], \label{fm} \end{equation}](/articles/aa/full_html/2015/03/aa23713-14/aa23713-14-eq194.png) (24)where ta and tb are the two intercepts between the M5007 = const. line and one of the M5007(tev) curves in Fig. 11. A is a normalization constant chosen such that ∫f dM = 1.
(24)where ta and tb are the two intercepts between the M5007 = const. line and one of the M5007(tev) curves in Fig. 11. A is a normalization constant chosen such that ∫f dM = 1.
In this way, we have computed the f(M5007) frequency rates for the PNe of the two bursts (f1 and f2, respectively), which are shown in Fig. 12. Also shown in this figure is the weighted sum f = 0.3f1 + f2.
We see that this weighted sum of the PNe distributions estimated for the two star formation bursts has two modes at about the same height, with a horizontal separation of ΔM5007 ~ 1.2. This distribution function is similar to the distribution that we have obtained from the PNe observed in NGC 6822 (see Fig. 4), which also has two peaks of similar heights, separated by Δm5007 ~ 1.4.
Therefore, we find that this simplified model qualitatively reproduces the general morphology of the NGC 6822 PNe distribution function. In order to obtain two peaks of similar heights (observed in the NGC 6822 distribution) it is necessary to have a second episode (creating the ~ 2.5 M⊙ stars giving rise to some of the present day PNe) which is substantially more massive than the first star formation episode (which created the ~1.4 M⊙ stars). This study could be extended to other galaxies which present a dip in the PNLF and a star formation with more than one burst (i.e., SMC, see Noël et al. 2008).
6. Summary
We have proposed an extension of the PN luminosity function of C89 and J90 to include two different stellar populations, and we have applied it to a sample of PNe in nine galaxies.
The most important parameter of the PNLF is M∗, the magnitude of the brigthest PNe expected in the PNe population, which has been found to be remarkably similar in many galaxies, and is therefore used as a distance estimator.
The original C89 and J90 PNLF adjusted two parameters for one population, m∗ and NT, which are the magnitude of the brightest PN and a normalization constant, respectively. To obtain these parameters with a large sample of PNe one could fit the functional form of the PNLF to a histogram of the sample. On the contrary, if the sample is small, as it is in many cases, a maximum likelihood method has to be used. In any case the data has to be restricted to the brightest PNe because of sample incompleteness.
In our two-mode PNLF a first mode dominates the brightest part of the sample, while the second mode becomes comparable, or dominant at fainter magnitudes. We have introduced a parameter mcut for the first mode, a sharp cutoff at the faintest magnitude. This is not included for the second mode to have as few parameters as possible. For the second mode the cutoff is artificially placed where the sample becomes incomplete. Therefore, we can in general fit two populations in a PNLF with five parameters, all of which go into a genetic fitting algorithm.
To obtain the parameters in our PNLFs we used a genetic algorithm to fit the cumulative luminosity function, which can be used with small or large samples. Since the two-mode PNLF considers the presence (or absence) of a dip in the PNLF we cover a larger magnitude range than the typically used with a single-mode PNLF.
In order to explore the PNLF for galaxies of different Hubble types, we have selected nine galaxies: four irregulars (SMC, LMC, NGC 6822, NGC 3109), three spirals (NGC 300, M31 and M33), the dwarf elliptical NGC 205, and the elliptical NGC 4697. We have fitted the two-mode PNLF to each of these galaxies and find a good agreement with the m∗ estimated by other authors. Our fitting procedure automatically finds a single-mode fit (returns a 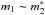 ) where the data is more consistent with a single mode. All of the irregular galaxies in our sample, except one, are consistent with two-modes. The situation is less clear for spiral and elliptical galaxies, and the sample of galaxies used here is not large enough to see any trend of the number of modes with the Hubble type. However, we can see a little trend to the star forming galaxies to present a PNLE with two modes.
) where the data is more consistent with a single mode. All of the irregular galaxies in our sample, except one, are consistent with two-modes. The situation is less clear for spiral and elliptical galaxies, and the sample of galaxies used here is not large enough to see any trend of the number of modes with the Hubble type. However, we can see a little trend to the star forming galaxies to present a PNLE with two modes.
Finally, comparing the results of our two-mode fit to the PNLF of NGC 6822 with the star formation history in this galaxy given by Carigi et al. (2006), we have shown that the two modes (two bursts of star formation) reproduce a combined frequency of PNe with two peaks separated by ~1.2 mag, which is consistent with the sample of PNe observed in NGC 6822.
Acknowledgments
We acknowledge support from CONACyT grant 167625 and DGAPA-UNAM grants IN105312 and IN106212. L.H.-M. & M.P. acknowledge the financial support from PAPIIT grant IN109614 (DGAPA-UNAM). L.H.-M. appreciates the hospitality of IA-UNAM.
References
- Cantó, J., Curiel, S., & Martínez-Gómez, E. 2009, A&A, 501, 1259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carigi, L., Colín, P., & Peimbert, M. 2006, ApJ, 644, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R. 2006, IAU Symp., 234, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R. 2012, Ap&SS, 341, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Jacoby, G., Ford, H., & Neill, J. D. 1989a, ApJ, 339, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Jacoby, G., & Ford, H. 1989b, ApJ, 344, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Jacoby, G. H., & Harris, W. E. 1991, ApJ, 383, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Feldmeier, J. J., Jacoby, G. H., et al. 2002, ApJ, 577, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., Durrell, P. R., Laychak, M. B., et al. 2004, ApJ, 614, 167 [Google Scholar]
- Ciardullo, R., Sigurdsson, S., Feldmeier, J. J., & Jacoby, G. H. 2005, ApJ, 629, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Corradi, R. L. M., Magrini, L., Greimel, R., et al. 2005, A&A, 431, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dopita, M. A., Jacoby, G. H., & Vassiliadis, E. 1992, ApJ, 389, 27. [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., & Babu, G. J. 2012, in Modern statistical methods for astronomy (Cambridge University Press), 107 [Google Scholar]
- Feldmeier, J. J., Ciardullo, R., & Jacoby, G. H. 1997, ApJ, 479, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Hanes, D. A., & Whittaker, D. G. 1987, AJ, 94, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Henize, K. G., & Westerlund, B. E. 1963, ApJ, 137, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández-Martínez, L., & Peña, M. 2009a, A&A, 495, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernández-Martínez, L., Peña, M., Carigi, L., & García-Rojas, J. 2009b, A&A, 505, 1027 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herrmann, K. A., Ciardullo, R., Feldmeier, J. J., & Vinciguerra, M. 2008, ApJ, 683, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Hogg, D. W. 2008 [arXiv:0807.4820] [Google Scholar]
- Jacoby, G. H. 1980, ApJS, 42, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H., & De Marco, O. 2002, AJ, 123, 269 [Google Scholar]
- Jacoby, G. H., Africano, John L., & Quigley, R. J. 1987, PASP, 99, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H., Ciardullo, R., Booth, J., & Ford, H. C. 1989, ApJ, 344, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H., Ciardullo, R., & Ford, H. C. 1990a, ApJ, 356, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H., Ciardullo, R., & Walker, A. R. 1990b, ApJ, 365, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H., Ciardullo, R., & Harris, W. E. 1996, ApJ, 462, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, L.C, Méndez, R. H., & Teodorescu, A. M. 2009, ApJ, 697, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Weiss, A., Groenewegen, M. A. T., & Chiosi, C. 2004, A&A, 423, 995 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McMillan, R., Ciardullo, R., & Jacoby, G. H. 1993, ApJ, 416, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez, R. H., Kudritzki, R. P., Ciardullo, R., & Jacoby, G. H. 1993, A&A, 275, 534 [NASA ADS] [Google Scholar]
- Méndez, R. H., Riffeser, A., Kudritzki, R.-P., et al. 2001, ApJ, 563, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez, R. H., Teodorescu, A. M., Schönberner, D., Jacob, R., & Steffen, M. 2008, ApJ, 681, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Noël, N. E. D. 2008, PASP, 120, 74 [Google Scholar]
- Peña, M., Richer, M. G., & Stasińska, G. 2007, A&A, 466, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peña, M., Reyes-Pérez, J., Hernández-Martínez, L., & Pérez-Guillén, M. 2012, A&A, 547, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pottasch, S. R. 1990, A&A, 236, 231 [NASA ADS] [Google Scholar]
- Reid, W. A., & Parker, Q. A. 2010, MNRAS, 405, 1349 [NASA ADS] [Google Scholar]
- Rodríguez-González, A., Esquivel, A., Raga, A. C., et al. 2012, AJ, 143, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Schönberner, D., Jacob, R., Steffen, M., & Sandin, C. 2007, A&A, 473, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scott, D. W. 1979, Biometrika, 66, 605 [CrossRef] [MathSciNet] [Google Scholar]
- Teodorescu, A. M., Méndez, R. H., Saglia, R. P., Riffeser, A., et al. 2005, ApJ, 635, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Wyder, T. K. 2001, AJ, 122, 2490 [NASA ADS] [CrossRef] [Google Scholar]
- Wyder, T. K. 2003, AJ, 125, 3097 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Cumulative PNLF of the Large Magellanic Cloud. The triangles are the data from Reid & Parker (2010) and the solid line is our two-mode fit. |
| In the text | |
 |
Fig. 2 Cumulative PNLF of the Small Magellanic Cloud. The plus symbols are the data from Jacoby & De Marco (2002), the solid is our two-mode fit. |
| In the text | |
 |
Fig. 3 Cumulative PNLF of NGC 6822. The plus signs and the dashed line are the data and the fit of HMP09, respectively. The solid line is our two-mode fit. |
| In the text | |
 |
Fig. 4 PNLF (non-cumulative) of NGC 6822. The thin solid line and the dashed line are the histogram of the observational data and the fit of HMP09, respectively. The dotted and dashed-dotted lines are the first and the second mode of our fitted function and the thick solid line is our two-mode fit. |
| In the text | |
 |
Fig. 5 Cumulative PNLF of NGC 3109. The plus signs and the dashed line are the observational data and the single mode fitted in Peña et al. (2007). The solid line and the dotted lines are the one- and two-mode best fits, respectively, obtained with our genetic algorithm. |
| In the text | |
 |
Fig. 6 Cumulative PNLF of M 31. |
| In the text | |
 |
Fig. 7 Cumulative PNLF of M 33. |
| In the text | |
 |
Fig. 8 Cumulative PNLF of NGC 300. |
| In the text | |
 |
Fig. 9 Cumulative PNLF of NGC 205. |
| In the text | |
 |
Fig. 10 Cumulative PNLF of NGC 4697. |
| In the text | |
 |
Fig. 11 M5007 (absolute magnitude of the 5007 line) versus PN age for two progenitor masses, 2.5 (dashed line) and 1.4 (solid line) M⊙ (taken from Fig. 10 in Marigo et al. 2004). |
| In the text | |
 |
Fig. 12 Frequency rate for the PNe of the two bursts versus M50007. The short-dashed line shows the normalized frequency for the second burst, and the long-dashed line shows the normalized frequency (multiplied by 0.3) for the first burst. The solid line is the sum. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


