| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 7 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201424690 | |
| Published online | 06 February 2015 | |
Applying the theory of general relativity to reducing geodetic VLBI data
1
Geoscience Australia, PO Box 378
Canberra,
ACT
2601,
Australia
e-mail:
oleg.titov@ga.gov.au
2
Institute of Applied Astronomy RAS, Kutuzov Quay 10, 191187
Saint-Petersburg,
Russia
e-mail:
girduik@ipa.nw.ru
Received: 28 July 2014
Accepted: 4 December 2014
Context. We present an alternate formula for calculating gravitational time delay.
Aims. We use this formula to reduce geodetic Very Long Baseline Interferometry (VLBI) data, taking into account gravitational effects within the solar system, and to test general relativity.
Methods. The alternate formula was obtained by expanding the conventional formula in a Taylor series. We show that the gravitational delay can be split into several terms including a term due to the coordinate transformation and terms that are explicitly linked to the light deflection angle.
Results. Our formula is compared numerically with the conventional formula, and difference in arrival times within 1 ps are found at 1° from the Sun for a full range of baseline lengths.
Conclusions. We conclude that the standard reduction of geodetic VLBI data for the effects of general relativity is equivalent to displacing the reference radio sources from their original catalogue positions in accordance with the classical light deflection formula across the whole sky.
Key words: methods: analytical / astrometry / proper motions / reference systems
© ESO, 2015
1. Introduction
With geodetic Very Long Baseline Interferometry (VLBI) precise group delays – the difference in arrival times of radio waves at two radio telescopes (Schuh & Behrend 2012) – can be measured, and very accurate radio source positions can be obtained (~40 microarcsec, Ma et al. 2009). There are numerous astrometric and geodetic effects that must be accounted for when reducing high-precision VLBI data. One of these effects is gravitational time delay, which is caused by the gravitational fields of massive objects along the observer’s line-of-sight (Shapiro 1964, 1967) and is responsible for the measured group delays. These massive objects also bend the path of light from distant objects, causing an apparent shift of their position in the sky, as predicted by general relativity (Einstein 1916). Within the solar system both the Sun and Jupiter are massive enough to produce these effects. The conventional equation for calculating gravitational delay is formulated in terms of the positions of the radio telescopes within the barycentric reference frame of the solar system (Kopeikin 1990; Eubanks et al. 1991; Soffel et al. 1991; Klioner 1991), rather than the baseline length between the radio telescopes. Moreover, the total VLBI delay formula includes a coordinate term to transform from the geocentric to the barycentric reference frame.
We propose an alternate gravitational delay formula using a Taylor series expansion. In Sect. 2 we show how the conventional formula can be split into a sum of several terms. All the terms are expressed as a ratio of the baseline length to the Earth barycentric distance. One of the terms links the gravitational delay and the well-known formula for the light deflection angle at an arbitrary elongation from the Sun. Another term cancels the coordinate term explicitly presented at the equation of the total VLBI delay. It is more convenient to formulate the effect of general relativity so that it is free from this complicating coordinate term.
In Sect. 3 a numerical comparison between the new and conventional formulae is presented for the cases of the gravitational field of the Sun and Jupiter. Kaplan (1998) compared the astrometric difference in general relativity effects between the group VLBI delay and optical observations, where the observables are measured in angular quantities. It was claimed that the difference is less than 1 microarcsec using some numerical algorithms. Our analytical approach shows that the two approaches are absolutely equivalent for all elongation angles (the difference is equal to zero), except for the small area around the gravitational body, which is a special case.
In Sect. 4 we show that the formulae for the post-post-Newtonian effect can be developed using the same approach as for the standard monopole light deflection.
In Sect. 5 we discuss the application of the new formula to estimate the proper motion of an extragalactic radio source induced by the solar gravitational field.
2. Developing the conventional formula for gravitational delay
In addition to the three classical tests of general relativity (GR), a fourth test – the delay of a signal propagating in the solar gravitational field – was proposed by Shapiro (1964) and is known as the Shapiro delay. The positions of astronomical instruments on Earth are referenced to the solar system barycentre, and the VLBI delay is equal to the terrestrial time (TT) coordinate time interval between two events of the signal arrival at the first and second radio telescopes (Petit et al. 2010). The difference between the two Shapiro delays as measured with two radio telescopes at the barycentric distances r1 and r2 from a body of mass M gives a gravitational delay, τgrav, which must be taken into account during the standard reduction of the high-precision geodetic VLBI data (Petit et al. 2010), 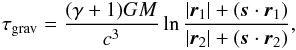 (1)where G is the gravitational constant, s is the unit vector in the direction of observed radio source, c is the speed of light, and γ is the parameter of the parametrised post-Newtonian (PPN) formalism (Will 1993), equal to unity in GR. The classical Shapiro delay formula includes the positions of the remote body and the receiver, but the differential delay (1) only depends on the positions of the two receivers in the adopted reference system. Therefore, the formula (1) is valid for all objects regardless of their distance unless the curvature of the observed light front cannot be ignored. All extragalatic radio sources meet this condition.
(1)where G is the gravitational constant, s is the unit vector in the direction of observed radio source, c is the speed of light, and γ is the parameter of the parametrised post-Newtonian (PPN) formalism (Will 1993), equal to unity in GR. The classical Shapiro delay formula includes the positions of the remote body and the receiver, but the differential delay (1) only depends on the positions of the two receivers in the adopted reference system. Therefore, the formula (1) is valid for all objects regardless of their distance unless the curvature of the observed light front cannot be ignored. All extragalatic radio sources meet this condition.
We introduce the baseline vector, b, as the difference between the two barycentre radius-vectors of two antennas b = r2 − r1. Then formula (1) may be re-written as follows (we recall that γ = 1): 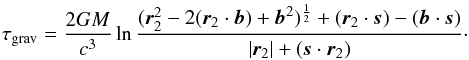 (2)For typical baselines, | b | ≪ | r2 | , and we can use the Taylor series expansion
(2)For typical baselines, | b | ≪ | r2 | , and we can use the Taylor series expansion 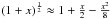 for x ≪ 1 to modify (2) as follows:
for x ≪ 1 to modify (2) as follows: ![\begin{eqnarray} \label{sh_new_2} \tau_{\rm grav}\approx\frac{2GM}{c^{3}} \ln \left[1+\frac{-({\vec r}_{2}\cdot{\vec b})/r_{2} -({\vec b}\cdot{\vec s})+\frac{b^2}{2r_2}-\frac{({\vec r}_{2}\cdot{\vec b})^2}{2r^3_2}}{r_{2}+({\vec r}_{2}\cdot{\vec s})}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2015/02/aa24690-14/aa24690-14-eq19.png) (3)Formula (3) may be re-written using the approximation ln(1 + y) ≈ y − y2/ 2 for y ≪ 1 because the baseline length is much smaller than the barycentric distance to the points on Earth
(3)Formula (3) may be re-written using the approximation ln(1 + y) ≈ y − y2/ 2 for y ≪ 1 because the baseline length is much smaller than the barycentric distance to the points on Earth ![\begin{eqnarray} \label{sh_new_3} \tau_{\rm grav} \approx \dfrac{2GM}{c^{3}} &&\left[\dfrac{-({\vec r}_{2}\cdot{\vec b})/r_{2}-({\vec b}\cdot{\vec s})+\dfrac{b^2}{2r_2}-\dfrac{({\vec r}_{2}\cdot{\vec b})^2}{2r^3_2}}{r_{2}+({\vec r}_{2}\cdot{\vec s})}\right. \nonumber\\ &&\left.\hspace*{-7.5mm}-\frac{1}{2}\left(\dfrac{-({\vec r}_{2}\cdot{\vec b})/r_{2}-({\vec b}\cdot{\vec s})}{r_{2}+({\vec r}_{2}\cdot{\vec s})\phantom{\frac{\frac{1^2}{2^2}}{\frac{1^2}{2^2}}}}\right)^{2}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2015/02/aa24690-14/aa24690-14-eq22.png) (4)One has to keep the barycentric coordinates r2 for the second station in the formulae below to provide consistency with the original gravitational delay model (1).
(4)One has to keep the barycentric coordinates r2 for the second station in the formulae below to provide consistency with the original gravitational delay model (1).
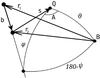 |
Fig. 1 Angles ϕ, ψ, θ, and A, originated from the position of gravitational mass (B), quasar (Q), and baseline vector (b). If the Sun plays the role of the gravitational mass, then the point B in Fig. 1 is also the position of the solar system barycentre. |
Converting the three dot products with angles ϕ,ψ,θ (Fig. 1), where 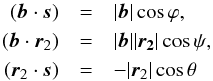 (5)and changing | r2 | to r2 and | b | to b for simplicity, one can obtain from Eq. (4)
(5)and changing | r2 | to r2 and | b | to b for simplicity, one can obtain from Eq. (4) ![\begin{eqnarray} \label{vrem} \tau_{\rm grav} &\approx&\dfrac{2GM}{c^{3}}\left [\dfrac{-b\cos\psi-b\cos\varphi+\dfrac{b^2}{2r_2}(1-\cos^2\psi)}{r_2(1-\cos\theta)}\right.\nonumber\\ &&\left. -\dfrac{1}{2}\left(\dfrac{-b\cos\psi-b\cos\varphi}{r_2(1-\cos\theta)\phantom{\frac{\frac{1^2}{2^2}}{\frac{1^2}{2^2}}}}\right)^2\right]\cdot \end{eqnarray}](/articles/aa/full_html/2015/02/aa24690-14/aa24690-14-eq32.png) (6)Angle θ is given here with respect to the second station, that is, θ = θ2 for the sake of simplicity. The difference between θ1 and θ2 is discussed in Sect. 3. Similar expressions (without terms that include
(6)Angle θ is given here with respect to the second station, that is, θ = θ2 for the sake of simplicity. The difference between θ1 and θ2 is discussed in Sect. 3. Similar expressions (without terms that include 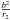 ) have been obtained for geodetic VLBI (e.g. Finkelstein et al. 1983; Hellings 1986) and for SIM interferometry mission model delays (Turyshev 2009).
) have been obtained for geodetic VLBI (e.g. Finkelstein et al. 1983; Hellings 1986) and for SIM interferometry mission model delays (Turyshev 2009).
For the general case of no coplanar vectors (Fig. 1) 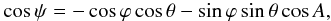 (7)and formula (6) for arbitrary angles ϕ and θ is given by
(7)and formula (6) for arbitrary angles ϕ and θ is given by ![\begin{eqnarray} \label{t_grav0} \tau_{\rm grav}&\approx&-\dfrac{2GMb}{r_2c^{3}}\cos\varphi + \dfrac{2GMb}{r_2c^{3}}\dfrac{\sin\varphi\sin\theta\cos A}{1-\cos\theta}\nonumber\\[3mm] & &+\dfrac{GM}{c^{3}}\dfrac{b^2}{r_2^2(1-\cos\theta)}\nonumber\\[4mm] & &-\dfrac{GM}{c^{3}}\dfrac{b^2(\cos\varphi\cos\theta+\sin\varphi\sin\theta\cos A)^2}{r_2^2(1-\cos\theta)}\nonumber\\[4mm] & &-\dfrac{GM}{c^{3}}\dfrac{b^2\sin^2\varphi\sin^2\theta\cos^2 A}{r_2^2(1-\cos\theta)^2}\nonumber\\[4mm] & &-\dfrac{GM}{c^{3}}\dfrac{b^2\cos^2\varphi}{r_2^2}+\dfrac{GM}{c^{3}}\dfrac{b^2\sin 2\varphi\sin\theta\cos A}{r_2^2(1-\cos\theta)} \cdot \end{eqnarray}](/articles/aa/full_html/2015/02/aa24690-14/aa24690-14-eq39.png) (8)Using the small-angle approximation (R ≪ r2),
(8)Using the small-angle approximation (R ≪ r2), 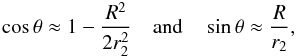 where R is the impact parameter and is equal to the solar radius for the case of grazing light. Therefore
where R is the impact parameter and is equal to the solar radius for the case of grazing light. Therefore 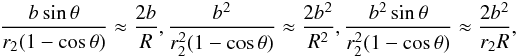 (9)and with a “typical” baseline of ~6000 km the first term ~160 ns, the second term is ~1.2 ns, and the third term is ~3 ps for grazing light. As we show below, the third term is less than 1 ps for observations at θ> 1° from the Sun. This term and other small terms in (8) may be neglected because VLBI observations are not undertaken closer than 4° from the Sun. Then, the gravitational delay is given by
(9)and with a “typical” baseline of ~6000 km the first term ~160 ns, the second term is ~1.2 ns, and the third term is ~3 ps for grazing light. As we show below, the third term is less than 1 ps for observations at θ> 1° from the Sun. This term and other small terms in (8) may be neglected because VLBI observations are not undertaken closer than 4° from the Sun. Then, the gravitational delay is given by ![\begin{eqnarray} \label{t_grav_1} \tau_{\rm grav}&\approx&-\dfrac{2GMb}{r_2c^{3}}\cos\varphi+\dfrac{2GMb}{r_2c^{3}}\dfrac{\sin\varphi\sin\theta\cos A}{1-\cos\theta}\nonumber\\ [4mm] & &+\dfrac{GM}{c^{3}}\dfrac{b^2}{r_2^2(1-\cos\theta)}-\dfrac{GM}{c^{3}}\dfrac{b^2\cos^2\varphi\cos^2\theta}{r_2^2(1-\cos\theta)}\nonumber\\[4mm] & &-\dfrac{GM}{c^{3}}\dfrac{b^2\sin^2\varphi\sin^2\theta\cos^2 A}{r_2^2(1-\cos\theta)^2}, \end{eqnarray}](/articles/aa/full_html/2015/02/aa24690-14/aa24690-14-eq45.png) (10)or, finally,
(10)or, finally, ![\begin{eqnarray} \label{t_grav_2} \tau_{\rm grav}&\approx&-\dfrac{2GMb}{r_2c^{3}}\cos\varphi+\dfrac{2GMb}{r_2c^{3}}\dfrac{\sin\varphi\sin\theta\cos A}{1-\cos\theta}\nonumber\\[4mm] & &+\dfrac{GM}{c^{3}}\dfrac{b^2(1-\cos^2\varphi\cos^2\theta)}{r_2^2(1-\cos\theta)}\nonumber\\[4mm] & &-\dfrac{GM}{c^{3}}\dfrac{b^2\sin^2\varphi\sin^2\theta\cos^2 A}{r_2^2(1-\cos\theta)^2}\cdot \end{eqnarray}](/articles/aa/full_html/2015/02/aa24690-14/aa24690-14-eq46.png) (11)This equation is sufficient for a picosecond level of accuracy. The first term of Eq. (11) can be excluded because it cancels out a similar term from the total geocentric delay (Petit et al. 2010, Eq. (11.9)). Indeed, this formula (11.9) from the IERS Conventions includes the term
(11)This equation is sufficient for a picosecond level of accuracy. The first term of Eq. (11) can be excluded because it cancels out a similar term from the total geocentric delay (Petit et al. 2010, Eq. (11.9)). Indeed, this formula (11.9) from the IERS Conventions includes the term 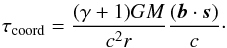 (12)Recalling that γ = 1, the resulting effect of general relativity, τGR, in the total VLBI delay model is therefore given by the sum of the gravitational delay τgrav and the coordinate term τcoord
(12)Recalling that γ = 1, the resulting effect of general relativity, τGR, in the total VLBI delay model is therefore given by the sum of the gravitational delay τgrav and the coordinate term τcoord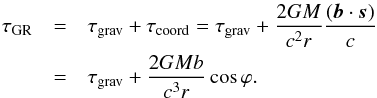 (13)The gravitational delay (11) includes the barycentric distance of the second station r2 in the denominator, whereas the term (12) includes the barycentric distance of the geocentre r. For the case of the Sun, the coordinate term may be as large as 400 ps (see Sect. 2.1) and should be considered carefully, but for Jupiter it does not exceed 1 ps.
(13)The gravitational delay (11) includes the barycentric distance of the second station r2 in the denominator, whereas the term (12) includes the barycentric distance of the geocentre r. For the case of the Sun, the coordinate term may be as large as 400 ps (see Sect. 2.1) and should be considered carefully, but for Jupiter it does not exceed 1 ps.
The difference between two terms 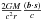 (12) and
(12) and 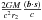 (11) is less than 0.1 ps, and it may be ignored for the current level of accuracy. Nonetheless, the angles θ and ψ are to be referred to the vector r2 for correct calculation.
(11) is less than 0.1 ps, and it may be ignored for the current level of accuracy. Nonetheless, the angles θ and ψ are to be referred to the vector r2 for correct calculation.
In the original form the gravitational delay is expressed in the BCRS system, whereas the baseline length in (12) is given in the GCRS system. This means that theoretically, one has to convert the baseline length b and r2 into Eq. (11) from BCRS to GCRS before comparing the coordinate terms from two different parts. However, in practice, the corresponding correction in time delay does not exceed 1 ps for grazing light and a baseline of 6000 km.
After all reductions, the total contribution of the relativistic effects to the total VLBI delay, τGR, can be written as follows: 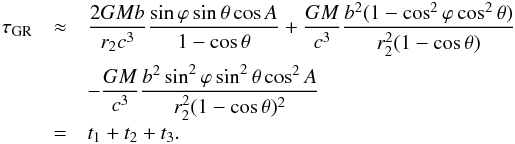 (14)For an arbitrary θ the gravitational delay (1) can be split into several terms in Eq. (13), and the main deflection term is given by
(14)For an arbitrary θ the gravitational delay (1) can be split into several terms in Eq. (13), and the main deflection term is given by 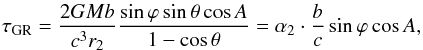 (15)where α2 is the deflection angle at arbitrary θ (Shapiro 1967; Ward 1970), and is given by
(15)where α2 is the deflection angle at arbitrary θ (Shapiro 1967; Ward 1970), and is given by 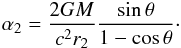 (16)The minor terms in (14) may be ignored for a sufficiently large θ. Therefore (15) may be used as an alternative to the conventional total delay formula for all sources that are far from to a gravitational body. Thus, formulae (15) and (16) present the deflection angle in a more convenient form for estimation from geodetic VLBI data than previously (Treuhaft & Lowe 1991; Kaplan 1998). These formulae also prove that the two approaches – based on angular observations and on the VLBI group delay – are equivalent for all ranges of elongation angles, therefore the difference between two types of quantities is equal to zero.
(16)The minor terms in (14) may be ignored for a sufficiently large θ. Therefore (15) may be used as an alternative to the conventional total delay formula for all sources that are far from to a gravitational body. Thus, formulae (15) and (16) present the deflection angle in a more convenient form for estimation from geodetic VLBI data than previously (Treuhaft & Lowe 1991; Kaplan 1998). These formulae also prove that the two approaches – based on angular observations and on the VLBI group delay – are equivalent for all ranges of elongation angles, therefore the difference between two types of quantities is equal to zero.
2.1. Alternative equation for the gravitational fields of the Sun and Jupiter
We consider two realistic cases and compare the alternative formula τGR (14) with the conventional formula τgrav (1). There are two bodies in the solar system that are able to cause a significant impact on the observations – the Sun and Jupiter. The Sun is the more massive of the two bodies, but observations of radio sources closer than 4° are very rare. Jupiter is three orders of magnitude less massive, but observations at its limb (i.e., at an extremely small impact parameter of 70 000 km) are possible. Other massive planets have a weaker effect (Klioner 2003).
The alternative formula (14) consists of three terms: the first term, t1, provides the main contribution to the GR effects, while the two other terms, t2 and t3, contribute much less than t1. However, we show that for very small angles (θ less than 30′′) all three terms have a similar contribution. At θ = 180° the relativistic contribution, τGR, to the total delay is equal to zero, whereas the gravitational delay, τgrav, is up to 400 ps at a “standard” baseline of ~6000 km as a result of the coordinate term (12) 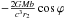 .
.
We illustrate this in Fig. 2, where the coordinate term (12) and the main deflection term (first term in (14)) are presented as a function of the impact parameter for A = 180°(cosA = 1) and ϕ = 45° (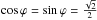 ), b = 6000 km, and r = 1 a.u. The coordinate term is always equal to 280 ps because it does not depend on the variable impact parameter θ. The gravitational delay model (1) does not contain the angle θ explicitly, the solid curve in Fig. 2 is calculated numerically. It is equal to zero at θ = 90° and –280 ps at θ = 180°. The main deflection term, t1 in (14) , is equal to zero at θ = 180, as was previously noted for the relativistic contribution, τGR.
), b = 6000 km, and r = 1 a.u. The coordinate term is always equal to 280 ps because it does not depend on the variable impact parameter θ. The gravitational delay model (1) does not contain the angle θ explicitly, the solid curve in Fig. 2 is calculated numerically. It is equal to zero at θ = 90° and –280 ps at θ = 180°. The main deflection term, t1 in (14) , is equal to zero at θ = 180, as was previously noted for the relativistic contribution, τGR.
 |
Fig. 2 Gravitational delay (1), coordinate term, and main deflection term (13) with respect to the angle θ (see more details in the text). |
To investigate the accuracy of the alternative formula (14), one has to sum the original gravitational delay formula (1) and the term (12) 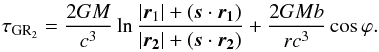 (17)Figure 3 shows the difference between the delays τGR (14) and τGR2 (17) for the Sun and a baseline of 10 000 km: the difference between the two formulae only exceeds 1 ps at
(17)Figure 3 shows the difference between the delays τGR (14) and τGR2 (17) for the Sun and a baseline of 10 000 km: the difference between the two formulae only exceeds 1 ps at 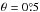 . Thus, the difference between the two formulae is negligible for the light propagation in the solar system as measured by geodetic VLBI at the current level of precision.
. Thus, the difference between the two formulae is negligible for the light propagation in the solar system as measured by geodetic VLBI at the current level of precision.
While the two minor terms, t2 and t3, contribute less than t1, they cannot be ignored completely. The contribution of these terms grows rapidly with baseline length (τ ~ b2) and is 72 ps at θ = 1° for b = 10 000 km (Fig. 4).
 |
Fig. 4 Contribution of the minor terms to the total GR delay for different baseline lengths. |
Herewith, we consider two observational VLBI sessions to separately investigate the effect of t1 separately during a standard 24 h session for the Sun and Jupiter. The VLBI experiment R&D1208 was carried out on 2–3 October, 2012 to track several reference radio sources in close vicinity to the Sun. While the Sun travelled along the ecliptic during the 24 h session, quasar 1243–072 was tracked in the range of angular distances from of 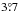 to
to 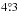 . The four curves in the left-hand of plot of Fig. 5 reflect the variation in t1 for four selected VLBI baselines of differing length: Kokee – Tsukub32 (KT; 5755 km), HartRAO – Wettzell (HtW; 7832 km), Onsala60 – Wettzell (OW; 920 km), and HartRAO – Onsala60 (HtO; 8525 km) with respect to the angle θ of the approach of the Sun to the radio source 1243-072. This varies steadily due to the relatively slow apparent motion of the Sun.
. The four curves in the left-hand of plot of Fig. 5 reflect the variation in t1 for four selected VLBI baselines of differing length: Kokee – Tsukub32 (KT; 5755 km), HartRAO – Wettzell (HtW; 7832 km), Onsala60 – Wettzell (OW; 920 km), and HartRAO – Onsala60 (HtO; 8525 km) with respect to the angle θ of the approach of the Sun to the radio source 1243-072. This varies steadily due to the relatively slow apparent motion of the Sun.
 |
Fig. 5 Main term t1 for 1243-072 (left) and for 1922-224 (right) vs. θ. |
The largest solar system planet Jupiter approached the radio source 1922-224 on 18–19 November, 2008. This event was observed during the 24 h experiment OHIG60. Four stations – Hobart26, Kokee, Tsukub32, and Parkes participated in tracking the radio source over only 12 h because of observing constraints. The angle θ between the radio source and Jupiter changed from 1.́4 to about 5′ within 12 h. The right plot of Fig. 5 shows the variations in t1 as a function of θ during this event. This term reaches its maximum of about 400 ps for the longest available baseline (Hobart26 – Tsukub32 (HT) of b = 8088 km) and becomes negligible after a short period of time. For the shorter baselines (Parkes – Tsukub32 (PT; 7233 km) and Hobart26 – Parkes (HP; 1089 km)), this term is lower in magnitude.
 |
Fig. 6 Variations of the coordinate term for 1243-072 (left) and for 1922-224 (right). |
The coordinate term calculated for both events (Fig. 6) is significant for the Sun (reaching 300 ps) but is negligible for Jupiter (less than 0.1 ps). In accordance with Eq. (17), the coordinate term does not depend on the impact parameter and, therefore, it does not grow at small angles, as seen in Fig. 2. All variations in Fig. 6 are caused by the variations in angle ϕ and baseline length.
 |
Fig. 7 Comparison of the two models for the approach of the Sun to 1243-072 (left) and of Jupiter to 1922-224 (right). The difference for baseline Hobart26 – Parkes in the right plot is not distinctive for this scale. |
Figure 7 illustrates the residuals between Eqs. (14) and (17) for these two events. The difference does not exceed 1 ps for either case. This proves that Eq. (14), proposed in this paper, can be used to model the relativistic effects along with the conventional model (17).
3. Small-angle approximation
The monopole effect of the general relativity results in a circular motion of the deflected object (Sazhin et al. 2001; Kopeikin & Makarov 2007). Therefore, the radio sources draw a regular pattern on the sky due to the light deflection. Here we consider an impact of the minor terms in Eq. (14) on the formula for the light deflection, in particular on the intraday time-scale, if a large planet such as Jupiter passes by a reference radio sources very quickly. In the small-angle approximation, Eq. (9), the effect of GR (14) is given by 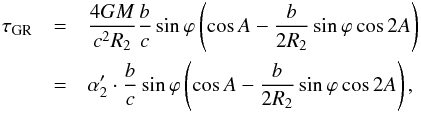 (18)where
(18)where 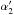 is the deflection angle for light propagated through a gravitation field (Einstein 1916) for the second station
is the deflection angle for light propagated through a gravitation field (Einstein 1916) for the second station 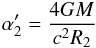 (19)and R2 = r2cosθ2.
(19)and R2 = r2cosθ2.
Re-arranging formula (18) provides an expression for the deflection angle, 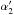 , for an arbitrary baseline length in the small-angle approximation as follows:
, for an arbitrary baseline length in the small-angle approximation as follows: 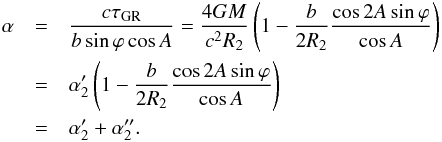 (20)Thus, once in single-telescope mode, only the main angle (19) is presented; in the two-telescope mode, the secondary deflection angle
(20)Thus, once in single-telescope mode, only the main angle (19) is presented; in the two-telescope mode, the secondary deflection angle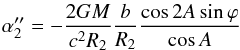 (21)represents the difference between angles
(21)represents the difference between angles 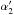 and
and 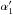 , if
, if 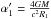 and R1 = r1cosθ1. Even though the parallactic shift of the Sun θ1 − θ2 is about 8′′ for b = 6000 km, this difference between
and R1 = r1cosθ1. Even though the parallactic shift of the Sun θ1 − θ2 is about 8′′ for b = 6000 km, this difference between 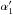 and
and 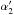 , is not negligible in the small-angle approximation. The formula shows that the secondary deflection angle depends on the baseline length, but it reduces to Einstein’s classical expression (19) for a zero-length baseline (i.e. b = 0).
, is not negligible in the small-angle approximation. The formula shows that the secondary deflection angle depends on the baseline length, but it reduces to Einstein’s classical expression (19) for a zero-length baseline (i.e. b = 0).
Table 1 shows the meaning of the angle 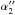 for the Sun and Table 2 for Jupiter with different combinations of the parameters θ2 and R2. This effect rapidly grows as b is decreasing and may be detected with a long-baseline radio-interferometer at a very close approach of the Sun (<5°) or large planets (<1′) to a distant radio source.
for the Sun and Table 2 for Jupiter with different combinations of the parameters θ2 and R2. This effect rapidly grows as b is decreasing and may be detected with a long-baseline radio-interferometer at a very close approach of the Sun (<5°) or large planets (<1′) to a distant radio source.
The angle 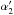 can change comparatively fast when Jupiter passing by a radio source. An example of the fast variations of
can change comparatively fast when Jupiter passing by a radio source. An example of the fast variations of 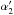 is shown in Fig. 8 for the approach of Jupiter and the radio source 1922-224 discussed in Sect. 2.1. The corresponding time delays as shown in the right plot of Fig. 5 are different, but the light deflection angles in Fig. 8. for all baselines are the same.
is shown in Fig. 8 for the approach of Jupiter and the radio source 1922-224 discussed in Sect. 2.1. The corresponding time delays as shown in the right plot of Fig. 5 are different, but the light deflection angles in Fig. 8. for all baselines are the same.
Einstein deflection angle and the secondary deflection angle for the Sun.
Einstein deflection angle and the secondary deflection angle for Jupiter.
 |
Fig. 8 Arc for baselines Hobart26-Tsukub32 (upper left), Kokee-Tsukub32 (upper right), Hobart26-Parkes (bottom left), Kokee-Parkes (bottom right). |
4. Post-post-Newtonian effect
As shown by (Klioner 1991), the main term of the post-post-Newtonian effect is given by ![\begin{eqnarray} \tau_{\rm PPN} &=& \frac{4G^2M^2}{c^5}\left[\dfrac{4}{|{\vec r}_1|+({\vec r}_1\cdot {\vec s})}-\dfrac{4}{|{\vec r}_2|+({\vec r}_2 \cdot {\vec s})}\right] \cdot \end{eqnarray}](/articles/aa/full_html/2015/02/aa24690-14/aa24690-14-eq106.png) (22)Using the mathematical transformation of Eqs. (2) and (5),
(22)Using the mathematical transformation of Eqs. (2) and (5), ![\begin{eqnarray} \label{ppn2} \tau_{\rm PPN} &=& \frac{4G^2M^2}{c^5}\left[\frac{4}{r_2(1-\cos\theta)\left(1-\frac{b\cos\psi+b\cos\varphi}{r_2(1-\cos\theta)}\right)}-\frac{4}{r_2(1-\cos\theta)}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2015/02/aa24690-14/aa24690-14-eq107.png) (23)If the baseline length is negligible with respect to the barycentric distance (b ≪ r2), one could recall
(23)If the baseline length is negligible with respect to the barycentric distance (b ≪ r2), one could recall 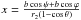 and apply the approximation
and apply the approximation 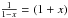 using Eq. (7) to solve the spherical triangle (Fig. 1) and to develop (23) as follows:
using Eq. (7) to solve the spherical triangle (Fig. 1) and to develop (23) as follows: 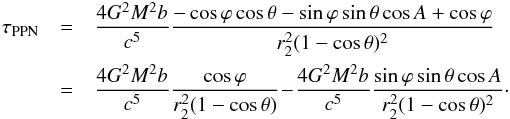 (24)In the small-angle approximation (R ≪ r2) (24) is given by
(24)In the small-angle approximation (R ≪ r2) (24) is given by 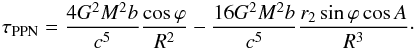 (25)For the grazing light the first term in Eq. (25) is about 1 ps, whereas the second one can reach 300 ps at a “standard” baseline of 6000 km (Klioner 1991).
(25)For the grazing light the first term in Eq. (25) is about 1 ps, whereas the second one can reach 300 ps at a “standard” baseline of 6000 km (Klioner 1991).
When the first term in Eq. (24) is negligible, we can introduce a new variable 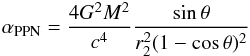 (26)and re-write the second term of Eq. (24) as follows:
(26)and re-write the second term of Eq. (24) as follows: 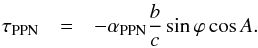 (27)It is obvious that the variable αPPN plays the role of the post-post-Newtonian deflection angle at arbitrary θ, and converting between the deflection angle and the corresponding part of gravitational delay uses the same factor
(27)It is obvious that the variable αPPN plays the role of the post-post-Newtonian deflection angle at arbitrary θ, and converting between the deflection angle and the corresponding part of gravitational delay uses the same factor 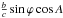 for the post-Newtonian effect as in Eqs. (15) and (16). It enables us to present the sum of the two delays τGR (15) and τPPN (27) in the form of two angles, Eqs. (19) and (26), multiplied by
for the post-Newtonian effect as in Eqs. (15) and (16). It enables us to present the sum of the two delays τGR (15) and τPPN (27) in the form of two angles, Eqs. (19) and (26), multiplied by 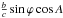 , that is,
, that is, 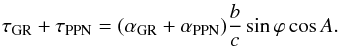 (28)Finally, we recall that the second term of Eq. (24) corresponds to formula (11.14) from the IERS Conventions (Petit et al. 2010).
(28)Finally, we recall that the second term of Eq. (24) corresponds to formula (11.14) from the IERS Conventions (Petit et al. 2010).
5. Proper motion of extragalactic radio sources induced by the Sun
The solar gravitational field will result in a proper motion of extragalactic radio sources if the effects of general relativity are not accounted for in VLBI data reduction. The rapid change of the observed positions during a typical 24 h VLBI session may be detected for observations within 10° from the Sun.
The partial derivative 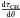 is given by
is given by 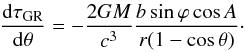 (29)For an arbitrary angle θ, the proper motion
(29)For an arbitrary angle θ, the proper motion 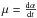 (where α is from (15)) may be presented by re-arranging Eq. (29) as follows:
(where α is from (15)) may be presented by re-arranging Eq. (29) as follows: 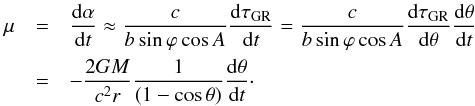 (30)Figure 9 illustrates Eq. (30) for a range of angles θ from 0° to 10°. It is obvious that all distant radio sources across the sky will display a circular motion if general relativity is not accounted for in VLBI data reduction. The magnitude of the effect is proportional to
(30)Figure 9 illustrates Eq. (30) for a range of angles θ from 0° to 10°. It is obvious that all distant radio sources across the sky will display a circular motion if general relativity is not accounted for in VLBI data reduction. The magnitude of the effect is proportional to 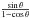 . In particular, a source near the ecliptic poles θ = 90° will draw a circle of 4 mas in size. The daily displacement between the consecutive days will be equal to
. In particular, a source near the ecliptic poles θ = 90° will draw a circle of 4 mas in size. The daily displacement between the consecutive days will be equal to 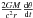 . For the Sun,
. For the Sun, 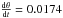 , and the daily displacement is ≈0.07 mas. For all other sources, the daily displacement will be proportional to the factor
, and the daily displacement is ≈0.07 mas. For all other sources, the daily displacement will be proportional to the factor 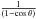 in Eq. (30).
in Eq. (30).
In the small-angle approxiation, Eq. (30) may be written as follows: 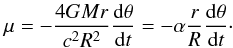 (31)For background radio sources that are co-planar with the plane of the body, the apparent motion, μ, rapidly grows from 0.5 μas/year at θ = 10°, to 1.6 μas/year at θ = 5° and 40 μas/year at θ = 1°. Therefore, a systematic pattern of proper motion in a particular area of the sky may serve as an indicator of a hidden mass in this direction.
(31)For background radio sources that are co-planar with the plane of the body, the apparent motion, μ, rapidly grows from 0.5 μas/year at θ = 10°, to 1.6 μas/year at θ = 5° and 40 μas/year at θ = 1°. Therefore, a systematic pattern of proper motion in a particular area of the sky may serve as an indicator of a hidden mass in this direction.
6. Conclusion
The effects of general relativity are explicitly contained in both components of the total VLBI delay model – the gravitational delay and the coordinate term with a factor of 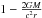 . While the former component uses the individual barycentre positions of the radio telescopes to calculate the effect, the latter component is expressed in terms of the baseline between the radio telescopes. Coupling between both parts has not been investigated until now.
. While the former component uses the individual barycentre positions of the radio telescopes to calculate the effect, the latter component is expressed in terms of the baseline between the radio telescopes. Coupling between both parts has not been investigated until now.
The Shapiro effect as measured by radars and the deflection of light measured with traditional astronomical instruments are considered two independent tests of general relativity. We showed that the total group delay model joins the two tests within one observational technique – geodetic VLBI. The gravitational delay that traditionally originated from the Shapiro effect is linked to the light deflection angle. Therefore, the two approaches, VLBI delay and angular, are absolutely equivalent.
For almost all realistic situations this angle does not depend on the baseline length, thus, a standard geodetic VLBI interferometer acts as a traditional astronomical instrument. In addition, the coordinate term explicitly presented in the conventional total delay model ceases to exist because it is compensated by the same effect in the gravitational delay with opposite sign. Thus, the proposed alternative version of the general relativity contribution to the total VLBI group delay model is free of the coordinate effects. Therefore, the two approaches, time delay and angular, are absolutely equivalent.
The final equation of the general relativity contribution expressed in angular terms also comprises two smaller terms that are significant at very small angular separation between
the deflecting body and distant radio source. These terms may be considered as an increment in the light deflection angle due to the additional time delay for the propagation of the light from station 1 to station 2. This effect becomes significant at 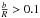 .
.
It is unlikely that the effect will be detected with ground-based interferometers, but it may be detected with space-baseline interferometers, for example, RadioAstron with b up to 300 000 km (Kardashev et al. 2013).
Acknowledgments
We thank Craig Harrison for proofreading the manuscript and valuable comments. We are also grateful to Slava Turyshev, Sergei Kopeikin, Laura Stanford, Sergei Klioner, Benedikt Soja, Natalia Pavlovskaya, Nicole Capitaine, Sebastien Lambert, Adrien Bourgoine, Pierre Teyssandier, Aurelien Hees, Christophe Le Ponchin-Lafitte, Vladimir Zharov and Mihail Sazhin for useful discussion on the mathematical details of general relativity. Oleg Titov was supported by the Russian fund “Dynasty” for two short-term working visits to Saint-Petersburg University in 2011 and 2013. A special “hand made” observing schedule was prepared by Dirk Behrend (GSFC) to track the radio source 1922-224 on 18–19 November, 2008. This paper is published with the permission of the CEO, Geoscience Australia.
References
- Einstein, A. 1916, Annalen der Physik, 354, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Eubanks, T. M., Carter, M. S., Josties, F. J., Matsakis, D. N., & McCarthy, D. D. 1991, IAU Colloq. 127: Reference Systems, 256 [Google Scholar]
- Finkelstein, A. M., Kreinovich, V. I., & Pandey, S. N. 1983, Ap&SS, 94, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Hellings, R. W. 1986, AJ, 91, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Kaplan, G. H. 1998, AJ, 115, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Kardashev, N. S., Khartov, V. V., Abramov, V. V., et al. 2013, Astron. Rep., 57, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Klioner, S. A. 1991, in Conf. Proc. Geodetic VLBI: Monitoring Global Change, Technical Report NOS 137NGS 49, 188 [Google Scholar]
- Klioner, S. A. 2003, AJ, 125, 1580 [Google Scholar]
- Kopeikin, S. M. 1990, Sov. Ast, 34, 5 [Google Scholar]
- Kopeikin, S. M., & Makarov, V. V. 2007, Phys. Rev. D, 75, 062002 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, C., Arias, E. F., Bianco, G., et al. 2009, IERS Technical Note, 35, 1 [Google Scholar]
- Petit, G., & Luzum, B. 2010, IERS Technical Note, 36, 1 [NASA ADS] [Google Scholar]
- Sazhin, M. V., Zharov, V. E., & Kalinina, T. A. 2001, MNRAS, 323, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Schuh, H., & Behrend, D. 2012, J. Geodynamics, 61, 68 [Google Scholar]
- Shapiro, I. I. 1964, Phys. Rev. Lett., 13, 789 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Shapiro, I. I. 1967, Science, 157, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Soffel, M. H., Wu, X., Xu, C., & Mueller, J. 1991, AJ, 101, 2306 [NASA ADS] [CrossRef] [Google Scholar]
- Treuhaft, R. N., & Lowe, S. T. 1991, AJ, 102, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Turyshev, V. G. 2009, Astron. Lett., 35, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Ward, W. R. 1970, ApJ, 162, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Will, C. M. 1993, Theory and Experiment in Gravitational Physics, ed. M. W. Clifford (Cambridge, UK: Cambridge University Press), 396 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Angles ϕ, ψ, θ, and A, originated from the position of gravitational mass (B), quasar (Q), and baseline vector (b). If the Sun plays the role of the gravitational mass, then the point B in Fig. 1 is also the position of the solar system barycentre. |
| In the text | |
 |
Fig. 2 Gravitational delay (1), coordinate term, and main deflection term (13) with respect to the angle θ (see more details in the text). |
| In the text | |
 |
Fig. 3 Difference between formulae (14) and (17) for a baseline of 10 000 km length. |
| In the text | |
 |
Fig. 4 Contribution of the minor terms to the total GR delay for different baseline lengths. |
| In the text | |
 |
Fig. 5 Main term t1 for 1243-072 (left) and for 1922-224 (right) vs. θ. |
| In the text | |
 |
Fig. 6 Variations of the coordinate term for 1243-072 (left) and for 1922-224 (right). |
| In the text | |
 |
Fig. 7 Comparison of the two models for the approach of the Sun to 1243-072 (left) and of Jupiter to 1922-224 (right). The difference for baseline Hobart26 – Parkes in the right plot is not distinctive for this scale. |
| In the text | |
 |
Fig. 8 Arc for baselines Hobart26-Tsukub32 (upper left), Kokee-Tsukub32 (upper right), Hobart26-Parkes (bottom left), Kokee-Parkes (bottom right). |
| In the text | |
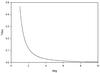 |
Fig. 9 Daily proper motion calculated from Eq. (30) near the Sun. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


