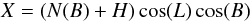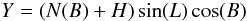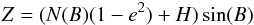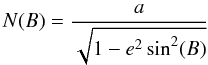| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 22 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201424653 | |
| Published online | 21 January 2015 | |
Representations of time coordinates in FITS
Time and relative dimension in space
1
Harvard-Smithsonian Center for Astrophysics/Smithsonian Astrophysical
Observatory,
60 Garden Street MS 67,
Cambridge,
MA
02138,
USA
e-mail:
arots@cfa.harvard.edu
2
Institute of Astronomy, Madingley Road, Cambridge
CB3 0HA,
UK
3
CSIRO Astronomy and Space Science, PO Box 76,
Epping
NSW
1710,
Australia
4
UCO/Lick Observatory, University of California,
Santa Cruz,
CA
95064,
USA
5
Adnet Systems, Inc., NASA Goddard Space Flight Center, Code 671,
Greenbelt,
MD
20771,
USA
Received: 22 July 2014
Accepted: 26 September 2014
Context. In a series of three previous papers, formulation and specifics of the representation of world coordinate transformations in FITS data have been presented. This fourth paper deals with encoding time.
Aims. Time on all scales and precisions known in astronomical datasets is to be described in an unambiguous, complete, and self-consistent manner.
Methods. Employing the well-established World Coordinate System (WCS) framework, and maintaining compatibility with the FITS conventions that are currently in use to specify time, the standard is extended to describe rigorously the time coordinate.
Results. World coordinate functions are defined for temporal axes sampled linearly and as specified by a lookup table. The resulting standard is consistent with the existing FITS WCS standards and specifies a metadata set that achieves the aims enunciated above.
Key words: time / standards / methods: data analysis / techniques: miscellaneous / astronomical databases: miscellaneous / reference systems
© ESO, 2015
1. Introduction
Time as a dimension in astronomical data presents challenges in its representation in FITS files as great as those met by the previous papers in this series. The first, Paper I (Greisen & Calabretta 2002), lays the groundwork by developing general constructs and related FITS header keywords and the rules for their usage in recording coordinate information. Paper II (Calabretta & Greisen 2002) addresses the specific problem of describing celestial coordinates in a two-dimensional projection of the sky. In Paper III, Greisen et al. (2006) apply these methods to spectral coordinates. A draft paper (Calabretta et al., in prep.) proposes an extension to the formalism in order to deal with general distortions of the coordinate grid.
This paper, the fourth in the series, formulates the representation of the time axis, or possibly multiple time axes, into the FITS World Coordinate System (WCS) previously described. We show how much of the basic structure is employed, while developing extensions to cope with the differences between time and other dimensions; notable amongst these differences is the huge dynamic range, covering the highest resolution timing relative to the age of the Universe.
The precision with which any time stamp conforms to any conventional time scale is highly dependent on the characteristics of the acquiring system. The definitions of many conventional time scales vary over their history along with the precision that can be attributed to any time stamp. The meaning of any time stamp may be ambiguous if a time scale is used for dates prior to its definition by a recognized authority, or for dates after that definition is abandoned. However, common sense should prevail and it would be overly pedantic to require a precision in the description of the time coordinate that far exceeds the accuracy of the temporal information in the data.
In the following sections we first define the terms of reference of this standard (Sect. 2). Section 3 deals with time values and representations of time. Section 4 forms the core of this standard, providing an explanation of the components that are involved and defining the keywords to be used for specifying those components. Section 5 provides some general comments on implementing this standard. Section 6 on usage context refers back to the terms of reference, illustrated with six header examples and including a sub-section on time-related coordinate axes. The prescriptive part of this standard is contained in Sects. 2−4, and Appendix A.
Generally helpful references may be found in Seidelmann (1992), Urban & Seidelmann (2012), and McCarthy & Seidelmann (2009). The report on the current (IAU 2009) system of astronomical constants is provided by Luzum et al. (2011)1.
The interpretation of the terms must, required, should, and may follows common usage in standards documents: An implementation is compliant if it satisfies all the must or required level requirements for the protocols it implements. An implementation that satisfies all the must or required level and all the should level requirements for its protocols is said to be “unconditionally compliant”; one that satisfies all the must level requirements but not all the should level requirements for its protocols is said to be “conditionally compliant”. Alternatively, one may apply the common-sense compliance criterion that requires all keywords needed for full interpretation of the data to be present, with the exception of those for which default values have been defined.
2. Terms of reference
Time WCS information needs to be supported in five contexts:
-
Recording time stamps in header keywords
-
Time coordinate axes in images
-
Time columns in tables
-
Time coordinate axes in table vector columns
-
Time in random groups2
We distinguish the following components in the specification of time:
-
Time coordinate frame, containing:
-
Time scale
-
Reference time (the zero point for relative times)
-
Time reference position
-
Time reference direction (if applicable)
-
Solar System ephemeris used (if applicable)
-
-
Time unit
-
Corrections, errors, etc.:
-
Time offsets
-
Absolute error
-
Relative error
-
Time resolution
-
-
Durations
The following use cases illustrate the scope of the requirements for time axes:
-
Photon arrival times (“event lists”)
-
Time-sampled data streams (referred to as “light curves” in some of our communities)
-
Pulsar pulse profiles and other folded or stacked light curves
-
Power spectra, cross-, and auto-correlation spectra
-
Image cubes: typically a series of two-dimensional images acquired at regular time spacing, and stacked so the third axis is time. Usually precision is not demanding, but the time axis must be integrated into a three-dimensional WCS
-
Simulation data
“Mixed” axes, where spatial or spectral coordinates change as a function of time (e.g., during an observation) represent a special challenge.
Where possible, we have adopted the same keywords as in the OGIP convention3, which has become a de facto standard for representing timing information within high-energy astrophysics data files, particularly from NASA as well as many ESA missions.
In addition to absolute time axes, we provide accommodation for three types of time-related coordinates: Phase, Timelag, and Frequency; see Sect. 4.5.
Contrary to the convention followed in previous FITS standards papers, Appendix A is to be considered part of this standard. The more subtle issues associated with the definition of time scales are, of necessity, germaine to the details of the standard, but it seemed unwieldy to include them in the main text of this paper.
3. Time values and representations of time
The three most common ways to specify time are: ISO-8601, Julian date (JD; see Herschel 1851), or modified Julian date (MJD = JD − 2 400 000.5; see IAU 1997). Julian dates are counted from Julian proleptic calendar date 1 January 4713 BCE at noon, or Gregorian proleptic calendar date 24 November 4714 BCE, also at noon. For an explanation of the calendars, see the note in Sect. 3.1.
Even though we may tend to think of certain representations of time as absolute (ISO-8601, JDs), time values in this paper shall all be considered relative: elapsed time since a particular reference point in time. It may help to view the “absolute” values as merely relative to a globally accepted zero point.
In the following we first treat the ISO-8601 representation, then floating point values of elapsed time since a reference value. For time, more than any other coordinate, precision may be a concern and naive use of double precision floating point parameters for time values (especially JDs) will be inadequate in some cases. However, a judicious combination of keywords and their values, as described in the remainder of this section, will allow almost any required precision to be achieved without having to resort to anything beyond double precision data types in handling keyword values. We urge creators of data products to apply special care, so that clients can rely on this being the case. If and when, in addition to the 32-bit (E) and 64-bit (D) floating point types, a 128-bit floating point data type becomes available and supported, we envision that such a type will also be used for time values, removing the need for any special provisions.
We conclude the section with a specification of epochs.
3.1. ISO-8601 datetime strings
FITS uses a subset of ISO-8601 (which in itself does not imply a particular time scale) for several time-related keywords (Bunclark & Rots 1997), such as DATE-xxx. In this paper we will use datetime as a pseudo data type to indicate its use. Following the current FITS standard (Pence et al. 2010) its values must be written as a character string in Aformat, but if and when an ISO-8601 data type is adopted, it should be used in table columns, rather than the string type.
The full specification for the format of the datetime string till now has been:
CCYY-MM-DD[Thh:mm:ss[.s...]]
All of the time part may be omitted (just leaving the date) or the decimal seconds may be omitted. Leading zeroes must not be omitted and timezone designators are not allowed.
This paper extends the definition to allow five-digit years with a (mandatory) sign, in accordance with ISO-8601. I.e., one shall either use the unsigned four-digit year format or the signed five-digit year format:
[ ±C]CCYY-MM-DD[Thh:mm:ss[.s...]]
Note the following:
-
In counting years, ISO-8601 follows the convention established by Cassini (1740) of including year zero. Consequently, for negative year numbers there is an offset of one from BCE dates which do not recognize a year zero. Thus year 1 corresponds to 1 CE, year 0 to 1 BCE, year −1 to 2 BCE, and so on.
-
The earliest date that may be represented in the four-digit year format is 0000-01-01T00:00:00 (in the year 1 BCE); the latest date is 9999-12-31T23:59:59. This representation of time is tied to the Gregorian calendar (Pope Gregorius XIII 1582)4. In conformance with the present ISO-8601:2004(E) standard (ISO 2004) we specify that, for use in FITS files, dates prior to 1582 must be interpreted according to the proleptic application of the rules of Gregorius XIII (1582). For dates not covered by the range we recommend the use of MJD or JD numbers or the use of the signed five-digit year format.
-
In the five-digit year format the earliest and latest dates are −99999-01-01T00:00:00 (i.e., −100000 BCE) and +99999-12-31T23:59:59.
-
Recalling the definition of JD provided at the top of Sect. 3, we can express its origin as −04713-11-24T12:00:00.
-
In time scale UTC the integer part of the seconds field runs from 00 to 60 (in order to accommodate leap seconds); in all other time scales the range is 00 to 59.
-
This data type is not allowed in image axis descriptions since CRVALis required to be a floating point value.
-
ISO-8601 datetime does not imply the use of any particular time scale (see Sect. 4.1.1).
-
As specified by Bunclark & Rots (1997), time zones are explicitly not supported in FITS and, consequently, appending the letter ‘Z’ to a FITS ISO-8601 string is not allowed. The rationale for this rule is that its role in the ISO standard is that of a time zone indicator, not a time scale indicator. As the concept of a time zone is not supported in FITS, the use of time zone indicator is inappropriate.
3.2. Single or double precision floating point relative time
These are existing data types that do not need any particular provisions and can be used when their precision suffices. In general, if higher precision is required, it will be possible to achieve this by judicious use of keyword values, without having to resort to exotic datatypes, as described in the next subsection.
3.3. Higher precision in keyword values
While the FITS standard (Pence et al. 2010, Sect. 4.2.4). allows header values to be written to as many as 70 decimal digits, it must be recognised that practical implementations are currently based on double-precision floating point values which are capable of representing only approximately 15 decimal digits. While this has not been a limitation in the past, it may not be adequate for certain high-precision timing applications. In the absence of the widespread availability of quad-precision floating point, timing software often obtains the extra required precision by using a pair of double-precision values, typically containing the integer and fractional part, whose (implied) sum forms the high-precision value. In like vein we provide the [M]JDREF[IF] and DATEREF keywords (see Sect. 4.1.2) to define a global time reference epoch to which all times in the HDU are relative, and these should be used judiciously where high-precision timing is required. Implementers of this standard should be aware that precision may be lost by adding relative times to the reference epoch, and maintain them as separate quantities until a final value is required (see Sect. 5.3).
3.4. Higher precision in binary tables: doublet vectors
In binary tables one may use pairs of doubles. The time column in such a table shall contain a vector of two doubles (TFORMn = ‘2D’) where the first component of the doublet contains the integer portion of the time value and the second one the fractional part, such that their sum equals the true value and where both have the same sign. This will ensure that retention of precision can be effected in as simple a way as possible and avoiding any sign ambiguities. We readily admit that a combination of an integer and a floating point number would be preferable, but the use of two doubles allows us to keep the time stamps in a single table column.
3.5. Julian and Besselian epochs
In a variety of contexts epochs are provided with astronomical data. Until 1976 these were commonly based on the Besselian year (see Sect. 4.2), with standard epochs B1900.0 and B1950.0. After 1976 the transition was made to Julian epochs based on the Julian year of 365.25 days, with the standard epoch J2000.0. They are tied to time scales ET and TDB, respectively. Table 1 provides conversion values for some Besselian and Julian epochs. See also Seidelmann (1992, Table 15.3). Note that the Besselian epochs are scaled by the variable length of the Besselian year (see Sect. 4.2 and its cautionary note, which also applies to this context). The Julian epochs are easier to calculate, as long as one keeps track of leap days.
See Sect. 6.6 for the use of Besselian and Julian epochs in FITS files.
Some Besselian and Julian epochs.
Caution: be aware of the offset of 1 in negative year numbers, compared with BCE dates (see Sect. 3.1).
4. Components of the standard
This section describes the components of the standard. The keywords used to specify times are summarized in Table 5. Section 5.a of the table contains data items: time values that have, in principle, global validity in the HDU. Section 5.b presents keywords that define the time reference frame for all time values in the HDU and their context-dependent override keywords. If the HDU contains a table, all keywords in the first two sections may be replaced by columns, with specific values for each row (“Green Bank convention”; Pence 2010). The last section of the table (5.c) lists the keywords that allow overriding the global HDU keyword values for the time axis in images.
In the following datetime-valued must be interpreted as string-valued where the string conforms to ISO-8601 format as defined in Sect. 3.1.
4.1. Time coordinate frame
This section defines the various components that constitute the time coordinate frame. For a full review of the IAU resolutions concerning space-time coordinate transformations, see Soffel et al. (2003).
4.1.1. Time scale
The time scale defines the temporal reference frame (in the terminology of the IVOA Space-Time Coordinate metadata standard; see Rots 2008). See also the USNO (2008) page on time scales, Wallace (2011), and SOFA (2010).
Table 2 lists recognized values. For a detailed discussion of the time scales we refer to Appendix A; that information will be of particular relevance for high-precision timing. In cases where this is significant, one may append a specific realization, in parentheses, to the values in the table; e.g., TT(TAI), TT(BIPM08), UTC(NIST). Note that linearity is not preserved across all time scales. Specifically, if the reference position remains unchanged (see Sect. 4.1.3), the first ten, with the exception of UT1, are linear transformations of each other (excepting leap seconds), as are TDBand TCB. On average TCBruns faster than TCGby approximately 1.6 × 10-8, but the transformation from TTor TCG(which are linearly related) is to be achieved through a time ephemeris, as provided by Irwin & Fukushima (1999).
The relations between coordinate time scales and their dynamical equivalents have been defined as (see Luzum et al. 2011; Wallace 2011; SOFA 2010):
T(TCG) = T(TT) + LG × 86400 × (JD(TT) − JD0)
T(TDB) = T(TCB) − LB × 86400 × (JD(TCB) − JD0) + TDB0
where:
T is in seconds
LG = 6.969290134 × 10-10
LB = 1.550519768 × 10-8
JD0 = 2 443 144.5003725
TDB0 = − 6.55 × 10-5 s
Linearity is virtually guaranteed since images and individual table columns do not allow more than one reference position to be associated with them and since there is no overlap between reference positions that are meaningful for the first nine time scales on the one hand, and for the barycentric ones on the other. All use of the time scale GMT in FITS files shall be taken to have its zero point at midnight, conformant with UT, including dates prior to 1925; see Sadler (1978). For high-precision timing prior to 1972, see Sect. A.9.
Global Navigation Satellite System (GNSS) time scales GLONASS, Galileo, and Beidou are not included, as they are less mature and/or less widely used than GPS. They may be added in the future if their use becomes more common in the scientific community.
Other time scales that are not listed in Table 2 are intrinsically unreliable and/or ill-defined. These should be tied to one of the existing scales with appropriate specification of the uncertainties; the same is true for free-running clocks. However, a local time scale, such as MET (Mission Elapsed Time) or OET (Observation Elapsed Time), may be defined for practical reasons. In those cases the time reference value (see Sect. 4.1.2) shall not be applied to the values and we strongly recommend that such timescales be provided as alternate time scales, with a defined conversion to a recognized time scale.
Most current computer operating systems adhere to the POSIX standard for time, and use Network Time Protocol (NTP) to synchronize closely to UTC. This reasonable approximation to UTC is then commonly used to derive timestamps for FITS data. However, authors of FITS writers and subsequent users of FITS timing information should be aware of the accuracy limitations of POSIX and NTP, especially around the time of a leap second.
Finally, it may be helpful, in order to put the different time scales into perspective, to emphasize that while UT1 is, in essence, an angle (of the Earth’s rotation – i.e., a clock), the others are SI-second counters (chronometers); UTC, by employing leapseconds, serves as a bridge between the two types of time scales.
Keywords.
The global keyword that records the time scale is
TIMESYS (string-valued)
time scale; default UTC.
In relevant context (e.g., time axes in image arrays, table columns, or random groups) it may be overridden by a time scale recorded in CTYPEia, its binary table equivalents, or PTYPEi (see Table 5).
The keywords TIMESYS, CTYPEia, TCTYPn, and TCTYna may assume the values listed in Table 2. In addition, for backward compatibility, all except TIMESYS and PTYPEi may also assume the value TIME(case-insensitive), whereupon the time scale shall be that recorded in TIMESYS or, in its absence, its default value, UTC. See also Sects. 6.2–6.4. See Sect. 4.5 regarding their use for specific time-related axes.
As noted above, local time scales other than those listed in Table 2may be used, but their use should be restricted to alternate coordinates in order that the primary coordinates will always refer to a properly recognized time scale; an example may be found in Sect. 6.3.
4.1.2. Time reference value
We allow the time reference point to be defined in the three common systems: ISO-8601, JD, or MJD. These reference values are only to be applied to time values associated with one of the recognized time scales listed in Table 2 and that time scale needs to be specified (see also Sect. 5.4).
Keywords.
The reference point in time, to which all times in the HDU are relative, shall be specified through one of three keywords:
MJDREF (floating-valued)
Reference time in MJD
JDREF (floating-valued)
Reference time in JD
DATEREF (datetime-valued)
Reference time in ISO-8601
MJDREF and JDREF may, for clarity and/ or precision reasons, be split into two keywords holding the integer and fractional parts separately:
MJDREFI (integer-valued)
Integer part of reference time in MJD
MJDREFF (floating-valued)
Fractional part of reference time in MJD
JDREFI (integer-valued)
Integer part of reference time in JD
JDREFF (floating-valued)
Fractional part of reference time in JD
If [M]JDREF and both [M]JDREFI and [M]JDREFF are present, the integer and fractional values shall have precedence over the single value. If the single value is present with one of the two parts, the single value shall have precedence. In the following, MJDREF and JDREF refer to their literal meaning or the combination of their integer and fractional parts.
If, for whatever reason, a header contains more than one of these keywords, JDREF shall have precedence over DATEREF and MJDREF shall have precedence over both the others. If none of the three keywords is present, there is no problem as long as all times in the HDU are expressed in ISO-8601; otherwise MJDREF = 0.0 must be assumed. If TREFPOS = ’CUSTOM’ (Sect. 4.1.3) it is legitimate for none of the reference time keywords to be present, as one may assume that we are dealing with simulation data.
Note:
The value of the reference time has global validity for all time values, but it does not have a particular time scale associated with it. Therefore, assuming the use of TT(TAI), if MJDREF = 50814.0 and TIMEUNIT= ’s’:
a time instant T = 86400.0 associated with TT will fall on
1998-01-02T00:00:00.0(TT) or
1998-01-01T23:59:27.816(TAI) or
1998-01-01T23:58:56.816(UTC),
but a time instant T = 86400.0 associated with TAI will fall on
1998-01-02T00:00:32.184(TT) or
1998-01-02T00:00:00.0(TAI) or
1998-01-01T23:59:29.0(UTC).
Table 10 provides examples of this; one may compare the reference pixel values of TT, TCG, and UTC for Col. 1, and of TDB and TCB for Col. 20.
4.1.3. Time reference position
An observation is an event in space-time. The reference position, specified by the keyword TREFPOS, specifies the spatial location at which the time is valid, either where the observation was made or the point in space for which light-time corrections have been applied. This may be a standard location (such as GEOCENTER or TOPOCENTER) or a point in space defined by specific coordinates. In the latter case one should be aware that a (3D) spatial coordinate frame needs to be defined that is likely to be different from the frame(s) that the data are associated with. Note that TOPOCENTERis only moderately informative if no observatory location is provided or indicated.
The commonly allowed standard values are shown in Table 3. Note that for the gaseous planets we use the barycenters of their planetary systems, including satellites, for obvious reasons. Our preference is to spell the location names out in full, but in order to be consistent with the practice of Paper III (2006) and the FITS Standard (Pence et al. 2010) the values are allowed to be truncated to eight characters. Furthermore, in order to allow for alternative spellings, only the first three characters of all these values shall be considered significant. The value of the keyword shall be case-sensitive. We envisage that at some time in the future we may need a provision to add minor planets to this list.
Some caution is in order here. Time scales and reference positions cannot be combined arbitrarily if one wants a clock that runs linearly at TREFPOS. Table 4 provides a summary of compatible combinations. BARYCENTER should only be used in conjunction with time scales TDBand TCBand should be the only reference position used with these time scales. With proper care GEOCENTER, TOPOCENTER, and EMBARYCENTERare appropriate for the first ten time scales in Table 2. However, one needs to be aware that relativistic effects introduce a (generally linear) scaling in certain combinations; highly eccentric spacecraft orbits are the exceptions. Problems will arise when using a reference position on another solar system body (including HELIOCENTER). At this point we recommend synchronizing the local clock with one of the time scales defined on the Earth’s surface, TT, TAI, GPS, or UTC(in the last case: beware of leap seconds). This is common practice for spacecraft clocks. Locally, such a clock will not appear to run at a constant rate, because of variations in the gravitational potential and in motions with respect to Earth, but the effects can be calculated and are probably small compared with errors introduced by the alternative: establishing a local time standard.
In order to provide a complete description, TOPOCENTER requires the observatory’s coordinates to be specified. We offer three options: the ITRS Cartesian coordinates (X, Y, Z) introduced in Paper III; a geodetic latitude/longitude/height triplet; or a reference to an orbit ephemeris file.
A non-standard location indicated by CUSTOM must be specified in a manner similar to the specification of the observatory location (indicated by TOPOCENTER). One should be careful with the use of the CUSTOM value and not confuse it with TOPOCENTER, as use of the latter imparts additional information on the provenance of the data.
Keywords.
The time reference position is specified by the keyword
TREFPOS (string-valued)
Time reference position; default TOPOCENTER
TREFPOS 5 shall apply to time coordinate axes in images as well. See Sect. 6.2.1 for an explanation.
In binary tables different columns may represent completely different Time Coordinate Frames. However, each column can have only one time reference position, thus guaranteeing linearity (see Sect. 4.1.1) and the following keyword may override TREFPOS:
TRPOSn (string-valued)
If the value of any of these keywords is TOPOCENTER, the observatory position needs to be specified. If the value is CUSTOM, the “custom” position needs to be specified. In either case we allow three mechanisms for this.
The ITRS Cartesian coordinates (with respect to the geocenter) as defined in Paper III:
OBSGEO-X (floating-valued)
ITRS Cartesian X in m
OBSGEO-Y (floating-valued)
ITRS Cartesian Y in m
OBSGEO-Z (floating-valued)
ITRS Cartesian Z in m
Similarly defined geodetic coordinates have to be recognized, although the ITRS Cartesian coordinates are strongly preferred:
OBSGEO-B (floating-valued)
Latitude in deg, North positive
OBSGEO-L (floating-valued)
Longitude in deg, East positive
OBSGEO-H (floating-valued)
Altitude in m
An orbit ephemeris file:
OBSORBIT (string-valued)
URI, URL, or name of orbit ephemeris file
Beware that only one set of coordinates is allowed in a given HDU. Cartesian ITRS coordinates are the preferred coordinate system; however, when using these in an environment requiring nanosecond accuracy, one should take care to distinguish between meters consistent with TCG or with TT. If one uses geodetic coordinates, the geodetic altitude OBSGEO-His measured with respect to IAU 1976 ellipsoid which is defined as having a semi-major axis of 6 378 140 m and an inverse flattening of 298.2577.
ITRS coordinates (X,Y,Z) may be derived from geodetic coordinates (L,B,H) through:
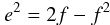 a is the semi major axis, f the inverse of the inverse flattening.
a is the semi major axis, f the inverse of the inverse flattening.
Nanosecond precision in timing requires that OBSGEO-[BLH] be expressed in a geodetic reference frame defined after 1984 in order to be sufficiently accurate.
4.1.4. Time reference direction
If any pathlength corrections have been applied to the time stamps (i.e., if the reference position is not TOPOCENTER for observational data), the reference direction that is used in calculating the pathlength delay should be provided in order to maintain a proper analysis trail of the data. However, this is useful only if there is also information available on the location from where the observation was made (the observatory location). The direction will usually be provided in a spatial coordinate frame that is already being used for the spatial metadata, although that is not necessarily the case. It is, for instance, quite conceivable that multiple spatial frames are already involved: spherical ICRS coordinates for celestial positions, and Cartesian FK5 for spacecraft ephemeris. We also acknowledge that the time reference direction does not by itself provide sufficient information to perform a fully correct transformation; however, within the context of a specific analysis environment it should suffice.
The uncertainty in the reference direction affects the errors in the time stamps. A typical example is provided by barycentric corrections where the time error terr is related to the position error poserr:
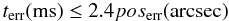 The reference direction is indicated through a reference to specific keywords. These keywords may hold the reference direction explicitly or indicate columns holding the coordinates. In event lists where the individual photons are tagged with a spatial position, those coordinates may have been used for the reference direction and the reference will point to the columns containing these coordinate values. The OGIP convention, on the other hand, uses the keywords RA_NOMand DEC_NOMindicating a globally applied direction for the entire HDU.
The reference direction is indicated through a reference to specific keywords. These keywords may hold the reference direction explicitly or indicate columns holding the coordinates. In event lists where the individual photons are tagged with a spatial position, those coordinates may have been used for the reference direction and the reference will point to the columns containing these coordinate values. The OGIP convention, on the other hand, uses the keywords RA_NOMand DEC_NOMindicating a globally applied direction for the entire HDU.
Keywords.
The time reference direction is specified by the keyword
TREFDIR (string-valued)
Pointer to time reference direction
TREFDIR shall apply to time coordinate axes in images as well. See Sect. 6.2.1 for an explanation.
In binary tables different columns may represent completely different Time Coordinate Frames. However, also in that situation the condition holds that each column can have only one Time Reference Direction. Hence, the following keyword may override TREFDIR:
TRDIRn (string-valued)
The value of the keyword shall consist of the name of the keyword or column containing the longitudinal coordinate, followed by a comma, followed by the name of the keyword or column containing the latitudinal coordinate. For the above quoted OGIP convention this would result in:
TREFDIR = ’RA_NOM,DEC_NOM’
For the example in Table 10:
TRDIR20= ’EventRA, EventDEC’
4.1.5. Solar System ephemeris
If applicable, the Solar System ephemeris used for calculating pathlength delays should be identified. This is particularly pertinent when the time scale is TCBor TDB.
The ephemerides that are currently most often used are JPL’s (NASA/JPL 2014a and 2014b):
-
DE200 (Standish 1990; considered obsolete, but still in use)
-
DE405 (Standish 1998; default)
-
DE421 (Folkner et al. 2009)
-
DE430, DE431, DE432 (Folkner et al. 2014)
Future ephemerides in this series shall be accepted and recognized as they are released.
Keyword.
The Solar System ephemeris used for the data (if required) is indicated by the value of the keyword:
PLEPHEM (string-valued)
Solar System ephemeris; default DE405.
Historically, the name PLEPHEMreferred to Planetary and Lunar Ephemeris; we continue the use of that keyword name.
4.2. Time unit
The specification of the time unit allows the values defined in Paper I (2002) and the FITS Standard (Pence et al. 2010), with the addition of the century. We recommend the following:
-
s: second (default)
-
d: day (=86 400 s)
-
a: (Julian) year (=365.25 d)
-
cy: (Julian) century (=100 a)
The following values are also acceptable:
-
min: minute (=60 s)
-
h: hour (=3600 s)
-
yr: (Julian) year (=a= 365.25 d)
-
ta: tropical year
-
Ba: Besselian year
The use of taand Bais not encouraged, but there are data and applications that require the use of tropical years or Besselian epochs (see Sect. 3.5). The length of the tropical year tain days is (based on Simon et al. 1994):
1ta = 365.24219040211236 − 0.00000615251349T
−6.0921 × 10-10T2 + 2.6525 × 10-10T3d
where T is in Julian centuries since J2000, using time scale TDB.
The length of the Besselian year Bain days is (based on Newcomb 1895 and 1898):
1Ba = 365.2421987817 − 0.00000785423Td
where T is in Julian centuries since J1900, using time scale ET – although for these purposes the difference with TDB is negligible.
A cautionary note is in order here. The subject of tropical and Besselian years presents a particular quandary for the specification of standards. The expressions presented here specify how to calculate them for use in data files while creating these. However, that is pretty much a non-statement since such practice is strongly discouraged. Our purpose in providing the expressions is to guide the user in how to interpret existing data that are based on these units. But there is no guarantee that the authors of the data applied these particular definitions and there is ample evidence that many did not (see, e.g., Meeus & Savoie 1992). An alternative definition of the Besselian epoch in common use (e.g., in SOFA 2010) is the one given by Lieske 1979:
B = 1900.0 + (JD − 2 415 020.31352) / 365.242198781
which is based on a Besselian year of fixed length leading to:
1Ba = 365.242198781d.
Therefore, all we can state here is that these are the most accurate available expressions for the units, but at the same time we strongly advise any user of existing data that contain them to pay special attention and attempt to ascertain what the data’s authors really used.
See Sect. 6.6 for the use of Besselian and Julian epochs in FITS files.
Keywords.
The time unit is set by the keyword
TIMEUNIT (string-valued)
Time unit; default s
that shall apply to all time instances and durations that do not have an implied time unit (such as is the case for JD, MJD, ISO-8601, J and B epochs). In relevant context, this may be overridden (see Sect. 6 for details) by the CUNITia keywords and their binary table equivalents (see Table 5).
4.3. Assorted items affecting time data: corrections, errors, etc.
All quantities enumerated below must be expressed in the prevailing time units (TIMEUNITor its local overrides), the default being s.
4.3.1. Time offset (not applicable to images)
It is sometimes convenient to be able to apply a uniform clock correction in bulk by just putting that number in a single keyword. A second use for a time offset is to set a zero offset to a relative time series, allowing zero-relative times, or just higher precision, in the time stamps. Its default value is zero.
Its value shall be added to MJDREF, JDREF, or DATEREF, and hence affects the values of TSTART, and TSTOP, as well as any time pixel values in a binary table.
However, this construct may only be used in tables and must not be used in images.
Keyword.
The time offset is set, in the units of TIMEUNIT, by:
TIMEOFFS (floating-valued)
Time offset; default 0.0
and has global validity for all times in the HDU. It has the same meaning as the keyword TIMEZERO in the OGIP convention – which we did not adopt out of concern for the potentially ambiguous meaning of the name. The net effect of this keyword is that the value of TIMEOFFS is to be added to the time stamp values in the file. Formally, this is effected by adding that value to MJDREF, JDREF, and/or DATEREF.
Keywords for specifying time coordinates.
4.3.2. Absolute error
The absolute time error is the equivalent of the systematic error defined in previous papers.
Keywords.
The absolute time error is set, in the units of TIMEUNIT, by:
TIMSYER (floating-valued)
Absolute time error
but may be overridden, in appropriate context (e.g., time axes in image arrays or table columns; see Sect. 6 for details) by the CSYERia keywords and their binary table equivalents (see Table 5).
4.3.3. Relative error
The relative time error specifies accuracy of the time stamps relative to each other. This error will usually be much smaller than the absolute time error. This error is equivalent to the random error defined in previous papers.
Keywords.
The relative time error (the random error between time stamps) is set, in the units of TIMEUNIT, by:
TIMRDER (floating-valued)
Relative time error
but may be overridden, in appropriate context (e.g., time axes in image arrays or table columns; see Sect. 6 for details) by the CRDERia keywords and their binary table equivalents (see Table 5).
4.3.4. Time resolution
The resolution of the time stamps (the width of the time sampling function) is represented by a simple double. In tables this may, for instance, be the size of the bins for time series data or the bit precision of the time stamp values.
Keyword.
The time resolution is global in the HDU, and set by the keyword
TIMEDEL (floating-valued)
Time resolution
in the units of TIMEUNIT.
4.3.5. Time binning (not applicable to images)
When data are binned in time bins (or, as a special case, events are tagged with a time stamp of finite precision) it is important to know to which position in the bin (or pixel) that time stamp refers. This is an important issue: the FITS standard assumes that coordinate values correspond to the center of all pixels; yet, clock readings are effectively truncations, not rounded values, and therefore correspond to the lower bound of the pixel.
However, this construct may only be used in tables and must not be used in images.
Keyword.
The relative position of the time stamp in each time bin (TIMEDEL in the case of an event list) is set universally in the HDU by the keyword:
TIMEPIXR (floating-valued)
Pixel position of the time stamp; from 0.0 to 1.0, default 0.5.
In conformance with the FITS pixel definition, the default is 0.5, although the value 0.0 may be more common in certain contexts. Note, for instance, that this is required when truncated clock readings are recorded, as is the case for almost all event lists. It seems unwise to allow this keyword to be specified separately for multiple time frames, rather than requiring its value to apply to all.
4.4. Keywords that represent global time values
Keywords.
The following time values may only be found in the header, independent of any time axes in the data. Except for DATE, they provide the top-level temporal bounds of the data in the HDU. As noted before, they may also be implemented as table columns.
DATE (datetime-valued)
Creation date of the HDU in UTC
DATE-OBS (datetime-valued)
Time of data in ISO-8601 according to TIMESYS
MJD-OBS (floating-valued)
Time of data in MJD according to TIMESYS
DATE-OBSis already defined in Sect. 4.4.2.2 of the FITS Standard. It is not specifically defined as the start time of the observation and has also been used to indicate some form of mean observing date and time. In order to specify a start date and time unambiguously one should use:
DATE-BEG (datetime-valued)
Start time of data in ISO-8601 according to TIMESYS
DATE-AVG (datetime-valued)
Average time of data in ISO-8601 according to TIMESYS; note: this standard does not prescribe how average times should be calculated
DATE-END (datetime-valued)
Stop time of data in ISO-8601 according to TIMESYS
MJD-BEG (floating-valued)
Start time of data in MJD according to TIMESYS
MJD-AVG (floating-valued)
Average time of data in MJD according to TIMESYS; note: this standard does not prescribe how average times should be calculated
MJD-END (floating-valued)
Stop time of data in MJD according to TIMESYS
TSTART (floating-valued)
Start time of data in units of TIMEUNIT relative to MJDREF, JDREF, or DATEREF and TIMEOFFS according to TIMESYS
TSTOP (floating-valued)
Stop time of data in units of TIMEUNIT relative to MJDREF, JDREF, or DATEREFand TIMEOFFSaccording to TIMESYS.
The alternate-axis equivalent keywords DOBSn, MJDOBn, DAVGn, and MJDAn, as defined in the FITS Standard (Pence et al. 2010, Table 22) are also allowed. Note that of the above only TSTART and TSTOP are relative to the time reference value.
As in the case of the time reference value (see Sect. 4.1.2), the JD values supersede DATE values, and MJD values supersede both, in cases where conflicting values are present.
It should be noted that, although they do not represent global time values within an HDU, the CRVALia and CDELTia keywords, and their binary table equivalents (see Table 5), also represent (binary) time values. They should be handled with the same care regarding precision when combining them with the time reference value as any other time value (see also Sect. 5.3).
Finally, Julian and Besselian epochs (see Sects. 3.5 and 4.2) may be expressed by these two keywords – to be used with great caution, as their definitions are more complicated and hence their use more prone to confusion:
JEPOCH (floating-valued)
Julian epoch; implied time scale TDB;
BEPOCH (floating-valued)
Besselian epoch; implied time scale ET.
When these epochs are used as time stamps in a table column their interpretation will be clear from the context. When the keywords appear in the header without obvious context, they must be regarded as equivalents of DATE-OBSand MJD-OBS, i.e., with no fixed definition as to what part of the dataset they refer to.
4.5. Other time-related coordinate axes
There are a few coordinate axes that are related to time and that are accommodated in this standard: (temporal) phase, timelag, and frequency. Phase results from folding a time series on a given period. Timelag is the coordinate of cross- and auto-correlation spectra. As a practical definition one may consider frequency as the Fourier transform equivalent of time and, particularly, the coordinate axis of power spectra, with the exception of spectra where the dependent variable is the electromagnetic field. Specifically, the latter (excluded) case applies to electromagnetic waveforms of cosmic origin with fixed transformations to related variables such as wavelength, Doppler velocity, and redshift which do not apply to periodic phenomena in general. That specific case is covered by Greisen et al. (2006).
These coordinate axes shall be specified by giving CTYPEi and its binary table equivalents one of the values:
PHASE, TIMELAG, FREQUENCY
Note that the frequency coordinate of the electromagnetic spectrum is indicated by the value FREQ.
Timelag’s units are the regular time units and frequency’s basic unit is Hz. Neither of these two coordinates is a linear or scaled transformation of time and therefore cannot appear in parallel with time as an alternate description. Phrased differently, a given vector of values for an observable can be paired with a coordinate vector of time, or timelag, or frequency, but not with more than one of these; the three coordinates are orthogonal.
Phase, on the other hand, can appear in parallel with time as an alternate description of the same axis. Its units may be deg, rad, or turn, the last of which is introduced here.
Time at the zero point of a phase axis shall be recorded in a new keyword
CZPHSia (floating-valued)
with binary table forms TCZPHn, TCZPna, iCZPHn, and iCZPna.
Optionally, the period of a phase axis may be recorded in a new keyword
CPERIia (floating-valued)
with binary table forms TCPERn, TCPRna, iCPERn, and iCPRna. One should be aware, however, that this can be used only if the period is a constant. When that is not the case, the period should either be absent or set to zero, and one should follow a convention like PSRFITS6 (see also Hotan et al. 2004, and Hobbs et al. 2006).
Phase period and zero point shall be expressed in the globally valid time reference frame and unit as defined by the global keywords (or their defaults) in the header.
4.6. Durations
Durations shall not be expressed in ISO-8601 format, but only as actual durations (i.e., numerical values) in the units of the specified time unit.
There is an extensive collection of header keywords that indicate time durations, such as exposure times, but there are many pitfalls and subtleties that make this seemingly simple concept treacherous. One may encounter similar-sounding keywords for concepts like: awarded exposure time; scheduled exposure time; on-target time; duration of the exposure, including dead time and lost time; exposure time charged against the awarded exposure time; exposure time corrected for lost (bad) data; and exposure time corrected for dead time. Related to these are various keywords providing dead time correction factors, dead time correction flags, and duty cycle information. We suggest that these are are excellent candidates for definition through an appropriate formally registered FITS convention, rather than inclusion in this standard.
Because of their crucial role and common use, keywords are defined here to record exposure and elapsed time; in addition, a standard for good time intervals is defined in Sect. 4.7.
Keyword.
The only defined durations shall indicated by the keywords:
XPOSURE (floating-valued)
in the units of TIMEUNIT. It shall be the effective exposure time for the data, corrected for dead time and lost time. If the HDU contains multiple time slices, it shall be the total accumulated exposure time over all slices. More obvious candidates for the keyword name (like EXPOSURE) had to be avoided since they have been used with conflicting definitions in various sub-communities.
TELAPSE (floating-valued)
also in the units of TIMEUNIT provides the amount of time elapsed between the start (TSTART, MJD-BEG, etc.) and the end (TSTOP, DATE-END, etc.) of the observation or data stream.
4.7. Good time interval (GTI) tables
Good-Time-Interval (GTI) tables are indispensable for data with “holes” in them, especially photon event files, as they allow one to discriminate between “no data received” versus “no data taken”. GTI tables shall contain two mandatory columns, STARTand STOP, and may contain one optional column, WEIGHT. The first two define the interval, the third, with a value from 0 to 1, the quality of the interval; i.e., a weight of 0 indicates a Bad-Time-Interval. WEIGHT has a default value of 1. Any time interval not covered in the table shall be considered to have a weight of zero.
5. General comments on implementation
In the following we discuss some practical implementation issues, before turning, in the next section, to usage in specific contexts.
As a general comment, we should point out that the distortion conventions described by Calabretta et al. (in prep.) are also very much applicable to the time coordinate axis.
5.1. Getting started
As a simple getting-started guide, we make the following recommendations (referring to Table 5):
-
The presence of the Informational DATE keyword is STRONGLY RECOMMENDED in all HDUs
-
One or more of the Informational keywords DATE-xxxand/or MJD-xxxSHOULD be present in all HDUs whenever a meaningful value can be determined. This also applies, for instance, to catalogs derived from data collected over a well-defined time range
-
The Global keyword TIMESYS is STRONGLY RECOMMENDED
-
The Global keywords MJDREF or JDREFor DATEREFare RECOMMENDED
-
The remaining Informational and Global keywords SHOULD be present whenever applicable
-
All Context-Specific keywords SHALL be present as needed and required by the context of the data
5.2. Global keywords and overrides
For reference to the keywords that are discussed here, see Table 5. The globally applicable keywords listed in Sect. 5.b of the table serve as default values for the corresponding C* and TC* keywords in that same section, but only when axis and column specifications (including alternate coordinate definitions) use a time scale listed in Table 2 or when the corresponding CTYPE or TTYPE keywords are set to the value TIME. Any alternate coordinate specified in a non-recognized time scale assumes the value of the axis pixels or the column cells, optionally modified by applicable scaling and/or reference value keywords; see also Sect. 4.1.1.
5.3. Precision
In order to maintain the precision that is provided by the HDU, one needs to be careful while processing the information for high timing precision applications. Although it is safe to read floating point values in headers and binary data in double precision, arithmetic performed with those values may need to be executed with extended precision. For example, if the header contains:
MJDREFI = 1243
MJDREFF = 0.3746369623
CRVAL = 0.0000000111111
CDELT = 0.00000000251537257213
then the relative value of the first pixel is:
T = CRVAL + 1*CDELT
= 0.00000001362647257213
while the final answer, expressed in MJD and performed in quad precision, is:
TIME = MJDREFI + MJDREFF + T
= 1243.374636975926472572130000.
The onus is on the application programmer to ensure that applications maintain their required precision.
5.4. Labeling
We have observed that there is a confusing variation in the labeling of time axes in figures and presentations. In particular, the usage of terms like “TJD”, “HJD”, and “BJD” is highly ambiguous. Julian and modified Julian date counts do not imply any particular time scale or any particular reference position. The “B” in “BJD” raises the question whether it refers to the reference position BARYCENTERor the time scale TDB. And an expression like “BJD−2 400 000” leaves the reader in doubt whether the value is to be taken literally or whether the author really meant “BJD−2 400 000.5”. Authors should be explicit about the times that are posted and we strongly recommend that they adopt the following convention for axis labeling:
JD|MJD(<timescale>;<reference position>)
In order to facilitate the correct labeling we recommend that these strings be provided in the CNAME* and TCNA* keywords if possible; for instance:
TCNAM1 = ’MJD(TDB;Barycenter)’
Also, see the examples of TCNA1Eand TCNA1Fin Table 10.
Example 1: Cube with two spatial and one time axis.
6. Usage contexts
In this section we discuss usage in the contexts to which this WCS time standard applies; these contexts refer back to Sect. 2.
6.1. Header keywords
The rules governing these keywords are explained in Sect. 4 and summarized in Table 5.
6.2. Time axis in images
Example 1 (Table 6) is a data cube in which the 3rd axis is time. It is in fact a sequence of 2D images stacked together.
The rules governing keywords defining the time axis in an image (which could be a one-dimensional time series or a multi-dimensional space-time-spectral hypercube) are also dealt with in Sect. 4 and summarized in Table 5, but there are some aspects that require further elaboration as presented in the following sub-sections.
6.2.1. Restrictions on alternate descriptions
An image will have at most one time axis as identified by having the CTYPEi value of TIMEor one of the values listed in Table 2. Consequently, as long as the axis is identified through CTYPEi, there is no need to have axis number identification on the global time-related keywords. In addition, we expressly prohibit the specification of multiple time reference positions on this axis for alternate time coordinate frames, since this would give rise to complicated model-dependent non-linear relations between these frames. Hence, time scales TDB and TCB(or ET, to its precision) may be specified in the same image, but cannot be combined with any of the first nine time scales in Table 2; those first nine can be expressed as linear transformations of each other, too, provided the reference position remains unchanged. Time scale LOCAL is by itself, intended for simulations, and should not be mixed with any of the others.
6.2.2. CRVAL ia
The WCS standard requires this keyword to be numeric and it cannot be expressed in ISO-8601 format. Therefore, CRVALia is required to contain the elapsed time in units of TIMEUNIT or CUNITia, even if the zero point of time is specified by DATEREF.
6.2.3. CDELTia, CDi_ja and PCi_ja
If the image does not use a matrix for scaling, rotation and shear (Paper I 2002), CDELTia provides the numeric value for the time interval.
If the PC form of scaling, rotation and shear (Paper I 2002) is used, CDELTia provides the numeric value for the time interval, and PCi_j, where i = j = the index of the time axis (in the typical case of an image cube with axis 3 being time, i = j = 3) would take the exact value 1, the default (Paper I 2002).
When the CDi_j form of mapping is used, CDi_j provides the numeric value for the time interval.
If one of the axes is time and the matrix form is used, then the treatment of the PCi_ja (or CDi_ja) matrices involves at least a Minkowsky metric and Lorentz transformations (as contrasted with Euclidean and Galilean). See Soffel et al. (2003) for a full review of the IAU resolutions concerning space-time coordinate transformations.
Sections 6.2.4 and 6.2.5 describe examples of the use of these keywords.
Example 2: Header extract of an image where Time is coupled with Space, built up from individual exposures from a stigmatic slit spectrograph stepped across the solar disk.
Example 3: Header extract of an image where Time is coupled with Space needing a PC matrix.
Example 4: Header extract of an image cube where Space is coupled with Time through rotation, using different CD matrices for the beginning and end of the observation.
6.2.4. Example of an image constructed by a moving slit
As an example we present a header in Table 7 (Example 2) based on a simplified version of a SOHO Coronal Diagnostic Spectrometer observation from October 1998 (Harris et al. 1992). An image of the Sun is focused onto the entrance slit of a stigmatic spectrograph, forming a spectral image on the intensified CCD detector with wavelength in one direction, and the latitudinal spatial dimension in the other direction. A spectrally resolved map of the Sun is formed by moving the slit from right to left during the observation; thus different parts (columns) of the data cube are observed at different times. The example header defines the relations between the different coordinate systems by specifying a degenerate Time axis that is related to the first spatial pixel axis through the PC4_2 matrix element.
Example 5: Header extract of a binary table (event list) with two time columns.
An alternative approach for the example in Table 7 would be to define the time axis as CTYPE2A, tying it directly to the longitude pixel coordinate. However, it is possible to devise a scenario where this simple alternative approach is not sufficient. In the actual observation that Table 7 is based on, the slit was tilted relative to solar north, so that the resulting PCi_j matrix would have non-trivial values for axes 2 and 3. If the data were then rotated to be aligned to solar north, time would be dependent on both spatial axes, which would be reflected as non-zero values for both PC4_2 and PC4_3.
This approach is shown in Example 3 (Table 8). One could still use the alternative description of Time as an alternate axis on longitude, but in that case it would need its own PC2_jA matrix.
6.2.5. Less tractable space-time interactions
The following example does not have a fool-proof solution, but it may be instructive. It is derived from the APF telescope at Lick Observatory. This is a telescope on an azimuth-elevation mount where the guider has no rotator, so the Celestial WCS changes as the telescope tracks. The guide camera software can produce movies as 3D FITS files.
There is no provision for a Celestial WCS which changes as a function of time (or position), so it is not possible for a FITS file to store a complete description of the WCS for every frame in a movie within the context of a single HDU.
However, it is possible to store a WCS for the beginning and end of a movie. That allows standard FITS WCS viewing programs to give some idea of the amount of field rotation that happens during a movie.
So the intent of the FITS header in Example 4 (Table 9) is to communicate that alternate WCS Sis valid at the beginning of the exposure and alternate WCS Ris valid at the end of the exposure.
Of course, an alternate approach would be to provide the WCS information for each frame in a binary table as a separate HDU. Each row in the table would represent a separate time step and the columns would contain the corresponding time-dependent WCS parameters using the Green Bank convention (Pence 2010). This solution has the benefit of providing exact WCS information. However, it does require introducing a separate HDU, whereas the merit of the example in Table 9 is that it provides the extremes within the image HDU itself. In conclusion, these two approaches may be considered complementary and are not mutually exclusive.
6.3. Time columns in tables
Example 5 (Table 10) is part of the header of an event list (a binary table in pixel list mode) with two time columns. Column 1 carries time in TT, with alternate time coordinate frames in UTC, TCG, Mission Elapsed Time, Observation Elapsed Time, MJD, and JD. Column 20 contains the time stamps in TDB with alternate frames in TCB and Julian epoch; Cols. 21 and 22 provide the events’ positions.
The rules governing keywords defining the time in table columns (pixel as well as vector columns) are largely dealt with in Sect. 4 and summarized in Table 5, but, again, there are some aspects that require further elaboration.
All times (other than ISO-8601), expressed in a recognized time scale (see Table 2), are relative (to MJDREF, JDREF or DATEREF). That means that they are elapsed times and that users have to take care of leap seconds when using UTC; the unit ‘d’ is defined as 86 400 elapsed seconds. But beware of the following: the reference time values are to be taken in the time scale specified for the coordinate one is dealing with. That is why the TCRV1Ain the Table 10 needs to account for the difference between MJDREF(TT) and MJDREF(UTC).
Times that are expressed in any other time scale (e.g., Mission Elapsed Time, a common scale) take the values in the table cells at face value, though they may be modified by applicable keywords such as TCRP*, TCRV*, and TCD*.
In the context of tables the most important point to keep in mind is that TCTYPn and/or TCTYna contain the time scale. However, it should also be pointed out that a binary table column with TTYPEn = ’TIME’ and either lacking any TC*n keywords or with TC*n = ’TIME’ will be controlled by the global keywords listed in Table 5. This is a common convention in existing files that will still be compliant with the present standard.
The keywords JEPOCH and BEPOCH, of course, may also be turned into table columns. However, one should be mindful that they are implicitly tied to specific time scales and represent absolute times. Consequently, they have no association with any of the global keywords.
Example 6: Header extract of a binary table with two phase columns.
6.3.1. Restrictions
The same restrictions imposed on the image time axis (see Sect. 6.2.1) also apply to individual table columns. However, since one can have more than one column with time information in the same table, it is possible to mix different time reference positions and time scales that are not linearly related to each other – provided that one does not mix these in the same column.
6.4. Time in random groups
As noted before, the Random Group structure is deprecated; we include it here for completeness, but this should not be construed as a statement in support of its continued use.
There are two ways in which time can enter into random group data (see Greisen & Harten 1981): as one of the subarray axes or through a group parameter. In the former case the situation is identical to that in images and we refer to Sect. 6.2 for the rules. If time is to be transmitted through a group parameter, it simply means that the PTYPEi keyword needs to be set to one of the time scale codes from Table 2, just like the CTYPEi. All the global time reference frame keywords (see Table 5) apply, just as they would if CTYPEi were set to the same time scale value, except that there is no possibility of override since the PUNITi, PSYERi, and PRDERi keywords are not defined in the standard.
6.5. The time-related coordinate axes
Summarizing the definition of phase, timelag, and frequency in Sect. 4.5, we emphasize three key concepts:
-
FREQUENCY may be used as the abscissa of any spectrum, except an electo-magnetic spectrum
-
phase can be used as an alternate description of the time coordinate; timelag and frequency cannot
-
The period of a phase axis may be provided through the keyword CPERIia and its equivalents, but only if that period is a constant; when that is not the case, the period should either be absent or set to zero
We provide an simple example of a binary table with one time and two phase columns in Example 6 (see Table 11). We readily admit that in this simple example the phase columns can also be projected onto the time column as linear alternate coordinate systems. The purpose of the example is to show the use of the phase coordinate, not an encouragement to make headers more complicated than necessary.
6.6. Use of Besselian and Julian epochs
Use of Besselian and Julian epochs requires special care, as discussed in Sects. 3.5 and 4.2. Their use is discouraged, but the fact remains that data exist with a time axis that is so labeled. We recommend the following convention for identifying these epochs (illustrated for binary table Col. 1, but easily translated to other use cases):
DATEREF = ’0000-01-01T00:00:00’
TCUNI1 = ’Ba’ / for Besselian epochs
TCUNI1 = ’a’ / or ’yr’; for Julian epochs
TCNAM1 = ’B epoch’ / or ’Besselian epoch’
TCNAM1 = ’J epoch’ / or ’Julian epoch’.
Current Best Estimates are maintained at http://maia.usno.navy.mil/NSFA/NSFA_cbe.html
This convention was developed by the Office of Guest Investigator Programs within the HEASARC (High Energy Astrophysics Science Archive Research Center) at the NASA Goddard Space Flight Center; (OGIP/GSFC/NASA 2008).
The Gregorian calendar was an improvement of the Julian calendar which was introduced by Julius Caesar in 46 BCE (Plinius 78), advised by Sosigenes of Alexandria and probably based on an earlier design by Ptolemaeus III Euergetes (246-221 BCE) (Encyclopædia Britannica 2014). Although the Julian calendar took effect in 45 BCE, the leap days were not properly implemented until at least 4 CE, requiring proleptic use of this calendar before that time. The Gregorian calendar reduced the average length of the year from 365.25 days (Julian calendar) to 365.2425 days, closer to the length of the tropical year. Further resources on these subjects can also be found in Wikipedia.
The OGIP convention uses the keyword TIMEREFand only allows values ‘LOCAL’ (i.e., Topocenter), ‘GEOCENTRIC’, ‘HELIOCENTRIC’, ‘SOLARSYSTEM’ (i.e., Barycenter); the convention contains also the somewhat peculiar keyword TASSIGN. We will not adopt these keywords in order to avoid confusion on allowed values and meaning. Instead, we adopt the keywords TREFPOS and TRPOSn.
http://www.bipm.org/en/committees/cc/cctf/ccds-1970.html (Note the 1980 amendment and the change implicit by the IAU 1991 Resolution A4)
Acknowledgments
The authors want to express their deep gratitude and appreciation for the dedication and tireless efforts of their colleague and friend Peter Bunclark in moving the work on this paper forward. We received his last email on 8 December 2008, just two days before his untimely death. We miss Pete dearly, not only as a great co-author who kept us on the straight and narrow, but especially as a very good friend. It was a privilege to have collaborated with him. We are also very much indebted to former IAU FITS Working Group chair Bill Pence, who provided valuable comments and kept exhorting us to finally finish this paper. A.H.R. gratefully acknowledges the many helpful discussions he had with Jonathan McDowell and the support by NASA under contract NAS 8-03060 to the Smithsonian Astrophysical Observatory for operation of the Chandra X-ray Center. We thank an anonymous referee for helpful comments that resulted in improved clarity. And we thank Patrick Wallace, Ken Seidelmann, and George Kaplan for their comments and suggestions.
References
- BIPM 2006, The International System of Units (SI), BIPM, Paris (The SI Brochure, 8th edn.) http://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf [Google Scholar]
- Brown, E. W., & Hedrick, H. B. 1919, Tables of the motion of the moon (Yale University Press) [Google Scholar]
- Bunclark, P. S., & Rots, A. H. 1997, FITS-Y2k agreement: http://fits.gsfc.nasa.gov/year2000.html [Google Scholar]
- Calabretta, M. R., &Greisen, E. W. 2002, A&A, 395, 1077 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassini, J. 1740, Tables astronomiques du Soleil et de la Lune, des planètes, des étoiles fixes et des satellites de Jupiter et de Saturne; avec l’explication et l’usage de ces mêmes tables [Google Scholar]
- CCIR 1970, Avis 460, Émissions de Fréquences Étalon et de Signaux Horaires, XIIe Assemblée Plénière [Google Scholar]
- Clemence, G. M. 1948, AJ, 53, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Encyclopædia Britannica 2014, Sosigenes of Alexandria, http://www.britannica.com/EBchecked/topic/555018/Sosigenes-of-Alexandria [Google Scholar]
- Folkner, W. M., Williams, J. G., & Boggs, D. H. 2009, IPN Progress Report 42-178: http://tmo.jpl.nasa.gov/progress_report/42-178/178C.pdf [Google Scholar]
- Folkner, W. M., Williams, J. G., Boggs, D. H. Park, R. S., & Kuchynka, P. 2014, IPN Progress Report 42-196: http://tmo.jpl.nasa.gov/progress_report/42-196/196C.pdf [Google Scholar]
- Fukushima, T.,Kaplan, G. H.,Krasinsky, G. A., et al. 2008, Transactions of the International Astronomical Union, Series A, 27, 5 [Google Scholar]
- Gregorius PP. XIII 1582, Inter gravissimas, in Clavius, C. Romani Calendarii A Gregorio XIII P. M. Restituti, Rome 1603; see also: http://www.fourmilab.ch/documents/calendar/IG_Latin.html [Google Scholar]
- Greisen, E. W., &Calabretta, M. R. 2002, A&A, 395, 1061 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greisen, E. W., &Harten, R. H. 1981, A&AS, 44, 371 [NASA ADS] [Google Scholar]
- Greisen, E. W.,Calabretta, M. R.,Valdes, F. G., &Allen, S. L. 2006, A&A, 446, 747 (Paper III) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harrison, R. A., et al. 1995, Sol. Phys., 162, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Herschel, J. 1851, Outlines of astronomy, 4th edn. [Google Scholar]
- Hobbs, G. M., Edwards, R. T., & Manchester, R. N. 2006, MNRAS, 369. 655 [NASA ADS] [CrossRef] [Google Scholar]
- Hotan, A. W., van Straten, W., &Manchester, R. N. 2004, PASA, 21, 302 [NASA ADS] [CrossRef] [Google Scholar]
- IAU 1928, IIIrd General Assembly – The International Astronomical Union meeting at Leiden, 1928 July 5–13, The Observatory, 51, 237 [Google Scholar]
- IAU 1991, XXIst General Assembly – Transactions of the IAU Vol. XXI B, ed. J. Bergeron (Kluwer Academic Publishers) [Google Scholar]
- IAU 1997, Resolution B1 of the XXIIIrd General Assembly – Transactions of the IAU Vol. XXIII B, ed. J. Andersen (Kluwer Academic Publishers) http://www.iau.org/static/resolutions/IAU1997_French.pdf http://www.iers.org/MainDisp.csl?pid=98-110 [Google Scholar]
- IAU 2000, XXIVth General Assembly – Transactions of the IAU Vol. XXIV B, ed. H. Rickman (ASP) [Google Scholar]
- IAU 2006, Proceedings of the XXVIth General Assembly Prague 2006 – Transactions of the IAU, Vol. XXVIB, ed. K. A. van der Hucht (Cambridge University Press) [Google Scholar]
- Irwin, A. W., &Fukushima, T. A. 1999, A&A, 348, 642 [NASA ADS] [Google Scholar]
- ISO 2004, International Standard ISO 8601:2004(E), Data elements and interchange formats – Information interchange – Representation of dates and times [Google Scholar]
- ITU 2004, Recommendation ITU-R TF.460-6, Standard-frequency and time-signal emission, Radio Regulations 4, 7 [Google Scholar]
- Jordi, C.,Morrison, L. V.,Rosen, R. D., et al. 1994, Geophys. J. Int., 117, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Lieske, J. H. 1979, A&A, 73, 282 [NASA ADS] [Google Scholar]
- Luzum, B.,Capitaine, N.,Fienga, A., et al. 2011, Celest. Mech. Dyn. Astr., 110, 293 [Google Scholar]
- McCarthy, D. D., & Seidelmann, P. K. 2009, TIME – From Earth Rotation to Atomic Physics (Wiley-VCH) [Google Scholar]
- Meeus, J., &Savoie, D. 1992, J. Br. Astron. Assoc., 102, 40 [NASA ADS] [Google Scholar]
- NASA/JPL Planetary Ephemerides 2014a: http://ssd.jpl.nasa.gov/?ephemerides [Google Scholar]
- NASA/JPL Solar and Planetary Ephemerides 2014b: http://ssd.jpl.nasa.gov/?planet_eph_export [Google Scholar]
- Newcomb, S. 1895, Tables of the Sun, Astr. Papers Amer. Ephemeris 6, Part I, Bureau of Equipment, Navy Department, Washington [Google Scholar]
- Newcomb, S. 1898, Tables of the Four Inner Planets, Astr. Papers Amer. Ephemeris 6, 2nd edn., Bureau of Equipment, Navy Department, Washington [Google Scholar]
- OGIP/GSFC/NASA 2008, FITS conventions: http://heasarc.gsfc.nasa.gov/docs/heasarc/ofwg/ofwg_recomm.html [Google Scholar]
- Pence, W. D. 2010, http://fits.gsfc.nasa.gov/registry/greenbank.html [Google Scholar]
- Pence, W. D.,Chiappetti, L.,Page, C. G., et al. 2010, A&A, 524, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plinius Secundus, Gaius 78, Naturalis Historia, Book 18, Chap. 57, http://www.perseus.tufts.edu/hopper/text?doc=Perseus:text:1999.02.0137:book=18:chapter=57 [Google Scholar]
- Rots, A. H. 2008, Space-Time Coordinate Metadata for the Virtual Observatory: http://www.ivoa.net/Documents/latest/STC.html [Google Scholar]
- Sadler, D. H. 1978, QJRAS, 19, 290 [NASA ADS] [Google Scholar]
- Seidelmann, P. K. 1992, Explanatory Supplement to the Astronomical Almanac, 2nd edn. (University Science Books) [Google Scholar]
- Seidelmann, P. K., &Fukushima, T. 1992, A&A, 265, 833 [NASA ADS] [Google Scholar]
- Simon, J. L.,Bretagnon, P.,Chapront, J., et al. 1994, A&A, 282, 663 [NASA ADS] [Google Scholar]
- SOFA 2010, SOFA Time Scale and Calendar Tools, http://www.iausofa.org/sofa_ts_c.pdf [Google Scholar]
- Soffel, M.,Klioner, S. A.,Petit, G., et al. 2003, AJ, 126, 2687 [NASA ADS] [CrossRef] [Google Scholar]
- Standish, E. M. 1990, A&A, 233, 252 [NASA ADS] [Google Scholar]
- Standish, E. M. 1998, JPL Memo IOM 312.F-98-048 [Google Scholar]
- Urban, S. E., & Seidelmann, P. K. 2012, Explanatory Supplement to the Astronomical Almanac, 3rd edn. (University Science Books) [Google Scholar]
- USNO Time Scales: http://tycho.usno.navy.mil/systime.html [Google Scholar]
- Wallace, P. T. 2011, Metrologia, 48, S200 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Time scales
If one is dealing with high-precision timing, there are more subtle issues associated with the various time scales that should be considered. This Appendix provides the necessary information that supplements Sect. 4.1.1 and Table 2. It also provides some background information on how some of the time scales are realized and how they relate to each other. To put this in context, measurement of time is based on the SI second which has been defined since 1967 as the duration of 9192631770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom (BIPM 2006). TT is an ideal time scale based on the SI second that serves as the independent time variable for all astronomical ephemerides, whereas TAI, as an observationally determined time scale, differs from an ideal one due to the limitations inherent in any observational activity. All currently maintained time scales, with the exception of UT1, are based on the SI second in the appropriate reference frame.
Appendix A.1: TT and TDT
TT is defined by Resolution B1.9 of the XXIVth General Assembly of the IAU in 2000 at Manchester (IAU 20007). This is a re-definition of TT as originally defined by Recommendation IV of Resolution A4 of the XXIst General Assembly of the IAU in 1991 at Buenos Aires (IAU 19918). By that resolution TT was recognized as a better-defined replacement for TDT.
The initial definition of TT was explained by Seidelmann & Fukushima (1992). For explanation of the redefinition see Petit in IERS Technical Note 299.
Due to the rotation of the Earth (and motion of other bodies), a point on the surface changes its depth in the gravitational potential of the solar system. As noted in Soffel et al. (2003), the proper time experienced by chronometers on the surface of Earth differs from TT with a diurnal variation at the picosecond level.
Because TDT never had a satisfactory definition its meaning is ambiguous at microsecond precision. For most uses other than historical tabulation it is more practical to express such time stamps as TT.
Appendix A.2: TCG and TCB
TCG and TCB are defined by Recommendation III of Resolution A4 of the XXIst General Assembly of the IAU in 1991 at Buenos Aires (IAU 199110). Note 4 suggests that precise use of these time scales requires specification of both the realized time scale (i.e., TAI) and the theory used to transform from the realized time scale to the coordinate time scale. All of the references given above for TT are also relevant for TCG and TCB.
Given that TT and TCG differ only by a constant rate, a precise value of TCG is specified by documenting the realization of TT. Thus we suggest that TCG(TAI) be shorthand for TCG computed from TT = TAI + 32.184 s or, alternatively, TCG(TT(TAI)). Likewise, we suggest that TCG(BIPMnn) be shorthand for TCG(TT(BIPMnn)).
Specifying a precise value for TCB requires documenting a precise value of TT and additionally a time ephemeris. A current example of a time ephemeris is TE405 given by Irwin & Fukushima (1999).
It is not immediately clear to us how best to express this in a concise value for the FITS keyword, for there is no guarantee of a controlled vocabulary for the time ephemerides: nothing prevents other authors from producing another time ephemeris based on DE405. However we may proceed on the assumption that the differences between any two time ephemerides will be inconsequentially small. Consequently, we suggest that TCB(BIPMnn,TE405) be shorthand for TCB computed from TT(BIPMnn) and TE405.
Appendix A.3: TDB
TDB is defined by Resolution B3 of the XXVIth General Assembly of the IAU in 2006 at Prague (IAU 200611). This definition is required for microsecond precision. Note that the reference frame for TDB is barycentric but it ticks with seconds approximately scaled to match the SI seconds of TT on the rotating geoid. For further details on this matter we refer to Chapter 3 in Urban & Seidelmann (2012).
Appendix A.4: ET
ET was defined by Clemence (1948), named by Resolution 6 of the 1950 Conference on the Fundamental Constants of Astronomy held at CNRS in Paris, and adopted by a recommendation from IAU Commission 4 during the VIIIth General Assembly in 1952 at Rome. The definition of ET is based on the works of Newcomb (1895 and 1898) and Brown & Hedrick (1919). At the IAU General Assemblies in 1961 and 1967 Commission 4 designated three improvements on ET named ET0, ET1, and ET2.
Because ET is nonrelativistic its meaning is ambiguous at millisecond precision. For most uses other than historical tabulation it is more practical to express such time stamps as TT or TDB. For the purposes of historical tabulation we might want to recommend the use of “ET(ET0)”, “ET(ET1)”, and “ET(ET2)”.
Starting in 1955 timestamps derived from radio signal distributions based on (national) atomic clocks became an option; see Sect. A.9.
Appendix A.5: TAI
TAI is defined by BIPM12.
Thus TAI is intended to be the best possible realization of TT, which means its aim is to be a geocentric coordinate time scale. Because of deficiencies in the realization, TAI is only approximately equal to TT − 32.184 s.
TAI is a special case of the atomic time scales because the only valid realization is the one in Circular T which is published in arrears by the BIPM. As such a FITS keyword value of ‘TAI’ should only be used for timestamps which have been reduced using a chain of chronometers traceable through Circular T. TAI should not be used casually. For example, there are GPS devices which provide time stamps that claim to be TAI.
TAI should be avoided prior to 1972 because:
-
TAI had not been authorized until the 14th CGPM in late 197113
-
TAI had not been available for any contemporary time stamping mechanisms prior to 1972-01-01
TAI should be used with caution prior to 1977 because of the 10-12 change in rate, and for precision work TAI should always be corrected using TT(BIPMnn).
For the recording of terrestrial time stamps between 1955 and 1972 we refer to Sect. A.9.
Appendix A.6: GPS time
GPS time is currently defined by the Interface Specification document “IS-GPS-200F, Revision F”14. Note that GPS time is aligned to a specific UTC(USNO) epoch, 19 s behind TAI, with the fractional part matching UTC(USNO) to within a microsecond.
GPS is a convenient source of accurate time. However, for precise timestamps it is necessary for applications to know whether the receiver has implemented the corrections to the satellite clocks and ionosphere given by the contents of Subframe 1 as documented in Sect. 20.3.3.3 of IS-GPS-200.
GPS system time should not be used before its date of inception (1980-01-06).
Appendix A.7: UTC
UTC is defined by ITU-R TF.460 (CCIR 1970 and ITU 2004). It is a time scale that is offset from TAI by an integer number of SI seconds and required to be within 0.9 s of UT1, Earth rotation time; this requirement is satisfied by the insertion of leap seconds as needed, (see also Sect. 4.1.1). According to the specification the broadcasters are required to match only to within a millisecond. Because of the international recommendations and treaty obligations regarding its use, most national metrology agencies have adopted UTC and disseminate it as part of their statutory obligation.
UTC should be used with caution prior to 1974 because the meaning of the name was unknown outside the metrology community.
UTC should be used with extreme caution prior to 1972-01-01 because different contemporary sources of timestamps were providing different time scales.
UTC with its current definition was not available prior to 1972. Aside from historical tabulations, most terrestrial time stamps prior to 1972 should be expressed as UT (see Sect. A.9) and we recommend specifically that GMT be interpreted as UT for such dates.
UTC should not be used prior to 1960-01-01 because coordination of broadcast time did not begin until then, and prior to 1961 only time sources in the US and UK were providing it.
UTC from any source is practical, but in order to provide precision timestamps one needs to know which realization was used.
UTC from a GPS receiver is also practical, but any tools that are to provide precision timestamps need to know whether the receiver has implemented the corrections given by the contents of Subframes 4 and 5 as documented in section 20.3.3.5 of IS-GPS-200.
Appendix A.8: GMT
Greenwich Mean Time (GMT) is an ill-defined timescale that nevertheless continues to persist in popular parlance as well as scientific papers. Its use is to be discouraged, but if encountered it should be interpreted as UTC, with the caveat that it is rather loosely defined as such and any assertions as to the precision of the time stamps should be regarded with caution.
Appendix A.9: UT
The underlying concept for UT originated at the International Meridian Conference held in Washington in 1884 which defined the Universal Day as a mean solar day to be reckoned from Greenwich midnight. UT was initially defined by Newcomb’s “fictitious mean sun” (Newcomb 1895 and 1898). The name Universal Time was established as the subdivision of the Universal Day by Commission 4 of the IAU at the IIIth General Assembly in 1928 at Leiden (IAU 192815).
Most terrestrial time stamps prior to 1972 should be expressed as UT. For events with time stamps established by radio transmissions we note that it is possible to use Bulletin Horaire of the BIH to obtain sub-second precision on one of the time scales here.
Particularly, if high time resolution is required for time stamps based on radio distributions of atomic clocks between 1955 and 1972 data providers should be specific about their time distribution source.
Example notations of time stamps before 1972 which were based on broadcasts that have not been corrected for propagation time from the transmitter:
UT(WWV)
UT(CHU)
Example notations for time stamps before 1972 which were based on broadcasts that have been corrected for propagation time from the transmitter:
UT(NBS)
UT(NRC)
Example notation for time stamps before 1972 which were based on broadcasts that have been corrected to Heure Définitive using Bulletin Horaire:
UT(BIH)
Example notations for time stamps since 1972-01-01 which were based on broadcasts that have not been corrected for propagation time from the transmitter:
UTC(JJY)
UTC(DCF77)UTC(MSF)
Example notations for time stamps since 1972-01-01 which were based on broadcasts that have been corrected for propagation time from the transmitter:
UTC(NICT)
UTC(PTB)
UTC(NPL)
Example notation for time stamps since 1972-01-01 which have been corrected using tabulations published in BIPM Circular T:
UTC(BIPM)
We also encourage the use of a similar convention to denote the flavor of UT used during that period:
UT(UT0)
UT(UT1)
UT(UT2)
We encourage data publishers to transform their time stamps to a uniform time scale such as TT, but we recognize that some data may have been acquired by systems for which time offsets were never characterized. Even when those offsets are known the transformation may require disproportionate research and consultation with the tabulated corrections for radio broadcasts published by a national time bureau, and the BIH Bulletin Horaire or BIPM Circular T. Therefore this standard requires minimally that the original time stamps be transformed from a local time zone to UT.
This paper cannot prescribe a historically complete set of notations for time stamps from radio transmissions and national laboratories. When any of these notations for precision time are used we recommend inclusion of comments describing how the time stamps should be interpreted.
In exceptional cases of events with time stamps established by chronometers at observatories with meridian instruments, calibration is possible to sub-second precision as far back as 1830 (Jordi et al. 1994).
All Tables
Example 2: Header extract of an image where Time is coupled with Space, built up from individual exposures from a stigmatic slit spectrograph stepped across the solar disk.
Example 3: Header extract of an image where Time is coupled with Space needing a PC matrix.
Example 4: Header extract of an image cube where Space is coupled with Time through rotation, using different CD matrices for the beginning and end of the observation.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.