| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 11 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201424394 | |
| Published online | 30 January 2015 | |
Benchmarking atomic data for astrophysics: Si iii⋆
1
DAMTP, Centre for Mathematical Sciences, Wilberforce Road,
Cambridge
CB3 0WA,
UK
e-mail:
g.del-zanna@damtp.cam.ac.uk
2
Department of Physics, University of Strathclyde,
Glasgow, G4 0NG, UK
Received: 13 June 2014
Accepted: 20 November 2014
We investigate the main spectral diagnostics for Si iii UV lines, which have been previously used to measure electron densities, temperatures, and to suggest that non-Maxwellian electron distributions might be present in the low transition region of the solar atmosphere. Previous atomic calculations and observations are reviewed. We benchmark the observations using a new large-scale R-matrix scattering calculation for electron collisional excitation of Si iii, carried out with the intermediate-coupling frame transformation (ICFT) method. We find generally good agreement between predicted and observed line intensities, if one takes into account the different temperature sensitivity of the lines, and the structure of the solar transition region. We find no conclusive evidence for the presence of non-Maxwellian electron distributions.
Key words: atomic data / techniques: spectroscopic / Sun: corona / line: identification
The full dataset (energies, transition probabilities and rates) are available in electronic form at our APAP website (www.apap-network.org)
© ESO, 2015
1. Introduction
Si iii lines are prominent in UV spectra of solar and many astrophysical plasmas (planetary nebulae, novae, stars, interstellar medium). They have been used for a variety of diagnostic applications, in particular to measure electron densities and temperatures. For example, Dufton et al. (1983) used Skylab observations obtained with the Naval Research Laboratory (NRL) slit spectrograph S082B to measure electron densities. Some discrepancies between observed and predicted line ratios were found. They involved the intercombination line 3s21S0−3s 3p 3P1 at 1892 Å and the 3s 3p 1P1 − 3s 4s 1S0 1312.6 Å line.
Dufton et al. (1984) suggested that these discrepancies could have been caused by the presence of non-Maxwellian electron distributions in the low transition region. The upper level of the 1312.6 Å line is populated from the ground state via a transition with a relatively high excitation energy, hence would be sensitive to the high-energy tail of any non-Maxwellian electron distribution. Since then, various authors have used solar observations of Si iii lines to suggest that non-Maxwellian electron distributions were present in the solar corona (see, e.g. Keenan et al. 1989; Pinfield et al. 1999; Dzifčáková & Kulinová 2011).
Clearly, it would be extremely interesting if non-Maxwellian electrons were present in the solar transition region. However, it is important beforehand to analyse the atomic data for this ion. This is done here by carrying out new atomic calculations and then reassessing the diagnostics using various solar and stellar observations. The scattering calculations are part of our UK APAP network work along the Mg-like sequence (Fernández-Menchero et al. 2014).
We first briefly review in Sect. 2 previous calculations for this ion. Sect. 3 presents our calculations, while Sect. 4 presents our comparisons with observations. We present in Sect. 5 our conclusions.
2. Previous calculations
2.1. Scattering calculations
Baluja & Hibbert (1980) used the CIV3 program (Hibbert 1975) to calculate wavefunctions and energies for the lowest 12 LS terms, which give rise to 20 fine-structure levels. The complete set of n = 3,4 configurations was adopted. These wavefunctions were later used for the scattering calculations for this ion with R-matrix codes in a series of papers (Baluja et al. 1980, 1981; Dufton et al. 1984). A paper that has been widely cited was that of Dufton & Kingston (1989), because the level-resolved effective collision strengths were made available in a tabulated form. These data were made available in the first version of the CHIANTI database (Dere et al. 1997) and are still in the last one, v.7.1 (Landi et al. 2013). Dufton & Kingston (1989) performed the calculations in LS coupling, including partial waves up to L = 12, for about 1050 impact energies (up to 10 Ryd). They then used the JAJOM code (Saraph 1978) to obtain level-resolved collision strengths.
Griffin et al. (1999) performed an intermediate-coupling frame transformation (ICFT) R-matrix calculation, with an LS close-coupling expansion which included all 25 terms arising from the 3s2, 3s 3p, 3p2, 3s 3d, 3p 3d, 3d2, 3s 4s, 3s 4p, and 3s 4d configurations. A full exchange calculation was performed on all partial waves up to L = 12, using 25 continuum basis orbitals. A non-exchange calculation in LS coupling for L = 10−50 was performed, and added, together with the usual top-up for high J contributions, to the exchange part. The number of mesh points used in the asymptotic part of the problem was 5032 and the maximum energy was 7.35 Ryd.
Wallbank et al. (1997) and Reisenfeld et al. (1999) published laboratory measurements of the cross sections for two transitions from the ground state (to 3s 3p 1P, 3P), finding good agreement with the previous R-matrix calculations, hence providing confidence in the ab-initio calculations, at least for these terms.
2.2. Transition probabilities
That radiative rates for several Si iii transitions differed significantly from one another was well known in the literature. Griffin et al. (1999) also suggested that several of the diagnostic line ratios commonly used could be significantly different, depending on which radiative rates one employs.
2.2.1. The intercombination line
The transition probability for the intercombination line 3s21S0−3s 3p 3P1 at 1892.0 Å has been the subject of many studies, because its value varies significantly between calculations. The 3P1 level has a weak mixing with the 1P1 level through the spin-orbit parameter of the 3p electron, so the radiative rate is sensitive to the energies of these levels. It turns out that ab-initio calculations are unable to obtain the energy of the 3s 3p 3PJ levels close enough to the experimental value, so many authors have applied empirical corrections.
Baluja & Hibbert (1980) provided a radiative rate of 1.2 × 104 s-1. Dufton et al. (1983) improved the Baluja & Hibbert (1980) calculations, by adjusting the diagonal energies of the Hamiltonian matrix (to reproduce the experimental energies), to obtain a value of 1.46 × 104 s-1, which has been widely used since.
Nussbaumer (1986) used the Superstructure program (Eissner et al. 1974) and different basis sets (66 and 120 configurations up to n = 8) to try to improve the energies of the lowest levels. At the end, the term energies were still not very accurate, so various semi-empirical corrections based on the observed energies were applied to the calculations. Nussbaumer (1986) obtained a value of 1.8 × 104 s-1. The atomic structure employed by Griffin et al. (1999) for the scattering calculation provided a lower value of 0.92 × 104 s-1. The energy-adjusted MCHF calculations of Tachiev and Froese Fisher (2002)1 produced a value of 1.75 × 104 s-1.
There is only one experiment, by Kwong et al. (1983), which produced lifetime measurements and an A-value of 1.67± 0.1 ×104 s-1. Various authors have adopted this experimental value for modelling. We also adopt it here, as discussed below, although we note that further measurements would be useful, to confirm this value.
We also note that Ojha et al. (1988) obtained the same value measured by Kwong et al. (1983). Laughlin & Victor (1979) carried out semi-empirical model potential calculations for the intercombination line along the Mg-like sequence. They also obtained a value close to experiment, 1.78 × 104 s-1.
2.2.2. The 1312.6 Å line
Despite its diagnostic importance in terms of non-Maxwellian electron distributions, the calculation of the radiative rate for the 3s 3p 1P1–3s 4s 1S0 1312.6 Å transition has received less attention from previous authors. Baluja & Hibbert (1980) noted that the inclusion of a 5s pseudo-orbital decreased the oscillator strength for this transition by a large factor, of three. In their model ion, Dufton et al. (1983) adopted the lower value calculated by Baluja & Hibbert (1980), which implies a transition rate of 2.84 × 108 s-1. The ab-initio value obtained by Griffin et al. (1999) is even lower, 1.81 × 108 s-1. Nussbaumer (1986) provided instead a much larger value of 4.0 × 108 s-1. The energy-adjusted MCHF calculations of Tachiev Froese Fisher (2002) produced an even larger value, 8.87 × 108 s-1.
3. Atomic calculations
Several authors in the previous literature pointed out the significant increases in the collision strengths calculated with the R-matrix codes, with respect to earlier distorted wave calculations. These are due to the resonances (see, e.g. Seaton 1975; Burke & Robb 1975). Our recent work on the more complex iron coronal ions (see. e.g. Del Zanna et al. 2012) has shown that larger targets often produce significant increases in the level populations, partly because of enhanced resonances, partly because of cascading from higher levels. We have therefore set out to perform a larger scattering calculation to see what effects additional levels have. Our target, described below, includes the 3s 4f levels, which in principle produce lines observed in the solar spectrum, and all the main n = 5 levels, to improve the calculations for the n = 4 levels.
3.1. The atomic structure
The target electron configuration basis and orbital scaling parameters λnl.
The atomic structure calculations were carried out using the Autostructure program (Badnell 2011) which constructs target wavefunctions using radial wavefunctions calculated in a scaled Thomas-Fermi-Dirac-Amaldi statistical model potential with a set of scaling parameters, in the same way as the superstructure program (Eissner et al. 1974). The program also provides radiative rates and infinite energy Born limits, used in the interpolation of the collision strengths at high energies.
We have chosen as our configuration basis the set of 33 n = 3,4,5 configurations listed in Table 1. They give rise to 149 LS terms and 283 fine-structure levels. The scaling parameters λnl for the potentials in which the orbital functions are calculated are also given in Table 1.
Level energies for Si iii.
Table 2 presents the 20 lowest fine-structure target level energies Et, compared to experimental energies Eexp. The experimental energies are taken from the NIST compilation (Kramida et al. 2013). We also list the target energies of the structure calculations of Baluja & Hibbert (1980) used by the following authors for the scattering calculations. We also list the Griffin et al. (1999) values. Overall, we have very good agreement between observed and predicted energies, although as we mentioned the small discrepancy in the 3s 3p 3PJ levels affects the radiative rate for the intercombination line.
We note that our target energies are worse than those of Baluja & Hibbert (1980), but better than those of Griffin et al. (1999) for all levels below the 3s 3d 3D1 level. The differences in the various targets do not significantly affect the oscillator strengths (and collisions strengths) for transitions involving these lowest 20 levels, with the exception of levels No. 14, 15. This occurs because the 3s 4s 1S0 level (No. 15) is LS-mixed with the nearby 3p21S0 level (No. 14). It turns out that the radiative rate for the 5−15 3s 3p 1P1–3s 4s 1S0 1312.6 Å transition is very sensitive to the target wavefunctions. We have carried out several calculations, to try and establish an accurate value. The minimization procedure that we employed to obtain the scaling parameters shown in Table 1 resulted in an energy difference of 4280 cm-1. The experimental energy difference is 5625 cm-1, while those of the Baluja & Hibbert (1980) and Griffin et al. (1999) targets are 2985 and 7730 cm-1, respectively.
We have carried out several large Laguerre pseudo-state structure calculations (Badnell & Gorczyca 1997) in order to try and establish an accurate value for the 5−15 1312.6 Å transition. We kept the Ne-like core fixed and then promoted the two remaining electrons to all nln′l′ configurations up to 18d. We also expanded further to 18f and 20d, independently, but this changed the f-value by only 1%. We used spectroscopic orbitals up to n = 4 and Laguerre pseudo-state orbitals thereon. The former were generated in the usual Thomas-Fermi potential. The f-value varied by < 1% between using the optimized (Table 1) and default (unity) values for the Thomas-Fermi scaling parameters. The Laguerre orbitals all used an effective charge of zn/ 2 – where z = 3 here. This is the default value that we use in all of our large R-matrix with pseudo-state calculations and has been found to converge the expansion most rapidly (Badnell & Griffin 2000). It is a property of the Laguerre pseudo-states that they form an approximate complete basis, i.e. span a wide range of energies even with a small number – here 50 Ry. Our final radiative rate for the 5−15 × 1312.6 Å transition is 2.76 × 108 and with length and velocity f-values of 0.0731 and 0.0688, respectively. The energy separation ranged between about 3800 and 4400 cm-1, i.e. inner-shell promotions (e.g. 2p) would be required to converge energies to the experimental values.
Using the experimental energies and the scaling parameters shown in Table 1, we obtain an A-value for the 5−15 1312.6 Å transition of 2.96 × 108 s-1, i.e. lower than the Nussbaumer (1986) value (4.0 × 108), and slightly higher than the Dufton et al. (1983) value (2.8 × 108).
 |
Fig. 1 Thermally-averaged collision strengths Υ for transitions to the lowest 20 levels, from the 3s2 and 3s 3p levels. The dashed lines indicate ±20%. |
Victor et al. (1976) carried out semi-empirical model potential calculations for the allowed transitions along the Mg-like sequence, obtaining in general very good agreement between the predicted and the (few) measured oscillator strengths. For the 5−15 transition, Victor et al. (1976) calculated gf = 5.3 × 10-2, while for the 5−14 transition gf = 0.84, i.e. quite close to our calculated values (7.6 × 10-2 and 0.88).
In terms of experiments, Livingston et al. (1976a) measured the lifetime of the 3s 4s 3S1 level to be 0.5 ± 0.1 ns. We predict a value of 0.44 ns, in close agreement. Unfortunately, there are no lifetime measurements of the 3s 4s 1S0 level. Livingston et al. (1976b) measured the lifetime of the 3p21S0 level (No. 14) to be 0.58 ± 0.04 ns. The main decay from this level is the 5−14 transition at 1417.24 Å. We predict a lifetime of 0.34 ns, i.e. not in agreement with the experimental result, but still within a factor of two. We will come back to this transition below.
A set of “best” energies Eb was obtained with a linear fit between the Eexp and Et values. The Eb values were used, whenever the Eexp ones are not available, to calculate the transition probabilities. Table 3 lists our A-values, together with those of Dufton et al. (1983) as given in the CHIANTI v.7.1 database, and those from Nussbaumer (1986), which we consider to be the best ones previously published. We can see the excellent agreement (within a relative 10%) in the A-values for most transitions, with a notable exception. Our A-value for the intercombination line is 1.1 × 104, i.e. smaller than experiment (we recall 1.67 × 104).
3.2. The scattering calculation
The R-matrix method used in the scattering calculation is described in Hummer et al. (1993) and Berrington et al. (1995). We performed the calculation in the inner region in LS coupling and included mass and Darwin relativistic energy corrections. The outer region calculation used the ICFT method (Griffin et al. 1998) and our standard assumptions and codes (see the APAP website). Details on the calculation can be found in Fernández-Menchero et al. (2014).
List of the strongest Si iii lines.
The thermally-averaged (effective) collisions strength Υ(i − j) were calculated by assuming a Maxwellian electron distribution and linear integration with the final energy of the colliding electron.
We compared the effective collisions strength with the previous R-matrix results of Dufton & Kingston (1989) and Griffin et al. (1999), finding generally good agreement. Figure 1 shows a comparison at log Te[ K ] = 4.65, the temperature near peak ion abundance in ionization equilibrium (Dere et al. 2009), for all transitions to the lowest 20 levels (the spectroscopically most important ones), from the 3s2 and 3s 3p levels (the main populating levels). As expected, there is an overall scatter, however in most cases it is within a very acceptable 20%. This comparison shows that the effect of resonances attached to higher levels is not significant at such temperatures. Some differences are present, but are likely attributable to the various factors: the position of the resonance thresholds, the resolution in energy, the target wavefunctions, etc.
A sample of thermally-averaged collision strengths is shown in Fig. 2. For strong dipole-allowed transitions such as the resonance 1–5 line, we find vey good agreement between the calculations. However, for several important transitions, we find generally good agreement with the Griffin et al. (1999) values, but some differences with the Dufton & Kingston (1989) effective collision strengths for some transitions. However, as we shall see below, these differences do not significantly affect the intensities of the main diagnostic lines.
 |
Fig. 2 Thermally-averaged collision strengths for a selection of transitions (see text). |
3.3. Line intensities
We have constructed an ion population model with our R-matrix collision strengths and A-values. We then calculated line intensities at log Ne [cm-3] = 10 (a typical solar density) and log Te[ K ] = 4.7, the temperature of maximum ion abundance in ionization equilibrium according to Dere et al. (2009; but see the discussion below). The calculated intensities of the brightest lines, relative to the resonance line (1−5, at 1206.5 Å), are listed in Table 3.
We also list (in brackets) the intensities calculated with the experimental A-value for the intercombination line, 1.67 × 104 s-1 by Kwong et al. (1983) instead of our value of 1.1 × 104 s-1. It is interesting to note that such large variation has a negligible effect on the intensity of the intercombination line, an issue that was pointed out by Jordan et al. (2001), but not noted by other studies on this ion. We have looked at the level population at log Ne [cm-3]=10 and log Te[ K ] = 4.7, corresponding to the relative intensities in Table 3. The 50% increase in the A-value for the intercombination line results in a similar decrease in the relative level population for the 3s 3p 3P1 level, hence a similar line intensity, relative to the strongest 1−5 resonance line, which is not affected by the population of the 3s 3p 3P1 level. On the other hand, the population of several higher levels is significantly affected by direct excitation from the 3s 3p 3P1 level, so a decrease in the population of the 3s 3p 3P1 level results in a decrease of the line intensities decaying from these levels. For example, the population of the 3p23P0 (No. 7) level is by about half due to direct excitation from the 3s 3p 3P1, so it decreases by about 25%, which decreases the relative intensity of the 3–7 1301.1 Å transition as shown in the table. In the ion model calculations that we use in the rest of this paper, we adopt the experimental A-value for the intercombination line.
Regarding the important 5−15 transition at 1312.59 Å, we note that the upper level (3s 4s 1S0) is mainly (by 84%) populated by direct excitation from the ground state. Only about 10% of its population comes from excitations from the 3s 3p 3Pj levels, and about 6% from radiative decays from upper levels. The 1312.59 Å line is the dominant decay from the upper level.
Table 3 also shows the intensities calculated with the CHIANTI v.7.1 model (which we recall is based on the Dufton & Kingston 1989 collision strengths), for comparison. Differences are within 20–30%, with the exception of the decays from the 3s 4p levels, for which we predict higher intensities. Some are due to increased population from lower levels. For example, about half of the population of level 19 comes from level 4, which has an increased population, due to increased collision strength form the ground state (see Fig. 2).
Finally, we note that collisional data for the 3s 4f levels were not previously calculated. Sandlin et al. (1986) reports four lines as due to 3s 3d−3s 4f transitions in Si iii, at 1210.45, 1500.23, 1501.187, and 1501.87 Å. We predict that the strongest transition is the 6–27 3p21D2–3s 4f 1F3 one (see Table 3). However, our predicted intensities of these 3d−4f transitions are far smaller (by factors of 8, 3, 6, 15, respectively in the plage spectrum) than the observed ones, which casts doubts on the identifications of these lines in the solar spectrum.
4. Comparison with observations
Ratios of observed and predicted QS line radiances.
The radiance of an optically thin transition is normally expressed as an integral along the line of sight 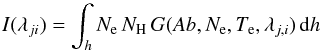 (1)where λji is the wavelength of the transition, Ne, NH are the electron and neutral hydrogen number densities, and G(Ab,Ne,T,λj,i) is the contribution function:
(1)where λji is the wavelength of the transition, Ne, NH are the electron and neutral hydrogen number densities, and G(Ab,Ne,T,λj,i) is the contribution function:
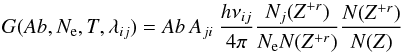 (2)which contains all of the relevant atomic physics parameters, and is mostly dependent on the electron temperature (for brevity, it is denoted below as G(T)). Aji is the spontaneous radiative transition probability, N(Z+ r) /N(Z) is the relative ion population, Nj(Z+ r) /N(Z+ r) is the fractional population of the upper level, and Ab is the element abundance relative to hydrogen. The fractional level population is obtained by solving a system of equations taking into account all the excitation and deexcitation mechanisms.
(2)which contains all of the relevant atomic physics parameters, and is mostly dependent on the electron temperature (for brevity, it is denoted below as G(T)). Aji is the spontaneous radiative transition probability, N(Z+ r) /N(Z) is the relative ion population, Nj(Z+ r) /N(Z+ r) is the fractional population of the upper level, and Ab is the element abundance relative to hydrogen. The fractional level population is obtained by solving a system of equations taking into account all the excitation and deexcitation mechanisms.
The ion population is normally obtained assuming equilibrium conditions, and taking into account all ionization and recombination rates. Several ion populations have been published over the years. Some are shown in Fig. 3. Most of them are obtained in the so-called low-density limit, whereby the density dependence of the dielectronic recombination rates and the presence of metastable levels is neglected. In this case, Si iii is relatively abundant in the range log T [ K ] = 4.6−4.8. Arnaud & Rothenflug (1985) calculated the silicon ion populations by including charge transfer (CT) effects as they were described in Baliunas & Butler (1980). The addition of charge transfer shifts the peak of the Si iii abundance to lower temperatures, about log T [ K ] = 4.5, as Fig. 3 shows. We note that most of the other ion population tabulations do not include CT effects.
 |
Fig. 3 Ion populations. |
Table 4 lists some of the quiet Sun observed intensities (described below) relative to the 1298.9 Å self-blend, as well as the isothermal ratios calculated with the present atomic data, for different temperatures. The relative intensity of the intercombination line is in agreement with an isothermal temperature of about log T [ K ] = 4.5, close to the peak of ion abundance suggested by Arnaud & Rothenflug (1985).
On the other hand, the relative intensity of the resonance line at 1206 Å is closer to the isothermal ratio at log Te [ K ] = 4.7. Such discrepancies had been noted in previous literature, but the lower temperature was assumed to be correct (Dufton et al. 1984; Keenan et al. 1989; Pinfield et al. 1999). The assumption of an isothermal emission at log Te [ K ] = 4.5 resulted in the intensity of the 1312.59 Å line being underestimated, which led to the introduction of non-Maxwellian electron distributions to explain the large intensity of the 1312.59 Å line.
The excitation energy of the transition (from the ground state) populating the upper level of the 1312.59 Å line is in fact significant (19.7 eV), much higher than that of the other lines observed nearby, so this line would be more sensitive to the high-energy tail of a non-Maxwellian electron distribution. Indeed Dufton et al. (1984) showed that, assuming a formation temperature of log Te [ K ] = 4.5, the intensity of the 1312.59 Å line becomes significantly enhanced in the non-Maxwellian case. This, according to the authors, provided plausible evidence for the presence of non-Maxwellian electron distributions at the base of the transition region.
However, the isothermal approximation adopted by previous authors is not the correct approach, since the various Si iii lines have a different temperature sensitivity. Figure 4 (top) shows the contribution functions G(T) for a selection of lines, obtained with the present level populations, the CHIANTI v.7.1 (Landi et al. 2013) ion population and the silicon photospheric abundance of Asplund et al. (2009). It is clear that the resonance and especially the intercombination line would mostly be produced by the lower-temperature layers of the solar atmosphere. It is well known that the plasma distribution in the lower transition-region has a very steep gradient, so to interpret the intensities of the Si iii lines, an understanding of the temperature structure of the lower atmosphere for each observation is needed. This is normally done by assuming that a continuous distribution of the plasma at different temperatures exist, and estimating the column differential emission measure (DEM) as a function of the electron temperature (from a set of selected transitions) ![\begin{equation} {\rm DEM} (T) = ~N_{\rm e} N_{\rm H} {{\rm d}h \over {\rm d}T} \quad~~~[{\rm cm}^{-5} {\rm K}^{-1}] . \end{equation}](/articles/aa/full_html/2015/02/aa24394-14/aa24394-14-eq174.png) (3)The DEM gives an indication of the amount of plasma along the line of sight that is emitting the radiation observed at a temperature between T and T + dT. Such analysis is however often not feasible for previous observations of Si iii lines, because lines emitted from different ions were not reported.
(3)The DEM gives an indication of the amount of plasma along the line of sight that is emitting the radiation observed at a temperature between T and T + dT. Such analysis is however often not feasible for previous observations of Si iii lines, because lines emitted from different ions were not reported.
To illustrate the effect of the plasma distribution for the case of the quiet Sun, we have considered two quiet Sun DEM distributions. The first was obtained from SOHO CDS observations using older atomic data and the Arnaud & Rothenflug (1985) ion populations (Andretta et al. 2003). The values are tabulated in the Appendix. We have also obtained a second DEM from the Skylab observations of Vernazza & Reeves (1978), using for consistency recent atomic data, in particular the CHIANTI v.7.1 (Landi et al. 2013) ion populations. The details of the calculations will be provided in a separate paper, while the DEM values are also tabulated in the Appendix.
 |
Fig. 4 Top: contribution functions G(T) for a selection of lines; bottom: G(T) values multiplied by the quiet Sun DEM obtained from Skylab data. |
Figure 4 (bottom) shows the G(T) × DEM(T) values using the Skylab DEM as an example. We recall that the intensities of the lines are the integral of these curves over temperature. Table 4 lists the theoretical ratios obtained by integrating G(T) × DEM(T) with the two DEM distributions. Clearly, all the lines that have the same temperature sensitivity as the 1298.9 Å line have isothermal ratios that are independent of the temperature and are the same as those obtained by integrating G(T) × DEM(T). The 1312.59 Å line deviates, however its isothermal ratio at log Te [ K ] = 4.65 has the same value as that one obtained by integrating G(T) × DEM(T), and is close to the observed ratios. This means that the isothermal assumption with log Te [ K ] ≃ 4.65 is a reasonable approximation for the 1312.59 Å line, as well as the other lines around 1300 Å, including the resonance 1206.5 Å line.
Differences in the predicted ratios are found if different DEM distributions or ion populations (e.g. Arnaud & Rothenflug 1985 instead of the CHIANTI v.7.1) are used; however, with the exception of the intercombination line they are relatively small (within 20%), as shown in the Table. Therefore, the uncertainities related to the ion populations and the shape of the DEM distributions do not appear to affect our main conclusion, that the intensity of the 1312.59 Å line in the quiet Sun agrees with theory, without the need to invoke for the presence of non-Maxwellian distributions.
To simplify an overall comparison for all the lines, instead of showing how single line ratios behave as a function of density or temperature as done in previous literature, we show the “emissivity ratio” curves, which are basically the ratios of the observed (Iob, energy units) and the calculated line emissivities as a function of the electron density Ne (or temperature Te): 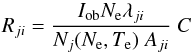 (4)where Nj(Ne,Te) is the population of the upper level j relative to the total number density of the ion, calculated at a fixed temperature Te (or density Ne). λji is the wavelength of the transition, Aji is the spontaneous radiative transition probability, and C is a scaling constant that is the same for all the lines within one observation. If agreement between experimental and theoretical intensities is present, all lines should be closely spaced or intersect, for a near isodensity (or isothermal) plasma. The value of C is chosen so that the emissivity ratios Rji are near unity where they intersect. The emissivity ratio curves as a function of the electron density are similar to the L-function curves introduced by Landi & Landini (1997), the differences being that in the latter case the observed intensities are divided by the line contribution functions G(Teff), calculated at an effective temperature Teff, which in turns depends on the differential emission measure.
(4)where Nj(Ne,Te) is the population of the upper level j relative to the total number density of the ion, calculated at a fixed temperature Te (or density Ne). λji is the wavelength of the transition, Aji is the spontaneous radiative transition probability, and C is a scaling constant that is the same for all the lines within one observation. If agreement between experimental and theoretical intensities is present, all lines should be closely spaced or intersect, for a near isodensity (or isothermal) plasma. The value of C is chosen so that the emissivity ratios Rji are near unity where they intersect. The emissivity ratio curves as a function of the electron density are similar to the L-function curves introduced by Landi & Landini (1997), the differences being that in the latter case the observed intensities are divided by the line contribution functions G(Teff), calculated at an effective temperature Teff, which in turns depends on the differential emission measure.
There are several solar observations of the UV lines, however in may instances either the calibration of the instruments was uncertain, or the lines were not observed simultaneously, or only lines emitted over a narrow spectral range were observed. A selection of observations is discussed below.
4.1. Skylab ATM observations
We start by considering one of the very few published solar observations where both the resonance and the intercombination lines were observed. The observations were performed with the Naval Research Laboratory (NRL) EUV spectrograph on the Skylab Apollo Telescope Mount (ATM) and were reported by Nicolas et al. (1977). The slit was positioned at various locations. In these and other subsequent observations, Si iii lines are rather weak, unless the observations are close to the solar limb, so we have chosen the observation that was 4′′ inside the limb, although we note that the resonance line at 1206 Å has a large optical depth (see, e.g. Burton et al. 1971; Nicolas et al. 1977; Sandlin et al. 1986) at the limb.
The intensity of the weak 1312.59 Å line was not reported by these authors, so we have included a measurement that we have obtained for it from the HRTS observation described by Brekke et al. (1991). These authors published an excellent HRTS spectrum, obtained during the second rocket flight in February 1978. The spectrum was radiometrically calibrated by matching the quiet Sun intensities with those measured by the Skylab S082B calibration rocket flight CALROC. Variations between the HRTS and the CALROC were small, about ±10%. The absolute calibration of the CALROC flight was ±25%. The long slit of the HRTS instrument scanned many solar regions, including the quiet Sun, plage, on disk and off-limb. We have analysed these spectra and measured line intensities for a selection of regions. One of them is a quiet Sun region close to the solar limb, one of the few where the 1312.59 Å line was visible. We have chosen this region because the calibrated radiances of the nearby stronger lines were similar to those reported by Nicolas et al. (1977).
Figure 5 (top) shows the corresponding emissivity ratio curves calculated at log Ne [cm-3] = 10.5, and shows visually what we discussed above, i.e. that, with the exception of the resonance and intercombination lines, all the other lines have a similar temperature sensitivity. We have shown in Table 4 that good agreement (within a relative 20%) is found between all the observed and predicted radiances, taking into account a quiet Sun DEM distribution. The bottom plot of Fig. 5 shows the corresponding emissivity ratio curves at log Te[K] = 4.7. A density of about log Ne [cm-3] = 10.5 provides good agreement for the lines observed around 1300 Å (No. 2 to 7). We note that the HRTS measurement of the 1312.59 Å line is in good agreement (within a relative 20%) with the other lines.
 |
Fig. 5 Emissivity ratio curves relative to the quiet Sun Skylab ATM observations 4′′ inside the limb reported by Nicolas et al. (1977), with the addition of an HRTS measurement of the 1312.59 Å line. Top: at a fixed log Ne [cm-3] = 10.5; bottom: at a fixed log Te[K] = 4.7. Iob indicates the measured intensity of a line in erg cm-2 s-1 sr-1. |
Kjeldseth Moe & Nicolas (1977) provided Skylab ATM observations close to the QS limb. The spectra were calibrated with a CALROC rocket flight which was calibrated on the ground, with typical uncertainties of 20%. We have considered a region 12′′inside the limb, because the same region was also observed by CALROC. The authors measured the intensities of the 1294.55, 1296.73, 1298.9, 1303.32, and 1892 Å lines. We find good agreement (to within 20%) with predicted intensities of the lines (they all have a similar density sensitivity), with the exception of the intercombination 1892 Å line, which is over a factor of three too bright with the isothermal assumption at log Te [ K ] = 4.7, as seen previously.
Dufton et al. (1983) reviewed older Skylab observations with the NRL slit spectrograph S082B, and provided some calibrated line ratios which we use here. They adopted a calibration proposed by Nicolas. Figure 6 shows the emissivity ratio curves calculated at log Te [ K ] = 4.7 relative to a quiet Sun and an active region observation, for a set of observed lines that have a similar temperature sensitivity. Excellent agreement (to within a ±10%) is found, for densities of log Ne [cm-3] = 10.1, 11.1 for the quiet Sun and active region, respectively.
 |
Fig. 6 Emissivity ratio curves relative to the Skylab NRL slit spectrograph S082-B observations (Dufton et al. 1983). Iob indicates the measured intensity of a line, normalised to the radiance of the 1296.73 Å line (energy units). |
Dufton et al. (1983) used a set of atomic data which included the R-matrix calculations of Baluja et al. (1980, 1981) and considered four line ratios. They obtained similar electron densities as we obtain, but noted large discrepancies in the ratios involving the 1892 Å (intercombination) and the 1312.59 Å lines. Around log Te [ K ] = 4.5, the ratios involving the intercombination line produce densities in agreement with the other lines, but the 1312.59 Å line is much brighter than predicted. As we mentioned, Dufton et al. (1984) pointed out that non-Maxwellian electrons would enhance the intensity of the 1312.59 Å line. Dufton et al. (1983) also suggested that perhaps the differences could be due to the temperature structure of the atmosphere, however the main uncertainity was related to the radiometric calibration of the Skylab NRL instrument, especially for the intercombination line (factor of two). However, we note that this would not explain the different discrepancies in different solar regions. Another problem with these Skylab observations is that lines were not recorded simultaneously.
4.2. HRTS observations
 |
Fig. 7 Emissivity ratio curves relative to the HRTS rocket flight spectrum recorded on 1975 Jul. 21, and regions No. 3, 4, relative to a quiet Sun and an active region (Nicolas et al. 1979). Iob indicates the measured intensity of a line in erg cm-2 s-1 sr-1. |
Nicolas et al. (1979) analysed a spectrum from a HRTS rocket flight on 1975 Jul. 21. They used for the calibration the absolutely calibrated rocket spectrum of 1976 Oct. 22. They provided calibrated intensities for four nearby lines in ten solar regions. The authors used older atomic data calculated with the DW approximation, and reported significant discrepancies in the electron densities obtained from different line ratios. On the contrary, the present atomic data provide excellent agreement for all the lines. Figure 7 shows the emissivity ratios calculated at log Te [ K ] = 4.7, for two of the ten observations, relative to a quiet Sun (lower density) and an active region. The agreement is to within a few percent, i.e. is much better than the expected uncertainties in the atomic data and instrument calibration. The intensity of the 1312.6 Å line is also in good agreement.
Keenan et al. (1989) analysed HRTS observations on 1985 Aug. 1 aboard Spacelab 2, providing calibrated ratios of the 1296.73, 1301.15, 1303, and 1312.59 Å lines in three different regions, a quiet Sun, an active region and a sunspot. The lines were recorded simultaneously. They also suggested that non-Maxwellian distributions may exist in all regions, because of the intensity of the 1312.59 Å line. On the other hand, with the present atomic data, we find good agreement between observed and predicted intensities at log Te [ K ] = 4.7, the approximate formation temperature of these lines. We also note that the 1312.59 Å line was very weak (with significant blends in its wings), especially in the sunspot, so the measured intensity of this line is very uncertain.
 |
Fig. 8 Emissivity ratio curves relative to HRTS observations of a plage and an umbra (Sandlin et al. 1986). Iob indicates the measured intensity of a line in erg cm-2 s-1 sr-1. |
Sandlin et al. (1986) published a well-known list of HRTS observations of different regions on the Sun, with accurate wavelengths and line intensities, in the 1175−1710 Å spectral range. We have considered the plage and umbra observations (where the 1312.59 Å line was observed), and again we find good agreement between observed and predicted intensities shown in Fig. 8, at log Te [ K ] = 4.7, the approximate formation temperature of the lines. As we have seen above, the exceptions are the resonance line and for the plage the 4−8 × 1303.32 Å, which is too bright, compared to the 2−81296.73 Å (which forms a branching ratio). The 5−14 transition at 1417.24 Å is extremely weak and difficult to measure even in the HRTS spectra. In the plage, the observed intensity of this line is about a factor of two too weak compared to our predicted intensity, while in the umbra the opposite is true, so we cannot reach any conclusions regarding the predicted intensity of this line.
4.3. SOHO SUMER observations
Pinfield et al. (1999) presented SOHO SUMER spectra of three solar regions, a coronal hole, a quiet Sun and an observation off the limb, within an active region. They also suggested that non-Maxwellian distributions were present, an argument followed up by Dzifčáková & Kulinová (2011).
The ratios of the quiet Sun values reported by Pinfield et al. (1999) are shown in Table 4, together with the Skylab + HRTS results. First, we note that the 1312.59 Å line is hardly visible in the coronal hole and quiet Sun data. Second, we note the unusually high intensity of the 1206 Å resonance line, and of the 1303.32 and 1312.6 Å lines, while the 1294.55 and 1296.73 Å ratios are in good agreement. This casts doubts on the observed intensities, in particular in the measurement of the 1303.32 Å line. Third, we note that Pinfield et al. (1999) obtained, using a combination of line ratios, log Te [ K ] = 4.45 and log Ne [ cm-3 ] = 10.3 for the quiet Sun. As we have seen, the best line for density measurements is the 3−7 × 1301.15 Å one, which was not observed, so it is not possible to measure the density accurately, although the quiet Sun value suggested by Pinfield et al. (1999) is in good agreement with previous results. The main problem is the low isothermal temperature obtained by Pinfield et al. (1999), which results in the observed intensity of the 1312.6 Å line being about a factor of three higher than predicted, as we can see from Table 4.
As we have seen, estimating the line ratios by taking into account a QS DEM distribution changes considerably the line ratios, and brings the relative intensity of the 1312.6 Å line within a factor of two the observed value.
Having said that, the intensity of the 1312.6 Å line in the off-limb AR observations of Pinfield et al. (1999) is indeed very high and at odds with the intensities of the other lines, so in that case the presence of a non-Maxwellian electron distribution is still a possible explanation. However, the SUMER lines were not observed simultaneously. The lower transition region lines are known to present strong variability on the shortest times observed, hence any non-simultaneous observations must be considered with great caution.
5. Conclusions
We aimed first to test if some of the reported discrepancies between observed and predicted Si iii line intensities were due to inaccuracies in the atomic data. We performed a new large-scale R-matrix scattering calculation which provides line intensities that are not largely different from those obtained from previous calculations. Variations are of the order of 20% so cannot explain the reported discrepancies.
Comparison with observation shows that the ratio of the 1301.15 Å line with any of the nearby lines is an excellent density diagnostic that is largely independent of the temperature structure of the solar transition region. Ratios involving the resonance and/or the intercombination lines can be used to measure electron temperatures, if the plasma is nearly isothermal. However, for the lower solar atmosphere, where strong gradients are present, understanding the Si iii spectrum is a complex matter, since the resonance, and especially the intercombination line, are typically formed at lower temperatures than the other lines. Furthermore, the resonance line, having a large oscillator strength, is often affected by opacity effects.
We have reviewed all the Si iii measurements of the 3s 3p 1P1−3s 4s 1S0 1312.6 Å line, since previous literature suggested that non-Maxwellian electron distributions were a possible option to explain the intensity of this line. Clearly, significant uncertainties in the formation temperature of the Si iii lines (i.e. ion populations) and the DEM distribution are present. However, they do not significantly affect the relative intensity of the 1312.6 Å line. By taking into account some example DEM distributions for the quiet Sun, we showed that the Si iii lines around 1300 Å are effectively formed at similar temperatures (around log Te [ K ] = 4.7 using the CHIANTI ion populations), so their ratio is not significantly affected by the thermal distribution of the transition region plasma.
We find in general very good agreement between the observed and predicted ratio of the 1312.6 Å line relative to the nearby lines. One exception are the SOHO SUMER observations (in particular the active region one), which are however uncertain, considering that lines were not observed simulaneously.
In summary, with the exception of the SUMER measurements, we find no conclusive evidence for the presence of non-Maxwellian electron distributions. Having said that, the solar transition region is very dynamic, and it is possible that non-equilibrium effects (including time-dependent ionisation) play a role in the formation of the Si iii lines. Future detailed modelling (which is beyond the scope of the present paper) should take that into account, together with the temperature structure of the transition region.
The 1312.6 Å, as well as the 1417.2 Å line, is very weak and its predicted intensity depends significantly on the atomic structure. We have provided what we believe are the best atomic data for these lines, however further laboratory and astrophysical measurements would be useful to confirm the present calculations.
Acknowledgments
The present work was funded by STFC (UK) through the University of Cambridge DAMTP astrophysics consolidated grant, and the University of Strathclyde UK APAP network grant ST/J000892/1. This work is one of several on-going studies GDZ is carrying out to study non-Maxwellian electron distributions, within an ISSI team led by E. Dzifčáková. We thank Carole Jordan for useful suggestions on how to improve the manuscript.
References
- Andretta, V., Del Zanna, G., & Jordan, S. D. 2003, A&A, 400, 737 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., & Rothenflug, R. 1985, A&AS, 60, 425 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R. 2011, Comput. Phys. Commun., 182, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R., & Gorczyca, T. W. 1997, J. Phys. B At. Mol. Phys., 30, 2011 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R., & Griffin, D. C. 2000, J. Phys. B At. Mol. Phys., 33, 2955 [NASA ADS] [CrossRef] [Google Scholar]
- Baliunas, S. L., & Butler, S. E. 1980, ApJ, 235, L45 [Google Scholar]
- Baluja, K. L., & Hibbert, A. 1980, J. Phys. B At. Mol. Phys., 13, L327 [NASA ADS] [CrossRef] [Google Scholar]
- Baluja, K. L., Burke, P. G., & Kingston, A. E. 1980, J. Phys. B At. Mol. Phys., 13, L543 [NASA ADS] [CrossRef] [Google Scholar]
- Baluja, K. L., Kingston, A. E., & Burke, P. G. 1981, J. Phys. B At. Mol. Phys., 14, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Berrington, K. A., Eissner, W. B., & Norrington, P. H. 1995, Comput. Phys. Commun., 92, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Brekke, P., Kjeldseth-Moe, O., Bartoe, J.-D. F., & Brueckner, G. E. 1991, ApJS, 75, 1337 [NASA ADS] [CrossRef] [Google Scholar]
- Burke, P. G., & Robb. 1975, Adv. At. Mol. Phys., 11, 143 [Google Scholar]
- Burton, W. M., Jordan, C., Ridgeley, A., & Wilson, R. 1971, Roy. Soc. London Philos. Trans. Ser. A, 270, 81 [Google Scholar]
- Del Zanna, G. 1999, Ph.D. Thesis, Univ. of Central Lancashire, UK [Google Scholar]
- Del Zanna, G., Landini, M., & Mason, H. E. 2002, A&A, 385, 968 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., Storey, P. J., Badnell, N. R., & Mason, H. E. 2012, A&A, 541, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Landi, E., Young, P. R., et al. 2009, A&A, 498, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dufton, P. L., & Kingston, A. E. 1989, MNRAS, 241, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Dufton, P. L., Hibbert, A., Kingston, A. E., & Doschek, G. A. 1983, ApJ, 274, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Dufton, P. L., Kingston, A. E., & Keenan, F. P. 1984, ApJ, 280, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Dzifčáková, E., & Kulinová, A. 2011, A&A, 531, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eissner, W., Jones, M., & Nussbaumer, H. 1974, Comput. Phys. Commun., 8, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández-Menchero, L., Badnell, N. R., & Del Zanna, G. 2014, A&A, 572, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffin, D. C., Badnell, N. R., & Pindzola, M. S. 1998, J. Phys. B At. Mol. Phys., 31, 3713 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, D. C., Badnell, N. R., Pindzola, M. S., & Shaw, J. A. 1999, J. Phys. B At. Mol. Phys., 32, 2139 [NASA ADS] [CrossRef] [Google Scholar]
- Hibbert, A. 1975, Comput. Phys. Commun., 9, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Hummer, D. G., Berrington, K. A., Eissner, W., et al. 1993, A&A, 279, 298 [NASA ADS] [Google Scholar]
- Jordan, C., Sim, S. A., McMurry, A. D., & Aruvel, M. 2001, MNRAS, 326, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Keenan, F. P., Dufton, P. L., Kingston, A. E., & Cook, J. W. 1989, ApJ, 340, 1135 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldseth Moe, O., & Nicolas, K. R. 1977, ApJ, 211, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramida, A., Ralchenko, Y., Reader, J., & NIST ASD Team 2013, NIST Atomic Spectra Database, http://physics.nist.gov/asd [Google Scholar]
- Kwong, H. S., Johnson, B. C., Smith, P. L., & Parkinson, W. H. 1983, Phys. Rev. A, 27, 3040 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., & Landini, M. 1997, A&A, 327, 1230 [NASA ADS] [Google Scholar]
- Landi, E., Young, P. R., Dere, K. P., Del Zanna, G., & Mason, H. E. 2013, ApJ, 763, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Laughlin, C., & Victor, G. A. 1979, ApJ, 234, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Livingston, A. E., Baudinet-Robinet, Y., Garnir, H. P., & Dumont, P. D. 1976a, J. Opt. Soc. Am., 66, 1393 [NASA ADS] [CrossRef] [Google Scholar]
- Livingston, A. E., Kernahan, J. A., Irwin, D. J. G., & Pinnington, E. H. 1976b, J. Phys. B At. Mol. Phys., 9, 389 [Google Scholar]
- Nicolas, K. R., Brueckner, G. E., Tousey, R., et al. 1977, Sol. Phys., 55, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Nicolas, K. R., Bartoe, J.-D. F., Brueckner, G. E., & Vanhoosier, M. E. 1979, ApJ, 233, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Nussbaumer, H. 1986, A&A, 155, 205 [NASA ADS] [Google Scholar]
- Ojha, P. C., Keenan, F. P., & Hibbert, A. 1988, J. Phys. B At. Mol. Phys., 21, L395 [NASA ADS] [CrossRef] [Google Scholar]
- Pinfield, D. J., Keenan, F. P., Mathioudakis, M., et al. 1999, ApJ, 527, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Reisenfeld, D. B., Gardner, L. D., Janzen, P. H., Savin, D. W., & Kohl, J. L. 1999, Phys. Rev. A, 60, 1153 [NASA ADS] [CrossRef] [Google Scholar]
- Sandlin, G. D., Bartoe, J.-D. F., Brueckner, G. E., Tousey, R., & Vanhoosier, M. E. 1986, ApJS, 61, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Saraph, H. E. 1978, Comput. Phys. Commun., 15, 247 [Google Scholar]
- Seaton, M. J. 1975, Adv. At. Mol. Phys., 11, 83 [Google Scholar]
- Strong, K. 1978, Ph.D. Thesis, University College London, UK [Google Scholar]
- Vernazza, J. E., & Reeves, E. M. 1978, ApJS, 37, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Victor, G. A., Stewart, R. F., & Laughlin, C. 1976, ApJS, 31, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Wallbank, B., Djurić, N., Woitke, O., et al. 1997, Phys. Rev. A, 56, 3714 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Quiet Sun DEM from Skylab ATM observations
We have taken the Vernazza & Reeves (1978) averaged quiet Sun radiances of a selection of lines formed from the chromosphere to the corona, and used the latest atomic data to obtain a differential emission measure DEM assuming the latest CHIANTI v.7.1 Landi et al. (2013) ionization equilibrium tables. In terms of atomic data, we employ CHIANTI v.7.1, but in several cases we use the new v.8 data (Del Zanna et al., in prep.). Finally, we assumed a constant pressure of 3 × 1014 cm-3 K and adopted the recommended photospheric abundances of Asplund et al. (2009). More details will be given in a separate paper. Table A.1 gives the DEM values, as well as the values obtained by Andretta et al. (2003) from SOHO CDS quiet Sun radiances and the Arnaud & Rothenflug (1985) ion populations.
Column quiet Sun DEM used here
All Tables
All Figures
 |
Fig. 1 Thermally-averaged collision strengths Υ for transitions to the lowest 20 levels, from the 3s2 and 3s 3p levels. The dashed lines indicate ±20%. |
| In the text | |
 |
Fig. 2 Thermally-averaged collision strengths for a selection of transitions (see text). |
| In the text | |
 |
Fig. 3 Ion populations. |
| In the text | |
 |
Fig. 4 Top: contribution functions G(T) for a selection of lines; bottom: G(T) values multiplied by the quiet Sun DEM obtained from Skylab data. |
| In the text | |
 |
Fig. 5 Emissivity ratio curves relative to the quiet Sun Skylab ATM observations 4′′ inside the limb reported by Nicolas et al. (1977), with the addition of an HRTS measurement of the 1312.59 Å line. Top: at a fixed log Ne [cm-3] = 10.5; bottom: at a fixed log Te[K] = 4.7. Iob indicates the measured intensity of a line in erg cm-2 s-1 sr-1. |
| In the text | |
 |
Fig. 6 Emissivity ratio curves relative to the Skylab NRL slit spectrograph S082-B observations (Dufton et al. 1983). Iob indicates the measured intensity of a line, normalised to the radiance of the 1296.73 Å line (energy units). |
| In the text | |
 |
Fig. 7 Emissivity ratio curves relative to the HRTS rocket flight spectrum recorded on 1975 Jul. 21, and regions No. 3, 4, relative to a quiet Sun and an active region (Nicolas et al. 1979). Iob indicates the measured intensity of a line in erg cm-2 s-1 sr-1. |
| In the text | |
 |
Fig. 8 Emissivity ratio curves relative to HRTS observations of a plage and an umbra (Sandlin et al. 1986). Iob indicates the measured intensity of a line in erg cm-2 s-1 sr-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


