| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201424130 | |
| Published online | 20 January 2015 | |
Evidence for enhanced mixing on the super-meteoritic Li-rich red giant HD 233517⋆
Leibniz-Institute for Astrophysics Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam,
Germany
e-mail: kstrassmeier@aip.de; tcarroll@aip.de; mweber@aip.de; tgranzer@aip.de
Received: 5 May 2014
Accepted: 7 July 2014
Context. HD 233517 is among the most Li-rich stars in the sky. It is a rapidly rotating, single K giant thought to be on its first ascent on the red giant branch. The star has also the highest known infrared excess among any of the known first-ascent giants.
Aims. We revisit the physical parameters of the system and aim to map its surface temperature distribution.
Methods. New time-series photometry and high-resolution spectroscopy were obtained with our robotic facilities STELLA and Amadeus Automatic Photoelectric Telescope (APT) in 2007–2011. Inverse line-profile modelling is performed on a total of 167 échelle spectra and six Doppler images are presented.
Results. Light and radial-velocity variations suggest a stellar rotation period of 47.6±0.3 d. The atmospheric parameters agree with previous studies and verify a super-meteoritic log 7Li abundance of 4.29±0.10 with undetected 6Li, while the metals are generally deficient by –0.4 dex with respect to the Sun. We determine a lower than normal isotopic carbon ratio of 12C/13C = 9+4-2. Our Doppler images indicate warm and cool spots with an average temperature contrast of just ±65 K with respect to the effective temperature. Doppler maps from Li i 670.78 reveal practically identical surface morphology, with a higher average contrast of ±160 K and errors that are five times larger. Reconstructions with simultaneously 1617 and 3007 spectral lines showed both a signal degradation with respect to our 56-line final image. An error analysis indicates an average temperature error per surface pixel of just ±4 K.
Conclusions. HD 233517 appears to be an old (≈10–Gyr) single 0.95–M⊙ giant currently undergoing mild mass loss in the form of a wind. The cool and warm photospheric features are interpreted to be merely locations of suppressed and enhanced convection, respectively, probably intermingled by a yet undetected weak magnetic field. The low carbon-isotope ratio is indicative of extra mixing rather than of an engulfing event. We tentatively conclude that HD 233517 operates an enhanced non-axisymmetric mixing process that leads to an inhomogeneous super-granulation pattern on the surface in form of large cool and warm features.
Key words: stars: activity / stars: atmospheres / stars: late-type / starspots / stars: imaging / stars: individual: HD 233517
© ESO, 2015
1. Introduction
Stellar evolution theory predicts strong Li dilution from the main sequence to the red giant branch (RGB). At the ascent of the RGB the expanding convective envelope already dilutes the remaining Li to an even larger volume and thereby further reduces its measurable surface abundance. Because Li is a fragile element it will be destroyed if it is mixed too deeply into the interior where the temperatures reach its destruction threshold. Consequently, one does not expect much surface Li left on a giant star even if it is just at the bottom of the first ascent of the RGB.
Therefore, it came as a surprise when the first Li-rich giants were discovered (Wallerstein & Sneden 1982; Brown et al. 1989) with some targets showing Li abundances even exceeding initial zero-age-main-sequence (ZAMS) abundances (also called the interstellar-medium abundance or the meteoritic abundance of log n(Li) ≈ 3.2 on the H = 12 scale). Li-rich giants are already rare, just around 1% (Brown et al. 1989), but the number of super-meteoritic Li-rich giants comes down to less than a dozen stars (e.g., de la Reza et al. 1997; Balachandran et al. 2000; Drake et al. 2002; Reddy & Lambert 2005; Kumar & Reddy 2009; Kumar et al. 2011, and further references therein). The details about this super-meteoritic Li enhancement in low-mass RGB stars are still unclear, but discussions tend toward two directions. One suggests an internal mixing mechanism with the synthesis of fresh Li via the Cameron-Fowler mechanism (e.g., Sackmann & Boothroyd 1999; Denissenkov & Herwig 2004). The other predicts the addition of external Li from the engulfing of close-in planets or brown dwarfs during the giant expansion phase. It also has become more clear that the initial protostellar abundance is more variable than originally thought (Carlberg et al. 2012). Kumar et al. (2011) found Li-rich red giants in the field that are too hot to be asymptotic giant branch (AGB) stars, but have chemical signatures verifying that Li dilution has completed. They suggested that these stars are red clump stars of ≈2 M⊙ that already regenerated Li during the He flash. One could speculate that also the low-mass super-meteoritic Li-rich giants, like HD 233517, are post-AGB stars that had already lost a substantial fraction of their mass. The existence of a strong infrared excess would support this picture in principle but requires a disk mass of order one solar mass, which is not observed.
An extra part of the puzzle is stellar rotation. Although most of the Li-rich giants are single stars and slow rotators, a few of these stars were found to be rapidly rotating with vsini ≥ 8 km s-1 and then appear also chromospherically, i.e., magnetically active (Fekel & Balachandran 1993; de Laverny et al. 2003; Lébre et al. 2006; Strassmeier et al. 2012). Many Li-rich stars are known among the chromospherically active binaries; dwarfs, subgiants, giants, and even bright giants. In these binaries we can expect enhanced stellar rotation due to forced orbital synchronization. Enhanced surface Li with rapid rotation is what is generally observed (Strassmeier et al. 2012). A recently-studied example of a moderately Li-rich K0 subgiant is HD 123351 (Strassmeier et al. 2011). This star not only turned out to be in a highly eccentric (e = 0.81) orbit with its unseen companion but also to be a very slow and strongly asynchronous rotator. HD 123351 is heavily spotted, exhibits a surface magnetic field of ≈540 G, and has a Li i 670.8 line broader than predicted from 7Li alone with a total logarithmic Li abundance of 1.70. Another group of Li-rich giants are the Hertzsprung-gap stars, typically of spectral type early G III. These stars are rapidly rotating at the surface and must be in the process of rearrangement of internal moment of inertia due to the exhaustion of core hydrogen. An example of this group is the single star 31 Comae (Strassmeier et al. 2010a) with log n(Li) = 3.0 and vsini = 67 km s-1. It is tempting to speculate that there is a joint mixing procedure in these two types of targets. Unfortunately, the incompleteness of the respective line lists for wavelengths around the Li lines, the still uncertain transition probabilities, and hyperfine-structure energy levels together with an incomplete treatment of surface convection has so far prohibited the conclusive detection of 6Li (see Cayrel et al. 2007).
 |
Fig. 1 A representative spectrum of HD 233517 (K2III, upper spectrum) in comparison with the neighboring star HD 233520 (K0III, grey-line) and the M-K standard star α Ari (K2III, grey dotted line). The spectrum of HD 233517 is shifted by +0.4 in intensity for better visibility. The panels show, from top left to bottom right, Balmer Hα, Na i D lines, Li i 610.36, Li i 670.78, Ca ii 866.2 irt triplet line, 12CN and 13CN lines, C2 primary and secondary Swan lines, Balmer Hβ, and Balmer Hγ. |
In this paper, we focus on HD 233517 (K2III, L/L⊙ ≈ 100, V = 9
 7), one of the most Li-rich single red giants in the sky. It is also the most rapidly rotating example among this class of stars with a vsini of 17.6 km s-1 (Balachandran et al. 2000). The combined 6Li+7Li abundance is given to ≈3.3 if a ratio of 7Li/6Li = 10 is assumed (Balachandran et al. 2000). Its logarithmic (7Li) non-local thermodynamic equilibrium (NLTE) surface abundance is ≈4.2, i.e., an order of magnitude above the maximum main-sequence Li abundance, however, the currently accepted primordial Li abundance (2.72 dex; Cyburt et al. 2008), is at odds with the WMAP satellite measurements, implying a primordial Li production three to five times higher than observed (e.g., Sbordone et al. 2010). The hypothesis of Li pollution from a previous generation of stars has also found further evidence from recent detections of Li-rich dwarfs in globular clusters (Koch et al. 2010; Monaco et al. 2012). Therefore, a detailed study of the surface lithium of a key star may also shed some light on these discrepancies.
7), one of the most Li-rich single red giants in the sky. It is also the most rapidly rotating example among this class of stars with a vsini of 17.6 km s-1 (Balachandran et al. 2000). The combined 6Li+7Li abundance is given to ≈3.3 if a ratio of 7Li/6Li = 10 is assumed (Balachandran et al. 2000). Its logarithmic (7Li) non-local thermodynamic equilibrium (NLTE) surface abundance is ≈4.2, i.e., an order of magnitude above the maximum main-sequence Li abundance, however, the currently accepted primordial Li abundance (2.72 dex; Cyburt et al. 2008), is at odds with the WMAP satellite measurements, implying a primordial Li production three to five times higher than observed (e.g., Sbordone et al. 2010). The hypothesis of Li pollution from a previous generation of stars has also found further evidence from recent detections of Li-rich dwarfs in globular clusters (Koch et al. 2010; Monaco et al. 2012). Therefore, a detailed study of the surface lithium of a key star may also shed some light on these discrepancies.
HD 233517 is a first-ascent red giant with an unusually large fractional infrared excess of 6% of the total stellar luminosity (Sylvester et al. 2001). Such a large IR excess cannot easily be explained by classic models invoking mass loss, but also appears extreme among a handful of rapidly-rotating, single K giants with exceptional lithium abundances (Fekel & Watson 1998). None of the other examples have an excess as large as HD 233517, but see Melis et al. (2009) for a comparable example (TYC 4144 329 2). Jura (2003) explained the IR excess of HD 233517 with an orbiting and flaring dust disk of ≈0.01 M⊙ and outer radius of ≈45 au. He speculated that HD 233517 had a low-mass companion that was engulfed when it became a red giant. The disk was confirmed by Spitzer follow-up observations (Jura et al. 2006) and also led to the discovery of polynuclear aromatic hydrocarbon molecules (PAHs) within the disk. The disk mass and the rapid stellar rotation together with the high lithium abundance would all be compatible with the engulfment of a close-in giant planet as recently favored by Carlberg et al. (2012). This scenario predicts an increased 12C/13C ratio compared to a normal RGB giant, opposite to the predictions from an enhanced mixing process.
In the present paper, we attempt to reconstruct the surface temperature distribution of HD 233517 from various optical spectral lines using the Doppler-imaging technique. Our aim is to compare an average photospheric temperature map to the temperature distribution from lithium to see whether there is a pattern indicative of either an enhanced mixing mechanism or an engulfing event. Section 2 describes our data. In Sect. 3, we redetermine basic stellar parameters from both the spectra and the photometry. In the same section, we also analyze spectra of HD 233520, a K0 giant very close to HD 233517 which was occasionally observed by the STELLA robot. Section 4 describes the Doppler imaging analysis and its results, while Sect. 5 discusses the overall scientific conclusions.
2. New observations and data reductions
2.1. STELLA SES spectroscopy
From March 6, 2007 to Feb. 21, 2011, we obtained 190 high-resolution échelle spectrograms of HD 233517 with the robotic 1.2 m STELLA-I telescope at the Izanã Observatory on Tenerife in the Canary islands (Strassmeier et al. 2010b). We used the fiber-fed STELLA Echelle Spectrograph (SES) with an e2v 2k×2k CCD detector. All spectra cover the wavelength range from 388–882 nm with increasing inter-order gaps near the red end starting at 734 nm toward 882 nm. The resolving power is R = 55 000 corresponding to a spectral resolution of 0.12 Å at 650 nm. The most recent observatory and instrument status is given in Weber et al. (2012).
The integration time was set to 7200 s because of the relative faintness of the target for a 1 m-class telescope. Of these spectra 167 achieved signal-to-noise ratios (S/N) between 60−160:1 per resolution element, depending on weather conditions, while 23 had S/N< 50−60:1 and are used for radial velocity measurements only. SES spectra are automatically reduced using the IRAF-based STELLA data-reduction pipeline (Weber et al. 2008). The images were corrected for bad pixels and cosmic-ray impacts. Bias levels were removed by subtracting the average overscan from each image followed by the subtraction of the mean of the (already overscan subtracted) master bias frame. The target spectra were flattened by dividing by a nightly master flat which has been normalized to unity. The nightly master flat itself is constructed from around 50 individual flats observed during dust, dawn, and around midnight. After the removal of scattered light, the one-dimensional spectra were extracted using an optimal-extraction algorithm. The blaze function was then removed from the target spectra, followed by a wavelength calibration using consecutively recorded Th-Ar spectra. Finally, the extracted spectral orders were continuum normalized by dividing by a flux-normalized synthetic spectrum of the same spectral classification as HD 233517.
Figure 1 shows an example spectrum from JD 2 455 222 (Jan. 26, 2010) for a number of wavelength ranges of interest. As a reference, the first-ascent RGB giant α Ari is shown for comparison (dotted line) along with star HD 233520. HD 233520 is 55′′ separated from our target and was accidentally observed. It is of comparable magnitude and color and was used as our photometric comparison star. During bad weather conditions the STELLA robot had a hard time correctly identifying the true target. Over the course of the four years, it was picked 27 times instead of HD 233517. The exposure time was nominally always the same as for HD 233517 (7200 s), but 11 aborts left spectra with exposure times of as short as 594 s. The S/N varied between 30:1 and 160:1, depending on the weather conditions and the exposure time. A good spectrum from JD 2 454 450 (Dec. 16, 2007) is shown in Fig. 1.
2.2. APT photometry
A campaign of Johnson-Cousins V(I)C photometry was carried out with the Amadeus Automatic Photoelectric Telescope (APT) at Fairborn Observatory in southern Arizona on 49 nights between Sept. 26, 2010 to Jan. 4, 2011. These measures were made differentially with respect to HD 233520 (V = 9
 35, B − V = 0
35, B − V = 0 96, K2; Miroshnichenko et al. 1996) as the comparison star and HD 70295 (V = 8
96, K2; Miroshnichenko et al. 1996) as the comparison star and HD 70295 (V = 8 40, B − V = 1
40, B − V = 1 01) as the check star. Balachandran et al. (2000) found HD 70295 to be a low-amplitude variable with a possible period of over 138 d. Two measures were taken per night where one measure consists of three 40 s integrations on the variable, four integrations on the comparison star, two integrations on the check star (with just 20 s integration), and two 10 s integrations on the sky. A 30′′ diaphragm was used. The standard error of a nightly mean from the overall seasonal mean was 0
01) as the check star. Balachandran et al. (2000) found HD 70295 to be a low-amplitude variable with a possible period of over 138 d. Two measures were taken per night where one measure consists of three 40 s integrations on the variable, four integrations on the comparison star, two integrations on the check star (with just 20 s integration), and two 10 s integrations on the sky. A 30′′ diaphragm was used. The standard error of a nightly mean from the overall seasonal mean was 0 006 in V and 0
006 in V and 0 008 in IC. For further details, we refer to Strassmeier et al. (1997) and Granzer et al. (2001).
008 in IC. For further details, we refer to Strassmeier et al. (1997) and Granzer et al. (2001).
 |
Fig. 2 Detections of rotational modulation. a) Differential APT V-band light curve from the observing season 2010. b) STELLA-SES radial velocities from 2008–2011. Both data sets were phased with P = 47.6 d from 2 455 000. |
3. Basic stellar parameters
3.1. Rotation
The APT data show a clear sign of periodic rotational modulation. A Lomb-Scargle analysis yields a period of 47.6±0.3 d with an amplitude of 0 02 in V (Fig. 2a). Balachandran et al. (2000) had already announced the detection of a photometric period from BV observations in 1995/96 of nearly the same value than we find.
02 in V (Fig. 2a). Balachandran et al. (2000) had already announced the detection of a photometric period from BV observations in 1995/96 of nearly the same value than we find.
We measured a total of 190 radial velocities with STELLA between 2007–2011. A zero point from 20 standard stars (Strassmeier et al. 2012) ties the STELLA velocities to the CORAVEL system when subtracting 503 m s-1 from the STELLA radial velocities. The mean radial velocity of HD 233517 was +46.63±0.07 km s-1 (+ 46.13 km s-1 in the CORAVEL system). The scatter appears variable over time and shows a maximum peak-to-valley variation of ≈200 m s-1 in 2008. The expected SES precision for the given line broadening is ≈50 m s-1 , according to the stars surveyed in Strassmeier et al. (2012). Thus, the 200 m s-1 scatter appears significant. We applied three different period-search techniques to the SES velocities (Lomb-Scargle, phase dispersion minimization, and string-length minimization) and found a period of 47.4±0.7 d and an amplitude of 60 m s-1 when data from 2008–2011 are combined (Fig. 2b). Early data from 2007 were excluded because of uncertain zero points as well as the few occasional (and underexposed) spectra in 2011. We interpret this period again to be the stellar rotation period and its amplitude due to spots rotating in and out of view. This naturally explains the higher than usual time-variable velocity scatter in our data.
Both periods, from photometry and from radial velocities, agree within their errors although both periods are possibly more uncertain than their quoted errors, for different reasons, e.g., when systematic errors like non-linear spectrograph drift or photometric comparison-star jitter could be quantified. We are now confident however, that we recovered the true stellar rotation period and not an alias. Consequently, we adopt the more precise photometric value of 47.6 d as the rotation period of HD 233517.
The rotational line broadening was initially measured by Balachandran et al. (2000) to 17.6±1.0 km s-1. Our Doppler-imaging analysis in Sect. 4 determines a more precise value of vsini of 17.8±0.1 km s-1, in very good agreement with Balachandran et al.’s (2000) value. With vsini and the rotation period from the photometry the star’s minimum radius Rsini is 16.7 ± 0.2 R⊙.
3.2. Temperature, gravity, metallicity
These parameters are determined from an iterative comparison of a grid of standard LTE model atmospheres from the MARCS collection (Gustafsson et al. 2008) with our SES spectra. The numerical tool PARameters from SES (PARSES; Allende-Prieto 2004) is employed based on the synthetic spectrum fitting procedure described in Allende-Prieto et al. (2006). We use the Gaia-ESO survey version 3 without molecules as line lists (Heiter et al., in prep.), and for wavelengths shorter than 480 nm the VALD3 list (Kupka et al. 2011). Five échelle orders of each SES spectrum are selected for the fitting with the following five free parameters; Teff, log g, [Fe/H], microturbulence, and macro line broadening 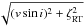 , where ζRT is the radial-tangential macroturbulence adopted from Gray (2005) and fixed during the fit. Internal errors are estimated from the rms of the solutions to the individual échelle orders and were for Teff ± 4 K, for log g ± 0.01 dex, and for [Fe/H] typically ±0.04 dex. The parameter vsini depends on the assumed macroturbulence, but internal errors for vsini of ≈0.4 km s-1 are routinely achieved. A microturbulence of 1.4±0.1 km s-1 is obtained for vsini = 17.1 km s-1. External errors are determined from a comparison with two other K giants. For this, we apply PARSES to SES spectra of α Ari and 35 Peg taken in the same configuration as HD 233517 and compare the results with averaged literature data. Systematic errors are then estimated from the differences to HD 233517 values assuming the α Ari and 35 Peg values are known and are without error. This yields differences for Teff of just 18 K and 5 K (for α Ari and 35 Peg, respectively), for log g between 0.02 dex (for α Ari) and 0.06 dex (for 35 Peg), and for [Fe/H] typically 0.04 dex. Note that the averaged values for α Ari were derived from nine literature sources, while for 35 Peg we used six literature sources for the average. We verified this approach by applying it to the ELODIE library (Prugniel & Soubiran 2001) and used linear regressions to determine the offsets with respect to the literature values and to our PARSES results. Absolute errors including observational zero points and model-atmosphere uncertainties are difficult to cite but are likely a factor 2–3 higher.
, where ζRT is the radial-tangential macroturbulence adopted from Gray (2005) and fixed during the fit. Internal errors are estimated from the rms of the solutions to the individual échelle orders and were for Teff ± 4 K, for log g ± 0.01 dex, and for [Fe/H] typically ±0.04 dex. The parameter vsini depends on the assumed macroturbulence, but internal errors for vsini of ≈0.4 km s-1 are routinely achieved. A microturbulence of 1.4±0.1 km s-1 is obtained for vsini = 17.1 km s-1. External errors are determined from a comparison with two other K giants. For this, we apply PARSES to SES spectra of α Ari and 35 Peg taken in the same configuration as HD 233517 and compare the results with averaged literature data. Systematic errors are then estimated from the differences to HD 233517 values assuming the α Ari and 35 Peg values are known and are without error. This yields differences for Teff of just 18 K and 5 K (for α Ari and 35 Peg, respectively), for log g between 0.02 dex (for α Ari) and 0.06 dex (for 35 Peg), and for [Fe/H] typically 0.04 dex. Note that the averaged values for α Ari were derived from nine literature sources, while for 35 Peg we used six literature sources for the average. We verified this approach by applying it to the ELODIE library (Prugniel & Soubiran 2001) and used linear regressions to determine the offsets with respect to the literature values and to our PARSES results. Absolute errors including observational zero points and model-atmosphere uncertainties are difficult to cite but are likely a factor 2–3 higher.
Figure 3 shows the PARSES results for all individual spectra. Average values for HD 233517 are Teff = 4390 ± 60 K, log g = 2.26 ± 0.04, and [ Fe/H ] = −0.42 ± 0.08. Errors are now estimated absolute errors, not internal rms errors. These values are in reasonable agreement with the study by Balachandran et al. (2000). Note that the few deviant points in Fig. 3 are due to spectra of low quality.
 |
Fig. 3 Atmospheric parameters of HD 233517 from the PARSES analysis. From top to bottom: effective temperature, gravity, and metallicity with long-term average values of 4390 K, 2.26 cm s-2, and −0.42 [M/H]⊙, respectively. |
3.3. Mass and age
Because of the lack of a Hipparcos parallax, we must rely on indirect determinations of the stellar luminosity. The dust maps of Schlegel et al. (1998) indicate a reddening of 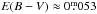 (AV = 0
(AV = 0 164) toward HD 233517. According to Jura (2003), HD 233517 has a uniquely high infrared excess due to an orbiting dust disk, which leaves us with the most likely situation that there must be a combination of interstellar and circumstellar extinction. Fekel et al. (1996) had already noted the blue-shifted Na D absorption lines in the optical spectrum and interpreted them to be of interstellar origin while Balachandran et al. (2000) determined the blueshift to –46.5 km s-1 with respect to the photospheric lines and estimated a distance of “a few hundred parsecs”. Our higher resolution spectra reveal a third narrow absorption component with a velocity offset of –33.1 km s-1 (Fig. 1). Both line systems appear sharp and stable over the time of our observations and we estimate equivalent widths of 200 mÅ and ≈100 mÅ for the second and the third components, respectively.
164) toward HD 233517. According to Jura (2003), HD 233517 has a uniquely high infrared excess due to an orbiting dust disk, which leaves us with the most likely situation that there must be a combination of interstellar and circumstellar extinction. Fekel et al. (1996) had already noted the blue-shifted Na D absorption lines in the optical spectrum and interpreted them to be of interstellar origin while Balachandran et al. (2000) determined the blueshift to –46.5 km s-1 with respect to the photospheric lines and estimated a distance of “a few hundred parsecs”. Our higher resolution spectra reveal a third narrow absorption component with a velocity offset of –33.1 km s-1 (Fig. 1). Both line systems appear sharp and stable over the time of our observations and we estimate equivalent widths of 200 mÅ and ≈100 mÅ for the second and the third components, respectively.
The Stefan-Boltzmann law suggests a luminosity of 124 ± 25 L⊙ based on R = 19.3 ± 1.3 R⊙ from Rsini of 16.7 ± 0.2 R⊙ (i of 60±10°) and Teff = 4390 ± 60 K. The error of the luminosity is simply the propagated error from Teff and R, with zero errors assumed for the solar values. With a BC of –0 685 (Flower 1996) its absolute visual magnitude is +0
685 (Flower 1996) its absolute visual magnitude is +0 35±0.26. The apparent V brightness at maximum light from our APT light curve is 9
35±0.26. The apparent V brightness at maximum light from our APT light curve is 9 66. This value is from an all-sky solution with 30 standard stars and is accurate to better than 0
66. This value is from an all-sky solution with 30 standard stars and is accurate to better than 0 05. Together with AV = 0
05. Together with AV = 0 164 from Schlegel et al. (1998), it places HD 233517 at a distance of 675±70 pc in agreement with the expectation from the spectral type. The primary luminosity indicator Sr ii 407.7 nm (as well as Sr ii 421.5 nm) appears almost identical to that in α Ari with an equivalent width of ≈400 mÅ and is comparable in strength to the nearby Fe i lines 407.1 and 406.3 nm. Other prominent line ratios such as Fe ii 643.2/Fe i 643.0, V i 645.2/Ca i 645.6 a.o., are also all in agreement with a K2 MK-class III giant, according to the calibration of Strassmeier & Fekel (1990).
164 from Schlegel et al. (1998), it places HD 233517 at a distance of 675±70 pc in agreement with the expectation from the spectral type. The primary luminosity indicator Sr ii 407.7 nm (as well as Sr ii 421.5 nm) appears almost identical to that in α Ari with an equivalent width of ≈400 mÅ and is comparable in strength to the nearby Fe i lines 407.1 and 406.3 nm. Other prominent line ratios such as Fe ii 643.2/Fe i 643.0, V i 645.2/Ca i 645.6 a.o., are also all in agreement with a K2 MK-class III giant, according to the calibration of Strassmeier & Fekel (1990).
 |
Fig. 4 Location of HD 233517 in the H-R diagram (dot with error bars, logarithmic presentation). The lines are the “best match” tracks from Bressan et al. (2013) for either solar metallicity (indicated as solar) or the measured metallicity [ Fe/H ] = −0.42 for post-main sequence (post) and pre-main sequence (pre). The mass is indicated in solar masses. Insert a) shows the best-match track (0.95 M⊙) and the two tracks that envelope the error box as indicated. Insert b) is a graphical zoom of the box in the main panel. |
Figure 4 shows the position of HD 233517 in the H-R diagram with respect to evolutionary tracks from the PARSEC grid (Bressan et al. 2013) for [ Fe/H ] = −0.42 and with moderate overshooting. The best match in the H-R diagram is provided with a mass of 0.95 ± 0.1 M⊙ and the biblical age of ≈10 Gyr if on the first ascent of the RGB. The age range is 7−14.8 Gyr from the error box of Teff and L/LSun. On the second ascent the best fit mass is even lower at ≈0.90 M⊙, with a difference of age of just 0.1 Gyr. If still on the pre-main sequence the best-fit mass is 1.3 M⊙ and an infant age of few thousands of years, according to the models of Bressan et al. (2013). In comparison, we assume solar abundances and plot the post-main-sequence and the pre-main-sequence models that would fit the observation. For these cases, the masses are 1.8 M⊙ on the RGB and 2.2 M⊙ on the pre-main sequence. The insert in Fig. 4 is a zoom and indicates the ambiguous situation of the evolutionary status. We also compared with the BaSTI model grid (Pietrinferni et al. 2004) and otherwise identical parameters and obtain comparable results typically with 20% lower masses. An independent check of the stellar mass from the relation g ∝ MR-2 and the measured radius and gravity suggests a mass of ≈2.5 M⊙, in contradiction with all of above values from the H-R diagram except maybe the 2.2-M⊙ pre-main-sequence model with solar abundances. Because we can not simply discharge our spectrum-synthesis metallicity, we tentatively conclude a mass of 0.95 ± 0.1 M⊙ and an age of ≈10 Gyr.
The 12C14N lines around 800.35 nm are strongly broadened and only detectable with a combined equivalent width of 110±10 mÅ. The equivalent width of the 13C14N line at 800.46 nm is with ≈12 mÅ close to our detection limit at this wavelength and S/N and suggests a low and fairly uncertain isotopic ratio of 12C/13C = 9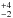 . This uncertainty also reflects the uncertainty due to unequal transition probabilities and saturation levels of the isotopic lines. We analyzed our reference giant α Ari in the same way and measured a 12C/13C ratio of 15±2 in excellent agreement with the ratio from a more detailed synthesis given in Luck & Challener (1995) (15) and still in agreement with the older measurement by Lambert & Ries (1981) (19). The nearby photometric-comparison star HD 233520 was measured with a ratio of just 6±3. Most other super Li-rich stars have significantly higher values of 12C/13C, between 12−28, with the exception of HD 77361, which has 4.3±0.5 (Kumar & Reddy 2009). Such low isotopic ratios generally support the RGB extra-mixing scenario over the engulfing scenario and could even help to constrain the exact mixing process. The very low ratio of HD 233517 is thus indicative for the first-ascent RGB scenario and, if our metallicity synthesis is correct, thus also for its low mass and old age. This is further supported by the detection of both the primary and secondary C2 Swan lines (Fig. 1).
. This uncertainty also reflects the uncertainty due to unequal transition probabilities and saturation levels of the isotopic lines. We analyzed our reference giant α Ari in the same way and measured a 12C/13C ratio of 15±2 in excellent agreement with the ratio from a more detailed synthesis given in Luck & Challener (1995) (15) and still in agreement with the older measurement by Lambert & Ries (1981) (19). The nearby photometric-comparison star HD 233520 was measured with a ratio of just 6±3. Most other super Li-rich stars have significantly higher values of 12C/13C, between 12−28, with the exception of HD 77361, which has 4.3±0.5 (Kumar & Reddy 2009). Such low isotopic ratios generally support the RGB extra-mixing scenario over the engulfing scenario and could even help to constrain the exact mixing process. The very low ratio of HD 233517 is thus indicative for the first-ascent RGB scenario and, if our metallicity synthesis is correct, thus also for its low mass and old age. This is further supported by the detection of both the primary and secondary C2 Swan lines (Fig. 1).
3.4. Magnetic activity
No Ca ii H&K emission nor infrared-triplet emission, or a He i D3 line, are detected in our R = 55 000 spectra. These lines are typical magnetic-activity indicators (see, e.g., Strassmeier et al. 2011) and are most prominent in young stars. The nondetection is surprising because the large rotational line broadening and the detection of a rotation period from broadband photometry, as well as from radial velocities, would normally hint at the existence of (magnetic) cool spots and thus also of chromospheric radiative losses. Our spectra are increasingly noisy at both ends of the wavelength range, i.e., at the Ca ii lines, sometimes reaching not more than 20:1. Therefore, very weak chromospheric emission could not be ruled out.
3.5. Balmer lines spectral appearance
All Balmer lines down to Hϵ are seen in absorption, but Hα appears with a weak blue shifted emission component (see Fig. 1). Its blue shift remains constant at –71.8 km s-1 throughout our observations and also its strength remains fairly constant and is qualitatively comparable to the line profiles of mass-outflow giants, e.g. like the ones in low-metallicity globular clusters (Meszaros et al. 2009). The asymmetry was already noticed by Fekel et al. (1996). The STELLA spectra have average equivalent widths of the full absorption line of 1650±20 mÅ for Hα, 1250±50 for Hβ, and 1000±100 for Hγ and thus a decrement of 1.32:1:0.8.
Most of the time our time-series data show a Hα profile like the one shown in Fig. 1. However, sometimes the profile appears with double absorption peaks, e.g., from mid to end of April 2008, and then again sometimes with an almost flat-bottomed profile, e.g., in early February 2008. These variations could be indicative of the rapid circumstellar-shell evolution proposed by de la Reza et al. (1996). We found no convincing relation to the photospheric Doppler maps.
3.6. Lithium abundance
A detailed spectrum synthesis is performed on the Li i resonance doublet and the two subordinate lines. We employ our iMap code in its forward radiative-transfer module (for a brief description see Sect. 4). We only used the 35 spectra from the observing season 2007/08 to create denoised, singular-value decomposed (SVD) profiles with a S/N ≈ 500:1 (see Sect. 4.2).
The synthesis fits are shown in Fig. 5. We adopted the VALD-3 (Kupka et al. 2011) line list as well as the Kurucz line list (Kurucz 1993) in conjunction with the Spectrum code (Gray 1999) in order to incorporate a significant number of TiO, VO, CN a.o. molecules. Fine-structure splittings were neglected given the large vsini of our target. All elements of lines that blend with Li were assumed to have solar abundances. Model atmospheres and other input are the same as for our Doppler-imaging in Sect. 4. For the Li i 670.78-nm fit, we first assume no 6Li contribution. With the stellar parameters from Table 1 the best-fit logarithmic 7Li LTE abundance is then 4.29 on the log n(H) = 12.00 scale. When we adopt the interstellar isotope ratio of 7Li/6Li ≈ 10 the Li abundance from the 670.78-line lowers to 3.58 but with a three times higher summed-squared fitting error (∑ (O−C)2). We interpret this as evidence that either there is no detectable 6Li on the surface of HD 233517 or that at least the ratio of 7Li/6Li must be significantly larger than 10. The zero-6Li fits to the subordinate lines at 610.36 nm and 812.65 nm give abundances of 4.33 and 4.24, respectively, in good agreement with the 670.8-nm line. However, the summed-squared error for the 610.36-nm fit is a factor 10 worse than for the 670.78 line due to its severe blending situation, while the 812.65-fit is just worse by 5% compared to the 670.78-line fit. The absolute abundance errors are likely 0.1 dex in this procedure and we thus consider the three 7Li abundances to be equal and average them to log n(Li) = 4.29 ± 0.10 for further reference. Therefore, we can not verify the abundance difference between the excited and the resonance 6+7Li lines seen by Balachandran et al. (2000) from two KPNO spectra. Such a difference between the abundances of the two Li lines was partly attributed to severe NLTE effects by Balachandran et al. (2000).
 |
Fig. 5 Lithium line fits. From top to bottom for the resonance line 670.78 nm and the two excited lines 610.36 nm and 812.65 nm. The dots are the STELLA SVD profiles from the observing season 2007/08 and the lines are the fits. |
An independent method to determine the Li abundance is to measure the line equivalent widths and compare them to theoretical curves of growths. The STELLA spectra yield an average Li i 670.78 equivalent width of 594±4 mÅ, compared to an average of 240 mÅ for the nearby Ca i 671.7-nm line. This still includes a significant Fe i and V i blend and some weaker CN lines totalling ≈34 mÅ. After subtraction of a shifted and broadened spectrum of the K0.5 giant 16 Vir, obtained with the same instrumental setup, the lithium equivalent width of HD 233517 is confirmed to be ≈565 mÅ. The NLTE curves of growth from Pavlenko & Magazzú (1996) for a model with 4400 K and log g = 3.0 convert this equivalent width to a logarithmic lithium abundance of 4.2±0.1 for the combined isotopes, in good agreement with the LTE spectrum synthesis. Note that the error is just an internal error and does not account for model deficiencies. We also note that the Pavlenko & Magazzú NLTE corrections generally agree quite well with the newer computations by Lind et al. (2009) and differ mostly because of the use of different model atmospheres (ATLAS9 vs. MARCS).
The equivalent width of the excited Li i line at 610.36 nm is on average ≈270 mÅ. It is difficult to measure because it is fully blended with two nearby Fe i and Ca i lines (the latter blended again with another Fe i line; see Fig. 1). Balachandran et al. (2000) gave values of 231 mÅ and 239 mÅ for two spectra, thus significantly lower than our average value. The curves of growth from Pavlenko & Magazzú (1996) convert the 270 mÅ into an abundance of 4.1±0.1 for both LTE and NLTE. The second Li i subordinate line at 812.65 nm is measured from our STELLA spectra with an equivalent width of 250 mÅ and converted to log n of 4.2±0.1 for the combined isotopes, again according to the theoretical curves of growth in Pavlenko & Magazzú (1996). Note that one has to extrapolate in these tables because 4.0 is the highest abundance tabulated in Pavlenko & Magazzú (1996). Although the curve-of-growth NLTE abundances are more uncertain there is good agreement with the LTE spectrum synthesis.
Astrophysical properties of HD 233517.
3.7. HD 233520
The 27 STELLA spectra of the close-by (55′′) star HD 233520 give a mean radial velocity of 8.41±0.15 km s-1 (7.91 in the CORAVEL zero-point system). For the PARSES analysis, we exempt the 11 spectra that all have S/N< 50:1 (see Sect. 3.2) and then derive average values of Teff = 4785 ± 20 K, log g = 2.16 ± 0.09, and [ Fe/H ] = −0.41 ± 0.03 (error bars are just internal rms deviations). These parameters are in agreement with canonical values of a K0 giant of luminosity class III rather than the K2 dwarf luminosity assigned by Miroshnichenko et al. (1996) from UBVRI photometry. The spectral appearance resembles HD 233517, except that HD 233520 shows no indications of asymmetric Balmer lines and that no lithium is detected for HD 233520. A Li i 670.78-nm equivalent width from the two best-exposed spectra must be below ≈5–7 mÅ. This also indirectly indicates that HD 233517 is of post-main-sequence status rather than a pre-main-sequence star.
The projected rotational velocity of HD 233520 is significantly smaller than for HD 233517 but still rotationally broadened. We find vsini of 8±1 km s-1 under the assumption of a radial-tangential macroturbulence velocity of 3 km s-1 taken from Gray (2005). No signs of magnetic activity are detected.
The similarity and vicinity of the two stars, HD 233517 and HD 233520, makes one wonder whether there is a gravitational connection. Neither of the two stars has a parallax but their brightness and MK-classifications are comparable so that they cannot be at vastly different distances. Their proper motions are in opposite directions and of comparable size, as expected for a wide visual binary of comparable mass.
4. Doppler imaging of HD 233517
4.1. Method and assumptions
We use our Doppler-imaging code iMap (Carroll et al. 2007, 2009) in its latest version described in Carroll et al. (2012). Reconstructing a stellar surface from a series of spectral line profiles is an inverse problem that amounts to solving the integral equation relating the surface temperature distribution to the observed line profiles while controlling the effects of noise in the data through a regularizing functional (see, e.g., the review by Rice 2002).
All of the line parameters necessary for the synthetic calculation are taken from the Vienna atomic line database (VALD-3; Kupka et al. 2011). A grid of model atmospheres with temperatures between Teff = 3500 and 6000 K in steps of 250 K and interpolated log g = 2.26 was taken from the ATLAS-9 CD (Castelli & Kurucz 2004). For each model atmosphere local line profiles were computed under the assumption of [ Fe/H ] = −0.42 and a microturbulence of 1.4 km s-1. Gray (2005) gives a typical radial-tangential macroturbulence velocity of 3 km s-1 for a K giant, which is adopted here.
A recent improvement in the iMap code is its inversion module, which now relies on an iteratively regularized Landweber method instead of conjugate gradients. The code rests on the idea of a simple fixed-point iteration derived from minimizing the sum of the squared errors. However, its choice over a conjugate gradient method with a local entropy regularization is only relevant for data with extremely low S/N, as encountered in spectropolarimetry. We do not expect a difference for the present application.
The stellar surface is partitioned into 6° × 6° segments whereas the radiative transfer is calculated on subpartitions of 3° × 3°. The initialization temperature was homogeneously set to 4400 K. Stellar parameters were adopted from Table 1.
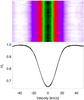 |
Fig. 6 Example time-series SVD line profiles of HD 233517 from data set Bb in 2007/08. Systematic errors are estimated from the standard deviation in two 20-km s-1 passbands at ±30–50 km s-1 away from the line center. In the dynamic plot in the top panel, time progresses from bottom to top for 63 d. The color denotes residual line depth (white is continuum, black is the line core). |
Doppler image log and temperature contrasts.
4.2. Data setup
We select only spectra with an initial S/N> 60 for the Doppler-imaging analysis. Each spectrum has 82 échelle orders of which the reddest 62 cover the wavelength ranges that contain most of the (relatively) unblended photospheric absorption lines. The line-profile inversions are preceded by a co-addition process to obtain an averaged line profile with an increased S/N level. Our best and favored choice is a hand-selection of 56 spectral lines based on their line strength, blend characteristics, and the availability of a nearby free continuum stretch. Spectral lines at the edges of the échelle orders are either completely removed, or averaged if repeated in two adjacent orders. Although the averaging of many line profiles is computationally more demanding because the same averaging must be done for the synthetic line profiles during the inversion, this process can lead to significantly lower least-squares errors (Carroll et al. 2012).
The noise in our averaged line profiles is estimated by the median-absolute deviation and results for our observations in S/N between 520 and 650:1 (initial S/N of ≈100). Visual inspection of the line profiles of HD 233517 does not directly reveal the typical migrating bumps due to starspots otherwise seen in rapidly rotating active K giants. Therefore, we first simulated and then corrected the sub-percent continuum-setting errors during data reduction. Figure 6 shows a time series of a subset of the original spectra. A single échelle spectrum of HD 233517 has a typical continuum error of 0.1% rms but few spectra have errors of up to 0.5% (the spectra with the lowest S/N). The latter error size weakens the algorithm in that it artificially increases the noise limit. During the regularization these spectra cannot constrain very weak spots and also introduce spurious surface features, albeit rather weak features. A test inversion with an immaculate star of the same astrophysical parameters as HD 233517 and the same continuum errors as in the real data reconstructs spurious temperature inhomogeneities of up to 50 K. These 50-K are then minimized during an inversion run with the continuum as the only free parameter by shifting the individual spectra. After continuum correction, the rms variations are reduced to a few Kelvin. The resulting corrections are then applied to the real data.
We determine the standard deviation in two 20-km s-1 passbands between 30 to 50 km s-1 around both sides of the line wings in the continuum and call this our systematic error. This systematic error can then be compared to the expected photon-noise error that we achieve by adding more and more lines to the inversion. Note that any intrinsic stellar contribution to the extreme ends of the line wings is thereby also interpreted as systematic noise. Among such contributions could be inhomogeneous stellar limb brightening due to chromospheric plages, which can indeed be considered systematic noise for a cool starspot reconstruction. Later, Fig. 9 shows the not-so-surprising result that the systematic error dominates the spectral lines, and thus the images, already at S/N of ≈300:1 (c/o Rice & Strassmeier 2000). If we want the photon noise to remain completely negligible, we arrive at the conclusion that the number of spectral lines that, say, double this S/N gives optimal results. Any further increase of the S/N due to adding more and more spectral lines will not increase the quality of the image but, as we will show below, even deteriorates the image because of the increased blend confusion combined with atmospheric stratification issues. The latter is most simply expressed by the fact that stellar atmospheres are not plane parallel, in particular, not those of K giants like HD 233517.
 |
Fig. 7 Average photospheric surface structure of HD 233517. Individual Doppler images were determined from a total of 56 selected absorption lines. Panels a)–f) are for the epochs identified in Table 2 and span three years from 2007–2010. |
List of 56 spectral lines with atomic parameters.
4.3. Simultaneous reconstructions from 56 spectral lines
Table 2 summarizes our Doppler-image log. The year indicates the mid-time of the image, then its Julian date range, the time elapsed in days, the number of spectra N, and the spot contrast in Kelvin. Spectra cover the range between 2007 to 2010 with emphasis on the 2007/08 observing season. This selection allows for in total six independent Doppler images, with three alone for the 2007/08 observing season. Our imagery incorporates data from between one to at most two stellar rotations sampled with between 18 to 38 spectra. Firstly, we employ the best sampled data set (Bb) to determine the best-fit vsini to 17.8±0.1 km s-1 and the inclination of the rotation axis to i = 60° ± 10°. These values are then kept fixed for the other seasons. Note that all inclination values within the range given are equally likely.
Figure 7 shows the surface images of the continuum-corrected data for the epochs from 2007 to 2010. We have selected 56 unblended spectral lines between 480−680 nm for simultaneous inversion. This line list is given in Table 3 for further use where χ is the excitation potential in eV and log (gf) the dimensionless transition probability. Wavelengths are given in Å.
The temperature contrast of the surface features is very small, varying between a range of approximately ±30 K to ±140 K, as already expected from the small light-curve amplitude. All images show warm and cool spots at the same time however and both with about the same amount of temperature contrast with respect to the average photospheric temperature of 4390 K. The average contrasts among the six maps are +66 K and –64 K for the warm and cool features, respectively. Such a low temperature contrast is not seen on the Sun in the case where a magnetic field is the sole cause of the cool feature, not even in spot penumbra when azimuthal fields dominate.
4.4. Reconstructions from the Li I 670.78 nm line
For the Li mapping, we rely on a principal component analysis (PCA) noise reduction before applying the data to the inversion. In this approach, a set of local lithium line profiles from one season is decomposed into their respective eigenprofiles. In a second step, we reconstruct each individual line profile with a reduced number of orthogonal eigenprofiles. By using only a limited number of eigenprofiles, we can significantly de-noise the line profiles and reduce high frequency noise as well as systematic noise. The number of significant eigenprofiles used for the reconstruction is determined by a randomized Monte Carlo procedure as described by Carroll et al. (2012).
Figure 8 shows the results from the line-profile inversion of the Li i 670.8-nm line. The maps generally agree with the average photospheric maps in Fig. 7 but are more uncertain. Unfortunately, the reconstruction from the other two Li lines is so severely hampered by blending lines that the small temperature contrast cannot be recovered properly. The spot contrasts in the Li maps appear on average larger by a factor three than in the averaged photospheric maps (which exclude the Li lines of course). The grand average from the Li maps is +170 K and –150 K for the warm and cool features, respectively.
4.5. Simultaneous reconstructions from 1617 and 3007 spectral lines
The VALD-3 data base is again searched for spectral lines in the wavelength range 480–680 nm. We first constrain line depth to larger than 0.4 and find 1617 spectral lines. Further relief of the constraint to line depths of larger than 0.14 results in 3007 lines. These two line lists are then used independently to denoise the Bb data set (2008.11) and to invert its 35 rotational phases. The resulting images show morphologically identical surface features compared to the 56-line image, but appear to show ever lower (temperature) contrast the more lines we co-add. This is already noticeable when one compares the single-line image from Li i in Fig. 8c with the 56-line image in Fig. 7c. We interpret this to be due to the injected increased vertical atmospheric-structure information that smears out the final signal (bump) in the co-added profiles. Because the model atmospheres are plane parallel and the radiative transfer along a single ray is just one dimensional, we further increase the smearing as soon as (very) weak and strong lines are mixed together (very strong, possibly saturated lines are omitted anyway).
4.6. Limits of the inversion and error maps
The temperature contrast in the Doppler images of HD 233517 is exceptionally low, on average just ±65 K average temperature contrast, so we ask ourselves to which extent noise and other systematic effects may contribute to the resulting cool and hot features within our calculated maps. To investigate this question, we performed the following randomization tests.
Each individual line profile of one season is randomly assigned to one of the available phases (observing times), i.e., we randomly mix all line profiles so that their time coherency is lost. By scrambling the observations through all available rotational phases, we diminish all signs of migrating bumps. Because the time correlation is then lost, only noise and other systematic effects can now contribute to coherent surface features within the Doppler images. We repeated this randomization process 100 times, i.e., calculated 100 inversions to obtain 100 randomized error maps. From these randomized error maps, we calculated the standard deviation map to estimate the mean error for each surface pixel. This is shown in Fig. 10 where we see that the mean value of the standard deviation is just 4 K with a peak value of 9 K for the 56-line images and 22 K with a peak of 38 K for the single-line images. We can now safely state that noise and remaining systematics in our data have only a small impact on the resulting Doppler images. The inversion code proves to be robust against these effects.
5. Summary and conclusions
Our enhanced Doppler imagery with iMap is now capable of revealing temperature contrasts on a stellar disk with an average error of just ±4 K. We achieve this by coadding well-defined spectral lines together with removing systematic noise due to continuum-setting errors. The latter is a hard limit for Doppler imaging and dominates the image error for S/N beyond ≈300:1. For HD 233517, we found the best line list from a 480–680 nm strip of spectrum with a total number of 56 lines. Reconstructions with 1617 and even 3007 lines showed a deterioration of the image quality. This is likely pronounced in HD 233517 because it is a giant star with an extended atmosphere. We could thus expect a significantly different vertical structure of the atmosphere than in a plane-parallel model. This deficiency would be more pronounced the more weaker and stronger lines are combined in a simultaneous solution.
 |
Fig. 9 Achieved S/N as a function of number of spectral lines. The curves for pure photon noise (dashed line) and for systematic noise (full line) are separated. Note the limitation due to systematic noise for S/N as low as a few hundred. |
The surface of HD 233517 shows coexisting, apparently cool and warm features. The temperature contrast with respect to a mean photospheric temperature is extremely low, ranging between just ±30 K to ±160 K for the three observing seasons. Such low contrasts are untypical for stars with magnetic starspots or faculae (cf. Berdyugina 2005; Strassmeier 2009) where the temperature contrasts are usually much higher between 800–2000 K for cool features and 300−1000 K for warm features, as for spots and white-light faculae on the Sun. Hot spots from the impact of funneled mass accretion appear even with higher temperature contrasts, typically 2000 K, even if unresolved, but dependent on how close the line formation is with respect to its shock front (e.g., Unruh et al. 2004; Strassmeier et al. 2005). Neither of these two scenarios give a satisfactory explanation for the low-contrast features observed on HD 233517.
An alternative explanation to pure magnetic features is an intermingling of a weak magnetic field with convection-driven horizontal velocity fields, similar to that found in an individual super-granulation cell on the Sun. Velocity fields due to certain nonspherical pulsation modes are not likely relevant given the late spectral type of HD 233517 and its evolutionary status on the RGB. We may also tentatively dismiss an enhanced chromospheric outflow (e.g., Lobel & Dupree 2000) because we detect no spectral signs of chromospheric activity in HD 233517. Inhomogeneous distributed granulation cells, on the other hand, could produce low-contrast dark and bright spots and lanes. This was shown in box simulations of rotating magneto-convection by Ziegler (2002) as well as for pure hydrodynamical simulations of rotating stars with very large pressure scale heights, e.g., for the M supergiant Betelgeuse by Steffen & Freytag (2007) and Chiavassa et al. (2010). Granulation on giant stars was simulated and discussed just recently by Tremblay et al. (2013). The cool and warm features on HD 233517 can be stable for a year, but sometimes also much shorter, and appear preferably at higher latitudes. We interpret them to be merely locations of suppressed and enhanced convection somehow related to the fast stellar rotation with P = 47.6 d. Whether any sort of a nonsolar super-granulation pattern is a sign of an enhanced internal mixing process linked to rotation remains speculative at this point, but is evident. Sackmann & Boothroyd (1999) had already demonstrated that deep circulation mixing at the base of the convective envelope and the associated cool bottom processing can account for very high Li abundances and low carbon-isotope ratios when approaching the RGB tip. The enhanced extra-mixing models of Denissenkov & Herwig (2004) predict 12C/13C between 8 and 17 compared to the expected value of ≈23 without the enhanced mixing, in agreement with our measurement of 9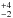 for HD 233517. Planet accretion, by contrast, should raise both the lithium abundance and the 12C/13C ratio. We tentatively conclude that HD 233517 exhibits an enhanced nonaxisymmetric mixing process that leads to an inhomogeneous super-granulation pattern on the surface with large high-latitude cool and warm regions.
for HD 233517. Planet accretion, by contrast, should raise both the lithium abundance and the 12C/13C ratio. We tentatively conclude that HD 233517 exhibits an enhanced nonaxisymmetric mixing process that leads to an inhomogeneous super-granulation pattern on the surface with large high-latitude cool and warm regions.
 |
Fig. 10 Error map deduced from the randomization test of the 56-line solution. See text. |
Just recently, Silva Aquirre et al. (2014) report the finding of the first confirmed Li-rich core-helium-burning giant, as revealed by asteroseismic analysis. The evolutionary timescales constrained by its asteroseismic mass suggest that Li production most likely took place through non-canonical mixing at the RGB tip, possibly during the helium flash. One possibility for independently constraining our own findings would be to detect similar surface Li structure on such superrich Li AGB stars, i.e., on stars after the second dredge up and during helium-core burning. Most, if not all, of the low-mass superrich Li stars however have not reached the AGB yet only the more massive stars reached the AGB. Because stellar rotation, and thus any rotation-induced mixing, should come to a minimum on the AGB because of its immense mass and therefore angular-momentum loss, we probably need such targets in spun-up binaries where the rotational line broadening is sufficiently high that the Doppler-imaging technique works. Alternatively, we could Doppler image low-mass RGB stars in a series of open clusters of known age, where the internal stellar structure is then better defined, assuming that no asteroseismic analysis would be available. Clearly, this asks for larger telescope aperture and higher spectral resolution.
Acknowledgments
We are grateful to the State of Brandenburg and the German federal ministry for education and research (BMBF) for their continuous support of the STELLA and APT activities. The STELLA facility is a collaboration of the AIP in Brandenburg with the IAC in Tenerife. We thank all engineers and technicians involved, in particular Manfred Woche and Emil Popow and his team, and Ignacio del Rosario and Miguel Serra of the IAC Tenerife day time crew. It is our pleasure to thank Eva Panofski for her bachelor thesis and Lou Boyd for nursing the APTs at Fairborn Observatory. An anonymous referee is thanked for his/her many helpful suggestions and comments.
References
- Allende-Prieto, C. 2004, Astron. Nachr., 325, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Allende-Prieto, C., Beers, T. C., Wilhelm, R., et al. 2006, ApJ, 636, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Balachandran, S. C., Fekel, F. C., Henry, G. W., & Uitenbroek, H. 2000, ApJ, 542, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V. 2005, Liv. Rev. Sol. Phys., 2 [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2013, MNRAS, 427, 127 [Google Scholar]
- Brown, J. A., Sneden, C., Lambert, D. L., & Dutchover, E. J., Jr. 1989, ApJS, 71, 293 [CrossRef] [Google Scholar]
- Carlberg, J. K., Cunha, K., Smith, V. V., & Majewski, S. R. 2012, ApJ, 757, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Carroll, T. A., Kopf, M., Ilyin, I., & Strassmeier, K. G. 2007, Astron. Nachr., 328, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Carroll, T. A., Kopf, M., Strassmeier, K. G., & Ilyin, I. 2009, in Cosmic Magnetic Fields: From Planets, to Stars and Galaxies (Cambridge Univ. Press), IAU Symp., 259, 633 [Google Scholar]
- Carroll, T., Strassmeier, K. G., Rice, J. B., & Künstler, A. 2012, A&A, 548, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004 [arXiv:astro-ph/0405087] [Google Scholar]
- Cayrel, R., Steffen, M., Chand, H., et al. 2007, A&A, 473, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiavassa, A., Haubois, X., Young, J. S., et al. 2010, A&A, 515, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cyburt, R. H., Fields, B. D., & Olive, K. A. 2008, J. Cosmol. Astropart. Phys., 11, 12 [Google Scholar]
- de la Reza, R., Drake, N. A., & da Silva, L. 1996, ApJ, 456, L115 [NASA ADS] [CrossRef] [Google Scholar]
- de la Reza, R., Drake, N. A., da Silva, L., Torres, C. A. O., & Martin, E. L. 1997, ApJ, 482, L77 [NASA ADS] [CrossRef] [Google Scholar]
- de Laverny, P., do Nascimento, J. D., Jr., Lebre, A., & De Medeiros, J. R. 2003, A&A, 410, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denissenkov, P. A., & Herwig, F. 2004, ApJ, 612, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Cameron, A. C., Semel, M., et al. 2003, MNRAS 345, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, N. A., de la Reza, R., da Silva, L., & Lambert, D. L. 2002, AJ, 123, 2703 [NASA ADS] [CrossRef] [Google Scholar]
- Dupree, A. K. 2011, in The Physics of Sun and Star Spots (Cambridge Univ. Press), IAU Symp., 273, 188 [Google Scholar]
- Fekel, F. C., & Balachandran, S. 1993, ApJ, 403, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Fekel, F. C., & Watson, L. C. 1998, AJ, 116, 2466 [NASA ADS] [CrossRef] [Google Scholar]
- Fekel, F. C., Webb, R. A., White, R. J., & Zuckerman, B. 1996, ApJ, 462, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Granzer, T., Reegen, P., & Strassmeier, K. G. 2001, Astron. Nachr., 322, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 2005, The observation and analysis of stellar photospheres, 3rd edn. (Cambridge Univ. Press) [Google Scholar]
- Gray, R. O. 1999, Spectrum: A stellar spectral synthesis program (ASC library), 9910.002 [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jura, M. 2003, ApJ, 582, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Jura, M., Bohac, C. J., Sargent, B., et al. 2006, ApJ, 637, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., Lind, K., & Rich, R. M. 2011, ApJ, 738, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, Y. B., & Reddy, B. E. 2009, ApJ, 703, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, Y. B., Reddy, B. E., & Lambert, D. L. 2011, ApJ, 730, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F., Dubernet, M.-L., et al. 2011, Balt. Astron., 20, 503 [Google Scholar]
- Kurucz, R. L. 1993, ATLAS-9, CD-ROM #13 [Google Scholar]
- Lambert, D. L., & Ries, L. M. 1981, ApJ, 248, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Lébre, A., Palacios, A., do Nascimento, J. D., et al. 2006, A&A, 450, 1173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lind, K., Asplund, M., & Barklem, P. S. 2009, A&A, 503, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lobel, A., & Dupree, A. K. 2000, ApJ, 545, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., & Challener, S. L. 1995, AJ 110, 2968 [NASA ADS] [CrossRef] [Google Scholar]
- Miroshnichenko, A. S., Bergner, Yu. K., & Kuratov, K. S. 1996, A&A, 312, 521 [NASA ADS] [Google Scholar]
- Melis, C., Zuckerman, B., Song, I., Rhee, J. H., & Metchev, S. 2009, ApJ, 696, 1964 [NASA ADS] [CrossRef] [Google Scholar]
- Meszaros, Sz., Dupree, A. K., & Szalai, T. 2009, AJ, 137, 4282 [NASA ADS] [CrossRef] [Google Scholar]
- Monaco, L., Villanova, S., Bonifacio, P., et al. 2012, A&A, 539, A137 [Google Scholar]
- Pavlenko, Ya. V., & Magazzú, A. 1996, A&A, 311, 961 [NASA ADS] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Prugniel, P., & Soubiran, C. 2001, A&A, 369, 1048 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reddy, B. E., & Lambert, D. L. 2005, AJ, 129, 2831 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, J. B. 2002, Astron. Nachr., 323, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, J. B., & Strassmeier, K. G. 2000, A&AS, 147, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sackmann, I.-J., & Boothroyd, A. I. 1999, ApJ, 510, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Scott Fisher, R., Telesco, C. M., Pina, R. K., & Knacke, R. F. 2003, ApJ, 586, L91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sbordone, L., Bonifacio, P., Caffau, E., et al. 2010, A&A, 522, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silva Aguirre, V., Ruchti, G. R., Hekker, S., et al. 2014, ApJ, 784, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, M., & Freytag, B. 2007, Astron. Nachr., 328, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G. 2009, A&ARv, 17, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., & Fekel, F. C. 1990, A&A, 230, 389 [NASA ADS] [Google Scholar]
- Strassmeier, K. G., Boyd, L. J., Epand, D. H., & Granzer, T. 1997, PASP, 109, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Rice, J. B., Ritter, A., et al. 2004, A&A, 440, 1105 [Google Scholar]
- Strassmeier, K. G., Granzer, T., Kopf, M., et al. 2010a, A&A, 520, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Granzer, T., & Weber, M. 2010b, Adv. Astron., 2010, 970306 [Google Scholar]
- Strassmeier, K. G., Carroll, T., Weber, M., et al. 2011, A&A, 535, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Weber, M., Granzer, T., & Järvinen, S. 2012, Astron. Nachr., 333, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Sylvester, R. J., Dunkin, S. K., & Barlow, M. J. 2001, MNRAS, 327, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Tremblay, P.-E., Ludwig, H.-G., Freytag, B., Steffen, M., & Caffau, E. 2013, A&A, 557, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Unruh, Y. C., Donati, J.-F., Oliveira, J. M., et al. 2004, MNRAS, 348, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Wallerstein, G., & Sneden, C. 1982, ApJ, 255, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, M., Granzer, T., Strassmeier, K. G., & Woche, M. 2008, Proc. SPIE, 7019, 70190L [NASA ADS] [CrossRef] [Google Scholar]
- Weber, M., Granzer, T., & Strassmeier, K. G. 2012, Proc. SPIE, 8451, 84510K [CrossRef] [Google Scholar]
- Ziegler, U. 2002, A&A, 386, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 A representative spectrum of HD 233517 (K2III, upper spectrum) in comparison with the neighboring star HD 233520 (K0III, grey-line) and the M-K standard star α Ari (K2III, grey dotted line). The spectrum of HD 233517 is shifted by +0.4 in intensity for better visibility. The panels show, from top left to bottom right, Balmer Hα, Na i D lines, Li i 610.36, Li i 670.78, Ca ii 866.2 irt triplet line, 12CN and 13CN lines, C2 primary and secondary Swan lines, Balmer Hβ, and Balmer Hγ. |
| In the text | |
 |
Fig. 2 Detections of rotational modulation. a) Differential APT V-band light curve from the observing season 2010. b) STELLA-SES radial velocities from 2008–2011. Both data sets were phased with P = 47.6 d from 2 455 000. |
| In the text | |
 |
Fig. 3 Atmospheric parameters of HD 233517 from the PARSES analysis. From top to bottom: effective temperature, gravity, and metallicity with long-term average values of 4390 K, 2.26 cm s-2, and −0.42 [M/H]⊙, respectively. |
| In the text | |
 |
Fig. 4 Location of HD 233517 in the H-R diagram (dot with error bars, logarithmic presentation). The lines are the “best match” tracks from Bressan et al. (2013) for either solar metallicity (indicated as solar) or the measured metallicity [ Fe/H ] = −0.42 for post-main sequence (post) and pre-main sequence (pre). The mass is indicated in solar masses. Insert a) shows the best-match track (0.95 M⊙) and the two tracks that envelope the error box as indicated. Insert b) is a graphical zoom of the box in the main panel. |
| In the text | |
 |
Fig. 5 Lithium line fits. From top to bottom for the resonance line 670.78 nm and the two excited lines 610.36 nm and 812.65 nm. The dots are the STELLA SVD profiles from the observing season 2007/08 and the lines are the fits. |
| In the text | |
 |
Fig. 6 Example time-series SVD line profiles of HD 233517 from data set Bb in 2007/08. Systematic errors are estimated from the standard deviation in two 20-km s-1 passbands at ±30–50 km s-1 away from the line center. In the dynamic plot in the top panel, time progresses from bottom to top for 63 d. The color denotes residual line depth (white is continuum, black is the line core). |
| In the text | |
 |
Fig. 7 Average photospheric surface structure of HD 233517. Individual Doppler images were determined from a total of 56 selected absorption lines. Panels a)–f) are for the epochs identified in Table 2 and span three years from 2007–2010. |
| In the text | |
 |
Fig. 8 Temperature Doppler images from the Li i 670.78 line. The epochs are the same as in Fig. 7. |
| In the text | |
 |
Fig. 9 Achieved S/N as a function of number of spectral lines. The curves for pure photon noise (dashed line) and for systematic noise (full line) are separated. Note the limitation due to systematic noise for S/N as low as a few hundred. |
| In the text | |
 |
Fig. 10 Error map deduced from the randomization test of the 56-line solution. See text. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


