| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A123 | |
| Number of page(s) | 13 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201423830 | |
| Published online | 05 February 2015 | |
Pre-hibernation performances of the OSIRIS cameras onboard the Rosetta spacecraft
1
Centro di Ateneo di Studi e Attivitá Spaziali “Giuseppe Colombo”,
University of Padova,
via Venezia 15,
35131
Padova,
Italy
e-mail:
sara.magrin.1@unipd.it
2
Department of Physics and Astronomy, University of
Padova, vicolo dell’Osservatorio
3, 35122
Padova,
Italy
3
CNR-IFN UOS Padova LUXOR, via Trasea 7,
35131
Padova,
Italy
4
Department of Information Engineering, University of
Padova, via Gradenigo
6, 35131
Padova,
Italy
5
Max-Planck-Institut für Sonnensystemforschung,
Justus-von-Liebig-Weg 3,
37077
Göttingen,
Germany
6
European Space Astronomy Centre, ESA, Villanueva de la
Cañada, 28691
Madrid,
Spain
7
LESIA, Observatoire de Paris, CNRS, UPMC Univ Paris 06, Univ. Paris Diderot, 5 Place J.
Janssen, 92195
Meudon Pricipal Cedex,
France
8
Université Paris Diderot, Sorbonne Paris Cité, 4 rue Elsa Morante,
75205
Paris,
France
9
Laboratoire d’Astrophysique de Marseille, CNRS and Université de
Provence, 38 rue Frédéric
Joliot-Curie, 13388
Marseille,
France
Received: 18 March 2014
Accepted: 6 December 2014
Context. The ESA cometary mission Rosetta was launched in 2004. In the past years and until the spacecraft hibernation in June 2011, the two cameras of the OSIRIS imaging system (Narrow Angle and Wide Angle Camera, NAC and WAC) observed many different sources. On 20 January 2014 the spacecraft successfully exited hibernation to start observing the primary scientific target of the mission, comet 67P/Churyumov-Gerasimenko.
Aims. A study of the past performances of the cameras is now mandatory to be able to determine whether the system has been stable through the time and to derive, if necessary, additional analysis methods for the future precise calibration of the cometary data.
Methods. The instrumental responses and filter passbands were used to estimate the efficiency of the system. A comparison with acquired images of specific calibration stars was made, and a refined photometric calibration was computed, both for the absolute flux and for the reflectivity of small bodies of the solar system.
Results. We found a stability of the instrumental performances within ±1.5% from 2007 to 2010, with no evidence of an aging effect on the optics or detectors. The efficiency of the instrumentation is found to be as expected in the visible range, but lower than expected in the UV and IR range. A photometric calibration implementation was discussed for the two cameras.
Conclusions. The calibration derived from pre-hibernation phases of the mission will be checked as soon as possible after the awakening of OSIRIS and will be continuously monitored until the end of the mission in December 2015. A list of additional calibration sources has been determined that are to be observed during the forthcoming phases of the mission to ensure a better coverage across the wavelength range of the cameras and to study the possible dust contamination of the optics.
Key words: instrumentation: detectors / space vehicles: instruments / techniques: photometric
© ESO, 2015
1. Introduction
The ESA Rosetta mission was launched on 2 March 2004, and since then, the Optical, Spectroscopic, and Infrared Remote Imaging System (OSIRIS, Keller et al. 2007), which is a two-camera system, performed many different scientific observations. It acquired data during a swing-by with Mars and Phobos in 2007, a fly-by with asteroid (2867) Steins in 2008, two swing-bys with Earth in 2007 and 2009, and a fly-by with asteroid (21) Lutetia in 2010, to mention only the main activities. On 8 June 2011, the spacecraft entered into deep-space hibernation mode. It successfully exited hibernation on 20 January 2014 for the cruise to the rendez-vous with the primary scientific target of the mission: the Jupiter-family comet 67P/Churyumov-Gerasimenko.
Establishing the stability of the instrument through time is vital to performing a correct absolute flux calibration of the cometary data.
Basic parameters of the NAC and WAC system and CCD specification (Keller et al. 2007).
In Sect. 2 we therefore study the past performances of the two cameras, the Narrow Angle and Wide Angle Camera (NAC and WAC), through the observations of calibration stars. In particular, we investigate the past responses of calibrator signal through time with different filters to be able to evaluate possible aging effects on the optics and to determine whether the photometric requirements set by the original mission science goals have remained stable. We also inspect the dynamical range of the two CCDs by checking the linear dependence between the stellar signal and the exposure time of observations. The transmission and reflectivity curves of each component of the two cameras, measured during on-ground calibration tests, is used to estimate the efficiency of the instrumentation. We thus check and compare the expected calibrator signals that are deduced from these instrumental efficiency curves and from the observed one, which is computed from images acquired in flight.
Following this investigation, we present in Sect. 3 the robust formulation for the absolute flux calibration of OSIRIS images. Section 4 is dedicated to the description of the conversion between the signal observed on the surface of solar system bodies and of their correct geometric reflectance.
The NAC is a three-mirror anastigmat system, while the WAC has an off-axis optical configuration obtained with two aspherical mirrors (Keller et al. 2007). In Table 1 we report the main characteristics of the NAC and WAC system, together with the specifications of the CCDs.
A plane-parallel antireflection coated plate, referred to as antiradiation plate (ARP), was added in front of the CCD for radiation shielding.
Both cameras are equipped with two filter wheels placed in front of the CCD. A passband is defined by a combination of two filters, hereafter (x,y), where x is the filter position on the first wheel and y is the position on the second wheel. In Table 2 we list all filters available for the two cameras by specifying their position on the wheels.
NAC and WAC filter names and wheel positions.
The WAC filters are located in seven of the eight positions of the two filter wheels, from 2 to 8, leaving the first position in both wheels empty. All seven filters of the first wheel can be used by setting the empty position in the second one, and vice-versa.
In the NAC the filter wheels have no empty position. Neutral or clear filters are used in combination with band-pass filters to optimize the camera performances either in the UV, in the visible, or in the IR range. A different focus range for near focus plate – visible (NFP-Vis) with respect to far focus plate – visible (FFP-Vis) is also planned, which will allow optimizing the resolution of the NAC for observations of the comet surface at a distance shorter than 4 km.
We can therefore define the filters as twins, which can be obtained by combining different clear filters in addition to the same band-pass filter. These combinations share the same passband, but have different efficiencies in general because clear filters have different efficiencies. Together with defining twin combinations, it is also possible to define a baseline filter combination by selecting a representative of the group and deduce the flux calibration of the whole group according to the baseline calibration.
In Appendix A we list and define the physical parameters and units we used.
2. Performance of OSIRIS cameras
2.1. Expected count rate
The expected total count rate, Kx,y in DN s-1, of a given source on an image acquired through the (x,y) filter combination is expressed by 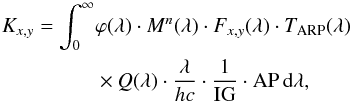 (1)where
(1)where
-
ϕ(λ) is the spectral irradiance of the source at the camera entrance aperture, expressed in W m-2 nm-1;
-
Q(λ) is the CCD quantum efficiency expressed in e−/ ph;
-
IG is the inverse gain, which hereafter is taken to be 3.1e−/ DN;
-
Mn(λ),Fx,y(λ),TARP(λ) are the mirror spectral reflectance (through n mirrors: n = 2 for WAC or n = 3 for NAC), filters, and antiradiation plate (ARP) transmissions as a function of the wavelength;
-
AP is the telescope aperture: 4.91 × 10-4 m2 for the WAC and 6.49 × 10-3 m2 for the NAC.
In Fig. 1 we report the reflectivity of the three-mirror (NAC) and two-mirror (WAC) systems together with filters and ARP transmission curves.
 |
Fig. 1 Efficiency curves of NAC and WAC optics: transmission curves of clear and band-pass filters, antiradiation plates (ARP), and reflectivity of mirrors. |
The integrand of Eq. (1)is the wavelength dependance of the count rate detected by the instrument. In particular, Q(λ) × λ/hc is the way to express the CCD efficiency in e−/(W s), where λ/ (hc) = λ/ (1.986 × 10-16) if λ is expressed in nm. Q(λ) × λ/ (hc·IG) hence gives the CCD efficiency in DN/(W s).
If the source flux is constant with time, then ϕ(λ) is time independent. Since in principle all instrument optics responses depend on age, the integrand of Eq. (1)and hence Kx,y are therefore time (age) dependent.
2.2. Observed count rate
Equation (1)gives the total count rate that is expected on the CCD in each (x,y) passband of a source with a known spectral irradiance ϕ(λ). As a first check of the OSIRIS performances, we compared these theoretical values with the real values observed by the instrument.
Two stars were regularly observed by OSIRIS during the past mission phases for calibration purposes: Vega and the double star 16 Cyg A+B. 16 Cyg B is a solar analog and is suitable for measuring the reflectance of small bodies of the solar system. The corresponding spectral irradiances that were taken into account to provide the theoretical values we compared our values with were taken from Bohlin & Gilliland (2004) for Vega and from Burlov-Vasiljev et al. (1995, 1998) for the solar spectrum properly scaled to match 16 Cyg A and B.
2.2.1. Aperture photometry
We derived the observed count rate from the calibration stars with the aperture photometry method.
The raw data were processed to remove the bias level. Flat-field correction was applied by means of images that were observed on the ground of the integrating sphere, which were acquired when the cameras were characterized in the laboratory. In-flight flat-field images are regularly acquired by illuminating the closed telescope front doors with internal lamps. However, internal lamps do not guarantee a completely flat source, and this method is only useful to monitor the flat-field stability, but not to create new reference images. Since no variation was detected on in-flight images, laboratory images are still used for the flat-field correction.
In the WAC images the 16 Cyg A+B pair is not separated, which forced us to apply the method to both stars at the same time. In the NAC images the 16 Cyg A and B centroids are separated by about ten pixels. This means that we can measure fluxes of 16 Cyg B alone only when the aperture radius is verified to be smaller than 5 pixels, to avoid contamination from 16 Cyg A.
 |
Fig. 2 PSF FWHM as number of pixels (geometric average of x and y direction values) in OSIRIS filters deduced from Vega observations. The largest size of four NAC filters is acquired by combining a near focus plate that can optimize the performances of the NAC camera for a target that is at a distance smaller than 4 km. |
On the CCD, different filters show different typical point spread function (PSF) profiles (see for example Figs. 2 and 3), so that the best aperture radius to use for the aperture photometry depends on the filter, which in many cases is larger than 5 pixels. For consistency between different cameras and among different filters, we therefore decided to derive the photometry from both stars in the NAC in the same way as we have to do with WAC images. See Appendix B for more details on the double star 16 Cyg A+B.
We finally had to define a general criterion to find the best value for the aperture radius. By investigating the stellar integral profile obtained at different aperture radius, we typically expect to find a plateau for aperture radii larger than a critical value after the background level is removed. For OSIRIS images, a typical aperture growth curve of Vega is reported in Fig. 4, where the sky level is estimated in a region here defined by sky apertures between 50 and 60 px. For both NAC and WAC, the sky background is normally found to be within ±3 DN, with a standard deviation of about 8.5 DN on NAC and 6.7 DN on the WAC, probably due to coherent noise. The plateau indicates that the total flux of the star was taken into account.
 |
Fig. 3 Shape of the Moffat fit of the PSF of OSIRIS camera filters in the following combinations: a) NAC-F16 (FFP-UV_Near-UV); b) NAC-F82 (Neutral_Orange); c) WAC-F12 (Red); and d) WAC-F18 (Vis610). |
In some OSIRIS images this cannot be achieved. We often found an oblique (instead of a horizontal) asymptote, regardless of our definition of the sky annuli. We ascribed this to an on-axis contamination, maybe due to diffuse light by optics micro-roughness or to ghosts.
The NAC ghosts are well described in Dohlen et al. (2010). First-generation ghosts are caused by the light reflection between pairs of optical surfaces. The most intense on-axis ghost, for example, can be produced by the reflection of the incident light on the surface of the CCD, reflected again by the nearest surface of the ARP. In the [800−1000] nm IR range the NAC CCD reflectivity increases from 10 to 30%. The ghost relative intensity, with respect to the scientific image, is thus three times higher at 1000 nm than at 800 nm. The two filters most affected by the oblique asymptote are the reddest ones, F61 and F71, which are centered at about 930 and 990 nm.
However, the CCD reflectivity and the ARP reflectivity in the whole [250−400] nm range are higher than at 1000 nm, which means that the ghost problem should affect the UV range much more than the IR, while we find that the contamination in UV NAC filter, where present, is not so evident. Therefore, further investigation is needed on this topic.
In the meanwhile, we had to find a new definition for the aperture radius for the NAC-F61 and NAC-F71 filters: we selected the smallest aperture radius r such that the flux in the annulus [r − 1,r] is below half the sky standard deviation. After that we considered the remnant contribution as background even if with a non-zero average.
2.2.2. CCD linearity and stability
We investigated the stability of the results of the aperture photometry method during different observational phases of the mission (from the Mars swing-by in 2007 to the Lutetia fly-by in 2010).
In Table 3 we report the mean value of the count rate computed from Vega images with different filter combinations, the maximum deviation, and the typical exposure times.
For the two NAC (F16 FFP-UV_Near-UV, and F82 Neutral_Orange) and two WAC filters (F12 Red, and F18 Vis610) the signal linearity with increasing exposure time was also investigated. The shortest exposure time is imposed by the shutter response tolerance, the longest time is defined by the CCD saturation level.
The OSIRIS CCDs are equipped with an antiblooming system, designed to “extract” overabundant electrons from the pixel potential well. This system is needed for the cometary target to allow overexposed images of the nucleus without saturation artifacts. This is necessary to acquire high signal-to-noise (S/N) data of the dust and gas in the inner coma against the brilliant nucleus. The saturation level was required to be about 120 000 e−/ px ≈ 40 000 DN / px (see Keller et al. 2007; Thomas et al. 1998) so that the pixel linearity is guaranteed only below this limit. Above the saturation, the CCD cannot collect any other electron, and we will find a constant signal regardless of the exposure time.
For point sources, which are dominated by the optics PSF, the peak value of the source must not exceed the saturation value, while the total flux of the source is split into more pixels and the total number of electrons collected can obviously exceed the limit. When the peak signal reaches the saturation levels, the antiblooming system prevents overabundant charges of only the overexposed pixels to spill over into the neighborhood above a given exposure time. Nearby unsaturated pixels, however, can continue to collect electrons, so that we would still experience an increase of the total point source signal with exposure time, even with a lower rate.
To study the linearity of the CCD response, we defined as outliers and consequently excluded from the data set the count rates that deviate from the mean value by more than three times the standard deviation. The iteration of this method defined a time interval where the linearity is satisfied. Figure 5 shows the distribution of Vega observations (reported as both counts and count rate) vs. exposure time in this interval. In Table 3 the time interval is specified for these four filters.
Table 3 shows that almost all the filters are stable within ±1.5%. In only one case, WAC-F51 at 295 nm, there is a deviation of + 2.79%, while in only two other filters, NAC-F41 at 880 nm and WAC-F61 at 308.5 nm, deviations exeed 1.5%. Moreover, we also verified that the data considered do not show any evident aging effect since there is no systematic trend with date: the data dispersion of about ±1.5% is found both in case of stellar observations acquired during the same day and during the whole OSIRIS activity period. This dispersion is also consistent with the photometry precision requirement of about 2% set by the original mission science goals (Keller et al. 2007).
From this investigation we found that the peak level of counts on a single pixel in raw images is above 57 000 DN for both NAC filters investigated, while it is about 47 000 and 50 000 DN for the two WAC filters investigated, well above the 40 000 DN limit foreseen. We verified for WAC that the centroids of the PSF were located in different positions on the CCD, with different efficiencies: if the saturation limit was found to be at 47 000 DN, the star always fell on some few cold pixels. This difference was then corrected by flat fielding. The difference between NAC and WAC values suggest that the two CCDs behave differently. For NAC-F82 we did not exclude any observation in the data-set with the longest exposure times, so that we did not confirme the saturation limit in this case. For new tests that are scheduled to study the CCD linearity, a wider range in texp for NAC-F82 must be considered.
 |
Fig. 4 Typical curve of the aperture flux growth. This curve was specifically obtained from Vega observations with the NAC F16 filter. |
In Fig. 3 we show the PSF for two NAC and two WAC filters in the case where the centroid of the PSF lies exactly on the center of a pixel. For the four selected filters the ratios between the peak value and the total integrated signal are about 17.5% for NAC-F16, 24.5% for NAC-F82, 34.5% for WAC-F12, and 34.3% for WAC-F18 of the total signal.
OSIRIS NAC and WAC filter characteristics and Vega observations.
2.3. Count rate: observed vs. expected
In Fig. 6 we show the ratio between observed and expected counts in each filter for Vega and 16 Cyg A+B. The count rate obtained for Vega and 16 Cyg A+B observations acquired during all mission phases was compared with the expected rate that we computed from the Vega reference spectrum (Bohlin & Gilliland 2004, CALSPEC version 004) and solar reference spectra (Burlov-Vasiljev et al. 1995, 1998), respectively, by means of Eq. (1). For this last source we computed a conversion factor of between 16 Cyg A+B and solar fluxes, based on the different visual absolute magnitudes, to allow a direct comparison with the solar spectrum. See Appendix B for further details.
The error bars in this plot were computed by propagating the photon noise deduced on the original images with errors defined on each instrument element. Horizontal bars refer to the FWHM of each passband.
The total relative (percentage) instrumental error is dominated by the CCD QE uncertainty.
Several considerations arise from the analysis of the plot:
-
In the UV range, that is, below 400 nm, fewercounts are observed than expected.
-
In the visible range, the WAC filters counts agree with the predicted counts. The NAC filter counts, however, seem to exceed the expected counts (in some cases they are even higher than the vertical error bars).
-
In the near-IR range, above 800 nm, fewer counts are observed counts than predicted.
-
The NAC twin filter values agree within error bars. However, we found some systematic differences among NAC FFP-Vis, NAC NFP-Vis, and NAC Neutral (second, third, and eighth position on filter wheel 1, respectively).
-
The agreement between observed and expected counts is verified from both Vega and 16 Cyg A+B counts in the range 470–890 nm.
-
The agreement between Vega and 16 Cyg A+B data is good above 470 nm.
-
The scatter among filters and between different stars is larger in the UV range. 16 Cyg A+B data are systematically lower than Vega data.
-
Around WAC F71 (centered on 325 nm) the plot behaves strangely in both Vega and 16 Cyg A+B data. This scatter is not due to an anomalous observation because the photometric values were computed for this filter, like for others, as the average of many observation in different phases, giving a positive and a negative maximum percentage error of +1.11% and −1.36%, respectively.
16 Cyg A+B data can be affected by an incorrect computation of the conversion from solar fluxes (computed from 10− 0.4(VSA − V⊙)). However, the match of 16 Cyg A+B data with Vega data above 470 nm suggests that this assumption is good at least in the visible and near-infrared range of the spectrum. In the UV range, there may be also some differences due to the imperfect match between 16 Cyg A and 16 Cyg B spectra and the solar spectrum, which can be variable in these wavelengths by up to 20% (Colina et al. 1996). Moreover, below 325 nm, 16 Cyg A+B counts are maybe unreliable as a result of the decreasing signal in this wavelength range that is typical of solar analog stars, which means that we can only trust the Vega counts.
 |
Fig. 5 Linearity measurements obtained by the Vega observations in terms of DN or DN/s vs exposure time. For each filter, the upper panels show counts vs. exposure time in the particular filter, the lower panels show the count rate vs. the exposure time. The investigation was made with the following filters: a) NAC-F16 (FFP-UV_Near-UV); b) NAC-F82 (Neutral_Orange); c) WAC-F12 (Red); and d) WAC-F18 (Vis610). |
 |
Fig. 6 Ratio between observed and expected counts from the CCD with a particular filter setting. Vertical error bars refer to photon noise and the propagation of instrumental uncertainties. Horizontal bars refer to the FWHM of each passband. Red data refer to counts computed from 16 Cyg A+B images and solar spectrum (Burlov-Vasiljev et al. 1995, 1998) scaled to 16 Cyg A+B magnitude; black data refer to Vega images and Vega spectrum (Bohlin & Gilliland 2004). |
Variability among twin filters that share the same passband (i.e., NAC F82-F22-F32, NAC F83-F23-F33, NAC F88-F28-F38, etc.) are probably due to different shapes of the actual transmission curves of clear filters (NAC FFP-Vis, NAC NFP-Vis, and NAC Neutral) with respect to laboratory data of the same filters obtained on the ground before the launch.
The lower count rate in the near IR can in principle be due to an incorrect computation of the counts within the selected aperture. For many NAC filters the aperture radii selected for the computation of Vega flux through the aperture photometry method were found to be 7−9 pixels. We recall here that for these filters we always found a plateau. However, throughout all the past mission phases, the signal was always found to increase for the NAC IR filters F61 and F71; it lay on an oblique asymptote. Taking into account a possible on-axis contamination, we decided to stop at an aperture of about 10−12 pixels for F61 and at 15−17 pixels for F71, depending on the background noise level on the different images. For the sake of completeness, we investigated wider apertures for the NAC-F61 and F71 filters. We found that even 40-pixel apertures are not enough to obtain the expected counts, hence wider apertures cannot improve the calibration in either case.
Absolute flux calibration of the OSIRIS NAC and WAC filters.
3. Absolute flux calibration
We call the factor needed to convert observed count rates per pixel into physical units the abscal factor (i.e., spectral radiance, expressed in W m-2 nm-1 sr-1) to obtain the absolute instrument calibration.
We present photometric calibration factors for each passband. We used images of stellar targets such as Vega and the pair 16 Cyg A+B. According to each filter combination (x,y), we can measure the total count rate due to the star (or pair), Kx,y, from these images.
The spectral radiance that we expect on each pixel with the same filter combination (x,y) is the weighted average of the incoming spectral radiance of the target star, with the instrumental response as the weight, divided by the pixel size (pxsz) of the CCD expressed in steradians (3.547e-010 sr for NAC and 9.982e-009 sr for WAC): 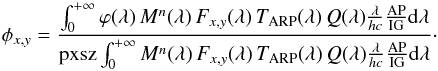 Consequently, the abscal factor, Ax,y, which links the total count rate (Kx,y) on the CCD for a particular filter combination to the spectral radiance within the passbands, φx,y, expressed in W m-2 nm-1 sr-1, is defined by
Consequently, the abscal factor, Ax,y, which links the total count rate (Kx,y) on the CCD for a particular filter combination to the spectral radiance within the passbands, φx,y, expressed in W m-2 nm-1 sr-1, is defined by 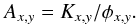 (2)In first approximation Ax,y is filter dependent (and hence in principle time (age) dependent) and star independent.
(2)In first approximation Ax,y is filter dependent (and hence in principle time (age) dependent) and star independent.
Because AP,hc, and IG are constant with wavelength and can be simplified, the abscal factor is 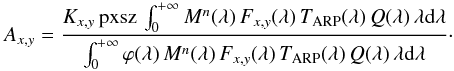 (3)The abscal factor is expressed in DN s-1·(Wm-2 nm-1 sr-1)-1.
(3)The abscal factor is expressed in DN s-1·(Wm-2 nm-1 sr-1)-1.
List of NAC filters without stellar calibration.
In Table 4 we report the abscal factor values for all different filters computed from this equation.
Q(λ) is roughly constant on the visible passbands and can be simplified from both integrals in Eq. (3): this means in particular that the abscal factors are little affected by the imperfect knowledge of the CCD quantum efficiency in the visible range (approximately [400−1000] nm).
3.1. Twin combinations
As said in the Introduction, we can calibrate scientific images acquired with any of the filters of a twin group by using the baseline calibration of a representative filter of the group. For example, we can calibrate both NAC-F87 and NAC-F37, or NAC-F84 and NAC-F34, simply by using the baseline calibration obtained with filter combinations NAC F27 or NAC F24, respectively. In Table 5 we show all the filters for which this is possible and the selected baseline filter.
In the following we describe the equations used to properly infer the absolute calibration in these cases. As an example, we use the calibration of NAC-F84 images through the NAC-F24 observation of the calibration star. The filter in the second position (2) on the NAC first filter wheel (FFP-Vis: far focus plate – visible) has a mean efficiency ≈95%, while filter 8 (neutral) has ≈5%. Accordingly, the two considered filters refer to Neutral_Blue or FFP-Vis_Blue (coded as NAC-F84 or and NAC-F24), respectively. To compute the abscal factor of the filter combination A84, we cannot use the usual expression 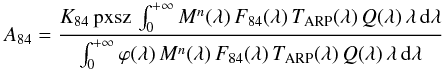 since we did not observe calibration stars through the F84 filter, we do not know the K84 count rate, but only K24. However, we expect from Eq. (1)that the counts of a star through a filter are proportional to the integral of the stellar spectrum multiplied by the passbands, so that
since we did not observe calibration stars through the F84 filter, we do not know the K84 count rate, but only K24. However, we expect from Eq. (1)that the counts of a star through a filter are proportional to the integral of the stellar spectrum multiplied by the passbands, so that 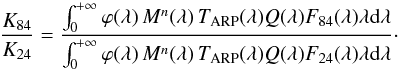 (4)This means that we can express A84 as
(4)This means that we can express A84 as 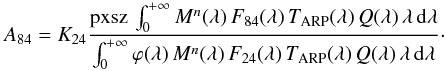 This method was applied to complete the absolute flux calibration presented in Table 4 for filters without a direct observation of the calibration stars.
This method was applied to complete the absolute flux calibration presented in Table 4 for filters without a direct observation of the calibration stars.
3.2. Theoretical and real abscal factor
Since the expected counts from a source should be expressed as in Eq. (1), the theoretic abscal factor should also be expressed as 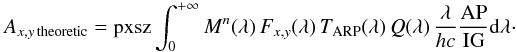 In this form we can see that the abscal factor should be calibrator independent. However, the expected counts in general may be not equal to the observed counts, as shown in Sect. 2.3. This is why the previous formulation is only the theoretical formulation and needs to be corrected for each variation on the instrumental response with time (age).
In this form we can see that the abscal factor should be calibrator independent. However, the expected counts in general may be not equal to the observed counts, as shown in Sect. 2.3. This is why the previous formulation is only the theoretical formulation and needs to be corrected for each variation on the instrumental response with time (age).
In the following, we call Cx,y the ratio between observed and expected counts in the (x,y) filter. It is defined by 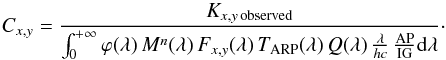 (5)This equation defines the correction factor that we need to apply to the optics profiles so that Eq. (1)gives the observed count rate. However, with this definition we only assume single correction factors, constant on wavelengths, for each (x,y) filter combination.
(5)This equation defines the correction factor that we need to apply to the optics profiles so that Eq. (1)gives the observed count rate. However, with this definition we only assume single correction factors, constant on wavelengths, for each (x,y) filter combination.
In this approximation the abscal factor we should use to convert our images becomes 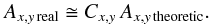 (6)We stress that this is not an exact equivalence. We should not only correct for Cx,y factors, constant on wavelength, but we should find a correction profile C(λ), dependent on the wavelength, deduced by Cx,y data, that can correct the shape of every passband profile.
(6)We stress that this is not an exact equivalence. We should not only correct for Cx,y factors, constant on wavelength, but we should find a correction profile C(λ), dependent on the wavelength, deduced by Cx,y data, that can correct the shape of every passband profile.
However, where the response diversity is a constant factor over the passband (or maybe even a slow symmetrical variation over the passband), the theoretical source flux weighted mean is the same as the observed one, and the previous equivalence is exact. This is verified for OSIRIS filters in the [470−900] nm range.
In this case, we can write 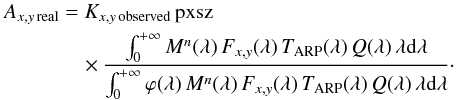 (7)Therefore, we can convert the count rate into the correct physical units in each passband (x,y) because the abscal factor compensates for every variation in the optics efficiencies:
(7)Therefore, we can convert the count rate into the correct physical units in each passband (x,y) because the abscal factor compensates for every variation in the optics efficiencies: 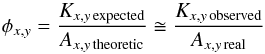 deduced from Eq. (2).
deduced from Eq. (2).
In contrast, where differences between actual and laboratory measured profiles are asymmetric over the passbands, Eq. (7)is valid only in a first approximation, and the goodness of the approximation depends on the real shape of the passbands. In this case we could also find different absolute flux calibrations for every source observed. This may be the reason why we see a mismatch between Vega and 16 Cyg A+B data in the UV range in Fig. 6. The steep UV behavior of the plot suggests that in this range, NAC and WAC passbands may have profiles with a shape different from that considered for the computation. These different shapes give an incorrect weight for computing the weighted arithmetic means that is at the base of the concept of Eq. (3).
These considerations are of fundamental importance for investigating possible aging or dust contamination of the optics during the last part of the mission around the comet, since we expect a wavelength-dependent variation of optical efficiencies in these cases. Therefore, we will have to continuously check this calibration: the computation of abscal factors may change with time, and the calibration will be good only because these factors compensate for efficiency variations. Moreover, an accurate computation of the correction profile C(λ) deduced from Cx,y must be implemented to improve the UV calibration.
One way to monitor the goodness of the approximation in Eq. (6)is to compute, for example, the flux calibration by means of different sources, with different spectra ϕ(λ).
3.3. List of UV calibrators
We should therefore observe different stars with different spectral type to be able to check the consistency of the calibration independently of the star spectrum so that we can try to fix calibration issues after the awakening of OSIRIS. As we stated before, 16 Cyg A and B are solar analogs, with a very low S/N in the UV, which is the reason why at the moment only Vega is used at these wavelengths. We need stars different from Vega (A0V) and hotter than a solar analog (G2V).
In Table 6 we present a list of stars in the Bruzual-Persson-Gunn-Stryker (BPGS) atlas with spectral type earlier than A3. These stars are cross-correlated with the TD1 catalog (Thompson et al. 1978) and the corresponding magnitudes are also provided (Hayes & Latham 1975).
The BPGS atlas consists of 175 spectra of stars covering a complete range of spectral types and luminosity classes. Each individual spectrum covers the [229–25 600] Å wavelength region. The fluxes were arbitrarily normalized to a visual magnitude of zero. More details about the spectra can be found in Gunn & Stryker (1983).
Selected UV calibrators from the BPGS catalog.
4. Reflectance calibration
If we are observing a small body in the solar system, at the first approximation and at least in the visible range, we detect that the solar spectrum is diffused from the body surface. Considering OSIRIS data, we can remove the solar contribution on each image by computing the solar flux that falls inside each filter passband to obtain the spectrophotometric reflectance of the observed object inside each passband. We are able, therefore, to investigate its optical properties and give hints on its surface mineralogical composition.
For example, we wish to scale the image count rate so that if the target is observed at zero phase angle, it will give the value of the geometric albedo on the given passband. For that purpose, we recall some photometric definitions.
The geometric albedo is the ratio of a body brightness at zero phase angle to the brightness of a perfectly diffusing (Lambertian) disk with the same position and apparent size as the body. A Lambertian surface follows the cosine emission law (Lambert 1760): the intensity seen by an observer from an ideal diffusing surface is proportional to the cosine of the angle θ between the observer’s line of sight and the normal to the surface, with peak luminous intensity (Ipeak) in the normal direction. The incident solar flux is equal to the total diffused flux that can be computed from the peak intensity by integrating the cosine law on the semi-sphere defined by the normal direction, obtaining Ftot = πIpeak.
The geometric albedo in a (x,y) given passband is expressed by 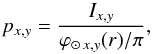 (8)where Ix,y is the body intensity at zero phase angle, ϕ⊙ x,y(r) is the incident solar spectral irradiance at the body distance r from the Sun, and the factor π comes from the integral on the semi-sphere of the Lambert cosine law.
(8)where Ix,y is the body intensity at zero phase angle, ϕ⊙ x,y(r) is the incident solar spectral irradiance at the body distance r from the Sun, and the factor π comes from the integral on the semi-sphere of the Lambert cosine law.
We can accordingly define the reflectance R of a solid object illuminated by the Sun at a given phase angle α as 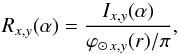 (9)where Ix,y(α) is the intensity emitted by the body in the (x,y) band at the phase angle α and ϕ⊙ x,y(r) is the peak of the solar flux diffused by the Lambertian disk with the same cross-section of the object at the distance r from the Sun in the same band.
(9)where Ix,y(α) is the intensity emitted by the body in the (x,y) band at the phase angle α and ϕ⊙ x,y(r) is the peak of the solar flux diffused by the Lambertian disk with the same cross-section of the object at the distance r from the Sun in the same band.
From the solar spectrum at 1 AU (Burlov-Vasiljev et al. 1995, 1998) we can compute the expected solar count rate at 1 AU, according to Eq. (1): 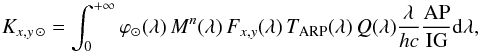 expressed in DN s-1, where ϕ⊙(λ) is the solar spectral irradiance at 1 AU expressed in W m-2 nm-1. The solar spectral irradiance at 1 AU inside a particular filter (x,y) is expressed by the weighted mean:
expressed in DN s-1, where ϕ⊙(λ) is the solar spectral irradiance at 1 AU expressed in W m-2 nm-1. The solar spectral irradiance at 1 AU inside a particular filter (x,y) is expressed by the weighted mean: 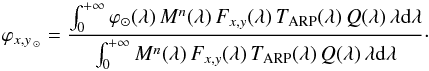 After dividing it by π and scaling it to the distance r of the target to the Sun expressed in astronomic units, we obtain the value ϕ⊙(r) /π, expressed in W m-2 nm-1 sr-1, used to obtain the (geometric) reflectance within a given passband. Note that the reflectance is a adimensional number.
After dividing it by π and scaling it to the distance r of the target to the Sun expressed in astronomic units, we obtain the value ϕ⊙(r) /π, expressed in W m-2 nm-1 sr-1, used to obtain the (geometric) reflectance within a given passband. Note that the reflectance is a adimensional number.
As already cited, we used the spectrum of the Sun measured by Burlov-Vasiljev et al. (1995, 1998). Solar analogs can be significantly different from the Sun, especially in the UV range, where the Sun can be variable by up to 20% (Colina et al. 1996). See Appendix B for more details.
In the following we use the expression 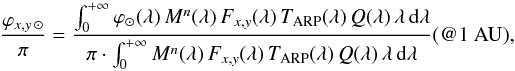 (10)or
(10)or 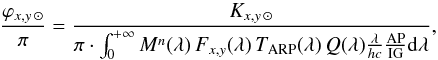 to indicate the mean spectral irradiance of the Sun at a distance of 1 AU in the wavelength range defined by the passband (x,y). Since the star observed by OSIRIS cannot be directly the Sun, but is a solar analog, the counts on the CCD refer to this second star. We can thus infer the “solar” counts from the analog counts (Kx,y SA) by using
to indicate the mean spectral irradiance of the Sun at a distance of 1 AU in the wavelength range defined by the passband (x,y). Since the star observed by OSIRIS cannot be directly the Sun, but is a solar analog, the counts on the CCD refer to this second star. We can thus infer the “solar” counts from the analog counts (Kx,y SA) by using 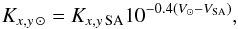 so that the reflectance factor is
so that the reflectance factor is 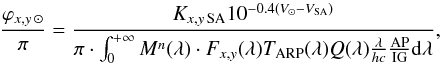 (11)where the use of the V magnitude, at each wavelength range, for the computation of the factor 10− 0.4(V⊙ − VSA) is justified since we assume the same spectral shape for the Sun and the solar analog. Some authors refer to the value of the solar flux as already divided by π. To avoid confusion, we always explicitly write ϕx,y ⊙/π as the solar intensity at 1 AU.
(11)where the use of the V magnitude, at each wavelength range, for the computation of the factor 10− 0.4(V⊙ − VSA) is justified since we assume the same spectral shape for the Sun and the solar analog. Some authors refer to the value of the solar flux as already divided by π. To avoid confusion, we always explicitly write ϕx,y ⊙/π as the solar intensity at 1 AU.
We can compute the reflectance directly from raw images (bias and flat-field corrected) by defining a composed abscal reflectance factor, multiplying the abscal factor defined in Eq. (3)and the new reflectance factor as expressed in Eq. (10).
Hence, the abscal reflectance factor defined is the value needed to convert the count rate into the reflectance of a body located at 1 AU from the Sun: 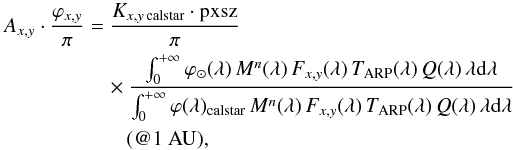 (12)where the “calstar” source (calibration star, usually Vega) used for the absolute flux calibration is generally different from the “SA” source (solar analog, usually 16 Cyg A+B, or 16 Cyg B) used to compute the solar value in Eq. (11). In Table 4 we report the abscal reflectance factor values computed by means of Eq. (12).
(12)where the “calstar” source (calibration star, usually Vega) used for the absolute flux calibration is generally different from the “SA” source (solar analog, usually 16 Cyg A+B, or 16 Cyg B) used to compute the solar value in Eq. (11). In Table 4 we report the abscal reflectance factor values computed by means of Eq. (12).
To derive the value needed for a body at a heliocentric distance r, we simply have to divide this factor by r2 if r is expressed in AU.
4.1. Counts from the solar analog
In the visible range the S/N of 16 Cyg B for the WAC is better than 100 with 180 s exposure time even with narrowband filters. For the NAC, the S/N is better than 200 with an exposure of a few seconds from about 480 nm to 1000 nm. In this spectral range we can also use this solar analog as a flux calibration star. Equation (12)can thus be further simplified by using “SA” as “calstar”, giving 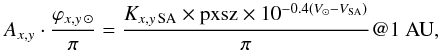 (13)since we used ϕ⊙ = ϕSA10− 0.4(V⊙ − VSA).
(13)since we used ϕ⊙ = ϕSA10− 0.4(V⊙ − VSA).
This leads to smaller error bars because we simplified every instrumental passband; the passbands are the parameters carrying the largest uncertainties. Moreover, through this method we can exclude some problems that are due to the instrumental variation with time (age) and with some uncertainties in the optics efficiencies because they all affect the target and stellar images in the same way.
However, we have to remember that there may be some differences between the Sun and the solar analog, especially in the UV, where the calibration with both 16 Cyg A+B may lead to further approximations, and that this solar analog is quite faint in this wavelength range so that we have to work with a low S/N in the UV filters.
UV counts of 16 Cyg A+B have large error bars because the spectrum is very weak in these wavelengths. In this case, the only way to find a reflectance value is to return to Eq. (12), computing the count rate from a star like Vega (which is much brighter than the Sun, especially in the UV). The division by the weighted Vega spectrum and the multiplication by the weighted Sun spectrum corrects the difference caused by the two different spectral types.
The two methods are expected to give the same values. If the absolute calibration is reliable and if the abscal factors are the same regardless of the calibration star used, we can choose one of the two formulations to compute the best reflectance factor just according to the smallest error bars associated with the result.
Vega is a single star and has a much better S/N than 16 Cyg A or B in each filter. After checking that the calibration is consistent when computed using different calibrators, we found that the best star to use is Vega, both for the abscal factor computation and for the solar values computation.
This formulation was verified to be valid. Good matches, within error bars, between OSIRIS spectrophotometry and literature reflectance spectra can be found for Phobos (Pajola et al. 2012, 2013) and Lutetia (Magrin et al. 2012).
4.2. Twin combinations
When we have to calibrate NAC F84 images from NAC F24 baseline acquisition, we have to substitute Eq. (4)into Eq. (12), finding 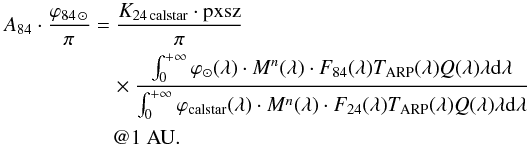 This method was applied to complete the absolute reflectance calibration presented in Table 4 for filters without direct observation of the calibration stars.
This method was applied to complete the absolute reflectance calibration presented in Table 4 for filters without direct observation of the calibration stars.
5. Conclusions
We detected a good stability within ±1.5% of the instrumental performances, without evidence of aging effects on the optics from 2007 to 2010. We found a good match between observed and expected data as deduced from on-ground laboratory measured optics and CCD efficiencies in the visible range. In the UV and IR wavelength range, however, we noted lower instrumental efficiencies than expected.
Properties of the Sun, 16 Cyg A, and 16 Cyg B according to Takeda (2005) and Takeda et al. (2005).
A reliable formulation for the flux calibration was proposed to be able to monitor this behavior from just after the exit from hibernation of the cameras and during the whole journey toward and around the comet, to study the possible dust contamination of the optics that would imply a wavelength-dependent variation of optical efficiencies. We also presented the formulation for the reflectance calibration. This formulation was verified to be valid, since there are good matches between OSIRIS spectrophotometry and literature reflectance spectra for Phobos (Pajola et al. 2012, 2013) and Lutetia (Magrin et al. 2012).
While the calibration compensates for instrumental efficiency variations in the visible and IR range, a deeper investigation of UV filters must be implemented. For this purpose, we finally suggested a list of other calibration sources. This will ensure a good calibration across the whole wavelength range during the entire last part of the mission.
Acknowledgments
OSIRIS was built by a consortium led by the Max-Planck-Institut für Sonnensystemforschung, Katlenburg-Lindau, Germany, in collaboration with CISAS, University of Padova, Italy, the Laboratoire d’Astrophysique de Marseille, France, the Instituto de Astrofisica de Andalucia, CSIC, Granada, Spain, the Research and Scientific Support Department of the European Space Agency, Noordwijk, The Netherlands, the Instituto Nacional de Tecnica Aeroespacial, Madrid, Spain, the Universidad Politechnica de Madrid, Spain, the Department of Astronomy and Space Physics of Uppsala University, Sweden, and the Institut für Datentechnik und Kommunikationsnetze der Technischen Universität Braunschweig, Germany. The support of the national funding agencies of Germany (DLR), France (CNES), Italy (ASI), Spain (MEC), Sweden (SNSB), and the ESA Technical Directorate is gratefully acknowledged. This activity has been realized under the WAC/Rosetta Agenzia Spaziale Italiana (ASI) contract to the Istituto Nazionale di Astrofisica (INAF) I/024/12/0. We also thank the anonymous referee of the manuscript for providing constructive comments that helped to improve this paper.
References
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1995, A&A, 297, 197 [NASA ADS] [Google Scholar]
- Bohlin, R. C., & Gilliland, R. L. 2004, AJ, 127, 3508 [NASA ADS] [CrossRef] [Google Scholar]
- Burlov-Vasiljev, K. A., Gurtovenko, E. A., & Matvejev, Y. B. 1995, Sol. Phys., 157, 51 [Google Scholar]
- Burlov-Vasiljev, K. A., Matvejev, Y. B., & Vasiljeva, I. E. 1998, Sol. Phys., 177, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Colina, L., Bohlin, R. C., & Castelli, F. 1996, AJ, 112, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Dohlen, K., Jorda, L., Lamy, P., Toth, I., & Origne, A. 2010, SPIE Conf. Ser., 7731 [Google Scholar]
- Gunn, J. E., & Stryker, L. L. 1983, ApJS, 52, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, D. S., & Latham, D. W. 1975, ApJ, 197, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, H. U., Barbieri, C., Lamy, P., et al. 2007, Space Sci. Rev., 128, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, J. H. 1760, Photometria, sive, De mensura et gradibus luminis, colorum et umbrae (Augustae Vindelicorum: V.E. Klett) [Google Scholar]
- Magrin, S., La Forgia, F., Pajola, M., et al. 2012, Planet. Space Sci., 66, 43 [Google Scholar]
- Pajola, M., Lazzarin, M., Bertini, I., et al. 2012, MNRAS, 427, 3230 [NASA ADS] [CrossRef] [Google Scholar]
- Pajola, M., Lazzarin, M., Dal le Ore, C. M., et al. 2013, ApJ, 777, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, Y. 2005, PASJ, 57, 83 [NASA ADS] [Google Scholar]
- Takeda, Y., Ohkubo, M., Sato, B., Kambe, E., & Sadakane, K. 2005, PASJ, 57, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, N., Keller, H. U., Arijs, E., et al. 1998, Adv. Space Res., 21, 1505 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, G. I., Nandy, K., Jamar, C., et al. 1978, Catalogue of stellar ultraviolet fluxes A compilation of absolute stellar fluxes measured by the Sky Survey Telescope (S2/68) aboard the ESRO satellite TD-1 [Google Scholar]
Appendix A: Units
In the following we list and define the physical parameters and units we used.
-
The irradiance is the power incident on a surface. It is expressedin the International System as W m-2.
-
The spectral irradiance is the power incident on a surface per unit wavelength, here expressed as W m-2 nm-1.
-
The radiance is the power emitted by a source per unit solid angle and unit area perpendicular to the emitting direction, expressed as W m-2 sr-1.
-
The spectral radiance is the power per unit solid angle per unit area per unit wavelength, here expressed as W m-2 nm-1 sr-1.
The abscal factor presented in this paper is the factor needed to convert images from count rate into spectral radiance, so that the pixel-per-pixel signal associated with the target, observed in a particular passband, is directly comparable with a flux calibrated spectrum of the target in a wavelength interval around the central wavelength of the band.
Appendix B: Description of the double star 16 Cyg A+B
The two stars 16 Cyg A and B are slightly different from the Sun. In particular, 16 Cyg A is larger than 16 Cyg B, and both are larger than the Sun. From Takeda (2005) and Takeda et al. (2005) we can find the log L of both 16 Cyg A and B, in terms of L⊙, transformed from the absolute visual magnitude MV by means of the bolometric correction (B.C.) obtained by interpolating the results reported in Alonso et al. (1995). We summarize these results in Table B.1, where Teff is computed for all stars from a spectroscopic method using the equivalent width values of FeI and FeII lines. Both 16 Cyg A and B are very close to the Sun.
If placed at the same distance as the Sun, the flux of 16 Cyg B is about 1.26 times the solar flux, and the flux of the pair 16 Cyg A+B is about three times the solar flux.
In summary: 16 Cyg A and B are slightly different from the Sun, but they seem to be similar enough to the Sun to allow us to assume the same spectral shape for the three stars, at least to the first order. Then, the simplest way to compute the scaling factor to convert the flux of 16 Cyg A+B into the solar flux is to consider V16 CygA = 5.99, V16 CygB = 6.25, and V⊙ = −26.74 at 1 AU. The magnitude V of the pair is then 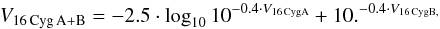 and the difference between the magnitude V of the 16 Cyg pair and the Sun leads to the relation
and the difference between the magnitude V of the 16 Cyg pair and the Sun leads to the relation 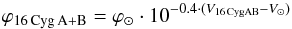 because we assume this factor to be a constant along the spectrum, since we assume the same spectral shape for the three stars.
because we assume this factor to be a constant along the spectrum, since we assume the same spectral shape for the three stars.
To estimate the count rate of the Sun from the count rate of 16 Cyg A+B, the relation is 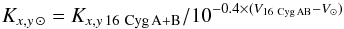 at 1 AU, as we wrote in previous paragraphs.
at 1 AU, as we wrote in previous paragraphs.
All Tables
Basic parameters of the NAC and WAC system and CCD specification (Keller et al. 2007).
Properties of the Sun, 16 Cyg A, and 16 Cyg B according to Takeda (2005) and Takeda et al. (2005).
All Figures
 |
Fig. 1 Efficiency curves of NAC and WAC optics: transmission curves of clear and band-pass filters, antiradiation plates (ARP), and reflectivity of mirrors. |
| In the text | |
 |
Fig. 2 PSF FWHM as number of pixels (geometric average of x and y direction values) in OSIRIS filters deduced from Vega observations. The largest size of four NAC filters is acquired by combining a near focus plate that can optimize the performances of the NAC camera for a target that is at a distance smaller than 4 km. |
| In the text | |
 |
Fig. 3 Shape of the Moffat fit of the PSF of OSIRIS camera filters in the following combinations: a) NAC-F16 (FFP-UV_Near-UV); b) NAC-F82 (Neutral_Orange); c) WAC-F12 (Red); and d) WAC-F18 (Vis610). |
| In the text | |
 |
Fig. 4 Typical curve of the aperture flux growth. This curve was specifically obtained from Vega observations with the NAC F16 filter. |
| In the text | |
 |
Fig. 5 Linearity measurements obtained by the Vega observations in terms of DN or DN/s vs exposure time. For each filter, the upper panels show counts vs. exposure time in the particular filter, the lower panels show the count rate vs. the exposure time. The investigation was made with the following filters: a) NAC-F16 (FFP-UV_Near-UV); b) NAC-F82 (Neutral_Orange); c) WAC-F12 (Red); and d) WAC-F18 (Vis610). |
| In the text | |
 |
Fig. 6 Ratio between observed and expected counts from the CCD with a particular filter setting. Vertical error bars refer to photon noise and the propagation of instrumental uncertainties. Horizontal bars refer to the FWHM of each passband. Red data refer to counts computed from 16 Cyg A+B images and solar spectrum (Burlov-Vasiljev et al. 1995, 1998) scaled to 16 Cyg A+B magnitude; black data refer to Vega images and Vega spectrum (Bohlin & Gilliland 2004). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


