| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 18 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201423513 | |
| Published online | 27 January 2015 | |
Total mass of six quiescent prominences estimated from their multi-spectral observations
1
Astronomical Institute, Academy of Sciences of the Czech
Republic,
25165
Ondřejov,
Czech Republic
e-mail: schwartz@asu.cas.cz; pheinzel@asu.cas.cz; pkotrc@asu.cas.cz; ffarnik@asu.cas.cz; kupry@asu.cas.cz
2
Astronomical Institute of Slovak Academy of
Sciences, 05960
Tatranská Lomnica, Slovak
Republic
e-mail:
pschwartz@astro.sk
3
Sternberg Astronomical Institute, 119899
Moscow,
Russia
4
Harvard-Smithsonian Center for Astrophysics, 60 Garden
Street, MA
02138
Cambridge,
USA
e-mail: edeluca@cfa.harvard.edu; lgolub@cfa.harvard.edu
Received: 27 January 2014
Accepted: 5 November 2014
Context. Total masses of six solar prominences were estimated using prominence multi-spectral observations (in EUV, X-rays, Hα, and Ca ii H). The observations were made during the observing campaign from April through June 2011.
Aims. The aim of the work was to apply a complex method for the prominence mass estimations that can be used later for other prominences observed during the observing campaign.
Methods. Our method is based on the fact that intensity of the EUV solar corona at wavelengths below 912 Å is reduced by the absorption in resonance continua of hydrogen and helium (photoionisation) and at the same time also by a deficit of the coronal emissivity in volume occupied by the cool prominence plasma. Both mechanisms contribute to intensity decrease simultaneously. The observations in X-rays allow us to separate these mechanisms from each other. Coronal emission behind a prominence is not estimated by any temporal or spatial interpolation, but by using a new method based on comparing the ratio of the optical thickness at 193 Å and 211 Å determined from the observations with the theoretical ratio.
Results. Values of the total mass estimated for six prominences are between 2.9 × 1011 and 1.7 × 1012 kg. The column density of hydrogen is of the order of 1018−1019 cm-2. Our results agree with results of other authors.
Conclusions. The method is now ready to be used for all 30 prominences observed during the campaign. Then in the near future it will be possible to obtain a statistics of the total mass of quiescent solar prominences.
Key words: Sun: filaments, prominences / Sun: corona / Sun: UV radiation / Sun: X-rays, gamma rays / techniques: spectroscopic
© ESO, 2015
1. Introduction
Quiescent prominences are objects formed by relatively cool plasma in the hot corona. Their cool material occurs mostly in the dipped magnetic field lines. In quiescent prominences, which can persist from several hours to several days, magnetic dips form quasi-vertical structures called threads. Quiescent prominences are often observed as part of magnetic structures composed of three coronal patterns: the prominence itself, surrounded by a low-density cavity and a dense helmet streamer overlying the cavity (Engvold 1989). The disruption of the helmet streamer often signifies the beginning of a coronal mass ejection (CME) that can reflect the three-part structure of the helmet streamer (when observed in the white light): the bright leading shell surrounding a dark cavity in which bright prominence material occurs (Crifo et al. 1983; Hundhausen 1999). As the masses of CMEs are most often inferred from the visible-light observations, the masses given in literature are usually only the masses of the leading shell. However, Burkepile et al. (2004) also saw highly structured material most probably originating from a prominence in 63% of CMEs associated with eruptive prominences at the limb observed in visible light using the broadband filter (λλ 5000−5350 Å). Although such observations are called as white light in literature, it would be better to consider them as observations in visible light, because naturally integral intensities in the visible spectral range are observed including both continuum and absorption lines, while white light is just a continuum caused by Thomson scattering on free electrons without the lines. Thus, the presence of absorption spectral lines in visible light complicates very much the estimation of prominence mass, but even if the influence of absorption lines was eliminated, continuum alone only allows us to estimate the mass of ionised material, thus mass of the prominence would be underestimated. Low (1996) stated that the contribution of an erupting prominence to the total mass of CME is usually one order of magnitude less than that of the shell, but in some cases these contributions can be comparable. Low et al. (2003) proposed theoretically an importance of the prominence mass for the deposit of magnetic energy for driving a CME. Thus, developing methods for the estimation of the total mass of prominences can help to explain the connection between prominences and CMEs and provide an important quantity for more accurate estimation of total mass ejected by a CME.
In the last two decades UV, EUV, and X-ray observations from space made it possible to estimate the total mass of prominences reliably without needing to solve problems that occur when using visible light as was described in the previous paragraph. One possibility would be to estimate column mass of hydrogen and/or helium plasma in prominences using spectral observations of UV and visible lines of hydrogen and helium (Balmer and Lyman lines) and sophisticated models in which plasma is assumed not being in the state of local thermodynamic equilibrium (NLTE models; see e.g. Labrosse et al.2010, and references therein). The problem can be a rather high complexity of such NLTE models which depend on various free parameters. Another possibility is to infer column mass and subsequently the total mass from the amount of radiation absorbed by the photoionisation in the prominence plasma at resonance continua of hydrogen and helium. This estimation of the mean column mass of prominences observed near the limb was first made by Kucera et al. (1998) using extreme-ultraviolet (EUV) observations from the Coronal Diagnostic Spectrometer (CDS; Harrison et al. 1995) on board the Solar and Heliospheric Observatory (SoHO) satellite. The advantage of the observations used by Kucera et al. (1998) was that CDS as a spectrograph observed only in spectral lines of interest, but spectrographs are able to obtain spectra from only one slit position during one exposure. Larger fields of view can be scanned by the spectrograph slit, as the CDS does, for example, but in such a case, intensities in different slit positions the scan is composed of were obtained at different times. In contrast, in filtergrams, intensities in all positions of the field of view are obtained at the same time, but the filter has transmission of certain width which can be wider than the spectral line of interest. The first estimation of the prominence mass using filtergrams was made by Golub et al. (1999) using Transition Region and Coronal Explorer (TRACE1) data. Similar studies were made by Gilbert et al. (2005, 2006) using observations of EUV Imaging Telescope (EIT; Delaboudinière et al. 1995) on board SoHO in the 195 Å channel. In those two works it was shown that it is necessary to estimate an amount of coronal emission behind and in front of the prominence (hereafter referred to as background and foreground radiation, respectively) to determine correctly the amount of absorbed radiation. The foreground radiation can be measured at the darkest place at a prominence, where it is assumed that all radiation from behind the prominence was absorbed. Then, the background radiation can be derived from the total coronal emission at the prominence location. Two ways to estimate the total emission were proposed and used. The spatial interpolative approach uses interpolation from intensities measured in the corona near a prominence. The temporal interpolative approach is suitable only for erupting prominences and it uses measurements of intensity in place of prominence after its eruption. In the work of Williams et al. (2013) these two approaches are also used to estimate the column mass of material returning to limb after prominence eruption. They used observations from the Atmospheric Imaging Assembly (AIA) instrument (Lemen et al. 2012) on board the Solar Dynamics Observatory (SDO) in several EUV coronal channels of wavelengths below 228 Å (head of the resonance continuum of He ii).
In this work we use multi-spectral observations from space and ground, i.e. combination of the XUV imaging and optical spectroscopy, to estimate values of the total mass of prominences. Hydrogen column densities and subsequently the total mass of a prominence is obtained from the amount of EUV coronal radiation absorbed by the prominence plasma in resonance continua of hydrogen and helium. We assume that except of the absorption, a coronal emissivity deficit (also called coronal emissivity blocking) can contribute remarkably to the coronal intensity depression at a prominence position (Anzer & Heinzel 2005). The coronal emissivity deficit is caused by the presence of cool and/or low-density material in volume occupied by the prominence or its cavity, which causes a lowering or even a lack of coronal emissivity in such a volume. Then the intensity, which is in fact the emissivity integrated along the whole line of sight, measured at the prominence and the cavity is lower than the intensity measured at the surrounding corona. To eliminate an effect of the coronal emissivity deficit, both X-ray observations (not absorbed by a prominence; Anzer et al.2007) and a method proposed by Heinzel et al. (2008), are used. Moreover, we use two novelties. First, we fix the prominence area according to observations in the AIA 304 Å channel (the He ii Lyman α line) where the whole prominence is visible, not only its front part on the limb as seen in EUV coronal lines. In addition, the fraction of coronal radiation from behind the prominence (background radiation) is estimated by comparing the ratio of the optical thickness of the prominence at two wavelengths estimated from observations with the theoretical value of this ratio.
The paper is organised as follows. In Sect. 2 the multi-spectral observations of prominences and co-alignment of data sets from different instruments are described, and in Sect. 3 the method of mass determination is described. In Sect. 4 our results are shown, Sect. 5 contains the discussion, and the conclusions are in Sect. 6.
2. Observations and co-alignment of different data sets
Morphological properties of the six prominences and dates and times of their observations.
More than 30 quiescent prominences were observed during a campaign held from April through June 2011. Prominences were selected according to Hα observations of two ground-based multi-camera spectrographs at the Ondřejov observatory: Solar Laboratory Spectrograph (SLS2) and Horizontal Sonnen Forschung Anlage No. 2 (HSFA2; Kotrč 2009). Observations from these two instruments are hereafter referred to as GBO. X-ray full-disc images obtained by the X-ray telescope (XRT) instrument (Golub et al. 2007) on board the Hinode satellite (Kosugi et al. 2007) on the same day as the SLS observations were used as well. As the AIA instrument on board the SDO satellite records images in all channels with very high cadence (approximately every 12 s), it is almost always possible to find quasi-simultaneous EUV full-disc observations. Thus it was not necessary to include the AIA instrument into the observing campaign. In this work we selected six prominence observations acquired during the campaign to estimate their total mass and ionisation degrees of hydrogen and helium. Dates and times of the observations, position angles, maximum heights above the surface, and areas of the observed prominences fixed according to AIA 304 Å images are listed in Table 1. Position angles were measured clockwise from the north heliographic pole. As an example, the prominence observations from 18 May 2011 (No. 6) are shown in Fig. 1. In the figure, Hα slit-jaw image of the HSFA2 spectrograph is not shown as it is similar to that of SLS shown in panel f. In panels a and f the whole big prominence is seen in the He ii 304 Å and Hα lines in emission. In contrast, in the coronal EUV lines of wavelengths below 912 Å (head of the hydrogen Lyman continuum) shown in panels b−d, only a small dark prominence structure due to both absorption and coronal emissivity deficit is visible, because only the front parts of the prominence are seen; the farther parts of the prominence are overradiated by the corona in front of them. The dark prominence structure is surrounded by a low-density cavity where the decrease of the coronal brightness is caused only by the coronal emissivity deficit. In X-ray observations shown in the panel e, mainly the cavity is shown as the prominence plasma does not absorb in X-rays (Anzer et al. 2007). In some cases when the prominence cool plasma is geometrically very thick along the line of sight, a prominence itself can also produce a visible dark structure with observable contrast in X-rays due to the coronal emissivity deficit, but the contrast of such a dark structure is much smaller than that caused by the absorption in EUV.
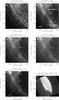 |
Fig. 1 Panels a)–e): observations of the prominence of 18 May 2011 (No. 6): cut-offs from the full-disc observations from the AIA instrument in the 304 Å, 193 Å, 211 Å, and 335 Å channels, and of the XRT telescope obtained using the Al-mesh filter. Rectangles drawn by a solid white line mark areas of interest. Positions of the prominence and surrounding cavity are marked in panels b) and e). Panel f): SLS spectrograph Hα slit-jaw image co-aligned with AIA observations. One of the eight slit positions is plotted by a black inclined dashed line. |
More details about the observations from individual instruments are written in the following subsections.
2.1. Ground-based observations
The SLS multi-camera spectrograph was designed as an instrument with a variable optical design, and so it can be used for many different purposes. Its optical schema used especially for the campaign observations is shown online3. Observations were carried out using four cameras: Hα slit-jaw image using wide-band filter and spectra of the Hα, infrared Ca ii 8542 Å, and D3 (He i 5875.6 Å) lines. Prominences were scanned by several slit positions during each block of observations and several blocks of observations for each prominence were made. Then, the best observations of each prominence were used in our analysis. Observed Hα spectra were reduced by the dark-frame subtraction and flat-fielding using the method of Wöhl et al. (2002). Then the spectra were absolutely calibrated using the comparison between the observed profile from the area at the solar disc close to the prominence with the reference Hα profile of David (1961) for μ (cosine of angle between the line of sight and normal to the solar surface) of the area. Finally, scattered light was subtracted assuming that the corona and prominence itself do not emit in continuum close to Hα and thus any non-zero intensity measured at the continuum must be scattered light. A special neutral filter was put in front of the slit in order to record prominences with long enough exposure time to achieve suitable contrast without overexposing the solar disc. The filter (hereafter called the prominence filter) consists of two parts; one with transmission of 12.7% that was put at the solar disc and the other with full transmission put at the prominence. Thus, intensities observed at the disc profile must be divided by the prominence filter transmission to obtain real intensities. In a case when it was not possible to observe disc and prominence at the same time (prominences close to position angles 90 and 270 degrees), the Hα spectrum at the centre of the solar disc was taken as the individual observation with the same exposure time as used for the prominence. The individual disc observation was made just after the prominence observations and the disc part of the prominence filter was put on the whole spectral image. Observed Hα profiles were used to estimate temperatures of prominence plasma from their widths, as it is described in detail later. Because the width of the Hα profile is determined by both temperature and microturbulence, spectral observations in a line of element much heavier than hydrogen that is much less sensitive to temperature was needed to estimate velocity of the microturbulence. The lines of Ca ii can be used for this reason. Because SLS observed only the infrared Ca ii line whose intensity is very low (measured signal very low even by exposure times twice as long as for Hα) and the optical thickness in this line is much lower than one (prominence is almost transparent). The optically thicker and more intense Ca ii H line, which was observed only by the HSFA2 spectrograph, is much more suitable.
HSFA2 is the second of the two multi-camera spectrographs with horizontal telescopes at Ondřejov Observatory. HSFA2 was greatly modernised several years ago. Except for the Hα slit-jaw images obtained using the filter of half-width of 0.7 Å (Kotrč 2009), it can record simultaneously spectra of the following lines: Hα, Hβ, D3, ionised Calcium H line (Ca ii 3968 Å), and infrared Calcium line (Ca ii 8542 Å)4. Prominence spectra were observed without using any filters, contrary to the SLS observations. Thus, observations with exposure times long enough to obtain prominence spectra with acceptable contrast led to overexposing the disc. Observations of the disc were made individually but with much shorter exposure times. In such a case, absolute calibration is still possible but one has to rely on linear dependency of intensity of the signal registered by the detector on length of exposure. Because we already had well calibrated Hα profiles from the SLS spectrograph it was not necessary to calibrate Hα from HSFA2. Only profiles of the Ca ii H line (not observed by SLS) were used to estimate the microturbulence velocities, for which absolutely calibrated data were not needed. Unfortunately, the HSFA2 observations of prominences 2, 3, and 5 are 1−4 days later than observations from SLS (see Table 1). The non-calibrated Hα spectra obtained by both spectrographs for those three observations were compared and no large changes in the average line width were observed. Thus, we can suppose that average temperatures and velocities of microturbulence (as only average values of the velocity are used for each prominence as is described in Sect. 3) did not change much.
2.2. X-ray observations from Hinode/XRT
The full-disc X-ray observations from XRT used in our analysis were obtained using the HOP 186 observing programme made every day between 10:00 and 12:00 UT when observations from the SLS spectrograph were also expected because of suitable atmospheric conditions at the Ondřejov observatory. The observations were made using an open aperture in the prefilter wheel (OPEN) and the Al-mesh filter from the second filter wheel located in the focal plane. Exposure time was 4.096 s and data were read out using full resolution of the detector with size of the pixel of 1 arcsec × 1 arcsec. Unfortunately, on 19 April 2011 (observation No. 1), the HOP 186 observations were left out because of preferred longterm observations of an active region. Therefore, the synoptic full-disc observations were taken instead. They were recorded with shorter exposure time of 1.024 s and binned 2 × 2. Nevertheless, the cavity around the prominence can also be seen well in an image of the binned X-ray observations.
Using the Al-mesh filter makes it possible to detect plasma of similar temperatures (log T around 6) as observed by AIA in channels 193, 211, and 335 Å. Only this filter has one of two maxima of the transmission function at temperatures ~106 K (Fig. 7 in Golub et al.2007). Unfortunately, the filter transmission also has the second and even higher maximum at log T ~ 6.9. Therefore, additional observations obtained with the filters Ti-poly or Be-thin were taken to detect plasma with temperature of log T ~ 6.9 and higher and areas in corona containing such hot plasma were left out from our analysis. For this purpose 2 × 2 binned images obtained with shorter exposures (2.05−2.9 s) were enough. Transmission function of the Ti-poly or Be-thin filters strongly increases with temperature of emitting plasma, reaches its maximum at log T ~ 6.9, and then slowly decreases. Plasma of temperatures below log T ~ 6.0 is not detected at all using the Be-thin filter.
2.3. EUV observations from AIA
Data from AIA, quasi-simultaneous with the HOP 186 XRT observations, were chosen. The AIA observations in the 304 Å channel – the He ii line – are suitable for fixing the prominence areas because prominences mainly emit above the limb in this line. The dark structures due to the absorption and coronal emissivity deficit at the prominences were seen in images of AIA in the 193 Å, 211 Å, and 335 Å channel which are dominated by the following EUV coronal lines: Fe xii 193.5 Å, Fe xiv 211.3 Å, and Fe xvi 335.4 Å (wavelengths according to the CHIANTI atomic database v.7; Dere et al.1997; Landi et al.2012). Observations in the 171 Å channel were not used because the Fe ix 171.1 Å line occurring in this channel can also be formed in the prominence-corona transition region (hereafter called PCTR) as was recently shown by Parenti et al. (2012).
As transmittances of the AIA channels are rather broad in wavelength, several other lines (except those mentioned above) are detected. Because many of them can be formed in PCTRs, it is necessary to evaluate their possible contributions to radiation detected by the instrument at the prominence. The Fe xxiv 192.03 Å line is also detected in the 193 Å channel, but its temperature of formation is as high as log T = 7.25. Areas in the corona with temperatures much higher than log T ~ 6 were already excluded from our analysis using XRT observations made with the Ti-poly or Be-thin filters, and so we can be sure that the Fe xxiv line formed at such high temperatures can occur only in those excluded areas. Moreover, the O v 192.8 Å, 192.904 Å, and Fe viii 194.661 Å lines formed mainly at temperatures log T of 5.4 and 5.6, respectively, can be detected in the 193 Å channel except for the hot coronal lines (log T ~ 6). However, their contributions to intensity detected at a prominence is negligible when compared with the intensity of the corona outside a prominence according to the calculations of Parenti et al. (2012, see their Table 1). In the 211 Å channel, several other coronal lines of Fe x, Fe xi, Fe xii, and Fe xiii are detected besides Fe xiv 211.3 Å. This channel is also contaminated by a radiation of the transition-region (hereafter referred to as TR) lines of ions O iv, O v, Ne v, N v, O vi, Fe viii, Cr viii, Fe ix, Cr ix, etc. (Parenti 2012, priv. comm.), which can also be formed in PCTR. Although their intensities are ten times lower than that of Fe xiv in the corona, their total contribution to radiation registered in the 211 Å channel at a prominence can be up to 15% of the intensity of the corona outside a prominence. In the 355 Å channel, coronal lines of Si x, Si xi, Fe xi Fe xii are also detected except for Fe xvi 335.41 Å as was calculated by CHIANTI (Dere et al. 1997; Landi et al. 2012), using spectral sensitivity of the channel in its main bandpass (approximately from 300 to 380 Å). The total contribution of the Mg v, Ne v, Mg vii, Mg viii, and Mg ix lines possibly formed in the PCTR should not exceed several percentage points of the coronal intensity (calculated using the CHIANTI ch_ss procedure with the built-in prominence DEM). Unfortunately, the 355 Å channel also has two narrow sensitivity peaks, one around 130 Å and the other at approximately 180 Å. The transition-region lines of ions O v, Ne vi, O vi, Ne vii, Fe viii, Fe ix of formation temperatures from log T of 5.5 up to 6, are detected in the two secondary sensitivity peaks. When assuming that temperatures in PCTR can encompass continuously from prominence values of several thousand Kelvins up to coronal values of ~106 K, these lines can be formed in the PCTR and their total contribution to intensity measured at a prominence can reach up to 60% of the intensity of the corona outside of a prominence.
The original dimensions of the AIA pixel in observed images were 0.6 arcsec × 0.6 arcsec. In order to eliminate pixel-to-pixel fluctuations, the spatial resolution was lowered by the 4 × 4 pixel binning.
The dates and times of the first and last AIA observation taken in our analysis for each prominence multi-spectral observations are listed in the seventh column of Table 1.
2.4. Mutual co-alignment of the multi-spectral data sets
The AIA observations from its different telescopes were co-aligned according to the solar disc centre using the Solar soft procedure aia_prep. Then the AIA and XRT images were resampled to the angular sizes as if they were obtained from Earth. That made it possible to co-align observations from the XRT and AIA instruments even when they are situated on different satellites with different distances from the Sun. The most suitable for the co-alignment was the AIA image in the 335 Å channel and X-ray XRT observations with the Al-mesh filter. The sizes and shapes of bright and dark areas on the disc were very similar in these images from the two instruments. Thus, the co-alignment was done by fitting their positions on the X-ray image with those on the 335 Å image. Slit-positions of GBO were determined by co-alignment of the Hα slit-jaw images with the AIA 304 Å images. We note that while images from both space instruments are correctly oriented with the solar north, the slit in GBO is oriented according to geographic north. Therefore, the slit-jaw images had to be rotated according to the position of the solar axis prior to the co-alignment. Even so, the co-alignment was sometimes difficult because the shapes and sizes of some prominences can be remarkably different in He ii 304 Å and Hα. The Hα prominence is often much smaller than that in the helium line. In such a case we were trying to find at least one structure which is similar in the both extended He ii and smaller Hα prominence.
3. Method
In the following sections, the individual steps of the method are described: calculation of the optical thickness at 193 Å (Sect. 3.1), estimation of the coronal asymmetry (3.2), ionisation degrees of hydrogen (3.3) and helium (3.4), and finally, the total mass calculation (3.5). Sections are not ordered according to sequential usage of the steps in the method, but according to the logical succession (first the formula for calculations of the optical thickness is explained, and then ways to estimate its input parameters). The order in which the steps are taken for calculations is as follows. First, the map of the ionisation degree of hydrogen is constructed from Hα spectral observations. Then, for different combinations of ionisation degrees of neutral and singly ionised helium, respectively (values of ionisation degree of hydrogen are already estimated from the Hα profiles), the total mass of a prominence is calculated from the map of the optical thickness τ193 of resonance continua of hydrogen and helium at 193 Å. A fraction of the EUV coronal emissivity from behind the prominence should be evaluated for the correct estimation of τ193 from the decrease of the EUV coronal intensity at a prominence. The fraction – the factor of coronal asymmetry – is estimated from comparison of the theoretical τ193/τ211 ratio (dependent on ionisation degrees of hydrogen and helium) with its value estimated from observations. The optical thickness τ211 of the resonance continua of hydrogen and helium at 211 Å is calculated from the decrease of intensity at 211 Å analogically to τ193 calculations. For the same combinations of the ionisation degrees of neutral and singly ionised helium as were used for the mass calculations from τ193, values of the total mass are also calculated from maps of the optical thickness τ335; values of τ335 are calculated from observations at 335 Å, the factor of coronal asymmetry is estimated by comparing of the theoretical ratio τ335/τ211 (dependent on ionisation degrees of hydrogen and helium) with that obtained from observations. Finally, values of the total mass calculated from τ193 and τ335 are compared. Ionisation degrees of neutral and singly ionised helium, for which difference between values of the mass calculated from τ193 and τ335 is the smallest, are taken as result. In addition, the mass calculated from map of τ193 for resulting ionisation degrees of helium is taken as the resulting mass.
 |
Fig. 2 Absorption and coronal emissivity deficit at a prominence and coronal emissivity deficit alone in the cavity cause decrease of the coronal intensity. Ip is the coronal intensity measured at a prominence, |
 |
Fig. 3 Upper-left panel: cut made tangentially to the limb through the prominence of 18 May 2011 (observation No. 6 according to Table 1). Upper-right panel: distributions of measured intensities along this cut in the He ii 304 Å line, coronal iron lines round 193 Å, and X-rays. In positions along the cut, where the AIA 304 Å intensity is increased, occurrence of prominence is assumed. The both 193 Å and X-ray intensities are decreased at the prominence and cavity positions. There is also a part of the prominence further beyond the plane of the limb that is overradiated by the corona but still visible in projection on the limb in 304 Å where the corona does not emit. Bottom panel: the distribution along the cut of intensity at 193 Å is shown together with X-rays while X-ray intensities were multiplied by such a factor that the X-ray and 193 Å distributions fit each other in the cavity and corona. At the prominence, the ratio between the intensities of these two distributions is proportional to the optical thickness. |
3.1. Calculations of maps of the optical thickness at 193 Å
We chose the AIA observations in 193 Å channel because contamination of the coronal emission detected in this channel by the TR lines radiated from PCTR is negligible. X-ray images of XRT made with the Al-mesh filter were used in order to eliminate the effect of the coronal emissivity deficit on the decrease of the EUV coronal intensities. As the calculation of the optical thickness along a cut made across a prominence tangentially to the limb has already been explained in Heinzel et al. (2008), we give here only a brief description of the method. As it can be seen in Fig. 2, the coronal intensities  , both in EUV and X-ray spectral regions, are lower than Ic measured in the corona due to reduced coronal emission in a low-density cavity. Assuming that the prominence plasma is composed mainly of hydrogen and helium and the X-ray coronal radiation is not absorbed in the prominence (Anzer et al. 2007), the X-ray intensity Ip(X - rays) measured by XRT at the prominence (denoted as Icp in Heinzel et al. 2008) is just simple addition of the intensities If and Ib of radiation emitted from corona in front of and behind a prominence, respectively:
, both in EUV and X-ray spectral regions, are lower than Ic measured in the corona due to reduced coronal emission in a low-density cavity. Assuming that the prominence plasma is composed mainly of hydrogen and helium and the X-ray coronal radiation is not absorbed in the prominence (Anzer et al. 2007), the X-ray intensity Ip(X - rays) measured by XRT at the prominence (denoted as Icp in Heinzel et al. 2008) is just simple addition of the intensities If and Ib of radiation emitted from corona in front of and behind a prominence, respectively: 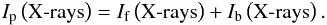 (1)Contrary to X-rays, the EUV radiation at wavelengths below 912 Å (head of the Lyman continuum of hydrogen) is absorbed by the prominence plasma in resonance continua of hydrogen (for λ< 912 Å) and neutral (for λ< 504 Å) and singly ionised (for λ< 228 Å) helium and thus for the intensity Ip(λ) we get
(1)Contrary to X-rays, the EUV radiation at wavelengths below 912 Å (head of the Lyman continuum of hydrogen) is absorbed by the prominence plasma in resonance continua of hydrogen (for λ< 912 Å) and neutral (for λ< 504 Å) and singly ionised (for λ< 228 Å) helium and thus for the intensity Ip(λ) we get 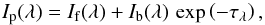 (2)where τλ is the optical thickness of the prominence plasma at the wavelength λ. It is important to note that in the intensities If and Ib, radiation both from the corona and cavity in front of and behind the prominence, respectively, is included. The If and Ib intensities can also be defined by using a branching factor α (hereafter called as the α factor or factor of coronal asymmetry) which defines fractions of the coronal emissivity in front of and behind a prominence:
(2)where τλ is the optical thickness of the prominence plasma at the wavelength λ. It is important to note that in the intensities If and Ib, radiation both from the corona and cavity in front of and behind the prominence, respectively, is included. The If and Ib intensities can also be defined by using a branching factor α (hereafter called as the α factor or factor of coronal asymmetry) which defines fractions of the coronal emissivity in front of and behind a prominence: 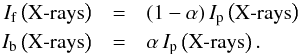 (3)The α factor is equal to 0.5 for the symmetrically distributed coronal emissivity. As the data of both AIA and XRT instruments are not absolutely calibrated, a direct evaluation of Eqs. (1) and (2) is not possible. Therefore ratios of the intensities Ip to Ic and optionally also to
(3)The α factor is equal to 0.5 for the symmetrically distributed coronal emissivity. As the data of both AIA and XRT instruments are not absolutely calibrated, a direct evaluation of Eqs. (1) and (2) is not possible. Therefore ratios of the intensities Ip to Ic and optionally also to  are defined. Here the ratios to the intensity Ic measured in the quiet corona are shown:
are defined. Here the ratios to the intensity Ic measured in the quiet corona are shown: 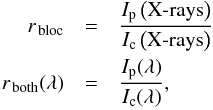 (4)where the r bloc and r both(λ) ratios represent the decrease of intensities at the prominence of X-ray radiation due to the coronal emissivity deficit alone and of EUV radiation at wavelength λ (below 912 Å) due to both absorption and coronal emissivity deficit, respectively. Applying definitions (4) and (3) to Eqs. (1) and (2) leads to:
(4)where the r bloc and r both(λ) ratios represent the decrease of intensities at the prominence of X-ray radiation due to the coronal emissivity deficit alone and of EUV radiation at wavelength λ (below 912 Å) due to both absorption and coronal emissivity deficit, respectively. Applying definitions (4) and (3) to Eqs. (1) and (2) leads to: ![\begin{equation} r_{\mathrm{\,both}}(\lambda)=\left\{1\rule{0pt}{0.8em}-\alpha\left[1-\exp\left(-\tau_{\lambda}\right)\right]\right\}\,r_{\mathrm{\,bloc}}. \label{eq:bastaueq} \end{equation}](/articles/aa/full_html/2015/02/aa23513-14/aa23513-14-eq57.png) (5)When a cut across a prominence is made tangentially to the limb, as is shown in the upper-left panel of Fig. 3, a wide dip in distributions of the AIA 193 Å and X-ray intensities along the cut occurs at the cavity surrounding the prominence as can be seen in the plot in the upper-right panel of the figure. The presence of this wide dip with strong decreases of intensities at its boundaries is due to the coronal emissivity deficit in the low-density cavity. In this dip several much deeper sections at 193 Å also occur, while they are not present in X-rays; they are due to absorption by the prominence plasma. Positions of these very deep regions correspond to increased intensity at 304 Å and are due to prominence emission in the He ii line. Except for this part of the prominence occurring at the limb or in front of it, there is also other part which is not seen at 193 Å because this part is further beyond the plane of the limb and is overradiated by the corona in front of it. But this part is visible at 304 Å in projections on the plane of the limb; we note the enhanced 304 Å intensity between positions along the cut between approximately 170 and 220 arcsec in the plot. It is not possible to estimate the optical thickness in this part, but it should be included to the mass calculation. The optical thickness in this part can be interpolated or if this overradiated part of the prominence is much larger than the area where the optical thickness was successfully estimated, an average value of the optical thickness is used for the whole prominence area. We explain this in more detail in Sect. 3.5 devoted to the mass calculation.
(5)When a cut across a prominence is made tangentially to the limb, as is shown in the upper-left panel of Fig. 3, a wide dip in distributions of the AIA 193 Å and X-ray intensities along the cut occurs at the cavity surrounding the prominence as can be seen in the plot in the upper-right panel of the figure. The presence of this wide dip with strong decreases of intensities at its boundaries is due to the coronal emissivity deficit in the low-density cavity. In this dip several much deeper sections at 193 Å also occur, while they are not present in X-rays; they are due to absorption by the prominence plasma. Positions of these very deep regions correspond to increased intensity at 304 Å and are due to prominence emission in the He ii line. Except for this part of the prominence occurring at the limb or in front of it, there is also other part which is not seen at 193 Å because this part is further beyond the plane of the limb and is overradiated by the corona in front of it. But this part is visible at 304 Å in projections on the plane of the limb; we note the enhanced 304 Å intensity between positions along the cut between approximately 170 and 220 arcsec in the plot. It is not possible to estimate the optical thickness in this part, but it should be included to the mass calculation. The optical thickness in this part can be interpolated or if this overradiated part of the prominence is much larger than the area where the optical thickness was successfully estimated, an average value of the optical thickness is used for the whole prominence area. We explain this in more detail in Sect. 3.5 devoted to the mass calculation.
Now it is possible to calculate the optical thickness τ193 along the prominence section (between approximately 50 and 170 arcsec) using Eq. (5) and ratios calculated using Eq. (4), although it is questionable at which position to take values of the intensities Ic. Assuming that both EUV at 193 Å and X-rays were emitted at the temperatures log T around 6 (hotter areas in X-rays are excluded using Ti-poly or Be-thin observations; see Sect. 2.2), distributions of the X-ray and EUV intensities outside a prominence should be similar except for some multiplicative factor. It is clearly noticeable in the upper-right panel of Fig. 3. The multiplicative factor is estimated by χ2 fitting of distributions along the cut of X-ray to EUV intensities in the cavity and the surrounding quiet corona. Distributions of EUV intensities at 193 Å and X-rays after fitting are shown in the bottom panel of Fig. 3. X-ray intensities at prominence after fitting are denoted as Ip, modif(X - rays). It is clear that after fitting, an effect of the emissivity deficit was cancelled in both cavity and prominence. The dip at the prominence position in the EUV intensity distribution is deeper than that in the X-rays after the fitting and is due to absorption only. After cancellation of the coronal emissivity deficit one gets from Eq. (5) ![\begin{equation} r^{\prime}_{\lambda}=1-\alpha\,\left[1-\exp\left(-\tau_{\lambda}\right)\right], \label{eq:finalbastaueq} \end{equation}](/articles/aa/full_html/2015/02/aa23513-14/aa23513-14-eq60.png) (6)where the ratio
(6)where the ratio 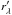 is defined as
is defined as 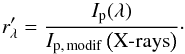 (7)Finally, the optical thickness at 193 Å can be calculated as
(7)Finally, the optical thickness at 193 Å can be calculated as 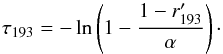 (8)As the α factor of the coronal asymmetry cannot be measured directly (there is a possibility of indirect measurement, see Sect. 5) we developed a method of its estimation and describe it in the next subsection.
(8)As the α factor of the coronal asymmetry cannot be measured directly (there is a possibility of indirect measurement, see Sect. 5) we developed a method of its estimation and describe it in the next subsection.
To eliminate noise, cuts of width of three XRT pixels were made and for each position along the cut an intensity averaged from the three pixels was taken. The map of τ193 calculated using Eq. (8) is then constructed covering the whole prominence area with such cuts.
3.2. Estimation of the α factor of coronal asymmetry
Analysing Eq. (8) mathematically it was found that calculated values of τ193 and the subsequently derived total mass strongly depend on correctly estimated α. Since it is not possible to measure α directly it can be derived indirectly by comparing the ratios of optical thickness estimated from observations at two wavelengths with such ratios calculated theoretically.
The optical thickness τλ of EUV radiation at wavelengths below 912 Å can be calculated using the following formula (Anzer & Heinzel 2005) ![\begin{eqnarray} \tau_{\lambda} & = & N(\mathrm{H})\left\{\rule{0pt}{2ex}\left(1-i\right)\,\sigma_{\mathrm{H}}\/(\lambda) +r_{\mathrm{He}}\left[\left(1-j_1-j_2\right)\,\sigma_{\mathrm{\ion{He}{i}}}\/(\lambda) \right.\right. \nonumber \\ & & \left.\left.+j_1\,\sigma_{\mathrm{\ion{He}{ii}}}\/(\lambda)\right]\rule{0pt}{2ex}\right\}, \label{eq:teortau} \end{eqnarray}](/articles/aa/full_html/2015/02/aa23513-14/aa23513-14-eq64.png) (9)where N(H) is the column density of hydrogen atoms; rHe the abundance of helium with respect to hydrogen; and σH(λ), σHe i(λ), and σHe ii(λ) are photoionisation cross sections of hydrogen, neutral, and singly ionised helium, respectively, dependent only on wavelength λ. Ionisation degrees of neutral hydrogen, neutral, and singly ionised helium are denoted as i, j1, and j2, respectively. The value of σHe i(λ) yields non-zero values only for wavelengths below 504 Å (the head of the resonance continuum of He i), while σHe ii(λ) below 228 Å (the head of helium Lyman continuum). For the helium abundance rHe a common solar value of 0.1 was used. The σH(λ) cross section can be calculated using (see e.g. Mihalas1978)
(9)where N(H) is the column density of hydrogen atoms; rHe the abundance of helium with respect to hydrogen; and σH(λ), σHe i(λ), and σHe ii(λ) are photoionisation cross sections of hydrogen, neutral, and singly ionised helium, respectively, dependent only on wavelength λ. Ionisation degrees of neutral hydrogen, neutral, and singly ionised helium are denoted as i, j1, and j2, respectively. The value of σHe i(λ) yields non-zero values only for wavelengths below 504 Å (the head of the resonance continuum of He i), while σHe ii(λ) below 228 Å (the head of helium Lyman continuum). For the helium abundance rHe a common solar value of 0.1 was used. The σH(λ) cross section can be calculated using (see e.g. Mihalas1978) 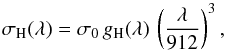 (10)where σ0 = 7.91 × 10-18 cm2 and the hydrogen Gaunt factors were tabulated by Karzas & Latter (1961). As He ii is the hydrogen-like ion, the formula for its photoionisation cross section is similar to Eq. (10), except that the multiplicative factor of 16 is added
(10)where σ0 = 7.91 × 10-18 cm2 and the hydrogen Gaunt factors were tabulated by Karzas & Latter (1961). As He ii is the hydrogen-like ion, the formula for its photoionisation cross section is similar to Eq. (10), except that the multiplicative factor of 16 is added 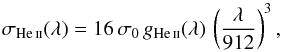 (11)where the He ii Gaunt factors are simply related to the hydrogen Gaunt factor by the n2λ-rule (n is the proton number). Thus, gHe ii(λ) = gH(4λ), and the σHe i(λ) cross section can be calculated using the polynomial fit of Rumph et al. (1994) who used data tabulated by Marr & West (1976).
(11)where the He ii Gaunt factors are simply related to the hydrogen Gaunt factor by the n2λ-rule (n is the proton number). Thus, gHe ii(λ) = gH(4λ), and the σHe i(λ) cross section can be calculated using the polynomial fit of Rumph et al. (1994) who used data tabulated by Marr & West (1976).
Then, if a theoretical ratio of optical thickness at two wavelengths below 912 Å is calculated using Eq. (9), the hydrogen column density is eliminated and the ratio depends only on ionisation degrees. As the ionisation degrees j1 and j2 of helium (the ionisation degree of hydrogen is estimated from the Hα spectra as explained in the next subsection) are not known, it is desirable to achieve as weak dependence as possible on j1 and j2. The AIA data from the 211 Å channel are suitable for this reason because radiation at 211 Å is absorbed by both neutral and singly ionised helium as well as the 193 Å radiation and radiation at the both wavelengths is emitted from the plasma of a similar temperature (log T ~ 6.2).
We were investigating variations of the theoretical τ193/τ211 ratio with i, j1, and j2 going from zero to unity and found that the ratio did not change much, reaching values between 0.76 and 0.83. Thus, the τ193/τ211 is suitable for α estimation. Although there is still some dependence on ionisation degrees that in some cases can cause large variations of estimated α (especially in a steep part of the dependency τ193/τ211 versus α). Thus, ionisation degrees i, j1, and j2 are still important and we devote Sects. 3.3 and 3.4 to methods of their estimation. The optical thickness τ211 can be calculated analogically to τ193, using observations in the AIA 211 Å channel, cuts at the same positions as in the AIA 193 Å observations but XRT X-ray data along cuts are fitted in the cavity and the surrounding corona to AIA 211 Å instead. In each point of the prominence area (estimated according to the AIA 304 Å image), both τ193 and τ211 are calculated from observations for values of α varying gradually from 0 to 1 with step of 0.01. Then, the τ193/τ211 ratios of optical thickness estimated from observations for various α are compared with the theoretical value. A value of α for which the observed ratio is closest to the theoretical one is considered as a correct value of α and τ193 calculated with this α as a correct value of the optical thickness at 193 Å. In such a way a map of α in the prominence area is also obtained.
We investigated the stability of the solution for α and found that in some positions in the prominence area even small errors in measured intensities can cause large errors in estimated α. Thus, we also estimated α for each prominence using indirect measurement from the intensities in the quiet corona just above the limb close to the prominence (the line of sight passing through the whole corona) and on the disc close to its edge (the line of sight passing through the corona in front of the prominence). A similar method for estimation of coronal radiation from behind a prominence was also used by Gilbert et al. (2005, 2006). Then we compare the α values estimated from τ193/τ211 with those measured indirectly (see Sect. 5). Sometimes errors in the intensities are so large that estimated τ193/τ211 is unrealistic (out of interval 0.76−0.83 of theoretical values) and therefore there is no solution for α. In such positions α is interpolated from the vicinity. If more than 30% of the prominence area is covered with α estimated from the τ193/τ211, bilinear interpolation in radial coordinates centred in the solar disc centre is used. If it is less than 30%, the Cartesian bilinear interpolation is used instead.
3.3. Estimations of ionisation degree of hydrogen from Hα observations
To derive the α factor of coronal asymmetry from the τ195/τ211 ratio or the hydrogen column density (necessary for mass calculations) from the optical thickness τ193 using Eq. (9), values of ionisation degrees i, j1, and j2 have to be known. The value of estimated total mass is very sensitive to the ionisation degrees. For example, varying all three ionisation degrees between zero and unity can cause such changes of calculated mass that highest value is almost three times larger than the lowest. Derivation of the ionisation degree of hydrogen from the Hα spectral observations is described in this subsection and the next subsection is devoted to the iterative estimation of the ionisation degrees of helium.
It is clear that radiation emitted in Hα from some position at a prominence should depend on the ionisation degree of hydrogen in the prominence plasma at this position. Each of the six prominences was observed by the SLS spectrograph in the complete Hα spectrum as it is shown in example of Hα observations of the prominence from 18 May 2011 in the upper panel of Fig. 4. In the bottom panel, an example of Hα profile from the position indicated by the horizontal dashed line is shown. The spectrum in Fig. 4 corresponds to the Hα slit-jaw image and the slit position shown in panel f of Fig. 1.
 |
Fig. 4 Upper panel: Hα spectrum of the prominence observed on 18 May 2011 by the SLS spectrograph. The bright solar disc with the Hα line in absorption and many other absorption lines is clearly distinguishable in the upper part of the image. Below the disc, fainter emission of the prominence in Hα is visible. Bottom panel: observed Hα profile from the position along the slit indicated by the white horizontal dashed line in the upper panel. Spectral intensities of the profile are marked with the “+” symbols. Errors in spectral intensities were derived from counts in raw spectra using Poisson statistics. The observed profile is fitted with synthetic profile calculated by a simple cloud model. The synthetic profile is plotted with the solid line. |
 |
Fig. 5 Log10τ0(Hα) versus log 10E(Hα). Integral intensities E(Hα) are in units erg / cm2/ s / sr. Results from the grid of simple 1D isobaric and isothermal models of Heinzel et al. (1994) are plotted with the “+” symbols. Models with different temperatures and geometrical thicknesses of the prominence were used to construct the plot. A clear trend can be seen, thus the points were fitted using a polynomial function (full line). |
 |
Fig. 6 Ionisation degree i versus τ0(Hα) from the results of the models of Heinzel et al. (1994) for three different temperatures and two geometrical thickness of the prominence. |
The ionisation degree i of hydrogen is estimated from an observed Hα profile in two steps. First, the optical thickness τ0(Hα) at the Hα line centre is estimated from the integral intensity E(Hα) using an empirical dependency derived by Heinzel et al. (1994). They calculated several hundreds of the simple 1D isobaric and isothermal models and put their results in the plot log 10E(Hα) versus log 10τ0(Hα) and found a linear trend for the optical thickness around unity. It is important to note that there is almost no dependency on temperature. As we need to derive the optical thickness from the integral intensity we make a plot with the integral intensity on the abscissa and the optical thickness on the ordinate as it is shown in Fig. 5. For τ0(Hα) farther from unity, a clear trend is also visible, although not simply linear. Thus, it was possible to fit the points with a polynomial function and then use this function to transform the log 10E(Hα) values into logarithm of τ0(Hα). Then in the second step the ionisation degree i of hydrogen is estimated from the optical thickness τ0(Hα) also using the models of Heinzel et al. (1994). When the values of i and τ0(Hα) from their models are plotted into a plot as shown in Fig. 6, it is clearly seen that the i – τ0(Hα) dependency varies remarkably with temperature. Variations with the geometrical thickness D is not so strong. Gunár et al. (2010, 2012) showed that the fine-structure prominence model composed of ten or a few tens of threads, each one 1000 km in width, reproduces well the observed Lyman line profiles. Therefore the geometrical thickness of a prominence of 10 000 km was assumed and the i – τ0(Hα) dependence for this geometrical thickness was used. Temperature can be estimated by fitting the prominence Hα profiles using the simple cloud model: When a prominence is approximated by the 1D vertically infinite slab irradiated at its sides from the solar surface, and it is assumed that prominence is not very optically thick (optical thickness at Hα does not exceed the unity by much), the intensity I(λ) of Hα emitted from the surface of the slab in the line of sight can be calculated as follows (Schwartz et al. 2012) ![\begin{equation} I(\lambda)=S\,\left[1-\exp\left(-\tau_{\lambda}\right)\right], \label{eq:ilambformsolsc} \end{equation}](/articles/aa/full_html/2015/02/aa23513-14/aa23513-14-eq93.png) (12)where S is the source function constant across the whole slab and τλ is the optical thickness at the wavelength λ. The wavelength dependency of the optical thickness can be expressed using the formula
(12)where S is the source function constant across the whole slab and τλ is the optical thickness at the wavelength λ. The wavelength dependency of the optical thickness can be expressed using the formula 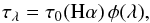 (13)where τ0(Hα) is the optical thickness at the Hα line centre and φ(λ) is absorption profile normalised to unity at its centre. To estimate the temperature from the Hα line, the Gaussian profile of Doppler width ΔλD and centred at λC is suitable for the absorption profile:
(13)where τ0(Hα) is the optical thickness at the Hα line centre and φ(λ) is absorption profile normalised to unity at its centre. To estimate the temperature from the Hα line, the Gaussian profile of Doppler width ΔλD and centred at λC is suitable for the absorption profile: ![\begin{equation} \phi(\lambda)=\exp\left[-\left(\frac{\lambda-\lambda_{\mathrm{C}}}{\Delta\lambda_{\mathrm{D}}}\right)^2\right]\cdot \label{eq:absprof} \end{equation}](/articles/aa/full_html/2015/02/aa23513-14/aa23513-14-eq100.png) (14)Then the temperature can be derived from the definition of the Doppler width
(14)Then the temperature can be derived from the definition of the Doppler width 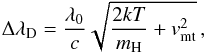 (15)where λ0 is the central wavelength of Hα according to some spectral atlas, c the speed of light in the vacuum, k the Boltzmann constant, mH mass of the hydrogen atom, and vmt is the velocity of microturbulence. The difference between λC and λ0 is due to the Doppler shift caused by a macroscopic velocity.
(15)where λ0 is the central wavelength of Hα according to some spectral atlas, c the speed of light in the vacuum, k the Boltzmann constant, mH mass of the hydrogen atom, and vmt is the velocity of microturbulence. The difference between λC and λ0 is due to the Doppler shift caused by a macroscopic velocity.
Values of vmt can be estimated from the Ca ii H line profiles observed by the HSFA 2 spectrograph Kotrč (2009). The mass of the calcium atom is approximately 40 times larger than the mass of the hydrogen atom. Therefore the expression 2kT/mCa in definition of the Doppler width (analogous to Eq. (15), except the central wavelength and mass for the Ca ii H line are used instead) reaches much smaller values compared to 2kT/mH. Therefore the width of the Ca ii H line is determined mainly by vmt. For example, for a temperature of 8000 K the contribution to the Doppler width from vmt of around 5 km s-1 is approximately 3 times larger than the contribution of the 2kT/mCa expression, but this ratio reaches almost 6 for a vmt of around 10 km s-1. Thus, it is more likely that larger velocities of microturbulence can be reliably estimated. Estimations of velocities vmt under 5 km s-1 have no physical meaning because in such a case the influence of temperature on width of the Ca ii H line profile is comparable to that of vmt.
 |
Fig. 7 Interpolated maps of temperature a), optical thickness τ0(Hα)b) and ionisation degree of hydrogen c) estimated from Hα spectral observations of the prominence of 18 May 2011. |
The optical thickness of a prominence at the Ca ii H line is comparable to that of Hα, thus the simple cloud model (Eqs. (12)−(14)) can be used to fit the observed Ca ii profiles as well. The difference is only that the optical thickness in the Ca ii H line is present in Eq. (13) instead of τ0(Hα). The advantage of the simple cloud model is that it can also be used for absolutely non-calibrated data (then only the source function is not expressed in physical units). As was already said in Sect. 2.1, the absolute calibration of the HSFA 2 data is somewhat problematic. Fortunately, the simple cloud model does not require absolutely calibrated data, thus the HSFA2 Ca ii H spectra were processed only by subtracting the dark frame, flat-fielding, correcting for the inclination of spectra on the detector, and finally subtracting the scattered light. Then profiles from the prominence section along the slit were fitted by the simple cloud model. A formula analogous to Eq. (15) with λ0 equal to 3968 Å and mCa instead of mH was used to estimate vmt from the Doppler width. Values of vmt were calculated for the temperature of 8000 K. Unfortunately, observations from the HSFA 2 and SLS spectrographs were not co-spatial (as for slit positions) for all prominence observations used in this work, and for three of them (see Table 1) observations from the both spectrographs were not made at the same time or even on the same day. Therefore, for each prominence observations, only one unique vmt value averaged from all slit positions of HSFA 2 was used. This problem could be solved if Hα observations from the HSFA 2 spectrograph were also used instead of those from SLS. However, absolute calibration of the Hα spectra from HSFA 2 was problematic (as was already explained) and absolutely calibrated intensities E(Hα) are necessary for τ0(Hα) estimations. Values of τ0(Hα) could also be estimated by fitting of the simple cloud model to the HSFA 2 non-calibrated Hα profiles, but values of τ0(Hα) obtained by the fitting are not reliable because τ0(Hα) occurs in the negative exponent in the simple cloud model that causes its high sensitivity in fitting to errors in profile intensities.
The fitting of the Hα and Ca ii H profiles was made by the non-linear least square method using the standard IDL procedure lmfit based on the Levemberg-Marquardt algorithm. First, fitting was made with τ0 fixed varying from 0 to 8 with step of 0.5 and the fit with the smallest χ2 was chosen. Then, the parameters of this best fit were used as starting values for fitting with τ0 also taken as a variable parameter.
For each prominence observation after the co-alignment of the SLS slit-jaw and AIA 304 Å images, it was possible to obtain values of temperature, τ0(Hα), and i along the co-aligned slit positions in a prominence area (fixed according to the AIA 304 Å observations). Then maps of these three quantities were constructed in two steps: first, values between the slit positions inside the prominence area were interpolated using the bilinear interpolation in the Cartesian coordinate system. Then, pixels outside an area covered by values in the previous step were filled in the vertical direction by values from the closest point on the boundary of the covered area (interpolated in the first step). The Hα observations of each prominence were made only in few slit positions, and these slit positions do not reach whole range of heights of the prominence area, which can cause the presence of vertical stripes in the maps reconstructed by the method explained above. Examples of the reconstructed maps of temperature, τ0(Hα), and i for the prominence of 18 May 2011 (No. 6 in Table 1) are shown in Fig. 7.
3.4. Estimation of the ionisation degrees of neutral and singly ionised helium
If the contribution to measured EUV intensities of the corona in front of a prominence were negligible, we could use ratios of intensities measured in 193, 211, and 335 Å channels at the prominence and Eqs. (2) and (9) to construct maps of ionisation degrees j1 and j2. It is clearly visible in observations that foreground coronal radiation cannot be neglected. Comparing the theoretical and observed optical thickness τ335 also does not help. Although 335 Å radiation is not absorbed in the resonance continuum of singly ionised helium (wavelength above the head of the resonance continuum of He ii) and thus the expression j1σHe ii(λ) is not present in Eq. (9), dependence on both j1 and j2 still persists. Thus, we are only able to estimate unique values of j1 and j2 for the whole prominence by comparing masses estimated from the AIA observations in the 193 Å channel with those estimated using the 335 Å channel for various combinations of j1 and j2, both from interval 0−1 with condition j1 + j2 ≤ 1. Moreover, if j1 + j2 is equal to unity and i = 1 at the same time, τ335 is equal to zero (see Eq. (9) assuming that σHe ii is equal to zero at 335 Å) and then the calculated mass is also equal to zero. Calculation of the total mass from the map of the optical thickness is described in Sect. 3.5. Values of j1 and j2, for which the minimal difference between the total masses calculated from the 193 and 335 Å AIA data is obtained, are considered as the correct ones.
The map of τ335 is calculated in a similar way as the τ193 computations described in Sect. 3.1. Thus, Eq. (8) with 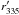 instead of
instead of 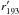 is used to calculate τ335 in all positions inside the prominence area along the tangential to the limb cuts across a prominence. In this case,
is used to calculate τ335 in all positions inside the prominence area along the tangential to the limb cuts across a prominence. In this case, 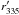 are ratios of intensities of the AIA 335 Å data to the XRT X-ray data along one cut. Before calculations of the ratios, distributions of X rays along the cuts are fitted to the AIA 335 Å intensities in the cavity and corona, in a similar way as was done for the τ193 calculations. The factors of coronal asymmetry α are estimated using the method described in Sect. 3.2, however, the ratio τ335/τ211 is used instead. As it was already said in previous paragraph, there is no absorption in the resonance continua of He ii at 335 Å contrary to 211 Å. Therefore τ335/τ211 is much more sensitive to the ionisation degrees j1 and j2 than τ193/τ211. For example, for i between 0.2 and 1, j1 and j2 from interval 0−1, the τ335/τ211 ratio ranges from 0.03 to 3.93, which is a much wider interval than for τ193/τ211. Therefore, α factor estimated using the τ335/τ211 ratio is remarkably sensitive to j1 and j2, and subsequently the value of the total mass estimated from the 335 Å AIA channel (hereafter called 335 Å based mass) also varies with the helium ionisation degrees much more than the mass determined from the AIA observations at 193 Å (hereafter referred to as 193 Å based mass). Such a behaviour of the 335 Å based mass makes it possible to find unambiguous values of j1 and j2 for which a difference between the masses obtained using the 193 and 335 Å channels is minimal.
are ratios of intensities of the AIA 335 Å data to the XRT X-ray data along one cut. Before calculations of the ratios, distributions of X rays along the cuts are fitted to the AIA 335 Å intensities in the cavity and corona, in a similar way as was done for the τ193 calculations. The factors of coronal asymmetry α are estimated using the method described in Sect. 3.2, however, the ratio τ335/τ211 is used instead. As it was already said in previous paragraph, there is no absorption in the resonance continua of He ii at 335 Å contrary to 211 Å. Therefore τ335/τ211 is much more sensitive to the ionisation degrees j1 and j2 than τ193/τ211. For example, for i between 0.2 and 1, j1 and j2 from interval 0−1, the τ335/τ211 ratio ranges from 0.03 to 3.93, which is a much wider interval than for τ193/τ211. Therefore, α factor estimated using the τ335/τ211 ratio is remarkably sensitive to j1 and j2, and subsequently the value of the total mass estimated from the 335 Å AIA channel (hereafter called 335 Å based mass) also varies with the helium ionisation degrees much more than the mass determined from the AIA observations at 193 Å (hereafter referred to as 193 Å based mass). Such a behaviour of the 335 Å based mass makes it possible to find unambiguous values of j1 and j2 for which a difference between the masses obtained using the 193 and 335 Å channels is minimal.
 |
Fig. 8 Interpolated maps of the α factor of asymmetry of EUV coronal emissivity a), and optical thickness τ193b) derived from prominence EUV and X-ray observations of 18 May 2011. Striation in the α map in panel a) is caused by problems of bilinear interpolation explained in the last paragraph of Sect. 3.3. |
3.5. The total mass calculations
Once the ionisation degrees i, j1, and j2 were estimated, the map of α can be calculated (Sect. 3.2) and then the pixels in the map with undefined values are interpolated using the bilinear interpolation in the radial coordinate system according to the centre of the solar disc. In addition, in the α maps the striation occurs because of the fitting method (see the last paragraph of Sect. 3.3). Because of errors in the data, the expression 1−(1−r′) /α in Eq. (8) can reach values that are outside the permitted interval: if it is negative or zero then it is not possible at all to calculate the optical thickness (non-positive argument of logarithm), and if it is greater than one negative values of the optical thickness are calculated. Positions in the prominence area where either of the two cases occurs, are considered as positions with undefined optical thickness, so-called black pixels in the τ193 map. Black pixels are interpolated using bilinear interpolation if the following three conditions are fulfilled: More than 30% of the prominence area is covered by defined optical thickness; the distance between the centre of gravity (all positions are weighted equally) of the whole prominence area and that of positions with defined optical thickness does not exceed several thousands km; and positions with defined optical thickness closest to the boundary of the prominence area are not farther away than several thousand km. If any of these three conditions is not fulfilled, an average value of optical thickness is taken for the whole prominence area. An example of interpolated maps of α and τ193 for the prominence observations of 18 May 2011 (prominence observation No. 6 in Table 1) is shown in Fig. 8.
Observation numbers and times of SLS observations are listed in the first two columns.
The column density NH of hydrogen atoms can be directly derived from Eq. (9). Thus, the map of τ193 can be simply transformed into a map of NH using this formula and the known ionisation degrees i, j1 and j2. The total mass M of a prominence is calculated by integration of the column mass of hydrogen and helium prominence plasma over the whole prominence area PA 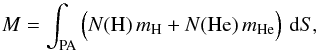 (16)where mH and mHe are masses of hydrogen and helium atoms and quantities N(H) and N(He) are column densities of hydrogen and helium, respectively. Using the definition of the abundance of helium according to hydrogen rHe = N(He) /N(H), and assuming that for the accuracy that we can achieve it is enough to take mHe as being four times mH, Eq. (16) simplifies as follows:
(16)where mH and mHe are masses of hydrogen and helium atoms and quantities N(H) and N(He) are column densities of hydrogen and helium, respectively. Using the definition of the abundance of helium according to hydrogen rHe = N(He) /N(H), and assuming that for the accuracy that we can achieve it is enough to take mHe as being four times mH, Eq. (16) simplifies as follows: ![\begin{eqnarray} M & = & \int_{\mathrm{PA}}N(\mathrm{H})\,\left(\rule{0pt}{1.7ex}m_{\mathrm{H}}+r_{\mathrm{He}}\,m_{\mathrm{He}}\right)\,{\rm d}S \nonumber \\[-0.5em] & & \\[-0.4em] & = & m_{\mathrm{H}}\,\int_{\mathrm{PA}}N(\mathrm{H})\,\left(\rule{0pt}{1.7ex}1+4\,r_{\mathrm{He}}\right)\,{\rm d}S. \nonumber \label{eq:totalmass2} \end{eqnarray}](/articles/aa/full_html/2015/02/aa23513-14/aa23513-14-eq136.png) (17)The abundance rHe is taken as being constant and a commonly used solar value 0.1 is adopted.
(17)The abundance rHe is taken as being constant and a commonly used solar value 0.1 is adopted.
4. Results
The intervals within which the temperature T, velocity of microturbulence vmt, optical thickness τ0(Hα) and ionisation degree i of hydrogen vary in the six prominences are shown in Table 2. These quantities were obtained from spectral observations of the Hα and Ca ii H lines made by the SLS and HSFA2 spectrographs, respectively, using the simple cloud model (Sect. 3.3). Together with the intervals, also mean values averaged from whole prominence areas are listed in the table. Except quantities mentioned above, values of the ionisation degrees j1 and j2 of neutral and singly ionised helium, respectively, are also listed in the table. Unique values of j1 and j2 were obtained for each prominence by searching of minimal difference between the 193 Å and 335 Å based masses as was explained in Sect. 3.4.
A small prominence No. 2 was visible in the AIA images in channels 304 Å, 193 Å, 211 Å, and 335 Å, but it was not visible in Hα observations from the SLS and HSFA2 spectrographs. Therefore, it was not possible to estimate the temperature, τ0(Hα) and i for this prominence. Thus, a unique value of i for the whole prominence was estimated, together with j1 and j2, by comparing the 193 Å and 335 Å based masses. The estimation of a high value of ionisation degree of hydrogen for this prominence agrees with its invisibility in Hα. A high value of ionisation degree of neutral helium and no double ionised helium (j2 = 0) derived for this prominence means that the prominence is composed mainly of singly ionised helium. This idea is also supported by the observation of the prominence as a very bright object in the 304 Å AIA image.
Further results of the spectroscopic analysis of the multi-spectral data leading to estimations of the total mass of prominences are shown in Table 3. The first two columns of the table are the same as in Table 2. Intervals within which the α factor of coronal asymmetry occurs are shown in the third column. Only for the small prominence No. 2, was a unique value of 0.2 estimated for the whole prominence. The α maps were calculated using ratios τ193/τ211 as was explained in Sect. 3.2. Together with the intervals, average values of α are also listed in the table. Possible errors of these average α values caused by noise in the data are calculated using the Monte Carlo method as follows: When extracting data from tangential cuts through a prominence to obtain maps of τ193 and α (see Sects. 3.1 and 3.2), both the EUV and X-ray data are modified by adding random errors. The random errors are normally distributed while the error estimated using the Poisson statistics is taken as σ of the distribution. Then, the α map is computed using the modified data and deviation of average α from that obtained from the unmodified data, is calculated. Computations of α maps using randomly modified data are made for several tens of cases and the deviations are plotted into a histogram. Finally, the σ parameter of the Gaussian fitted to the histogram was taken as the error. Therefore we call such an error the 1σ error and it is listed in Col. 4 of Table 3. In Cols. 5 and 6, the values of the mean column density of hydrogen and total mass are shown. Numbers of the mass preceded by “=” were obtained from the τ193 map in which the black pixels (positions with undefined τ193) were interpolated (see Sect. 3.5). Instead, a mass value given with the “≈” symbol was calculated using a mean value of τ193 for a whole prominence due to lack of pixels with defined values of τ193. The 1σ errors of the mass are listed in Col. 7. In the last column, relative differences between the 335 Å and 193 Å based masses are expressed as a percentage. Estimated values of j1 and j2 (unique for the whole prominence) characterise well the real distributions of ionisation degrees throughout the prominence if the difference between the 335 Å and 193 Å based masses is small (not exceeding few tens of percentage points).
When investigating the dependency of the resulting total masses (Table 3) on morphological characteristics of the six prominences, such as maximum apparent height above the limb or area according to AIA 304 Å images (Table 1), no simple and clear dependencies between mass and these quantities can be found because not only is the size of a prominence responsible for its total mass, but also the column densities of its plasma. Moreover, the mean column density of hydrogen can vary very much from prominence to prominence. For example, Berlicki et al. (2011) used a NLTE model with one order of magnitude lower column mass for one thread of a prominence than was used by Gunár et al. (2010) for a different prominence. On the other hand, there is almost perfect linear dependence of the total mass on a product of the prominence area according to AIA 304 Å images and mean hydrogen column density. Thus, one does not need maps of the column densities for comparison of the masses of different prominences, knowledge of the mean column densities and prominence areas estimated from observations in the 304 Å helium line are enough for this reason. However, only 4−65% of prominence areas according to the AIA 304 Å images were covered by the prominence structures visible in the Hα slit-jaw images of the SLS spectrograph. Thus, these slit-jaw images are not suitable for using in the total mass calculations. There were no any other simple relations found between resulting parameters, and six prominence observations is too few for the statistical sample suitable for such an analysis. We can do more reliable analysis after the masses of all 30 prominences observed during the campaign are obtained.
Values of the α factor of coronal asymmetry and total mass estimated for the six multi-spectral observations of prominences.
5. Discussion
Values of the total mass of the six observed prominences range from 2.9 × 1011 to 1.7 × 1012 kg. Only the mass of the small prominence No. 2, which seems to be a small part of a large filament, is of order of 109 kg. The column densities averaged for each prominence observation range from 3.8 × 1018 to 1.6 × 1019 cm-2. Burkepile et al. (2004) estimated masses of CMEs observed in visible light associated with eruptive prominences on the limb ranging from 1.6 × 1011 kg, which is comparable to our prominence mass estimations, up to 2.5 × 1013 kg, which is one order of magnitude larger. This agrees with the statement of Low (1996) that the contribution of an erupting prominence to the total mass of a CME is one order of magnitude lower than the mass of its leading shell, but he also claimed that in some cases it can be comparable. Because some fraction of ejected prominence material can return back to the solar surface after a CME, the contribution of a prominence to a following magnetic cloud in interplanetary space could be even smaller. Carlyle et al. (2014) studied material returning in several blobs to the chromosphere after a CME initialised by the filament eruption on 7 June 2011. They estimated mass returning in one blob being of the order of 1010 kg, which is at the most a small percentage of the prominence masses estimated here.
It is important to briefly mention three problems with our mass estimations. First, saturation of absorption: The τ193 optical thickness in some positions at a prominence can reach such a critical value that almost no radiation is transmitted. For example, only 5% of radiation is transmitted through the plasma of the optical thickness equal to three. Such a small intensity can be beyond the detection limit of an instrument and/or below the level of noise in the data. Thus, any increase of the optical thickness above the critical value does not make a detectable additional decrease of intensity. It is not possible to estimate the error in our mass estimations caused by the saturation without comparing it with values estimated by other methods not affected by saturation. For example, it is possible to calculate mass from densities determined from NLTE modelling of profiles of the hydrogen Lyman lines and Hα. Unfortunately we do not have such observations for our prominences, but we plan to do it in a future paper using data obtained during our recent observing campaign. The second problem is the possibility of an absorption of X-rays by the prominence plasma. We already know that hydrogen and helium, which are the most abundant elements in the prominence plasma, practically do not absorb X rays, but continua of some metals can absorb X-rays. It was already shown by Anzer et al. (2007) that there is negligible absorption at 50 Å, but possibility of absorption at 10 Å, where the XRT Al-mesh filter has the highest transmission, has not been investigated yet. We will deal with this problem in our future paper. The last problem is contamination of the XRT signal by the EUV radiation when using the Al-mesh filter. The filter has a secondary maximum of transmission around 171 Å. Although the transmission of the filter in EUV is approximately one hundred times lower than in X-rays, the contribution from EUV is not negligible because the intensity of X-rays around 10 Å is approximately one hundred times lower than the intensity of the coronal radiation around 171 Å. Using the CHIANTI atomic database (Dere et al. 1997; Landi et al. 2012), quiet-Sun distributions of electron density and temperature with distance from the Sun’s centre taken from Saito et al. (1970) and Lemaire (2011), respectively, and the transmission curve of the Al-mesh filter, we found that the contamination varies between 18 and 25%. We developed a simple method for removing the EUV contamination from XRT Al-mesh data using a quasi-simultaneous AIA 171 Å image: The image after co-alignment is multiplied by such a factor that data values in several selected quiet-Sun areas are equal to the EUV contaminations calculated for their distances from the disc centre. After such manipulation this image is subtracted from the XRT Al-mesh data. It was found that percentual errors of mass estimations caused by the EUV contamination were approximately four times smaller than the 1σ errors caused by errors in the observed data (Table 3) for the large prominence No. 2 and for prominence No. 5. The errors caused by the EUV contamination are comparable to the 1σ errors for prominences Nos. 3, 6, and the small prominence No. 2. Only for prominence No. 4 the contamination causes an error of 63%, which is approximately four times as large as the 1σ error. When adding 63% to the mass estimated for prominence No. 4, we get a value comparable to the mass estimated for the large prominence No. 2, which is the same prominence observed one day earlier. Thus, the EUV contamination of XRT data obtained using the Al-mesh filter cannot be neglected in some cases. This needs more investigation; in our next paper we plan to compare masses of a prominence estimated using Al-mesh XRT data and observations in the green coronal line instead.
Estimations of hydrogen column density for two absorption features in the corona were previously made by Kucera et al. (1998). They used observations of two prominences made on 14 May and 18 June 1997 by the CDS spectrometer on board the SoHO with four hot (T> 600 000 K) coronal EUV lines of wavelengths between 504 and 912 Å where only the absorption in the hydrogen Lyman continuum occurs. They found the hydrogen column density to be of the order of 1018 cm-2, which agrees with our estimations. Hydrogen column density with an upper limit of 7.5 × 1018 cm-2 of Golub et al. (1999) from the first TRACE observations of a prominence on 9 May 1998 in 171 Å and 195 Å channels also falls into the range of values estimated in this work. Gilbert et al. (2005) estimated the total mass of the prominence observed by SoHO/EIT on 12 July 1999. The prominence was partially visible off-limb and partially on-disc which made it possible to estimate the emissivity of the corona in front of the prominence (foreground intensity). Background radiation was estimated by the both temporal-interpolative and spatial-interpolative approaches and they found values of the total mass 6.0 × 1011 kg with the error ± 41% and 7.4 × 1011 kg with the larger error of ± 62. Both values lie in the interval of the total masses estimated here. Later they published the work on a similar analysis of EIT prominence observations made from July 1999 through July 2004 and they found average values of 4.18 × 1011 kg for quiescent prominences, 9.09 × 1011 kg for eruptive prominences, and 1.53 × 1011 kg for surges (Gilbert et al. 2006). The average total mass 7.48 × 1011 kg for prominences studied in this work (the small prominence of observations No. 2 excluded) is closer to their average value for eruptive prominences than their average mass of quiescent prominences, but all prominences studied here behaved quiescently and it was not investigated whether any of them erupted later. This discrepancy can be explained in two ways: first, Gilbert et al. (2006) took only a dark structure observed in the EUV coronal radiation, which can be only a small part of whole prominence. Instead, we integrated the column density of hydrogen and helium throughout the whole prominence area fixed according to projection of a prominence on the limb as seen in the AIA 304 Å image. Second, when the spatial-interpolative approach of background radiation was used, only prominences that were seen partly off-limb and partly on-disc, were suitable for such an analysis. Then the mass of a prominences were underestimated because just their off-limb parts were taken. Recently, Williams et al. (2013) estimated the mass of returning matter after a filament eruption from observations from AIA/SDO in channels 94, 131, 171, 193, and 211 Å. The filament eruption occurred during the large CME of 7 Jun. 2011. In their work both approaches for the estimation of background radiation were used. For material returning unhindered by the magnetic field a polychromatic method, which uses simultaneous observations in the all five EUV coronal AIA channels, was used and values of the hydrogen column densities within a range 1019−1020 cm-2 were estimated (see their Fig. 5). This is comparable to or even one order of magnitude higher than our values. Higher values of the hydrogen column density could be explained by changes in concentration of a filament/prominence material after the eruption, but this still needs further research. Using a monochromatic method (only 193 Å channel was used) for the filament material returning to the coronal magnetic null point, only lower-limit estimates of the hydrogen column density between 3 × 1018 and 5 × 1018 cm-2 were obtained (Fig. 7 of Williams et al.2013). These values are comparable to those obtained here.
The estimated values of ionisation degrees j1 and j2 reproduce reality more accurately when the difference M335 − M193 between the 335 Å and 193 Å based masses is smaller. The differences are listed in Table 3 while the corresponding j1, j2 in Table 2. Comparing these two tables one can see that only for prominence No. 3, j1 and j2 are equal to 1 and 0, respectively, are well suitable for the whole prominence. For prominence No. 1, the difference around 30% is still acceptable. For all other prominences analysed here, the differences are already rather large (between 60 and 90%). That means that j1 and j2 vary much throughout a prominence. We note that differences for all six prominences are negative, which means that values of the 335 Å based mass are underestimated, most probably because TR lines radiated from prominence PCTRs are detected in two secondary peaks of the transmission function of the AIA 335 Å filter. This problem could be solved in future missions by using a filter with narrower transmission and without unwanted secondary maxima. A spectrometer similar to SoHO/CDS or EIS on Hinode observing in spectral ranges of resonance continua of hydrogen and helium would be another solution.
Comparison of values of α estimated from the ratio of optical thickness τ193/τ211 and indirectly from measurements.
The method for α estimations from comparing the observed and theoretical τ193/τ211 ratio is not very stable (Sect. 3.2). Thus, even small errors in the data can cause large errors in α. Values estimated by the method are hereafter referred to as the estimated α. High sensitivity of the estimated α on data errors are manifested by rather large 1σ errors of average α listed in Table 3 for prominences Nos. 1, 4, and 5. Therefore, it is necessary to compare the estimated α with values obtained by a different method. Approximate values of α were determined using measurements of the intensities ILMB and IDSK at the vicinity of a prominence just off-limb and just on-disc, respectively (a so-called indirect measurement of α). The intensities were measured as follows. A radial cut crossing the disc and limb was made in the quiet vicinity of a prominence. Then, the 193 Å intensities along the on-disc section of the cut outside any brightenings were fitted by a polynomial of the 3rd or 4th degree and the value of the fit at the limb was taken as IDSK. Intensities along the off-limb part of the cut were fitted by an exponential function and the value of the fit at limb was taken as ILMB. Finally, α was calculated by a very simple formula: 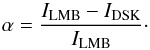 (18)Values of α determined in such a way are hereafter referred to as the measured α. If radial cuts are made in different positions, various values of measured α are obtained. It means that the quiet corona in the prominence vicinity is also rather inhomogeneous. Therefore, an average distribution of intensity from several radial cuts made on both sides of each studied prominence was used instead. Values of the estimated and measured α are compared in Table 4. They are close to each other only for prominence No. 3 and the small prominence No. 2. In addition, the total masses calculated for these two prominences using the estimated and measured α differ only by less than 30%. For prominence No. 5, the mass difference is only a little larger, although the measured α differs greatly from the mean estimated α. For the remaining four prominences, the total mass differences are much larger, between 50 and 80%. Values of the measured α are close to or even inside the intervals within which the estimated α varies in these prominences.
(18)Values of α determined in such a way are hereafter referred to as the measured α. If radial cuts are made in different positions, various values of measured α are obtained. It means that the quiet corona in the prominence vicinity is also rather inhomogeneous. Therefore, an average distribution of intensity from several radial cuts made on both sides of each studied prominence was used instead. Values of the estimated and measured α are compared in Table 4. They are close to each other only for prominence No. 3 and the small prominence No. 2. In addition, the total masses calculated for these two prominences using the estimated and measured α differ only by less than 30%. For prominence No. 5, the mass difference is only a little larger, although the measured α differs greatly from the mean estimated α. For the remaining four prominences, the total mass differences are much larger, between 50 and 80%. Values of the measured α are close to or even inside the intervals within which the estimated α varies in these prominences.
6. Conclusions
In this paper we introduced a complex method based on work of Heinzel et al. (2008) for the estimation of the total mass of solar prominences from their multi-spectral observations (in EUV, X-rays, Hα, and Ca ii H). The method was used for six prominence observations obtained during an observation campaign from April through June 2011. The estimated values of the total mass and hydrogen column density are comparable with results published in earlier and recent works of other authors. Hydrogen column densities are derived from an amount of the EUV coronal radiation absorbed by a prominence plasma in the resonance continua of hydrogen and helium, similarly to Kucera et al. (1998), Golub et al. (1999), Gilbert et al. (2005, 2006) and Williams et al. (2013). Contrary to our method, lack of the coronal emission that would be present in a volume occupied by a cool prominence plasma – the so-called coronal emissivity deficit – was not taken into account or was neglected in those works. Neglecting its contribution to decrease of the EUV coronal line intensities can lead to overestimation of the optical thickness and subsequently to larger hydrogen column densities mainly for prominences geometrically rather thick along the line of sight. For example, neglecting the coronal emissivity deficit leads to overestimation of hydrogen column densities by 5−11% for the geometrical thickness of 10 000 km. The overestimation can reach up to 70% for the geometrical thickness of 40 000 km.
The total EUV coronal emission (sum of the background and foreground emissivities) at the prominence position had to be known for an estimation of the emission from behind a prominence in works listed in the first paragraph. The total emission was estimated by an interpolation in space or time. Values of the total emission obtained in such a way need not be reliable because interpolations in space or time calculate the total emission from the prominence vicinity or from times when a prominence was not present, respectively, but the corona along the line of sight at the prominence position can be rather inhomogeneous and dynamic. Instead, our method estimates the total EUV coronal emission at the prominence position using X-ray observations (no absorption by hydrogen and helium plasma) as a proxy. Then values of fraction of the coronal emissivity from behind a prominence are obtained using almost simultaneous and co-spatial observations in two EUV coronal lines. Our estimation of the background emission has a disadvantage in a sort of uncertainty principle: the closer the wavelengths of the two EUV lines are, the less stable the solution is. And the larger is the difference in wavelengths of the two lines, the more sensitive is the solution to ionisation degrees of hydrogen and helium.
Unlike other works, where only small dark structures visible in the EUV coronal lines were considered in the mass calculation, we take whole areas of prominences as visible in the He ii 304 Å observations. Because such small dark structures are usually only front parts (not overradiated by the corona in front of them) of much bigger prominences, the mass calculated using just areas of these small structures can be underestimated. For example, for the six prominences studied in this work the mass underestimation can reach up to 96%.
For our next paper we plan to calculate the total mass for the 24 remaining prominence observations made during the campaign using the method described here and then to analyse the results statistically.
See SLS web page http://radegast.asu.cas.cz/MFS/prominence_archiv/sls.html
More details about the HSFA2 instrument itself and data reduction can be found at http://www.asu.cas.cz/~sos/hsfa2.html
Acknowledgments
P.S. and P.H. acknowledge the support from grant P209/12/0906 of the Grant Agency of the Czech Republic. Work of P.S. and P.H. was supported by the project RVO: 67985815. Work of P.S. was also supported by the grant project VEGA 2/0108/12 of the Science Grant Agency. P.S. acknowledges support from the Slovak Research and Development Agency under the contract No. APVV-0816-11. The AIA data are courtesy of NASA/SDO and the AIA science team. CHIANTI is a collaborative project involving George Mason University, the University of Michigan (USA) and the University of Cambridge (UK).
References
- Anzer, U., & Heinzel, P. 2005, ApJ, 622, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Anzer, U., Heinzel, P., & Fárnik, F. 2007, Sol. Phys., 242, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Berlicki, A., Gunar, S., Heinzel, P., Schmieder, B., & Schwartz, P. 2011, A&A, 530, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burkepile, J. T., Hundhausen, A. J., Stanger, A. L., St. Cyr, O. C., & Seiden, J. A. 2004, J. Geophys. Res. (Space Physics), 109, 3103 [Google Scholar]
- Carlyle, J., Williams, D. R., van Driel-Gesztelyi, L., et al. 2014, ApJ, 782, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Crifo, F., Picat, J. P., & Cailloux, M. 1983, Sol. Phys., 83, 143 [NASA ADS] [CrossRef] [Google Scholar]
- David, K.-H. 1961, ZAp, 53, 37 [Google Scholar]
- Delaboudinière, J.-P., Artzner, G. E., Brunaud, J., et al. 1995, Sol. Phys., 162, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Engvold, O. 1989, in Dynamics and Structure of Quiescent Solar Prominences, ed. E. R. Priest, Astrophys. Space Sci. Lib., 150, 47 [Google Scholar]
- Gilbert, H. R., Holzer, T. E., & MacQueen, R. M. 2005, ApJ, 618, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Gilbert, H. R., Falco, L. E., Holzer, T. E., & MacQueen, R. M. 2006, ApJ, 641, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Golub, L., Bookbinder, J., Deluca, E., et al. 1999, Phys. Plasmas, 6, 2205 [NASA ADS] [CrossRef] [Google Scholar]
- Golub, L., Deluca, E., Austin, G., et al. 2007, Sol. Phys., 243, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Gunár, S., Schwartz, P., Schmieder, B., Heinzel, P., & Anzer, U. 2010, A&A, 514, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunár, S., Mein, P., Schmieder, B., Heinzel, P., & Mein, N. 2012, A&A, 543, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harrison, R. A., Sawyer, E. C., Carter, M. K., et al. 1995, Sol. Phys., 162, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Heinzel, P., Gouttebroze, P., & Vial, J.-C. 1994, A&A, 292, 656 [NASA ADS] [Google Scholar]
- Heinzel, P., Schmieder, B., Fárník, F., et al. 2008, ApJ, 686, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Hundhausen, A. 1999, in The many faces of the sun: a summary of the results from NASA’s Solar Maximum Mission., eds. K. T. Strong, J. L. R. Saba, B. M. Haisch, & J. T. Schmelz (New York: Springer), 143 [Google Scholar]
- Karzas, W. J., & Latter, R. 1961, ApJS, 6, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Kotrč, P. 2009, Central European Astrophysical Bulletin, 33, 327 [Google Scholar]
- Kucera, T. A., Andretta, V., & Poland, A. I. 1998, Sol. Phys., 183, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Labrosse, N., Heinzel, P., Vial, J.-C., et al. 2010, Space Sci. Rev., 151, 243 [Google Scholar]
- Landi, E., Del Zanna, G., Young, P. R., Dere, K. P., & Mason, H. E. 2012, ApJ, 744, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Lemaire, J. F. 2011 [arXiv:1112.3850] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Low, B. C. 1996, Sol. Phys., 167, 217 [Google Scholar]
- Low, B. C., Fong, B., & Fan, Y. 2003, ApJ, 594, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Marr, G. V., & West, J. B. 1976, Atomic Data and Nuclear Data Tables, 18, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D. 1978, Stellar atmospheres 2nd edn. (San Francisco: Freeman & Co) [Google Scholar]
- Parenti, S., Schmieder, B., Heinzel, P., & Golub, L. 2012, ApJ, 754, 66 [Google Scholar]
- Rumph, T., Bowyer, S., & Vennes, S. 1994, AJ, 107, 2108 [NASA ADS] [CrossRef] [Google Scholar]
- Saito, K., Makita, M., Nishi, K., & Hata, S. 1970, Annals of the Tokyo Astronomical Observatory, 12, 53 [Google Scholar]
- Schwartz, P., Rybák, J., Kučera, A., et al. 2012, Contributions of the Astronomical Observatory Skalnate Pleso, 42, 135 [NASA ADS] [Google Scholar]
- Williams, D. R., Baker, D., & van Driel-Gesztelyi, L. 2013, ApJ, 764, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Wöhl, H., Kučera, A., Rybák, J., & Hanslmeier, A. 2002, A&A, 394, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Morphological properties of the six prominences and dates and times of their observations.
Observation numbers and times of SLS observations are listed in the first two columns.
Values of the α factor of coronal asymmetry and total mass estimated for the six multi-spectral observations of prominences.
Comparison of values of α estimated from the ratio of optical thickness τ193/τ211 and indirectly from measurements.
All Figures
 |
Fig. 1 Panels a)–e): observations of the prominence of 18 May 2011 (No. 6): cut-offs from the full-disc observations from the AIA instrument in the 304 Å, 193 Å, 211 Å, and 335 Å channels, and of the XRT telescope obtained using the Al-mesh filter. Rectangles drawn by a solid white line mark areas of interest. Positions of the prominence and surrounding cavity are marked in panels b) and e). Panel f): SLS spectrograph Hα slit-jaw image co-aligned with AIA observations. One of the eight slit positions is plotted by a black inclined dashed line. |
| In the text | |
 |
Fig. 2 Absorption and coronal emissivity deficit at a prominence and coronal emissivity deficit alone in the cavity cause decrease of the coronal intensity. Ip is the coronal intensity measured at a prominence, |
| In the text | |
 |
Fig. 3 Upper-left panel: cut made tangentially to the limb through the prominence of 18 May 2011 (observation No. 6 according to Table 1). Upper-right panel: distributions of measured intensities along this cut in the He ii 304 Å line, coronal iron lines round 193 Å, and X-rays. In positions along the cut, where the AIA 304 Å intensity is increased, occurrence of prominence is assumed. The both 193 Å and X-ray intensities are decreased at the prominence and cavity positions. There is also a part of the prominence further beyond the plane of the limb that is overradiated by the corona but still visible in projection on the limb in 304 Å where the corona does not emit. Bottom panel: the distribution along the cut of intensity at 193 Å is shown together with X-rays while X-ray intensities were multiplied by such a factor that the X-ray and 193 Å distributions fit each other in the cavity and corona. At the prominence, the ratio between the intensities of these two distributions is proportional to the optical thickness. |
| In the text | |
 |
Fig. 4 Upper panel: Hα spectrum of the prominence observed on 18 May 2011 by the SLS spectrograph. The bright solar disc with the Hα line in absorption and many other absorption lines is clearly distinguishable in the upper part of the image. Below the disc, fainter emission of the prominence in Hα is visible. Bottom panel: observed Hα profile from the position along the slit indicated by the white horizontal dashed line in the upper panel. Spectral intensities of the profile are marked with the “+” symbols. Errors in spectral intensities were derived from counts in raw spectra using Poisson statistics. The observed profile is fitted with synthetic profile calculated by a simple cloud model. The synthetic profile is plotted with the solid line. |
| In the text | |
 |
Fig. 5 Log10τ0(Hα) versus log 10E(Hα). Integral intensities E(Hα) are in units erg / cm2/ s / sr. Results from the grid of simple 1D isobaric and isothermal models of Heinzel et al. (1994) are plotted with the “+” symbols. Models with different temperatures and geometrical thicknesses of the prominence were used to construct the plot. A clear trend can be seen, thus the points were fitted using a polynomial function (full line). |
| In the text | |
 |
Fig. 6 Ionisation degree i versus τ0(Hα) from the results of the models of Heinzel et al. (1994) for three different temperatures and two geometrical thickness of the prominence. |
| In the text | |
 |
Fig. 7 Interpolated maps of temperature a), optical thickness τ0(Hα)b) and ionisation degree of hydrogen c) estimated from Hα spectral observations of the prominence of 18 May 2011. |
| In the text | |
 |
Fig. 8 Interpolated maps of the α factor of asymmetry of EUV coronal emissivity a), and optical thickness τ193b) derived from prominence EUV and X-ray observations of 18 May 2011. Striation in the α map in panel a) is caused by problems of bilinear interpolation explained in the last paragraph of Sect. 3.3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


