| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 4 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201424824 | |
| Published online | 14 January 2015 | |
Influence of celestial light on lunar surface brightness determinations: Application to earthshine studies
1
Danish Climate Centre, Danish Meteorological Institute,
Lyngbyvej 100,
2100
Copenhagen Ø,
Denmark
e-mail:
pth@dmi.dk
2
Centre for Atmosphere and Observations at DMI,
Lyngbyvej 100, 2100
Copenhagen Ø,
Denmark
3
Centre for Astrophysics and Supercomputing, Swinburne
University, Hawthorn
VIC
3122,
Australia
Received: 18 August 2014
Accepted: 22 September 2014
Aims. We consider the influence of celestial-sphere brightness on determinations of terrestrial albedo from earthshine intensity measurements. In particular, the contributions from zodiacal light and starlight are considered.
Methods. Using published data for the zodiacal light (ZL) and stellar brightness distribution across the sky, we calculate the expected contribution to the sky at the position of the Moon in typical earthshine observations, and the magnitude relative to typical earthshine intensities. We derive terrestrial albedo with and without the ZL correction in order to gauge the magnitude of the effect.
Results. We find that celestial-sphere surface brightness can be so large that a considerable and unacceptable error level would have an impact on half of typical earthshine-based albedo-determinations if left unaccounted for. Considering the empirical uncertainty on ZL, we show that almost all our earthshine data can be used if a sky correction is made. In real observations we find up to a 1% effect on albedo results of correcting for the celestial brightness.
Conclusions. Correction for ZL and starlight brightness is essential to earthshine measurements if climate-science relevant levels of terrestrial albedo accuracy are to be achieved, something that has not yet been realized. With ZL and starlight corrections the earthshine method can potentially yield accurate terrestrial albedo values.
Key words: zodiacal dust / Moon / techniques: photometric / atmospheric effects
© ESO, 2015
1. Introduction
Earthshine is the light from Earth that falls on the Moon. Near new moon the Earth is almost full and earthshine is brightest; this is when it is easiest to see the normally dark side of the Moon. The intensity of the earthshine is not only a function of celestial geometry, but is also proportional to the state of the Earth’s surface: bright clouds, deserts, and ice reflect a great deal of light, while forests and oceans are darker. The shortwave albedo is an important regulator of the climatic energy balance, but it is also dependent on the state of the climate system. Studying the albedo is therefore of interest to climate research; in particular, long-term studies could provide important independent insights into mean climate trends. Satellites cannot yet observe terrestrial albedo with long-term accuracy beyond the 1% limit (Kieffer & Stone 2005). Careful ground-based observations of earthshine intensity potentially offer a way to obtain albedo data more accurately and at a fraction of the cost of space-based systems (MacDonald et al. 1992; Flatte et al. 1992).
Historically, earthshine on the dark side of the Moon has been studied quantitatively since the 1930s (Danjon 1933; Dubois 1955; Bakos 1964; Rydgren 1966; Franklin 1967), although the full realization of what earthshine actually was had been written down some 500 years ago (Longshaw 2010). Today, modern equipment and analysis methods are able to obtain much more accurate data, but precision is dominated by natural variability in the Earth climate system. Albedo itself varies by several percentage points from day to day as a result of drifting cloud masses, and observing through an atmosphere makes the method susceptible to subtle transparency variations. It was understood early on that the use of relative intensity measurements could be an efficient counter to this problem, but the variable scattered light in the halo around the bright side of the Moon was not efficiently dealt with until modern observations began (Goode et al. 2001) at the Big Bear Solar Observatory (BBSO). Here, the spatial trend of the scattered light was mapped thanks to CCD imaging and thus became subtractable (Qiu et al. 2003).
Earthshine intensity determination with the modern method is essentially an exercise in surface brightness determination for an extended source, and is thus challenging: point sources are easier to study photometrically. In considering the problems of reducing image data of the Moon with the strong halo of scattered light around it, we have come to realize that an important variable factor is being ignored or incorrectly accounted for in data reductions: the sky behind the Moon is routinely assumed to be completely black. It is not, of course; there are faint sources of light, some resolved, some not. If the sources are bright enough, a basic data reduction step in current techniques is invalid, leading to biases of up to 1% in terrestrial albedo determined from earthshine intensity measurements.
Earthshine studies are currently of interest to the exoplanet community, and has always been of interest to investigations into Earth’s albedo in planetology, astronomy, climate, and climate change contexts. The method offers an estimate of terrestrial albedo that is independent from satellite-based measurements which in turn are dealing with calibration and drift issues at a level of several percentage points (Kieffer & Stone 2005; Wu et al. 2006; Viticchiè et al. 2013). Long-term stability in data is needed in order to have an impact on climate change issues in the face of a large natural variability of the albedo: long time-series without instrumental drift need to be generated so that averages can reduce the scatter and reveal, if present, drifts in terrestrial albedo (Herman et al. 2013), or subtle cycles due to external forcing (e.g. solar cycle effects on cloud cover, e.g. Shindell et al. 1999), or internal dynamics (e.g. the ENSO phenomenon). Bender et al. (2006) reviewed the satellite-based data on terrestrial albedo and show annual cycles in albedo at the 9% level driven by well-understood changes in the weather system, and standard deviations of monthly binned values of that cycle at the 1.7% level. Small trends in albedo are difficult to detect under such conditions, unless long series of observations are available. To beat the variability and also offer an advantage over current levels of absolute-photometry calibration of satellites, we have set ourselves a design goal of 0.1% error. That is, we do not wish to knowingly have sources of error (bias, mainly) larger than this in single measurements. Scatter is another matter: BBSO report obtaining albedo-determinations in single images of the Moon with typically 1% uncertainty, a level of scatter (i.e. precision) we concur with. Averaging over many such determinations (approximately 100) can meaningfully drive down the error to near the 0.1% level provided there is no large bias present.
2. Earthshine data reduction procedures
In reducing observed images of the earthlit Moon, the basic reduction steps consist of bias-subtraction and flat-fielding followed by some sort of sky subtraction to account for interfering lights. This light is to a large extent from the Moon itself, but some also arises in the atmosphere (airglow, and for some latitudes, aurora), or is ground-reflected Moonlight. The halo around the bright side (BS) of the Moon has a strong spatial gradient and is caused by scattering in the atmosphere itself and by the optics of the telescope. This halo stretches onto the dark side (DS) of the Moon in the image. The early measurements of earthshine corrected for the level of sky brightness near the Moon, but ignored (and did not record) the spatial gradient, probably making current-day reduction of the historical measurements impossible.
The BBSO earthshine group introduced the estimation of the gradient by fitting a line to the brightness of the halo on the sky near the DS and extrapolating this onto the DS near the edge, thus enabling the removal of the scattered light. Our own methods (described in more detail in Appendix A) are centred on the complete forward modelling of the halo of scattered light in multi-parametric fitting of theoretically generated lunar images (illuminated by the Sun and a simple model of the Earth) to the observations, thereby determining the best-fitting Lambertian equivalent reflectivity of the Earth model.
Central to our own efforts, and also to those of the BBSO, was the idea that the intensity of light on the sky near the DS can be used to define a model of the scattered light on the disc itself so that you can clean the observed image.
This is insufficient if the space behind the Moon is bright (see Fig. 1). It is quite dark, of course, but so is the DS, and the combined brightness of zodiacal light (ZL), unresolved stars, distant galaxies, and interstellar scattered starlight is significant compared to the earthshine. Omission of this light in reduction methods causes a negative albedo bias because too much light is subtracted from the DS image.
In this paper we quantitatively analyse the effect of neglecting a ZL and starlight (SL) contribution. We estimate the ZL and SL contributions using observed distributions of ZL and stars. We use ZL tables found in the literature such as Allen (1975); Levasseur-Regourd & Dumont (1980); Leinert et al. (1997); Kwon et al. (2004) and here choose Kwon et al. (2004) who provide an independent, more highly resolved model of the ZL, based on extensive analogue visual-band observational material obtained at Mt. Haleakala, Hawaii, in the 1960s and recently digitized. The data, where comparable to the lower-resolution data of Leinert et al. (1997), differ by 10−15%. The ZL is concentrated near the Sun and along the ecliptic. For starlight we use the fitted formula of Benn & Ellison (1998) which is based on Roach & Megill (1961). Starlight is concentrated along the Galactic plane. Starlight is more accurately quantified than the ZL.
Both the ZL and SL estimates we use are based on visual-band values because we used the Johnson V-band data that we already had. Adjustments to the actual wavelength bands used in our observations and the basis given in the above references are possible using information in Leinert et al. (1997), but are on the order of 10% and have not been carried out in this paper. Below, we shall see whether a 15% uncertainty is an important source of error in our earthshine work, since accounting for background sky brightness propagates the relative uncertainty to the albedo determination.
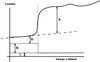 |
Fig. 1 Brightness contributions on the DS of the Moon and adjacent sky. Vertical dotted line shows the edge of the lunar dark-side (DS) disc. C indicates an atmospheric brightness contribution (airglow and ambient diffuse light) that affects the brightness of the lunar disc as well as the adjacent sky. B is a contribution from background space (such as Zodiacal light, unresolved stars, and scattered starlight) that affects only the sky part of the image. D is a spatially varying halo; it is the scattered light from the bright side of the Moon. A is an incorrect estimate of the earthshine because it is based on the assumption that B is zero. |
3. Method
Tabulations of the ZL and starlight brightness are often in units of the number of 10th-magnitude stars per square degree. We thus need to convert this into fluxes and counts so that a comparison can be made to observations.
We convert the number of 10th-magnitude stars per square degree, n10, to V-band magnitudes per square degree: 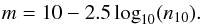 Next, we transform the mag/◦2 to mag/′′2,
Next, we transform the mag/◦2 to mag/′′2, 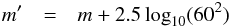 and then to mag per pixel using the known pixel size
and then to mag per pixel using the known pixel size 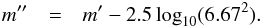 Based on the known camera calibration (Thejll et al. 2014) we can further convert this to counts per second (cps),
Based on the known camera calibration (Thejll et al. 2014) we can further convert this to counts per second (cps), 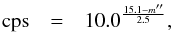 (1)where a small B − V colour-term has been omitted in (1).
(1)where a small B − V colour-term has been omitted in (1).
For comparison to the counts in a pixel on an actual image we need the exposure time, t, and thus have: 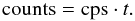 (2)
(2)
4. Results
We know the sky position and exposure time for our V-band Moon observations, obtained in 2012 at Mauna Loa, Hawaii (Thejll et al. 2014), and can therefore look up (Kwon et al. 2004) the celestial visual-band sky brightness next to the DS of the Moon for each image.
We find that the intensity of the zodiacal light and the starlight, in the sky next to the Moon, for all our observations varies by 2 orders of magnitude and lie in the range 0.0003−0.03 counts. Whether this is a lot or a little depends on the intensity of the DS in each image. In Fig. 2 we show the ZL+starlight near the Moon as a percentage of the increment in brightness in going from the sky adjacent to the Moon to the dark side itself immediately near the edge. It appears that half of our observations have an expected ZL+starlight intensity larger than the 0.1% level, suggesting that ignoring the light will bias half of our results by this much or more, which is unacceptable in terms of our science goals.
As it is, ZL intensity can be described to within ±15% and the error contributed to the albedo scales proportionally. Taking the worst-case 1% level ZL brightness relative to DS, we see that the error propagated to the albedo would be 0.15%, which is acceptable.
 |
Fig. 2 Histogram of zodiacal light + starlight intensity as a percentage of the DS step size, i.e. the increment in surface brightness in going from DS sky to lunar DS. The vertical dashed line shows the median value of the distribution. |
In Fig. 3 we show the actual change in fitted albedo when all suitable data are reduced with and without the celestial sphere brightness correction. Results for only the V-band filter are shown. Seventy-nine percent of the data undergo an increase in albedo and half of the albedo determinations rise by more than 0.18%. A few albedos are changed by more than 1%. We see that 20% of the albedo changes are negative. This is an indication of the workings of the fitting process itself: during fitting eight model parameters are determined, and albedo is one of them. It is not yet clear whether the negative change is due to an incorrect estimate of the celestial brightness, or is an effect of model-fitting. As a sensitivity-study, we repeated the fitting of all V-band data with negative ZL+SL corrections and found (not shown) an equivalent negative shift of the distribution peak in Fig. 3. The shift of the peak is therefore due to the sky-light correction itself.
However, the main point is clear: omission of a celestial brightness correction causes an underestimation of fitted albedo for 79% of our data. This applies to all determinations of earthshine intensity that utilize the offset from the surrounding sky to find the DS brightness. Longer exposure times do not affect the matter since the background sky and the DS fluxes both scale linearly with the exposure time.
 |
Fig. 3 Effect of removing zodiacal light and starlight, on fitted albedo, for V-band filter images. Shown is the percentage change in fitted albedo: positive values indicate a rise in albedo upon removal of background sky brightness. 79% of the changes are positive (dotted line); 50% (dashed line) are greater than 0.18. We note that there is both a shifted peak of the distribution and a broader scatter. The origins of the broader scatter is not due to uncertainties in the applied ZL+SL corrections, but can originate in the stochasticity of the lunar dark-side data themselves. |
5. Discussion
Allowing for the brightness of the celestial sphere adjacent to the DS of the Moon is just the first order correction – the zodiacal light and the starlight also illuminate the DS itself, which interferes with the earthshine measurement. The celestial hemisphere visible from a given surface element on the Moon receives light and scatters it back into space so it mixes with the earthshine reflecting from the same surface element, towards the observer. Since lunar surface reflectance is a steep function of phase angle (see Fig. 6 in Kieffer & Stone 2005) we assume that only small areas of the sky could contribute significantly to the beam along which the earthshine observer looks. One of these is the area just behind the observer, essentially the Gegenschein region, which has low intensity despite the name; however, the strongest ZL light comes from near the Sun and these rays scatter towards the observer at a very low angle where reflectance is relatively small. A full understanding of this oppositely directed effect on terrestrial albedo determinations from the disc illumination awaits a full quantitative treatment, potentially possible with ray-tracing models.
6. Conclusions
We see that the sky brightness must be estimated and subtracted from at least half our images if the bias on albedo is not to be larger than 0.18%. We also see that even if we estimate the ZL + starlight and subtract it we will inherit a small relative error (about 15%), mainly from the published ZL predictions, but also from slight mismatches in the wavelength bands that ZL and SL and our Johnson V-band filter are based on. The error is acceptable for most of our V-band data, given our science goals. We note that the larger spread in Fig. 3 is likely due to factors unrelated to the ZL+SL corrections, and represent a data-reduction problem yet to be solved.
Our conclusion is that we must correct for the zodiacal light and starlight. Future improvements in the quantification of zodiacal light brightness will benefit present and future earthshine observations. Calculation of the opposite effect of celestial light on the brightness of the lunar surface itself, must be performed.
Acknowledgments
We thank Sukminn Kwon for giving us the zodiacal light tables in a machine-readable format.
References
- Allen, C. W. 1975, Astrophysical Quantities (University of London, The Athlone Press) [Google Scholar]
- Bakos, G. A. 1964, SAO Spec. Rep., 162 [Google Scholar]
- Bender, F. A.-M., Rodhe, H., Charlson, R. J., Ekman, A. M. L., & Loeb, N. 2006, Tellus Ser. A, 58, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Benn, C., & Ellison, S. 1998, New Astron. Rev., 42, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Danjon, A. 1933, Annales de l’Observatoire de Strasbourg, 3, 138 [NASA ADS] [Google Scholar]
- Dubois, J. 1955, L’Astronomie, 69, 242 [NASA ADS] [Google Scholar]
- Flatte, S., Koonin, S., & MacDonald, G. 1992, Global change and the dark of the moon, Final Report Mitre Corp, http://www.dtic.mil/dtic/tr/fulltext/u2/a255181.pdf [Google Scholar]
- Franklin, F. A. 1967, J. Geophys. Res., 72, 2963 [NASA ADS] [CrossRef] [Google Scholar]
- Goode, P., Qiu, J., Yurchyshyn, V., et al. 2001, Geophys. Res. Lett., 28, 1671 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 1963, AJ, 68, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Herman, J., DeLand, M. T., Huang, L.-K., et al. 2013, Atmospheric Chemistry & Physics, 13, 8505 [NASA ADS] [CrossRef] [Google Scholar]
- Kieffer, H. H., & Stone, T. C. 2005, AJ, 129, 2887 [NASA ADS] [CrossRef] [Google Scholar]
- Kwon, S. M., Hong, S. S., & Weinberg, J. L. 2004, New Astron., 10, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Leinert, C., Bowyer, S., & Haikala, L. 1997, A&AS, 127, 1 [Google Scholar]
- Levasseur-Regourd, A. C., & Dumont, R. 1980, A&A, 84, 277 [NASA ADS] [Google Scholar]
- Longshaw, N. 2010, British Astronomical Association, 120, 243 [NASA ADS] [Google Scholar]
- MacDonald, G., Koonin, S., MacDonald, G., & Koonin, S. 1992, The Observatory, 112, 59 [NASA ADS] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Qiu, J., Goode, P. R., Pallé, E., et al. 2003, J. Geophys. Res. D, 108, 4709 [NASA ADS] [CrossRef] [Google Scholar]
- Roach, F. E., & Megill, L. L. R. 1961, AJ, 133, 228 [Google Scholar]
- Robinson, M., & Riner, M. 2005, J. Earth Syst. Sci., 114, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Rydgren, B. 1966, Arkiv for Astronomi, 4, 131 [NASA ADS] [Google Scholar]
- Shindell, D., Rind, D., Balachandran, N., Lean, J., & Lonergan, P. 1999, Science, 284, 305 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Thejll, P., Flynn, C., Gleisner, H., et al. 2014, A&A, 563, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viticchiè, S. B., Wagner, T., & Stone, T. 2013, Global Space-based Inter-Calibration System Quarterly, 7, 3 [Google Scholar]
- Wu, X., Stone, T. C., Yu, F., & Han, D. 2006, in SPIE Conf. Ser., 6296 [Google Scholar]
Appendix A: Scattered-light modelling
Given an observed image of the Moon (O), showing well-exposed dark side and bright side, construct an adjustable model (M) of what the Moon should look like at the moment of observation on the basis of ephemerides, an assumption about terrestrial albedo, and geometric information about the positions of objects. Then fit M to O, using least squares methods, so that residual R is minimized. Include convolution with an adjustable point spread function so that model light is scattered from the bright parts of the model image across the image plane, 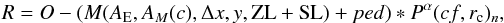 where Δx,y are model image shifts along rows and columns; α is the power to which we raise an empirical point spread function P; cf is a core factor on that part of the PSF that lies inside a radius rc (fixed at 3 pixels) from the PSF peak; the subscript n indicates that the PSF is normalized following adjustment of the parameters that define it; ZL + SL are the contributions, from zodiacal and star-light, respectively, to the image pixels outside the disc of the Moon; ped is a constant term added to the
where Δx,y are model image shifts along rows and columns; α is the power to which we raise an empirical point spread function P; cf is a core factor on that part of the PSF that lies inside a radius rc (fixed at 3 pixels) from the PSF peak; the subscript n indicates that the PSF is normalized following adjustment of the parameters that define it; ZL + SL are the contributions, from zodiacal and star-light, respectively, to the image pixels outside the disc of the Moon; ped is a constant term added to the
whole model image, representing the bright atmosphere in the image frame (from airglow and scattered/reflected light from the ground). The parameters AE,AM(c) are terrestrial and lunar albedos used in generating the model image M: AE is just a single number, the Lambertian equivalent albedo, while the lunar albedo AM(c) is a contrast-scaled version of the Clementine 750 nm albedo image (Robinson & Riner 2005); c is the factor applied to the albedo map (newmap = (oldmap − median(oldmap))·c + median(oldmap)). Thus, 10 parameters determine the model image M, along with an assumed bidirectional reflectance model; we used the simple Hapke BRDF (Hapke 1963). Using MPFIT (Markwardt 2009) we minimized the sum of squared residuals in some region of R. We chose two regions: one is a region on the DS of the lunar disc including sky as well as DS, the other is a region on the sky near the BS. Above, ∗ indicates convolution.
All Figures
 |
Fig. 1 Brightness contributions on the DS of the Moon and adjacent sky. Vertical dotted line shows the edge of the lunar dark-side (DS) disc. C indicates an atmospheric brightness contribution (airglow and ambient diffuse light) that affects the brightness of the lunar disc as well as the adjacent sky. B is a contribution from background space (such as Zodiacal light, unresolved stars, and scattered starlight) that affects only the sky part of the image. D is a spatially varying halo; it is the scattered light from the bright side of the Moon. A is an incorrect estimate of the earthshine because it is based on the assumption that B is zero. |
| In the text | |
 |
Fig. 2 Histogram of zodiacal light + starlight intensity as a percentage of the DS step size, i.e. the increment in surface brightness in going from DS sky to lunar DS. The vertical dashed line shows the median value of the distribution. |
| In the text | |
 |
Fig. 3 Effect of removing zodiacal light and starlight, on fitted albedo, for V-band filter images. Shown is the percentage change in fitted albedo: positive values indicate a rise in albedo upon removal of background sky brightness. 79% of the changes are positive (dotted line); 50% (dashed line) are greater than 0.18. We note that there is both a shifted peak of the distribution and a broader scatter. The origins of the broader scatter is not due to uncertainties in the applied ZL+SL corrections, but can originate in the stochasticity of the lunar dark-side data themselves. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


